Percentile Study of χ Distribution. Application to Response Time Data
Abstract
1. Introduction
2. Methodology
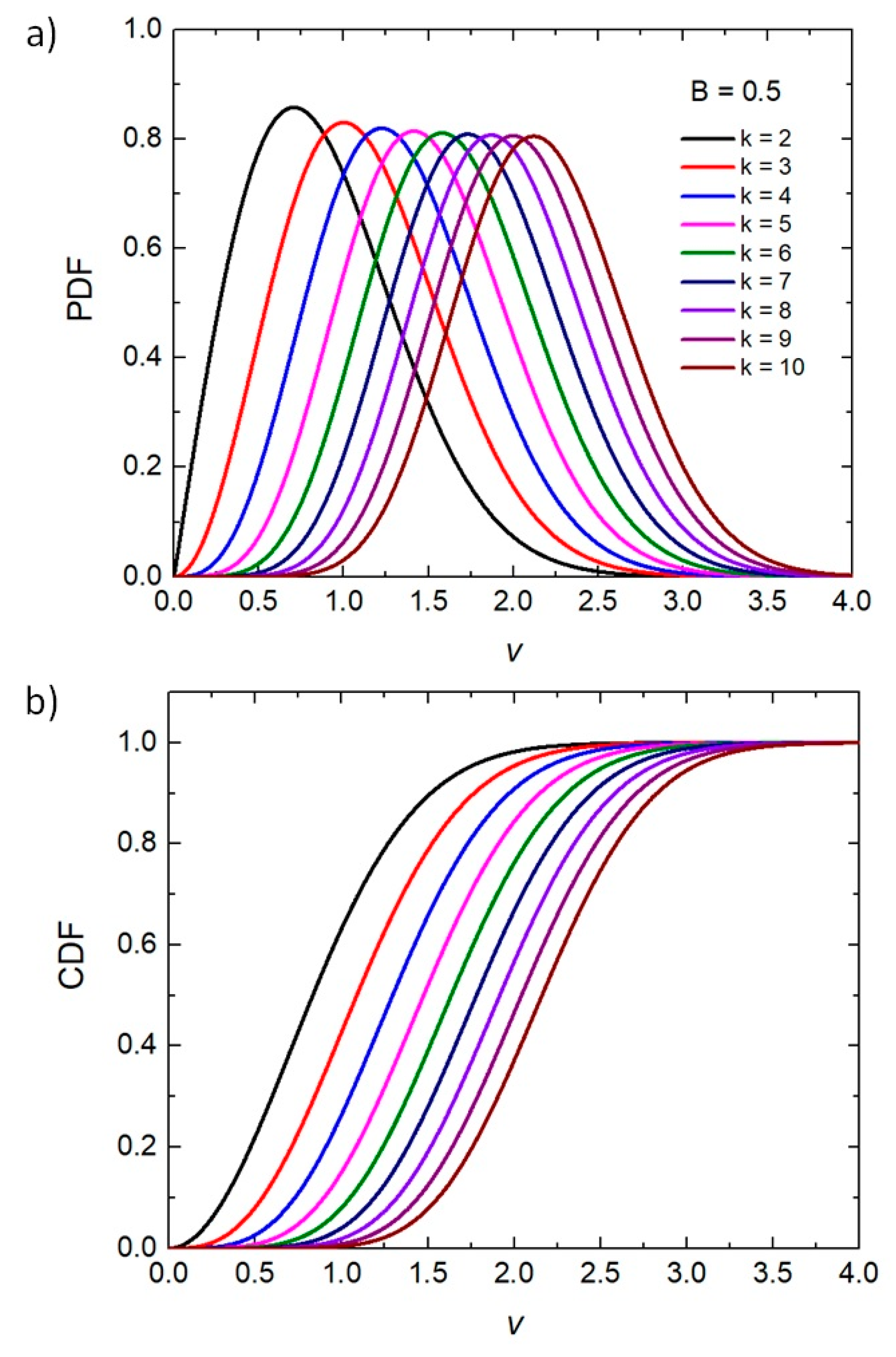
2.1. Percentile Analysis of the χ Distribution (from k = 2 to k = 10)
2.2. Response Time Experiments. A case for k = 3
3. Results and Discussions
3.1. Multidimensional, Anisotropic Ideal Gas (χ of k Degrees of Freedom)
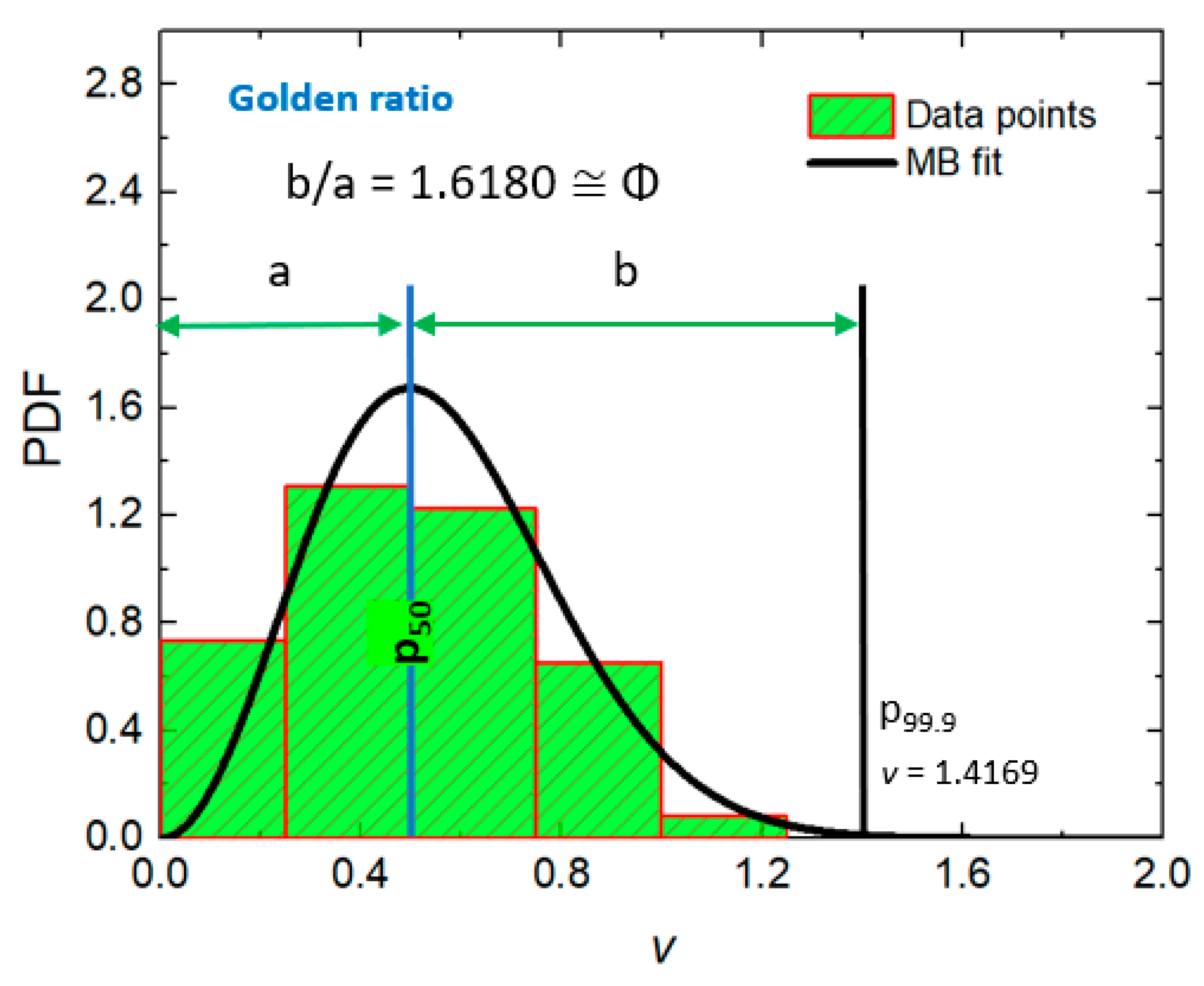
3.2. Reaction Times and Ideal Gas. Appearance of the Golden Ratio
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doob, J.L. Stochastic Processes; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1966. [Google Scholar]
- Tolman, R. The Principles of Statistical Mechanics; Dover Publications Inc.: New York, NY, USA, 2003. [Google Scholar]
- Hernaiz-Guijarro, M.; Castro-Palacio, J.C.; Navarro-Pardo, E.; Isidro, J.M.; Fernández de Córdoba, P. A Probabilistic Classification Procedure Based on Response Time Analysis towards a Quick Pre–diagnosis of Student’s Attention Deficit. Mathematics 2019, 7, 473. [Google Scholar] [CrossRef]
- Castro-Palacio, J.C.; Fernández de Córdoba, P.; Isidro, J.M.; Navarro-Pardo, E. Brain reaction times: Linking Individual and Collective Behaviour through Physics modelling. arXiv 2019, arXiv:1910.12725. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Meisner, G.B. The Golden Ratio: The Divine Beauty of Mathematics; Race Point Publishing: London, UK, 2018. [Google Scholar]
- World Medical Association. Declaration of Helsinki: Ethical Principles for Medical Research Involving Human Subjects. J. Am. Med. Assoc. 2013, 310, 2191–2194. [Google Scholar] [CrossRef] [PubMed]
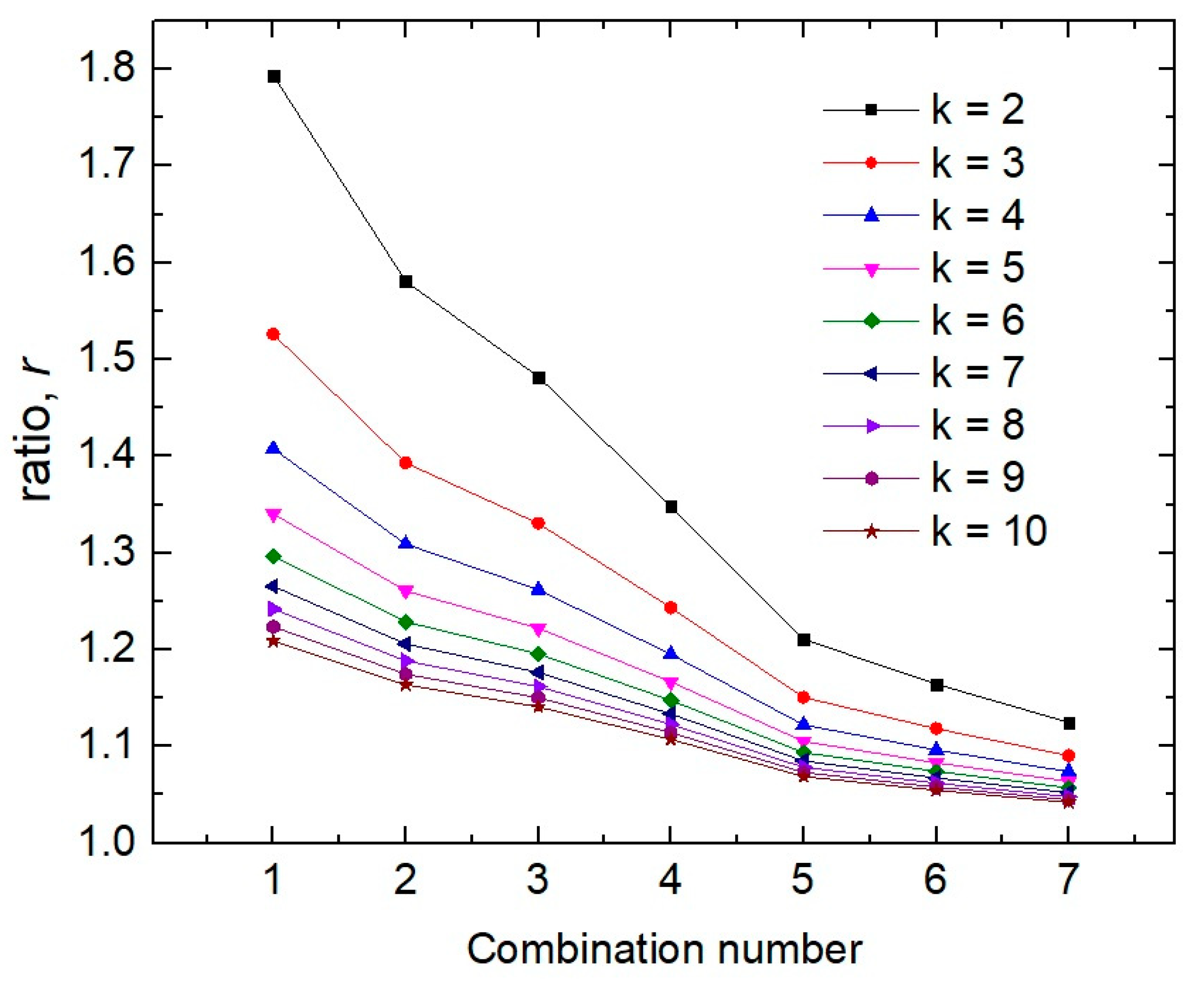
| Combinations | k = 2 | k = 3 | k = 4 | k = 5 | k = 6 | k = 7 | k = 8 | k = 9 | k = 10 |
|---|---|---|---|---|---|---|---|---|---|
| 1 (p1-p50-p99) | 1.7935 | 1.5259 | 1.4075 | 1.3404 | 1.2966 | 1.2655 | 1.2421 | 1.2237 | 1.2088 |
| 2 (p3-p50-p97) | 1.5805 | 1.3930 | 1.3090 | 1.2607 | 1.2287 | 1.2058 | 1.1884 | 1.1747 | 1.1635 |
| 3 (p5-p50-p95) | 1.4821 | 1.3305 | 1.2619 | 1.2220 | 1.1955 | 1.1764 | 1.1618 | 1.1502 | 1.1408 |
| 4 (p10-p50-p90) | 1.3483 | 1.2435 | 1.1951 | 1.1666 | 1.1474 | 1.1335 | 1.1228 | 1.1143 | 1.1073 |
| 5 (p20-p50-p80) | 1.2108 | 1.1506 | 1.1221 | 1.1051 | 1.0935 | 1.0850 | 1.0784 | 1.0731 | 1.0688 |
| 6 (p25-p50-p75) | 1.1643 | 1.1183 | 1.0963 | 1.0831 | 1.0740 | 1.0673 | 1.0622 | 1.0580 | 1.0547 |
| 7 (p30-p50-p70) | 1.1248 | 1.0904 | 1.0738 | 1.0638 | 1.0570 | 1.0519 | 1.0480 | 1.0448 | 1.0422 |
| k | r | Relative Error | ||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 0.26789 | 0.005 | 3.5831 | 0.995 | 1.5382 | 1.6098 | 1.6180 | 0.5% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro-Palacio, J.C.; Fernández-de-Córdoba, P.; Isidro, J.M.; Navarro-Pardo, E.; Selvas Aguilar, R. Percentile Study of χ Distribution. Application to Response Time Data. Mathematics 2020, 8, 514. https://doi.org/10.3390/math8040514
Castro-Palacio JC, Fernández-de-Córdoba P, Isidro JM, Navarro-Pardo E, Selvas Aguilar R. Percentile Study of χ Distribution. Application to Response Time Data. Mathematics. 2020; 8(4):514. https://doi.org/10.3390/math8040514
Chicago/Turabian StyleCastro-Palacio, Juan Carlos, Pedro Fernández-de-Córdoba, J. M. Isidro, Esperanza Navarro-Pardo, and Romeo Selvas Aguilar. 2020. "Percentile Study of χ Distribution. Application to Response Time Data" Mathematics 8, no. 4: 514. https://doi.org/10.3390/math8040514
APA StyleCastro-Palacio, J. C., Fernández-de-Córdoba, P., Isidro, J. M., Navarro-Pardo, E., & Selvas Aguilar, R. (2020). Percentile Study of χ Distribution. Application to Response Time Data. Mathematics, 8(4), 514. https://doi.org/10.3390/math8040514







