Computer Simulation and Iterative Algorithm for Approximate Solving of Initial Value Problem for Riemann-Liouville Fractional Delay Differential Equations

Abstract

The main aim of this paper is to suggest an algorithm for constructing two monotone sequences of mild lower and upper solutions which are convergent to the mild solution of the initial value problem for Riemann-Liouville fractional delay differential equation. The iterative scheme is based on a monotone iterative technique. The suggested scheme is computerized and applied to solve approximately the initial value problem for scalar nonlinear Riemann-Liouville fractional differential equations with a constant delay on a finite interval. The suggested and well-grounded algorithm is applied to a particular problem and the practical usefulness is illustrated.

1. Introduction

Fractional differential operators are applied successfully to model various processes with anomalous dynamics in science and engineering [1,2]. At the same time, only a small number of fractional differential equations could be solved explicitly. It requires the application of different approximate methods for solving nonlinear factional equations.

This paper deals with an initial value problem for a nonlinear scalar Riemann-Liouville (RL) fractional differential equation with a delay on a closed interval is studied. Mild lower and mild upper solutions are defined. An algorithm for constructing two convergent monotone functional sequences $\left\{v^n\right\}$, $\left\{w^n\right\}$ are given. It is proved both sequences $\left\{{(t-t_0)}^{1-q}{v}^n\right\}$ and $\left\{{(t-t_0)}^{1-q}{w}^n\right\}$ are the mild minimal and the mild maximal solutions of the given problem. The uniform convergence of both sequences is proved. A special computer program is built and applied to solve particular problems and to illustrate the practical application of the suggested schemes.

Note the monotone iterative techniques combined with lower and upper solutions are applied in the literature to solve various problems in ordinary differential equations [3], differential equations with maxima [4], difference equations with maxima [5], Caputo fractional differential equations [6], Riemann-Liouville fractional differential equations [7,8,9,10].

In this paper, we consider an initial value problem for a scalar nonlinear Riemann-Liouville fractional differential equation with a constant delay on a finite interval. We apply the method of lower and upper solutions and monotone-iterative technique to suggest an algorithm for approximate solving of the studied problem. The suggested and well-grounded algorithm is used in an appropriate computer environment and it is applied to a particular problem to illustrate the practical usefulness.

2. Preliminary and Auxiliary Results

Let $m:[0,\infty )\to \mathbb{R}$ be a given function and $q\in (0,1)$ be a fixed number. Then the Riemann- Liouville fractional derivative of order $q\in (0,1)$ is defined by (see, for example, [2]

$${}_0^{RL}{D}_t^{q}m\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(1-q\right)}\frac{d}{dt}\left(\underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{-q}m\left(s\right)ds\right),t\ge 0.$$

We will give RL fractional derivatives of some elementary functions which will be used later:

Proposition 1.

Reference [2] the following equalities are true:

$$\begin{array}{cc}\hfill {}_0^{RL}{D}_t^{q}C& =\frac{1}{\mathrm{\Gamma }(1-q)}{t}^{-q},\hfill \\ \hfill {}_0^{RL}{D}_t^q{t}^{\beta }& =\frac{\mathrm{\Gamma }(1+\beta )}{\mathrm{\Gamma }(1+\beta -q)}{t}^{\beta -q}.\hfill \end{array}$$

Consider the initial value problem (IVP) for the nonlinear Riemann-Liouville delay fractional differential equation (FrDDE)

$$\begin{array}{c}{}_0^{RL}{D}_t^{q}x\left(t\right)=F(t,x\left(t\right),x(t-\tau ))\mathrm{for}t\in (0,T]\hfill \\ x\left(s\right)=\psi \left(s\right)\mathrm{for}s\in [-\tau ,0]\hfill \\ t^{1-q}{x\left(t\right)|}_{t=0}=\underset{t\to 0+}{lim}{t}^{1-q}x\left(t\right)=\psi \left(0\right),\hfill \end{array}$$

(1)

where $q\in (0,1)$, $F:[0,T]\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$, $\psi :[-\tau ,0]\to \mathbb{R}:\psi \left(0\right)<\infty$ with $T\in \left(\right(N-1)\tau ,N\tau ]$, N is a natural number, and $\tau >0$ is a given number.

The solution of the IVP (1) could have a discontinuity at $t=0$.

Denote the interval $I=[-\tau ,T]/\left\{0\right\}.$

Denote

$$C_{1-q}\left([a,b]\right)=\{x\left(t\right):[a,b]\to \mathbb{R}:{(t-a)}^{1-q}x\left(t\right)\in C([a,b],\mathbb{R})\},$$

where $a,b,a<b$ are real numbers.

Define the norm in $C_{1-q}\left([a,b]\right)$ by ${\left|\right|x\left|\right|}_{C_{1-q}[a,b]}=\underset{t\in [a,b]}{max}\left|{(t-a)}^{1-q}x\left(t\right)\right|.$

Consider the linear scalar delay RL fractional equation of the type

$$\begin{array}{c}{}_0^{RL}{D}_t^{q}x\left(t\right)=\lambda x\left(t\right)+\mu x(t-\tau )+f\left(t\right)\mathrm{for}t\in (0,T],\hfill \\ x\left(t\right)=\psi \left(t\right)\mathrm{for}t\in [-\tau ,0],t^{1-q}{x\left(t\right)|}_{t=0}=\psi \left(0\right),\hfill \end{array}$$

(2)

where $\lambda ,\mu$ are real constant, $f\in C\left(\right[0,T],\mathbb{R})$. There exits an explicit formula for the solution of (2) given by see [11]:

$$x\left(t\right)=\left\{\begin{array}{c}\psi \left(t\right)\mathrm{for}t\in [-\tau ,0],\hfill \\ {\displaystyle \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(\lambda t^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(\lambda {(t-s)}^q\right)\left(f\left(s\right)+\mu x(s-\tau )\right)ds,t\in (0,T]}\hfill \end{array}\right.$$

(3)

where $E_{\alpha ,\beta }\left(z\right)={\sum }_{k=0}^{\infty }\frac{z^k}{\mathrm{\Gamma }(\alpha k+\beta )}$ is the Mittag-Leffler function with two parameters.

Note that the solution in the simplest linear case is not easy to obtain. It requires the application of some approximate methods.

Similar to References [12], we have the following result:

Proposition 2.

Let $f\in C\left(\right[0,T],\mathbb{R})$, $\psi \in C\left(\right[-\tau ,0],\mathbb{R})$, $\lambda \in \mathbb{R},\mu \ge 0$ be constants and

$$\begin{array}{c}{}_0^{RL}{D}_t^{q}v\left(t\right)\le \lambda v\left(t\right)+\mu v(t-\tau )+f\left(t\right)fort\in (0,T],\hfill \\ v\left(t\right)=\psi \left(t\right)fort\in [-\tau ,0],t^{1-q}{v\left(t\right)|}_{t=0}=\psi \left(0\right).\hfill \end{array}$$

Then

$$v\left(t\right)\le \left\{\begin{array}{c}\psi \left(t\right),t\in [-\tau ,0],\hfill \\ {\displaystyle \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(\lambda t^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(\lambda {(t-s)}^q\right)\left(f\left(s\right)+\mu v(s-\tau )\right)ds,t\in (0,T].}\hfill \end{array}\right.$$

Similar to References [7], we define the mild solutions:

Definition 1.

The function $x\in C(I,\mathbb{R})$ is a mild solution of the IVP for FrDDE (1), if it satisfies

$$x\left(t\right)=\left\{\begin{array}{c}\psi \left(t\right)fort\in [-\tau ,0],\hfill \\ {\displaystyle \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(\lambda t^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(\lambda {(t-s)}^q\right)f(s,x\left(s\right),x(s-\tau ))ds,}t\in (0,T].\hfill \end{array}\right.$$

(4)

Remark 1.

Note that the mild solution $x\left(t\right)\in C(I,\mathbb{R})$ of the IVP for FrDDE (1) might not be from $C_{1-q}\left([0,T]\right)$ and it might not have the fractional derivative ${}_0^{RL}{D}_t^{q}x\left(t\right)$.

Definition 2.

The function $x\in C(I,\mathbb{R})$ is a mild maximal solution (a mild minimal solution) of the IVP for FrDDE (1), if it is a mild solution of (1) and for any mild solution $u\left(t\right)\in C(I,\mathbb{R})$ of (1) the inequality $x\left(t\right)\le u\left(t\right)$ ($x\left(t\right)\ge u\left(t\right)$) holds on I and $t^{1-q}x\left(t\right){{|}_{t=0}\le (\ge )t^{1-q}u\left(t\right)|}_{t=0}$.

3. Mild Lower and Mild Upper Solutions of FrDDE

Definition 3.

The function $v\left(t\right)\in C(I,\mathbb{R})$ is a mild lower (a mild upper) solution of the IVP for FrDDE (1), if it satisfies the integral inequalities

$$v\left(t\right)\le (\ge )\left\{\begin{array}{c}\psi \left(t\right)fort\in ]-\tau ,0],\hfill \\ {\displaystyle \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(\lambda t^q\right)t^{q-1}}+\hfill \\ {\displaystyle +{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(\lambda {(t-s)}^q\right)f(s,v\left(s\right),v(s-\tau ))ds,t\in (0,T]}\hfill \end{array}\right.$$

(5)

and $t^{1-q}{v\left(t\right)|}_{t=0}=\psi \left(0\right)$.

Definition 4.

We say that the function $v\left(t\right)\in C_{1-q}(I,\mathbb{R})$ is a lower (an upper) solution of the IVP for FrDDE (1), if

$$\begin{array}{c}{}_0^{RL}{D}_t^{q}v\left(t\right)\le (\ge )F(t,v\left(t\right),v(t-\tau ))fort\in (0,T],\hfill \\ v\left(t\right)=\psi \left(t\right)fort\in [-\tau ,0],t^{1-q}{v\left(t\right)|}_{t=0}=\psi \left(0\right).\hfill \end{array}$$

Remark 2.

A function could be a mild lower solution or a mild upper solution, respectively, of the IVP for FrDDE (1) but it could not be a lower solution or an upper solution, respectively, of the IVP for FrDDE (1).

Remark 3.

Note that the mild lower solution (mild upper solution) is not unique. At the same time, because of the inequalities in (5) it is much easier to obtain at least one mild lower solution (mild upper solution) than a mild solution of the IVP for FrDDE (1).

4. Monotone-Iterative Techniques for FrDDE

Now we will consider a nonlinear RL fractional differential equation with a constant delay. We will apply a monotone iterative technique to obtain approximate solution. The idea of the formulas for the successive approximations is based on linear RL-fractional differential equations of type (2) and its explicit formula for the solution obtained in [11].

For any two $u,v\in PC\left(\right[-\tau ,T],\mathbb{R})$ and the constants $M,L$ define the operator (the values of the constants $M,L$ will be defined later):

$$\mathrm{\Omega }(u,v)\left(t\right)=\left\{\begin{array}{c}\psi \left(t\right),t\in [-\tau ,0]\hfill \\ {\displaystyle \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,u\left(s\right),u(s-\tau ))ds}\hfill \\ {\displaystyle -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(Mu\left(s\right)+L\left(u\right(s-\tau )-v(s-\tau \left)\right)\right)ds,t\in (0,T].}\hfill \end{array}\right.$$

Theorem 1.

Let the following conditions be fulfilled:

• Let the functions $v,w\in C(I,\mathbb{R})\cup C_{1-q}\left([0,T]\right)$ be a lower solution and an upper solution, respectively, of the IVP for FrDDE (1) such that $v\left(t\right)\le w\left(t\right)$ for $t\in [0,T]$ and $v\left(0\right)-\psi \left(0\right)\le v\left(s\right)-\psi \left(s\right)$, $w\left(0\right)-\psi \left(0\right)\ge w\left(s\right)-\psi \left(s\right)$ for $s\in [-\tau ,0)$.
• The function $F\in C\left(\right[0,T]\times \mathbb{R}\times \mathbb{R},\mathbb{R})$ and there exist constants $M\in \mathbb{R}$ and $L>0:\frac{L{T}^q}{\mathrm{\Gamma }\left(1_q\right)}<1$ such that for any $t\in [0,T],x,y,u,v\in \mathbb{R}:v\left(t\right)\le x\le y\le w\left(t\right),v(t-\tau )\le u\le v\le w(t-\tau )$ the inequality $F(t,x,u)-F(t,y,v)\le M(x-y)+L(u-v)$ holds.

Then there exist two sequences of functions ${\left\{v^{\left(n\right)}\left(t\right)\right\}}_0^{\infty }$ and ${\left\{w^{\left(n\right)}\left(t\right)\right\}}_0^{\infty }$, $t\in [-\tau ,T]$, such that:

a. 

The sequences $\left\{v^{\left(n\right)}\left(t\right)\right\}$ and $\left\{w^{\left(n\right)}\left(t\right)\right\}$ are defined by $v^{\left(0\right)}\left(t\right)=v\left(t\right),w^{\left(0\right)}\left(t\right)=w\left(t\right)$ and

$$v^{\left(n\right)}\left(t\right)=\mathrm{\Omega }\left(v^{(n-1)},v^{\left(n\right)}\right)\left(t\right),w^{\left(n\right)}\left(t\right)=\mathrm{\Omega }\left(w^{(n-1)},w^{\left(n\right)}\right)\left(t\right)\mathrm{for}n\ge 1,$$

that is,

$$v^{\left(n\right)}\left(t\right)=\left\{\begin{array}{c}\psi \left(t\right),t\in [-\tau ,0],\hfill \\ {\displaystyle \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+}\hfill \\ {\displaystyle +{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,v^{(n-1)}\left(s\right),v^{(n-1)}(s-\tau ))ds-}\hfill \\ {\displaystyle -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\times }\hfill \\ {\displaystyle \times \left(M{v}^{(n-1)}\left(s\right)+L(v^{(n-1)}(s-\tau )-v^{\left(n\right)}(s-\tau ))\right)ds,t\in (0,T],}\hfill \end{array}\right.$$

$$w^{\left(n\right)}\left(t\right)=\left\{\begin{array}{c}\psi \left(t\right),t\in [-\tau ,0],\hfill \\ {\displaystyle \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}}\hfill \\ {\displaystyle +{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,w^{(n-1)}\left(s\right),w^{(n-1)}(s-\tau ))ds}\hfill \\ {\displaystyle -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\times }\hfill \\ {\displaystyle \times \left(M{w}^{(n-1)}\left(s\right)+L(w^{(n-1)}(s-\tau )-w^{\left(n\right)}(s-\tau ))\right)ds,t\in (0,T],}\hfill \end{array}\right.$$

where the constants $M,L$ are defined in condition 2.

b. 

The sequence ${\left\{v^{\left(j\right)}\left(t\right)\right\}}_{j=0}^{\infty }$ is increasing, that is, $v^{(j-1)}\left(t\right)\le v^{\left(j\right)}\left(t\right)$ for $t\in (0,T],$$j=1,2,\dots$.

c. 

The sequence ${\left\{w^{\left(j\right)}\left(t\right)\right\}}_{j=0}^{\infty }$ is decreasing, that is, $w^{(j-1)}\left(t\right)\ge w^{\left(j\right)}\left(t\right)$ for $t\in (0,T]$, $j=1,2,\dots$.

d. 

The inequality

$$v^{\left(k\right)}\left(t\right)\le w^{\left(k\right)}\left(t\right)\mathrm{for}t\in (0,T],k=1,2,\dots$$

(6)

holds.

e. 

The sequences ${\left\{t^{1-q}{v}^{\left(n\right)}\left(t\right)\right\}}_0^{\infty }$ and ${\left\{t^{1-q}{w}^{\left(n\right)}\left(t\right)\right\}}_0^{\infty }$ converge uniformly on $[0,T]$ and $t^{1-q}V\left(t\right)=\underset{k\to \infty }{lim}{t}^{1-q}{v}^{\left(n\right)}\left(t\right)$, $t^{1-q}W\left(t\right)=\underset{k\to \infty }{lim}{t}^{1-q}{w}^{\left(n\right)}\left(t\right)$ on $[0,T]$.

f. 

The limit functions $V\left(t\right)$ and $W\left(t\right)$ are mild solutions of the IVP for FrDDE (1) on $[-\tau ,T]$.

g. 

The inequalities $v^{\left(n\right)}\left(t\right)\le V\left(t\right)\le W\left(t\right)\le w^{\left(n\right)}\left(t\right)$ hold on $(0,T]$ for any $n=0,1,2,\dots$.

Proof of Theorem 1. 

Let $v\left(t\right)$ be a lower solution of the IVP for FrDDE (1), that is,

$$\begin{array}{c}\hfill {}_{{\theta }_0}^{RL}{D}_t^{q}v\left(t\right)\le Mv\left(t\right)+Lv(t-\tau )+G(t,v\left(t\right),v(t-\tau )),\end{array}$$

(7)

where $G(t,u,v)=F(t,u,v)-Mu-Lv,t\in [0,T],u,v\in \mathbb{R}.$

According to Proposition 2, the inequality

$$\begin{array}{cc}\hfill v\left(t\right)& \le \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)G(s,v\left(s\right),v(s-\tau ))ds\hfill \\ & +L{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)v(s-\tau )ds,t\in (0,T]\hfill \end{array}$$

(8)

holds.

Let $v^{\left(0\right)}\left(t\right)=v\left(t\right)$ and $w^{\left(0\right)}\left(t\right)=w\left(t\right)$ for $t\in [-\tau ,T].$

We use induction w.r.t. the interval to prove properties of the sequences of successive approximations.

From the definition of the operator $\mathrm{\Omega }$ and equality $E_{q,q}\left(0\right)=\frac{1}{\mathrm{\Gamma }\left(q\right)}$ it follows that $t^{1-q}{w}^{\left(n\right)}\left(t\right){{|}_{t=0}=t^{1-q}{v}^{\left(n\right)}\left(t\right)|}_{t=0}=\underset{t\to 0+}{lim}{t}^{1-q}{v}^{\left(n\right)}\left(t\right)=\underset{t\to 0+}{lim}\psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)=\psi \left(0\right)$ for all integers $n\ge 1$.

Let $t\in (0,\tau ]$. From the definition of the operator $\mathrm{\Omega }$ and inequalities (8) we obtain

$$\begin{array}{cc}\hfill v^{\left(0\right)}\left(t\right)\le & \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)G(s,v^{\left(0\right)}\left(s\right),v^{\left(0\right)}(s-\tau ))ds\hfill \\ & +L{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\psi (s-\tau )ds=v^{\left(1\right)}\left(t\right)fort\in (0,\tau ].\hfill \end{array}$$

(9)

From the definition of the operator $\mathrm{\Omega }$, condition 2, the inequality (9) and the equality $v^{\left(1\right)}(s-\tau )-v^{\left(2\right)}(s-\tau )=0$ for $s\in (0,\tau ]$ we get

$$\begin{array}{cc}\hfill v^{\left(1\right)}\left(t\right)& =\psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+L{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)v^{\left(1\right)}(s-\tau )ds\hfill \\ & +{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,v^{\left(0\right)}\left(s\right),v^{\left(0\right)}(s-\tau ))ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(M{v}^{\left(0\right)}\left(s\right)+L{v}^{\left(0\right)}(s-\tau )\right)ds\hfill \\ & \le \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+L{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)v^{\left(2\right)}(s-\tau )ds\hfill \\ & +{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,v^{\left(1\right)}\left(s\right),v^{\left(1\right)}(s-\tau ))ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(M{v}^{\left(1\right)}\left(s\right)+L{v}^{\left(1\right)}(s-\tau )\right)ds\hfill \\ & =v^{\left(2\right)}\left(t\right)\mathrm{for}t\in (0,\tau ].\hfill \end{array}$$

(10)

Similarly, we can prove

$$v^{\left(n\right)}\left(t\right)\le v^{(n+1)}\left(t\right),\mathrm{for}t\in (0,\tau ],n=2,\dots ,$$

and

$$w^{\left(n\right)}\left(t\right)\ge w^{(n+1)}\left(t\right),\mathrm{for}t\in (0,\tau ],n=0,1,2,\dots .$$

Let $t\in (\tau ,2\tau ]$. From the definition of the operator $\mathrm{\Omega }$, the inequalities (8) and $v^{\left(0\right)}(t-\tau )\le v^{\left(1\right)}(t-\tau )$ for $t\in (\tau ,2\tau ]$ we obtain

$$\begin{array}{cc}\hfill v^{\left(0\right)}\left(t\right)& \le \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,v^{\left(0\right)}\left(s\right),v^{\left(0\right)}(s-\tau ))ds\hfill \\ & +L{\int }_0^{\tau }{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)v^{\left(1\right)}(s-\tau )ds\hfill \\ & +L{\int }_{\tau }^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)v^{\left(1\right)}(s-\tau )ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(M{v}^{\left(0\right)}\left(s\right)+L{v}^{\left(0\right)}(s-\tau )\right)ds=v^{\left(1\right)}\left(t\right).\hfill \end{array}$$

(11)

Also, from condition 2, the inequalities (8) and $v^{\left(1\right)}(t-\tau )\le v^{\left(2\right)}(t-\tau )$ for $t\in (\tau ,2\tau ]$ we get

$$\begin{array}{cc}\hfill v^{\left(1\right)}\left(t\right)& =\psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,v^{\left(0\right)}\left(s\right),v^{\left(0\right)}(s-\tau ))ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(M{v}^{\left(0\right)}\left(s\right)+L(v^{\left(0\right)}(s-\tau )-v^{\left(1\right)}(s-\tau )\right)ds\hfill \\ & \le \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,v^{\left(1\right)}\left(s\right),v^{\left(1\right)}(s-\tau ))ds\hfill \\ & +{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(M(v^{\left(0\right)}\left(s\right)-v^{\left(1\right)}\left(s\right))+L(v^{\left(0\right)}(s-\tau )-v^{\left(1\right)}(s-\tau ))\right)ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(M{v}^{\left(0\right)}\left(s\right)+L(v^{\left(0\right)}(s-\tau )-v^{\left(1\right)}(s-\tau ))\right)ds\hfill \\ & =\psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,v^{\left(1\right)}\left(s\right),v^{\left(1\right)}(s-\tau ))ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)M{v}^{\left(1\right)}\left(s\right)ds\hfill \\ & \le \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,v^{\left(1\right)}\left(s\right),v^{\left(1\right)}(s-\tau ))ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(M{v}^{\left(1\right)}\left(s\right)+L(v^{\left(1\right)}(s-\tau )-v^{\left(2\right)}(s-\tau ))\right)ds\hfill \\ & =v^{\left(2\right)}\left(t\right),t\in (\tau ,2\tau ].\hfill \end{array}$$

Similarly, we can prove

$$v^{\left(n\right)}\left(t\right)\le v^{(n+1)}\left(t\right),fort\in (\tau ,2\tau ],n=2,3\dots ,$$

and

$$w^{\left(n\right)}\left(t\right)\ge w^{(n+1)}\left(t\right),fort\in (\tau ,2\tau ],n=0,1,2,\dots .$$

Following the induction process w.r.t. the interval we prove the claims (b) and (c).

Now, we will prove the claim (d). Let $t\in (0,\tau ]$. From the definition of the operator $\mathrm{\Omega }$, condition 2, the inequality (9) we get

$$\begin{array}{cc}\hfill v^{\left(1\right)}\left(t\right)-w^{\left(1\right)}\left(t\right)& ={\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,v^{\left(0\right)}\left(s\right),v^{\left(0\right)}(s-\tau ))ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,w^{\left(0\right)}\left(s\right),w^{\left(0\right)}(s-\tau ))ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\times \hfill \\ & \times \left(M{v}^{\left(0\right)}\left(s\right)+L(v^{\left(0\right)}(s-\tau )-v^{\left(1\right)}(s-\tau ))\right)ds\hfill \\ & +{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\times \hfill \\ & \times \left(M{w}^{\left(0\right)}\left(s\right)+L{w}^{\left(0\right)}(s-\tau )-L{w}^{\left(1\right)}(s-\tau )\right)ds\hfill \\ & \le L{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)(v^{\left(1\right)}(s-\tau )-w^{\left(1\right)}(s-\tau ))ds\hfill \\ & =0\mathrm{for}t\in (0,\tau ].\hfill \end{array}$$

(12)

Similarly, we can prove

$$v^{\left(n\right)}\left(t\right)\le w^{(n+1)}\left(t\right),fort\in (0,\tau ],n=2,3,\dots .$$

Let $t\in (\tau ,2\tau ]$. From condition 2, the inequalities (8) and $v^{\left(1\right)}(t-\tau )\le w^{\left(1\right)}(t-\tau )$ for $t\in (\tau ,2\tau ]$ we obtain we get

$$\begin{array}{cc}\hfill v^{\left(1\right)}\left(t\right)& =\psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,v^{\left(0\right)}\left(s\right),v^{\left(0\right)}(s-\tau ))ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\left)\right(M{v}^{\left(0\right)}\left(s\right)+L(v^{\left(0\right)}(s-\tau )-v^{\left(1\right)}(s-\tau ))\right)ds\hfill \\ & \le \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,w^{\left(0\right)}\left(s\right),w^{\left(0\right)}(s-\tau ))ds\hfill \\ & +{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(M(v^{\left(0\right)}\left(s\right)-w^{\left(0\right)}\left(s\right))+L(v^{\left(0\right)}(s-\tau )-w^{\left(0\right)}(s-\tau ))\right)ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(M{v}^{\left(0\right)}\left(s\right)+L(v^{\left(0\right)}(s-\tau )-v^{\left(1\right)}(s-\tau ))\right)ds\hfill \\ & \le \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,w^{\left(0\right)}\left(s\right),w^{\left(0\right)}(s-\tau ))ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)M{w}^{\left(0\right)}\left(s\right)\hfill \\ & \le \psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{q-1}+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,w^{\left(0\right)}\left(s\right),w^{\left(0\right)}(s-\tau ))ds\hfill \\ & -{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(M{w}^{\left(0\right)}\left(s\right)+L(w^{\left(0\right)}(s-\tau )-w^{\left(1\right)}(s-\tau ))\right)ds\hfill \\ & =w^{\left(1\right)}\left(t\right),t\in (\tau ,2\tau ].\hfill \end{array}$$

Similarly, we can prove

$$v^{\left(n\right)}\left(t\right)\le w^{\left(n\right)}\left(t\right),\mathrm{for}t\in (\tau .2\tau ],n=2,3,\dots .$$

Now consider the sequences ${\left\{t^{1-q}{v}^{\left(n\right)}\left(t\right)\right\}}_0^{\infty }$ and ${\left\{t^{1-q}{w}^{\left(n\right)}\left(t\right)\right\}}_0^{\infty }$. They are increasing and decreasing, respectively, and bounded. Thus, they are equicontinuous on $[0,T]$ (the proof is similar to that in [13] and we omit it). Therefore, they are uniformly convergent on $[0,T]$. Denote, $\tilde{V}\left(t\right)=\underset{n\to \infty }{lim}{t}^{1-q}{v}^{\left(n\right)}\left(t\right)$ and $\tilde{W}\left(t\right)=\underset{n\to \infty }{lim}{t}^{1-q}{w}^{\left(n\right)}\left(t\right),t\in [0,T].$ According to the above (b), (c) and (d) the inequalities

$$\begin{array}{c}{t}^{1-q}{v}^{\left(n\right)}\left(t\right)\le \tilde{V}\left(t\right),t\in [0,T],\tilde{W}\left(t\right)\le t^{1-q}{w}^{\left(n\right)}\left(t\right),t\in [0,T],n=0,1,2,\dots ,\hfill \\ \tilde{V}\left(t\right)\le \tilde{W}\left(t\right),t\in [0,T].\hfill \end{array}$$

(13)

hold.

From the uniform convergence of the sequences ${\left\{t^{1-q}{v}^{\left(n\right)}\left(t\right)\right\}}_0^{\infty }$ and ${\left\{t^{1-q}{w}^{\left(n\right)}\left(t\right)\right\}}_0^{\infty }$ we have the point-wise convergence of the sequences ${\left\{v^{\left(n\right)}\left(t\right)\right\}}_0^{\infty }$ and ${\left\{w^{\left(n\right)}\left(t\right)\right\}}_0^{\infty }$ on $(0,T]$ to $V\left(t\right)=\frac{\tilde{V}\left(t\right)}{t^{1-q}}\in C_{1-q}\left([0,T]\right)$ and $W\left(t\right)=\frac{\tilde{W}\left(t\right)}{t^{1-q}}\in C_{1-q}\left([0,T]\right)$, respectively.

Consider the continuous extension of the integral form of $t^{1-q}{v}^{(n+1)}\left(t\right)$ on $[0,T]$:

$$\begin{array}{cc}\hfill t^{1-q}{v}^{\left(n\right)}\left(t\right)& =\psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)\hfill \\ & +t^{1-q}{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)F(s,v^{(n-1)}\left(s\right),v^{(n-1)}(s-\tau ))ds\hfill \\ & -t^{1-q}{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\times \hfill \\ & \times \left(M{v}^{(n-1)}\left(s\right)+L(v^{(n-1)}(s-\tau )-v^{\left(n\right)}(s-\tau ))\right)ds.\hfill \end{array}$$

(14)

Take the limit in (14) and we obtain the Volterra fractional integral equation

$$\begin{array}{cc}\hfill \tilde{V}\left(t\right)& =\psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)\hfill \\ & +t^{1-q}{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(F(s,V(s),V(s-\tau \left)\right)-MV\left(s\right)\right)ds,fort\in (0,T],\hfill \end{array}$$

(15)

or

$$\begin{array}{cc}\hfill V\left(t\right)& =\psi \left(0\right)\mathrm{\Gamma }\left(q\right)E_{q,q}\left(M{t}^q\right)t^{1-q}\hfill \\ & +{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(M{(t-s)}^q\right)\left(F(s,V(s),V(s-\tau \left)\right)-MV\left(s\right)\right)ds,fort\in (0,T].\hfill \end{array}$$

(16)

From equalities $t^{1-q}{V\left(t\right)|}_{t=0}=\tilde{V}\left(t\right){{|}_{t=0}=\underset{n\to \infty }{lim}{(t-0)}^{1-q}{v}^{\left(n\right)}\left(t\right)|}_{t=0}=\underset{n\to \infty }{lim}\psi \left(0\right)=\psi \left(0\right)$ according to Proposition 2 applied to Equation (16) the limit function $V\left(t\right)$ is a solution of the linear FrDDE

$${}_{t_0}^{RL}{D}_t^{q}v\left(t\right)=Mv\left(t\right)-\left(F(t,v(t),v(t-\tau \left)\right)-Mv\left(t\right)\right)=F(t,v\left(t\right),v(t-\tau )),t\in (0,T].$$

Therefore, the function $v\left(t\right)$ is a solution of the IVP for FrDDE (1).

The proof about $w\left(t\right)$ is similar.

Proof of claim g). From claim (d) and the inequality (6) it follows that $t^{1-q}{v}^{\left(k\right)}\left(t\right)\le t^{1-q}{w}^{\left(k\right)}\left(t\right)$ for any fixed $t\in (0,T]$ and $k=1,2,\dots$. Then applying claim (e) we get $t^{1-q}{v}^{\left(k\right)}\left(t\right)\le t^{1-q}V\left(t\right)\le t^{1-q}W\left(t\right)\le t^{1-q}{w}^{\left(k\right)}\left(t\right)$ for any fixed $t\in (0,T]$. Therefore, $v^{\left(k\right)}\left(t\right)\le V\left(t\right)\le W\left(t\right)\le w^{\left(k\right)}\left(t\right)$ for any on $t\in (0,T]$. □

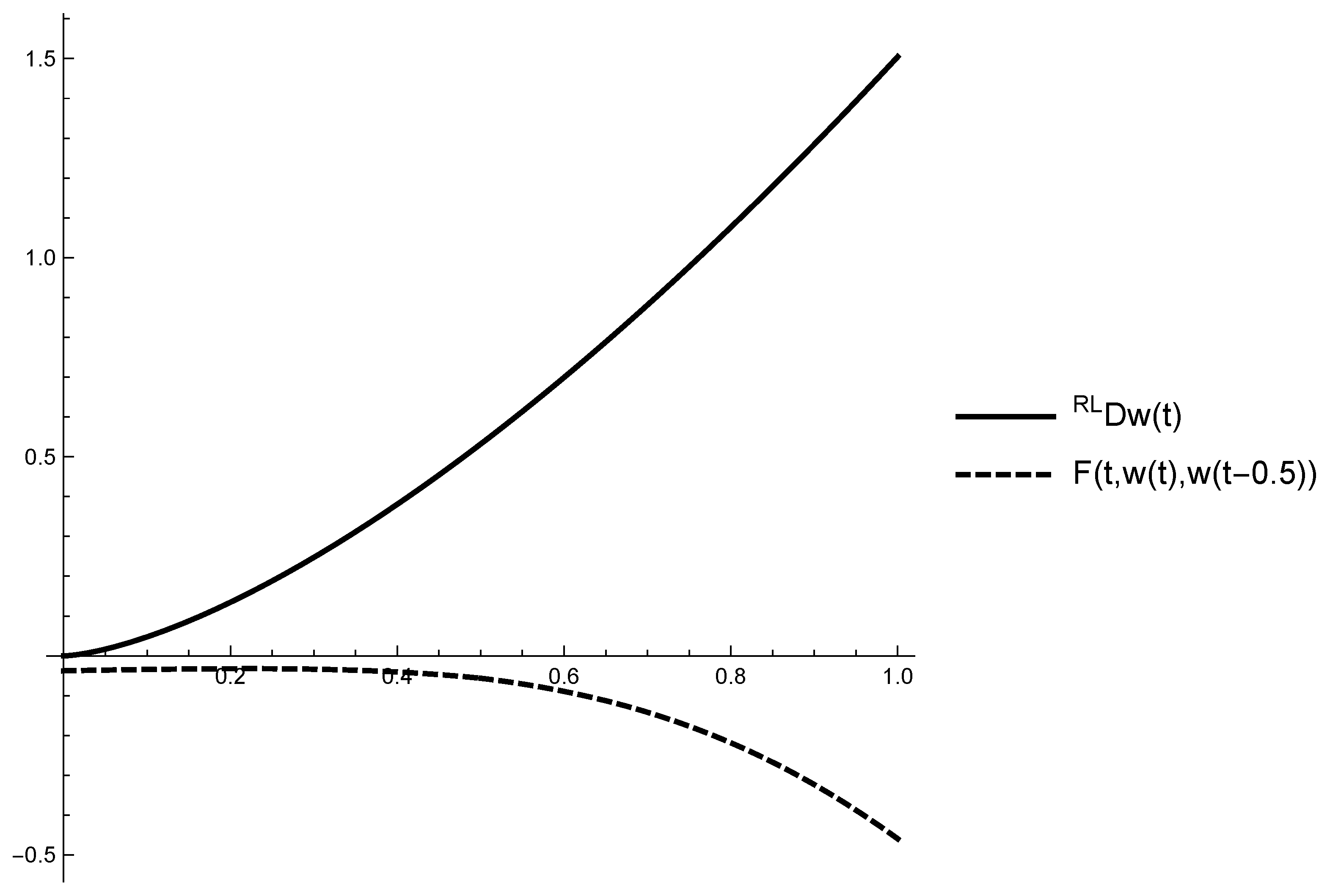
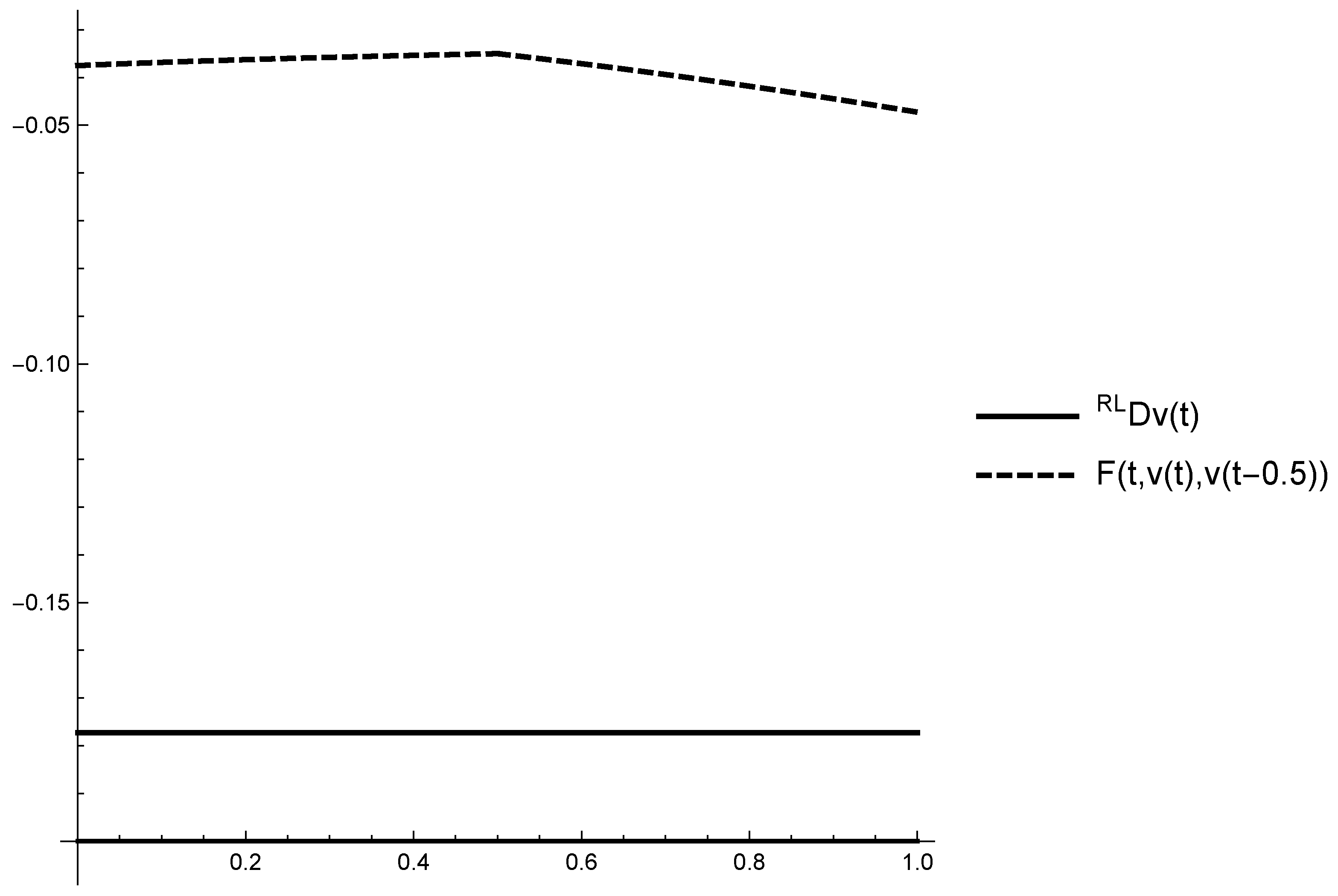
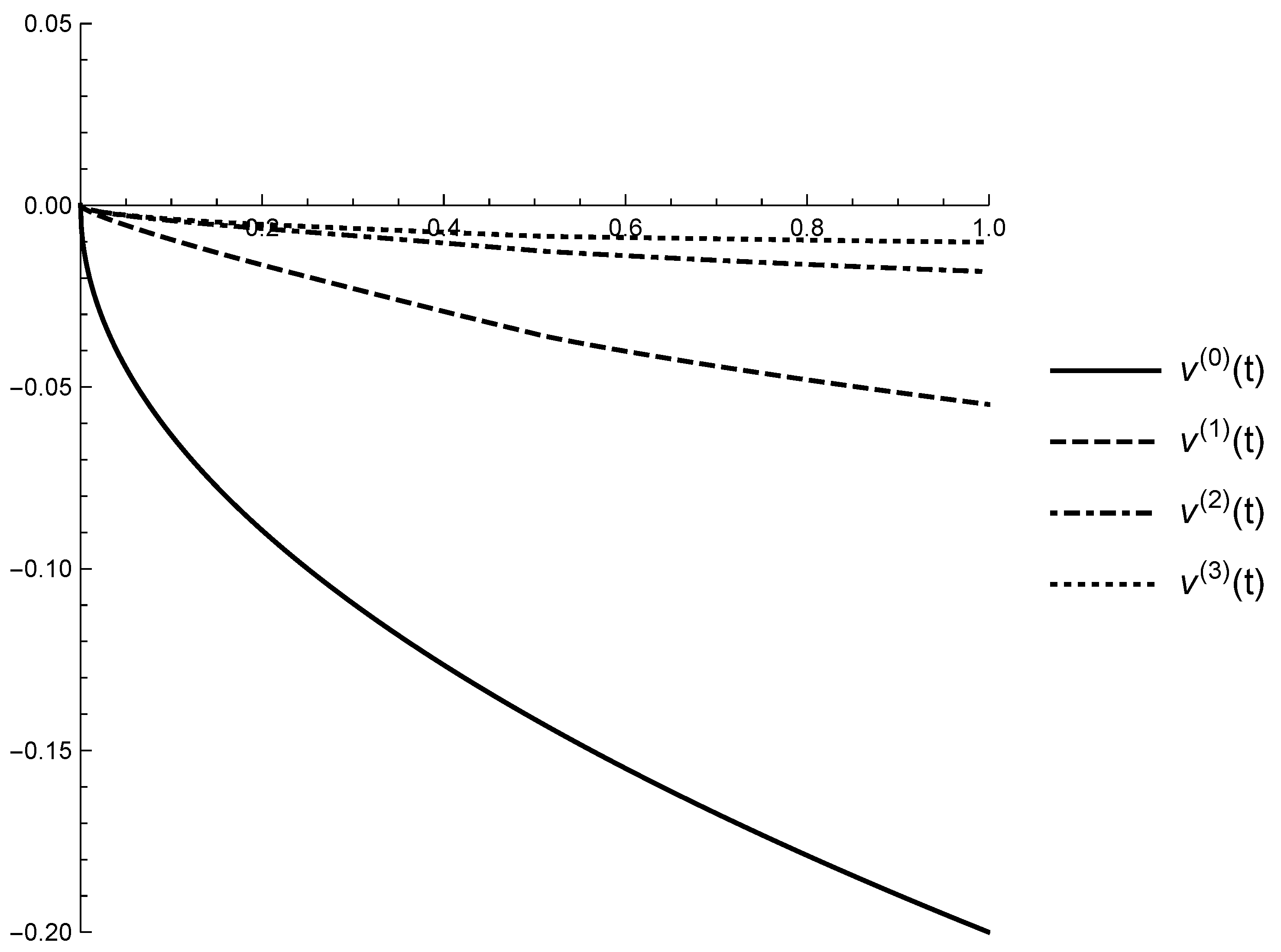
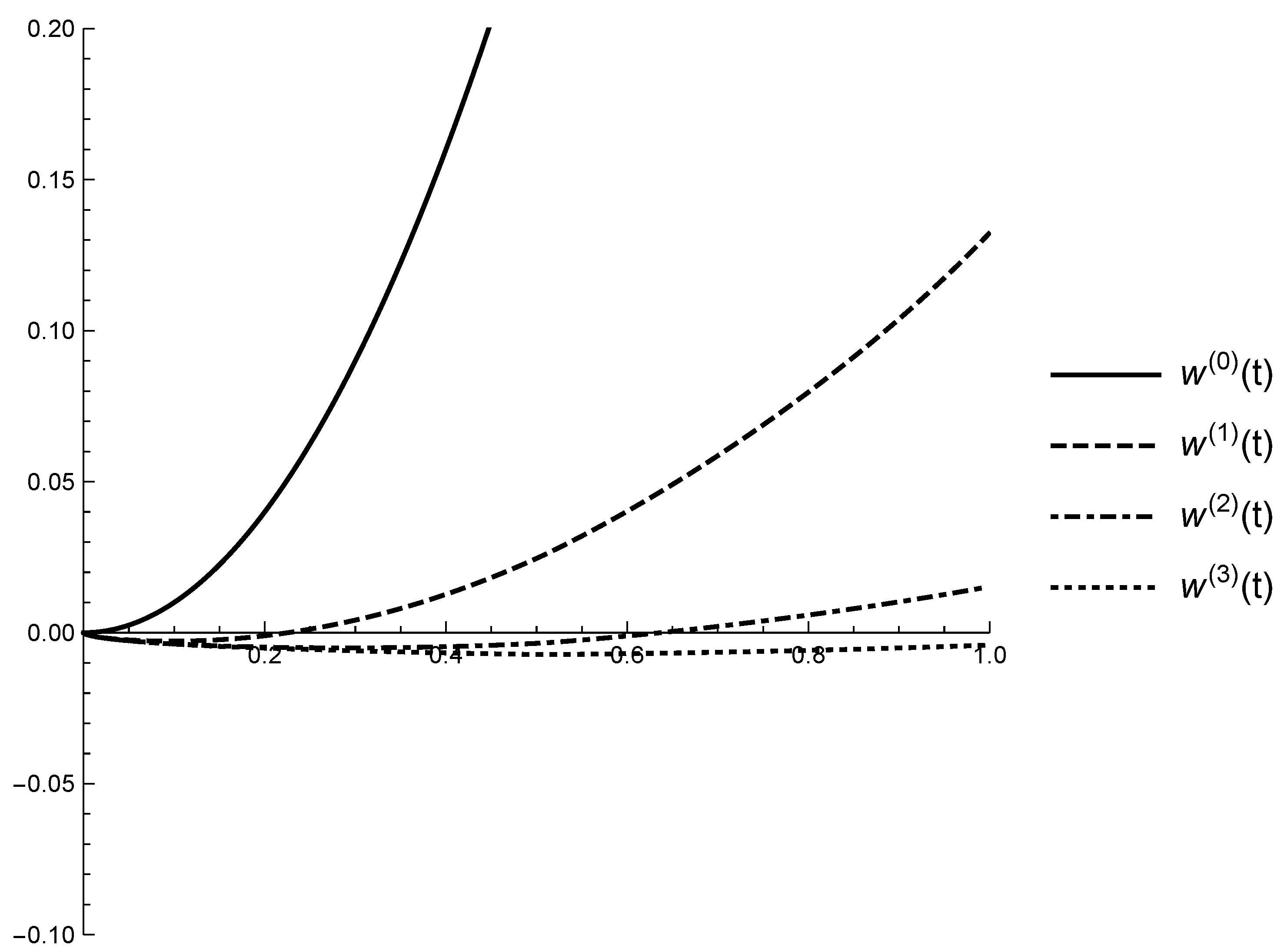
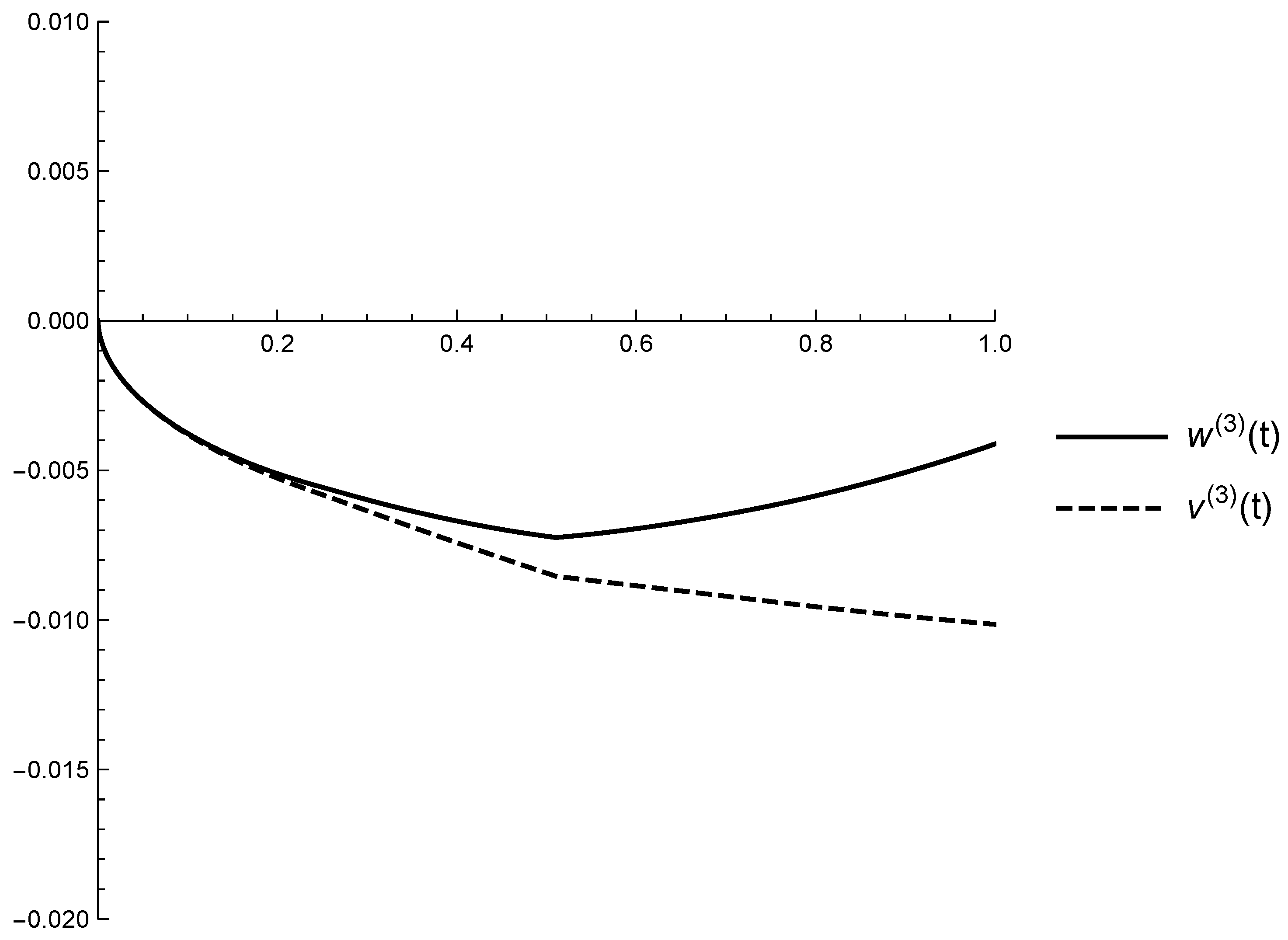
5. Application of the Suggested Algorithm

Now we will apply the algorithm suggested in Theorem 1 for approximate obtaining of the solution of nonlinear RL fractional differential equation with a delay. We will use computer realization of this algorithm to obtain the values of the approximate solutions and to graph them.

Example 1.

Let $\tau =0.5,T=1$ and consider the IVP for scalar nonlinear Riemann-Liouville FrDDE

$$\begin{array}{c}{}_0^{RL}{D}_t^{0.5}x\left(t\right)=(x^2\left(t\right)+0.05)\left(-0.5+\frac{x(t-0.5)}{t+1}\right)fort\in (0,1],\hfill \\ x\left(t\right)=0.5tfort\in [-0.5,0],\hfill \\ t^{0.5}{x\left(t\right)|}_{t=0}=0\hfill \end{array}$$

(17)

with $\psi \left(t\right)=0.5t,t\in [-0.5,0]$, and $F(t,x,y)=(x^2+0.05)(-0.5+\frac{y}{t+1})$.

The function

$$w\left(t\right)=\left\{\begin{array}{cc}0.5t,\hfill & t\in [-0.5,0]\hfill \\ t^2,\hfill & t\in (0,1]\hfill \end{array}\right.$$

is an upper solution on $[-0.5,1]$ of the IVP for FrDE (17) since $t^{0.5}{t}^2{|}_{t=0}=0$ and according to Proposition 1 with $q=0.5$ and $\beta =2$ the following inequalities

$${}_0^{RL}{D}_t^{0.5}{t}^2=\frac{\mathrm{\Gamma }\left(3\right)}{\mathrm{\Gamma }\left(2.5\right)}{t}^{1.5}\ge \left\{\begin{array}{cc}(t^4+0.05)\left(-0.5+\frac{0.5(t-0.5)}{t+1}\right),\hfill & t\in (0,0.5]\hfill \\ (t^4+0.05)\left(-0.5+\frac{{(t-0.5)}^2}{t+1}\right),\hfill & t\in (0.5,1]\hfill \end{array}\right.$$

are satisfied (see Figure 1).

Figure 1. Graphs of the fractional derivative of the function $w\left(t\right)$ and the right side part of the equation on $[0,1]$.

The function

$$v\left(t\right)=\left\{\begin{array}{cc}0.5t,\hfill & t\in [-0.5,0]\hfill \\ -0.2t^{0.5},\hfill & t\in (0,1]\hfill \end{array}\right.$$

is a lower solution on $[-0.5,1]$ of the IVP for FrDDE (17) because $t^{0.5}(-5t^{0.5}){|}_{t=0}=0$ holds and according to Proposition 1 with $q=\beta =0.5$ the following inequalities

$${}_0^{RL}{D}_t^{0.5}(-0.2t^{0.5})=-0.2\mathrm{\Gamma }\left(1.5\right)\le \left\{\begin{array}{cc}\left({\left(0.2t^{0.5}\right)}^2+0.05\right)\left(-0.5+0.5\frac{t-0.5}{t+1}\right),\hfill & t\in (0,0.5]\hfill \\ \left({(-0.2t^{0.5})}^2+0.05\right)\left(-0.5-0.2\frac{{(t-0.5)}^{0.5}}{t+1}\right),\hfill & t\in (0.5,1]\hfill \end{array}\right.$$

are satisfied (see Figure 2).

Figure 2. Graphs of the fractional derivative of the functions $v\left(t\right)$ and the right side part of the equation on $[0,1]$.

Note that the lower and upper solutions $v\left(t\right)$ and $w\left(t\right)$ are not unique. For example the function

$$w\left(t\right)=\left\{\begin{array}{cc}0.5t,\hfill & t\in [-0.5,0]\hfill \\ t^3,\hfill & t\in (0,1]\hfill \end{array}\right.$$

is also an upper solution. But we take just one lower (upper) solution to start the procedure.

Also, the inequality $v\left(t\right)\le w\left(t\right)$ on $[-0.5,1]$ holds.

For any $t\in [0,1],x,y,u,v\in \mathbb{R}$ we have $-0.2\le -0.2t^{0.5}=v\left(t\right)\le x\le y\le w\left(t\right)=t^2\le 1$, $-0.25\le v(t-0.5)\le u\le v\le w(t-0.5)\le \sqrt{0.5}$ and therefore,

$$\begin{array}{cc}\hfill F(t,x,u)-F(t,y,v)& =(x^2+0.05)\left(-0.5+\frac{u}{t+1}\right)-(y^2+0.05)\left(-0.5+\frac{v}{t+1}\right)\hfill \\ & =-0.5(x^2+0.05-y^2-0.05)+(x^2+0.05)\frac{u}{t+1}\hfill \\ & -(y^2+0.05)\frac{u}{t+1}+(y^2+0.05)\frac{u}{t+1}-(y^2+0.05)\frac{v}{t+1}\hfill \\ & =\left(\frac{u}{t+1}-0.5\right)(x+y)(x-y)+\frac{y^2+0.05}{t+1}(u-v).\hfill \end{array}$$

Applying the inequalities $-0.5\le (\frac{u}{t+1}-0.5)\le \sqrt{0.5}-0.5$, $-0.4\le x+y\le 2$, and $(\frac{u}{t+1}-0.5)(x+y)\ge -1$, $\frac{y^2+0.05}{t+1}\ge 0.05$, we get the inequality $F(t,x,u)-F(t,y,v)\le M(x-y)+L(u-v)$ with $M=-1,L=0.05>0$. Therefore, all conditions of Theorem 1 are fulfilled.

We apply the iterative scheme, suggested in Theorem 1, to obtain the successive approximations to the mild solution and to illustrate the claims of Theorem 1.

Define the zero approximation by $v^{\left(0\right)}\left(t\right)=v\left(t\right)$ and $w^{\left(0\right)}\left(t\right)=w\left(t\right)$ for $t\in [-0.5,1]$.

Starting from the function $v^{\left(0\right)}\left(t\right)$ we obtain the first lower approximation

$$v^{\left(1\right)}\left(t\right)=\left\{\begin{array}{c}0.5t,t\in [-0.5,0]\hfill \\ {\displaystyle {\int }_0^t{(t-s)}^{-0.5}{E}_{0.5,0.5}(-{(t-s)}^{0.5})({\left(v^{\left(0\right)}\left(s\right)\right)}^2+0.05)(-0.5+\frac{v^{\left(0\right)}(s-0.5)}{s+1}))ds}\hfill \\ {\displaystyle -{\int }_0^t{(t-s)}^{-0.5}{E}_{0.5,0.5}(-{(t-s)}^{0.5})\times }\hfill \\ {\displaystyle \times (-\left(v^{\left(0\right)}\left(s\right)\right)+0.05)(v^{\left(0\right)}(s-0.5)-v^{\left(1\right)}(s-0.5))ds},t\in (0,1],\hfill \end{array}\right.$$

(18)

the second lower approximation

$$v^{\left(2\right)}\left(t\right)=\left\{\begin{array}{c}0.5t,t\in [-0.5,0]\hfill \\ {\displaystyle {\int }_0^t{(t-s)}^{-0.5}{E}_{0.5,0.5}(-{(t-s)}^{0.5})({\left(v^{\left(1\right)}\left(s\right)\right)}^2+0.05)(-0.5+\frac{v^{\left(1\right)}(s-0.5)}{s+1}))ds}\hfill \\ {\displaystyle -{\int }_0^t{(t-s)}^{-0.5}{E}_{0.5,0.5}(-{(t-s)}^{0.5})\times }\hfill \\ {\displaystyle \times (-\left(v^{\left(1\right)}\left(s\right)\right)+0.05)(v^{\left(1\right)}(s-0.5)-v^{\left(2\right)}(s-0.5))ds},t\in (0,1]\hfill \end{array}\right.$$

(19)

and so on.

About the upper approximations we start from $w^{\left(0\right)}\left(t\right)$ and obtain the first upper approximation

$$w^{\left(1\right)}\left(t\right)=\left\{\begin{array}{c}0.5t,t\in [-0.5,0]\hfill \\ {\displaystyle {\int }_0^t{(t-s)}^{-0.5}{E}_{0.5,0.5}(-{(t-s)}^{0.5})({\left(w^{\left(0\right)}\left(s\right)\right)}^2+0.05)(-0.5+\frac{w^{\left(0\right)}(s-0.5)}{s+1}))ds}\hfill \\ {\displaystyle -{\int }_0^t{(t-s)}^{-0.5}{E}_{0.5,0.5}(-{(t-s)}^{0.5})\times }\hfill \\ {\displaystyle \times (-\left(w^{\left(0\right)}\left(s\right)\right)+0.05)(w^{\left(0\right)}(s-0.5)-w^{\left(1\right)}(s-0.5))ds},t\in (0,1],\hfill \end{array}\right.$$

the second upper approximation

$$w^{\left(2\right)}\left(t\right)=\left\{\begin{array}{c}0.5t,t\in [-0.5,0]\hfill \\ {\displaystyle {\int }_0^t{(t-s)}^{-0.5}{E}_{0.5,0.5}(-{(t-s)}^{0.5})({\left(w^{\left(1\right)}\left(s\right)\right)}^2+0.05)(-0.5+\frac{w^{\left(1\right)}(s-0.5)}{s+1}))ds}\hfill \\ {\displaystyle -{\int }_0^t{(t-s)}^{-0.5}{E}_{0.5,0.5}(-{(t-s)}^{0.5})\times }\hfill \\ {\displaystyle \times (-\left(w^{\left(1\right)}\left(s\right)\right)+0.05)(w^{\left(1\right)}(s-0.5)-w^{\left(2\right)}(s-0.5))ds},t\in (0,1],\hfill \end{array}\right.$$

and so on.

The numerical values of the lower/upper approximations, given analytically above, are obtained by a computer program written in C#. We will briefly describe the computerized algorithm for obtaining these successive approximations:

The numerical values of the sequences of successive approximations $v^{\left(k\right)}\left(t\right)$ and $w^{\left(k\right)}\left(t\right)$, $k=0,1,2,3,\dots$, $t\in [-0.5,1]$, are written in two dimensional arrays. The length of any of these arrays depends on the step in the interval $[-0.5,1]$.

We calculate in advance the values of the Mittag-Leffler function $E_{0.5,0.5}(-t^{0.5}),t\in [0,1),$ in the points t, which will be used for numerical solving of the integrals ${\int }_0^t\dots ds,t\in (0,1)$ (see Equations (18) and (19)). In the same points we also obtain the values of ${\left(t\right)}^{-0.5}$. These results are written in arrays with lengths, depending on the step on interval $(0,1)$. Note that the values of the Mittag-Leffler function are calculated by the help of the main definition (as an infinite sum) with an initially given error.

We use the trapezoid method with an initially given error to solve numerically the integrals of the type ${\int }_0^t{(t-s)}^{-0.5}{E}_{0.5,0.5}(-{(t-s)}^{0.5})\dots ds$ for each approximation k and any fixed $t\in (0,1]$. The values of both multipliers ${(t-s)}^{-0.5}$ and $E_{0.5,0.5}(-{(t-s)}^{0.5})$ are taken from initially formed arrays. Note that it could be used another numerical method for solving the required definite integrals.

For example, to calculate the values of $v^{\left(k\right)}\left(t\right)$ we use the following function

private double Calc_v_t(double[,] v, int k, long it)

    {

        double f, pf, sum = 0, s = 0, q = 0.5;

        long shift = (long)(0.5/eps)+1;

        long sh2 = shift/2;

        long i = shift, ie = it;

 

        pf = PowTmS[ie] * Eqq[ie] *

                 ((v[k-1,i]*v[k-1,i]+0.05) * (-q+v[k-1,i-sh2]/(s+1)) -

                   (-v[k-1,i]+0.05*(v[k-1,i-sh2]-v[k,i-sh2])));

 

        while (s < tval)

        {

             i++; ie--; s += eps;

             f = PowTmS[ie] * Eqq[ie] *

                    ((v[k-1,i]*v[k-1,i]+0.05) * (-q+v[k-1,i-sh2]/(s+1)) -

                         (-v[k-1,i]+0.05*(v[k-1,i-sh2]-v[k,i-sh2])));

             sum += (pf + f) * eps;

             pf = f;

        }

        return sum / 2;

    }

A part of the obtained numerical values of the successive approximations are given in Table 1 and they are used to generate the graphs on Figure 3, Figure 4, Figure 5 and Figure 6).

Table 1. Values of successive approximations $w^{\left(n\right)}\left(t\right)$ and $v^{\left(n\right)}\left(t\right)$, $n=0,1,2,3$ for $t\in [0,1]$.

t	${\mathit{w}}^{\left(0\right)}\left(\mathit{t}\right)$	${\mathit{w}}^{\left(1\right)}\left(\mathit{t}\right)$	${\mathit{w}}^{\left(2\right)}\left(\mathit{t}\right)$	${\mathit{w}}^{\left(3\right)}\left(\mathit{t}\right)$	${\mathit{v}}^{\left(3\right)}\left(\mathit{t}\right)$	${\mathit{v}}^{\left(2\right)}\left(\mathit{t}\right)$	${\mathit{v}}^{\left(1\right)}\left(\mathit{t}\right)$	${\mathit{v}}^{\left(0\right)}\left(\mathit{t}\right)$
0	0	0	0		0	0	0	0
…	…	…	…	…	…	…	…	…
0.05	0.0025000	−0.0024014	−0.002669875	−0.0026830	−0.0026910	−0.0028370	−0.0054822	−0.0447213
…	…	…	…	…	…	…	…	…
0.1	0.0100000	−0.0028030	−0.003707587	−0.0037665	−0.0038006	−0.0042116	−0.0094143	−0.0632455
…	…	…	…	…	…	…	…	…
0.15	0.0225000	−0.0023273	−0.004371989	−0.0045293	−0.0046100	−0.0053537	−0.0130148	−0.0774596
…	…	…	…	…	…	…	…	…
0.2	0.0400000	−0.0010073	−0.004782033	−0.0051102	−0.0052606	−0.0063855	−0.0164157	−0.0894427
…	…	…	…	…	…	…	…	…
0.25	0.0625000	0.0011752	−0.004974678	−0.0055640	−0.0058104	−0.0073536	−0.0196715	−0.1000000
…	…	…	…	…	…	…	…	…
0.3	0.0900000	0.0041728	−0.005025551	−0.0059818	−0.0063535	−0.0083442	−0.0228876	−0.1095445
…	…	…	…	…	…	…	…	…
0.35	0.1225000	0.0080102	−0.004920663	−0.0063617	−0.0068915	−0.0093546	−0.0260671	−0.1183215
…	…	…	…	…	…	…	…	…
0.4	0.1600000	0.0127018	−0.004640016	−0.0066932	−0.0074170	−0.0103733	−0.0291992	−0.1264911
…	…	…	…	…	…	…	…	…
0.45	0.2025000	0.0182403	−0.004175051	−0.0069743	−0.0079311	−0.0113985	−0.0322849	−0.1341640
…	…	…	…	…	…	…	…	…
0.5	0.2500000	0.0246100	−0.003520597	−0.0072042	−0.0084358	−0.0124294	−0.0353267	−0.1414213
…	…	…	…	…	…	…	…	…
0.55	0.3025000	0.0320137	−0.002426030	−0.0071326	−0.0086820	−0.0131993	−0.0378996	−0.1483239
…	…	…	…	…	…	…	…	…
0.6	0.3600000	0.0402038	−0.001086952	−0.0069496	−0.0088569	−0.0138649	−0.0401436	−0.1549193
…	…	…	…	…	…	…	…	…
0.65	0.4225000	0.0490747	0.000417801	−0.0067284	−0.0090315	−0.0145008	−0.0422464	−0.1612451
…	…	…	…	…	…	…	…	…
0.7	0.4900000	0.0585998	0.002078399	−0.0064716	−0.0092072	−0.0151118	−0.0442469	−0.1673320
…	…	…	…	…	…	…	…	…
0.75	0.5625000	0.0687781	0.003887027	−0.0061807	−0.0093841	−0.0157009	−0.0461668	−0.1732050
…	…	…	…	…	…	…	…	…
0.8	0.6400000	0.0796462	0.005842443	−0.0058527	−0.0095575	−0.0162662	−0.0480153	−0.1788854
…	…	…	…	…	…	…	…	…
0.85	0.7225000	0.0912844	0.007949841	−0.0054815	−0.0097203	−0.0168024	−0.0497938	−0.1843908
…	…	…	…	…	…	…	…	…
0.9	0.8100000	0.1038155	0.010211677	−0.0050684	−0.0098728	−0.0173114	−0.0515115	−0.1897366
…	…	…	…	…	…	…	…	…
0.95	0.9025000	0.1174206	0.012636895	−0.0046141	−0.0100154	−0.0177952	−0.0531754	−0.1949358
…	…	…	…	…	…	…	…	…
0.999	0.9980010	0.1320345	0.015188142	−0.0041287	−0.0101456	−0.0182462	−0.0547594	−0.1998999

Figure 3. Graphs of the upper/lpwer successive approximations $v^{\left(n\right)}\left(t\right)$ and $w^{\left(n\right)}\left(t\right)$, $n=0,1,2,3$, on the interval $[0,1]$.

Figure 4. Graphs of the successive lower approximations $v^{\left(n\right)}\left(t\right)$, $n=0,1,2,3$, on the interval $[0,1]$.

Figure 5. Graphs of the successive upper approximations $w^{\left(n\right)}\left(t\right)$, $n=0,1,2,3$, on the interval $[0,1]$.

Figure 6. Graphs of the successive approximations $v^{\left(3\right)}\left(t\right)$ and $w^{\left(3\right)}\left(t\right)$ on the interval $[0,1]$.

Table 1 and Figure 3, Figure 4, Figure 5 and Figure 6 illustrate the claims of Theorem 1 for the obtained successive approximations:

-

claim (b) - the sequence of lower approximate solutions $v^{\left(n\right)}\left(t\right)$, $n=0,1,2,3$ is increasing (see Figure 4 and the last four columns of Table 1);

-

claim (c)- the sequence of upper approximate solutions $w^{\left(n\right)}\left(t\right)$, $n=0,1,2,3$ is decreasing (see Figure 5 and the first four columns of Table 1);

-

claim (d) - the inequality $v^{\left(3\right)}\left(t\right)\le w^{\left(3\right)}\left(t\right),t\in [0,1]$ holds (see Figure 6 and the 5-th and 6-th columns of Table 1).

According to the claim (g) of Theorem 1 the mild solutions $V\left(t\right)$ and $W\left(t\right)$ of the FrDDE (17) are between the last obtained lower solution $v^{\left(3\right)}\left(t\right)$ and upper solution $w^{\left(3\right)}\left(t\right)$. So, practically the suggested algorithm for the approximate solving of IVP for FrDDE gives us a lower and upper bounds of the unknown exact solution.

6. Conclusions

The main aim of the paper is to suggest a scheme for the approximate solving of the initial value problem for scalar nonlinear Riemann-Liouville fractional differential equations with a constant delay on a finite interval. The iterative scheme is based on the method of lower and upper solutions. In connection with this, mild lower and mild upper solutions are defined. An algorithm for constructing two monotone sequences of mild lower and mild upper solutions, respectively, is given. It is proved both sequences are convergent to the exact solution of the studied problem. The iterative scheme is used in a computer environment to illustrate its application for solving a particular nonlinear problem. The suggested and computerized algorithm can be applied to solve approximately and to study the behavior of scalar models with RL fractional derives and delays. The practical application requires the next step in the investigations, more exactly to obtain an algorithm for approximate solving of systems with RL derivatives and delays.