Synchronization of Butterfly Fractional Order Chaotic System
Abstract
:1. Introduction
2. Main Results
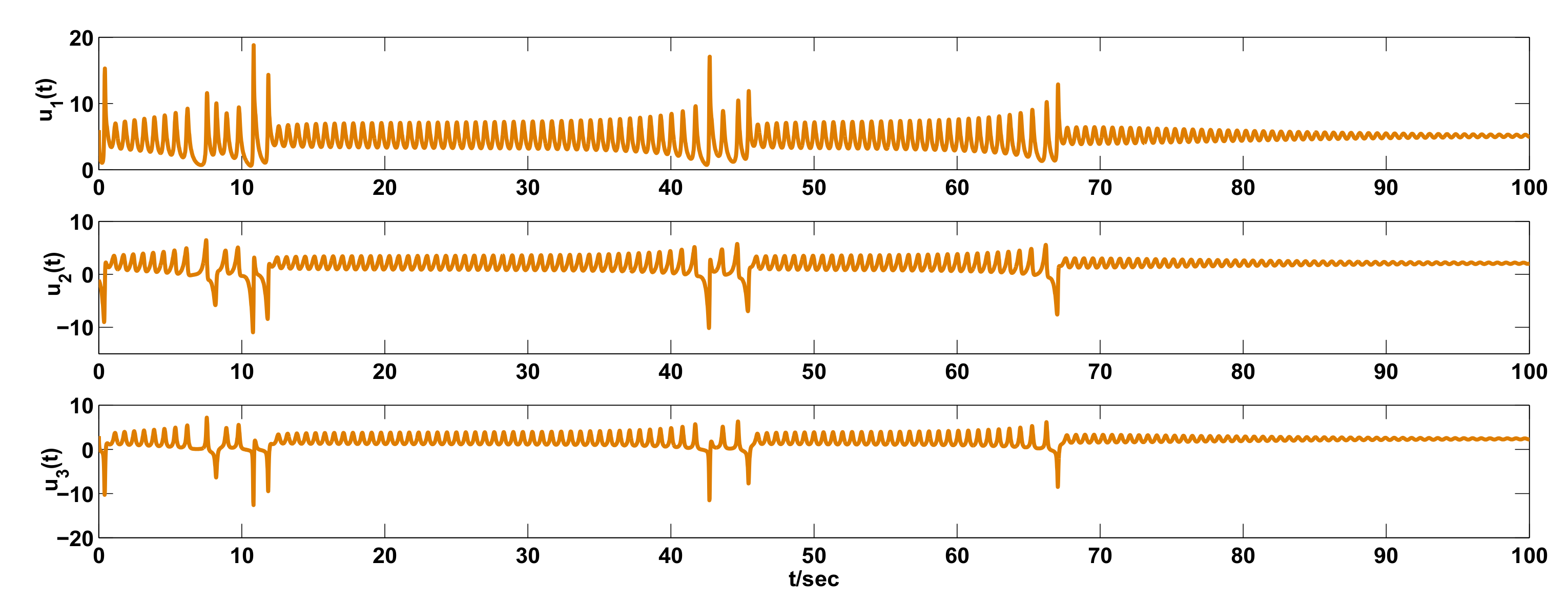
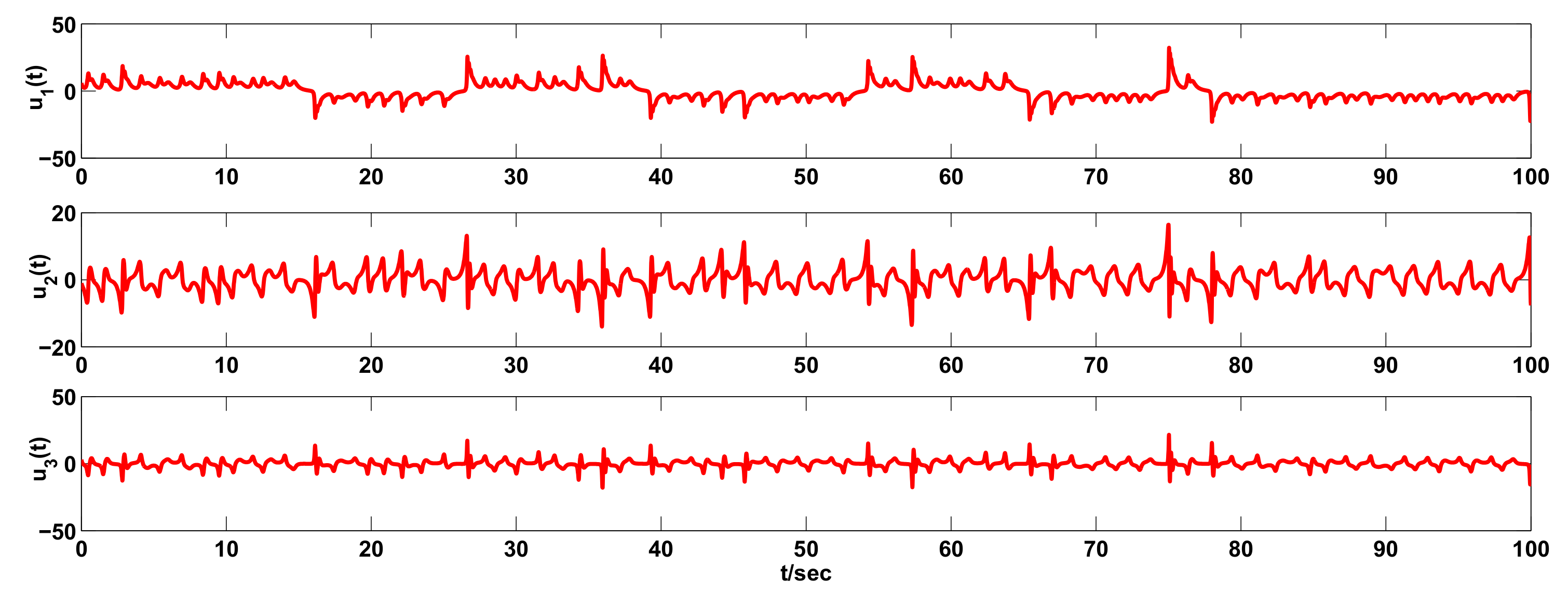
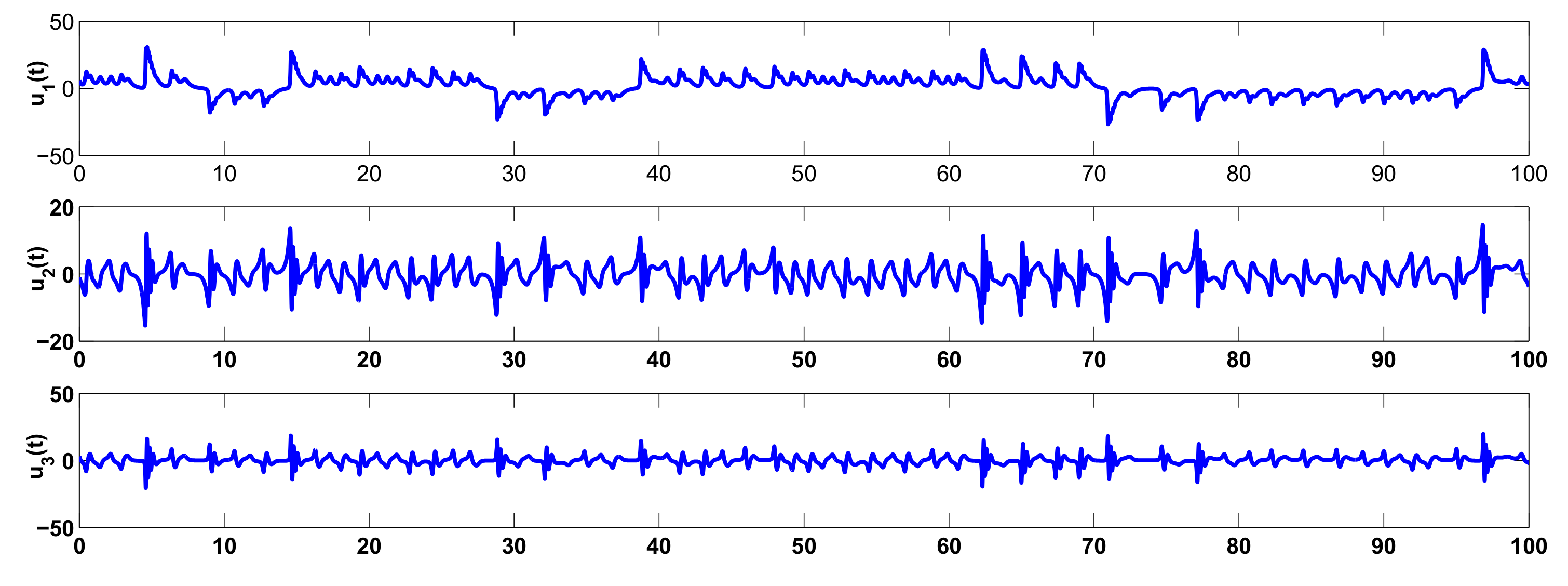
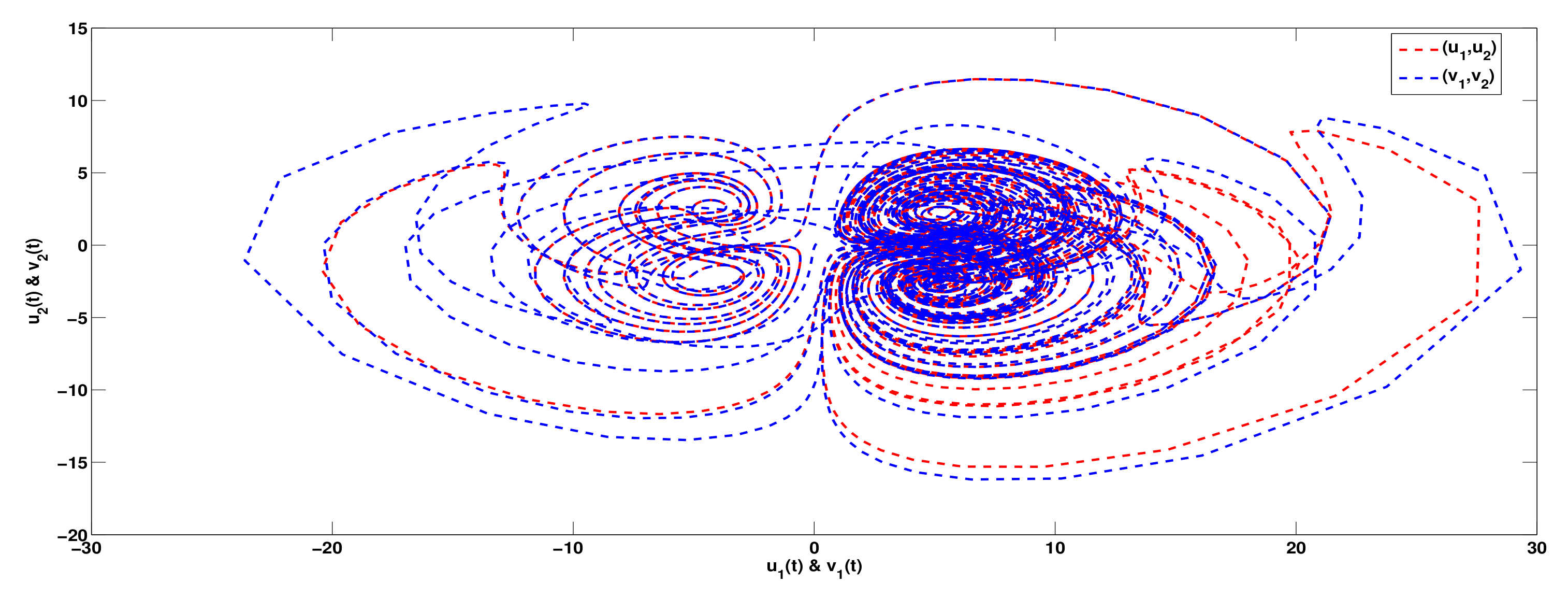
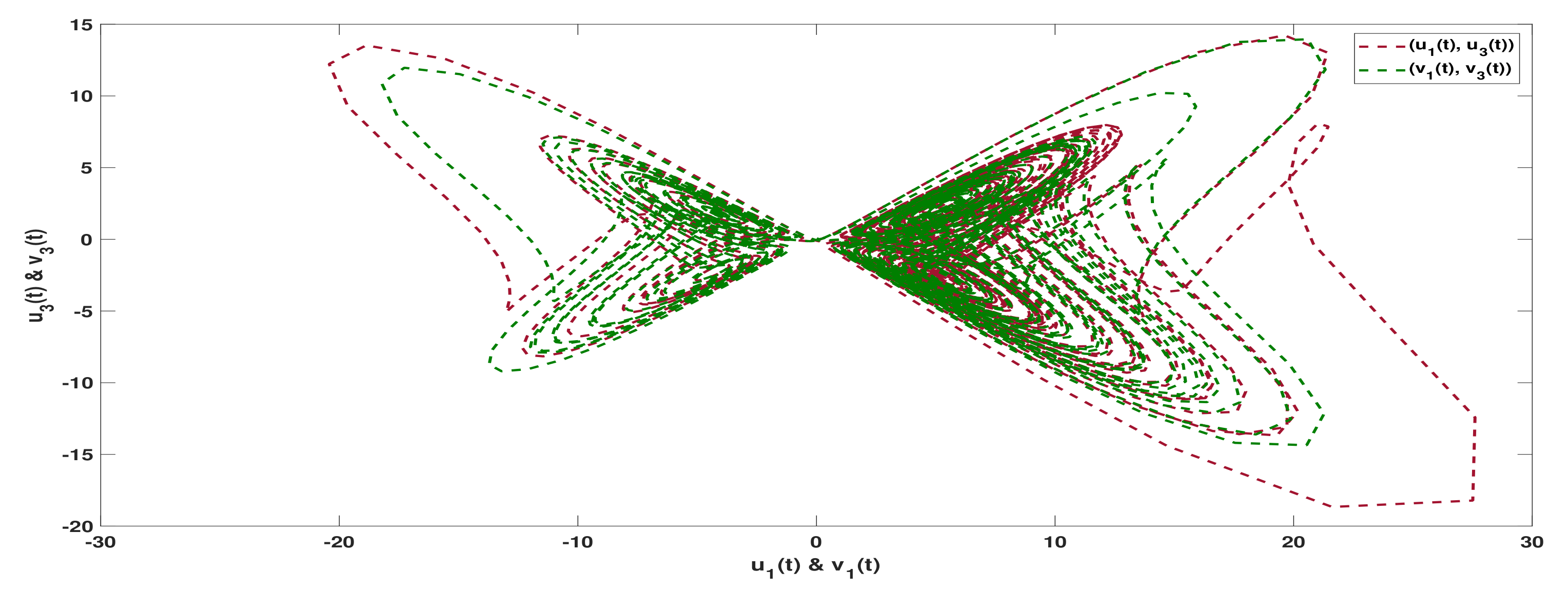
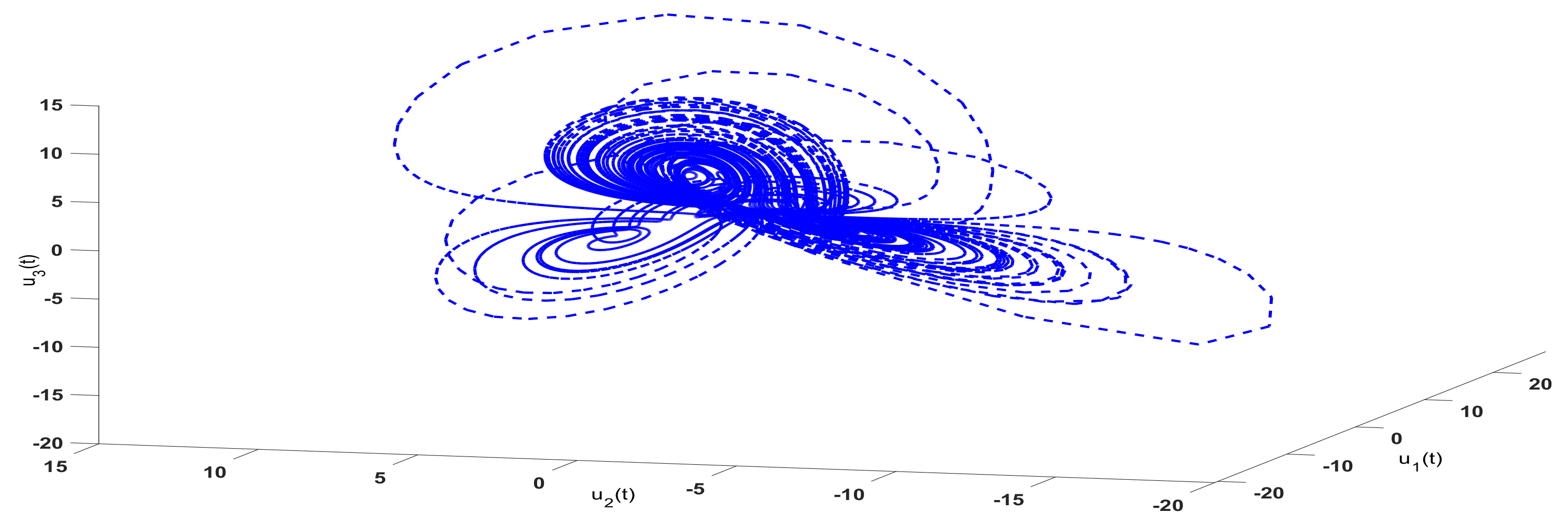
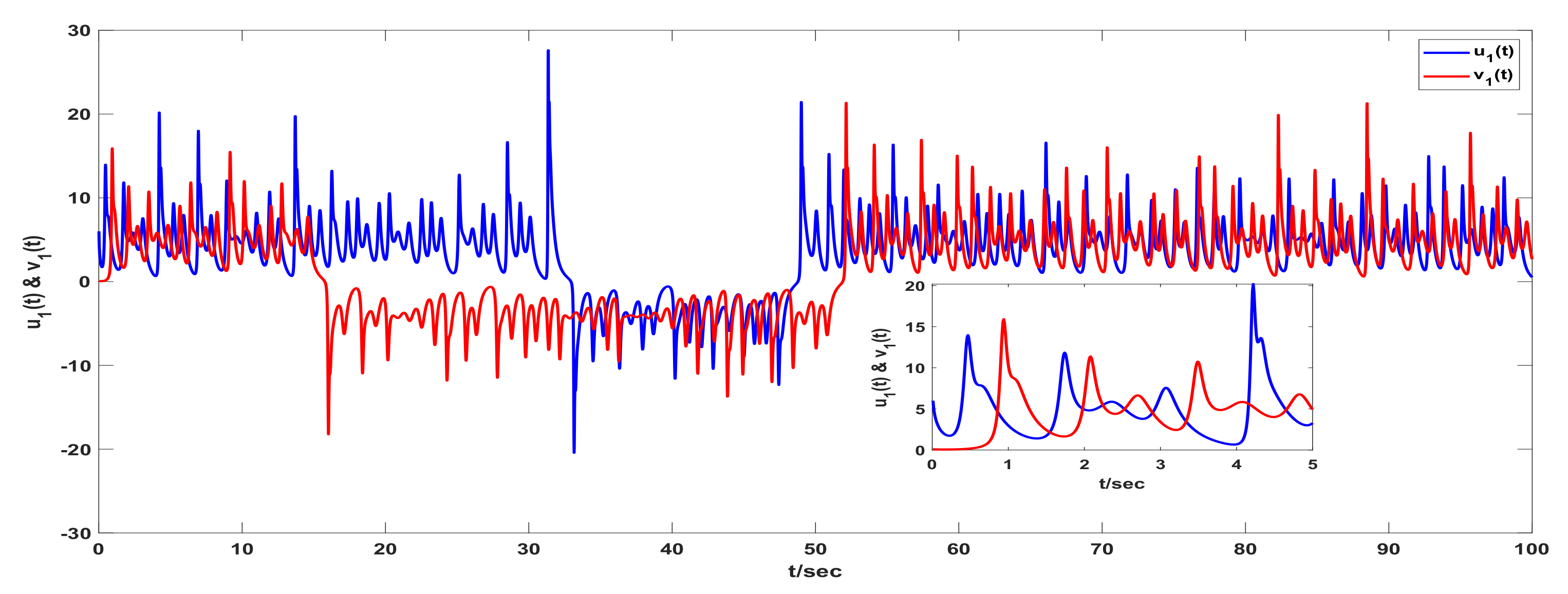
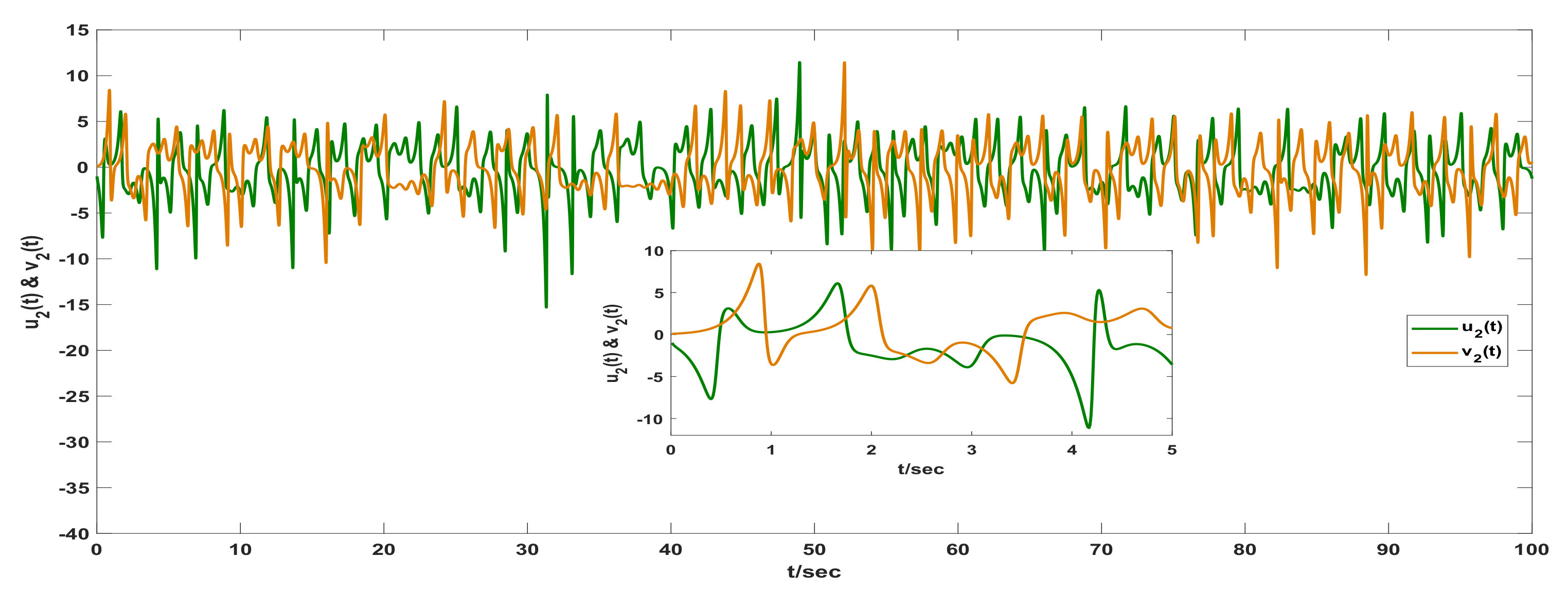
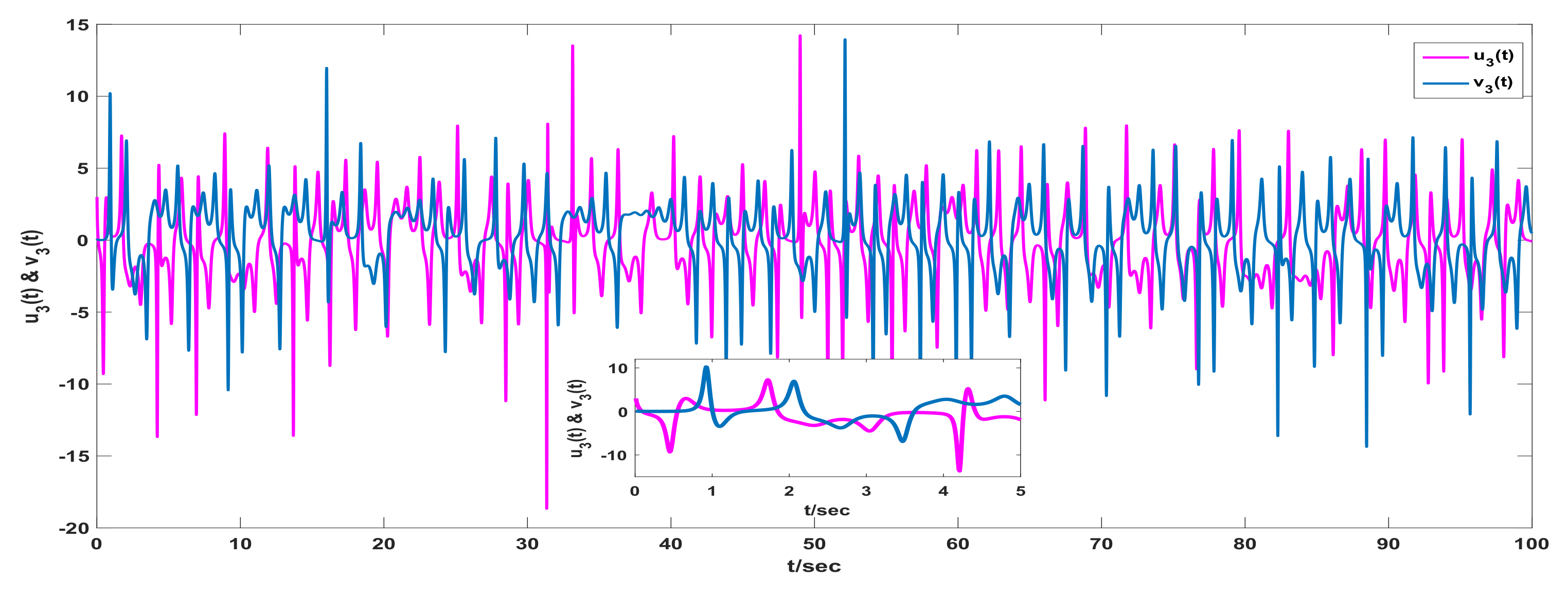
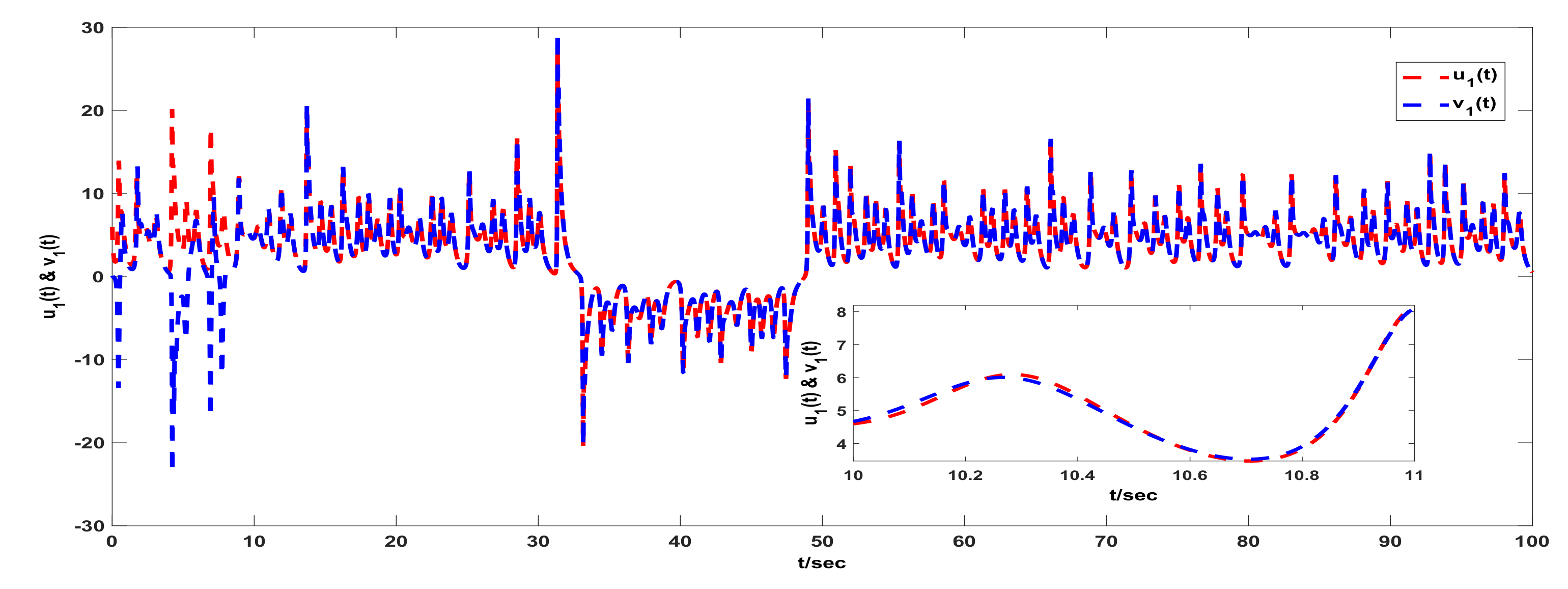
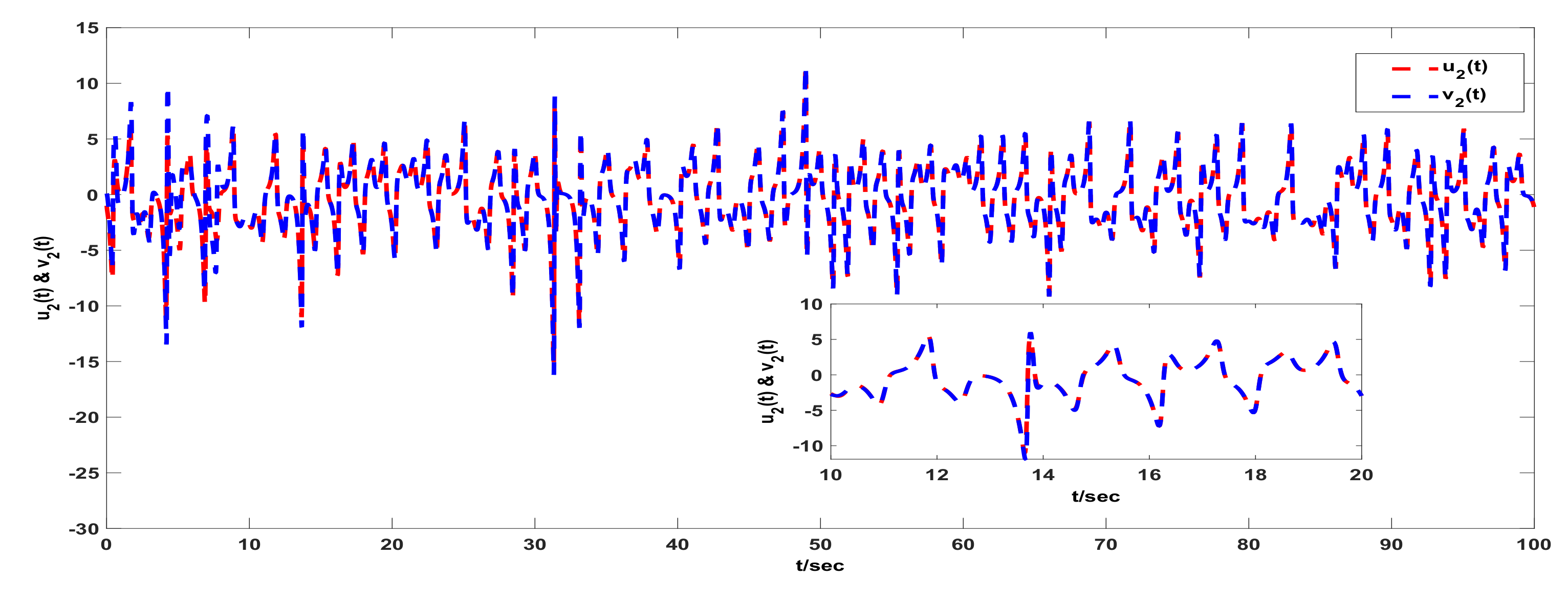
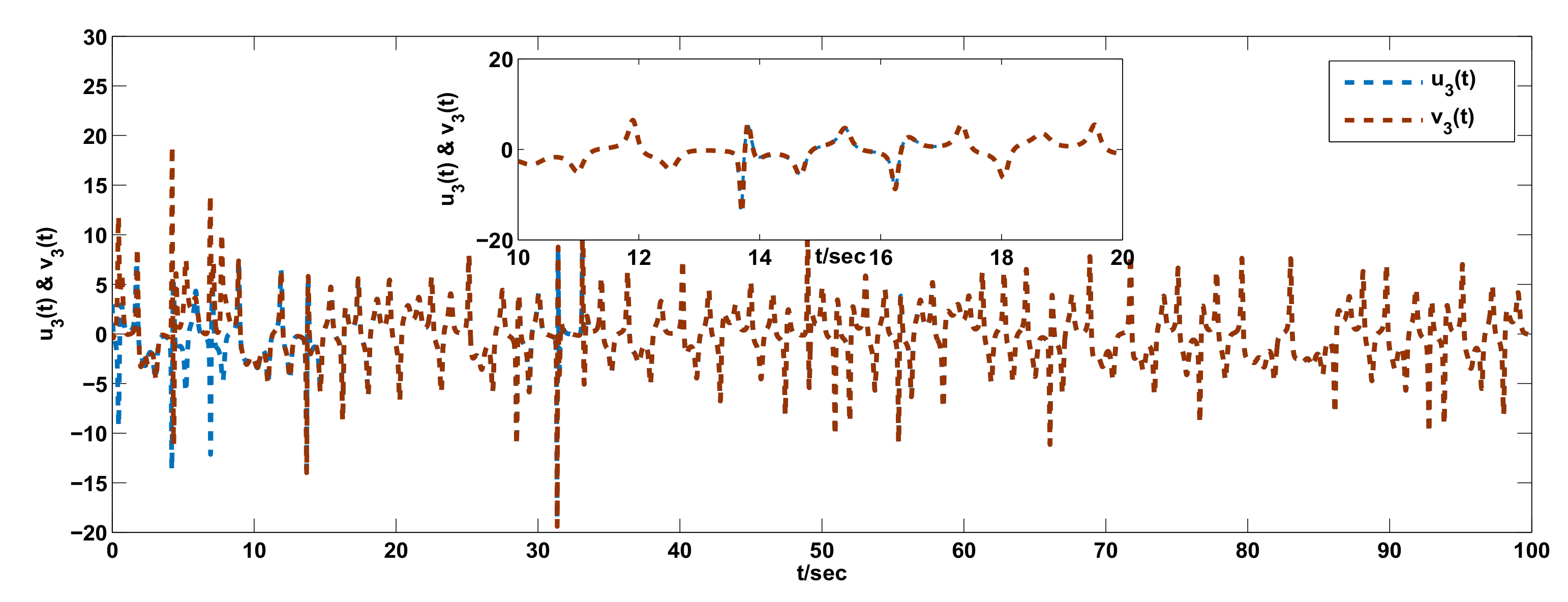
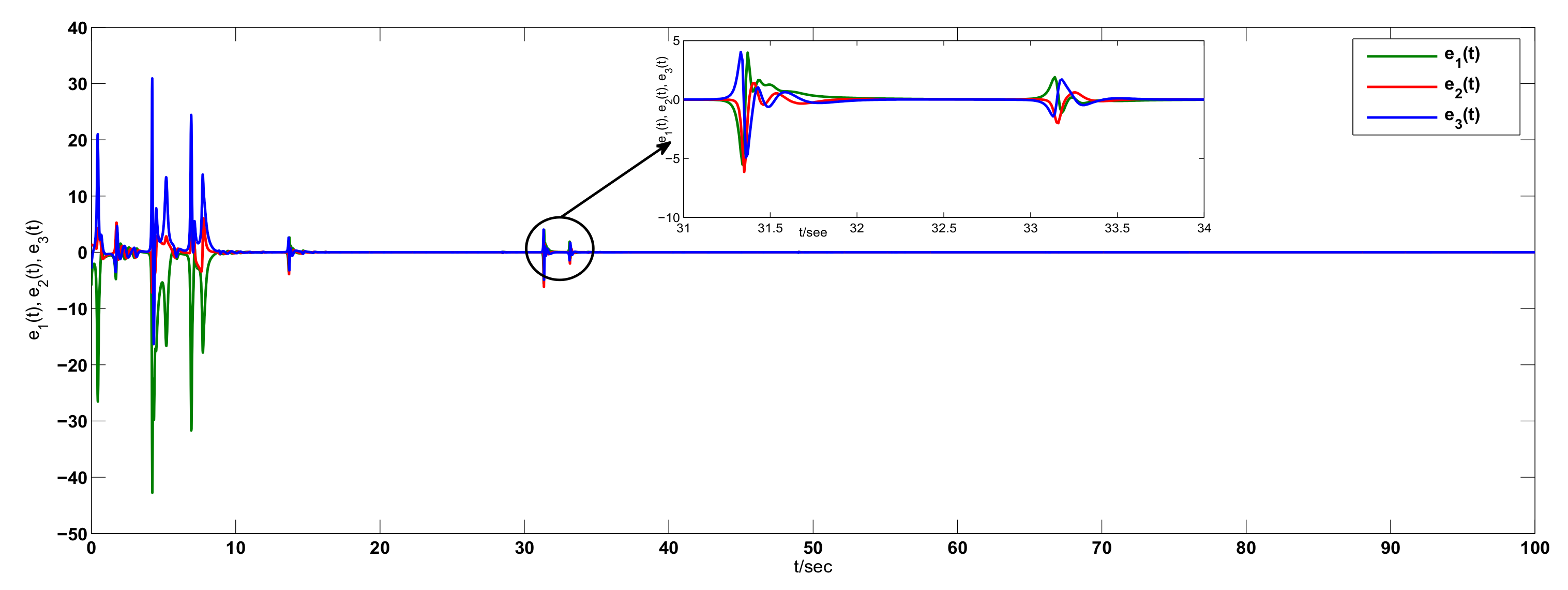
3. Examples
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bagley, R.L.; Calico, R.A. Fractional order state equations for the control of viscoelastically damped structures. J. Guid. Control. Dyn. 1991, 14, 304–311. [Google Scholar] [CrossRef]
- Sun, H.H.; Abdelwahab, A.A.; Onaral, B. Linear approximation of transfer function with a pole of fractional power. IEEE Trans. Autom. Control 1984, 29, 441–444. [Google Scholar] [CrossRef]
- Ichise, M.; Nagayanagi, Y.; Kojima, T. An analog simulation of non-integer order transfer functions for analysis of electrode processes. J. Electroanal. Chem. Interfacial Electrochem. 1971, 33, 253–265. [Google Scholar] [CrossRef]
- Heaviside, O. Electromagnetic Theory; Chelsea: New York, NY, USA, 1971. [Google Scholar]
- Laskin, N. Fractional market dynamics. Physica A 2000, 287, 482–492. [Google Scholar] [CrossRef]
- Kusnezov, D.; Bulgac, A.; Dang, G.D. Quantum Lévy Processes and Fractional Kinetics. Phys. Rev. Lett. 1999, 82, 1136–1139. [Google Scholar] [CrossRef] [Green Version]
- Milanovic, V.; Zaghloul, M.E. Synchronization of chaotic neural networks and applications to communications. Int. J. Bifurc. Chaos 1996, 6, 2571–2585. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–825. [Google Scholar] [CrossRef] [PubMed]
- Odibat, Z.M.; Corson, N.; Aziz-Alaoui, M.A.; Bertelle, C. Synchronization of chaotic fractional-order systems via linear control. Int. J. Bifurc. Chaos 2010, 20, 81–97. [Google Scholar] [CrossRef] [Green Version]
- Zhou, P.; Ding, R. Chaotic synchronization between different fractional-order chaotic systems. J. Frankl. Inst. 2011, 348, 2839–2848. [Google Scholar] [CrossRef]
- Agrawal, S.K.; Srivastava, M.; Das, S. Synchronization of fractional order chaotic systems using active control method. Chaos Solitons Fractals 2012, 45, 737–752. [Google Scholar] [CrossRef]
- Li, C.; Su, K.; Tong, Y.; Li, H. Robust synchronization for a class of fractional-order chaotic and hyperchaotic systems. Optik 2013, 124, 3242–3245. [Google Scholar] [CrossRef]
- Hu, T.; Zhang, X.; Zhong, S. Global asymptotic synchronization of nonidentical fractional-order neural networks. Neurocomputing 2018, 313, 39–46. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M.; Yan, X. Adaptive sliding mode synchronization for a class of fractional-order chaotic systems with disturbance. Nonlinear Dyn. 2016, 83, 1855–1866. [Google Scholar] [CrossRef]
- Wang, Q.; Qi, D.L. Synchronization for fractional order chaotic systems with uncertain parameters. Int. J. Control. Autom. Syst. 2016, 14, 211–216. [Google Scholar] [CrossRef]
- Mathiyalagan, K.; Park, J.H.; Sakthivel, R. Exponential synchronization for fractional-order chaotic systems with mixed uncertainties. Complexity 2015, 21, 114–125. [Google Scholar] [CrossRef]
- Li, C.; Zhang, J. Synchronization of a fractional-order chaotic system using finite-time input-to-state stability. Int. J. Syst. Sci. 2016, 47, 2440–2448. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Li, K.; Peng, J. Laplace transform and fractional differential equations. Appl. Math. Lett. 2011, 24, 2019–2023. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Goreno, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin, Germany, 2014. [Google Scholar]
- Peng, S.; Wang, J. Existence and Ulam-Hyers stability of ODEs involving two Caputo fractional derivatives. Electron. J. Qual. Theory Differ. Equ. 2015, 52, 1–16. [Google Scholar] [CrossRef]
- Cong, N.D.; Doan, T.S.; Siegmund, S.; Tuan, H.T. On stable manifolds for fractional differential equations in high-dimensional spaces. Nonlinear Dyn. 2016, 86, 1885–1894. [Google Scholar] [CrossRef] [Green Version]
- Pazy, A. Semigroup of Linear Operators and Applications to Partial Differential Equations; Springer: New York, NY, USA, 1983. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fečkan, M.; Sathiyaraj, T.; Wang, J. Synchronization of Butterfly Fractional Order Chaotic System. Mathematics 2020, 8, 446. https://doi.org/10.3390/math8030446
Fečkan M, Sathiyaraj T, Wang J. Synchronization of Butterfly Fractional Order Chaotic System. Mathematics. 2020; 8(3):446. https://doi.org/10.3390/math8030446
Chicago/Turabian StyleFečkan, Michal, T. Sathiyaraj, and JinRong Wang. 2020. "Synchronization of Butterfly Fractional Order Chaotic System" Mathematics 8, no. 3: 446. https://doi.org/10.3390/math8030446
APA StyleFečkan, M., Sathiyaraj, T., & Wang, J. (2020). Synchronization of Butterfly Fractional Order Chaotic System. Mathematics, 8(3), 446. https://doi.org/10.3390/math8030446






