A Study of the Eigenfunctions of the Singular Sturm–Liouville Problem Using the Analytical Method and the Decomposition Technique

Abstract

The history of boundary value problems for differential equations starts with the well-known studies of D. Bernoulli, J. D’Alambert, C. Sturm, J. Liouville, L. Euler, G. Birkhoff and V. Steklov. The greatest success in spectral theory of ordinary differential operators has been achieved for Sturm–Liouville problems. The Sturm–Liouville-type boundary value problem appears in solving the many important problems of natural science. For the classical Sturm–Liouville problem, it is guaranteed that all the eigenvalues are real and simple, and the corresponding eigenfunctions forms a basis in a suitable Hilbert space. This work is aimed at computing the eigenvalues and eigenfunctions of singular two-interval Sturm–Liouville problems. The problem studied here differs from the standard Sturm–Liouville problems in that it contains additional transmission conditions at the interior point of interaction, and the eigenparameter $\lambda$ appears not only in the differential equation, but also in the boundary conditions. Such boundary value transmission problems (BVTPs) are much more complicated to solve than one-interval boundary value problems ones. The major difficulty lies in the existence of eigenvalues and the corresponding eigenfunctions. It is not clear how to apply the known analytical and approximate techniques to such BVTPs. Based on the Adomian decomposition method (ADM), we present a new analytical and numerical algorithm for computing the eigenvalues and corresponding eigenfunctions. Some graphical illustrations of the eigenvalues and eigenfunctions are also presented. The obtained results demonstrate that the ADM can be adapted to find the eigenvalues and eigenfunctions not only of the classical one-interval boundary value problems (BVPs) but also of a singular two-interval BVTPs.

1. Introduction

In this study we are interested in the eigenvalues and eigenfunctions of two-interval Sturm–Liouville problems that arise when modeling many real problems appearing in physics, engineering and other branches of natural science. For example, they arise when considering Kirchoff’s law in electrical circuits, the balance of tension in elastic, the steady-state temperature in a heated rod, the vibrations of a string or the energy eigenfunctions of a quantum mechanical oscillator, in which eigenvalues correspond to the resonant frequencies or energy levels (See, [1,2]).

It is evident that not all equations of Sturm–Liouville type have exact solutions. Some special cases are solved by different numerical methods, such as the Runge–Kutta method, the finite difference method, the shooting method, the weighed residual method, Picard’s successive approximation method, the variational iteration method and the differential transformation method.

Chen and Ho [3] used the differential transformation method (DTM) to calculate the eigenvalues of the linear Sturm–Liouville problem

$$\frac{d}{dx}\left[p\left(x\right)\frac{dy\left(x\right)}{dx}\right]+[q\left(x\right)+\lambda w\left(x\right)]y\left(x\right)=0$$

$$y\left(0\right)+\alpha y^{\prime }\left(0\right)=0,y\left(1\right)+\beta y^{\prime }\left(1\right)=0$$

and the results were compared with those calculated by other analytical methods. Golmankhaneh et al. [4] used the homotop perturbation method (HPM), the variational iteration method (VIM) and the new iteration method (NIM) for finding approximation solutions of nonlinear Sturm–Liouville equation

$$-u^{″}+u^k\left(x\right)=\lambda u\left(x\right),$$

with the initial conditions

$$u_0=u\left(0\right)=A,u_0^{\prime }=u^{\prime }\left(0\right)=B$$

where $k\ge 2.$ By comparing the obtained results, they deduced that HPM gives better approximation solutions than VIM and NIM.

In the 1980s, George Adomian [5,6,7] developed a new decomposition method, called the Adomian decomposition method (ADM), for solving linear or nonlinear equations; ordinary or partial differential equations; various types of integral, algebraic and delay equations; and stochastic systems. An advantage of this method is that it can provide analytical approximations to a rather wide class of problems requiring no linearization, perturbation, closure approximations or discretization methods, which can require massive numerical computation.

S. Somali and G. Gokmen [8] considered ADM for computing eigenvalues and eigenfunctions of nonlinear Sturm–Liouville equation

$$-y^{″}\left(t\right)+y^p\left(t\right)=\lambda y\left(t\right)$$

together with simple boundary conditions

$$y\left(0\right)=y\left(1\right)=0.$$

By using the shooting technique and the direct integrating method, Malathi et al. [9] computed eigenvalues of periodic Sturm–Liouville problems.

Attili et al. [10] used ADM for computing eigenvalues of a one-interval boundary value problem for the Sturm–Liouville equation. Al-Hayani [11] considered a modified ADM to solve linear and nonlinear boundary-value problems with Neumann boundary conditions. Momani and Noor [12] used the DTM, ADM and HPM for solving a special class of boundary value problems for a fourth-order ordinary differential equation.

Recently a great deal of interest has been focused on the application of different types of approximation methods for the solutions of linear and nonlinear problems (See, [13,14,15,16,17]).

Bibi and Merahi [13] derived approximate solutions of linear stochastic differential equations. They showed the efficiency of ADM in the field of sthochastic differential equations. Erturk and Momani [18] presented a numerical comparison between DTM and ADM applied to the solution of fourth-order boundary value problems.

We will be interested in the computation of the eigenvalues and eigenfunctions of a new type of SLPs (Sturm–Liouville problems), the main feature of which is the nature of the boundary conditions imposed. Namely, the boundary conditions contain not only end points of the considered interval, but also an interior point of discontinuity at which given supplementary conditions are called transmission conditions. Moreover, the spectral parameter appears not only in the differential equation, but also in the boundary conditions. Such two-interval boundary value problems arise in various type problems of natural science, such as in heat and mass transfer problems; diffraction problems; vibrating string problems when the string is loaded additionally with point masses; and thermal conduction problems for a thin laminated plate.

We want emphasize that two-interval boundary-value problems with additional transmission conditions are much more complicated to solve than one-interval boundary value problems. The existence and uniqueness theorems for the solution of a two-interval boundary value transmission problem (BVTP) can be found in many articles by the first author and his collaborators (see, for example, [19,20,21,22,23,24].)

The organization of the rest of this study will be as follows. In Section 2 we explain the application of the Adomian decomposition method to computing the solution of the linear and nonlinear Sturm–Liouville equations. In Section 3 we present a new analytical method for the computing of exact eigenelements. In Section 4 we adapt the ADM to obtain approximate values of eigenvalues and eigenfunctions.

The graphical illustration of the obtained eigenfunctions is given in Section 3 and Section 4. The results are illustrated graphically in the Section 3 and Section 4. Concluding remarks are presented in Section 5.

Remark 1.

Our motivation for this work comes from the problem regarding the Earth’s seismic behavior, the stability and velocity of large-scale waves in the atmosphere, etc. If the Earth is assumed to be spherically symmetric and non-rotating, and to consist of an isotropic, perfect elastic medium, then the mathematical model can be written in singular Sturm–Liouville form with interior discontinity, where discontinuities in the elastic parameters are transformed to discontinuities in the eigenfunctions. The transmission conditions for the solutions come from continuity of displacement and stress at an interface. Since the Earth has several discontinuities in the upper mantle, we are motivated to consider singular Sturm–Liouville problems with additional transmission conditions at one interior point of discontinuity.

2. Outline of the Decomposition Method for Linear and Nonlinear Sturm–Liouville Problems

Let us recall basic principles of the Adomian decomposition method (see [5,6,7]) for solving linear or nonlinear differential equations of the form $Fy=g,$ where the operator F is the differential operator involving both linear and nonlinear terms. The linear term is decomposed into $L+R$, where L is highest order derivation and R is the reminder of the linear term. Thus, the equation $Fy=g$ may be rewritten in the following form.

$$Ly+Ry+Ny=g\left(x\right),$$

(1)

Here $Ny$ represents the nonlinear term. Since the highest order derivation operator L is easily invertable, from (1) we have

$$y=-\left(L^{-1}R\right)y-\left(L^{-1}N\right)y+L^{-1}g.$$

(2)

A solution we can be expanded as following series

$$y=\sum _{n=0}^{\infty }{y}_n.$$

(3)

and the nonlinear term $Ny$ can be decomposed by the infinite series of polynomials $A_n,n=0,1,2\dots$, so-called Adomian polynomials, as $Ny={\sum }_{n=0}^{\infty }{A}_n,$ where

$$A_0\left(y_0\right)=N\left(y_0\right),$$

$$A_1(y_0,y_1)=y_1{N}^{\prime }\left(y_0\right),$$

$$A_2(y_0,y_1,y_2)=y_2{N}^{\prime }\left(y_0\right)+\frac{y_1^2}{2!}{N}^{″}\left(y_0\right),$$

$$A_3(y_0,y_1,y_2,y_3)=y_3{N}^{\prime }\left(y_0\right)+y_1{y}_2{N}^{″}\left(y_0\right)+\frac{y_1^3}{3!}{N}^{″}\left(y_0\right)$$

and so on. Then with a reasonable $u_0$ which may be identified with respect to the representation of the inverse operator $L^{-1}$, we have the following recurrence formula.

$$\begin{array}{ccc}\hfill y_1& =& -\left(L^{-1}R\right)y_0-L^{-1}{A}_0\hfill \\ \hfill y_{n+1}& =& -\left(L^{-1}R\right)y_n-L^{-1}{A}_n,n=1,2,3,\dots \hfill \end{array}$$

Now consider the Sturm–Liouville equation

$$\left(\frac{d}{dx}\left(p\left(x\right)\frac{dy}{dx}\right)\right)+(q\left(x\right)-\lambda )y+f\left(y\right)=g\left(x\right)$$

(4)

where the function $p\left(x\right)$ is continuously differentiable and nonzero for all x, and $q\left(x\right)$ is a continuous function. Define the Adomian’s operators L, R and N as

$$Ly:=\frac{d}{dx}\left(p\left(x\right)\frac{dy}{dx}\right),Ry:=(q\left(x\right)-\lambda )y,Ny:=f\left(y\right)$$

The Equation (4) reduces to an operator form

$$Ly+Ry+Ny=g\left(x\right).$$

(5)

By integrating twice, the equation

$$Ly:=\frac{d}{dx}\left(p\left(x\right)\frac{dy}{dx}\right)=h\left(x\right),$$

we see that the inverse operator $L^{-1}$ has the form

$$L^{-1}\left(h\right)={\int }_0^x\frac{dx}{p\left(x\right)}\left({\int }_0^{x}h\left(s\right)ds+p\left(0\right)h^{\prime }\left(0\right)\right)+h\left(0\right)$$

Operating $L^{-1}$ on both sides of the operator, Equation (5) yields

$$\begin{array}{ccc}{L}^{-1}L\left(y\left(x\right)\right)\hfill & =& {\int }_0^x\frac{1}{p\left(x\right)}{\left({\int }_0^x(p\left(x\right)y^{\prime }\left(x\right)dx\right)}^{\prime }dx\hfill \\ & =& {\int }_0^x\frac{1}{p\left(x\right)}(p\left(x\right)y^{\prime }\left(x\right)-p\left(0\right)y^{\prime }\left(0\right))dx\hfill \\ & =& y\left(x\right)-(y\left(0\right)+p\left(0\right)y^{\prime }\left(0\right){\int }_0^x\frac{dx}{p\left(x\right)})\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}\hfill y\left(x\right)& =& \left(L^{-1}g\right)\left(x\right)-p\left(0\right)\left(\frac{d}{dx}(q\left(x\right)-\lambda )y\left(x\right)\right){|}_{x=0}{\int }_0^x\frac{ds}{p\left(s\right)}-(q\left(0\right)-\lambda )y\left(0\right)\hfill \\ & -& L^{-1}\left(Ry\right)-L^{-1}\left(Ny\right)\hfill \end{array}$$

(6)

The ADM assumes that the solution y of the Equation (6) can be decomposed into an infinite series

$$y=\sum _{n=0}^{\infty }{y}_n\left(x\right).$$

(7)

Now, assuming $f\left(y\right)$ is analytic, we can write

$$Ny=\sum _{n=0}^{\infty }{A}_n(y_0,y_1,\dots ,y_n)$$

where the terms $A_n(y_0,y_1,\dots ,y_n)$ are specially defined polynomials (so-called Adomian polynomials), which depend only on the first $n+1$ components and form a rapidly convergent series (see [7]). These polynomials are defined by

$$A_0\left(y_0\right)=f\left(y_0\right),A_1(y_0,y_1)=y_1\left(\frac{d}{dy}\right)f\left(y_0\right),$$

$$A_2(y_0,y_1,y_2)=y_2\left(\frac{d}{dy}\right)f\left(y_0\right)+\frac{y_1^2}{2!}\left(\frac{d^2}{d{y}^2}\right)f\left(y_0\right),$$

$$A_3(y_0,y_1,y_2,y_3)=y_3\left(\frac{d}{dy}\right)f\left(y_0\right)+y_1{y}_2\left(\frac{d^2}{d{y}^2}\right)f\left(y_0\right)+\frac{y_1^3}{3!}\left(\frac{d^3}{d{y}^3}\right)f\left(y_0\right),\dots$$

The solution $y\left(x\right)$ can now be written as

$$\begin{array}{c}\hfill y\left(x\right)=y_0\left(x\right)-\left(L^{-1}R\right)\left(\sum _{n=0}^{\infty }{y}_n\left(x\right)\right)-L^{-1}\left(\sum _{n=0}^{\infty }{A}_n(y_0,y_1,\dots ,y_n)\right).\end{array}$$

Therefore, in accordance with the well-known fixed-point theorem, we can choose successive approximations $y_0\left(x\right),y_1\left(x\right),\dots$ of the solution $y\left(x\right)$ as

$$\begin{array}{c}\hfill y_0\left(x\right)=\left(L^{-1}g\right)\left(x\right)-(q\left(0\right)-\lambda )y\left(0\right)-p\left(0\right)\left(\frac{d}{dx}(q\left(x\right)-\lambda )y\left(x\right)\right){|}_{x=0}{\int }_0^x\frac{1}{p\left(s\right)}ds\end{array}$$

(8)

$$\begin{array}{ccc}\hfill y_1\left(x\right)& =& -\left(L^{-1}R\right)y_0\left(x\right)-\left(L^{-1}{A}_0\left(y_0\right)\right)\left(x\right)\hfill \\ \hfill y_2\left(x\right)& =& -\left(L^{-1}R\right)y_1\left(x\right)-\left(L^{-1}{A}_1(y_0,y_1)\right)\left(x\right)\hfill \\ \hfill y_3\left(x\right)& =& -\left(L^{-1}R\right)y_2\left(x\right)-\left(L^{-1}{A}_2(y_0,y_1,y_2)\right)\left(x\right)\hfill \end{array}$$

(9)

and so on.

The first approximation $y_0\left(x\right)$ can be obtained by using initial and boundary conditions. Thus we have recurrence formulas (8) and (9) for obtaining other components $y_1\left(x\right),y_2\left(x\right),\dots$ of the decomposition (7). Convergence of this decomposition and rapidity of this convergence have been established by Y. Cherrualt [25].

3. A New Analytical Technique for Computing Exact Eigenvalues and Eigenfunctions of the BVTP for Two-Interval SLPs

Let us consider the following two-interval Sturm–Liouville equation.

$$y^{″}(x,\lambda )+\lambda y(x,\lambda )=0,x\in [-1,0)\cup (0,1]$$

(10)

together with eigenparameter dependent boundary conditions, given by

$$\lambda y(-1,\lambda )+y^{\prime }(-1,\lambda )=0,y(1,\lambda )+\lambda y^{\prime }(1,\lambda )=0$$

(11)

and with additional transmission conditions at the point of interaction $x=0$, given by

$$y(-0,\lambda )=y(+0,\lambda ),y^{\prime }(-0,\lambda )=2y^{\prime }(+0,\lambda )$$

(12)

where $\lambda$ is an eigenparameter. Recall that the values of the parameter $\lambda$ for which the BVTP (10)–(12) has a nontrivial solution are called eigenvalues, and nontrivial solutions corresponding to an eigenvalues are called eigenfuncions.

Remark 2.

The considered problem (10)–(12) differs from the classical Sturm–Liouville problems in that it contains not only end-point boundary conditions, but also the additional transmission conditions at the interior point of interaction $x=0$. Moreover the eigenparameter λ appears not only in the differential equation but also in the boundary conditions. The major difficulty lies in the existence of eigenvalues. It is well-known that the classical Sturm–Liouville problems have infinitely many real eigenvalues which can be ordered in a monotonous increasing magnitude ${\lambda }_1<{\lambda }_2<{\lambda }_3<\dots$ such that ${\lambda }_n\to \infty$ as $n\to \infty$. Nevertheless there are Sturm–Liouville problems with transmission conditions that do not have infinitely many eigenvalues. Moreover, the set of eigenvalues of such BVTPs may even be empty. For example, we can show that the simple two-interval Sturm–Liouville BVTP

$$-y^{″}\left(x\right)=\lambda y\left(x\right),x\in [-1,0)\cup (0,1]$$

$$y(-1)=y^{\prime }\left(1\right)=0,y(-0)=y(+0),y^{\prime }(-0)=-y^{\prime }(+0)$$

has only the trivial solution $y=0$ for arbitrary real λ; i.e., the simplest BVTP has no real eigenvalue.

Now, to find the exact eigenvalues and eigenfunctions we shall construct some auxiliary initial value problems on the left side interval $[-1,0)$ and right side interval $(0,1]$ separately. At first we shall consider the following initial value problem, given by

$$y^{″}(x,\lambda )+\lambda y(x,\lambda )=0,x\in [-1,0)$$

$$y(-1,\lambda )=1,y^{\prime }(-1,\lambda )=-\lambda$$

It is easy to show that for each $\lambda$, this initial-value problem has a unique solution

$$y={\varphi }_1(x,\lambda )=cos\left(\sqrt{\lambda }(1+x)\right)-\sqrt{\lambda }sin\left(\sqrt{\lambda }(1+x)\right).$$

Now consider the following initial-value problem on the right side $[0,1)$, given by

$$y^{″}(x,\lambda )+\lambda y(x,\lambda )=0,x\in (0,1]$$

$$y(0,\lambda )=cos\sqrt{\lambda }-\sqrt{\lambda }sin\sqrt{\lambda },y^{\prime }(0,\lambda )=\frac{\sqrt{\lambda }}{2}sin\sqrt{\lambda }+\lambda cos\sqrt{\lambda }$$

This initial-value problem has an exact solution

$$\begin{array}{ccc}\hfill y& =& {\varphi }_2(x,\lambda )\hfill \\ & =& (cos\sqrt{\lambda }-\sqrt{\lambda }sin\sqrt{\lambda })cos\sqrt{\lambda }x+\frac{1}{2}(-sin\sqrt{\lambda }-\sqrt{\lambda }cos\sqrt{\lambda })sin\sqrt{\lambda }x\hfill \end{array}$$

It is easy to verify that the function $y=\varphi (x,\lambda )$ defined by

$$\begin{array}{c}\hfill \varphi (x,\lambda )=\left\{\begin{array}{c}cos\left(\sqrt{\lambda }(1+x)\right)-\sqrt{\lambda }sin\left(\sqrt{\lambda }(1+x)\right),forx\in [-1,0)\hfill \\ (cos\sqrt{\lambda }-\sqrt{\lambda }sin\sqrt{\lambda })cos\sqrt{\lambda }x-\frac{1}{2}\left(sin\sqrt{\lambda }\sqrt{\lambda }cos\sqrt{\lambda }\right)sin\sqrt{\lambda }x,forx\in (0,1]\hfill \end{array}\right.\end{array}$$

(13)

satisfies the differential Equation (10) in the whole of $[-1,0)\cup (0,1]$, the first boundary condition $\lambda y(-1,\lambda )+y^{\prime }(-1,\lambda )=0$ and both transmission conditions (12). Now, substituting (13) in the second boundary condition $y(1,\lambda )+\lambda y^{\prime }(1,\lambda )=0$, we have the following characteristic equation.

$$\begin{array}{c}\hfill w\left(\lambda \right):=(cos\sqrt{\lambda }-\sqrt{\lambda }sin\sqrt{\lambda })cos\sqrt{\lambda }-\frac{1}{2}(sin\sqrt{\lambda }+\sqrt{\lambda }cos\sqrt{\lambda })sin\sqrt{\lambda }\\ \hfill +\lambda (\lambda sin\sqrt{\lambda }-\sqrt{\lambda }cos\sqrt{\lambda })sin\sqrt{\lambda }-\frac{\lambda }{2}(\lambda cos\sqrt{\lambda }+\sqrt{\lambda }sin\sqrt{\lambda })cos\sqrt{\lambda }=0\end{array}$$

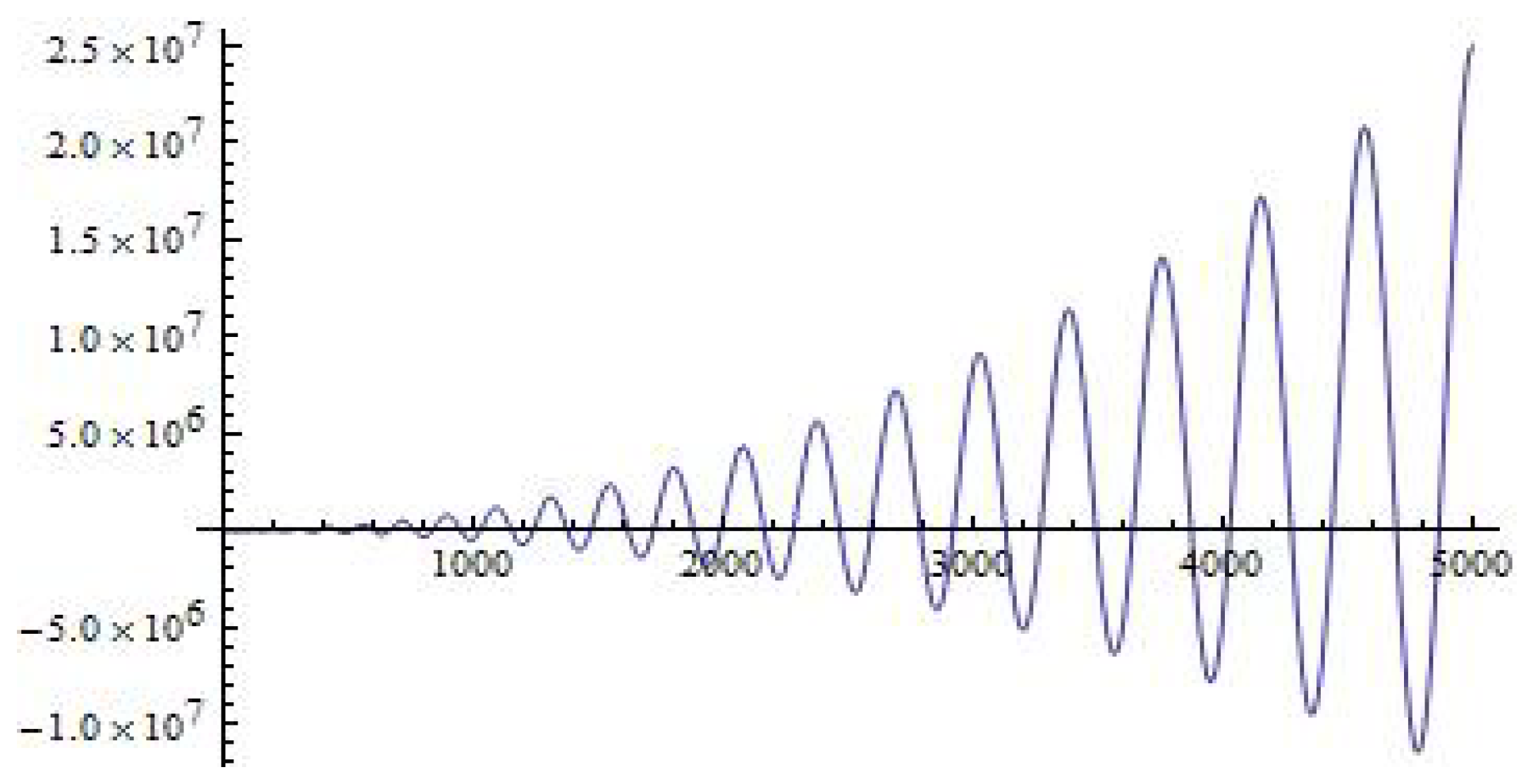
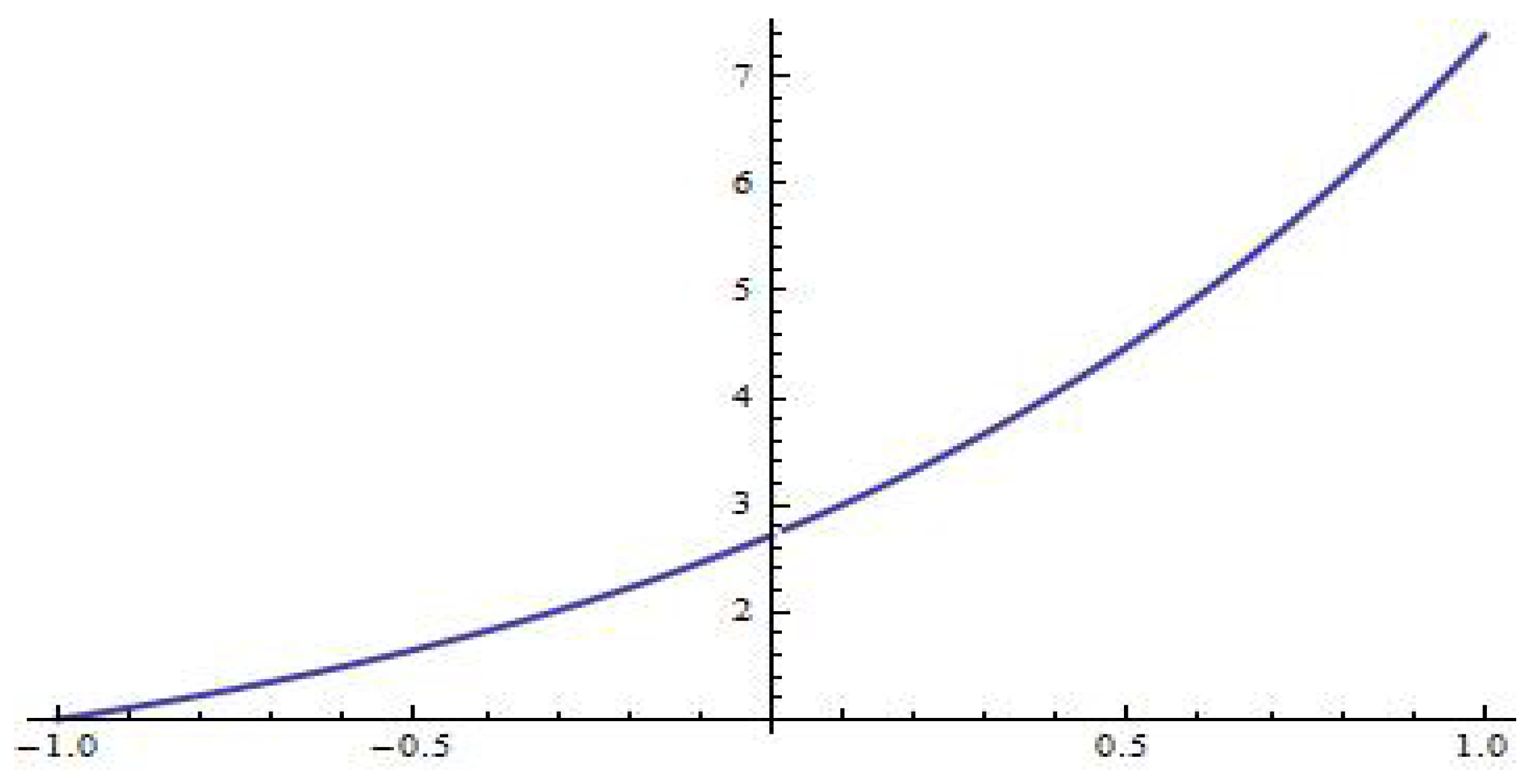
A graph of the characteristic function $w\left(\lambda \right)$ is given below in Figure 1.

We can show that the characteristic function $w\left(\lambda \right)$ has infinitely many real zeros ${\lambda }_1,{\lambda }_2,\dots$ which coincide with the set of eigenvalues of the considered BVTP (10)–(12). Then the functions $y_n=\varphi (x,{\lambda }_n),n=1,2,\dots$ form a sequence of the corresponding eigenfunctions.

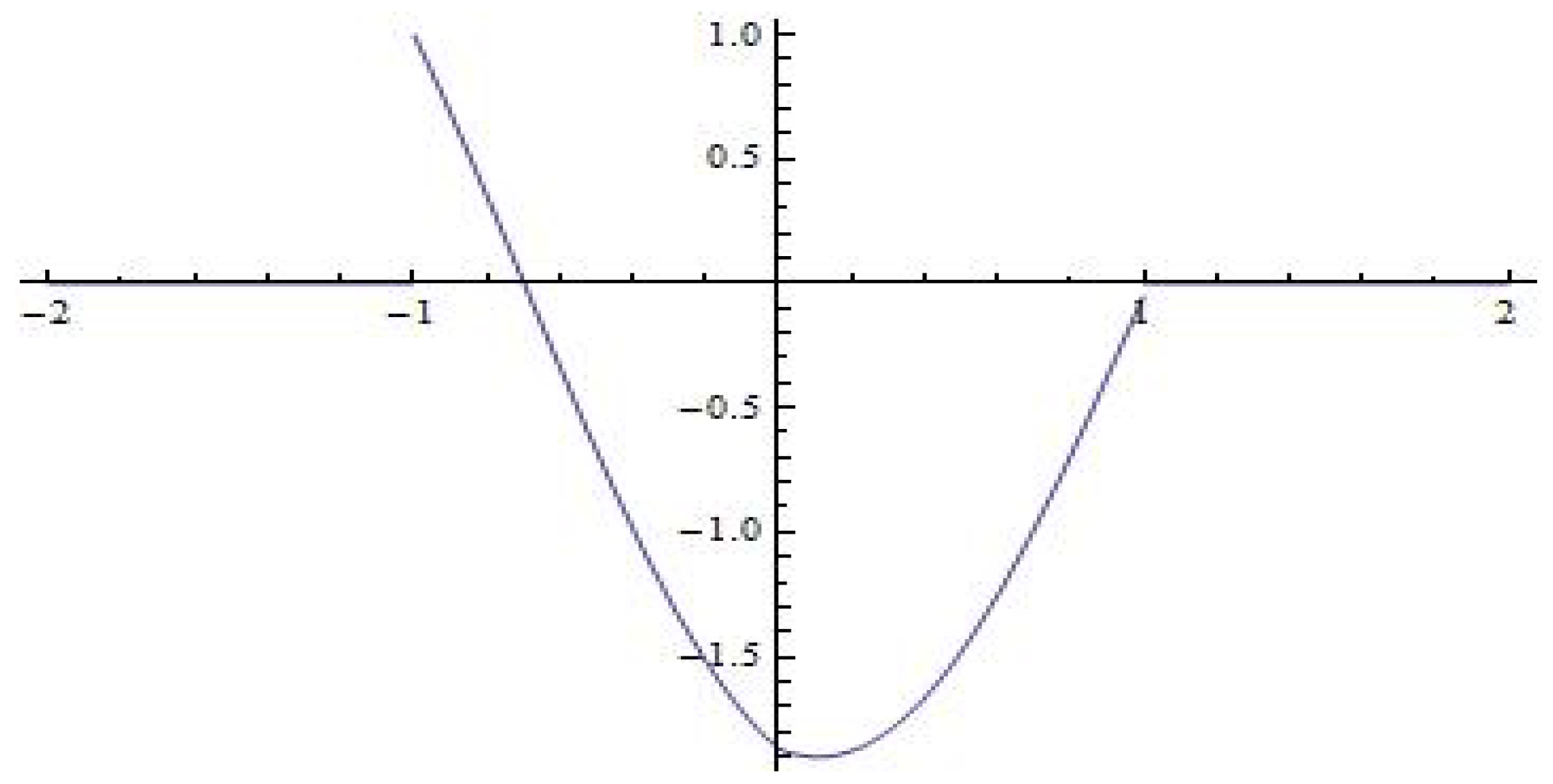
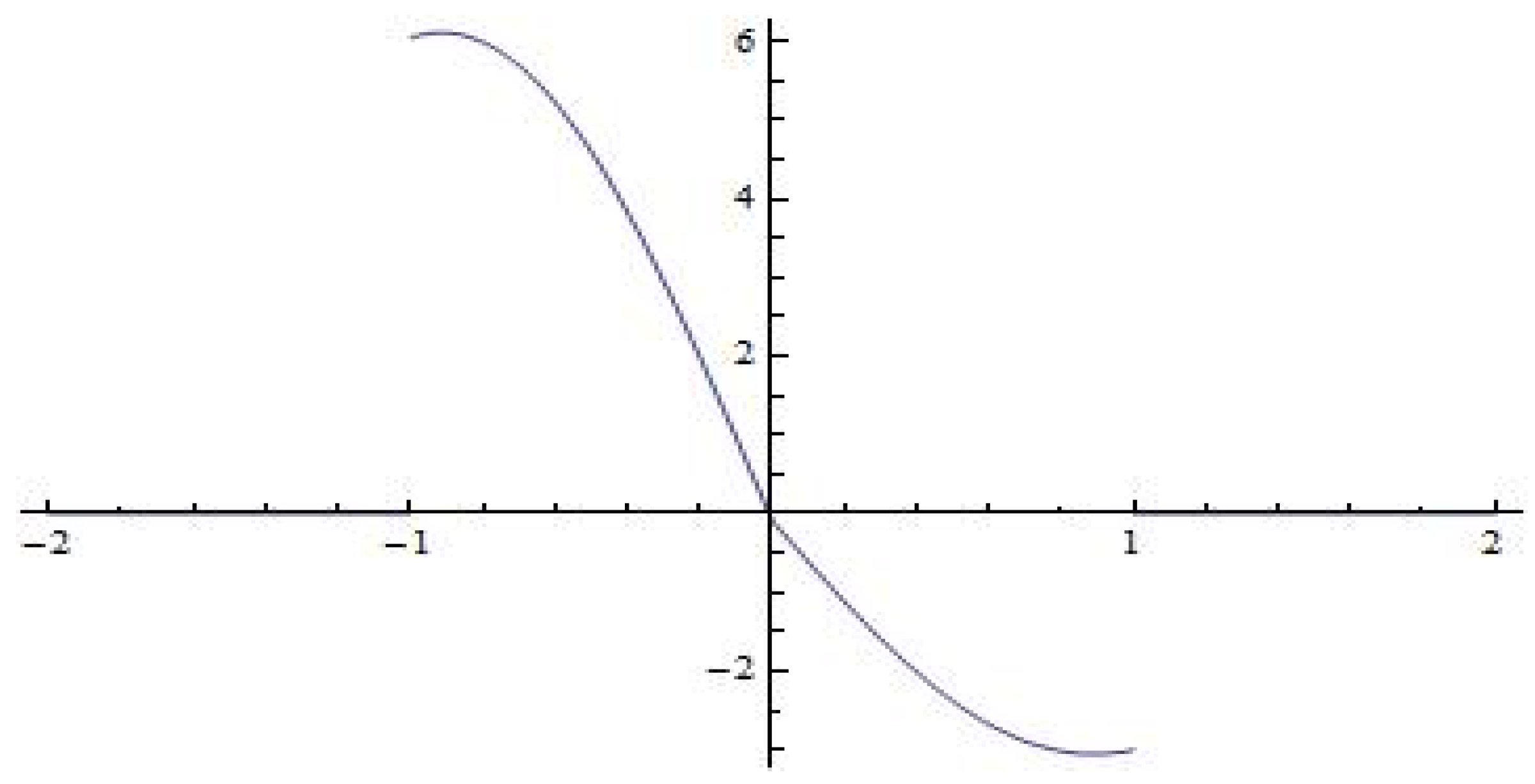
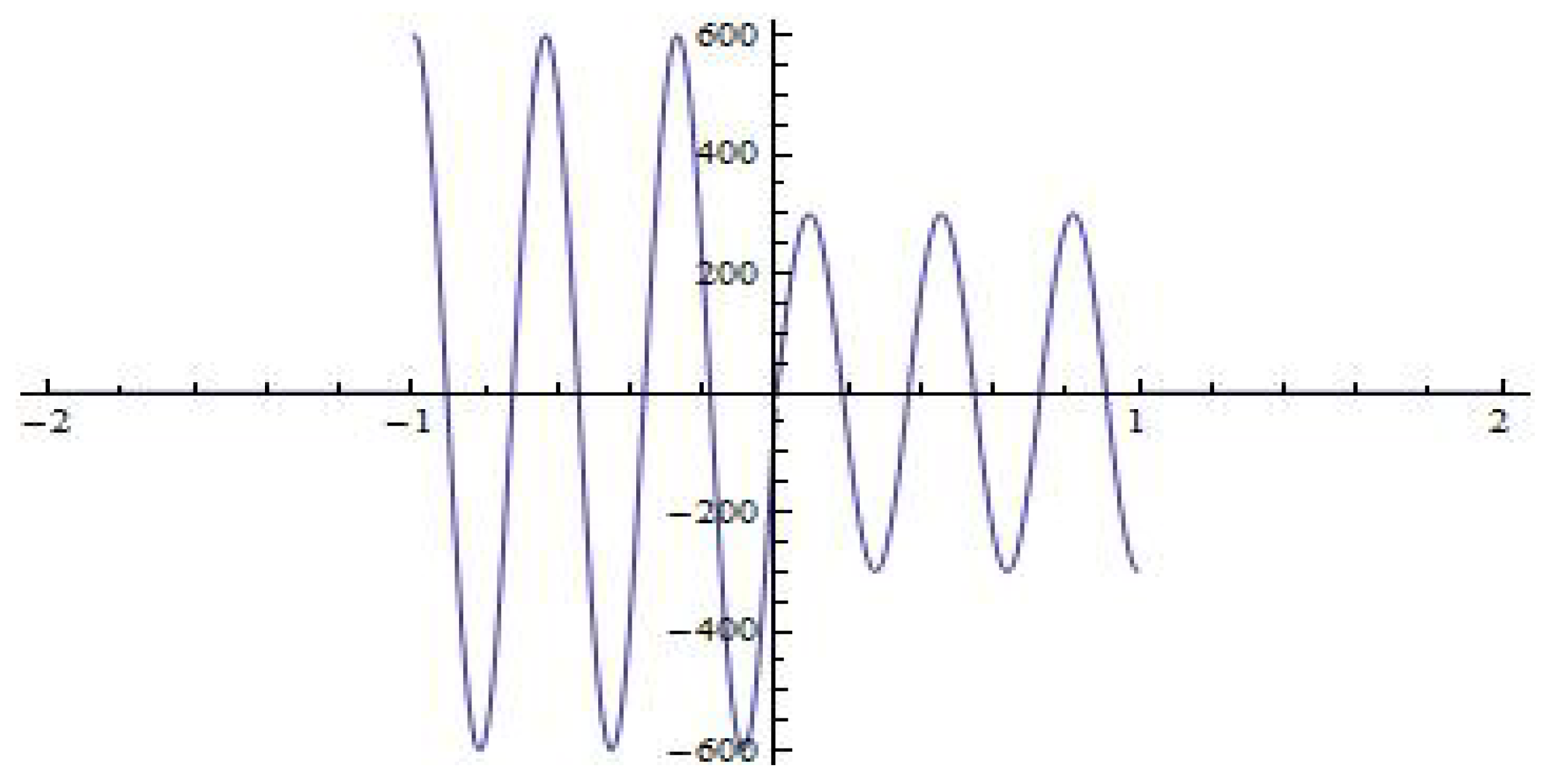
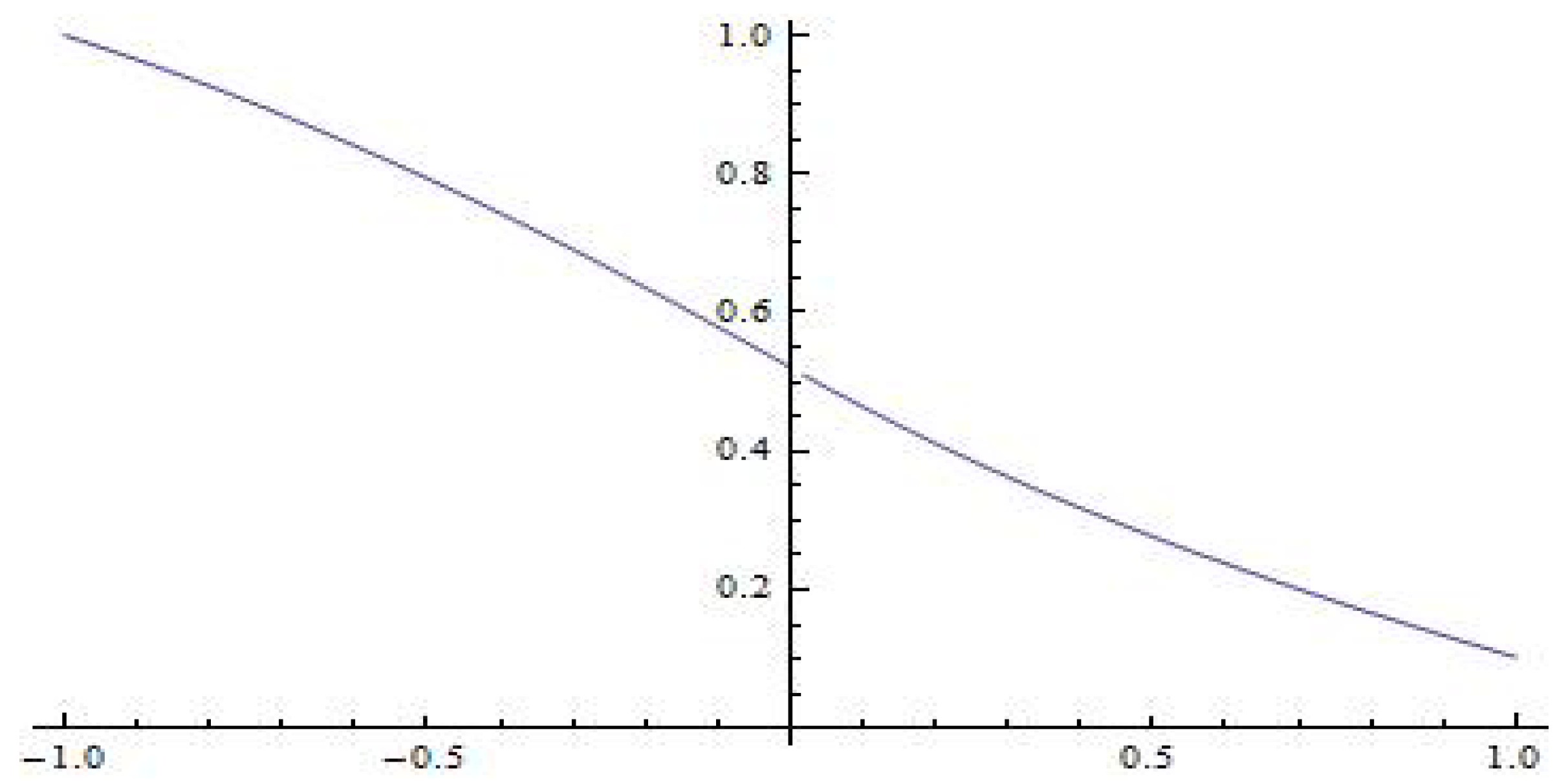
Below we illustrate the graphical simulations of the first fundamental solution $y=\varphi (x,\lambda )$ for some values of the eigenparameter $\lambda$. Namely, the graphs of the first fundamental solutions $\varphi (x,\lambda )$ for $\lambda =3,$ $\lambda =30$ and $\lambda =300$ are shown in Figure 2, Figure 3 and Figure 4, respectively.

Now by applying the same analytical technique, we can show that the function $y=\chi (x,\lambda )$ defined by

$$\begin{array}{c}\hfill \chi (x,\lambda )=\left\{\begin{array}{cc}\left(\frac{-\lambda \sqrt{\lambda }cos\sqrt{\lambda }-sin\sqrt{\lambda }}{\sqrt{\lambda }}\right)cos\sqrt{\lambda }x+\frac{2}{\sqrt{\lambda }}(cos\sqrt{\lambda }-\lambda \sqrt{\lambda }sin\sqrt{\lambda })sin\sqrt{\lambda }x,\hfill & x\in [-1,0)\hfill \\ (-\lambda )cos\left(\sqrt{\lambda }(x-1)\right)-\frac{1}{\sqrt{\lambda }}sin\left(\sqrt{\lambda }(1-x)\right),\hfill & x\in (0,1]\hfill \end{array}\right.\end{array}$$

satisfies the differential equation (10), the second boundary condition $\chi (1,\lambda )+\lambda {\chi }^{\prime }(1,\lambda )=0$ and the both transmission conditions

$$\begin{array}{c}\hfill \chi (-0,\lambda )=\chi (+0,\lambda ),{\chi }^{\prime }(-0,\lambda )=2{\chi }^{\prime }(+0,\lambda ).\end{array}$$

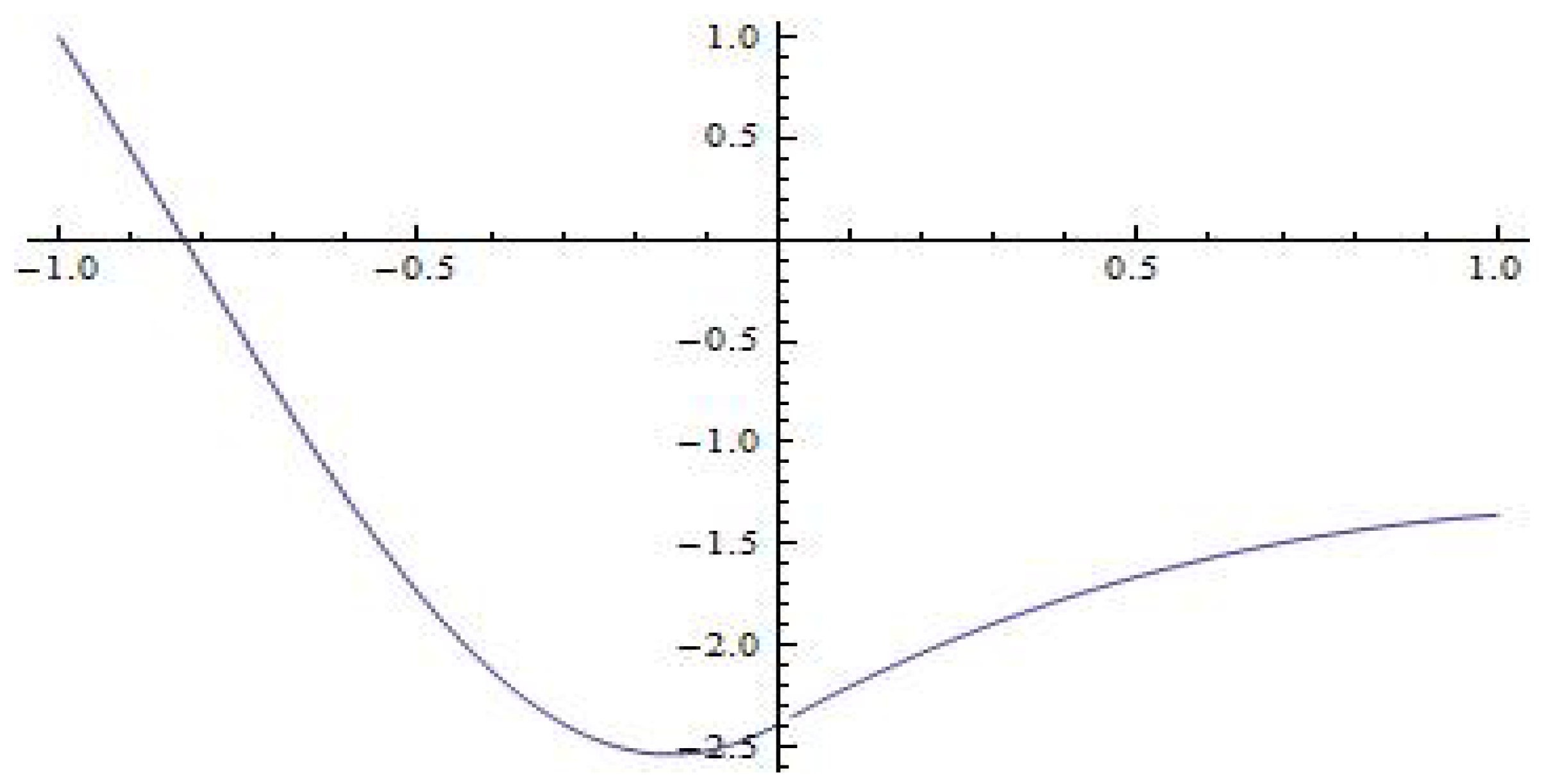
Below we illustrate the graphical simulation of the second fundamental solution $y=\chi (x,\lambda )$ for some values of eigenparameter $\lambda$. Namely, the graphs of the second fundamental solution $\chi (x,\lambda )$ for $\lambda =3$, $\lambda =30$ and $\lambda =300$ are shown in Figure 5, Figure 6 and Figure 7, respectively.

4. A New Iterative Technique Based on the Decomposition Method

In order to solve the BVTP (10)–(12) by means of the decomposition method, we shall consider some auxiliary initial-value problems as follows:

First, consider the following left-side initial-value problem, given by

$$y_l^{″}(x,\lambda )+\lambda y_l(x,\lambda )=0,x\in [-1,0]$$

(14)

$$y_l(-1,\lambda )=1,y_l^{\prime }(-1,\lambda )=-\lambda .$$

(15)

By using the decomposition method which is described in Section 2, we can calculate the successive approximations of the left solution $y_l\left(x\right)$; that is, we can find the decomposition $y_l={\sum }_{n=0}^{\infty }{\left(y_l\right)}_n$ of the solution $y_l$ of the initial value problem (14)–(15).

Namely, by applying the recurrence formulas (8) and (9), we have

$${\left(y_l\right)}_0(x,\lambda )=1-\lambda x-\lambda$$

$${\left(y_l\right)}_1(x,\lambda )=-\lambda \left[\left(\frac{1}{2}-\frac{\lambda }{6}\right)+\left(1-\frac{\lambda }{2}\right)x+\left(\frac{1}{2}-\frac{\lambda }{2}\right)x^2-\frac{\lambda }{6}{x}^3\right]$$

$${\left(y_l\right)}_2(x,\lambda )={\lambda }^2\frac{-1}{120}{(1+x)}^4(\lambda -5+x\lambda )$$

$${\left(y_l\right)}_3(x,\lambda )={\lambda }^3\frac{1}{5040}{(1+x)}^6(\lambda -7+x\lambda )$$

$$......................$$

Thus, the left-side solution $y_l(x,\lambda )$ is readily obtained in a series form by

$$\begin{array}{ccc}\hfill y_l(x,\lambda )& =& 1-\lambda x-\lambda +(-\lambda )\left(\frac{1}{2}+x+\frac{x^2}{2}-\frac{\lambda }{6}-\frac{\lambda }{2}x-\frac{1}{2}\lambda x^2-\frac{1}{6}\lambda x^3\right)\hfill \\ \hfill & -& \frac{1}{120}{\lambda }^2{(1+x)}^4(\lambda -5+\lambda x)+\frac{1}{5040}{\lambda }^3{(1+x)}^6(\lambda -7+\lambda x)\hfill \\ \hfill & +& .....\hfill \end{array}$$

(16)

Obviously it is possible to calculate more components in this decomposition series to improve the approximation. We next consider the following right-side initial-value problem, given by

$$y_r^{″}(x,\lambda )+\lambda y_r(x,\lambda )=0,$$

(17)

$$\begin{array}{c}\hfill y_r(0,\lambda )=1-\lambda -(\frac{1}{2}-\frac{\lambda }{6})\lambda +\frac{1}{120}(5-\lambda ){\lambda }^2-\frac{1}{5040}(7-\lambda ){\lambda }^3\end{array}$$

(18)

$$\begin{array}{c}\hfill y_r^{\prime }(0,\lambda )=2(-\lambda -(1-\frac{\lambda }{2})\lambda -\frac{1}{30}(-5+\lambda ){\lambda }^2-\frac{{\lambda }^3}{120}+\frac{1}{840}(-7+\lambda ){\lambda }^3+\frac{{\lambda }^4}{5040})\end{array}$$

Similarly to the calculation of the left-side solution $y_l\left(x\right)$, we can calculate the following components of the decomposition $y_r={\sum }_{n=0}^{\infty }{\left(y_r\right)}_n$ of the right-side solution $y_r$ of the problem (17)–(18) given by

$$\begin{array}{ccc}\hfill {\left(y_r\right)}_0(x,\lambda )& =& y_r(0,\lambda )+x{y}_r^{\prime }(0,\lambda )\hfill \\ & =& 1-\lambda -(\frac{1}{2}-\frac{\lambda }{6})\lambda +\frac{1}{120}(5-\lambda ){\lambda }^2-\frac{1}{5040}(7-\lambda ){\lambda }^3\hfill \\ & +& x(-\lambda -(1-\frac{\lambda }{2})\lambda -\frac{1}{30}(-5+\lambda ){\lambda }^2-\frac{{\lambda }^3}{120}+\frac{1}{840}(-7+\lambda ){\lambda }^3+\frac{{\lambda }^4}{5040})\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\left(y_r\right)}_1(x,\lambda )& =& (-\lambda )\left[\frac{x^2}{2}-\frac{3}{4}{x}^2\lambda -\frac{1}{3}{x}^3\lambda +\frac{5}{48}{x}^2{\lambda }^2+\frac{1}{9}{x}^3{\lambda }^2-\frac{7}{1440}{x}^2{\lambda }^3\right]\hfill \\ & +& (-\lambda )\left[\frac{-1}{120}{x}^3{\lambda }^3+\frac{1}{10080}{x}^2{\lambda }^4+\frac{1}{4320}{x}^3{\lambda }^4\right]\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\left(y_r\right)}_2(x,\lambda )& =& {\lambda }^2\frac{1}{604800}(x^4(25200+25\lambda (-7560+\lambda (1050+(-49+\lambda )\lambda )))\hfill \\ & +& {\lambda }^2\frac{1}{604800}\left(7x\lambda (-1440+\lambda (480+(-36+\lambda )\lambda ))\right)\hfill \end{array}$$

$${\left(y_r\right)}_3(x,\lambda )=(-{\lambda }^3)\frac{t^6(5040+\lambda (-7560+\lambda (1050+(-49+\lambda )\lambda )+x(-1440+\lambda (480+(-36+\lambda )\lambda ))))}{3628800}$$

$$......................$$

Consequently, the right-side solution $y_r(x,\lambda )$ is obtained in a series form by

$$\begin{array}{ccc}\hfill y_r(x,\lambda )& =& 1-\lambda -(\frac{1}{2}-\frac{\lambda }{6})\lambda +\frac{1}{120}(5-\lambda ){\lambda }^2-\frac{1}{5040}(7-\lambda ){\lambda }^3\hfill \\ \hfill & +& x(-\lambda -(1-\frac{\lambda }{2})\lambda -\frac{1}{30}(-5+\lambda ){\lambda }^2-\frac{{\lambda }^3}{120}+\frac{1}{840}(-7+\lambda ){\lambda }^3+\frac{{\lambda }^4}{5040})\hfill \\ \hfill & +& (-\lambda )\left[\frac{x^2}{2}-\frac{3}{4}{x}^2\lambda -\frac{1}{3}{x}^3\lambda +\frac{5}{48}{x}^2{\lambda }^2+\frac{1}{9}{x}^3{\lambda }^2-\frac{7}{1440}{x}^2{\lambda }^3\right]\hfill \\ \hfill & +& (-\lambda )\left[\frac{-1}{120}{x}^3{\lambda }^3+\frac{1}{10080}{x}^2{\lambda }^4+\frac{1}{4320}{x}^3{\lambda }^4\right]\hfill \\ \hfill & +& {\lambda }^2\frac{1}{604800}(x^4(25200+25\lambda (-7560+\lambda (1050+(-49+\lambda )\lambda )))\hfill \\ \hfill & +& {\lambda }^2\frac{1}{604800}\left(7x\lambda (-1440+\lambda (480+(-36+\lambda )\lambda ))\right)\hfill \\ \hfill & -& {\lambda }^3\frac{t^6(5040+\lambda (-7560+\lambda (1050+(-49+\lambda )\lambda )+x(-1440+\lambda (480+(-36+\lambda )\lambda ))))}{3628800}\hfill \\ \hfill & +& \dots \hfill \end{array}$$

(19)

Consequently, the approximate solution is given by

$$\begin{array}{c}\hfill y(x,\lambda )=\left\{\begin{array}{cc}{y}_l(x,\lambda ),\hfill & x\in [-1,0)\hfill \\ y_r(x,\lambda ),\hfill & x\in (0,1]\hfill \end{array}\right.\end{array}$$

where the left and right side solutions $y_l(x,\lambda )$ and $y_r(x,\lambda )$ are given by (16) and (19) respectively. Substituting (19) in the formula

$$\tilde{w}\left(\lambda \right)=y_r(1,\lambda )+\lambda y_r^{\prime }(1,\lambda )$$

we have that the characteristic function $\tilde{w}\left(\lambda \right)$ has the following representation

$$\begin{array}{ccc}\hfill \tilde{w}\left(\lambda \right)& =& \frac{3}{2}-\frac{43\lambda }{12}-(1-\frac{\lambda }{2})\lambda +\frac{55{\lambda }^2}{144}-\frac{1}{24}(-5+\lambda ){\lambda }^2-\frac{31{\lambda }^3}{1440}+\frac{1}{720}(-7+\lambda ){\lambda }^3+\frac{{\lambda }^4}{1890}\hfill \\ & +& \frac{25200+5\lambda (-7560+\lambda (1050+(-49+\lambda )\lambda \left)\right)+7\lambda (-1440+\lambda (480+(-36+\lambda )\lambda \left)\right)}{604800}\hfill \\ & +& \frac{5040+\lambda (-9000+\lambda (1050+(-49+\lambda )\lambda )+\lambda (480+(-36+\lambda )\lambda \left)\right)}{3628800}\hfill \\ & +& \lambda (1-\frac{7\lambda }{2}-(1-\frac{\lambda }{2})\lambda +\frac{13{\lambda }^2}{24}-\frac{1}{30}(-5+\lambda ){\lambda }^2-\frac{31{\lambda }^3}{720}+\frac{1}{840}(-7+\lambda ){\lambda }^3+\frac{11{\lambda }^4}{10080})\hfill \\ & +& \lambda \frac{43\lambda (-1440+\lambda (480+(-36+\lambda )\lambda \left)\right)}{3628800}\hfill \\ & +& \lambda \frac{25200+5\lambda (-7560+\lambda (1050+(-49+\lambda )\lambda \left)\right)+7\lambda (-1440+\lambda (480+(-36+\lambda )\lambda \left)\right)}{151200}\hfill \\ & +& \lambda \frac{5040+\lambda (-9000+\lambda (1050+(-49+\lambda )\lambda )+\lambda (480+(-36+\lambda )\lambda \left)\right)}{604800}\hfill \end{array}$$

Since the zeros of $\tilde{w}\left(\lambda \right)$ correspond to the approximate eigenvalues, solving the equation $\tilde{w}\left(\lambda \right)=0$ by using Mathematica 8 and the transcendental equation, we can find the following approximate eigenvalues.

${\lambda }_1=-1.00008,$${\lambda }_2=0.334608,$${\lambda }_3=5.41871,\dots$

Finally, we can illustrate the graphical simulation of approximate eigenfunctions

$$\begin{array}{c}\hfill y_n\left(x\right)=y(x,{\lambda }_n)=\left\{\begin{array}{cc}{y}_l(x,{\lambda }_n),for\hfill & x\in [-1,0)\hfill \\ y_r(x,{\lambda }_n),for\hfill & x\in (0,1]\hfill \end{array}\right.\end{array}$$

for the eigenvalues ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$ as follows.

The graphs of the first three eigenfunctions $y_1\left(x\right)$, $y_2\left(x\right)$ and $y_3\left(x\right)$ are shown in Figure 8, Figure 9 and Figure 10, respectively.

Discussion of Figure 8, Figure 9 and Figure 10:

As it seems from Figure 8, Figure 9 and Figure 10, the modified Adomian decomposition method used in this paper proved to be very efficient for computing the eigenfunctions even of singular Sturm–Liouville problems under additional transmission conditions at the interior point of discontinuity.

5. Conclusions

In this paper we have investigated a new type singular Sturm–Liouville problem. First, by proposing new analytical approaches, we derived exact formulas for eigenvalues and corresponding exact eigenfunctions. Then, we modified the Adomian decomposition method for computing left and right side solutions. Moreover, some graphical illustrations are presented for the first and second fundamental solutions, and for characteristic functions, the roots of which coincide with the eigenvalues. In the final part of our study, we present a graphical illustration of the corresponding eigenfunctions. The obtained results showed that the ADM can be adapted for solving two-interval Sturm–Liouville problems with additional transmission conditions.