A Numerical Computation of Zeros of q-Generalized Tangent-Appell Polynomials
Abstract
1. Introduction and Preliminaries
2. q-Generalized Tangent-Appell Polynomials
3. Identities Involving q-Generalized Tangent-Appell Polynomials
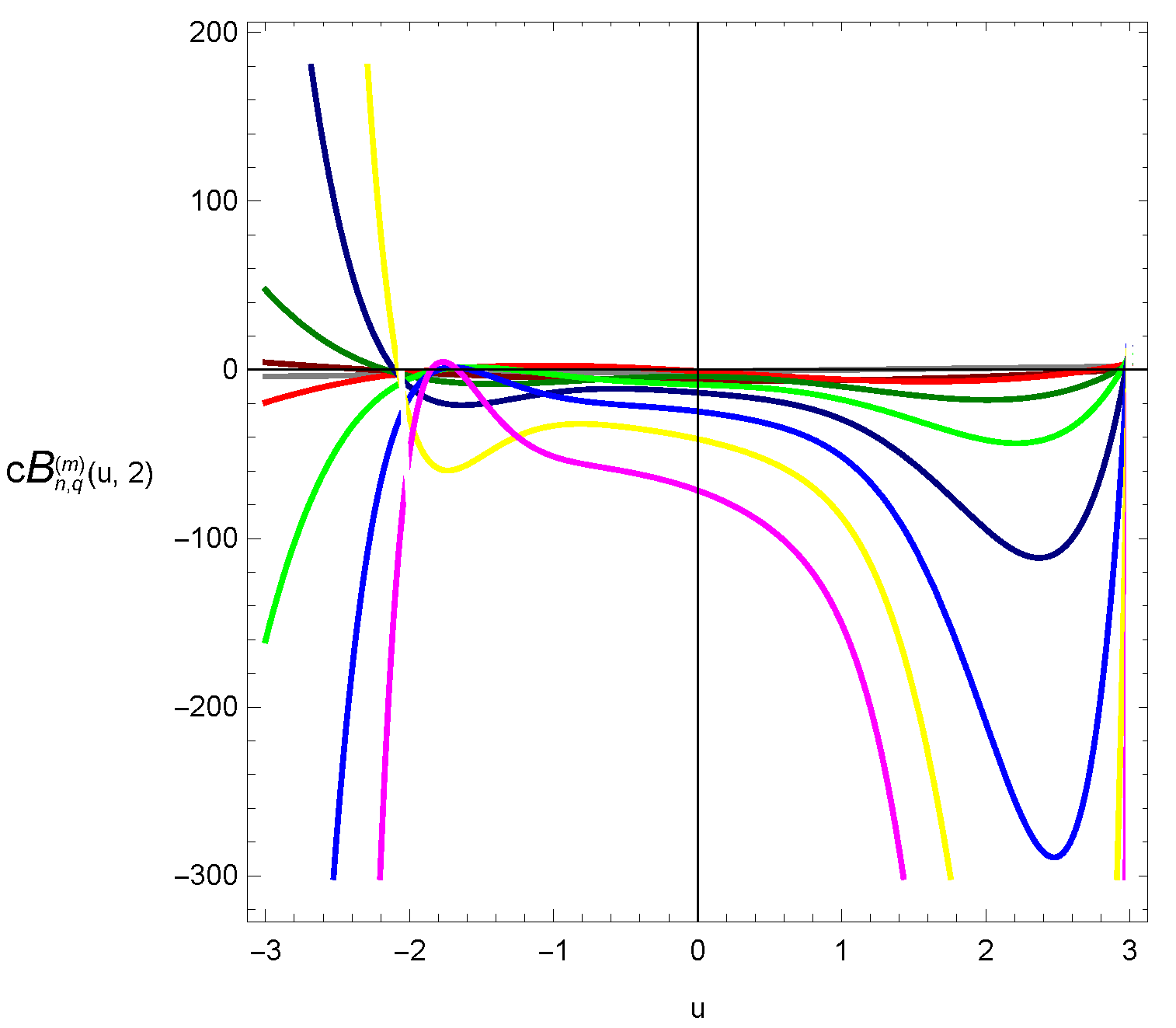
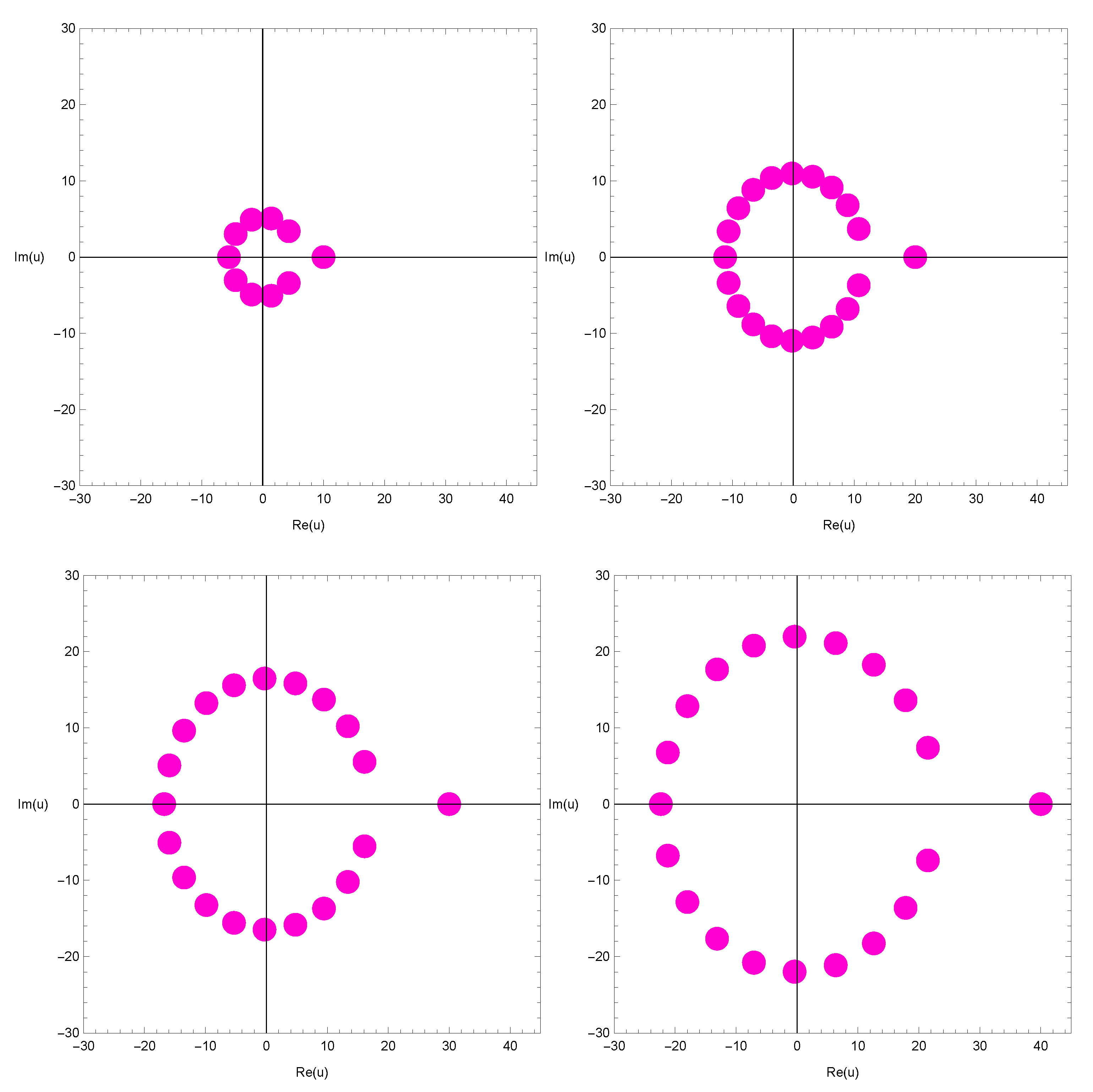
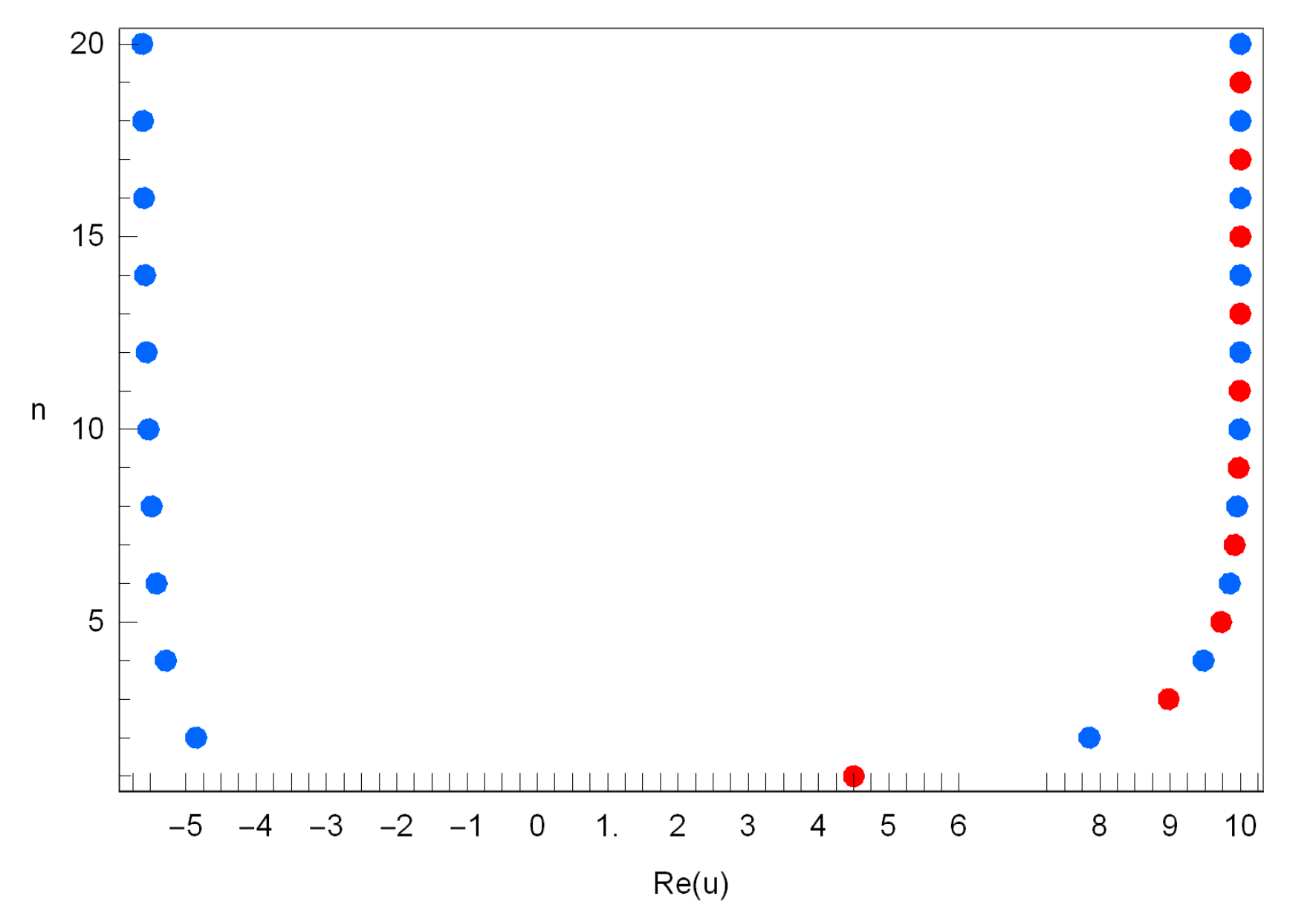
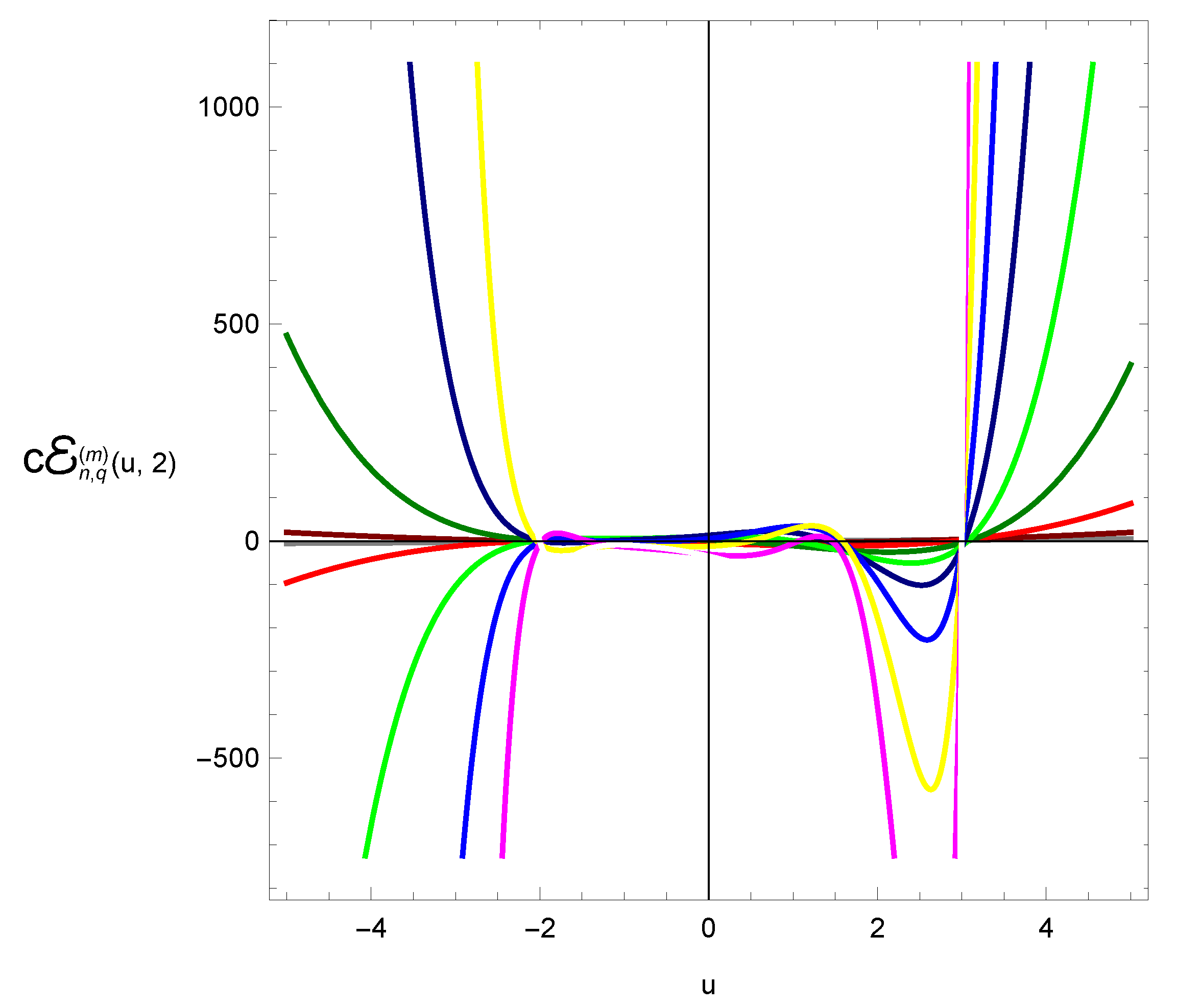
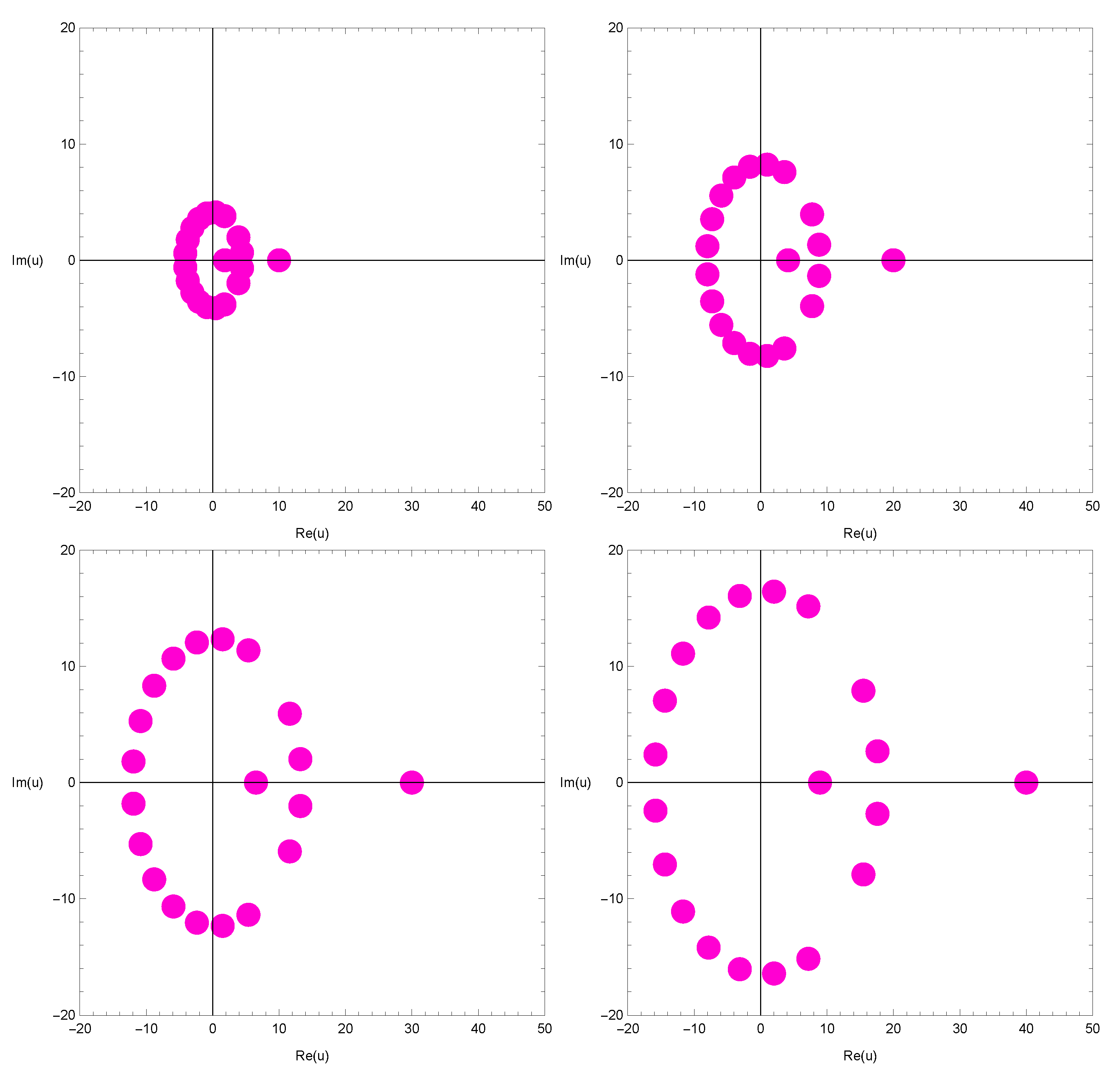
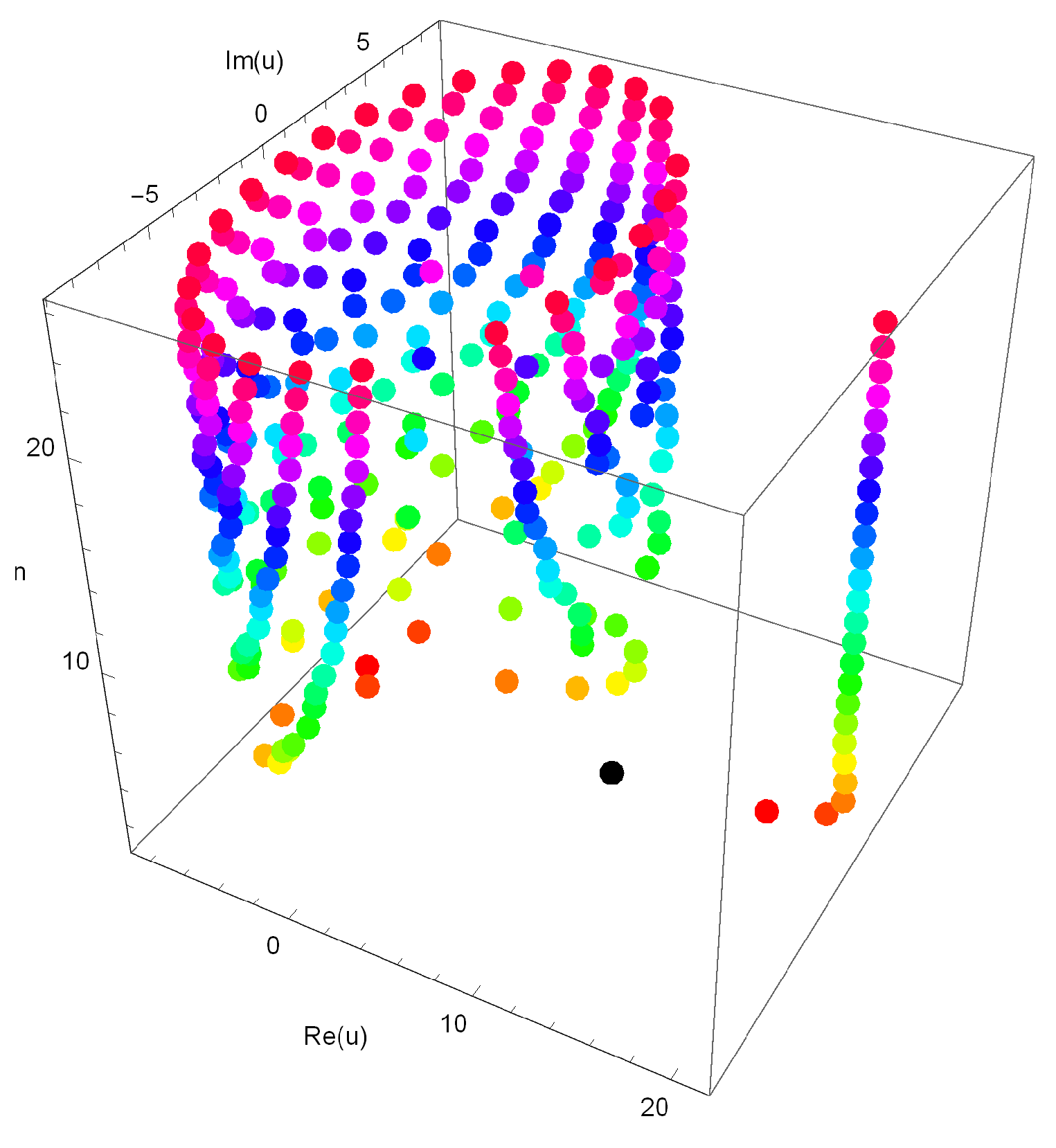
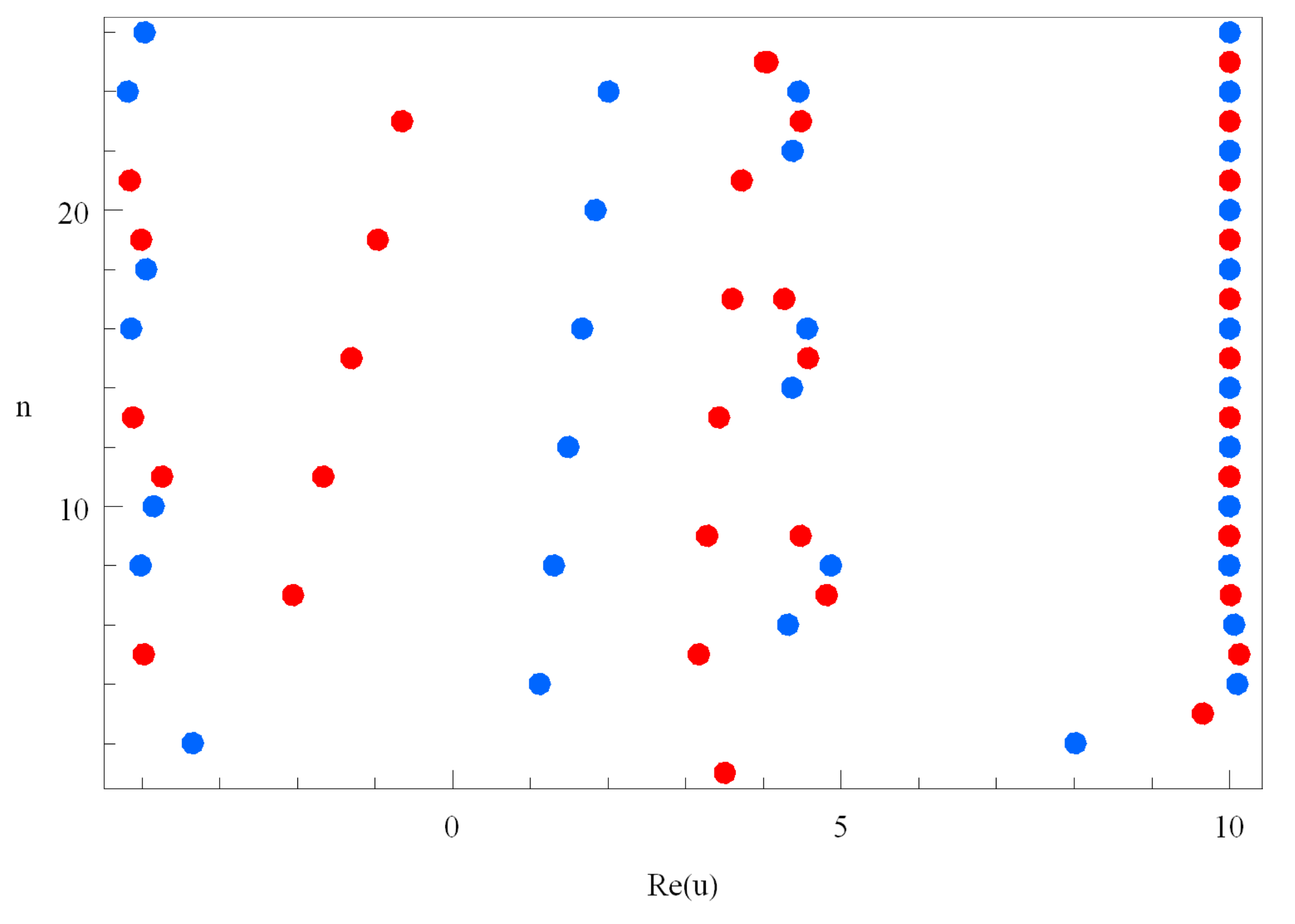
4. Graphical Representation and Computation of Zeros
Author Contributions
Funding
Conflicts of Interest
References
- Andrews, G.E.; Askey, R.; Roy, R. Special Functions—Encyclopedia of Mathematics and its Applications; Cambridge University Press: Cambridge, UK; London, UK; New York, NY, USA, 2000; Volume 71. [Google Scholar]
- Bildirici, C.; Acikgoz, M.; Araci, S. A note on analogues of tangent polynomials. J. Algebra Number Theory Acad. 2014, 4, 21. [Google Scholar]
- Ryoo, C.S. Generalized Tangent numbers and polynomials associated with p-adic integral on zp. Appl. Math. Sci. 2013, 7, 4929–4934. [Google Scholar] [CrossRef]
- Ryoo, C.S. A note on the tangent numbers and polynomials. Adv. Studies Theor. Phys. 2013, 7, 447–454. [Google Scholar] [CrossRef]
- Yasmin, G.; Muhyi, A. Certain results of 2-variable q-generalized tangent-Apostol type polynomials. J. Math. Computer Sci. 2020, in press. [Google Scholar]
- Mahmudov, N.I. On a class of q-Bernoulli and q-Euler polynomials. Adv. Difference Equ. 2013, 2013, 108. [Google Scholar] [CrossRef]
- Ryoo, C.S. Some properties of two dimensional q-tangent numbers and polynomials. Glob. J. Pure Appl. Math. 2016, 12, 2999–3007. [Google Scholar]
- Appell, P. Sur une Classe de Polynômes; Gauthier-Villars: Paris, France, 1880. [Google Scholar]
- Al-Salam, W.A. q-Appell polynomials. Ann. Mat. Pura Appl. 1967, 77, 31–45. [Google Scholar] [CrossRef]
- Keleshteri, M.E.; Mahmudov, N.I. A study on q-Appell polynomials from determinantal point of view. Appl. Math. Comput. 2015, 260, 351–369. [Google Scholar] [CrossRef]
- Al-Salam, W.A. q-Bernoulli numbers and polynomials. Math. Nachr. 1958, 17, 239–260. [Google Scholar] [CrossRef]
- Ernst, T. q-Bernoulli and q-Euler polynomials, an umbral approach. Int. J. Difference Equ. 2006, 1, 31–80. [Google Scholar]
- Yasmin, G.; Muhyi, A.; Araci, S. Certain results of q-Sheffer-Appell polynomials. Symmetry 2019, 11, 159. [Google Scholar] [CrossRef]

| Name of q-Special | ||||
|---|---|---|---|---|
| S. No. | Polynomials and Its | Generating Function | Series Definition | |
| Associated Numbers | ||||
| I | q-Bernoulli polynomials; | |||
| q-Bernoulli numbers | ||||
| [11,12] | ||||
| II | q-Euler polynomials; | |||
| q-Euler numbers | ||||
| [6,12] |
| S. No. | Name of the | Generating Function | Generating Function | |
|---|---|---|---|---|
| Resultant Member | of Resultant Polynomial | of Resultant Number | ||
| I | q-generalized tangent | |||
| -Bernoulli polynomials (qGTBP) | ||||
| II | q-generalized tangent | |||
| -Euler polynomials (qGTEP) |
| S. No. | Results | qGTBP | qGTEP |
|---|---|---|---|
| I | Series | ||
| Expansions | |||
| II | Summation | ||
| Formulae | |||
| III | Differential | ||
| Recurrence | |||
| Relations | |||
| S. No. | Identities Involving q-Generalized Tangent | Identities Involving q-Generalized Tangent |
|---|---|---|
| -Bernoulli Polynomials qGTBP | -Euler Polynomials qGTEP | |
| I | ||
| II | ||
| III | ||
| IV | ||
| V | ||
| VI | ||
| VII | ||
| Degree n | Number of Real Zeros | Number of Complex Zeros |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 2 | 0 |
| 3 | 3 | 0 |
| 4 | 2 | 2 |
| 5 | 3 | 2 |
| 6 | 2 | 4 |
| 7 | 3 | 4 |
| 8 | 2 | 6 |
| 9 | 3 | 6 |
| Degree n | u |
|---|---|
| 1 | 1.0000 |
| 2 | −2.2609, 2.9276 |
| 3 | −1.8173, −0.15699, 2.7521 |
| 4 | −2.1632, 2.9221 |
| 5 | −1.7892, −1.2772, 2.9430 |
| 6 | −2.1077, 2.9725 |
| 7 | 1.8001, −1.5784, 2.9835 |
| 8 | −2.0768, 2.9910 |
| 9 | −1.8504, −1.6667, 2.9948 |
| Degree n | Number of Real Zeros | Number of Complex Zeros |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 2 | 0 |
| 3 | 3 | 0 |
| 4 | 2 | 2 |
| 5 | 3 | 2 |
| 6 | 4 | 2 |
| 7 | 5 | 2 |
| 8 | 4 | 4 |
| 9 | 5 | 4 |
| 10 | 2 | 8 |
| Degree n | u |
|---|---|
| 1 | 0 |
| 2 | −2.1602, 2.1602 |
| 3 | −2.1498, −0.73464, 2.8845 |
| 4 | 0.30406, 3.0659 |
| 5 | −2.0953, 1.0226, 3.0658 |
| 6 | −1.9820, 1.4174, 3.0287 |
| 7 | −1.9583, −1.2749, −0.42473, 1.5804, 3.0043 |
| 8 | −2.0338, 0.48493, 1.5889, 2.9970 |
| 9 | −1.9779, −1.4188, 1.0634, 1.4592, 2.9975 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasmin, G.; Ryoo, C.S.; Islahi, H. A Numerical Computation of Zeros of q-Generalized Tangent-Appell Polynomials. Mathematics 2020, 8, 383. https://doi.org/10.3390/math8030383
Yasmin G, Ryoo CS, Islahi H. A Numerical Computation of Zeros of q-Generalized Tangent-Appell Polynomials. Mathematics. 2020; 8(3):383. https://doi.org/10.3390/math8030383
Chicago/Turabian StyleYasmin, Ghazala, Cheon Seoung Ryoo, and Hibah Islahi. 2020. "A Numerical Computation of Zeros of q-Generalized Tangent-Appell Polynomials" Mathematics 8, no. 3: 383. https://doi.org/10.3390/math8030383
APA StyleYasmin, G., Ryoo, C. S., & Islahi, H. (2020). A Numerical Computation of Zeros of q-Generalized Tangent-Appell Polynomials. Mathematics, 8(3), 383. https://doi.org/10.3390/math8030383





