Improved Decentralized Fractional PD Control of Structure Vibrations
Abstract
:1. Introduction
2. Preliminaries and Model Description
2.1. Fractional Calculus Theory
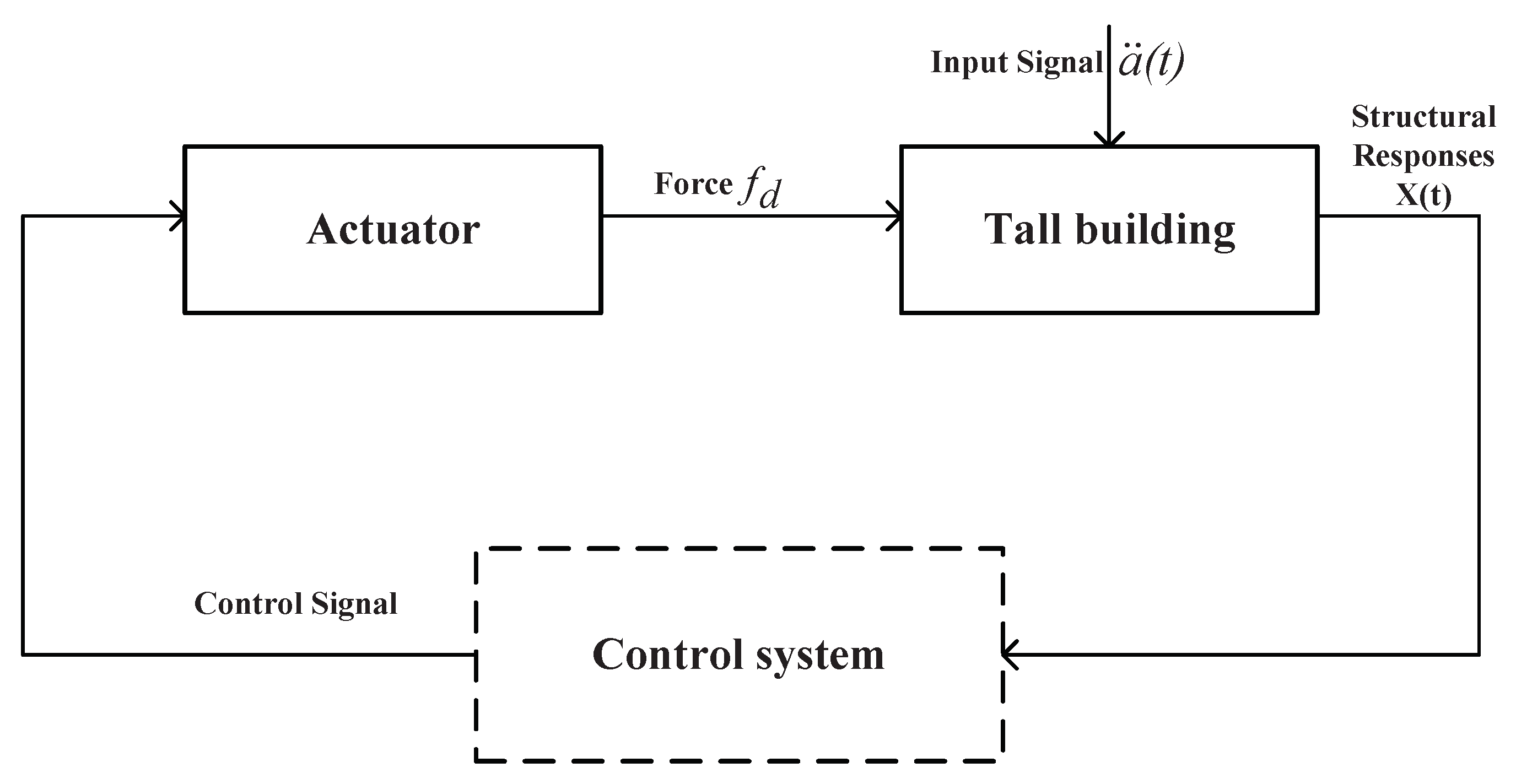
2.2. Vibration Control System of Building Structures
3. Improved Control Strategy
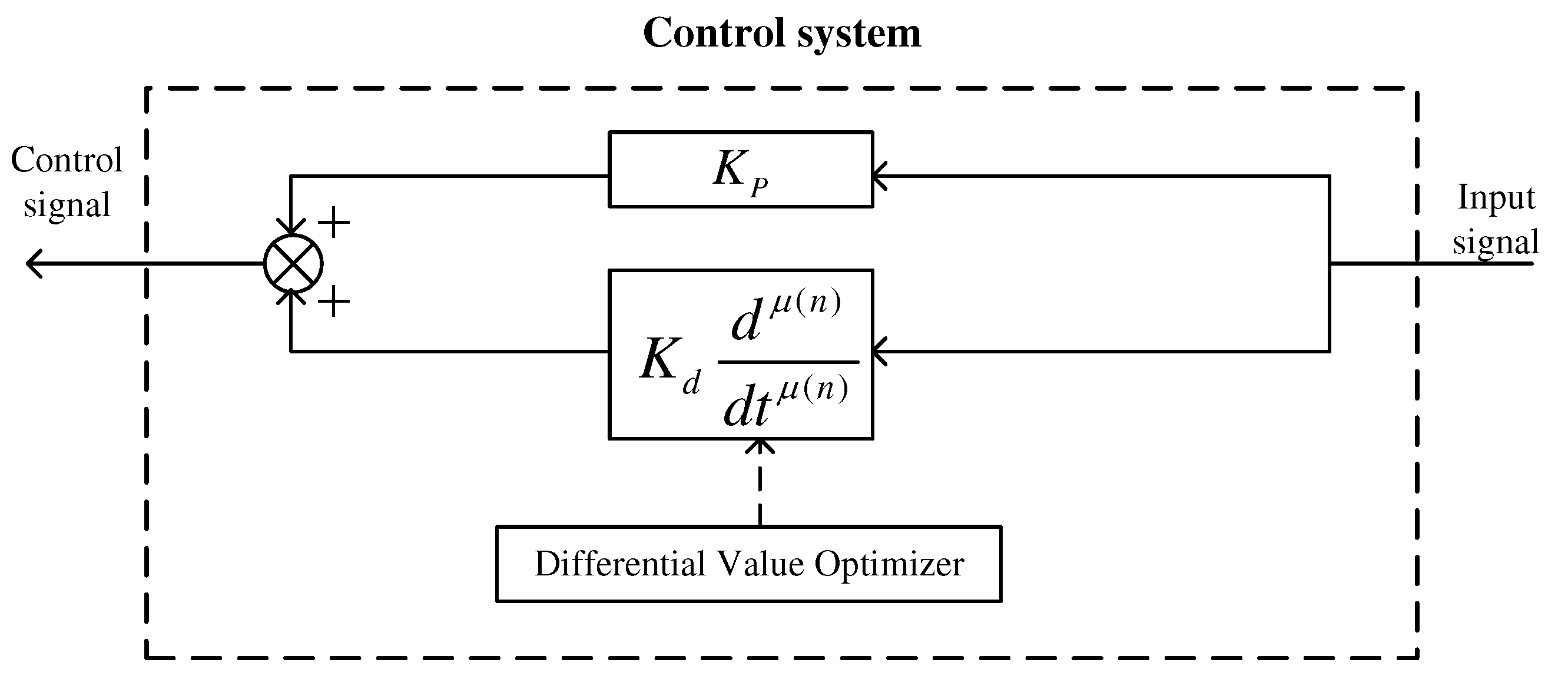
3.1. An Improved FOPD Controller
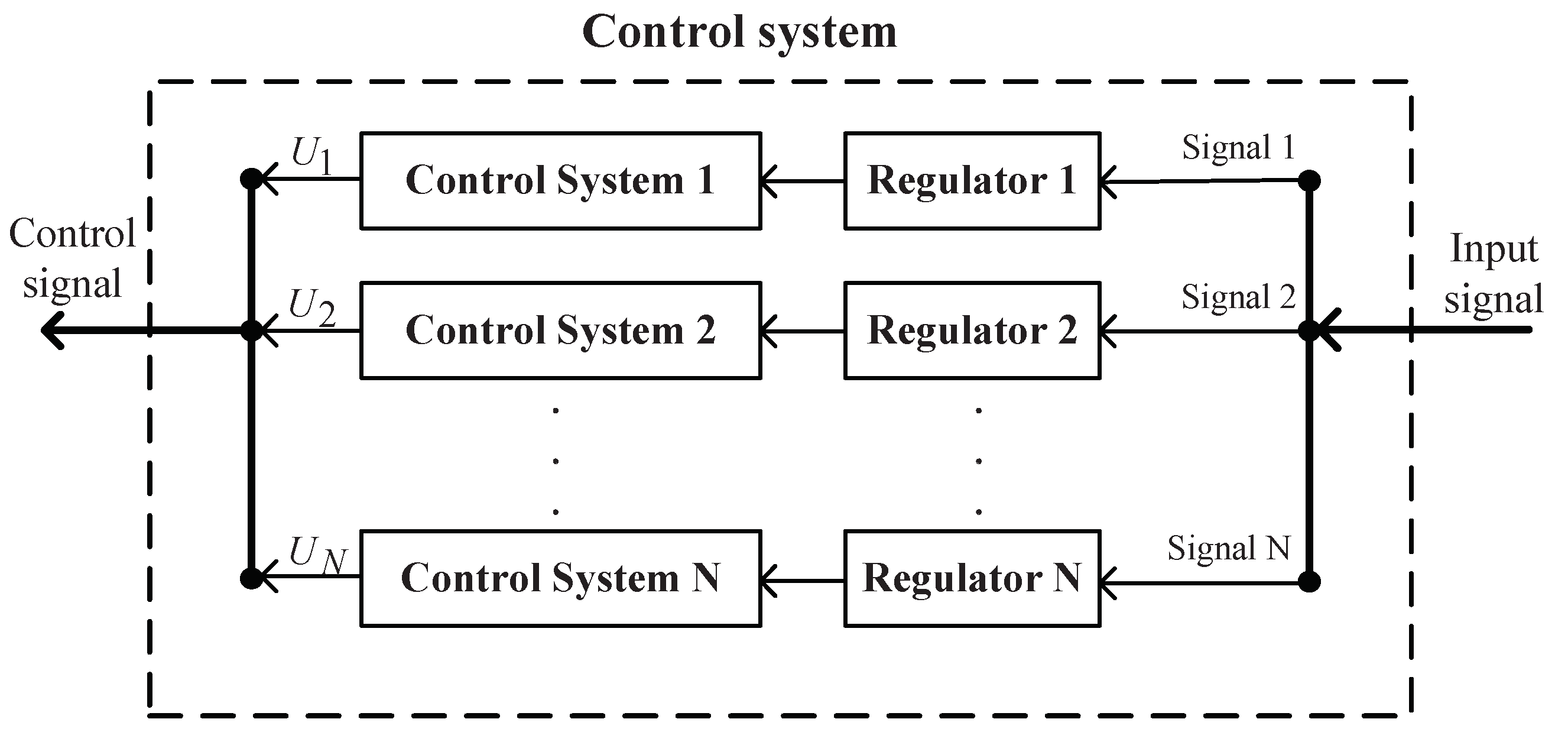
3.2. An Improved Decentralized Control Strategy
- Step 1: Check if there is a fault in the control subsystem. If “yes”, jump to step 2; otherwise, if “no”, jump to step 3;
- Step 2: Update the control system parameters according to the fault situation;
- Step 3: Run the control system and output the corresponding control actions.
4. Simulation Analysis
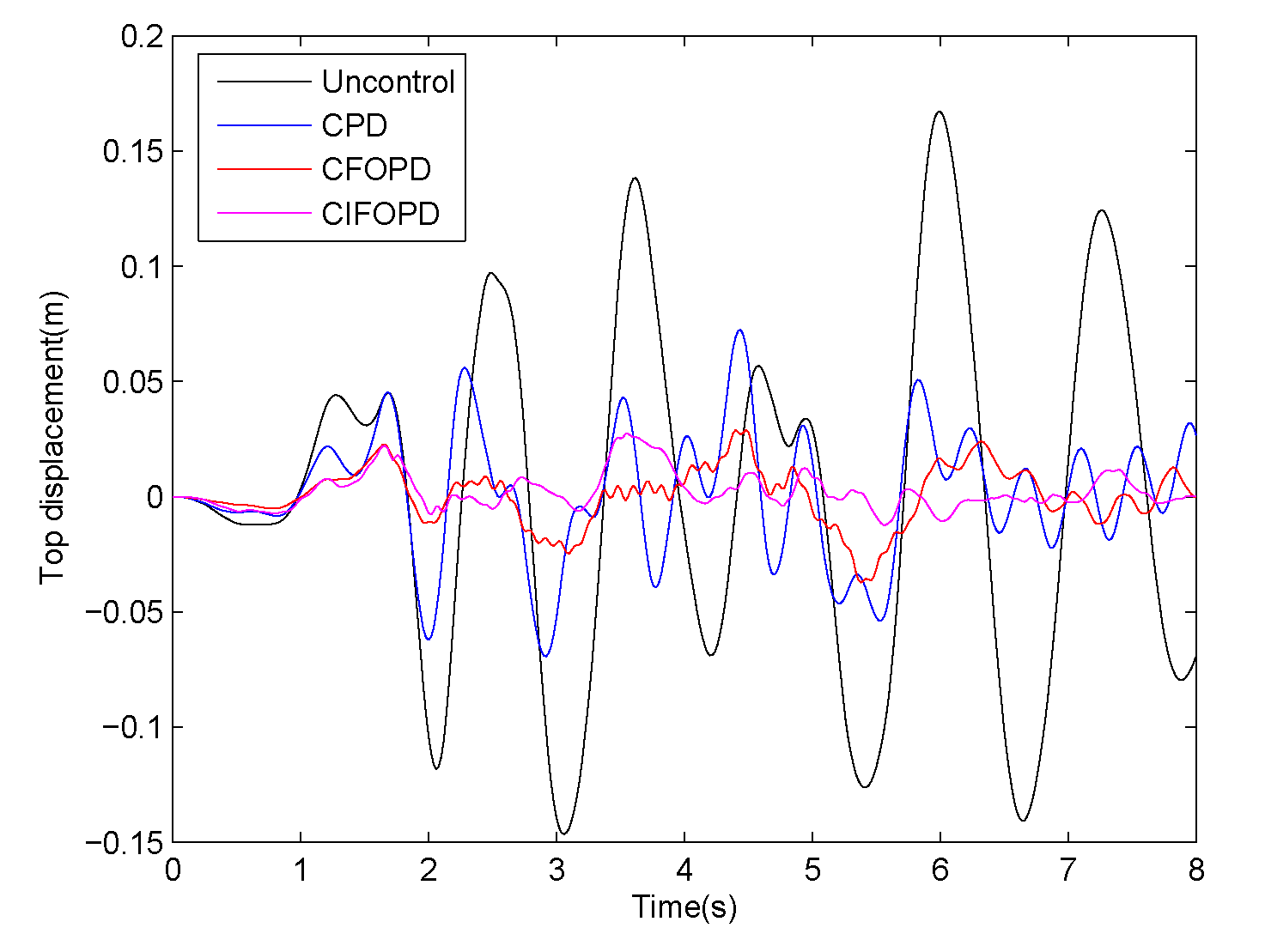
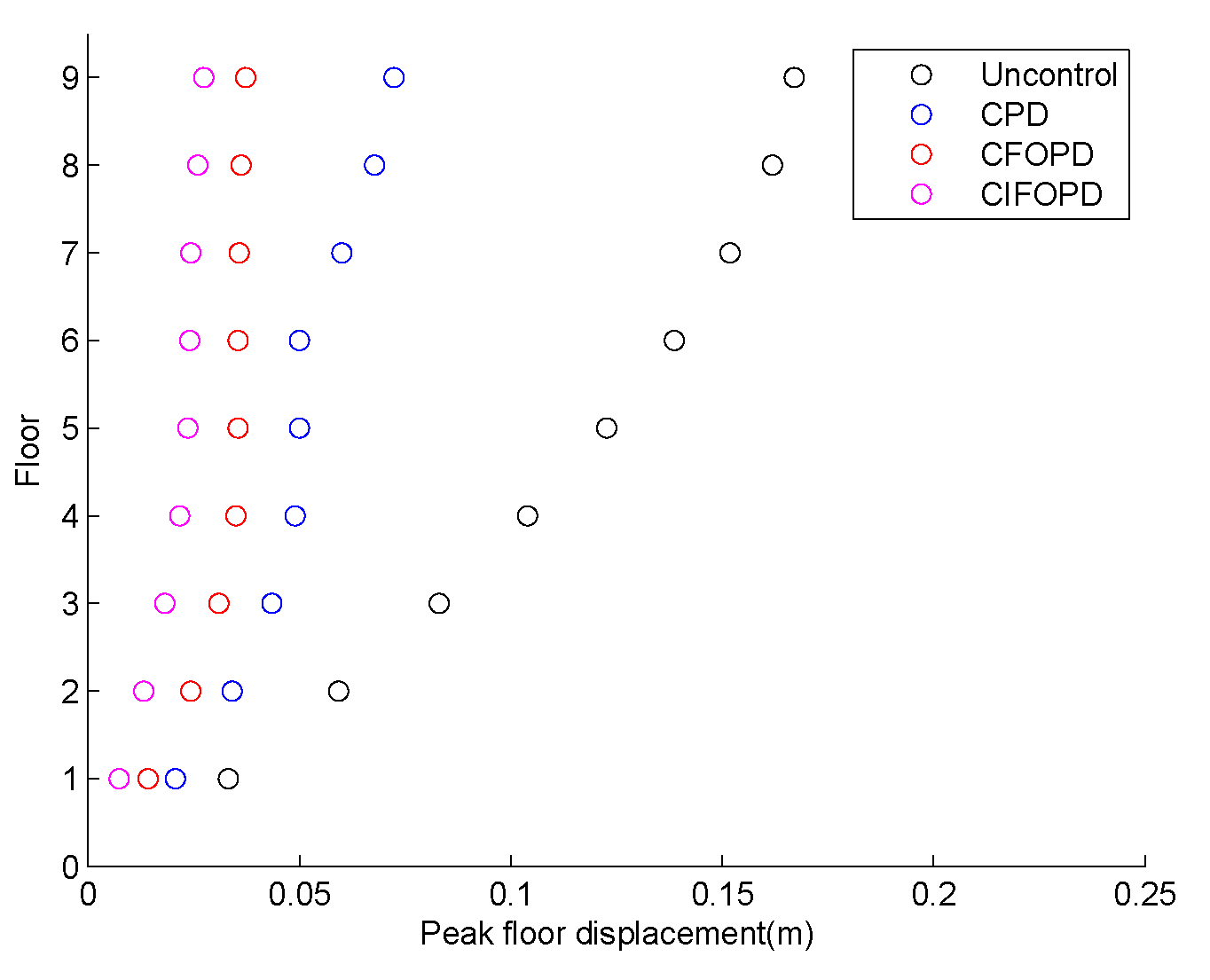
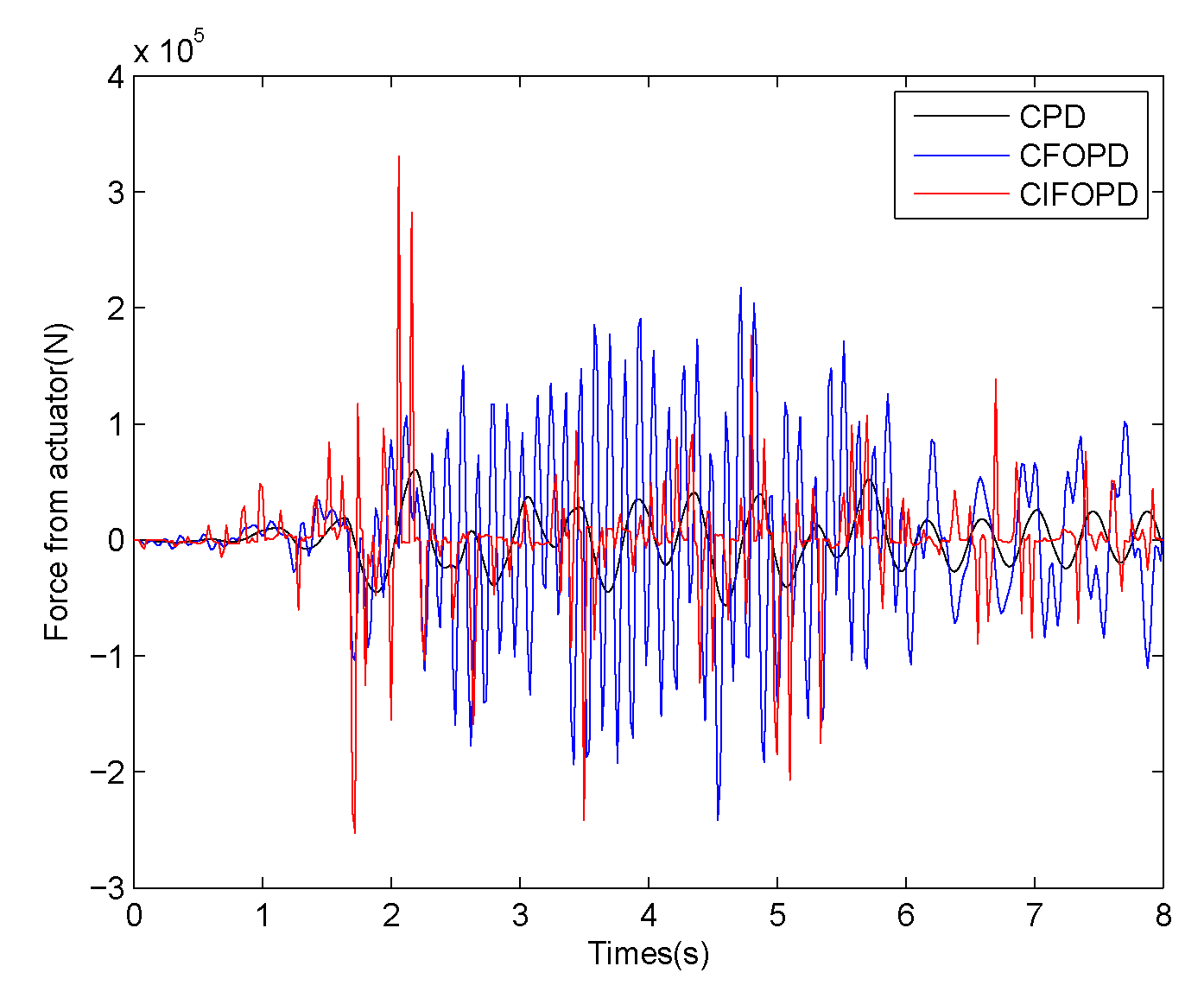
4.1. Analysis of the Centralized Control
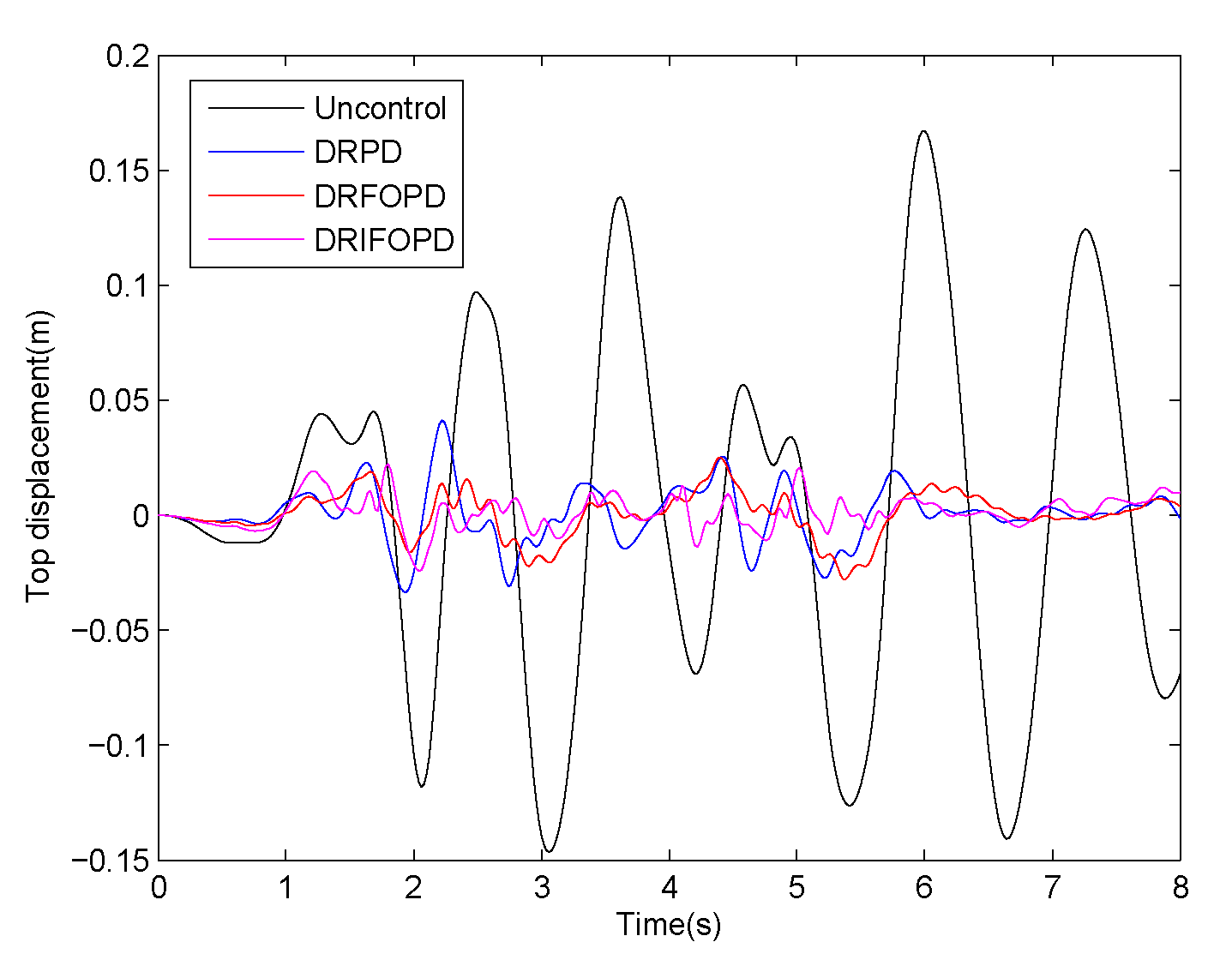
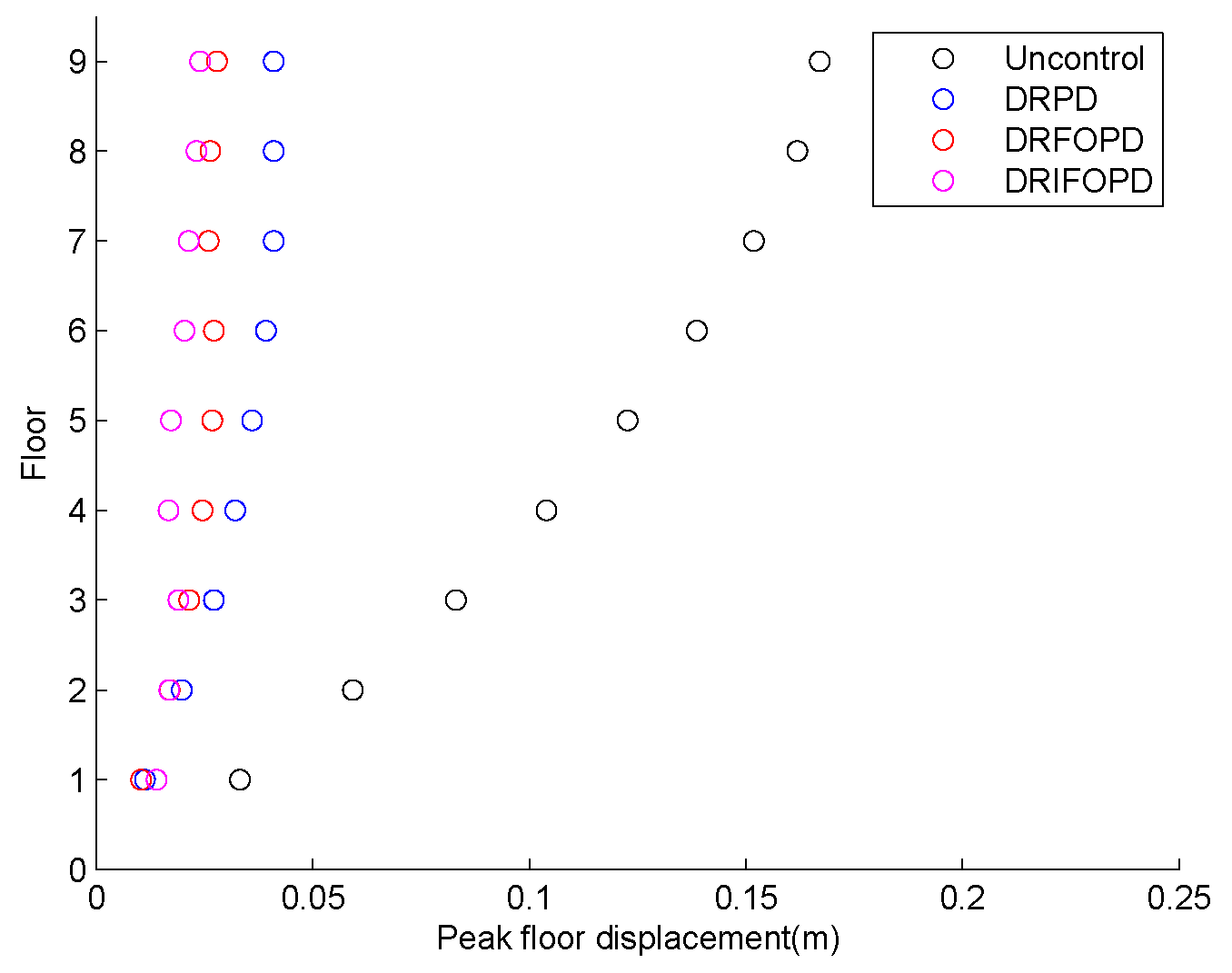
4.2. Analysis of the Decentralized Control
4.3. Fault Analysis
4.3.1. Fault Case 1
4.3.2. Fault Case 2
4.3.3. Fault Case 3
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Floor | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Height (m) | 4 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 |
| Quality (kg) | 29890 | 21700 | 21700 | 21700 | 21700 | 21700 | 21700 | 21700 | 21700 |
| Rigidity ( N/m) | 1.764 | 2.08 | 2.08 | 2.08 | 2.08 | 2.08 | 2.08 | 2.08 | 2.08 |
| Name of Parameters | Value of Parameters |
|---|---|
| Particle number | 50 |
| Number of Iterations/Number of repeated experiments | 300/50 |
| Scaling factors | , , , |
| Parameter optimization range | , , |
| Name of Control System | Control System Parameter Value |
|---|---|
| CPD | |
| CFOPD | |
| CIFOPD | |
| DRPD | |
| DRFOPD | |
| DRIFOPD | |
| Fault case 1: DIFOPD | |
| Fault case 1: DRIFOPD | |
| Fault case 2: DIFOPD | |
| Fault case 2: DRIFOPD | |
| Fault case 3: DIFOPD | |
| Fault case 3: DRIFOPD | |
References
- Rahimi, Z.; Sumelka, W.; Ahmadi, S.R.; Baleanu, D. Study and control of thermoelastic damping of in-plane vibration of the functionally graded nano-plate. J. Vib. Control. 2019, 25, 2850–2862. [Google Scholar] [CrossRef]
- Jajarmi, A.; Hajipour, M.; Sajjadi, S.S.; Baleanu, D. A robust and accurate disturbance damping control design for nonlinear dynamical systems. Optim. Control. Appl. Methods 2019, 40, 375–393. [Google Scholar] [CrossRef]
- Chuang, C.H.; Wu, D.N.; Wang, Q. LQR for state-bounded structural control. J. Dyn. Syst. Meas. Control. 1996, 118, 113–119. [Google Scholar] [CrossRef]
- Soleymani, M.; Abolmasoumi, A.H.; Bahrami, H.; Khalatbari-S, A.; Khoshbin, E.; Sayahi, S. Modified sliding mode control of a seismic active mass damper system considering model uncertainties and input time delay. J. Vib. Control. 2018, 24, 1051–1064. [Google Scholar] [CrossRef]
- Zizouni, K.; Fali, L.; Sadek, Y.; Bousserhane, I.K. Neural network control for earthquake structural vibration reduction using MRD. Front. Struct. Civ. Eng. 2019, 13, 1171–1182. [Google Scholar] [CrossRef]
- Maruani, J.; Bruant, I.; Pablo, F.; Gallimard, L. Active vibration control of a smart functionally graded piezoelectric material plate using an adaptive fuzzy controller strategy. J. Intell. Mater. Syst. Struct. 2019, 30, 2065–2078. [Google Scholar] [CrossRef]
- Wang, J.; Chen, W.; Chen, Z.; Huang, Y.; Huang, X.; Wu, W.; He, B.; Zhang, C. Neural Terminal Sliding-Mode Control for Uncertain Systems with Building Structure Vibration. Complexity 2019, 2019, 1507051. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Zhang, S.Q.; Wang, Z.X.; Qin, X.S.; Wang, R.X.; Schmidt, R. Disturbance rejection control with H∞ optimized observer for vibration suppression of piezoelectric smart structures. Mech. Ind. 2019, 20, 202. [Google Scholar] [CrossRef]
- Thenozhi, S.; Yu, W. Stability analysis of active vibration control of building structures using PD/PID control. Eng. Struct. 2014, 81, 208–218. [Google Scholar] [CrossRef]
- Guclu, R.; Yazici, H. Vibration control of a structure with ATMD against earthquake using fuzzy logic controllers. J. Sound Vib. 2008, 318, 36–49. [Google Scholar] [CrossRef]
- Etedali, S.; Zamani, A.A.; Tavakoli, S. A GBMO-based PIλDμ controller for vibration mitigation of seismic-excited structures. Autom. Constr. 2018, 87, 1–12. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Torres, F.; Gómez-Aguilar, J.; Escobar-Jiménez, R.; Guerrero-Ramírez, G. On the trajectory tracking control for an SCARA robot manipulator in a fractional model driven by induction motors with PSO tuning. Multibody Syst. Dyn. 2018, 43, 257–277. [Google Scholar] [CrossRef]
- Zhong, J.; Li, L. Fractional-order system identification and proportional-derivative control of a solid-core magnetic bearing. ISA Trans. 2014, 53, 1232–1242. [Google Scholar] [CrossRef] [PubMed]
- Silva, M.F.; Machado, J.T.; Lopes, A. Fractional order control of a hexapod robot. Nonlinear Dyn. 2004, 38, 417–433. [Google Scholar] [CrossRef]
- Zamani, A.A.; Tavakoli, S.; Etedali, S. Fractional order PID control design for semi-active control of smart base-isolated structures: A multi-objective cuckoo search approach. ISA Trans. 2017, 67, 222–232. [Google Scholar] [CrossRef] [PubMed]
- Petráš, I.; Vinagre, B. Practical application of digital fractional-order controller to temperature control. Acta Montan. Slovaca 2002, 7, 131–137. [Google Scholar]
- Delavari, H.; Ranjbar, A.; Ghaderi, R.; Momani, S. Fractional order control of a coupled tank. Nonlinear Dyn. 2010, 61, 383–397. [Google Scholar] [CrossRef]
- Chen, L.; Wu, R.; He, Y.; Yin, L. Robust stability and stabilization of fractional-order linear systems with polytopic uncertainties. Appl. Math. Comput. 2015, 257, 274–284. [Google Scholar] [CrossRef]
- Chen, L.; Cao, J.; Wu, R.; Machado, J.T.; Lopes, A.M.; Yang, H. Stability and synchronization of fractional-order memristive neural networks with multiple delays. Neural Netw. 2017, 94, 76–85. [Google Scholar] [CrossRef]
- Raji, R.; Hadidi, A.; Ghaffarzadeh, H.; Safari, A. Robust decentralized control of structures using the LMI H-infinity controller with uncertainties. Smart Struct. Syst. 2018, 22, 547–560. [Google Scholar]
- Lei, Y.; Wu, D.; Liu, L. A decentralized structural control algorithm with application to the benchmark control problem for seismically excited buildings. Struct. Control. Health Monit. 2013, 20, 1211–1225. [Google Scholar] [CrossRef]
- Linderman, L.E.; Spencer Jr, B. Decentralized active control of multistory civil structure with wireless smart sensor nodes. J. Eng. Mech. 2016, 142, 04016078. [Google Scholar] [CrossRef]
- Baghani, O. Solving state feedback control of fractional linear quadratic regulator systems using triangular functions. Commun. Nonlinear Sci. Numer. Simul. 2019, 73, 319–337. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Moore, K.L. Discretization schemes for fractional-order differentiators and integrators. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2002, 49, 363–367. [Google Scholar] [CrossRef]
- Zhenbin, W.; Zhenlei, W.; Guangyi, C.; Xinjian, Z. Digital implementation of fractional order PID controller and its application. J. Syst. Eng. Electron. 2005, 16, 116–122. [Google Scholar]
- Hall, J.F. Problems encountered from the use (or misuse) of Rayleigh damping. Earthq. Eng. Struct. Dyn. 2006, 35, 525–545. [Google Scholar] [CrossRef]
- Del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.C.; Harley, R.G. Particle swarm optimization: Basic concepts, variants and applications in power systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Kulkarni, R.V.; Venayagamoorthy, G.K. Particle swarm optimization in wireless-sensor networks: A brief survey. IEEE Trans. Syst. Man, Cybern. Part C (Appl. Rev.) 2010, 41, 262–267. [Google Scholar] [CrossRef] [Green Version]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Chen, L.; Wang, M.; Lopes, A.M.; Tenreiro Machado, J.A.; Zhai, H. Improved Decentralized Fractional PD Control of Structure Vibrations. Mathematics 2020, 8, 326. https://doi.org/10.3390/math8030326
Xu K, Chen L, Wang M, Lopes AM, Tenreiro Machado JA, Zhai H. Improved Decentralized Fractional PD Control of Structure Vibrations. Mathematics. 2020; 8(3):326. https://doi.org/10.3390/math8030326
Chicago/Turabian StyleXu, Kang, Liping Chen, Minwu Wang, António M. Lopes, J. A. Tenreiro Machado, and Houzhen Zhai. 2020. "Improved Decentralized Fractional PD Control of Structure Vibrations" Mathematics 8, no. 3: 326. https://doi.org/10.3390/math8030326
APA StyleXu, K., Chen, L., Wang, M., Lopes, A. M., Tenreiro Machado, J. A., & Zhai, H. (2020). Improved Decentralized Fractional PD Control of Structure Vibrations. Mathematics, 8(3), 326. https://doi.org/10.3390/math8030326








