Predictive Modeling the Free Hydraulic Jumps Pressure through Advanced Statistical Methods
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Statistical Data Analysis
3. Results and Discussion
3.1. Skewness and Kurtosis Coefficient
3.2. Cumulative Pressure Curves
3.3. Proposition of New Relationships
3.4. Comparison between Sample and Estimated Pressure Data
4. Conclusions
- (1)
- Sample skewness (S) and kurtosis (K) coefficients indicated that the pressure distribution along the hydraulic jumps does not follow a normal distribution. Some characteristic points are the maximum pressure fluctuations point (X*σmax) with Smax; the flow detachment point (X*d) with S ≈ 0; the roller endpoint (X*r) with Smin; and the hydraulic jump endpoint (X*j) with S ≈ 0.
- (2)
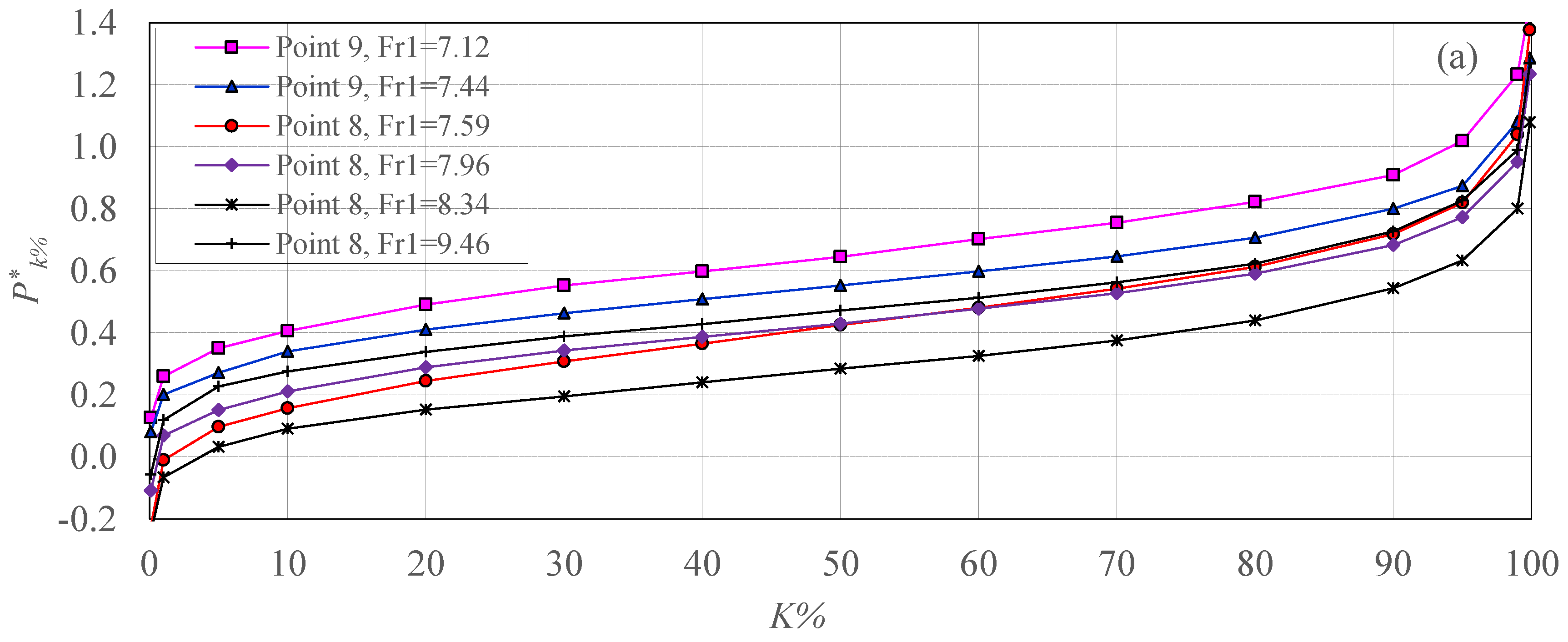
- From the pressure data with different non-exceedance probabilities (P*k%), the cumulative pressure curves are presented for P*k% related to the characteristic points of X*σmax, X*d, X*r, and X*j, respectively. For the positions close to the spillway toe, pressures with low and high probability (P*1% and P*99%), have lower and higher values, with the maximum differences than P*m. P*1% data, reach negative values down to −0.2, at the position X* ≈ 2, indicating regions with low pressures.
- (3)
- From the analysis of the probability distribution of the sample data as collected by pressure transducers, pressures data of P*k% can be determined.
- (4)
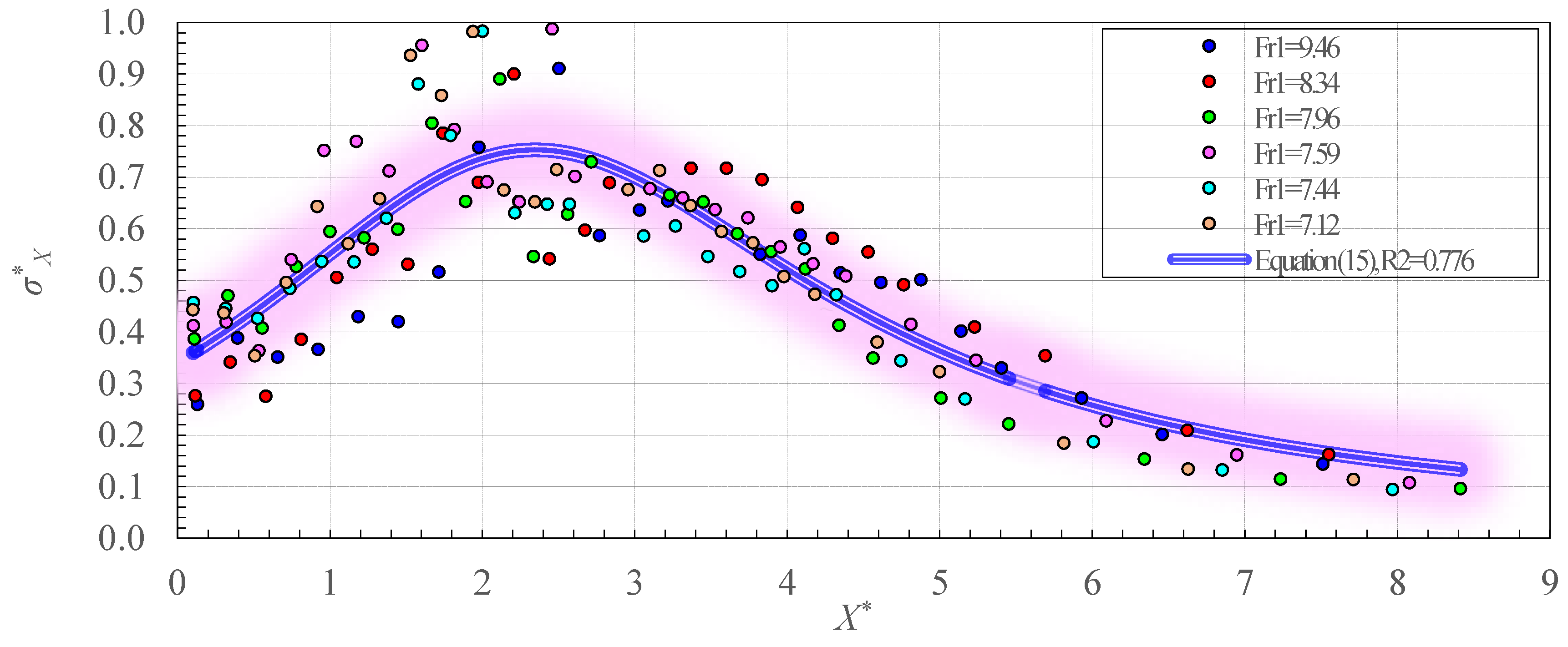
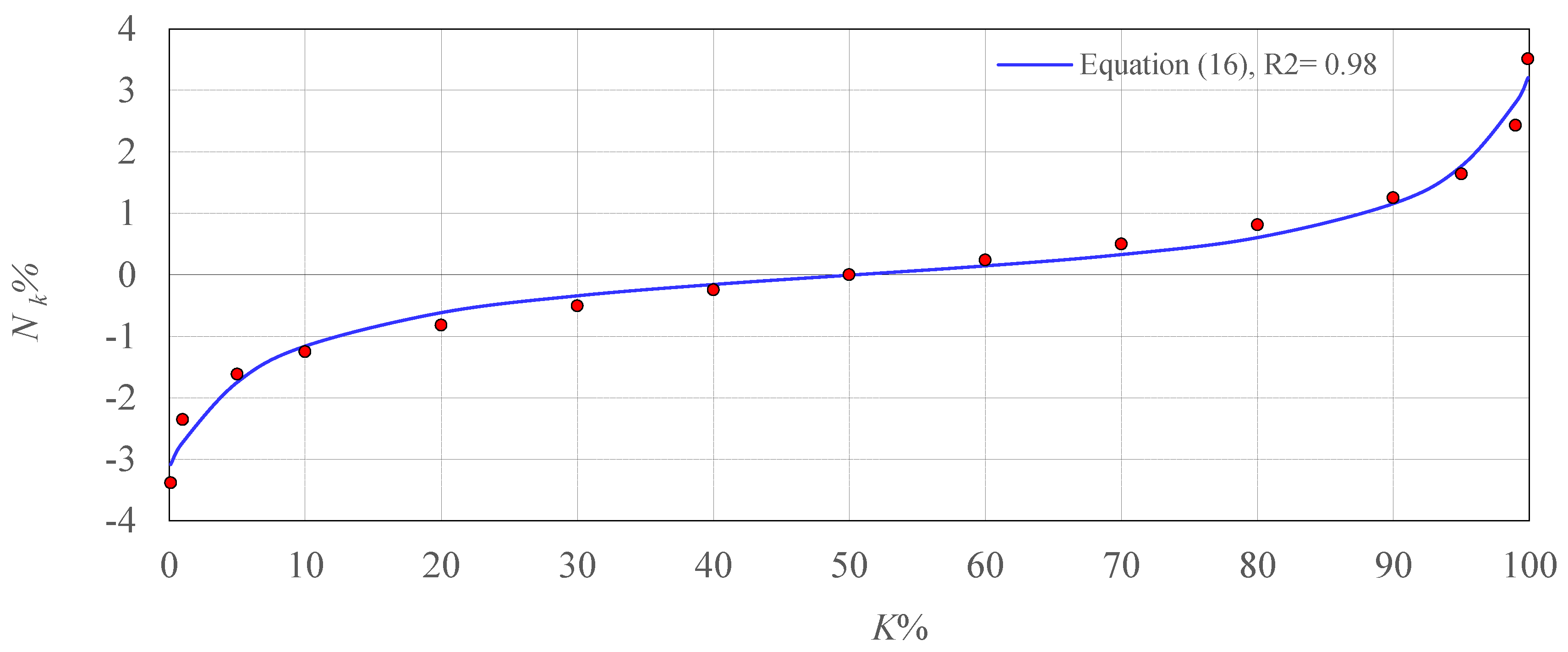
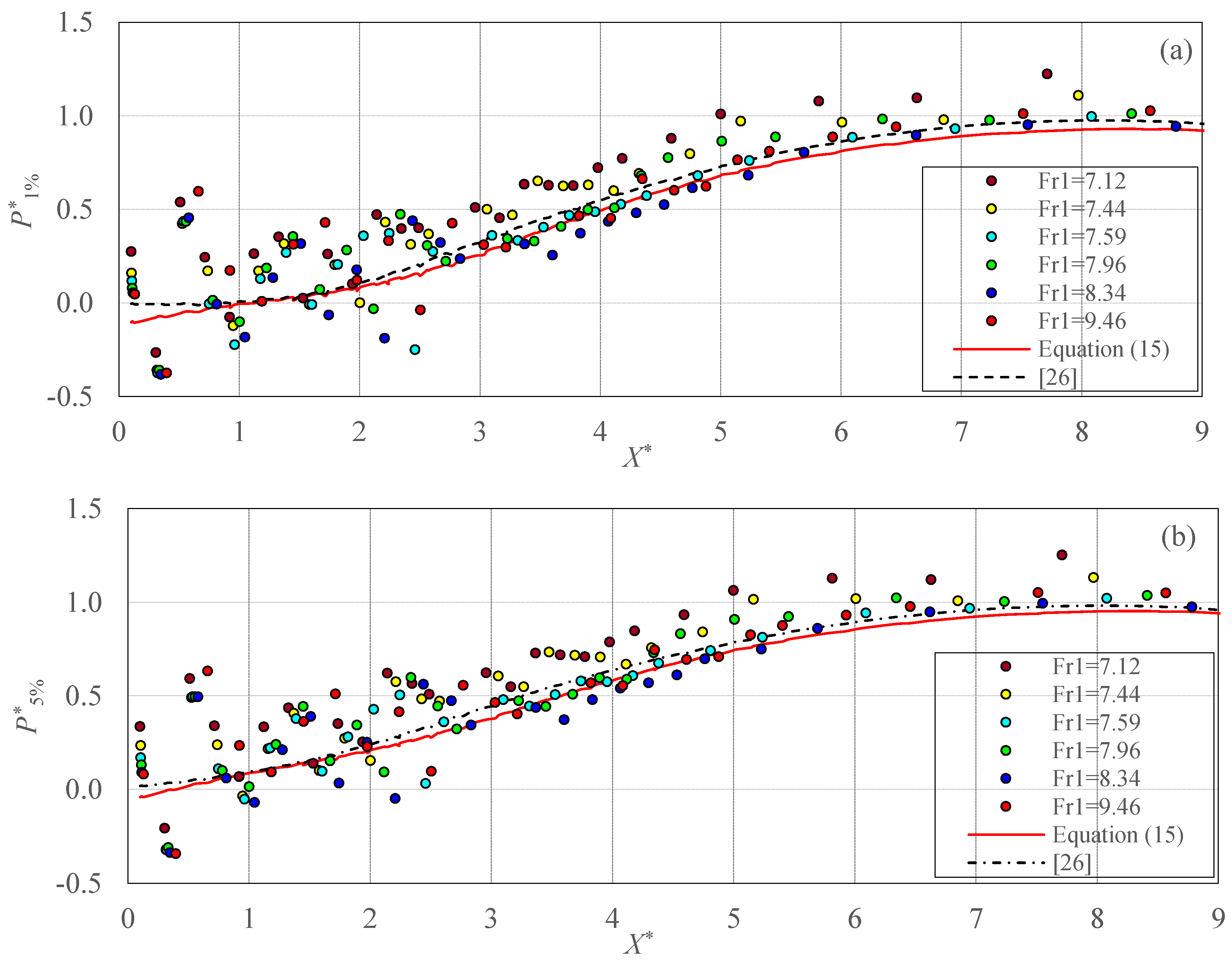
- Based on the results obtained, it was observed that the method proposed by Teixeira [26] could be optimized to be used for present data, or in similar conditions by using another relationship for the dimensionless standard deviation of pressure fluctuations (σ*X), and the statistical coefficient of the probability distribution (Nk%). Thus, a new second-order fractional relationship, as a function of the dimensionless position along the stilling basin (X*), is introduced for σ*X. This relationship is valid for the dimensionless positions (X*) in the range of 0 to 8.4. To assess the accuracy of this relationship, some performance criteria are used. For the new proposed relationship (σ*X) in this study, the values of R2, RMSE, MAE, and WI were achieved 0.776, 0.097, 0.075, and 0.931, respectively. The constant values of Nk% are developed along the jump. Therefore, depending on the probability, the values of the Nk% coefficient indicate a single mean value for each probability. A new second-order fractional relationship was proposed to estimate the Nk% coefficient with R2 = 0.98. The new relationships should be validated against sample data taken in similar conditions to our case study here.
- (5)
- The results contribute to enhancing the knowledge of the flow in a USBR Type I stilling basin that can be used to improve their design. This work only includes the case of free jumps. Future advancements will cover the behavior of submerged jumps with variable submergence degrees, resulting in modified pressure fields concerning those observed here for free jumps. As well, the efficiency of blocks and sills with different sizes may be investigated. A more extensive range of flow discharge will need to be explored. In the future, the more specific effort may be devoted to testing other possible distributions, fitting the observed pressure fields and their use in practice design. Also, velocity fields within the hydraulic jump may be investigated to define the turbulent components of flow fields.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notation
| B | Basin width (L) |
| Fr1 | Incident Froude number |
| g | Gravitational acceleration (LT−2) |
| K | Kurtosis coefficient |
| L | Spillway length (L) |
| Lb | Length of the USBR Type I stilling basin (L) |
| MAE | Mean Absolute Error |
| Nk% | Statistical coefficient of probability distribution at point X |
| H | Spillway height (L) |
| Pk% | Pressure with a certain non-exceedance probability (L) |
| P*k% | Dimensionless pressure with a certain non-exceedance probability |
| Pi | Instantaneous pressure of each pressure tap (L) |
| Pm | Mean pressure of each pressure tap (L) |
| P*m | Dimensionless mean pressure of each pressure tap |
| Q | Flow discharge (L3T−1) |
| q | Flow discharge per unit width (L2T-1) |
| R1 | Hydraulic radius of the incoming flow (L) |
| R2 | Determination coefficient |
| Re1 | Incident Reynolds number |
| RMSE | Root Mean Squared Error |
| S | Skewness coefficient |
| SX | Sample standard deviation |
| V1 | Mean supercritical velocity (LT−1) |
| WI | Willmott’s index of agreement |
| X | Distance of each pressure tap from the spillway toe (L) |
| X* | Dimensionless distance of each pressure tap from the spillway toe, i.e., X/ (Y2 − Y1) |
| X*d | Point of the flow detachment |
| X*j | Endpoint of the hydraulic jump |
| X*r | Endpoint of the roller |
| X*σmax | Point of the maximum pressure fluctuations |
| Y1 | Supercritical depth (L) |
| Y2 | Sequent depth (L) |
| ΔE | Energy head loss along the hydraulic jump (L) |
| σX | Standard deviation of pressure fluctuations at point x (L) |
References
- Valero, D.; Viti, N.; Gualtieri, C. Numerical simulation of hydraulic jumps. Part 1: Experimental data for modelling performance assessment. Water 2019, 11, 36. [Google Scholar] [CrossRef]
- Toso, J.W.; Bowers, C.E. Extreme pressures in hydraulic-jump stilling basins. J. Hydraul. Eng. 1988, 114, 829–843. [Google Scholar] [CrossRef]
- Khatsuria, R.M. Hydraulics of spillways and energy dissipators; Marcel Dekker: New York, NY, USA, 2005. [Google Scholar]
- Bukreev, V. Statistical characteristics of the pressure fluctuation in a hydraulic jump. J. Appl. Mech. Tech. Phys. 1966, 7, 97–99. [Google Scholar] [CrossRef]
- Locher, F.A. Some Characteristics of Pressure Fluctuations on Low-Ogee Crest Spillways Relevant to Flow-Induced Structural Vibrations; Iowa Institute of Hydraulic Research, The University of Iowa: Iowa City, IA, USA, 1971. [Google Scholar]
- Schiebe, F.R. The Stochastic Characteristics of Pressure Fluctuations on a Channel Bed due to The Macroturbulence in a Hydraulic Jump. Ph.D. Thesis, University of Minnesota, Twin Cities, MN, USA, 1971. [Google Scholar]
- Abdul Khader, M.; Elango, K. Turbulent pressure field beneath a hydraulic jump. J. Hydraul. Res. 1974, 12, 469–489. [Google Scholar] [CrossRef]
- Lopardo, R.; Vernet, G.; Ronaldo, R. Correlation of instantaneous pressures induced by a free and stable hydraulic jump. In Proceedings of the XI Latin American Congress of Hydraulics IAHR, Ezeiza, Argentina, 3 April 1984; pp. 23–34. (In Spanish). [Google Scholar]
- Lopardo, R.A. Methodology for estimating instantaneous pressures in dissipation basins. In Proceedings of the Annals of the University of Chile, Santiago, Chile, 20 June 1985; pp. 437–455. (In Spanish). [Google Scholar]
- Farhoudi, J.; Narayanan, R. Force on slab beneath hydraulic jump. J. Hydraul. Eng. 1991, 117, 64–82. [Google Scholar] [CrossRef]
- Fiorotto, V.; Rinaldo, A. Turbulent pressure fluctuations under hydraulic jumps. J. Hydraul. Res. 1992, 30, 499–520. [Google Scholar] [CrossRef]
- Fiorotto, V.; Rinaldo, A. Fluctuating uplift and lining design in spillway stilling basins. J. Hydraul. Eng. 1992, 118, 578–596. [Google Scholar] [CrossRef]
- Armenio, V.; Toscano, P.; Fiorotto, V. On the effects of a negative step in pressure fluctuations at the bottom of a hydraulic jump. J. Hydraul. Res. 2000, 38, 359–368. [Google Scholar] [CrossRef]
- Yan, Z.-M.; Zhou, C.-T.; Lu, S.-Q. Pressure fluctuations beneath spatial hydraulic jumps. J. Hydrodyn. 2006, 18, 723–726. [Google Scholar] [CrossRef]
- Onitsuka, K.; Akiyama, J.; Shige-Eda, M.; Ozeki, H.; Gotoh, S.; Shiraishi, T. Relationship between pressure fluctuations on the bed wall and free surface fluctuations in weak hydraulic jump. In New Trends in Fluid Mechanics Research—Proceedings of the Fifth International Conference on Fluid Mechanics, Shanghai, China, 15–19 August 2007; pp. 300–303. [Google Scholar]
- Lian, J.; Wang, J.; Gu, J. Similarity law of fluctuating pressure spectrum beneath hydraulic jump. Chin. Sci. Bull. 2008, 53, 2230–2238. [Google Scholar] [CrossRef]
- Lopardo, R.A.; Romagnoli, M. Pressure and velocity fluctuations in stilling basins. In Advances in Water Resources and Hydraulic Engineering; Springer: Berlin/Heidelberg, Germany, 2009; pp. 2093–2098. [Google Scholar]
- Lopardo, R.A. Extreme velocity fluctuations below free hydraulic jumps. J. Eng. 2013, 2013, 1–5. [Google Scholar] [CrossRef][Green Version]
- Wang, H.; Murzyn, F.; Chanson, H. Total pressure fluctuations and two-phase flow turbulence in hydraulic jumps. Exp. Fluids 2014, 55, 1847. [Google Scholar] [CrossRef]
- Fiorotto, V.; Barjastehmaleki, S.; Caroni, E. Stability analysis of plunge pool linings. J. Hydraul. Eng. 2016, 142, 1–11. [Google Scholar] [CrossRef]
- Barjastehmaleki, S.; Fiorotto, V.; Caroni, E. Spillway stilling basins lining design via Taylor hypothesis. J. Hydraul. Eng. 2016, 142, 1–11. [Google Scholar] [CrossRef]
- Barjastehmaleki, S.; Fiorotto, V.; Caroni, E. Design of stilling basin linings with sealed and unsealed joints. J. Hydraul. Eng. 2016, 142, 1–10. [Google Scholar] [CrossRef]
- Gu, S.; Bo, F.; Luo, M.; Kazemi, E.; Zhang, Y.; Wei, J. SPH simulation of hydraulic jump on corrugated riverbeds. Appl. Sci. 2019, 9, 436. [Google Scholar] [CrossRef]
- Güven, A.; Günal, M.; Cevik, A. Prediction of pressure fluctuations on sloping stilling basins. Can. J. Civ. Eng. 2006, 33, 1379–1388. [Google Scholar] [CrossRef]
- Hager, W.H. B-jump in sloping channel. J. Hydraul. Res. 1988, 26, 539–558. [Google Scholar] [CrossRef]
- Teixeira, E.D. Scale effect on estimating extreme pressure values on the bed of the hydraulic dissipation basins. Ph.D. Thesis, Hydraulic Reseach Institute, Federal University of Rio Grande do Sul, Porto Alegre, Brazil, 2008. (In Portuguese). [Google Scholar]
- Teixeira, E.D.; Neto, E.F.T.; Endres, L.A.M.; Marques, M.G. Analysis of pressure fluctuations near the bed in hydraulic jump dissipation basins. In Proceedings of the Brazilian Dam Committee, XXV Large Dams National Seminar, Salvador, Brazil, 12–15 October 2003; pp. 188–198. (In Portuguese). [Google Scholar]
- Souza, P.E.d.A.; Marques, M.G.; Neto, E.F.T.; Teixeira, E.D. Pressure fluctuation in a low-drop and low Froude numbers of hydraulic jump downstream of a spillway. In Proceedings of the Brazilian Dam Committee, XXX - Large Dams National Seminar, Foz do Iguaçu, Brazil, 11–13 May 2015; pp. 1–14. (In Portuguese). [Google Scholar]
- Prá, M.D.; Teixeira, E.D.; Marques, M.G.; Priebe, P.d.S. Evaluation of Pressure Fluctuation in Hydraulic Jump by Dissociation of Hydraulic Forces. Braz. J. Water Resour. (Rbrh) 2016, 21, 221–231. (In Portuguese) [Google Scholar]
- Novakoski, C.K.; Hampe, R.F.; Conterato, E.; Marques, M.G.; Teixeira, E.D. Longitudinal distribution of extreme pressures in a hydraulic jump downstream of a stepped spillway. Braz. J. Water Resour. (Rbrh) 2017, 22, e42. [Google Scholar] [CrossRef][Green Version]
- Marques, M.G.; Drapeau, J.; Verrette, J.-L. Pressure fluctuation coefficient in a hydraulic jump. Braz. J. Water Resour. (Rbrh) 1997, 2, 45–52. (In Portuguese) [Google Scholar]
- Farhoudi, J.; Sadat-Helbar, S.; Aziz, N.I. Pressure fluctuation around chute blocks of SAF stilling basins. J. Agric. Sci. Technol. 2010, 12, 203–212. [Google Scholar]
- Padulano, R.; Fecarotta, O.; Del Giudice, G.; Carravetta, A. Hydraulic design of a USBR Type II stilling basin. J. Irrig. Drain. Eng. 2017, 143, 04017001. [Google Scholar] [CrossRef]
- USBR. Spillways. In Design of small dams, 3rd ed.; US Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1987; pp. 339–437. [Google Scholar]
- Chanson, H.; Carvalho, R. Hydraulic jumps and stilling basins. In Energy Dissipation in Hydraulic Structures; Chanson; CRC Press: Leiden, The Netherlands, 2015; pp. 65–104. [Google Scholar]
- Rajaratnam, N. Hydraulic jumps. In Advances in Hydroscience; Elsevier: Edmonton, Canada, 1967; Volume 4, pp. 197–280. [Google Scholar]
- Peterka, A.J. Hydraulic Design of Stilling Basins and Energy Dissipators, 8th ed.; U.S. Dept. of the Interior, Bureau of Reclamation: Denver, CO, USA, 1984.
- Chaudhry, M.H. Open-Channel Flow, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Bennett, N.D.; Croke, B.F.; Guariso, G.; Guillaume, J.H.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.; Norton, J.P.; Perrin, C. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Bono, R.; Arnau, J.; Alarcón, R.; Blanca, M.J. Bias, precision, and accuracy of skewness and kurtosis estimators for frequently used continuous distributions. Symmetry 2020, 12, 19. [Google Scholar] [CrossRef]
- Sharma, C.; Ojha, C. Statistical parameters of hydrometeorological variables: standard deviation, SNR, skewness and kurtosis. In Advances in Water Resources Engineering and Management; Springer Singapore: Singapore, 2020; Volume 39, pp. 59–70. [Google Scholar]
- Wiest, R.A. Evaluation of the pressure field in hydraulic jump formed downstream of a spillway with different submergence degrees. Master’ Thesis, Hydraulic Reseach Institute, Federal University of Rio Grande do Sul, Porto Alegre, Brazil, 2008. (In Portuguese). [Google Scholar]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]

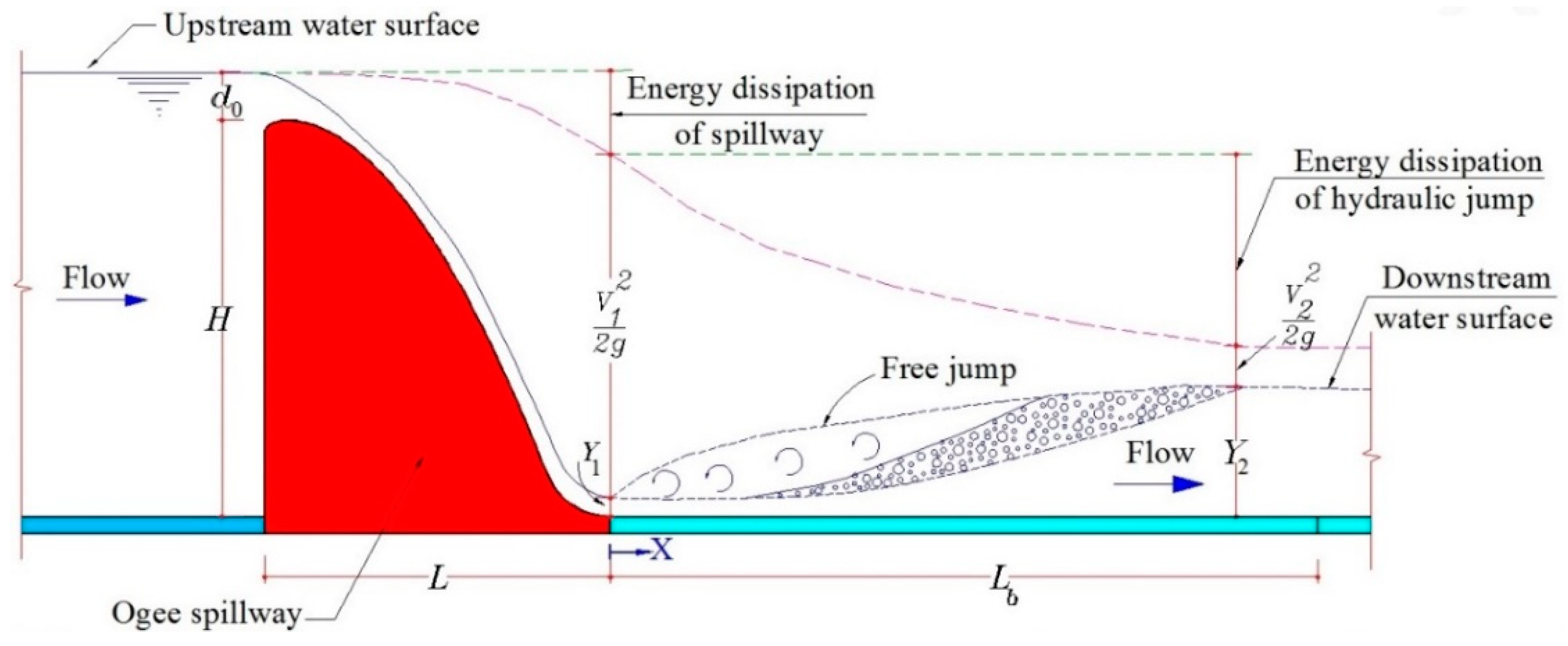
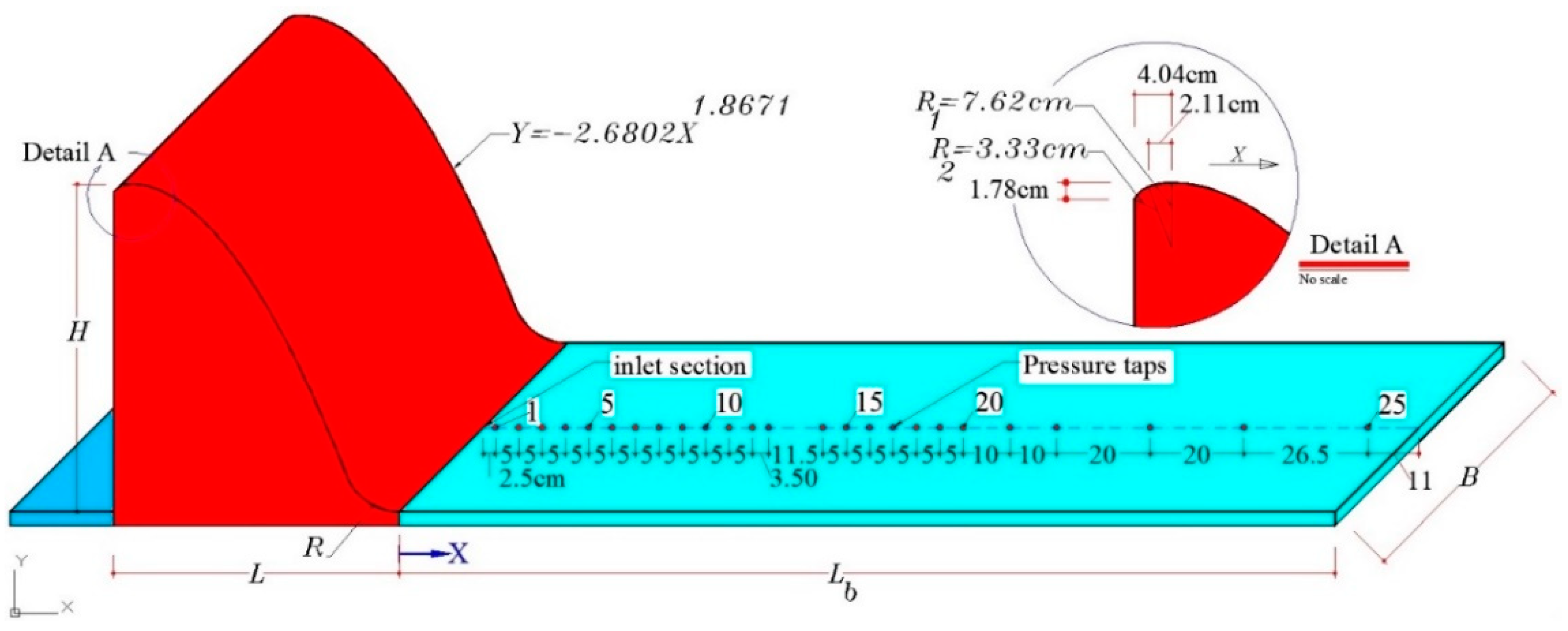
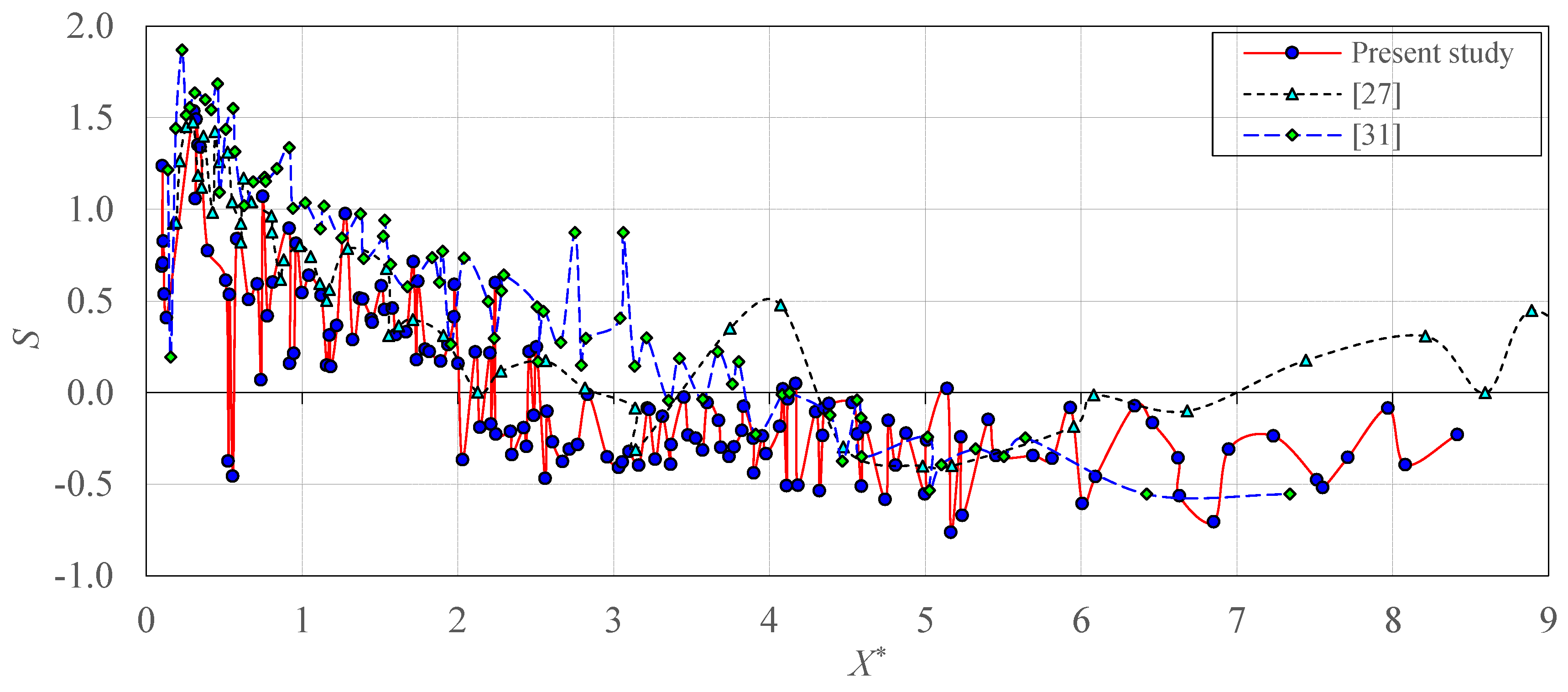
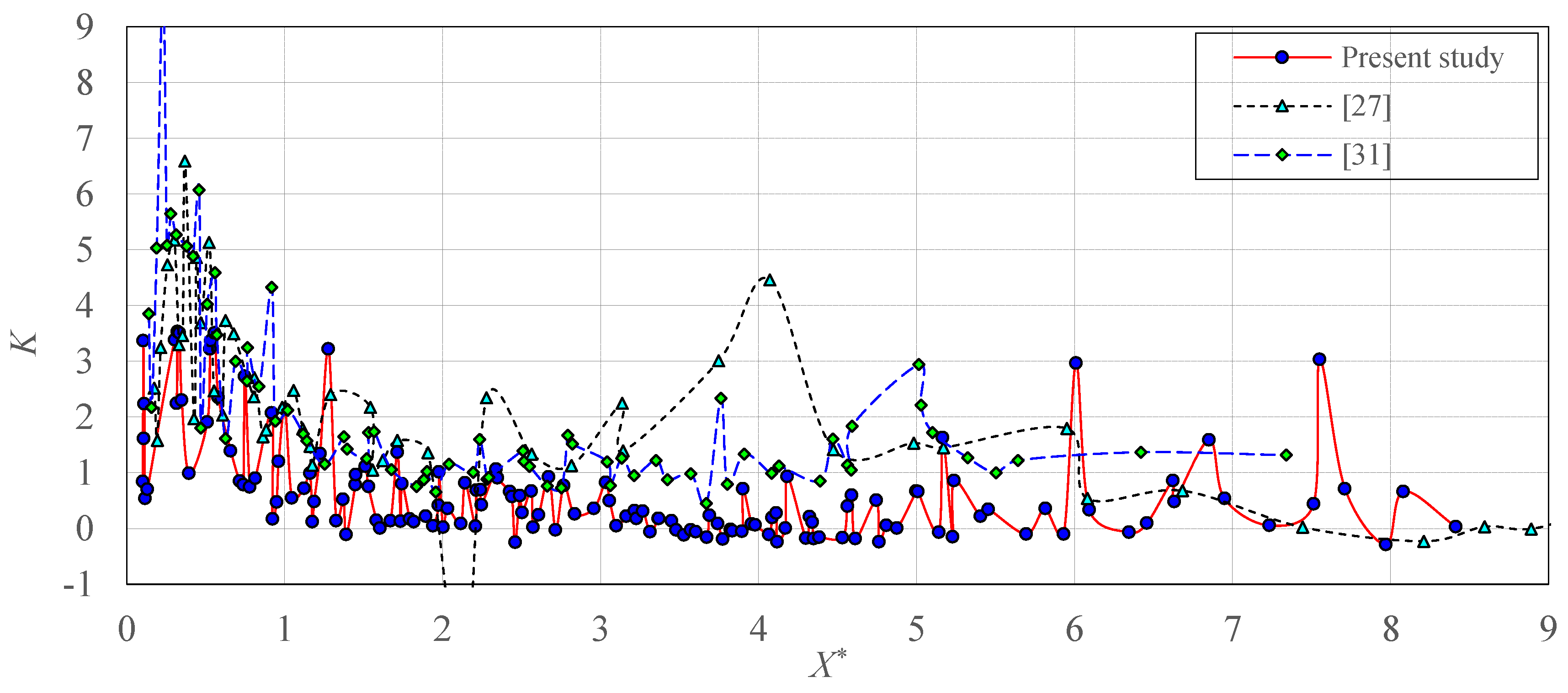



| Q (L/s) | Y1 (cm) | Y2 (cm) | V1 (m/s) | Fr1 (−) |
|---|---|---|---|---|
| 60.4 | 3.04 | 27.55 | 3.89 | 7.12 |
| 55.0 | 2.78 | 26.49 | 3.88 | 7.44 |
| 52.7 | 2.66 | 26.05 | 3.88 | 7.59 |
| 47.5 | 2.41 | 24.87 | 3.87 | 7.96 |
| 43.0 | 2.18 | 23.70 | 3.86 | 8.34 |
| 33.0 | 1.68 | 20.65 | 3.84 | 9.46 |
| k% | α | b | c | R2 |
| 1% | +0.0512 | −0.4480 | −1.6601 | 0.92 |
| 5% | +0.0130 | −0.1323 | −1.3061 | 0.73 |
| 10% | +0.0032 | −0.0450 | −1.0869 | 0.59 |
| 90% | +0.0048 | −0.0325 | +1.2695 | 0.26 |
| 95% | +0.0171 | −0.1393 | +1.8624 | 0.81 |
| 99% | +0.0317 | −0.3598 | +3.3008 | 0.86 |
| Fr1 | X*σmax | X*d | X*r | X*j |
|---|---|---|---|---|
| 7.12 | 1.734 | 3.98 | 5.81 | 7.71 |
| 7.44 | 1.79 | 4.11 | 6.01 | 7.97 |
| 7.59 | 1.60 | 3.95 | 6.09 | 8.08 |
| 7.96 | 1.67 | 3.89 | 5.45 | 8.41 |
| 8.34 | 1.74 | 3.83 | 5.69 | 7.55 |
| 9.46 | 2.00 | 4.09 | 5.40 | 7.51 |
| [31] | 1.75 | 4.00 | 6.00 | 8.50 |
| Method | R2 | RMSE | MAE | WI |
|---|---|---|---|---|
| Equation (15) | 0.776 | 0.097 | 0.075 | 0.931 |
| [26] | 0.674 | 0.140 | 0.115 | 0.875 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mousavi, S.N.; Júnior, R.S.; Teixeira, E.D.; Bocchiola, D.; Nabipour, N.; Mosavi, A.; Shamshirband, S. Predictive Modeling the Free Hydraulic Jumps Pressure through Advanced Statistical Methods. Mathematics 2020, 8, 323. https://doi.org/10.3390/math8030323
Mousavi SN, Júnior RS, Teixeira ED, Bocchiola D, Nabipour N, Mosavi A, Shamshirband S. Predictive Modeling the Free Hydraulic Jumps Pressure through Advanced Statistical Methods. Mathematics. 2020; 8(3):323. https://doi.org/10.3390/math8030323
Chicago/Turabian StyleMousavi, Seyed Nasrollah, Renato Steinke Júnior, Eder Daniel Teixeira, Daniele Bocchiola, Narjes Nabipour, Amir Mosavi, and Shahabodin Shamshirband. 2020. "Predictive Modeling the Free Hydraulic Jumps Pressure through Advanced Statistical Methods" Mathematics 8, no. 3: 323. https://doi.org/10.3390/math8030323
APA StyleMousavi, S. N., Júnior, R. S., Teixeira, E. D., Bocchiola, D., Nabipour, N., Mosavi, A., & Shamshirband, S. (2020). Predictive Modeling the Free Hydraulic Jumps Pressure through Advanced Statistical Methods. Mathematics, 8(3), 323. https://doi.org/10.3390/math8030323








