Existence of Bounded Solutions to a Modified Version of the Bagley–Torvik Equation
Abstract
:1. Introduction
2. Fundamental Notions about Fractional Calculus and the Bagley–Torvik Equation
2.1. Fundamental Notions of Fractional Calculus
2.2. Short Survey of Special Functions
2.3. Deduction of the Bagley–Torvik Equation
3. Stability for the Motion of a Plate Immersed in a Newtonian Fluid
3.1. Assimilable Cases
3.1.1. The Classical Pure Harmonic Oscillator
3.1.2. The Classical Damped Harmonic Oscillator
3.2. The Immersed Plate in a Fluid
- Solutions fulfilling .
- Solutions fulfilling .
3.2.1. Case
3.2.2. Case
- Now, we have coefficients for the degrees zero and .
- The rest of the coefficients coincide with those of the previous case, but after a multiplication by .
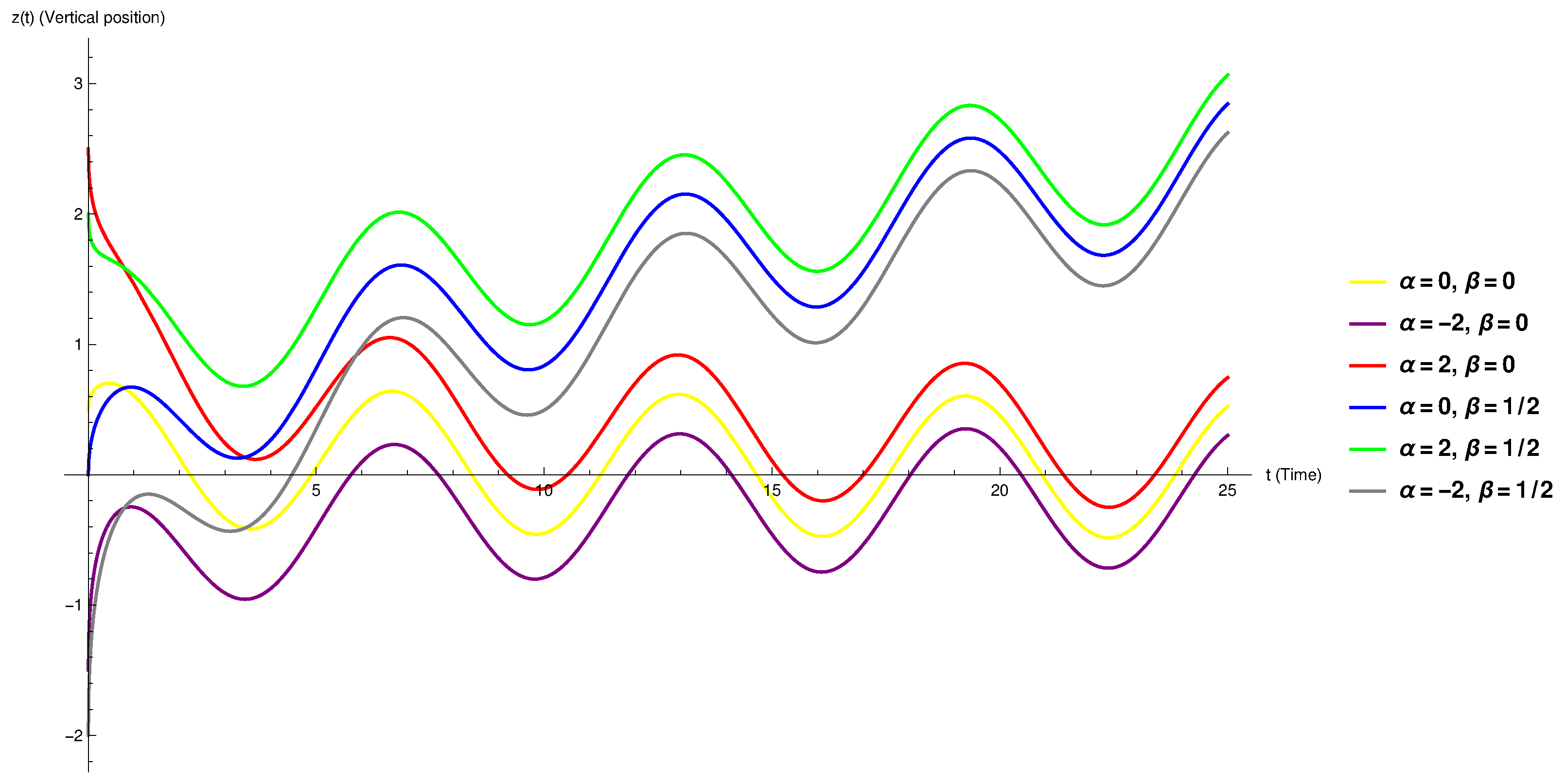
3.3. An Example
- If , then . In this case, .
- If , then . In this case, .
- If , then . In this case, .
4. Sufficient Conditions for Bounded Solutions
- 1.
- 2.
- 3.
Author Contributions
Funding
Conflicts of Interest
References
- Kochubei, A.; Luchko, Y. Handbook of Fractional Calculus with Applications: Basic Theory; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Kochubei, A.; Luchko, Y. Handbook of Fractional Calculus with Applications: Fractional Differential Equations; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Karniadakis, G. Handbook of Fractional Calculus with Applications: Numerical Methods; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Tarasov, V. Handbook of Fractional Calculus with Applications: Applications in Physics, Part A; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Tarasov, V. Handbook of Fractional Calculus with Applications: Applications in Physics, Part B; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Petráš, I. Handbook of Fractional Calculus with Applications: Applications in Control; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Baleanu, D.; Lopes, A.M. Handbook of Fractional Calculus with Applications: Applications in Engineering, Life and Social Sciences, Part A; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Baleanu, D.; Lopes, A.M. Handbook of Fractional Calculus with Applications: Applications in Engineering, Life and Social Sciences, Part B; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Ebaid, A. Analysis of projectile motion in view of fractional calculus. Appl. Math. Model. 2011, 35, 1231–1239. [Google Scholar] [CrossRef]
- Devillanova, G.; Marano, G.C. A free fractional viscous oscillator as a forced standard damped vibration. Fract. Calc. Appl. Anal. 2016, 19, 319–356. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Lopes, A.M. Fractional-order modeling of a diode. Commun. Nonlinear Sci. Numer. Simul. 2019, 70, 343–353. [Google Scholar] [CrossRef]
- Machado, J.T. Fractional generalization of memristor and higher order elements. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 264–275. [Google Scholar] [CrossRef] [Green Version]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Valério, D.; da Costa, J. Introduction to Fractional Control (b 2013); IET: London, UK, 2013. [Google Scholar]
- Cao Labora, D.; Lopes, A.M.; Machado, J.A.T. The Lorentz transformations and one observation in the perspective of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2019, 78, 104855. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin, Germany, 2011. [Google Scholar]
- Torvik, P.J.; Bagley, R.L. On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley-Interscience: Hoboken, NJ, USA, 1993. [Google Scholar]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Valério, D.; Trujillo, J.J.; Rivero, M.; Machado, J.A.T.; Baleanu, D. Fractional calculus: A survey of useful formulas. Eur. Phys. J. Spec. Top. 2013, 222, 1827–1846. [Google Scholar] [CrossRef]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler functions and their applications. J. Appl. Math. 2011, 2011, 1–51. [Google Scholar] [CrossRef] [Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao Labora, D.; Tenreiro Machado, J.A. Existence of Bounded Solutions to a Modified Version of the Bagley–Torvik Equation. Mathematics 2020, 8, 289. https://doi.org/10.3390/math8020289
Cao Labora D, Tenreiro Machado JA. Existence of Bounded Solutions to a Modified Version of the Bagley–Torvik Equation. Mathematics. 2020; 8(2):289. https://doi.org/10.3390/math8020289
Chicago/Turabian StyleCao Labora, Daniel, and José António Tenreiro Machado. 2020. "Existence of Bounded Solutions to a Modified Version of the Bagley–Torvik Equation" Mathematics 8, no. 2: 289. https://doi.org/10.3390/math8020289
APA StyleCao Labora, D., & Tenreiro Machado, J. A. (2020). Existence of Bounded Solutions to a Modified Version of the Bagley–Torvik Equation. Mathematics, 8(2), 289. https://doi.org/10.3390/math8020289





