Some Alternative Solutions to Fractional Models for Modelling Power Law Type Long Memory Behaviours
Abstract
1. Introduction
- -
- to illustrate these drawbacks and to show that alternative solutions exist for power law-type long memory behaviours modelling;
- -
- to clarify the limits and benefits of fractional models.
2. Power Law-Type Long Memory Behaviours
2.1. Spectral Density and Autocorrelation Functions of the Input Output Signals of an LTI System
2.2. Power Law Concept Extended to LTI Systems
- Its impulse response slowly decays with respect to time according to:
- For a white noise input of variance , its output autocorrelation function is:
- For a white noise input of variance , its output power spectral density is:
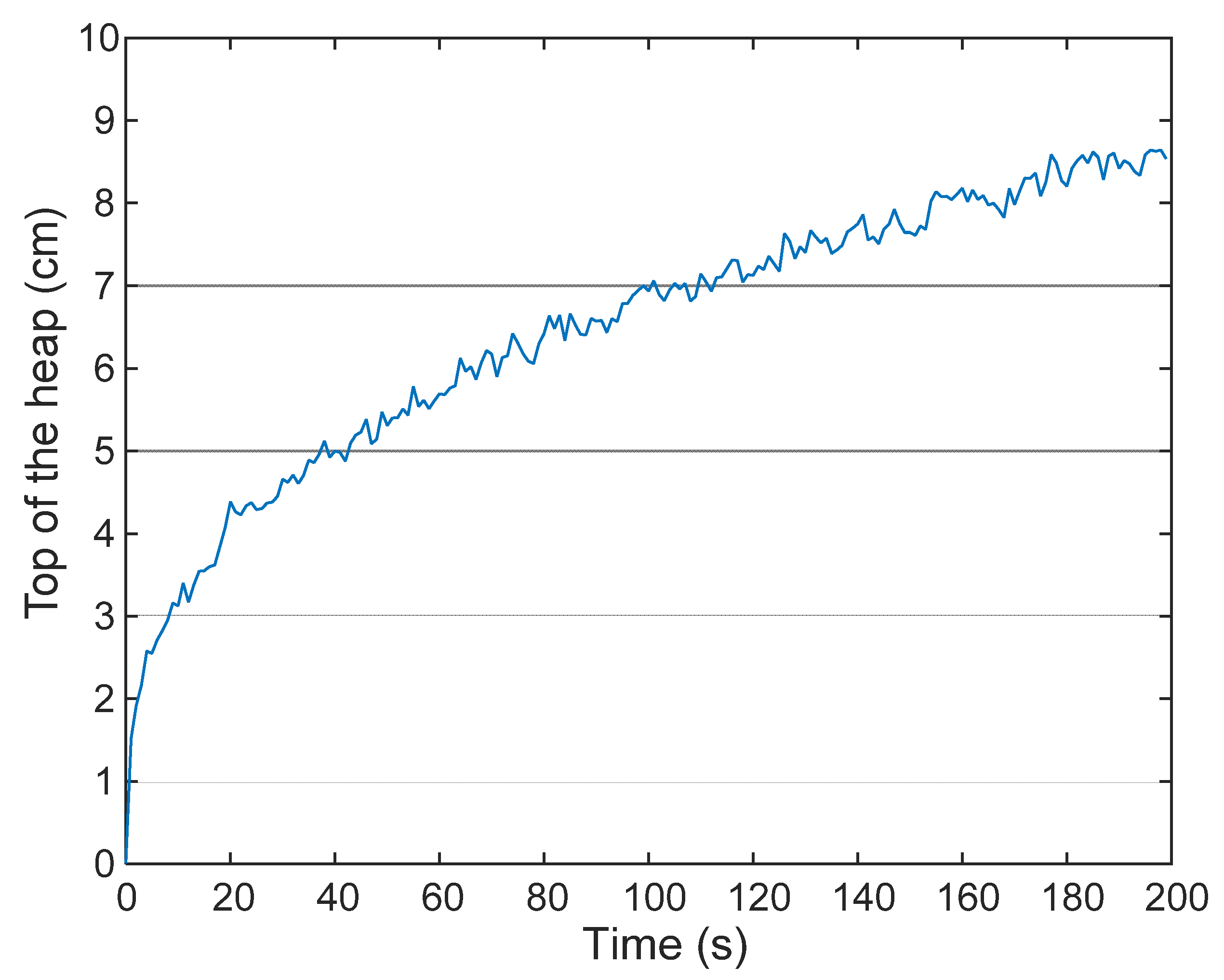
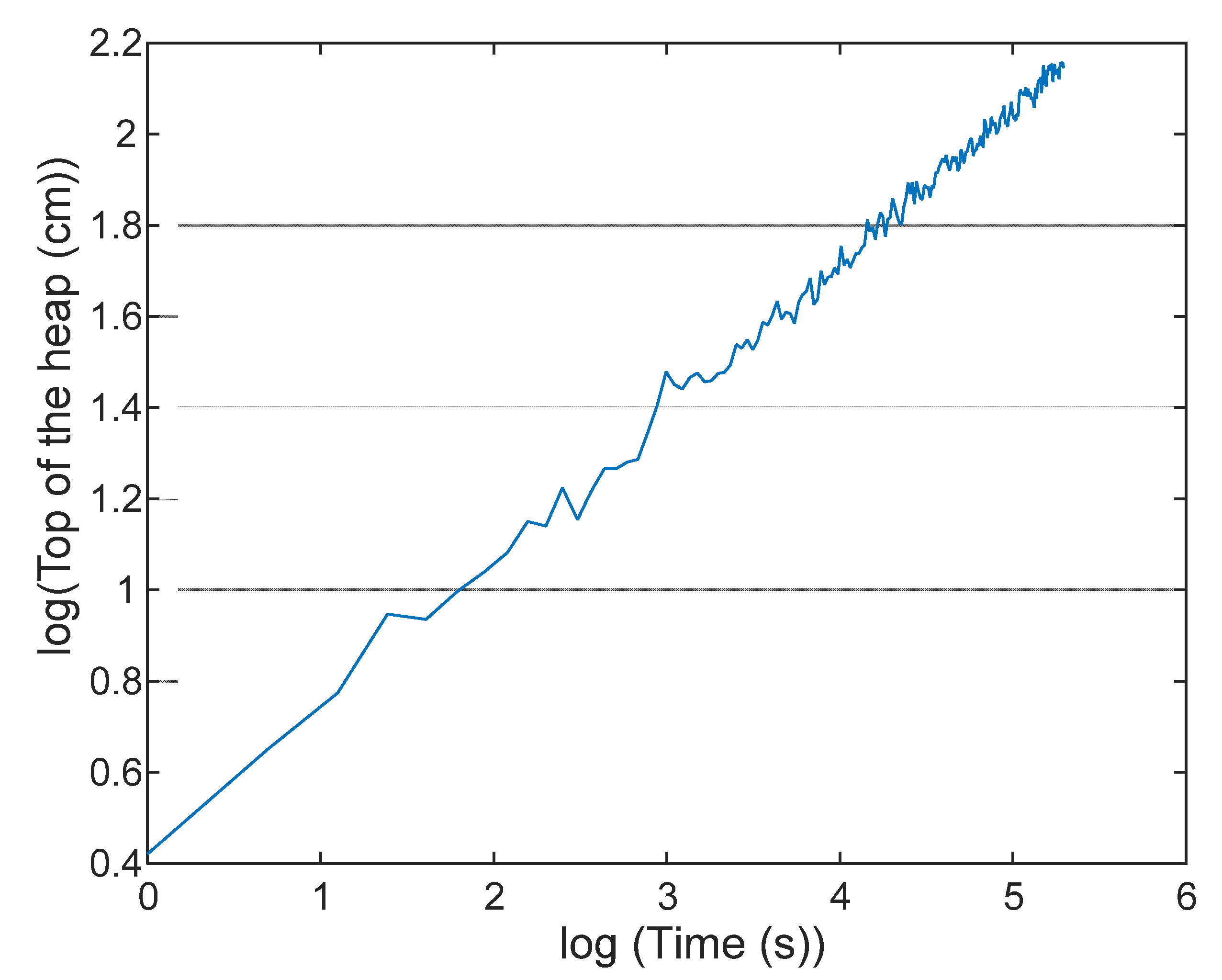
3. Sand Heap Growth: An Example of Power Law-Type Long Memory Behaviour
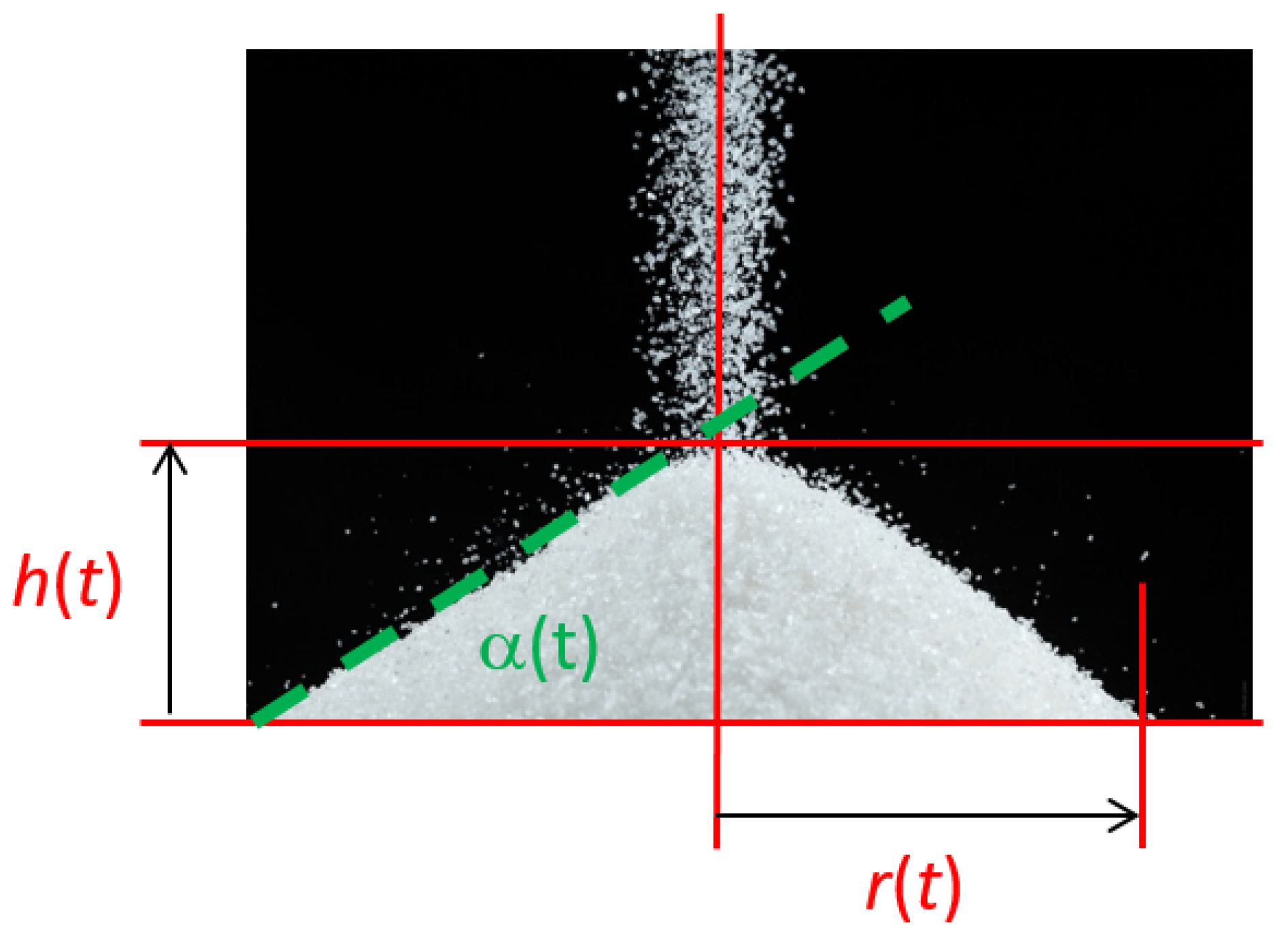
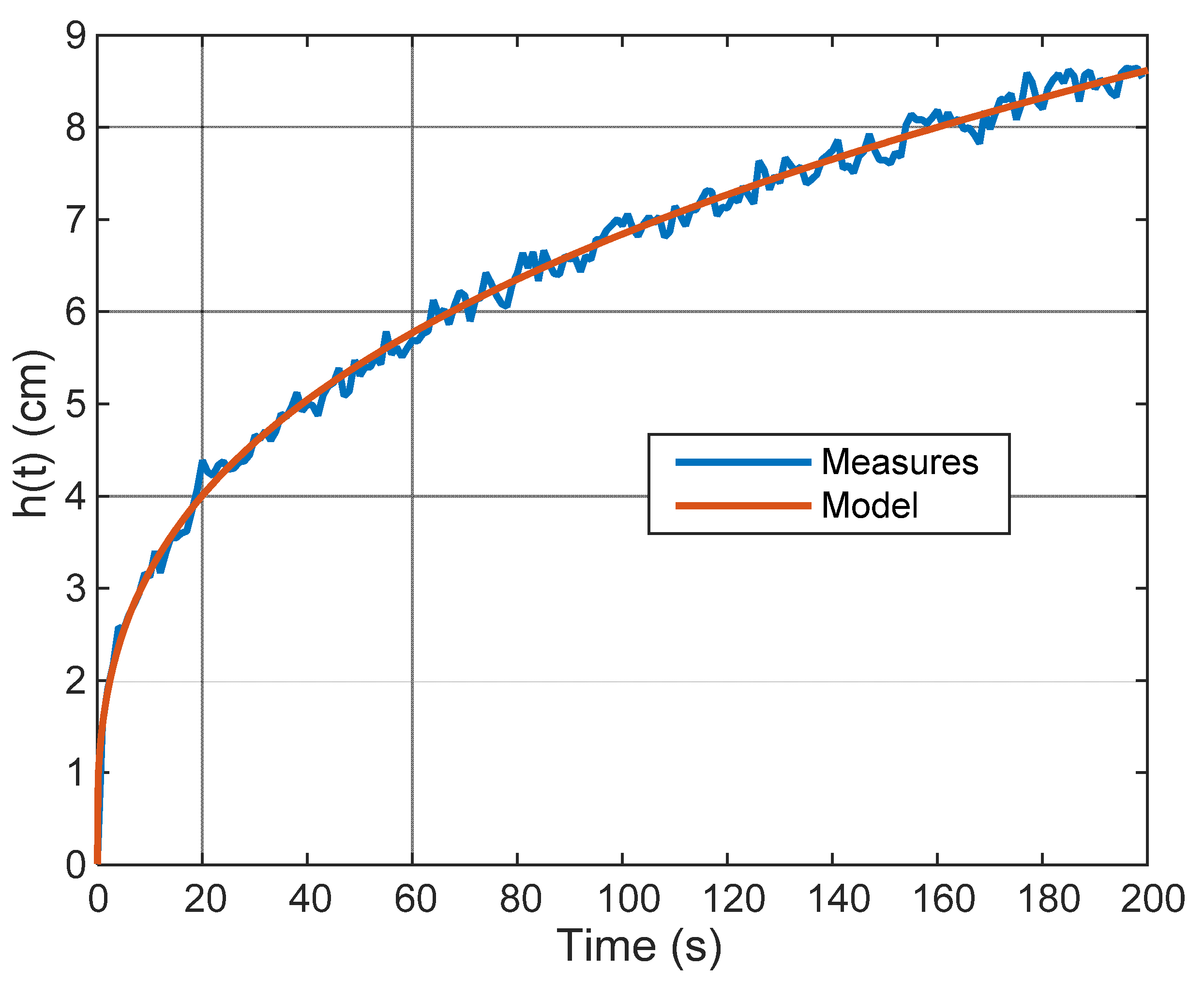
3.1. System Description
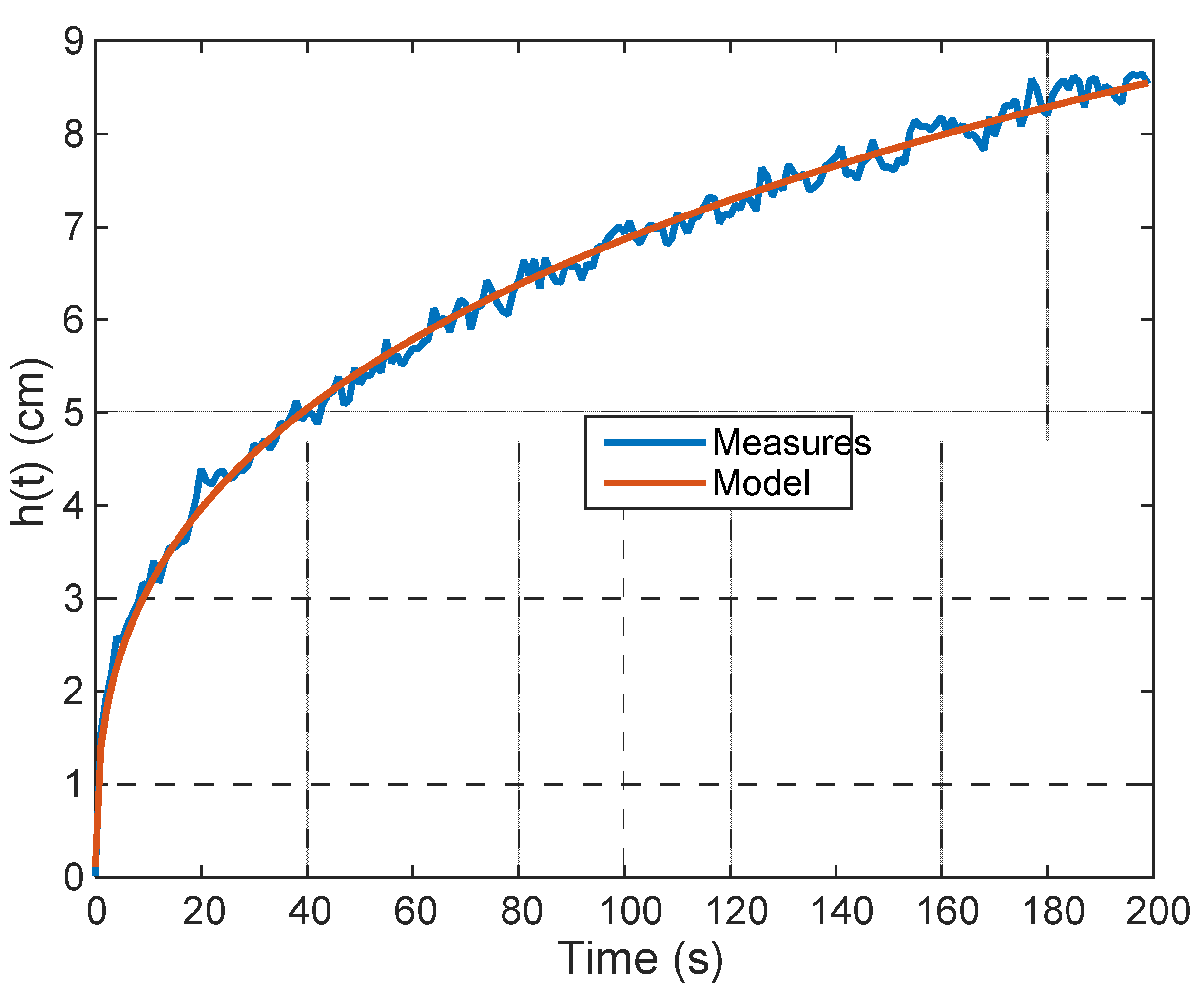
3.2. Fractional Modelling of the Sand Pile Growth
4. Drawbacks of Fractional Modelling
- -
- the temperature measure is done at the point where the heat flux is applied; or
- -
- an infinite dimension medium is considered.
5. Another Possible Model
6. Beyond Fractional Models
6.1. Some Classes of Non-Linear Models
- -
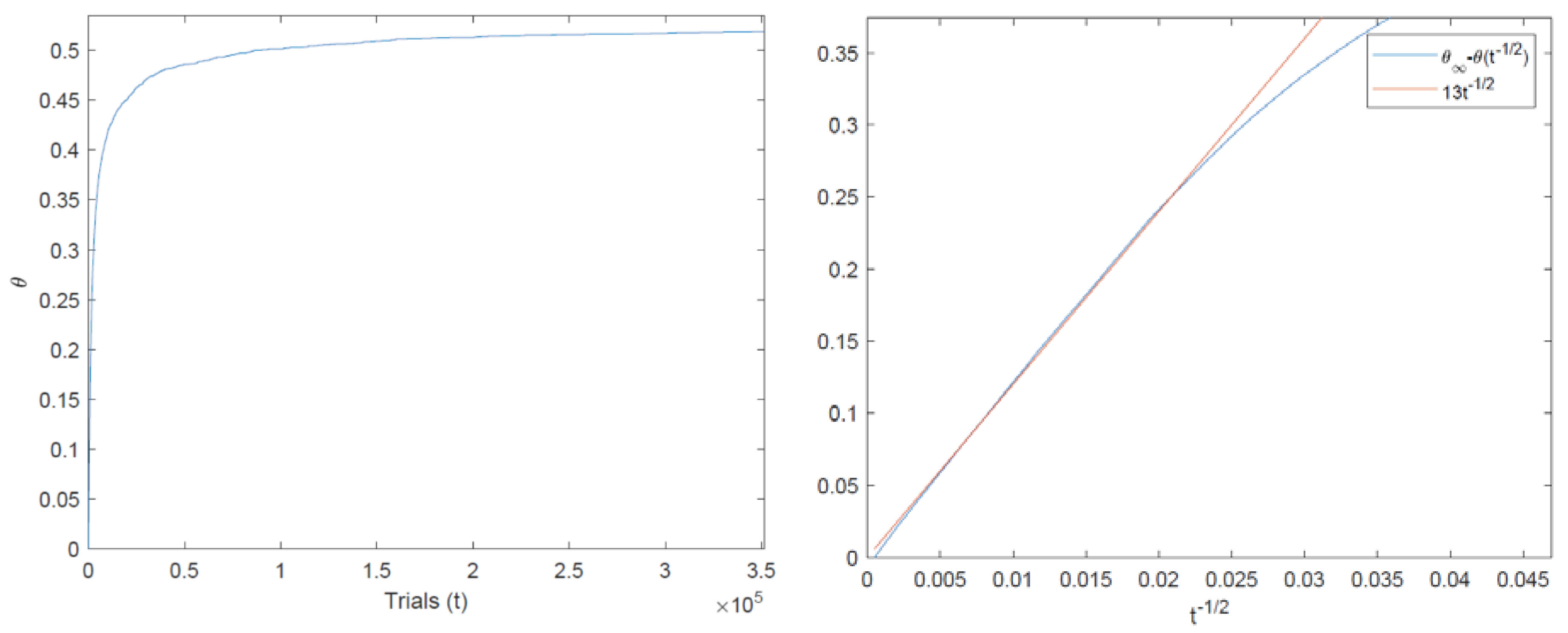
- With the RSA process (as for the sand pile process), if the flow is stopped, then the surface filling stops. If the flow restarts, the surface filling restarts from the same state. Such behaviour cannot be reproduced with a classical linear fractional model whose output relaxes for a null input.
- -
- With a fractional modelling approach, an infinite dimensional model is obtained, requiring the entire model past knowledge for a proper initialisation. However, in practice, such knowledge is not required. Initialisation of the RSA process only requires the knowledge of the density and a uniform distribution of the disks on the surface. Exact knowledge of the position of all the disks on the surface is not necessary, and thus not all the process history is required.
- -
- It permits an accurate fitting of the RSA process kinetic in spite of its power law behaviour;
- -
- It takes into account some non-linear behaviours in relation to the flow of incoming disks (or particles for the case of a real adsorption process);
- -
- Its state is only of one dimension, and its initialisation only requires knowledge of the covered density;
- -
- Its implementation does not require any approximation step.
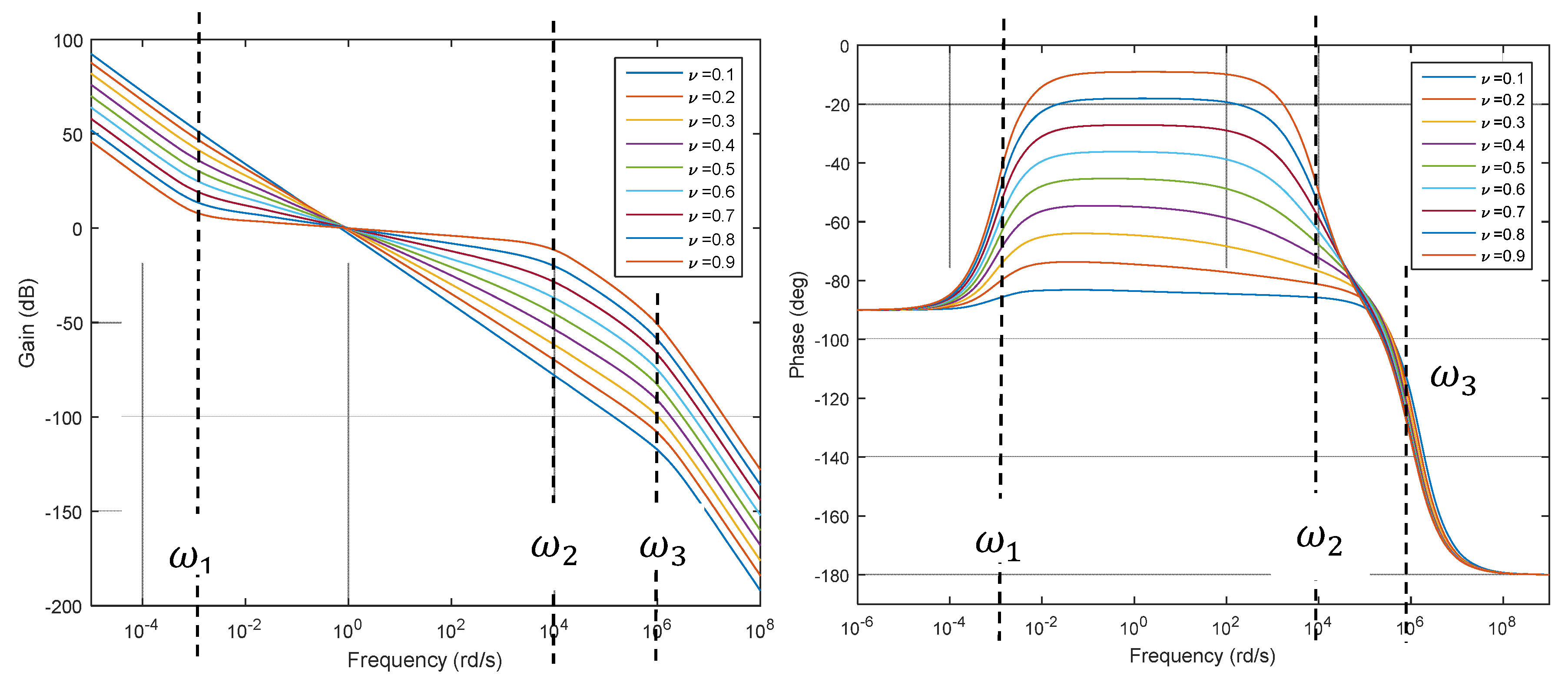
6.2. Distributed Time Delay Models
- -
- In Relation (43), the variable can be viewed as a real state and a physical meaning can be associated to it;
- -
- There is no longer any ambiguity in the operator used for the definition of Relation (43) (in Equation (32), Caputo’s, Riemann–Liouville, or another can be chosen);
- -
- Kernel in Relation (43) is not singular, unlike the definition of fractional derivative in Equation (32);
- -
- The memory of Model (43) is of finite length;
- -
- Initialisation of Model (43) requires knowledge of its state on a finite length and is well defined.
6.3. First Kind Volterra Equations
- Adapting the kernel in Relation (48) (see also [29], it is possible to produce, with the same kind of equation, power law behaviours of various types (denoted explicit, implicit), but also many other long memory behaviours;
- In Relation (48), if , is a matrix of kernels such that , thus permitting great flexibility in the tuning of Relation (48). The case comes closer to the non-commensurate fractional pseudo-state space representation case, but it should be remembered that physical interpretations invalidate this kind of model [18].
7. Conclusions
- -
- Even if fractional models permit an accurate fitting of power law-type input–output behaviours, they can give birth to disconnected issues of the system considered (initialisation, dimension, interpretations, …)
- -
- simpler more physical models can be obtained if we try to understand the physical origin of the behaviour.
Author Contributions
Funding
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Theory and Applications of Differentiation and Integration to Arbitrary Order (Mathematics in Science and Engineering, V); Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations. Mathematics in Sciences and Engineering; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: London, UK, 1993. [Google Scholar]
- Bagley, R.L.; Calico, R.A. Fractional order state equations for the control of viscoelastically damped structures. J. Guid. Control Dyn. 1991, 14, 304–311. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Alan SWillsky, A.S.; Hamid, S. Signals and Systems, Pearson New International Edition; Pearson Education Limited: Harlow, UK, 1996. [Google Scholar]
- Mandal, S.; Khakhar, D. Granular surface flow on an asymmetric conical heap. J. Fluid Mech. 2019, 865, 41–59. [Google Scholar] [CrossRef]
- Pacheco-Vazquez, F.; Moreau, F.; Vandewalle, N.; Dorbolo, S. Sculpting sandcastles grain by grain: Self-assembled sand towers. Phys. Rev. E 2012, 86, 051303. [Google Scholar] [CrossRef] [PubMed]
- Oustaloup, A. Diversity and Non-Integer Differentiation for System Dynamics; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Ben Adda, F. Geometric interpretation of the fractional derivative. J. Fract. Calc. 1997, 11, 21–52. [Google Scholar]
- Podlubny, I. Geometric and physical interpretation of fractional integration and fractional differentiation. J. Fract. Calc. Appl. Anal. 2002, 5, 357–366. [Google Scholar]
- Gorenflo, R. Afterthoughts on interpretation of fractional derivatives and integrals. In Transform Methods and Special Functions, Varna’96, Institute of Mathematics and Informatics; Rusev, P., Dimovski, I., Kiryakova, V., Eds.; Bulgarian Academy of Sciences: Bulgarian, Sofia, 1998. [Google Scholar]
- Mainardi, F. Considerations on fractional calculus: Interpretations and applications. In Transform Methods and Special Functions, Varna’96, Institute of Mathematics and Informatics; Rusev, P., Dimovski, I., Kiryakova, V., Eds.; Bulgarian Academy of Sciences: Bulgarian, Sofia, 1998. [Google Scholar]
- Nigmatullin, R.R. A fractional integral and its physical interpretation. Theoret. and Math. Physics 1992, 90, 242–251. [Google Scholar] [CrossRef]
- Rutman, R.S. On physical interpretations of fractional integration and differentiation. Theor. Math. Phys. 1995, 105, 393–404. [Google Scholar] [CrossRef]
- Sabatier, J.; Merveillaut, M.; Malti, R.; Oustaloup, A. On a Representation of Fractional Order Systems: Interests for the Initial Condition Problem. In Proceedings of the 3rd IFAC Workshop on “Fractional Differentiation and its Applications” (FDA’08), Ankara, Turkey, 5–7 November 2008. [Google Scholar]
- Tenreiro Machado, J.A. A probabilistic Interpretation of the Fractional-Order differentiation. J. Fract. Calc. Appl. Anal. 2003, 6, 73–80. [Google Scholar]
- Dokoumetzidis, A.; Magin, R.; Macheras, P. A commentary on fractionalization of multi-compartmental models. Pharm. Pharm. 2010, 37, 203–207. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, C.; Merveillaut, M.; Feneteau, L. On observability and pseudo state estimation of fractional order systems. Eur. J. Control 2012, 18, 260–271. [Google Scholar] [CrossRef]
- Matignon, D. Stability properties for generalized fractional differential systems. ESAIM Proc. 1998, 5, 145–158. [Google Scholar] [CrossRef]
- Montseny, G. Diffusive representation of pseudo-differential time-operators. ESAIM Proc. 1998, 5, 159–175. [Google Scholar] [CrossRef]
- Sabatier, J.; Merveillaut, M.; Malti, R.; Oustaloup, A. How to Impose Physically Coherent Initial Conditions to a Fractional System? Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1318–1326. [Google Scholar] [CrossRef]
- Sabatier, J.; Nguyen, H.C.; Farges, C.; Deletage, J.Y.; Moreau, X.; Guillemard, F.; Bavoux, B. Fractional models for thermal modeling and temperature estimation of a transistor junction. Adv. Differ. Equ. 2011. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, C.; Trigeassou, J.C. Fractional systems state space description: Some wrong ideas and proposed solutions. J. Vib. Control 2014, 20, 1076–1084. [Google Scholar] [CrossRef]
- De Oliveira, E.C.; Tenreiro Machado, J.A. A Review of Definitions for Fractional Derivatives and Integral. Math. Probl. Eng. 2019, 2014, 238459. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, C. Comments on the description and initialization of fractional partial differential equations using Riemann-Liouville’s and Caputo’s definitions. J. Comput. Appl. Math. 2018, 339, 30–39. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Coito, F.J. Initial Conditions: What Are We Talking about? In Proceedings of the Third IFAC Workshop on Fractional Differentiation, Ankara, Turkey, 5–7 November 2008. [Google Scholar]
- Sabatier, J.; Rodriguez Cadavid, S.; Farges, C. Advantages of limited frequency band fractional integration operator in fractional models definition. In Proceedings of the Conference on Control, Decision and Information Technologies (CoDIT 2019), Paris, France, 23–26 April 2019. [Google Scholar]
- Sabatier, J. Non-Singular Kernels for Modelling Power Law Type Long Memory Behaviours and Beyond. Cybernetics 2020. accepted. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Tartaglione, V.; Farges, C.; Sabatier, J. Dynamical Modelling of Random Sequential Adsorption. In Proceedings of the European Control Conference ECC 2020, St-Petersburg, Russia, 12–15 May 2020. [Google Scholar]
- Feder, J.; Giaever, I. Adsorption of ferritin. J. Colloid Interface Sci. 1980, 78, 144–154. [Google Scholar] [CrossRef]
- Viot, P.; Tarjus, G.; Ricci, S.; Talbot, J. Random sequential adsorption of anisotropic particles. I. jamming limit and asymptotic behavior. J. Chem. Phys. 1992, 97, 5212–5218. [Google Scholar] [CrossRef]
- Sabatier, J. Distributed time delay systems for power law long memory behaviors modelling. In Proceedings of the 58th Conference on Decision and Control (CDC 2019), Nice, France, 11–13 December 2019. [Google Scholar]
- Sabatier, J. Power Law Type Long Memory Behaviors Modeled with Distributed Time Delay Systems. Fract. Fractals 2020, 4, 1. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabatier, J.; Farges, C.; Tartaglione, V. Some Alternative Solutions to Fractional Models for Modelling Power Law Type Long Memory Behaviours. Mathematics 2020, 8, 196. https://doi.org/10.3390/math8020196
Sabatier J, Farges C, Tartaglione V. Some Alternative Solutions to Fractional Models for Modelling Power Law Type Long Memory Behaviours. Mathematics. 2020; 8(2):196. https://doi.org/10.3390/math8020196
Chicago/Turabian StyleSabatier, Jocelyn, Christophe Farges, and Vincent Tartaglione. 2020. "Some Alternative Solutions to Fractional Models for Modelling Power Law Type Long Memory Behaviours" Mathematics 8, no. 2: 196. https://doi.org/10.3390/math8020196
APA StyleSabatier, J., Farges, C., & Tartaglione, V. (2020). Some Alternative Solutions to Fractional Models for Modelling Power Law Type Long Memory Behaviours. Mathematics, 8(2), 196. https://doi.org/10.3390/math8020196




