Using Cuckoo Search Algorithm with Q-Learning and Genetic Operation to Solve the Problem of Logistics Distribution Center Location
Abstract
1. Introduction
- (1)
- In the DMQL-CS algorithm, the step size strategy is considered as an action which applies multiple step control strategies (linear decreasing strategy, non-linear decreasing strategy, and adaptively step-size strategy). In the DMQL-CS algorithm, according to multi-step effect of individual for a few steps forward, the optimal step size control strategy is learned. During each learning evolution step size, finally, the optimal individual and corresponding optimal step size strategy are derived by calculating the Q function value. The current individual continues to evolve through the step size obtained, which increases the adaptability of individual evolution.
- (2)
- The research introduces two genetic operators, crossover and mutation, into the DMQL-CS algorithm, intended for accelerating convergence. During crossover and mutation process, chromosomes are divided into pairs according to certain probability. We introduce the specifically designed crossover operation into problem of logistics distribution center location in this paper, which determines the performance of the algorithm to some extent. To improve the search ability of the CS algorithm, numerous strategies have been designed to adjust the crossover rate. In this work, a self-adaptive scheme is used to adjust the crossover rate. Genetic operators expand the search area of the population to improve the exploration and maintain the diversity of the population, which also helps to improve the exploration of the population of learners.
2. Related Work
3. Cuckoo Search
- (1)
- Each cuckoo lays one egg at a time, and places it in a randomly chosen nest.
- (2)
- The best nests with the highest-quality eggs (solutions) will be carried over to the next generations.
- (3)
- The number of available host nests is fixed, and the alien egg is discovered by the host bird with the probability . If the alien egg is discovered, the nest is abandoned and a new nest is built in a new location.
| Algorithm 1 CS Algorithm. |
| (1) randomly initialize population of n host nests |
| (2) calculate fitness value for each solution in each nest |
| (3) while (stopping criterion is not meet do) |
| (4) Generate as new solution by using Lévy flights; |
| (5) Choose candidate solution ; |
| (6) if |
| (7) Replace with new solution ; |
| (8) end if |
| (9) Throw out a fraction (pa) of worst nests; |
| (10) Generate solution using Equation (3); |
| (11) if |
| (12) Replace with new solution ; |
| (13) end if |
| (14) Rank the solution and find the current best. |
| (15) end while |
4. Cuckoo Search Algorithm with Q-Learning and Genetic Operations
4.1. Q-Learning Model
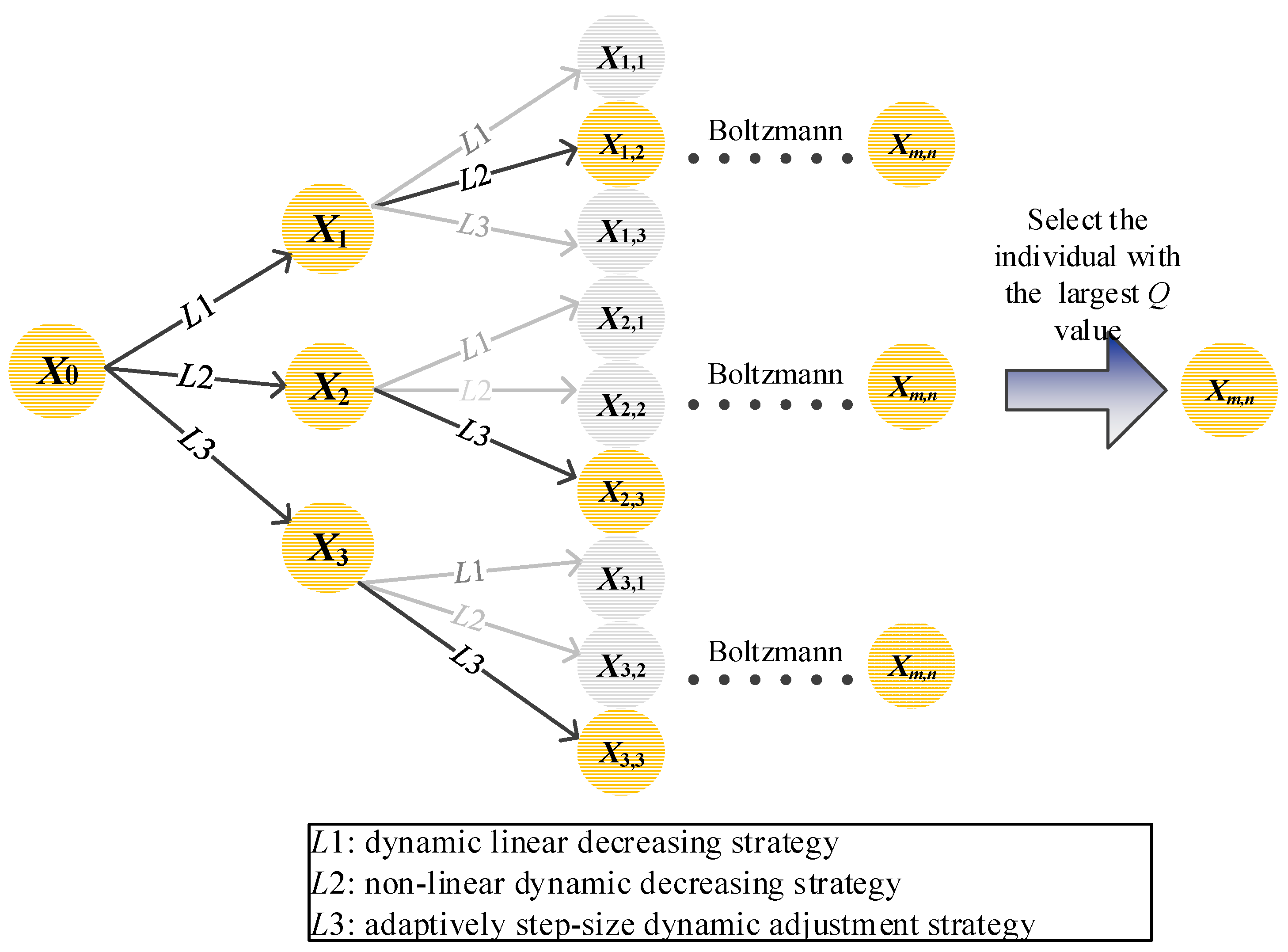
4.2. Step Size Control Model by Using Q-Learning
| Algorithm 2 Step size with Q-Learning. |
| (1) Each individual is expressed as (x, σ), and the number of learning steps M is set; |
| (2) Generate three new offspring for each individual by using the given step size control strategy (Linear decreasing strategy, non-linear decreasing strategy, adaptively step-size dynamic adjustment strategy), and set t = 1; |
| (3) Do while t < m |
| Each individual generates three offspring by using the given step size control strategy, as shown in Equations (9)–(12). |
| Calculate the probability of the newly generated offspring by using the Boltzmann distribution, and an individual is selected according to the probability. |
| t = t + 1; |
| (4) Calculate the corresponding Q value of each retained individual according to the three-step selection strategy. The step size corresponding to the step control strategy is retained when Q is maximized, the corresponding offspring are selected, and other offspring will be discarded. |
4.3. Genetic Operation
4.3.1. Crossover Process
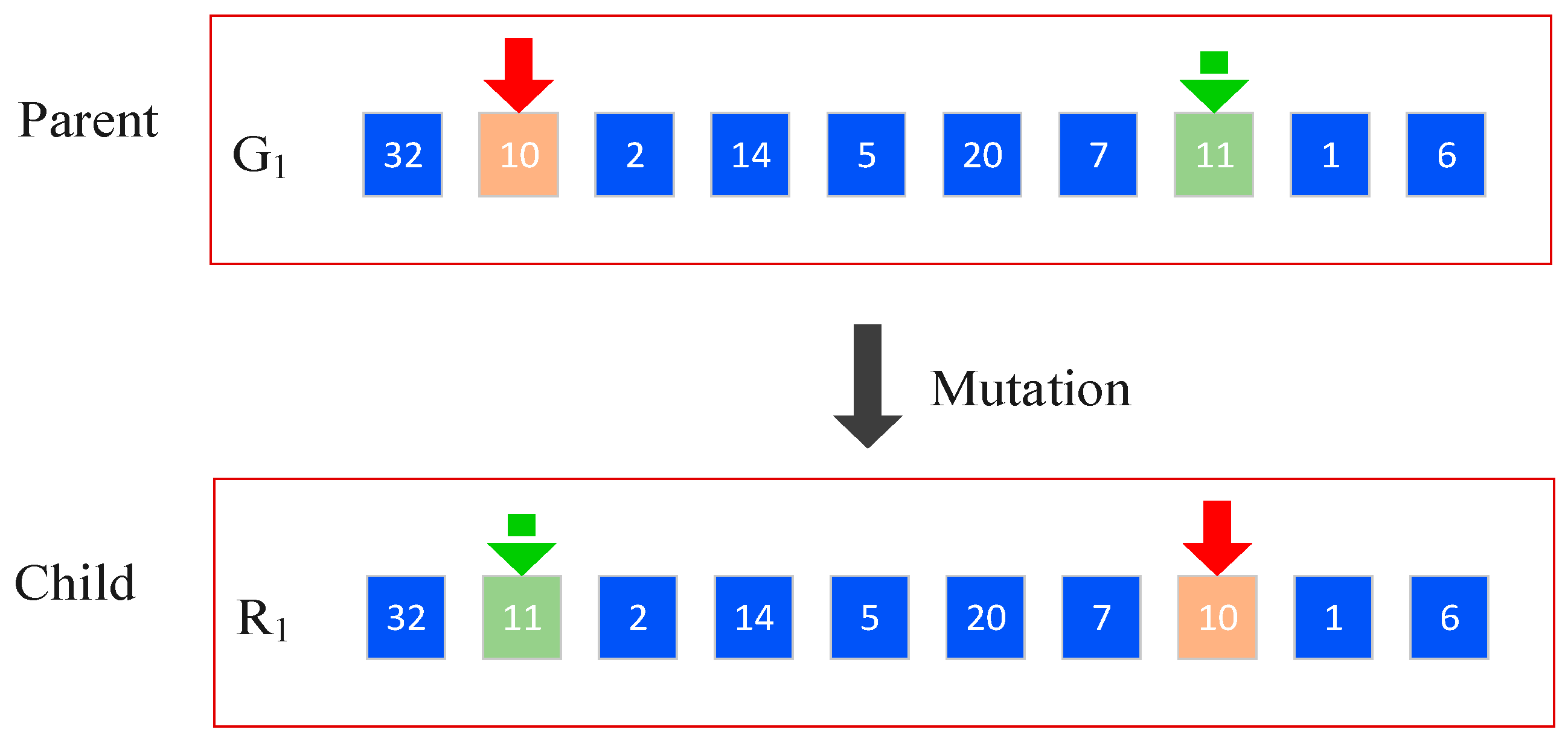
4.3.2. Mutation Process
4.3.3. Cuckoo Search Algorithm with Q-Learning Model and Genetic Operator
| Algorithm 3 DMQL-CS Algorithm. |
| Input: Population size, NP; Maximum number of function evaluations, MAX_FES, LP |
| (1) Randomly initialize position of NP nest, FES = NP; |
| (2) Calculate the fitness value of each initial solution; |
| (3) while (stopping criterion is not meet do) |
| (4) Select the best step size control strategy according to Algorithm 2; |
| (5) Generate new solution with the new step size by Lévy flights; |
| (6) Randomly choose a candidate solution ; |
| (7) if |
| (8) Replace with new solution ; |
| (9) end if |
| (10) Generate new solution by using crossover operator and mutation operator; |
| (11) Throw out a fraction (pa) of worst nests, generate solution using Equation (3); |
| (12) if |
| (13) Replace with new solution ; |
| (14) end if |
| (15) Rank the solution and find the current best. |
| (16) end while |
4.3.4. Analysis of Algorithm Complexity
5. Results
5.1. Optimization of Functions and Parameter Settings
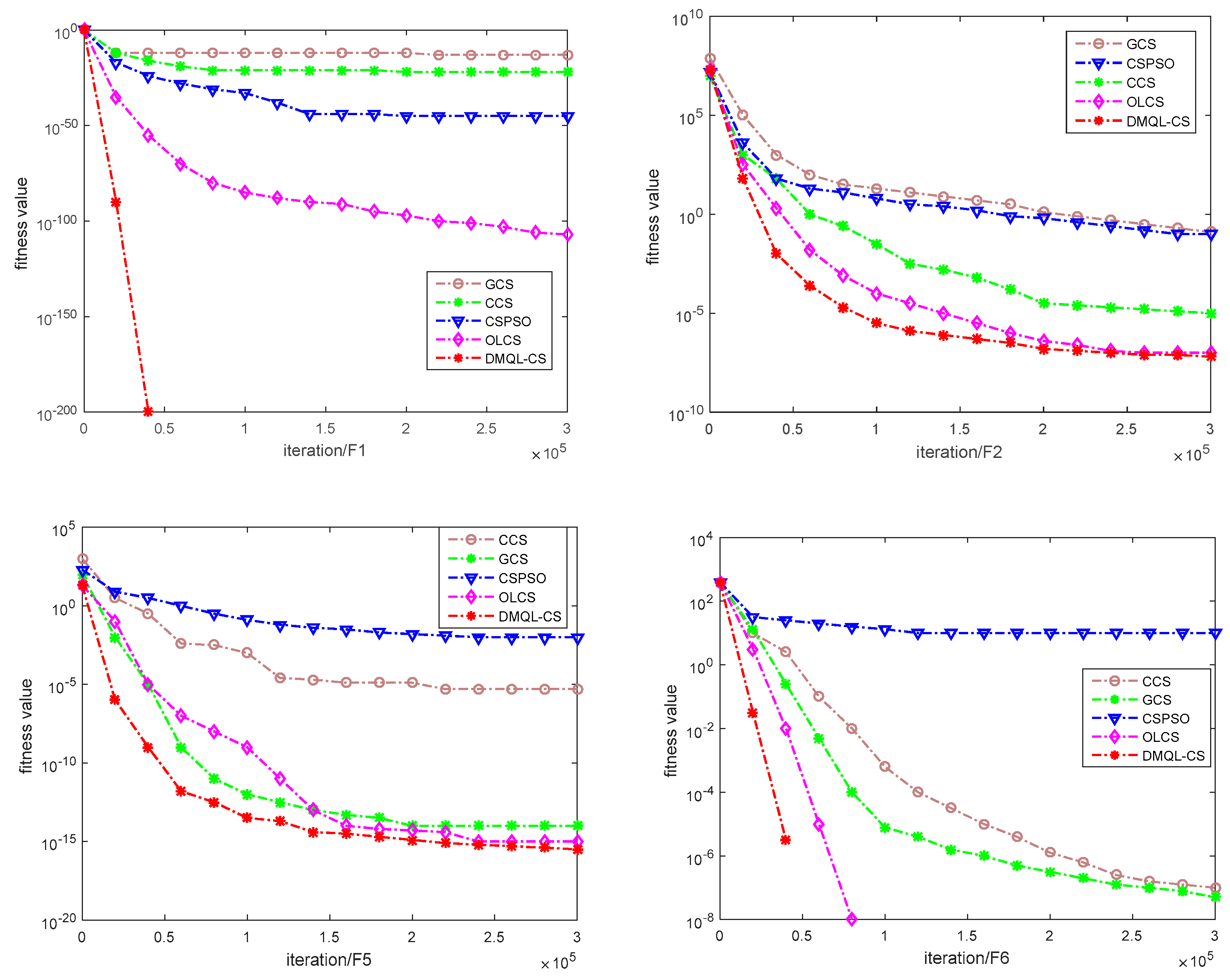
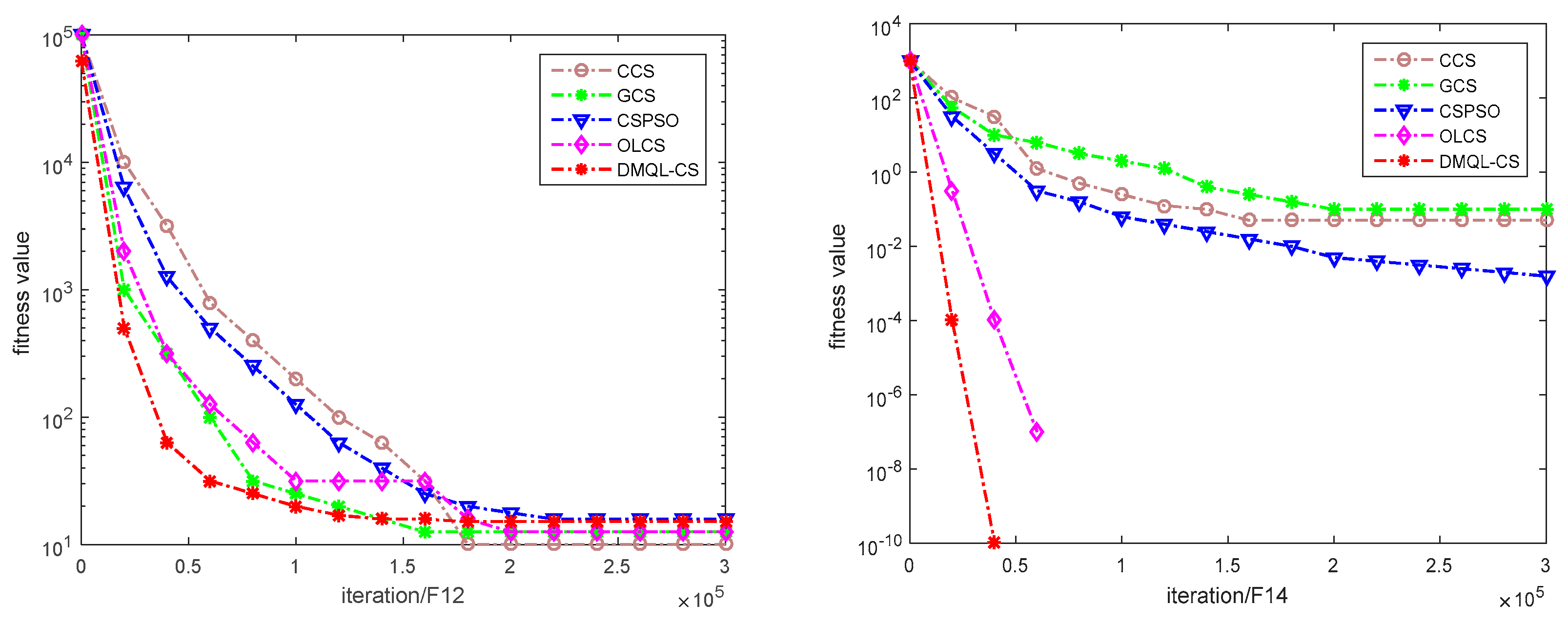
5.2. Comparison with Other CS Variants and Rank Based Analysis
5.3. Statistical Analysis of Performance for the CEC 2013 Test Suite
5.4. Application in the Problem of Logistics Distribution Center Location
5.4.1. Problem Description
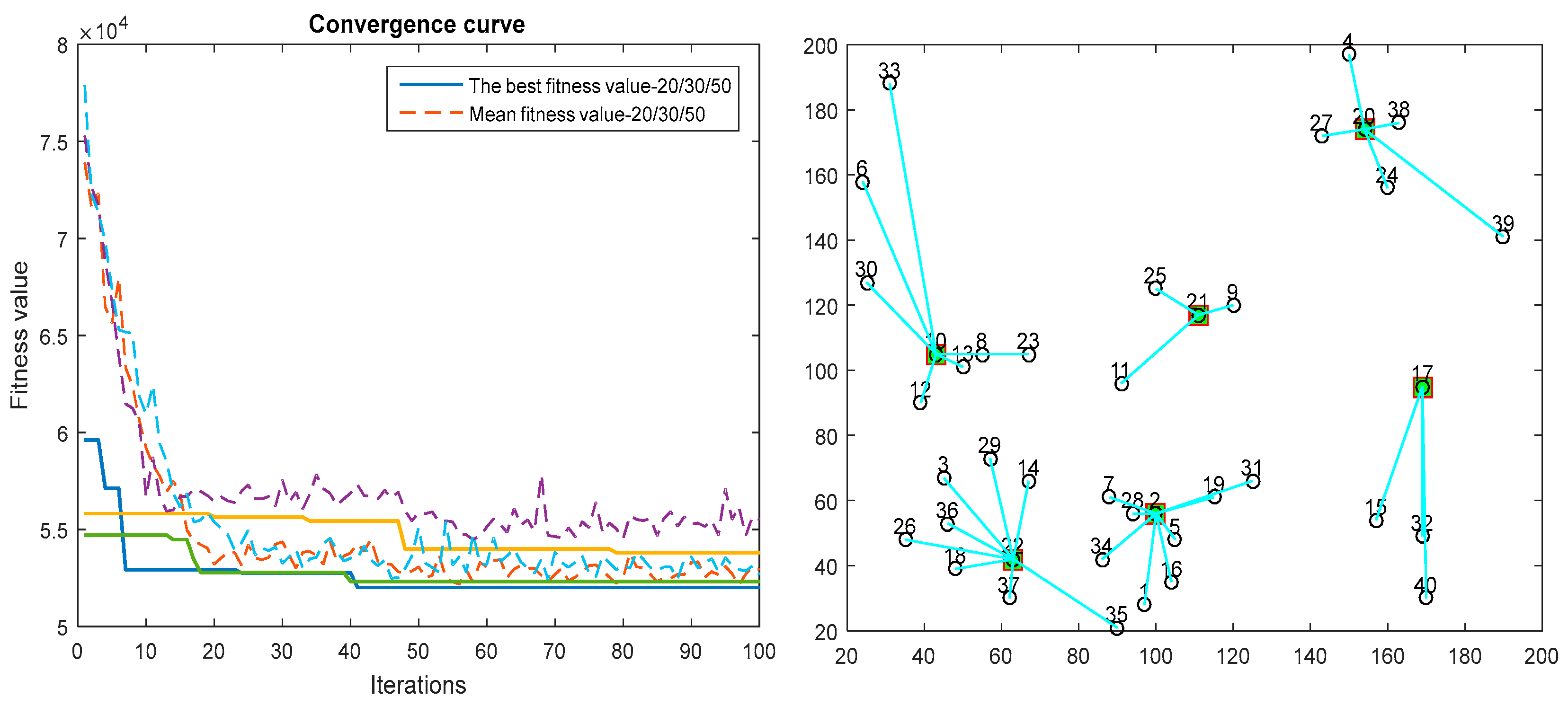
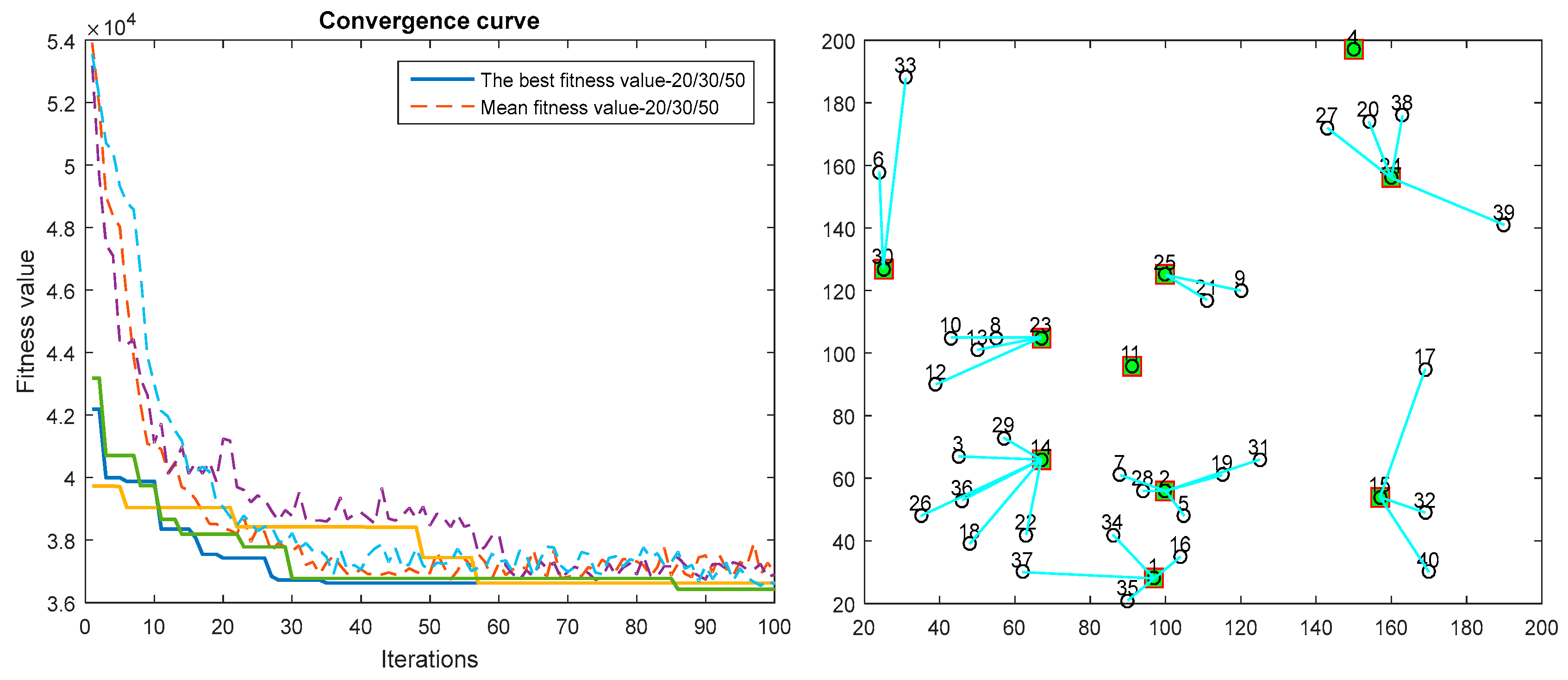
5.4.2. Analysis of Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sang, H.-Y.; Pan, Q.-K.; Duan, P.-Y.; Li, J.-Q. An effective discrete invasive weed optimization algorithm for lot-streaming flowshop scheduling problems. J. Intell. Manuf. 2015, 29, 1337–1349. [Google Scholar] [CrossRef]
- Sang, H.-Y.; Pan, Q.-K.; Li, J.-Q.; Wang, P.; Han, Y.-Y.; Gao, K.-Z.; Duan, P. Effective invasive weed optimization algorithms for distributed assembly permutation flowshop problem with total flowtime criterion. Swarm Evol. Comput. 2019, 44, 64–73. [Google Scholar] [CrossRef]
- Li, M.; Xiao, D.; Zhang, Y.; Nan, H. Reversible data hiding in encrypted images using cross division and additive homomorphism. Signal Process. Image Commun. 2015, 39, 234–248. [Google Scholar] [CrossRef]
- Li, M.; Guo, Y.; Huang, J.; Li, Y. Cryptanalysis of a chaotic image encryption scheme based on permutation-diffusion structure. Signal Process. Image Commun. 2018, 62, 164–172. [Google Scholar] [CrossRef]
- Fan, H.; Li, M.; Liu, D.; Zhang, E. Cryptanalysis of a colour image encryption using chaotic APFM nonlinear adaptive filter. Signal Process. 2018, 143, 28–41. [Google Scholar] [CrossRef]
- Dong, W.; Shi, G.; Li, X.; Ma, Y.; Huang, F. Compressive sensing via nonlocal low-rank regularization. IEEE Trans. Image Process. 2014, 23, 3618–3632. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.; Hu, Y.; Zhang, W. Feature selection algorithm based on bare bones particle swarm optimization. Neurocomputin 2015, 148, 150–157. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, X.-F.; Gong, D.-W. A return-cost-based binary firefly algorithm for feature selection. Inf. Sci. 2017, 418, 561–574. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Tang, J.; Li, Y. Predicting remaining useful life of rolling bearings based on deep feature representation and long short-term memory neural network. Adv. Mech. Eng. 2018, 10, 1687814018817184. [Google Scholar] [CrossRef]
- Jian, M.; Lam, K.-M.; Dong, J. Facial-feature detection and localization based on a hierarchical scheme. Inf. Sci. 2014, 262, 1–14. [Google Scholar] [CrossRef]
- Wang, G.-G.; Chu, H.E.; Mirjalili, S. Three-dimensional path planning for UCAV using an improved bat algorithm. Aerosp. Sci. Technol. 2016, 49, 231–238. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H.; Shao, M. Path planning for uninhabited combat aerial vehicle using hybrid meta-heuristic DE/BBO algorithm. Adv. Sci. Eng. Med. 2012, 4, 550–564. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.-w.; Gao, X.-z.; Tian, T.; Sun, X.-y. Binary differential evolution with self-learning for multi-objective feature selection. Inf. Sci. 2020, 507, 67–85. [Google Scholar] [CrossRef]
- Wang, G.-G.; Cai, X.; Cui, Z.; Min, G.; Chen, J. High performance computing for cyber physical social systems by using evolutionary multi-objective optimization algorithm. IEEE Trans. Emerg. Top. Comput. 2017. [Google Scholar] [CrossRef]
- Cui, Z.; Sun, B.; Wang, G.-G.; Xue, Y.; Chen, J. A novel oriented cuckoo search algorithm to improve DV-Hop performance for cyber-physical systems. J. Parallel Distrib. Comput. 2017, 103, 42–52. [Google Scholar] [CrossRef]
- Jian, M.; Lam, K.-M.; Dong, J. Illumination-insensitive texture discrimination based on illumination compensation and enhancement. Inf. Sci. 2014, 269, 60–72. [Google Scholar] [CrossRef]
- Jian, M.; Lam, K.M.; Dong, J.; Shen, L. Visual-patch-attention-aware saliency detection. IEEE Trans. Cybern. 2015, 45, 1575–1586. [Google Scholar] [CrossRef]
- Wang, G.-G.; Lu, M.; Dong, Y.-Q.; Zhao, X.-J. Self-adaptive extreme learning machine. Neural Comput. Appl. 2016, 27, 291–303. [Google Scholar] [CrossRef]
- Mao, W.; Zheng, Y.; Mu, X.; Zhao, J. Uncertainty evaluation and model selection of extreme learning machine based on Riemannian metric. Neural Comput. Appl. 2013, 24, 1613–1625. [Google Scholar] [CrossRef]
- Liu, G.; Zou, J. Level set evolution with sparsity constraint for object extraction. IET Image Process. 2018, 12, 1413–1422. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; El-Sehiemy, R.A.; Deb, S.; Wang, G.-G. A novel fruit fly framework for multi-objective shape design of tubular linear synchronous motor. J. Supercomput. 2017, 73, 1235–1256. [Google Scholar] [CrossRef]
- Yi, J.-H.; Xing, L.-N.; Wang, G.-G.; Dong, J.; Vasilakos, A.V.; Alavi, A.H.; Wang, L. Behavior of crossover operators in NSGA-III for large-scale optimization problems. Inf. Sci. 2020, 509, 470–487. [Google Scholar] [CrossRef]
- Yi, J.-H.; Deb, S.; Dong, J.; Alavi, A.H.; Wang, G.-G. An improved NSGA-III Algorithm with adaptive mutation operator for big data optimization problems. Future Gener. Comput. Syst. 2018, 88, 571–585. [Google Scholar] [CrossRef]
- Sun, J.; Miao, Z.; Gong, D.; Zeng, X.-J.; Li, J.; Wang, G.-G. Interval multi-objective optimization with memetic algorithms. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Wang, G.-G. Binary moth search algorithm for discounted {0-1} knapsack problem. IEEE Access 2018, 6, 10708–10719. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.-G.; Wang, L. Solving randomized time-varying knapsack problems by a novel global firefly algorithm. Eng. Comput. 2018, 34, 621–635. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Zhou, Y. An elite opposition-flower pollination algorithm for a 0-1 knapsack problem. Int. J. Bio-Inspired Comput. 2018, 11, 46–53. [Google Scholar] [CrossRef]
- Yi, J.-H.; Wang, J.; Wang, G.-G. Improved probabilistic neural networks with self-adaptive strategies for transformer fault diagnosis problem. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Li, Y.; Yan, Y. Bearing fault diagnosis with auto-encoder extreme learning machine: A comparative study. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 1560–1578. [Google Scholar] [CrossRef]
- Mao, W.; Feng, W.; Liang, X. A novel deep output kernel learning method for bearing fault structural diagnosis. Mech. Syst. Signal Process. 2019, 117, 293–318. [Google Scholar] [CrossRef]
- Duan, H.; Zhao, W.; Wang, G.; Feng, X. Test-sheet composition using analytic hierarchy process and hybrid metaheuristic algorithm TS/BBO. Math. Probl. Eng. 2012, 2012, 1–22. [Google Scholar] [CrossRef]
- Wang, G.G.; Tan, Y. Improving metaheuristic algorithms with information feedback models. IEEE Trans. Cybern. 2019, 49, 542–555. [Google Scholar] [CrossRef] [PubMed]
- Rong, M.; Gong, D.; Zhang, Y.; Jin, Y.; Pedrycz, W. Multidirectional prediction approach for dynamic multiobjective optimization problems. IEEE Trans. Cybern. 2019, 49, 3362–3374. [Google Scholar] [CrossRef] [PubMed]
- Gong, D.; Sun, J.; Miao, Z. A Set-Based Genetic Algorithm for Interval Many-Objective Optimization Problems. IEEE Trans. Evol. Comput. 2018, 22, 47–60. [Google Scholar] [CrossRef]
- Gong, D.; Sun, J.; Ji, X. Evolutionary algorithms with preference polyhedron for interval multi-objective optimization problems. Inf. Sci. 2013, 233, 141–161. [Google Scholar] [CrossRef]
- Sergeyev, Y.D.; Kvasov, D.E.; Mukhametzhanov, M.S. On the efficiency of nature-inspired metaheuristics in expensive global optimization with limited budget. Sci. Rep. 2018, 8, 453. [Google Scholar] [CrossRef]
- Kvasov, D.E.; Mukhametzhanov, M.S. Metaheuristic vs. deterministic global optimization algorithms: The univariate case. Appl. Math. Comput. 2018, 318, 245–259. [Google Scholar] [CrossRef]
- Sergeyev, Y.D.; Kvasov, D.E.; Mukhametzhanov, M.S. Operational zones for comparing metaheuristic and deterministic one-dimensional global optimization algorithms. Math. Comput. Simul. 2017, 141, 96–109. [Google Scholar] [CrossRef]
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Dorigo, M.; Stutzle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Wang, G.-G.; Deb, S.; Coelho, L.d.S. Earthworm optimization algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Int. J. Bio-Inspired Comput. 2018, 12, 1–22. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Coelho, L.d.S. Elephant herding optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI), Bali, Indonesia, 7–9 December 2015; pp. 1–5. [Google Scholar]
- Wang, G.-G.; Deb, S.; Gao, X.-Z.; Coelho, L.d.S. A new metaheuristic optimization algorithm motivated by elephant herding behavior. Int. J. Bio-Inspired Comput. 2016, 8, 394–409. [Google Scholar] [CrossRef]
- Wang, G.-G. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memetic Comput. 2018, 10, 151–164. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspired Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Wang, H.; Yi, J.-H. An improved optimization method based on krill herd and artificial bee colony with information exchange. Memetic Comput. 2018, 10, 177–198. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Liu, F.; Sun, Y.; Wang, G.-G.; Wu, T. An artificial bee colony algorithm based on dynamic penalty and chaos search for constrained optimization problems. Arab. J. Sci. Eng. 2018, 43, 7189–7208. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Zhao, X.; Chu, H.E. Hybridizing harmony search algorithm with cuckoo search for global numerical optimization. Soft Comput. 2016, 20, 273–285. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2019, 31, 1995–2014. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Zhao, X.; Cui, Z. A new monarch butterfly optimization with an improved crossover operator. Oper. Res. Int. J. 2018, 18, 731–755. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Sun, Y.; Jiao, L.; Deng, X.; Wang, R. Dynamic network structured immune particle swarm optimisation with small-world topology. Int. J. Bio-Inspired Comput. 2017, 9, 93–105. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Multi-stage genetic programming: A new strategy to nonlinear system modeling. Inf. Sci. 2011, 181, 5227–5239. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H. An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl. Math. Model. 2014, 38, 2454–2462. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H.; Deb, S. A multi-stage krill herd algorithm for global numerical optimization. Int. J. Artif. Intell. Tool 2016, 25, 1550030. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H.; Gong, D. A comprehensive review of krill herd algorithm: Variants, hybrids and applications. Artif. Intell. Rev. 2019, 51, 119–148. [Google Scholar] [CrossRef]
- Wang, G.-G.; Guo, L.; Gandomi, A.H.; Hao, G.-S.; Wang, H. Chaotic krill herd algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Gandomi, A.H.; Alavi, A.H. Opposition-based krill herd algorithm with Cauchy mutation and position clamping. Neurocomputing 2016, 177, 147–157. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H. Stud krill herd algorithm. Neurocomputing 2014, 128, 363–370. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.J.; Cao, X.; Zhang, J.; Fen, L. An improved genetic algorithm based on immune principle. Minimicro Syst. 1999, 20, 120. [Google Scholar]
- Li, J.; Li, Y.-x.; Tian, S.-s.; Zou, J. Dynamic cuckoo search algorithm based on Taguchi opposition-based search. Int. J. Bio-Inspired Comput. 2019, 13, 59–69. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Engineering optimisation by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Gandomi, A.H.; Zhang, Z.; Alavi, A.H. Chaotic cuckoo search. Soft Comput. 2016, 20, 3349–3362. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Mlakar, U.; Fister, I.; Fister, I. Hybrid self-adaptive cuckoo search for global optimization. Swarm Evol. Comput. 2016, 29, 47–72. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Yin, M. Enhancing the performance of cuckoo search algorithm using orthogonal learning method. Neural Comput. Appl. 2013, 24, 1233–1247. [Google Scholar] [CrossRef]
- Ouaarab, A.; Ahiod, B.; Yang, X.-S. Discrete cuckoo search algorithm for the travelling salesman problem. Neural Comput. Appl. 2013, 24, 1659–1669. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Li, T.-H.S.; Lin, C.-J. Backward Q-learning: The combination of Sarsa algorithm and Q-learning. Eng. Appl. Artif. Intell. 2013, 26, 2184–2193. [Google Scholar] [CrossRef]
- Alexandridis, A.; Chondrodima, E.; Sarimveis, H. Cooperative learning for radial basis function networks using particle swarm optimization. Appl. Soft Comput. 2016, 49, 485–497. [Google Scholar] [CrossRef]
- Rakhshani, H.; Rahati, A. Snap-drift cuckoo search: A novel cuckoo search optimization algorithm. Appl. Soft Comput. 2017, 52, 771–794. [Google Scholar] [CrossRef]
- Samma, H.; Lim, C.P.; Saleh, J.M. A new reinforcement learning-based memetic particle swarm optimizer. Appl. Soft Comput. 2016, 43, 276–297. [Google Scholar] [CrossRef]
- Abed-alguni, B.H. Action-selection method for reinforcement learning based on cuckoo search algorithm. Arab. J. Sci. Eng. 2017, 43, 6771–6785. [Google Scholar] [CrossRef]
- Ma, H.-S.; Li, S.-X.; Li, S.-F.; Lv, Z.-N.; Wang, J.-S. An improved dynamic self-adaption cuckoo search algorithm based on collaboration between subpopulations. Neural Comput. Appl. 2018, 31, 1375–1389. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Modified cuckoo search algorithm with self adaptive parameter method. Inf. Sci. 2015, 298, 80–97. [Google Scholar] [CrossRef]
- Yang, B.; Miao, J.; Fan, Z.; Long, J.; Liu, X. Modified cuckoo search algorithm for the optimal placement of actuators problem. Appl. Soft Comput. 2018, 67, 48–60. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.-X.; Tian, S.-S.; Xia, J.-L. An improved cuckoo search algorithm with self-adaptive knowledge learning. Neural Comput. Appl. 2019. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, L.; Xiong, Y. Ensemble of cuckoo search variants. Comput. Ind. Eng. 2019, 135, 299–313. [Google Scholar] [CrossRef]
- Long, W.; Cai, S.; Jiao, J.; Xu, M.; Wu, T. A new hybrid algorithm based on grey wolf optimizer and cuckoo search for parameter extraction of solar photovoltaic models. Energy Convers. Manag. 2020, 203, 112243. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, S.; Jia, W. A hybrid optimization algorithm based on cuckoo search and differential evolution for solving constrained engineering problems. Eng. Appl. Artif. Intell. 2019, 85, 254–268. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.-T.; Yin, M.-H. Hybrid cuckoo search algorithm with covariance matrix adaption evolution strategy for global optimisation problem. Int. J. Bio-Inspired Comput. 2019, 13, 102–110. [Google Scholar] [CrossRef]
- Tang, H.; Xue, F. Cuckoo search algorithm with different distribution strategy. Int. J. Bio-Inspired Comput. 2019, 13, 234–241. [Google Scholar] [CrossRef]
- Ong, P.; Zainuddin, Z. Optimizing wavelet neural networks using modified cuckoo search for multi-step ahead chaotic time series prediction. Appl. Soft Comput. 2019, 80, 374–386. [Google Scholar] [CrossRef]
- Kamoona, A.M.; Patra, J.C. A novel enhanced cuckoo search algorithm for contrast enhancement of gray scale images. Appl. Soft Comput. 2019, 85, 105749. [Google Scholar] [CrossRef]
- Naidu, M.N.; Boindala, P.S.; Vasan, A.; Varma, M.R. Optimization of Water Distribution Networks Using Cuckoo Search Algorithm. In Advanced Engineering Optimization Through Intelligent Techniques; Springer: Singapore, 2020. [Google Scholar]
- Ibrahim, A.M.; Tawhid, M.A. A hybridization of cuckoo search and particle swarm optimization for solving nonlinear systems. Evol. Intell. 2019, 12, 541–561. [Google Scholar] [CrossRef]
- Osaba, E.; del Ser, J.; Camacho, D.; Bilbao, M.N.; Yang, X.-S. Community detection in networks using bio-inspired optimization: Latest developments, new results and perspectives with a selection of recent meta-heuristics. Appl. Soft Comput. 2020, 87, 106010. [Google Scholar] [CrossRef]
- Rath, A.; Samantaray, S.; Swain, P.C. Optimization of the Cropping Pattern Using Cuckoo Search Technique. In Smart Techniques for a Smarter Planet; Springer: Cham, Switzerland, 2019; p. 19. [Google Scholar]
- Abdel-Basset, M.; Wang, G.-G.; Sangaiah, A.K.; Rushdy, E. Krill herd algorithm based on cuckoo search for solving engineering optimization problems. Multimed. Tools Appl. 2017, 78, 3861–3884. [Google Scholar] [CrossRef]
- Cao, Z.; Lin, C.; Zhou, M.; Huang, R. Scheduling semiconductor testing facility by using cuckoo search algorithm with reinforcement learning and surrogate modeling. IEEE Trans. Autom. Sci. Eng. 2019, 16, 825–837. [Google Scholar] [CrossRef]
- Hu, H.; Li, X.; Zhang, Y.; Shang, C.; Zhang, S. Multi-objective location-routing model for hazardous material logistics with traffic restriction constraint in inter-city roads. Comput. Ind. Eng. 2019, 128, 861–876. [Google Scholar] [CrossRef]
- Wang, F.; He, X.-s.; Wang, Y. The cuckoo search algorithm based on Gaussian disturbance. J. Xi’an Polytech. Univ. 2011, 25, 566–569. [Google Scholar]
- Wang, F.; Luo, L.; He, X.S.; Wang, Y. Hybrid optimization algorithm of PSO and Cuckoo Search. In Proceedings of the 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC), Dengleng, China, 8–10 August 2011; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-Adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Zhao, S.A.; Qu, C.W. An Improved Cuckoo Algorithm for Solving the Problem of Logistics Distribution Center Location. Math. Pract. Theory 2017, 47, 206–213. [Google Scholar]
- del Ser, J.; Osaba, E.; Molina, D.; Yang, X.-S.; Salcedo-Sanz, S.; Camacho, D.; Das, S.; Suganthan, P.N.; Coello, C.A.C.; Herrera, F. Bio-inspired computation: Where we stand and what’s next. Swarm Evol. Comput. 2019, 48, 220–250. [Google Scholar] [CrossRef]






| Type | Function | Name | Search Range | Acceptable Accuracy | Global Optimum |
|---|---|---|---|---|---|
| Unimodal | F1 | Sphere | [−100, 100] | 1 × 10−8 | 0 |
| F2 | Rosenbrock | [−30, 30] | 1 × 10−8 | 0 | |
| F3 | Step | [−100, 100] | 1 × 10−8 | 0 | |
| F4 | Schwefel2.22 | [−10, 10] | 1 × 10−8 | 0 | |
| Multimodal Shifted multimodal | F5 | Ackley | [−32, 32] | 1 × 10−8 | 0 |
| F6 | Rastrigin | [−5.12, 5.12] | 10 | 0 | |
| F7 | Griewank | [−600, 600] | 0.05 | 0 | |
| F8 | Generalized Penalized1 | [−50, 50] | 1 × 10−8 | 0 | |
| F9 | Generalized Penalized2 | [−50, 50] | 1 × 10−8 | 0 | |
| F10 | Shifted Schwefels Problem 1.2 | [−100, 100] | 1 × 10−8 | −450 | |
| F11 | Shifted Rotated High Conditioned Elliptic Function | [−100, 100] | 1 × 10−8 | −450 | |
| F12 | Shifted Rosenbrock | [−100, 100] | 2 | 390 | |
| F13 | Shifted Rotated Ackleys | [−32, 32] | 2 | −140 | |
| F14 | Shifted Griewanks | [−600, 600] | 0.2 | 0 | |
| F15 | Shifted Rotated Rastrigin | [−5.12, 5.12] | 10 | −330 |
| Algorithms | Parameter Configurations |
|---|---|
| CCS [68] | pa = 0.2, a = 0.5, b = 0.2, xi = (0, 1) |
| GCS [96] | a = 1/3, pa = 0.25 |
| CSPSO [97] | pa = 0.25, a = 0.1, W = 0.9~0.4, c1 = c2 = 2.0 |
| OLCS [71] | pa = 0.2, a = 0.5, K = 9, Q = 3 |
| DMQL-CS | pa = 0.25, M = 3, = 0.5 |
| Func | CCS | GCS | CSPSO | OLCS | DMQL-CS |
|---|---|---|---|---|---|
| F1 | 3.21 × 10−12 ± 2.09 × 10−12 | 4.34 × 10−10 ± 3.23 × 10−11 | 4.77 × 10−45 ± 3.65 × 10−44 | 2.89 × 10−106 ± 1.43 × 10−105 | 0.00 ± 0.00 |
| F2 | 3.96 × 10−5 ± 8.01 × 10−5 | 1.54 × 10−1 ± 1.82 × 10−1 | 1.66 × 10−1 ± 2.95 × 100 | 1.45 × 10−7 ± 4.01 × 10−7 | 0.76 × 10−7 ± 5.12 × 10−7 |
| F3 | 4.12 × 100 ± 3.11 × 100 | 7.09 × 100 ± 2.13 × 100 | 7.12 × 100 ± 3.31 × 100 | 0.00 ± 0.00 | 4.88 × 10−2 ± 5.19 × 10−1 |
| F4 | 5.56 × 10−33 ± 3.21 × 10−32 | 4.11 × 10−24 ± 5.01 × 10−23 | 2.76 × 10−76 ± 4.43 × 10−76 | 4.09 × 10−34 ± 3.88 × 10−34 | 8.88 × 10−35 ± 5.78 × 10−34 |
| F5 | 4.67 × 10−5 ± 3.21 × 10−6 | 4.11 × 10−14 ± 5.01 × 10−13 | 2.76 × 10−2 ± 4.43 × 10−2 | 7.21 × 10−15 ± 0.00 | 1.01 × 10−15 ± 2.87 × 10−14 |
| F6 | 6.22 × 10−7 ± 1.12 × 10−5 | 3.13 × 10−7 ± 2.98 × 10−6 | 3.87 × 101 ± 2.01 × 101 | 0.00 ± 0.00 | 0.00 ± 0.00 |
| F7 | 3.13 × 10−10 ± 1.11 × 10−10 | 2.87 × 10−11 ± 2.12 × 10−10 | 5.77 × 10−6 ± 3.03 × 10−6 | 0.00 ± 0.00 | 0.00 ± 0.00 |
| F8 | 4.90 × 10−7 ± 2.77 × 10−7 | 3.96 × 10−7 ± 3.31 × 10−5 | 1.39 × 10−6 ± 1.17 × 10−5 | 1.88 × 10−8 ± 4.09 × 10−8 | 3.38 × 10−7 ± 2.99 × 10−7 |
| F9 | 2.22 × 10−23 ± 1.05 × 10−22 | 3.04 × 10−22 ± 1.99 × 10−22 | 4.67 × 10−4 ± 2.89 × 10−6 | 4.39 × 10−29 ± 6.50 × 10−26 | 2.45 × 10−22 ± 6.89 × 10−22 |
| F10 | 6.01 × 10−15 ± 3.77 × 10−16 | 3.66 × 10−15 ± 2.19 × 10−16 | 3.21 × 10−16 ± 5.33 × 10−16 | 3.21 × 10−15 ± 3.17 × 10−11 | 9.55 × 10−15 ± 7.09 × 10−13 |
| F11 | 2.76 × 109 ± 5.77 × 109 | 2.81 × 109± 3.06 × 109 | 2.28 × 109 ± 9.02 × 108 | 5.63 × 106 ± 2.22 × 106 | 5.11 × 106 ± 3.90 × 106 |
| F12 | 1.23 × 101 ± 2.77 × 100 | 1.42 × 101 ± 2.93 × 100 | 5.23 × 101 ± 2.91 × 10+1 | 2.65 × 101 ± 4.23 × 100 | 4.21 × 101 ± 1.09 × 101 |
| F13 | 1.90 × 103 ± 3.97 × 103 | 5.88 × 103 ± 3.08 × 103 | 4.34 × 104 ± 1.88 × 103 | 4.70 × 103 ± 2.26 × 103 | 2.06 × 102 ± 3.77 × 101 |
| F14 | 2.71 × 10−1 ± 2.09 × 100 | 4.01 × 10−1 ± 7.00 × 100 | 1.37 × 10−2 ± 8.01 × 10−2 | 0.00 ± 0.00 | 0.00 ± 0.00 |
| F15 | 5.90 × 101 ± 3.78 × 100 | 7.88 × 101 ± 2.89 × 100 | 0.98 × 102 ± 3.56 × 101 | 3.65 × 101 ± 4.11 | 2.87 × 101 ± 4.77 × 101 |
| CCS | GCS | CSPSO | OLCS | MP-QL-CS | |
|---|---|---|---|---|---|
| Friedman rank | 3.18 | 3.82 | 4.31 | 2.53 | 2.44 |
| Final rank | 3 | 4 | 5 | 2 | 1 |
| Func | CCS | GCS | CSPSO | OLCS | MP-QL-CS |
|---|---|---|---|---|---|
| F1 | 3.76 × 10−6 ± 2.21 × 10−6 | 2.78 × 10−8 ± 5.67 × 10−9 | 3.99 × 10−19 ± 6.43 × 10−18 | 4.45 × 10−29 ± 6.33 × 10−28 | 6.55 × 10−30 ± 2.90 × 10−28 |
| F2 | 3.88 × 101 ± 3.09 × 101 | 2.89 × 101 ± 1.22 × 102 | 5.98 × 10−1 ± 2.99 × 10−1 | 3.10 × 101 ± 2.90 × 101 | 1.99 × 10−1 ± 4.56 × 10−1 |
| F3 | 3.78 × 101 ± 2.66 × 100 | 3.67 × 101 ± 4.52× 100 | 5.34 × 100± 2.11× 100 | 0.00± 0.00 | 4.77 × 10−2 ± 3.21 × 10−12 |
| F4 | 4.02 × 10−2 ± 1.55 × 10−2 | 3.78 × 10−2 ± 2.90 × 10−2 | 3.88 × 10−4 ± 1.89 × 10−4 | 4.65 × 10−5 ± 4.09 × 10−5- | 4.90 × 10−7 ± 2.11 × 10−8 |
| F5 | 1.89 × 10−2 ± 2.87 × 10−2 | 5.97 × 10−7 ± 5.22 × 10−7 | 4.77 × 10−2 ± 4.44 × 10−1 | 5.09 × 10−12 ± 4.89 × 10−14 | 2.99 × 10−12 ± 3.09 × 10−14 |
| F6 | 5.34 × 10−1 ± 3.87 × 10−1 | 6.44 × 10−6 ± 3.72 × 10−6 | 9.28 × 103 ± 4.73 × 103 | 0.00 ± 0.00 | 3.98 × 10−2 ± 2.22 × 10−1 |
| F7 | 3.12 × 10−2 ± 4.78 × 10−2 | 4.33 × 10−2 ± 9.21 × 10−2 | 6.34 × 10−2 ± 3.18 × 10−2 | 0.00 ± 0.00 | 0.00 ± 0.00 |
| F8 | 6.67 × 10−5 ± 1.90 × 10−5 | 5.78 × 10−7 ± 3.77 × 10−7 | 8.90 × 10−7 ± 2.30 × 10−7 | 3.77 × 10−8 ± 7.56 × 10−8 | 1.77 × 10−4 ± 2.12 × 10−4 |
| F9 | 5.78 × 10−3 ± 0.55 × 10−3 | 7.78 × 10−20 ± 6.23 × 10−20 | 3.66 × 10−1 ± 3.41 × 10−1 | 4.67 × 10−25 ± 1.23 × 10−26 | 3.90 × 10−10 ± 3.66 × 10−9 |
| F10 | 5.78 × 10−10 ± 5.55 × 10−10 | 3.99 × 10−10 ± 2.98 × 10−10 | 7.90 × 10−10 ± 8.11 × 10−10 | 7.34 × 10−10 ± 5.45 × 10−9 | 2.78 × 10−10 ± 1.34 × 10−6 |
| F11 | 3.66 × 1012 ± 3.89 × 1012 | 2.89 × 1012 ± 5.78 × 1012 | 2.90 × 107 ± 3.11 × 107 | 5.89 × 108 ± 9.90 × 108 | 4.89 × 1011 ± 3.67 × 1010 |
| F12 | 4.89 × 103 ± 3.78 × 103 | 2.90 × 103 ± 2.22 × 103 | 5.98 × 103 ± 2.09 × 103 | 6.99 × 102 ± 3.90 × 101 | 2.97 × 103 ± 1.86 × 103 |
| F13 | 4.89 × 105 ± 2.17 × 105 | 5.89 × 104 ± 1.12 × 104 | 5.33 × 105± 4.56 × 105 | 5.02 × 104 ± 2.09 × 104 | 1.09 × 103 ± 3.89 × 103 |
| F14 | 6.98 × 101 ± 1.11 × 102 | 5.56 × 101 ± 2.98 × 102 | 5.89 × 102 ± 2.21 × 102 | 0.00 ± 0.00 | 2.90 × 101 ± 3.76 × 101 |
| F15 | 6.25 × 102 ± 3.33 × 102 | 4.28 × 102 ± 1.77 × 102 | 3.45 × 103 ± 2.76 × 103 | 8.89 × 102 ± 4.11 × 102 | 2.22 × 102 ± 1.78 × 102 |
| CCS | GCS | CSPSO | OLCS | MP-QL-CS | |
|---|---|---|---|---|---|
| Friedman rank | 4.19 | 3.62 | 4.15 | 2.41 | 2.46 |
| Final rank | 5 | 3 | 4 | 1 | 2 |
| Dim | Algorithm | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 |
|---|---|---|---|---|---|---|---|---|---|
| 30 | CCS | 4 | 3 | 3 | 3 | 4 | 4 | 4 | 4 |
| GCS | 5 | 4 | 4 | 2 | 3 | 3 | 3 | 3 | |
| CSPSO | 3 | 5 | 5 | 4 | 5 | 5 | 5 | 5 | |
| OLCS | 2 | 1 | 1 | 5 | 2 | 1 | 1 | 2 | |
| DMQL-CS | 1 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | |
| 50 | CCS | 5 | 5 | 5 | 5 | 4 | 4 | 3 | 3 |
| GCS | 4 | 3 | 4 | 4 | 3 | 2 | 4 | 2 | |
| CSPSO | 3 | 2 | 3 | 3 | 5 | 5 | 5 | 4 | |
| OLCS | 2 | 4 | 1 | 2 | 2 | 1 | 1 | 1 | |
| DMQL-CS | 1 | 1 | 2 | 1 | 1 | 3 | 1 | 5 |
| Dim | Algorithm | F9 | F10 | F11 | F12 | F13 | F14 | F15 |
|---|---|---|---|---|---|---|---|---|
| 30 | CCS | 3 | 4 | 4 | 1 | 2 | 4 | 4 |
| GCS | 4 | 3 | 5 | 2 | 4 | 3 | 3 | |
| CSPSO | 5 | 1 | 3 | 5 | 5 | 2 | 5 | |
| OLCS | 1 | 2 | 2 | 3 | 3 | 1 | 2 | |
| DMQL-CS | 2 | 5 | 1 | 4 | 1 | 1 | 1 | |
| 50 | CCS | 4 | 3 | 5 | 4 | 4 | 3 | 2 |
| GCS | 2 | 2 | 4 | 2 | 3 | 4 | 4 | |
| CSPSO | 5 | 5 | 1 | 5 | 5 | 5 | 3 | |
| OLCS | 1 | 4 | 2 | 1 | 2 | 1 | 5 | |
| DMQL-CS | 3 | 1 | 3 | 3 | 1 | 2 | 1 |
| Dim | Rank | Algorithms | ||||
|---|---|---|---|---|---|---|
| CCS | GCS | CSPSO | OLCS | DMQL-CS | ||
| 30 | Total rank | 49 | 53 | 63 | 29 | 25 |
| Final rank | 3 | 4 | 5 | 2 | 1 | |
| 50 | Total rank | 60 | 47 | 55 | 30 | 29 |
| Final rank | 5 | 3 | 4 | 2 | 1 | |
| Algorithms | Parameter Configurations |
|---|---|
| jDE [98] | F = 0.5, CR = 0.9 |
| SaDE [99] | F~N(0.5, 0.3), CR0 = 0.5, CR~N(CRm, 0.1), LP = 50 |
| CLPSO [100] | W = 0.7298, c = 1.49618, m = 7, pc = 0.05~0.5 |
| DMQL-CS | pa = 0.25, PL = 20, = 0.015 |
| Function | Mean Std | Algorithms | |||
|---|---|---|---|---|---|
| SaDE | jDE | CLPSO | DMQL-CS | ||
| CEC 2013-F1 | Mean/Std | 0.00/0.00 | 0.00/0.00 | 2.16 × 10−13/0.00 | 0.00/0.00 |
| CEC 2013-F2 | Mean/Std | 4.21 × 105/1.21 × 105 | 1.27 × 105/6.86 × 105 | 2.99 × 107/2.10 × 106 | 1.12 × 105/4.88 × 105 |
| CEC 2013-F3 | Mean/Std | 2.98 × 107/2.99 × 107 | 2.99 × 106/3.01 × 106 | 3.16 × 108/2.92 × 108 | 3.78 × 107/5.87 × 106 |
| CEC 2013-F4 | Mean/Std | 3.22 × 103/2.98 × 103 | 0.97 × 101/1.88 × 101 | 4.87 × 104/1.09 × 103 | 8.09 × 100/7.90 × 100 |
| CEC 2013-F5 | Mean/Std | 0.00/0.00 | 1.19 × 10−13/3.55 × 10−14 | 3.54 × 10−11/2.01 × 10-12 | 4.56 × 10−14/1.90 × 10-12 |
| CEC 2013-F6 | Mean/Std | 2.78 × 101/5.66 × 101 | 1.23 × 101/9.78 × 100 | 3.56 × 101/1.00 × 101 | 5.62 × 10−2/9.89 × 100 |
| CEC 2013-F7 | Mean/Std | 2.22 × 101/1.38 × 100 | 2.12 × 101/1.38 × 100 | 6.97 × 101/3.20 × 101 | 8.90 × 101/5.12 × 100 |
| CEC 2013-F8 | Mean/Std | 2.11 × 101/6.45 × 101 | 2.01 × 100/6.11 × 100 | 2.09 × 101/3.73 × 10-2 | 2.07 × 101/1.78 × 10−2 |
| CEC 2013-F9 | Mean/Std | 1.78 × 101/2.33 × 100 | 2.59 × 101/4.45 × 100 | 3.19 × 101/3.62 × 100 | 1.01 × 101/7.90 × 100 |
| CEC 2013-F10 | Mean/Std | 2.73 × 10−1/2.33 × 10−1 | 4.37 × 10−2/4.73 × 10−2 | 3.99 × 101/2.01 × 100 | 2.77 × 10−3/6.89 × 10−2 |
| CEC 2013-F11 | Mean/Std | 3.87 × 10−2/3.64 × 10−1 | 0.00/0.00 | 6.14 × 101/3.01× 101 | 0.00/0.00 |
| CEC 2013-F12 | Mean/Std | 4.19 × 101/2.65× 101 | 5.56 × 101/1.49× 101 | 1.23 × 102/2.11× 101 | 9.01 × 100/4.67 × 101 |
| CEC 2013-F13 | Mean/Std | 1.10 × 101/3.21 × 102 | 1.29 × 101/5.22× 101 | 1.78 × 102/3.91× 101 | 1.11 × 102/3.99 × 102 |
| CEC 2013-F14 | Mean/Std | 7.34 × 100/2.22 × 100 | 1.06 × 10−4/4.24 × 10−3 | 5.77 × 102/4.79× 102 | 1.89 × 102/0.00 |
| CEC 2013-F15 | Mean/Std | 4.90 × 103/5.67 × 102 | 5.03 × 103/6.02 × 102 | 6.01 × 103/4.25× 102 | 4.98 × 103/2.67 × 103 |
| CEC 2013-F16 | Mean/Std | 2.24 × 100/5.12 × 10−1 | 3.05 × 100/2.26 × 10−1 | 3.22 × 100/2.21 × 10-1 | 1.18 × 100/2.05 × 10−1 |
| CEC 2013-F17 | Mean/Std | 6.12 × 101/1.16 × 10−2 | 6.13 × 101/3.65 × 100 | 7.23 × 101/5.51 × 100 | 5.89 × 102/4.24 × 101 |
| CEC 2013-F18 | Mean/Std | 1.02 × 102/2.57× 101 | 1.61 × 102/3.21 × 101 | 2.25 × 101/1.11× 101 | 1.78 × 101/1.12 × 101 |
| CEC 2013-F19 | Mean/Std | 4.91 × 100/6.18 × 10−1 | 1.05 × 100/3.81 × 10−1 | 3.18 × 100/1.03 × 10−1 | 3.27 × 100/3.99 × 10−1 |
| CEC 2013-F20 | Mean/Std | 1.10 × 101/5.23 × 100 | 1.15 × 101/4.09 × 100 | 1.41 × 101/2.55 × 100 | 1.02 × 101/5.12 × 100 |
| CEC 2013-F21 | Mean/Std | 2.80 × 102/3.55 × 101 | 2.65 × 102/1.29 × 101 | 3.12 × 102/4.11 × 101 | 2.01 × 102/4.88 × 102 |
| CEC 2013-F22 | Mean/Std | 1.25 × 103/2.23 × 102 | 1.17 × 103/2.23 × 102 | 7.35 × 102/1.01 × 102 | 8.23 × 102/6.98 × 102 |
| CEC 2013-F23 | Mean/Std | 4.83 × 103/0.21 × 103 | 4.90 × 103/2.21 × 102 | 6.23 × 103/3.83 × 102 | 2.00 × 103/3.23 × 102 |
| CEC 2013-F24 | Mean/Std | 2.35 × 102/2.56 × 100 | 2.21 × 102/5.56 × 101 | 2.89 × 102/7.38 × 100 | 2.67 × 102/3.21 × 100 |
| CEC 2013-F25 | Mean/Std | 2.45 × 102/1.28 × 101 | 2.66 × 102/1.01 × 100 | 2.80 × 102/6.33 × 100 | 2.02 × 102/3.98 × 100 |
| CEC 2013-F26 | Mean/Std | 2.23 × 102/2.09 × 103 | 2.17 × 102/2.51 × 101 | 1.97 × 102/1.66 × 10−1 | 1.04 × 102/1.09 × 102 |
| CEC 2013-F27 | Mean/Std | 5.48 × 102/4.23 × 101 | 6.34 × 102/3.32 × 102 | 8.13 × 102/2.65 × 102 | 6.89 × 102/3.89 × 102 |
| CEC 2013-F28 | Mean/Std | 3.05 × 102/0.00 | 3.05 × 102/0.00 | 3.03 × 102/2.98 × 10-3 | 3.02 × 102/3.20 × 102 |
| SaDE | jDE | CLPSO | DMQL-CS | |
|---|---|---|---|---|
| Friedman rank | 3.34 | 2.95 | 4.26 | 2.59 |
| Final rank | 3 | 2 | 4 | 1 |
| Function | SaDE | jDE | CLPSO | DMQL-CS |
|---|---|---|---|---|
| Rank | Rank | Rank | Rank | |
| CEC 2013-F1 | 1 (≈/=) | 1 (≈/=) | 4 (-) | 1 |
| CEC 2013-F2 | 4 (-) | 2 (-) | 3 (-) | 1 |
| CEC 2013-F3 | 2 (-) | 1 (+) | 4 (-) | 3 |
| CEC 2013-F4 | 3 (-) | 2 (-) | 4 (-) | 1 |
| CEC 2013-F5 | 1 (+) | 3 (+) | 2 (+) | 4 |
| CEC 2013-F6 | 3 (-) | 2 (-) | 4 (-) | 1 |
| CEC 2013-F7 | 2 (+) | 1 (+) | 3 (+) | 4 |
| CEC 2013-F8 | 4 (-) | 1 (+) | 3 (-) | 2 |
| CEC 2013-F9 | 2 (-) | 3 (-) | 4 (-) | 1 |
| CEC 2013-F10 | 2 (-) | 3 (-) | 4 (-) | 1 |
| CEC 2013-F11 | 3 (-) | 1 (≈/=) | 4 (-) | 1 |
| CEC 2013-F12 | 2 (-) | 3 (-) | 4 (-) | 1 |
| CEC 2013-F13 | 1 (+) | 3 (+) | 4 (+) | 2 |
| CEC 2013-F14 | 2 (+) | 1 (+) | 4 (-) | 3 |
| CEC 2013-F15 | 1 (+) | 3 (-) | 4 (-) | 2 |
| CEC 2013-F16 | 2 (-) | 3 (-) | 4 (-) | 1 |
| CEC 2013-F17 | 1 (+) | 2 (+) | 3 (+) | 4 |
| CEC 2013-F18 | 2 (-) | 3 (-) | 4 (-) | 1 |
| CEC 2013-F19 | 4 (-) | 1 (+) | 2 (+) | 3 |
| CEC 2013-F20 | 2 (-) | 3 (-) | 4 (-) | 1 |
| CEC 2013-F21 | 3 (-) | 2 (-) | 4 (-) | 1 |
| CEC 2013-F22 | 3 (+) | 2 (+) | 1 (+) | 4 |
| CEC 2013-F23 | 2 (-) | 3 (-) | 4 (-) | 1 |
| CEC 2013-F24 | 2 (+) | 1 (+) | 4 (-) | 3 |
| CEC 2013-F25 | 1(+) | 2 (+) | 3 (+) | 4 |
| CEC 2013-F26 | 4 (-) | 3 (-) | 2 (-) | 1 |
| CEC 2013-F27 | 1 (+) | 2 (+) | 4 (-) | 3 |
| CEC 2013-F28 | 3 (-) | 3 (-) | 2 (-) | 1 |
| Rank_Sun | 63 | 60 | 96 | 56 |
| Rank_Final | 3 | 2 | 4 | 1 |
| No | Coordinates | Demand | No | Coordinates | Demand | No | Coordinates | Demand | No | Coordinates | Demand | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | y | x | y | x | y | x | y | ||||||||
| 1 | 97 | 28 | 94 | 11 | 91 | 96 | 85 | 21 | 111 | 117 | 92 | 31 | 125 | 66 | 45 |
| 2 | 100 | 56 | 11 | 12 | 39 | 90 | 54 | 22 | 63 | 42 | 99 | 32 | 169 | 49 | 98 |
| 3 | 45 | 67 | 50 | 13 | 50 | 101 | 25 | 23 | 67 | 105 | 98 | 33 | 31 | 188 | 31 |
| 4 | 150 | 197 | 88 | 14 | 67 | 66 | 87 | 24 | 160 | 156 | 88 | 34 | 86 | 42 | 91 |
| 5 | 105 | 48 | 80 | 15 | 157 | 54 | 66 | 25 | 100 | 125 | 47 | 35 | 90 | 21 | 79 |
| 6 | 24 | 158 | 29 | 16 | 104 | 35 | 82 | 26 | 35 | 48 | 47 | 36 | 46 | 53 | 47 |
| 7 | 88 | 61 | 93 | 17 | 169 | 95 | 48 | 27 | 143 | 172 | 34 | 37 | 62 | 30 | 84 |
| 8 | 55 | 105 | 10 | 18 | 48 | 39 | 78 | 28 | 94 | 56 | 33 | 38 | 163 | 176 | 52 |
| 9 | 120 | 120 | 18 | 19 | 115 | 61 | 16 | 29 | 57 | 73 | 43 | 39 | 190 | 141 | 10 |
| 10 | 43 | 105 | 38 | 20 | 154 | 174 | 49 | 30 | 25 | 127 | 100 | 40 | 170 | 30 | 77 |
| Distribution Center | Distribution Scope |
|---|---|
| 10 | 33, 6, 30, 12, 13, 8, 23 |
| 21 | 11, 25, 9 |
| 20 | 4, 27, 38, 24, 39 |
| 22 | 14, 29, 3, 36, 26, 18, 37, 7 |
| 1 | 28, 25, 16, 19, 34, 35 |
| 15 | 31, 17, 32, 40 |
| Distribution Center | Distribution Scope |
|---|---|
| 30 | 6, 33 |
| 23 | 8,12, 13, 10 |
| 14 | 3, 29 |
| 18 | 26, 36, 22, 37 |
| 11 | - |
| 28 | 7, 34, 2, 19, 31, 5 |
| 21 | 25, 9 |
| 1 | 16, 35 |
| 20 | 4, 27, 38, 24, 39 |
| 15 | 17, 32, 40 |
| CS | IGA | CCS | |||
|---|---|---|---|---|---|
| D-C | Distribution Scope | D-C | Distribution Scope | D-C | Distribution Scope |
| 3 | 30, 12, 10, 13, 29, 14, 36, 26 | 10 | 33, 6, 30, 12, 8, 23, 13 | 23 | 33, 6, 30, 10, 12, 13, 8, 11 |
| 11 | 8, 23, 6, 33, 25, 21, 9 | 22 | 26, 36, 3, 18, 29, 14, 37, 35 | 21 | 9, 25 |
| 22 | 18, 37, 7 | 21 | 25, 11, 9 | 22 | 26, 36, 3, 29, 14, 18, 37 |
| 1 | 34, 35, 28, 2, 5, 16, 19 | 2 | 7, 34, 28, 19, 31, 1, 16, 5, 19 | 16 | 1, 35, 34, 7, 28, 2, 5, 19 |
| 15 | 31, 32, 17, 40 | 20 | 4, 27, 24, 38, 39 | 15 | 31, 17, 32, 40 |
| 20 | 27, 4, 38, 24, 39 | 17 | 15, 32, 40 | 20 | 4, 27, 24, 38, 39 |
| CS | IGA | CCS | |||
|---|---|---|---|---|---|
| D-C | Distribution Scope | D-C | Distribution Scope | D-C | Distribution Scope |
| 6 | 30, 33 | 30 | 6, 33 | 6 | 33 |
| 8 | 10, 12, 13, 23, 19 | 23 | 12, 10, 13, 8 | 10 | 30, 12, 13, 8 |
| 18 | 3, 26, 36, 22, 37 | 14 | 29, 3, 26, 36, 18, 22 | 23 | 11 |
| 11 | - | 1 | 34, 37, 35, 16 | 14 | 3, 29 |
| 21 | 25, 9 | 2 | 7, 28,5,19,31 | 22 | 36, 26, 18, 37 |
| 28 | 14, 7, 34, 2, 19, 31 | 11 | - | 25 | 21, 9 |
| 16 | 5 | 25 | 21, 9 | 7 | 34, 28, 2,19 |
| 1 | 35 | 24 | 17, 20, 38, 39 | 16 | 1, 35, 5 |
| 20 | 4, 27, 38, 24, 39 | 15 | 17, 32, 40 | 15 | 31, 17, 32, 40 |
| 15 | 17, 32, 40 | 4 | - | 20 | 4, 27, 38, 24, 39 |
| Algorithm | Distribution Points | Algorithms | ||||
|---|---|---|---|---|---|---|
| Best | Mean | Worst | Std | Time (s) | ||
| CS | 6 | 4.9629 × 104 | 6.1392 × 104 | 7.9211 ×104 | 2.4874 × 105 | 4.5187 |
| 10 | 3.2435 × 104 | 3.9502 × 104 | 4.3961 × 104 | 3.9872 × 105 | 4.5530 | |
| CCS | 6 | 4.7913 × 104 | 4.9009 × 104 | 5.2085 × 104 | 4.9009 × 105 | 4.9486 |
| 10 | 3.1619 × 104 | 3.3815 × 104 | 3.4209 × 104 | 3.3815 × 104 | 4.8706 | |
| IGA | 6 | 5.2032 × 104 | 5.3008 × 104 | 5.3814 × 104 | 5.9226 × 105 | 4.4255 |
| 10 | 3.5424 × 104 | 3.6460 × 104 | 3.6980 × 104 | 9.0172 × 105 | 4.5235 | |
| ICS | 6 | 4.5748 × 104 | 4.6187 × 104 | 4.6919 × 104 | 5.8622 × 104 | 4.7245 |
| 10 | 3.1034 × 104 | 3.2197 × 104 | 3.3113 × 104 | 8.0172 × 104 | 4.7811 | |
| DMQL-CS | 6 | 4.5013 × 104 | 4.8060 × 104 | 4.9253 ×104 | 1.2763 × 104 | 4.6255 |
| 10 | 2.9811 × 104 | 3.0157 × 104 | 3.2132 ×104 | 2.7651 × 104 | 4.6509 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Xiao, D.-d.; Lei, H.; Zhang, T.; Tian, T. Using Cuckoo Search Algorithm with Q-Learning and Genetic Operation to Solve the Problem of Logistics Distribution Center Location. Mathematics 2020, 8, 149. https://doi.org/10.3390/math8020149
Li J, Xiao D-d, Lei H, Zhang T, Tian T. Using Cuckoo Search Algorithm with Q-Learning and Genetic Operation to Solve the Problem of Logistics Distribution Center Location. Mathematics. 2020; 8(2):149. https://doi.org/10.3390/math8020149
Chicago/Turabian StyleLi, Juan, Dan-dan Xiao, Hong Lei, Ting Zhang, and Tian Tian. 2020. "Using Cuckoo Search Algorithm with Q-Learning and Genetic Operation to Solve the Problem of Logistics Distribution Center Location" Mathematics 8, no. 2: 149. https://doi.org/10.3390/math8020149
APA StyleLi, J., Xiao, D.-d., Lei, H., Zhang, T., & Tian, T. (2020). Using Cuckoo Search Algorithm with Q-Learning and Genetic Operation to Solve the Problem of Logistics Distribution Center Location. Mathematics, 8(2), 149. https://doi.org/10.3390/math8020149




