Abstract
Algebraic thinking, combinatorial thinking and reasoning skills are considered as playing central roles within teaching and learning in the field of mathematics, particularly in solving complex open-ended mathematical problems Specific relations between these three abilities, manifested in the solving of an open-ended ill-structured problem aimed at mathematical modeling, were investigated. We analyzed solutions received from 33 groups totaling 131 students, who solved a complex assignment within the mathematical contest Mathematics B-day 2018. Such relations were more obvious when solving a complex problem, compared to more structured closed subtasks. Algebraic generalization is an important prerequisite to prove mathematically and to solve combinatorial problem at higher levels, i.e., using expressions and formulas, therefore a special focus should be put on this ability in upper-secondary mathematics education.
1. Introduction
Mathematics education is constantly evolving based on the requirements of contemporary society. Consequently, the curriculum development is strongly influenced by 21st-century learning skills in particular critical thinking, problem solving, communication and collaboration [1]. It is obvious that any problem without some known algorithm or procedural tool can be considered as a challenge [2]. Students intending to inquire as defined in [3] feature the following characteristics: asking questions, attempting and experimenting, identifying the problem, choosing the right strategy in problem solving. The nature of open-ended problems represents the means how to implement the inquiry in mathematics education [4] and help students to learn how to think independently for using the problem solving strategies [5]. Over the course of many years, solving open-ended problems in mathematics has evolved into an activating method that supports the 21st-century learning skills mentioned above.
The ability to solve complex open-ended problems is anchored in some various different factors including the following: (i) metacognitive knowledge [6,7], (ii) positive attitude towards mathematics [8,9,10,11,12], (iii) mastering mathematics processes as are reasoning, generalization, communicating the results or mathematical modeling [13,14,15,16,17,18] and (iv) high level of mathematical proficiency in both, procedures [19,20] and conceptual understanding [21,22,23], including arithmetic, algebraic and combinatorial thinking. These aforementioned factors are not isolated, but they rather support each other mutually in the influence of the ability to solve complex open mathematical problems [24,25].
The distinction between arithmetic and algebraic thinking is sometimes oversimplified as a work with numbers, or a work with variables. In contrast, Radford [26] distinguishes between the arithmetic generalization, algebraic generalization and naive inductive reasoning based on the distinctive ways of thinking. It is more than clear that algebraic generalization builds on the observance of commonalities, by abduction from particulars. Then, a hypothesis, if formulated, and an expression, are or can be produced. On the other hand, just the arithmetic generalization often uses some recurrent relations and, following that, pupils, using this way of thinking are not able to provide a formula for a general case. However, the least sophisticated are the naive inductions based on probable reasoning. The type of generalization can be related to the type of problem occurring, however, the students equipped with well-connected problem solving schemas are not surprisingly more successful in transferring their knowledge [27]. On the other hand, the algebraic generalization raises specific problems for almost every student, even in the course of studying higher grades [28]. Our recent research findings indicate an ability to produce some general algebraic expressions as a crucial factor in solving open-ended non-routine problems in mathematics, even by high-achievers [29].
For the students the use of justification, proving strategies and techniques of various forms of proofs in mathematics, providing them with a crucial importance of mathematical reasoning, is conclusive. Therefore, such abilities clearly involve obtaining strategic knowledge in the specific areas related to the given problem at hand, as well as knowledge and norms specific for proving and reasoning [30], especially in mathematical open-ended problem-solving situations. Pedemonte [31] stresses the structural gap between the argumentation and proof. It is clear that just the argumentation inferences are based on the content, while in case of any proof they follow a deductive scheme. Within the work in the classroom environment, usually, students mostly experience some memorized algorithmic reasoning [32] or with some formal proofs, a sequence of formulas in the formal language [33] instead of the actual creative mathematical reasoning within a complex mathematical inquiry that enables understanding and construction of a new knowledge.
The ability to make some generalizations and to provide appropriate reasoning are both considered as high-level mathematical skills. Pedemonte further [34] studied certain relations between the level of the generalization and reasoning skills. However, generalization as such and concurrently as a process appears to be required for construction of mathematical induction, although, on the other hand, some relation was pointed out as a structural distance between them. Therefore, just the open-ended problems are considered suitable ways to develop required reasoning skills by students. Thus, the abductive reasoning serves for passing from the inductive to deductive reasoning [26]. It is not clear how the classifications or characteristics of generalization and justification arising from the studies that have focused on generalizing a number patterns apply to other mathematics topics or tasks. Nor do these frameworks make clear other reasoning processes that enable generalization and justification to occur [35].
Combinatorics has a special place in the field of mathematics and mathematics education. It is considered as a source of frequent and hard difficulties of students at various levels [15]. The fact is that just the combinatorial thinking presents the process of creating various possible combinations of ideas and cognitive operations [36]. The use of combinatorial thinking in combinatorial situations means developing a special ability to create abstract models and to find the structure of a set of outcomes [37]. When given enough time and hands-on problems, even usually low-achieving students can do well in solving combinatorial problems, and vice-versa, usually high-achieving students can lose track when dealing with novel problems in combinatorics [38]. Jones et al. [39] considered the following four levels of combinatorial thinking development: subjective, transitional, and informal quantitative, and numerical. Lockwood [40] stresses the role of the listing of elements forming a set of outcomes while solving any combinatorial problems. The suggested trajectory of solving the problems from some concrete elements to some general expressions seemed productive in helping students to gain familiarity with a context before generalizing, using variables. Problems in combinatorics provide a reasonable environment for generalization of the solution as “counting problems are often accessible yet challenging and these accessible problems provide a natural structure from which students may generalize” [41] (p. 311). During the process of generalization based on the combinatorial problem-solving any gifted students tried to understand the combinatorial situation more deeply, to identify some assumptions more precisely and a formulated plan was global in nature [42].
Little is known about the connections between the mathematical reasoning and combinatorial thinking. One of a few studies [41] investigating the affordances of combinatorial proof which can be considered as a valuable instrument for development of combinatorial thinking and for their proving skills is worth mentioning. The students participating in the study seem to be more convinced by the algebraic arguments than by the combinatorial reasoning.
The standard memorization of common algorithms and the routine calculations repetition have been slowly abandoned in mathematics education today. Instead, students are motivated to thinking about the given problem more deeply, analyzing and discussing the possibilities of different solutions [43] and looking for other mathematical aspects related to the mathematical content of the given problem. Therefore, any mathematics contest can be considered as a challenge [44] improving the students inquiring and using various problem-solving strategies. The development of the mathematical reasoning and problem solving strategies is supported in any mathematical contest especially aimed at students’ mutual collaboration [2].
Group-work in mathematics education represents the learning method based on the definition of collaborative problem solving by PISA (the OECD’s Programme for International Student Assessment) [45] as following: “an individual’s capacity to use cognitive processes to confront and resolve real, cross-disciplinary situations where the solution path is not immediately obvious and where the content areas or curricular areas that might be applicable are not within a single subject area of mathematics, science or reading” (p. 7). Mathematical open-ended problems requiring the higher mathematical thinking skills, can provide students an opportunity to share their knowledge [46], to discuss the strategies [47] and create the conclusion from the team as the unit [48].
As stated by Ericson and Lockwood [49] in order to prove a combinatorial identity various cognitive models are needed in order to understand the algebraic notations. Furthermore, it seems that the ability to provide plausible reasoning within solving combinatorial problems is influenced by a variety of representations at students’ disposal, including different algebraic notation [50]. Therefore, we consider as important to shed some light on the relations between the three mathematical competencies within a solution of complex open-ended mathematical problem by high-achieving students. Furthermore, the relations are usually studied for individual students. However, several researchers [51,52] suggest that especially cognitive abilities develop through social interactions, thus the group solutions should be investigated when producing highly cognitively demanding activity such as solving complex mathematical problems. Collaboration in groups is well suited to accessing skills manifested in problem-solving because it encourages students to explain their thinking and engage in joint elaboration of the final assignment [53].
We are not aware of any study investigating relations between the various mathematical abilities while studying group solutions of highly-demanding complex mathematical problems.
Our research is focused on the analysis of the team mathematical contest known as Mathematics B-day in the two particular perspectives: quantitative and qualitative. The assignment of the contest was analyzed as a coherent set of the mathematical problems aimed at inquiry in mathematics. We analyzed the correctness of the solution of subtasks with the different level of combinatorial thinking, algebraic generalization and mathematical reasoning. Then, the results of the analysis were compared with the authentic solutions of groups consisting of 3–4 students.
The research question was formulated as follows: what are the (implicative) relations between the levels of algebraic generalization, mathematical reasoning and combinatorial thinking manifested in the course of solving non-routine mathematical problems by groups of high-achieving upper-secondary students?
2. Materials and Methods
The Mathematics B-day contest [54] is a unique opportunity for upper secondary students to collaborate on the real mathematical open problem solving and demonstrate their mathematical knowledge and competences by conjecturing and proving in mathematics. In the Slovak Republic the Department of Mathematics of Constantine the Philosopher University in Nitra is an organizer of such an event, although the origin of this contest was in the Netherlands. The essence of the Mathematics B-day contest is based on the educational program of mathematics for the prospective university level of technical studies and studies in science and mathematics.
Students, divided into three or four member teams, are solving the assignment created with an intent motivating inquiry in mathematics. The assignment represents a set of subsequent problems related to the one chosen situation composed in the continuous text.
The goal of Mathematics B-day 2018 assignment [55] was inspired by the mathematical open ended problem called “The Moser’s Worm Problem” formulated as follows: “What is the surface of the smallest flat shape that can cover all lines of length 15 cm?” [56] (p.153). The situation was represented for students like a story of a certain snake with its length of 15 cm, that needs a blanket for every position while this snake is sleeping. The assigned problems were aimed at explaining specific relations, while generalizing and proving, and finally, at the mathematical modeling as such. Students could use recommended manipulatives (copper wire, sheet of graph paper, compass, scissors, etc.) for their experimenting in the first phase of the solution process and later the dynamic software GeoGebra was recommended. It is more than obvious that a success solution requires some elemental pieces of knowledge, stemming from geometry (e.g., planar geometry and trigonometry) as well as combinatorics (e.g., enumeration of combinations to produce a pattern).
In 2018, 131 students gathered into 33 teams solved the assignment of the Mathematics B-day contest. The relatively high achievement in mathematics is assumed because only two best reports from each participating school can be submitted for the final national assessment. The actual and real abilities to solve non-routine mathematical problems are one of the basic components of the general problem-solving ability [57]. The non-routine problems will demand a high cognitive load [58], therefore, the high-achievers’ solutions need to be analyzed to a greater extent. For this reason, the solvers, who participated in the Mathematical B-day event, can represent an appropriate sample for observing the level of generalization and proving in mathematics.
2.1. Assignment of Mathematical B-Day 2018: Snake Nest
The full text of the assignment represents 14 pages of continuous mathematical text, containing several kinds of non-routine problem, aimed at the following topics and themes: experimenting, calculations, and then, explanation, generalizing, as well as proving some relevant and real relations. This study was focused on some necessary subtasks, requiring some higher-order mathematical thinking skills, vested, especially, in the fields of proving and generalizing. The assignment is composed from the 6 tasks further divided into more subtasks characterized like open-ended problems.
The introductory subtasks (1a–1e) were aimed at the shape of a circle covering the all positions of the snake represented by a 15 cm long curve. Students had to find the smallest possible radius and properties in specific cases. In the subtasks 2a–2e, the positioning strategy of the snake is explained to students based on a special example: the snake bended in a rectangle.
The following tasks 3, 4, and 6, are aimed at discovering the smallest planar shape represented by several shapes like a half and quarter of the circle, triangle or diamond. Subsequently, students are asked to arrange the smallest possible area of a blanket by cutting off any useless parts of the aforementioned shapes. Apparently and definitely, some combinatorial thinking skills are required in the task 5. The problem about the smallest area of the blanket is viewed by means of a simplified model represented by the tetra-snake. The body of any tetra-snake consists of squares and the centers thereof can be connected by lines. Any given broken line can determine any position of the snake according to their shape, as shown in Figure 1.
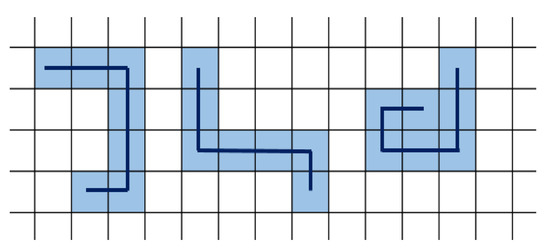
Figure 1.
Visual aid for subtask aimed at the combinatorial thinking (adapted from [55]).
The findings from the introductory assignments should be useful for creating a mathematical model of Final assignments assigned as follows: “Design the smallest possible blanket for the 15 cm snake” [55] (p. 14). The proposed approach is generalized in the following six steps:
- Limit what type of snakes and what type of blankets do you are consider.
- Experimenting.
- Give a positioning strategy for the all shapes for those blankets.
- Find the corresponding minimum dimensions.
- Explain that the all forms remain under the blanket with the strategy from the third step.
- Cut bits away from the blanket to make it even smaller.
As mentioned above, the assignment consists of several types of interconnected task characterized as the open-ended problems. The subtasks were sorted based on the level of required abilities into the three groups: (a) experimenting and applying, (b) reasoning and hypothesizing, (c) generalizing and proving. The first group of subtasks requires some basic abilities for solving routine problems aimed at estimating the concrete result or problems with a closed goal but open approach. The other two groups represent problems requiring a higher level of abilities. Figure 2 below shows how the subtasks of the all assignments are interconnected.
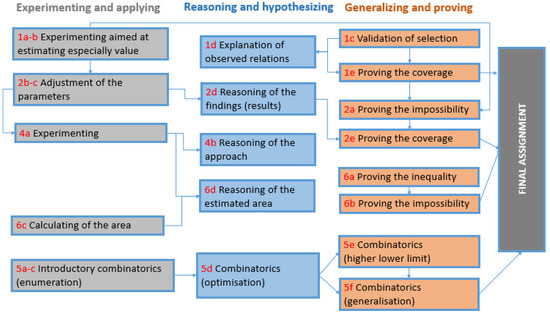
Figure 2.
Schema of interconnected subtasks.
The schema (Figure 2) shows that any assignment is composed in the sense of the recommended steps in the final assignment. To achieve success, the use of the students’ wide abilities on all levels are required. Task 5 is based on the essence of the main problem to find the smallest blanket for the snake but in view of using combinatorics. Therefore, the subtasks 5a–5f appear to be independent of the whole text of the assignment and the assumption that the previous tasks can influence and affect the success of a solution of the task 5 is omitted. The Moser’s Worm Problem can be included in the field of combinatorial geometry. Thus, specifically, we aimed at the subtasks where the investigated skills were supposed to be manifested, particularly the subtasks 1c, 1e, 2a, 2e, 5e, 5f, 6a, 6b (see the full assignment in [55]), while in the case of the subtasks 5a–5f for combinatorial thinking as well as final assignment, being focused mainly on the skills of mathematical modeling.
2.2. Statistical Analysis
The descriptive correlational research was used in this study to assess the relationships between students’ level of algebraic generalization, mathematical reasoning and combinatorial thinking. The assignment described in Section 2.1 was solved by 33 groups of students from 11 upper-secondary schools in Slovakia within the contest Mathematical B-day 2018. Each group consisted of 3–4 students. The intended output of the contest, final report of each group was assessed and following variables were investigated.
The level of reasoning skills was assigned to every student’s solution of the all investigated subtasks (2a, 5f, 6a, 6b, 6d), and the final assignment (FA) as well. The level of algebraic generalization was assigned to every student’s solution of the subtask 5f, and the final assignment (FA) as well. The subtasks 5a, 5c, 5f and final assignment were assessed for the level of combinatorial thinking. Table 1 shows the all data covering assessing the mathematical abilities.

Table 1.
Description of the levels of algebraic pattern generalization, reasoning and proving, and combinatorial thinking.
Following this, the subsequent statistical analysis of the obtained data was performed, using the software environment R [59], applying the packages RVAideMemoire [60], lsr [61], and rchic [62]. The success-rates in the subtasks of the given assignment were compared by the Cochran Q test that is the generalization of the McNemar test for the two independent samples. The partial problems were considered as independent samples. Subsequently, the post-hoc analysis, comparing each pair of problems, was performed by the McNemar test. The levels of reasoning skills and algebraic generalization in the analyzed subtasks were compared, and then, post-hoc analyzed by the Friedman test.
The mutual relationships between the assessed features of the group solutions of the complex problem were assessed. Different statistical characteristics were implemented based on the scale used for the particular variable. The relationship between a Boolean variable describing the correctness of the solution of particular subtasks was assessed by coefficient. The Spearman’s rank correlation coefficient was used to assess a relationship among the level reasoning skills, combinatorial thinking and algebraic pattern generalization manifested in particular subtasks. The corrected Cramer’s V was calculated to measure an association between the correctness of a solution of the particular subtask and levels of generalization, reasoning, and combinatorial thinking.
The statistical implicative analysis (SIA) [63] was applied to explore some mutual relations between the defined attributes of assessing and to evaluate relations between the subtasks in the basic assignment and the students’ performance in the final assignment.
3. Results
Out of a total 33 submitted team solutions 27 attempted to solve the final assignment. The relative frequency of investigated items differed significantly , a pairwise comparison by the McNemar test is summarized in Table 2. The null hypothesis was formulated for each pair of subtasks as follows: “There is no significant difference between the ratio of incorrectly solved subtasks for the subtask A and subtask B”. The levels of reasoning skills varied between the tasks (), contrasting to the level of algebraic generalisation (). The three subtasks were aimed at proving inequality/impossibility (2a, 6a, 6b). The subtask 2a was solved correctly and significantly more often than the other two subtasks (). Surprisingly, one of the parts of the assignment with the highest success rate was the final assignment requiring higher order thinking. However, it is an open-ended problem and students were allowed to choose their own objects of investigation according to their involvement and self-efficacy. Furthermore, the analyzed materials were not their hand-out versions, but the final report where they present only chosen results.

Table 2.
Success rate and levels of reasoning skills and algebraic generalization manifested in team solutions.
The results of SIA (see Figure 3) indicate an evident interconnection between correctness of the investigated subtasks. The correct solution of the subtask 5f aimed at assessing an ability to generalize algebraically implied correct solution of another subtask aimed at assessing the generalization skills, namely the subtask 2e. Although it was implied by the correct solution of the generalization of the subtasks 6b, it was also implied by the high level experimentation and application manifested in the team solution of subtask 6c. Furthermore, the correct solution of 6a implied the correct solution of two generalizations of the subtasks, 2e and 2a. The success in 2a was implied also by the correct solution of FA. Direct implications from the subtasks 6a and 6b to the success in 6d were not confirmed there. It may indicate that just the generalization is a hidden driving ability supporting mathematical reasoning.
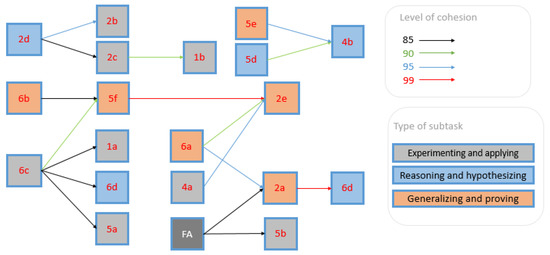
Figure 3.
Implication tree of correctness of the results.
The correctness of the team solutions correlated between the introductory combinatorial subtasks and between combinatorics subtasks aimed at optimization and generalizations (). It is worth commenting that the correct solution of the final assignment did not correlate with any of investigated subtasks (Table 3).

Table 3.
Correlation matrix of correctness of the team solution in selected subtask (phi coefficient).
Based on the results summarized in Table 4 we can claim that the levels of reasoning skill manifested in team solutions of the subtasks 6a, 6b and 6d correlated mutually (). On the other hand, the level of algebraic generalizations was not correlated between the subtask 5f and final assignment. The level of combinatorial thinking correlated with the generalization level, manifested in the final assignment ().

Table 4.
Correlation matrix of the level of reasoning, algebraic generalizations and combinatorial thinking manifested in the team solutions of selected subtasks (Spearman’s rho).
The level of combinatorial thinking manifested in the team solutions of the assessed partial subtasks 5a, 5c and 5f was correlated. Furthermore, the combinatorial thinking manifested in the solutions of the subtasks 5c and 5f correlated with algebraic generalization assessed in team solution of the subtask 5f The correlation between the combinatorial thinking manifested in the team solution of the subtask 5c and algebraic generalization in 5f is not caused by a simultaneous use of the two mathematical competencies, but rather in the design of the task as such, when the correct solution of the subtasks 5c was necessary for solving the subtask 5f. On the contrary, in the subtask 5f both competencies were necessary for a successful solution. It seems that contrasting to the mathematical reasoning and algebraic generalization, the ability to use combinatorial thinking appears to be very consistent among the partial subtasks of an investigated complex problem. Due to the special kind of problems as well as high-achieving solvers as participants in the study it is not possible to state whether this consistency is a general characteristic of combinatorial thinking, or it is a feature of the problem or of the solvers.
We tried to relate the correctness of the solution of the particular subtask with the different level of abilities. Correctness of the solution was associated with the reasoning skills manifested in solutions of several investigated subtasks (Table 5). The reasoning skills in solutions of the subtasks 6a, 6b and 6d were associated with correctness of 6a Furthermore, the subtask 5e was the only subtask in which correctness of the solution was related to the level of reasoning skills in FA ().

Table 5.
Correlation matrix of the solution correctness of and the levels of reasoning, algebraic generalization and combinatorial thinking manifested in the team solution of selected subtasks (Cramer’s V).
Out of 6 teams who were able to produce the correct algebraic expression in the solution of the subtask 5f used an inductive approach, one team did not provide any reasoning for it, and one team used an abductive reasoning approach. The level of generalization was related to correctness of the solution of this subtask (). The level of generalization in 5f was related to correctness of the subtask 5a (). Correctness of the final assignment was related to the reasoning-skills level (), however, it was not related to the level of generalization (), nor with the manifested level of combinatorial thinking in this complex problem (). It might again be caused by the different, more open, nature of the final assignment compared to partial subtasks.
3.1. Example of the Authentic Team Solutions of the Subtask 2a
The subtask 2a was classified to the third group as aimed at the generalizing and proving, but only the actual levels of reasoning and proving skills were observed in students’ solutions of this subtask. The goal of the subtasks is verifying the impossibility of the assigned argument.
3.1.1. Solution 2a.A
“Based on the previous experiment, we found an interval of the angles, for which there is not possible to cover the Lena. There is an interval of angles between the largest angel from the position 1 (41.81°) and the smallest angle from the position 2 (96.38°), which is not possible to fit under the cover. For example, the angle of size 60° creates the isosceles triangle; therefore the lengths of the heights on the triangles sides are equal and greater than 5 cm. Both rectangles, 5 × 15 as well as 5 × 14, are not covering Lena in every case.”
Students used an experiment as the main method to find a solution (Figure 4). The crucial parameter represents estimated lengths of the highs of the triangles created by a bent line based on the strategies set out in the assignment of the subtask (see the full assignment [55]). Subsequently, students found an interval of the angles that do not match the dimensions of the given rectangle. This approach was aimed at both assigned rectangles. The conclusion of students’ experimentation was expressed in the simple statements.

Figure 4.
Students’ experimenting by the GeoGebra and with the copper wire in solution 2a.A.
3.1.2. Solution 2a.B
“Let us deal with the specific group of snakes, especially with some snakes composed of the two line segments 7.5 cm long with a mutual boundaries point, which we are going to call as the vertex of the snake. The two remaining boundary points of line segments are going to be called the tails of the snake. Let these two line segments form an angle α. We are going to call these snakes laptops, because they remind us of a laptop from their profile.
“First, let us have a look at the rectangle with the dimensions 14 cm and 4 cm. This blanket is not enough for our snake. Therefore, it is obvious that the snake obtains a form of a line segment with its length 15 cm for α = 180°. The diagonal represents the longest line segment in the rectangle. And the length of this diagonal can be calculated by the Pythagorean Theorem. In our case the length of diagonal is just . The widest part of the blanket is less than our snake for the given angle, and thus for this reason the snake cannot fit under the blanket.
“Let us try the blanket with the dimensions 15 cm and 5 cm. The snake is not going to fit under this blanket. Let us take the snake at 60° angles. This snake has the shape of an equilateral triangle and the whole triangle must be placed inside the rectangle. The shortest distance between the vertex and the point of the opposite side, the height of the triangle, is approximately 6.63 cm long. If we rotate this triangle in the coordinate system, for every turn will be there the y-dimension greater than 5, and so it cannot fit in the rectangle, which has for some turns this dimension equal to 5.”
In solution 2a.B, students described their approach of a solution in the two parts for the two assigned rectangles. In the first case of the rectangle with the specific dimensions, students used the Pythagorean theorem. For the conclusion, there is enough to show if the diagonal of the rectangle can cover the whole length of the non-bended snake. Similar to the previous example of the solution, students were approaching by estimating the lengths of triangles created by a bended snake for the second assigned rectangle. However, the approach is not based on the strategies set out in the assignment of the subtask. Students originally showed in the one chosen example the impossibility of the argument, but a detailed description or a picture from experimenting is missing there in the students’ solution.
Thus the ways students were thinking in both approaches of the solution were correct. The solution reached the first level of reasoning and proving skills, because their description contains the reasoning by the one particular example.
3.2. Example of the Authentic Team Solutions of the Subtask 6d
The following subtask was classified in the second group based on a schema of interconnected subtasks, vested in reasoning and hypothesizing steps and jobs, but this all requires in addition some reasoning and proving skills. The subtask 6d is similar to the previous subtask 2a, but the goal is not to refute an argument. By contrast, students are asked to show that the snake will fit in an estimated area under some specific conditions.
3.2.1. Solution 6d.A
“Let us have a blanket created by joining the two equilateral triangles with the height 7.5 cm long and then we will put the middle of the snake on the common edge of the triangles [Figure 5A].
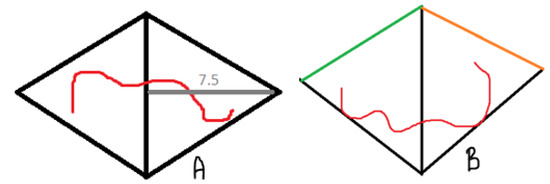
Figure 5.
Students’ solution A of the subtask 6d.
“We can estimate the side of the triangle x by Pythagorean theorem: , so we get by all adjustments, so that . Well, then the area of the one triangle is , and so the area of the whole blanket can be estimated as . But is this blanket enough?
“Put the snake into the position, that its middle is placed on the common sides of the two triangles and the snake is touching the two sides of triangles like given in the figure B [Figure 5B] (one half is touching the one side, the second half is touching the second one).
“Then we can see that the one half cannot pass through the two sides, because the heights of the triangle, the distance of these two sides, are equal to the length of the half of the snake.”
In the first step of solution 6d.A, students calculated the length of the side of the equilateral triangle for estimating an area of the diamond. Even if the final result of the area is correct, students made a mistake in the notation of the equation. However, the estimation of the diamonds’ area was not necessary in the case of a solution of the subtask 6d. Focusing on the reasoning of the argument was more important here. But the students’ conclusion does not consist of any mathematical evidence, even any mathematical reasoning which would reach out to the goal of this subtask. The reasoning and proving skills as such manifested in the solution A of the subtask 6d stay on the level 0.
3.2.2. Solution 6d.B
“Both parts of the shape (of the diamond) are the two equilateral triangles, so we just have to look at one of them, because in addition, an equally large piece of snake exceeds upon both sides. Let the equilateral triangle have a height 7.5 cm long. We will choose a point M on the one of the sides of the triangle. We will draw a line from this point, touching on the other side and our goal is to have a snake not exceeding through the third side. For this reason, let us take the shortest possible way. We will find out this way that we will reflect the third side in the axial symmetry based on the second side and extend the perpendicular from the first side.
“In Figure 6 we can see that the green line—a projection of the third side based on the second one —is parallel to the first side—and the point A lies on it. The perpendicular is always the shortest distance, and when a perpendicular line is parallel to another line, that means that the line with the shortest distance will be perpendicular also to the first line. For this reason, the distance is equal with the height of the triangle, therefore 7.5 cm.”
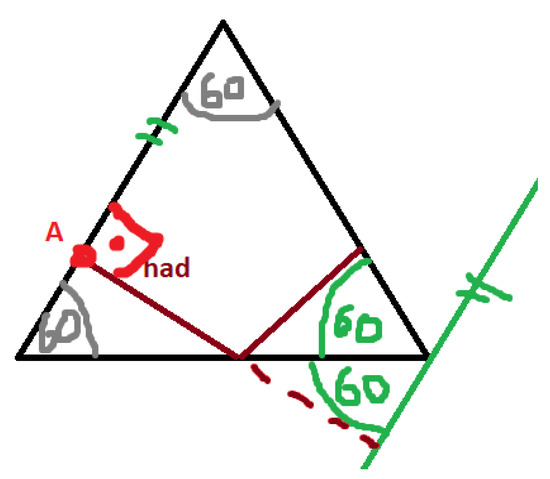
Figure 6.
Students’ solution B of the subtask 6d.
Students used the proper methods and tools to find the correct mathematical evidence, but the students’ description is not clear. At first, the final (underlined) conclusion is written in a confusing way. The description of the sides of triangles is not exactly named. In addition, the added picture does not contain an exact label. For example, there is a point M defined at the beginning of the solution. But in the following explanation as well as in the picture, the point A is marked.
3.3. Example of the Authentic Team Solutions of the Subtask 5f
The whole task 5 is aimed at the combinatorial thinking skills. Every single subtask requires some different skills on the different levels. The subtask 5f was chosen as the following example mainly because it required all the observed skills in this research, hence, algebraic generalization, reasoning and proving as well as combinatorial thinking.
3.3.1. Solution A
“If we bend a snake only one time in any point, then the area of the blanket can be calculated as follows for all kinds of snakes, except for the snake with the length of the body 1 because the formula is not valid for it.”
The students’ solution is giving a short expression, formula, or hypothesis, for the estimating of the wanted area. However, a closer mathematical description or formulation of this hypothesis is missing there. For this reason, students did not put any efforts into the possible combinations of some bended snakes. To sum it up, students manifested the algebraic generalization skill on the level 2, their reasoning and proving skills on the level 0 and their combinatorial thinking is not observable in the solution 5f.A.
3.3.2. Solution B
“Let’s have a bended tetra-snake with the length of the body n; and n cannot be equal to 1 or 2, as the possible smallest bendable tetra-snake has the length of the body 3. In a bent tetra-snake, one square represents a bending point, and other squares are divided between the two arms. Utmost, the first arm is composed from square and the second arm from the one square. It represents the most disproportionate distribution. In the next step, we will move the squares from the longer arm to the shorter one. In the most proportionate distribution, if n is an even number, there is the same amount of the squares in the arms of the tetra-snake and if n is an odd number, there are squares in the one arm and squares in the other arm. When we add another square (for example there are arms of a tetra-snake with the length 5 and 3, then 4 and 4, and then 3 and 5), we already have this option and, therefore, we can tilt the tetra-snake very easily.
This means that the one arm of the blanket must have a length of squares (in the utmost case) and the other arm has a length of if is an even number and if is an odd number. Then, the area of the blanket is is for which is even and for odd number . The general form of the formula is:
Students offered the general expression of the formula for estimating the area of covering the bent snake, so the algebraic generalization skills were well manifested at the level 3. However, their findings are not formalized in a form of the proof or the theorem. Therefore, students achieved level 2 in the reasoning and proving skills. As far as to the combinatorial thinking skills, level 2 is demonstrated in the solution 5f.B.
3.3.3. Solution C
“Now we are going to focus on the one-bent tetra-snakes, but without a condition that their bending point must be in the middle of the snake. We draw (Figure 7A) for all possible situations for

Figure 7.
Students’ solution of the subtask 5f (A) the generative strategy for expressing the formula and (B) the table of expressed general formula. Translations: Obsah obdĺžnikovej prikrývky = Area of the rectangular blanket; Obsah najmenšej prikrývky = Area of the smallest blanket; Párne n = Even n; Nepárne n = Odd n.
“We will try to generalize the observed properties for getting a formula expressing the smallest possible blanket for the tetra-snake with the length of n (Figure 7B).
“Note: we are not going to consider any tetra-snakes with their length of 1 and 2 squares, because these tetra-snakes represent special cases and they cannot be bent.”
Definitely, there can be observed some higher skills in the solution 5f.C. Students manifested level 3 in the algebraic generalization skills as well as in combinatorial thinking skills. Based on the chosen approach and tools, students found out a general formula (Figure 7B). However, also in this case it is not formalized in a form of the proof. Students reached level 2 in the reasoning and proving skills.
4. Discussion
In this paper we tried to investigate specific relations between the ability to generalize algebraically, to use combinatorial thinking and to prove mathematically that were manifested during solving complex open-ended mathematical problems within the team contest. The complex assignment called on a diverse set of knowledge of individual students contributing to the team solutions, as well as on their skills, abilities and expertise [64].
Certain correlations between the algebraic generalization and reasoning skills were confirmed in cases when students solved an open mathematical problem, requiring both, meaning the use of some reasoning skills as well as some generalization skills concurrently. However, the same relation between these two abilities was not confirmed among the all investigated subtasks. This confirms the findings that the mathematical reasoning is not necessarily related to students’ achievement in solving problems that do not pose high cognitive demands [65]. Furthermore, Nunes et al. [66] considered mathematical reasoning and algebraic skill as the two separate contributions to the achievement in mathematical problem solving. Relations between several aspects of mathematical problem-solving were investigated and the ability between control of variables and reasoning was confirmed also by [67]. However, Chimoni and Pitta-Pantazi [68] identified the ability to provide reasoning by analogy, serial or deductive reasoning as a significant predictor for lower-secondary students’ algebraic thinking. Students have to look beyond the surface characteristics of the problem to be able to construct a mathematical model which is sufficiently general and captures the essence of the situation [69]. The distance between the reasoning skills based on the generalized pattern produced could be an obstacle for students and a possible or probable cause of their failure in the construction of mathematical induction [31]. The correlations between the level of generalization and reasoning skills can be based in the nature of mathematical proof when “construction of deductive proof is performed only when inductive argumentation is based on a process pattern generalization” [70] (p. 147).
The subtasks in combinatorics analyzed were highly intercorrelated and correlated to the level of generalization. However, such correlation is not surprising, whereas the highest level of combinatorial thinking as defined by Jones et al. [39] leads to a solution of the combinatorial problem by the means of an expression or formula [14]. On the other hand, based on findings reported by Lockwood et al. [71] the re-invention of combinatorial formulas puts some higher demands on the level of combinatorial thinking than on algebraic generalization.
The manifested reasoning skills were significantly higher as far as to the subtasks 2a, 6a and 6b compared to the subtask 6d solution. A similar relation can be observed in the case of the correctness of the students’ solution. Our results indicate that it is easier to prove that the assigned situation is not possible or equality is not valid than to prove validity of a statement, even though this kind of task is usually unknown or even novel to many students [72]. Whereas the attitudes in mathematics can result from automatizing a repeated emotional reaction, students with a negative attitude towards geometric proofs may attach that same attitude to the all proofs in other mathematical fields [73], hence the use of the aforementioned kinds of proof can reduce negative attitude towards the mathematical proof as such. The seeming independence between ability to provide mathematical reasoning and combinatorial thinking can have a resource in the fact that algebra is typically the first part of mathematics where students are asked to provide abstract mathematical reasoning [74].
The problems investigated were aimed at the reasoning skills and mathematical proof (2a, 6a, 6b and 6d) and at algebraic generalization as such (5f). The subtasks were structured and strongly focused on the particular students’ ability. While solving a complex ill-structured open-ended problem aimed at mathematical modeling, i.e., the final assignment, our students have more freedom to investigate mathematically and incorporate the distinct mathematical abilities. This may fulfill the requirement formulated by Novotná [75], showing that the students should have a real chance to experience some pleasure while discovering, but also concurrently having a chance to learn, to acquire some new pieces of knowledge or skills, they would be able to apply in other situations subsequently. Thus, to conclude, any mathematical modeling job allows and requires both, the production of an expression, and proving the validity of the produced result. The interaction between the investigated abilities supports a more sophisticated solution of the problem than each of the skills occurring in isolation from the others [76].
Limitations of the Study
When generalizing the results of the presented study, one should be aware that the sampling was not random, nor stratified. The data came from the results of the contestants of Mathematics B-day what adds self-selection bias to the results. By contrast, any relations between the different sources of mathematical proficiency are most visible when solving a challenging problem by high-achieving students [57]. The groups are usually even more successful when handling complex problems [52], so the relations are more feasible for investigation in this kind of setting. Therefore, the group result was analyzed instead of individual contributions. As the “collaborative partnerships draw on different contributors across different tasks” [64] (p. 254), we focused on the results of shared activity regardless the previous experience with group-work and distribution of workload among the members of the team. Although the analysis of the work of groups of students may appear to be not sufficient to investigate all the cognitive aspects in relationship between the reasoning skills, combinatorial thinking and algebraic generalization, and some underlying variables may perhaps be hidden, some specific relations were observable nevertheless.
As reported in the meta-analysis by Lou et al. [77] the shared group goal (in this case the participation in a mathematical contest) is needed to make the group collaboration effective. Even though the results of this study may be related only to the special group of students, they extrapolate the relations among the ordinary students as solvers of mathematical problems.
5. Conclusions
Herein we have explored specific relations between the reasoning skills and the ability to generalize algebraically in the case of a team solution of a complex open-ended problem by high-achieving upper-secondary students. We found out that some relations can be observed mainly in cases of open-ended problem solving that generally require a higher-order level of thinking.
Based on the results of our study, we can suggest using or utilizing more problems aimed at proving an inequality or impossibility in the every-day mathematics classroom environment. Students, it seems to us, are or can be more successful in these kinds of proofs, and it might improve both, their reasoning skills as well as their self-efficacy in the field of mathematical proving. The highest level of combinatorial thinking is related to the work with combinatorial formulas and expressions. When students are asked to solve a combinatorial task using an expression or formula, then they should be able to generalize algebraically. Similarly, to our previous study [29] the role of algebraic generalization in solving problems from the different parts of mathematics was confirmed. Thus we can conclude that the algebraic generalization abilities should be in the focus of the upper-secondary mathematics education. It seems worthwhile to study how the generalization and reasoning skills are related to other observable mathematical competencies, e.g., factual combinatorial thinking ability, or factual probability reasoning ability as well.
Author Contributions
Conceptualization, S.Č.; methodology, J.M.; software, K.O.B.; validation, J.M., K.O.B. and S.Č.; quantitative analysis, J.M.; qualitative analysis, K.O.B.; investigation, J.M. and K.O.B.; resources, S.Č.; data curation, J.M. and K.O.B.; writing—original draft preparation, J.M. and K.O.B.; writing—review and editing, J.M. and K.O.B.; visualization, J.M. and K.O.B.; supervision, S.Č.; project administration, S.Č.; funding acquisition, S.Č. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Slovak Research and Development Agency under the contract No. APVV-15-0368 and by the Scientific Grant Agency of the Ministry of Education, Science, Research and Sport of the Slovak Republic under the contract No. VEGA 1/0815/18. The work was supported also by the Ministry of Education, Youth and Sports of the Czech Republic under the contract RO60201015025.
Conflicts of Interest
The authors declare no conflict of interest.
References
- National Research Council. Assessing 21st Century Skills; National Academies Press: Washington, DC, USA, 2011; p. 154. [Google Scholar]
- Powel, A.B. Challenging Tasks and Mathematics Learning. In Challenging Mathematics in and beyond the Classroom; Barbeau, E.J., Taylor, P.J., Eds.; ICMI Study Series 12; Springer: Berlin/Heidelberg, Germany, 2009; pp. 133–171. [Google Scholar]
- Jaworski, B. Theory and practice in mathematics teaching development: Critical inquiry as a mode of learning in teaching. J. Math. Teach. Educ. 2006, 9, 187–211. [Google Scholar] [CrossRef]
- Nohda, N. Teaching by Open-Approach Method in Japanese Mathematics Classroom. In Proceedings of the Conference of the International Group for the Psychology of Mathematics Education, Hiroshima, Japan, 23–27 July 2000; Volume 1, pp. 39–53. [Google Scholar]
- Frobisher, A.; Frobisher, L. Didaktika Matematiky II; Raabe: Bratislava, Slovakia, 2015; p. 169s. [Google Scholar]
- Artzt, A.F.; Armour-Thomas, E. Development of a Cognitive-Metacognitive Framework for Protocol Analysis of Mathematical Problem Solving in Small Groups. Cogn. Instr. 1992, 9, 137–175. [Google Scholar] [CrossRef]
- Veenman, M.V.J. The role of intellectual and metacognitive skills in math problem solving. In Metacognition in Mathematics Education; Desoete, A., Veenman, M., Eds.; Nova Science: Haupauge, NY, USA, 2006; pp. 35–50. [Google Scholar]
- Chytry, V.; Rican, J.; Korinkova, R. The influence of a teacher′s innovation on a pupil′s relationship to mathematics. In Proceedings of the ICERI19, 12th International Conference of Education, Research and Innovation, Seville, Spain, 11–13 November 2019; Chova, L.G., Martinez, A.L., Torres, I.C., Eds.; IATED-Int Assoc Technology Education & Development: Valencia, Spain, 2019; pp. 128–133. [Google Scholar]
- Mason, L. High school students′ beliefs about maths, mathematical problem solving, and their achievement in maths: A cross-sectional study. Educ. Psychol. 2003, 23, 73–85. [Google Scholar] [CrossRef]
- Pajares, F.; Miller, M.D. Role of self-efficacy and self-concept beliefs in mathematical problem solving: A path analysis. J. Educ. Psychol. 1994, 86, 193. [Google Scholar] [CrossRef]
- Stage, F.K.; Kloosterman, P. Measuring beliefs about mathematical problem solving. Sch. Sci. Math. 1992, 92, 109–115. [Google Scholar]
- Švecová, V. Mathematics Anxiety and Other Psycho Didactic Aspects in University Students. J. Educ. Soc. Policy 2018, 5, 246–250. [Google Scholar] [CrossRef]
- Kosyvas, G. Levels of arithmetic reasoning in solving an open-ended problem. Int. J. Math. Educ. Sci. Technol. 2015, 47, 356–372. [Google Scholar] [CrossRef]
- Lockwood, E. The Strategy of Solving Smaller, Similar Problems in the Context of Combinatorial Enumeration. Int. J. Res. Undergrad. Math. Educ. 2015, 1, 339–362. [Google Scholar] [CrossRef][Green Version]
- Lockwood, E.; Wasserman, N.H.; McGuffey, W. Classifying Combinations: Investigating Undergraduate Students′ Responses to Different Categories of Combination Problems. Int. J. Res. Undergrad. Math. Educ. 2018, 4, 305–322. [Google Scholar] [CrossRef]
- Mousoulides, N.G.; Christou, C.; Sriraman, B. A modeling perspective on the teaching and learning of mathematical problem solving. Math. Think. Learn. 2008, 10, 293–304. [Google Scholar] [CrossRef]
- Samková, L. Investigating the Variety and Usualness of Correct Solution Procedures of Mathematical Word Problems. J. Effic. Responsib. Educ. Sci. 2020, 13, 10–26. [Google Scholar] [CrossRef]
- Wong, T.T.-Y. Is conditional reasoning related to mathematical problem solving? Dev. Sci. 2017, 21, e12644. [Google Scholar] [CrossRef]
- Abramovich, S.; Pieper, A. Fostering recursive thinking in combinatorics through the use of manipulatives and computing technology. Math. Educ. 1995, 6, 4–12. [Google Scholar]
- Swafford, J.O.; Langrall, C.W. Grade 6 Students′ Preinstructional Use of Equations to Describe and Represent Problem Situations. J. Res. Math. Educ. 2000, 31, 89–112. [Google Scholar] [CrossRef]
- Kazemi, E. Discourse that promotes conceptual understanding. Teach. Child. Math. 1998, 4, 410. [Google Scholar] [CrossRef]
- Mula, M.; Hodnik, T. The PGBE Model for Building Students′ Mathematical Knowledge about Percentages. Eur. J. Educ. Res. 2020, 9, 257–276. [Google Scholar]
- Schüler-Meyer, A.; Prediger, S.; Kuzu, T.; Wessel, L.; Redder, A. Is formal language proficiency in the home language required to profit from a bilingual teaching intervention in mathematics? A mixed methods study on fostering multilingual students′ conceptual understanding. Int. J. Sci. Math. Educ. 2017, 17, 317–339. [Google Scholar] [CrossRef]
- Cheng, S.C.; She, H.C.; Huang, L.Y. The impact of problem-solving instruction on middle school students′ physical science learning: Interplays of knowledge, reasoning, and problem solving. Eurasia J. Math. Sci. Technol. Educ. 2017, 14, 731–743. [Google Scholar]
- Burch, L.; Pinhero, W.A.; Tillema, E. Opportunities for generalising within pre-service secondary teachers′ symbolisation of combinatorial tasks. In Proceedings of the Forty-First Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education; Otten, S., Candela, A.G., de Araujo, Z., Haines, C., Munter, C., Eds.; University of Missouri: St Louis, MO, USA, 2019. [Google Scholar]
- Radford, L. Iconicity and contraction: A semiotic investigation of forms of algebraic generalizations of patterns in different contexts. ZDM 2007, 40, 83–96. [Google Scholar] [CrossRef]
- Hodnik-Cadez, T.; Manfreda-Kolar, V. Comparison of types of generalizations and problem-solving schemas used to solve a mathematical problem’. Educ. Stud. Math. 2015, 89, 283–306. [Google Scholar] [CrossRef]
- Ayalon, M.; Watson, A.; Lerman, S. Progression towards Functions: Students’ Performance on Three Tasks about Variables from Grades 7 to 12. Int. J. Sci. Math. Educ. 2015, 14, 1153–1173. [Google Scholar] [CrossRef]
- Bulková, K.; Medová, J.; Čeretková, S. Identification of Crucial Steps and Skills in High-Achievers′ Solving Complex Mathematical Problem within Mathematical Contest. J. Effic. Responsib. Educ. Sci. 2020, 13, 67–78. [Google Scholar]
- Robinson, J.A. Proof = guarantee + explanation. In Intellectics and Computational Logic; Hölldobler, S., Ed.; Kluwer: Dordrecht, The Netherlands, 2000; pp. 277–294. [Google Scholar]
- Pedemonte, B. Argumentation and algebraic proof. ZDM 2008, 40, 385–400. [Google Scholar] [CrossRef]
- Lithner, J. A research framework for creative and imitative reasoning. Educ. Stud. Math. 2007, 67, 255–276. [Google Scholar] [CrossRef]
- Andersen, L.E. Acceptable gaps in mathematical proofs. Synthese 2018, 197, 1–15. [Google Scholar] [CrossRef]
- Pedemonte, B. How can the relationship between argumentation and proof be analysed. Educ. Stud. Math. 2007, 66, 23–41. [Google Scholar] [CrossRef]
- Vale, C.; Widjaja, W.; Herbert, S.; Bragg, L.A.; Loong, E.Y.-K. Mapping Variation in Children’s Mathematical Reasoning: The Case of ‘What Else Belongs’? Int. J. Sci. Math. Educ. 2017, 15, 873–894. [Google Scholar] [CrossRef]
- Wigfield, A.; Eccles, J.S.; Pintrich, P.R. Development between the ages of 11 and 25. In Handbook of Educational Psychology; Berliner, D.C., Calfee, R.C., Eds.; Routledge: New York, NY, USA, 1996; pp. 148–185. [Google Scholar]
- Scholtzová, I. Cesty Diskrétnej Matematiky (Kombinatoriky) na základnú školu [Routes of Discrete Mathematics (Combinatoric) to Elementary School]; Prešovská univerzita v Prešove: Prešov, Slovakia, 2007. [Google Scholar]
- English, L.D. Children’s construction of mathematical knowledge in solving novel isomorphic problems in concrete and written form. J. Math. Behav. 1996, 15, 81–112. [Google Scholar] [CrossRef]
- Jones, G.; Langrall, C.; Thornton, C.; Mogill, A.T. A framework for assessing and nurturing young children‘s thinking in probability. Educ. Stud. Math. 1997, 32, 101–125. [Google Scholar] [CrossRef]
- Lockwood, E. A model of students’ combinatorial thinking. J. Math. Behav. 2013, 32, 251–265. [Google Scholar] [CrossRef]
- Reed, Z.; Lockwood, E. Generalizing in combinatorics through categorization. RUME 2018. In Proceedings of the 21st annual conference on research in undergraduate mathematics education, San Diego, CA, USA, 22–27 February 2018; pp. 311–325. [Google Scholar]
- Sriraman, B. Mathematical giftedness, problem solving, and the ability to formulate generalizations: The problem-solving experiences of four gifted students. J. Second. Gift. Educ. 2003, 14, 151–165. [Google Scholar] [CrossRef]
- Krejčová, L. Žáci Potřebují Přemýšlet [Students Need to Think]; Portál: Praha, Czech Republic, 2013; p. 174. [Google Scholar]
- Häkkinen, P.; Järvelä, S.; Mäkitalo-Siegl, K.; Ahonen, A.; Näykki, P.; Valtonen, T. Preparing teacher-students for twenty-first-century learning practices (PREP21): A framework for enhancing collaborative problem-solving and strategic learning skills. Teach. Teach. Theory Pract. 2017, 23, 25–41. [Google Scholar] [CrossRef]
- PISA 2015. Collaborative Problem Solving Framework. 2017. Available online: http://www.oecd.org/pisa/pisaproducts/Draft%20PISA%202015%20Collaborative%20Problem%20Solving%20Framework%20.pdf (accessed on 7 December 2020).
- Kocak, Z.F.; Bozan, R.; Isik, Ö. The importance of group work in mathematics. Procedia Soc. Behav. Sci. 2009, 1, 2363–2365. [Google Scholar] [CrossRef]
- Frobisher, A.; Frobisher, L. Didaktika Matematiky I; Raabe: Bratislava, Slovakia, 2015; p. 169s. [Google Scholar]
- Fawcett, L.M.; Garton, A. The effect of peer collaboration on children’s problem-solving ability. Br. J. Educ. Psychol. 2005, 75, 157–169. [Google Scholar] [CrossRef] [PubMed]
- Erickson, S.A.; Lockwood, E. Investigating Combinatorial Provers‘ Reasoning about Multiplication. Int. J. Res. Undergrad. Math. Educ. 2020. [Google Scholar] [CrossRef]
- Lockwood, E.; Caughman, J.S.; Weber, K. An essay on proof, conviction, and explanation: Multiple representation systems in combinatorics. Educ. Stud. Math. 2020, 103, 173–189. [Google Scholar] [CrossRef]
- Stahl, G. The constitution of group cognition. In Handbook of Embodied Cognition; Shapiro, L., Ed.; Routledge: New York, NY, USA, 2014; pp. 335–346. [Google Scholar]
- Kirschner, P.; Sweller, J.; Kirschner, F.; Zambrano, R.J. From Cognitive Load Theory to Collaborative Cognitive Load Theory. Int. J. Comput. Collab. Learn. 2018, 13, 213–233. [Google Scholar] [CrossRef] [PubMed]
- Plass, J.L.; O’Keefe, P.A.; Homer, B.D.; Case, J.; Hayward, E.O.; Stein, M.; Perlin, K. The impact of individual, competitive, and collaborative mathematics game play on learning, performance, and motivation. J. Educ. Psychol. 2013, 105, 1050–1066. [Google Scholar] [CrossRef]
- FISME. Mathematics B-Day. 2020. Available online: https://www.uu.nl/en/education/mathematics-b-day (accessed on 17 December 2020).
- FISME: Snakes’ nest: Mathematics B-Day 2018. Available online: https://wiskundeinteams.sites.uu.nl/wp-content/uploads/sites/463/2019/03/assignment2018.pdf (accessed on 20 September 2020).
- Norwood, R.; Poole, G.; Laidacker, M. The worm problem of Leo Moser. Discret. Comput. Geom. 1992, 7, 153–162. [Google Scholar] [CrossRef]
- Pantziara, M.; Gagatsis, A.; Elia, I. Using diagrams as tools for the solution of non-routine mathematical problems. Educ. Stud. Math. 2009, 72, 39–60. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In Handbook for Reasearch on Mathematics Teaching and Learning; Grous, D., Ed.; Macmillan: New York, NY, USA, 2016. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Hervé, M. RVAideMemoire: Testing and Plotting Procedures for Biostatistics, R Package Version 0.9–70; 2020. Available online: https://cran.r-project.org/web/packages/RVAideMemoire (accessed on 15 September 2020).
- Navarro, D.J. Learning Statistics with R: A Tutorial for Psychology Students and Other Beginners; Version 0.5. [Lecture notes]; School of Psychology, University of Adelaide: Adelaide, Australia, 2015. [Google Scholar]
- Couturier, R. ‘rchic: Statistical Implicative Analysis’, R Package Version 0.25; 2018. Available online: https://github.com/rchic/Rchic/ (accessed on 12 January 2020).
- Gras, R.; Almouloud, S.A.; Bailleul, M.; Lahrer, A.; Polo, M.; Ratsimba-Rajohn, H. L’implication statistique: Nouvelle méthode exploratoire de données, applications à la didactique. In La Pensée Sauvage; Pron: Paris, France, 1996. [Google Scholar]
- Care, E.; Scoular, C.; Griffin, P. Assessment of Collaborative Problem Solving in Education Environments. Appl. Meas. Educ. 2016, 29, 250–264. [Google Scholar] [CrossRef]
- Adegoke, B. Modelling the relationship between mathematical reasoning ability and mathematics attainment. J. Educ. Pract. 2013, 4, 54–61. [Google Scholar]
- Nunes, T.; Bryant, P.; Barros, R.; Sylva, K. The relative importance of two different mathematical abilities to mathematical achievement. Br. J. Educ. Psychol. 2011, 82, 136–156. [Google Scholar] [CrossRef] [PubMed]
- Hejnová, E.; Eisenmann, P.; Cihlář, J.; Přibyl, J. Relations between Scientific Reasoning and Culture of Problem Solving. J. Effic. Responsib. Educ. Sci. 2018, 11, 38–44. [Google Scholar] [CrossRef]
- Chimoni, M.; Pitta-Pantazi, D. Connections between algebraic thinking and reasoning processes. In Proceedings of the CERME 9, Ninth Congress of the European Society for Research in Mathematics Education (ERME), Prague, Czech Republic, 4–8 February 2015; pp. 398–404. [Google Scholar]
- English, L.D.; Sharry, P.V. Analogical reasoning and the development of algebraic abstraction. Educ. Stud. Math. 1996, 30, 135–157. [Google Scholar] [CrossRef]
- Martinez, V.A.; Pedemonte, B. Relationship between inductive arithmetic argumentation and deductive algebraic proof. Educ. Stud. Math. 2014, 86, 125–149. [Google Scholar] [CrossRef]
- Lockwood, E.; Swinyard, C.; Caughman, J. Patterns, Sets of Outcomes, and Combinatorial Justification: Two Students’ Reinvention of Counting Formulas. Int. J. Res. Undergrad. Math. Educ. 2015, 1, 27–62. [Google Scholar] [CrossRef][Green Version]
- Stein, M.; Burchartz, B. The Invisible Wall Project: Reasoning and Problem Solving Processes of Primary and Lower Secondary Student. Math. Think. Learn. 2006, 8, 65–90. [Google Scholar] [CrossRef]
- McLeod, D.B. Beliefs, Attitudes, and Emotions. New Views of Affect in Mathematics Education. In Affect and Mathematical Problem Solving: A New Perspective; McLeod, D.B., Adams, V.M., Eds.; Springer: New York, NY, USA, 1989; pp. 245–258. [Google Scholar]
- Susac, A.; Bubic, A.; Vrbanc, A.; Planinic, M. Development of abstract mathematical reasoning: The case of algebra. Front. Hum. Neurosci. 2014, 8, 679. [Google Scholar] [CrossRef]
- Novotná, J. Heuristic Strategies in Solving of Mathematical Problems at School. In Proceedings of the ERIE 2016 13th International Conference Efficiency and Responsibility in Education 2016, Prague, Czech Republic, 2–3 June 2016; pp. 429–439. [Google Scholar]
- Ellis, A.B. Connections between generalizing and justifying students’ reasoning with linear relationships. J. Res. Math. Educ. 2007, 38, 194–229. [Google Scholar]
- Lou, Y.; Abrami, P.C.; Spence, J.C.; Poulsen, C.; Chambers, B.; d′Apollonia, S. Within-class grouping: A meta-analysis. Rev. Educ. Res. 1996, 66, 423–458. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).