On the ‘Definability of Definable’ Problem of Alfred Tarski †
Abstract
| Contents | ||
| 1 | Introduction | 2 |
| 1.1 The Problem................................................................................................................................................................... | 3 | |
| 1.2 Further Reformulations and Harrington’s Statement............................................................................................... | 3 | |
| 1.3 The Main Theorem........................................................................................................................................................ | 4 | |
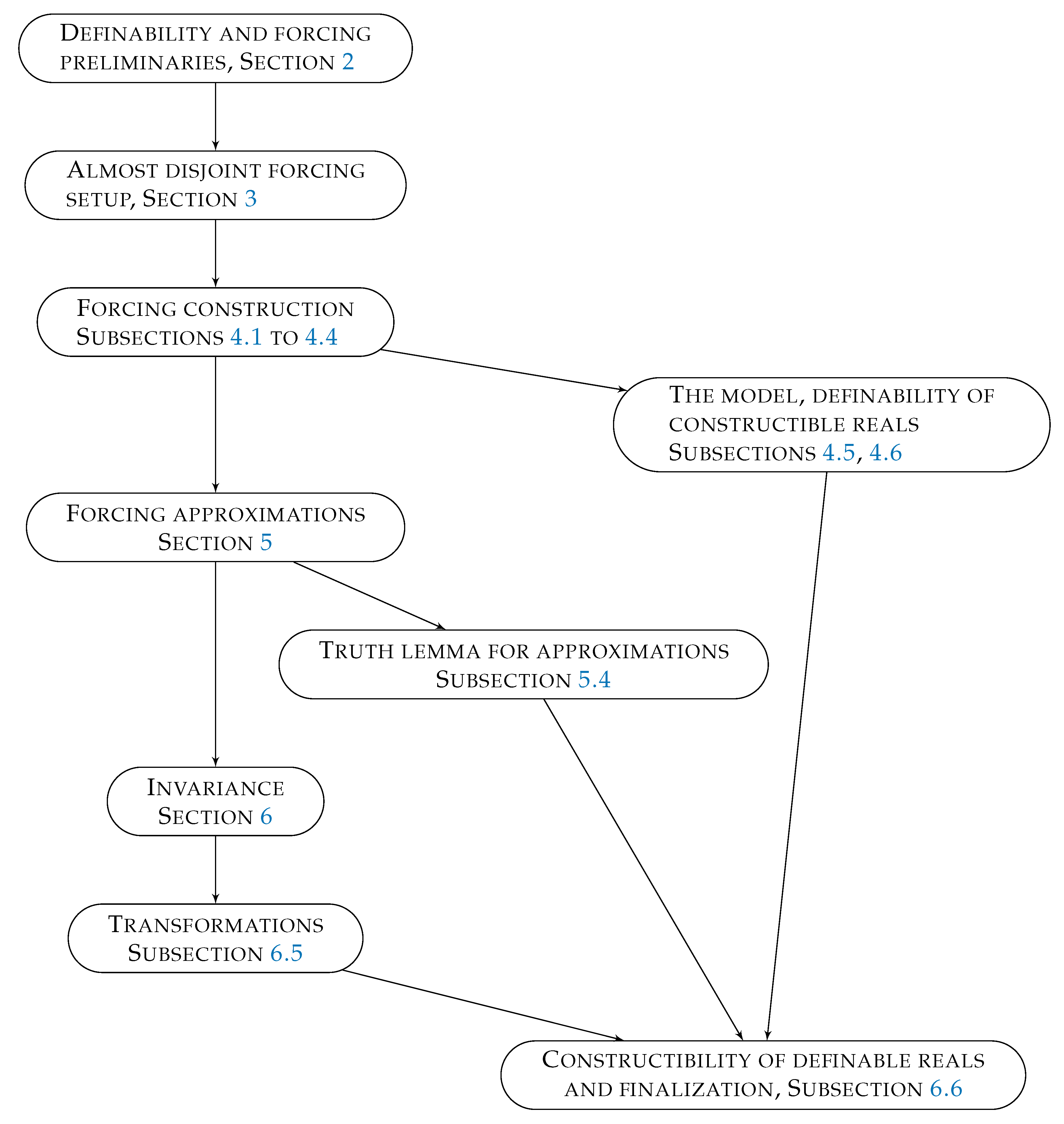
| 1.4 Structure of the Proof.................................................................................................................................................... | 5 | |
| Flowchart.................................................................................................................................................................................. | 6 | |
| 2 | Preliminaries | 7 |
| 2.1 Definability Issues......................................................................................................................................................... | 7 | |
| 2.2 Constructibility Issues.................................................................................................................................................. | 7 | |
| 2.3 Type-Theoretic Definability vs. ∈-Definability......................................................................................................... | 8 | |
| 2.4 Reduction to the Powerset Definability...................................................................................................................... | 9 | |
| 2.5 A Useful Result in Forcing Theory............................................................................................................................. | 10 | |
| 2.6 Definable Names.......................................................................................................................................................... | 11 | |
| 2.7 Collapse Forcing........................................................................................................................................................... | 13 | |
| 3 | Almost Disjoint Forcing, Uncountable Version | 13 |
| 3.1 Introduction to almost Disjoint Forcing.................................................................................................................... | 13 | |
| 3.2 Product Almost Disjoint Forcing............................................................................................................................... | 15 | |
| 3.3 Structure of Product almost Disjoint Generic Extensions....................................................................................... | 16 | |
| 4 | The Forcing Notion and the Model | 17 |
| 4.1 Systems, Definability Aspects..................................................................................................................................... | 17 | |
| 4.2 Complete Sequences.................................................................................................................................................... | 17 | |
| 4.3 Preservation of the Completeness............................................................................................................................. | 19 | |
| 4.4 Key Definability Engine............................................................................................................................................. | 20 | |
| 4.5 We Specify ............................................................................................................................................................... | 22 | |
| 4.6 The Model.................................................................................................................................................................... | 23 | |
| 5 | Forcing Approximation | 24 |
| 5.1 Language...................................................................................................................................................................... | 25 | |
| 5.2 Forcing Approximation.............................................................................................................................................. | 26 | |
| 5.3 Consequences for the Complete Forcing Notions................................................................................................... | 27 | |
| 5.4 Truth Lemma.............................................................................................................................................................. | 27 | |
| 6 | Invariance | 28 |
| 6.1 Hidden Invariance...................................................................................................................................................... | 28 | |
| 6.2 The Invariance Theorem............................................................................................................................................. | 29 | |
| 6.3 Proof of Theorem 9 from the Invariance Theorem.................................................................................................. | 29 | |
| 6.4 The Invariance Theorem: Setup................................................................................................................................ | 30 | |
| 6.5 Transformation........................................................................................................................................................... | 30 | |
| 6.6 Finalization................................................................................................................................................................. | 32 | |
| 7 | Conclusions and Discussion | 33 |
| References | 34 | |
1. Introduction
1.1. The Problem
the solution of the problem is (trivially) positive if ; the solution is negative if ; in the (perhaps most interesting) case the problem remains open.
1.2. Further Reformulations and Harrington’s Statement
1.3. The Main Theorem
- (i)
- , that is, constructible reals are precisely reals in — in particular, is a set, hence, , and even moreso,
- (ii)
- if then
- (iii)
- the general continuum hypothesis GCH holds.
- (A)
- a model [3] in which, for a given , there exists a countable non-empty set of reals, containing no OD element, while every countable set of reals contains only OD reals;
- (B)
- a model [28] in which, for a given , there is a real singleton that effectively codes a cofinal map , minimal over , while every real is constructible;
- (C)
- a model [29] in which, for a given , there exists a planar non-ROD-uniformizable lightface set, all of whose vertical cross-sections are countable, whereas all boldface sets with countable cross-sections are -uniformizable;
- (D)
- a model [30] in which, for a given , the Separation principle fails for .
1.4. Structure of the Proof
- (*)
- if in then covers f (that is, for unbounded-many ) iff (Lemma 15).
- -
- Increasing, i.e., for all and ,
- -
- Small, i.e., in for all , and,
- -
- Disjoint, i.e., the components are pairwise disjoint.
2. Preliminaries
2.1. Definability Issues
- = all sets , definable in H by a parameter-free formula;
- = all sets , definable in H by a formula with any sets in H as parameters.
2.2. Constructibility Issues
- 1°.
- The set belongs to and is equal to .
- 2°.
- The restriction is a wellordering of of length and a relation.
- 3°.
- On the other hand, the set and relation belong to and to .
- 4°.
- The map is as well.
- 5°.
- Assume that and is . If , then let be the -least witness. Then is as well.
2.3. Type-Theoretic Definability vs. -Definability
2.4. Reduction to the Powerset Definability
2.5. A Useful Result in Forcing Theory
- Is -closed, if any -decreasing sequence in P, of length , has a lower bound in P;
- Is -distributive, if the intersection of -many open dense sets is open dense, and a set is open, iff , and dense, iff for any there is , .
- Satisfies -chain condition, or -CC, if every antichain has cardinality strictly less than
- (i)
- P remains ϑ-distributive in ,
- (ii)
- Ω is still a cardinal in ,
- (iii)
- Every set , , bounded in Ω, belongs to .
- (A)
- “ is open dense in P”
- (B)
- If , , and then there exist and such that , , and -forces over .
- (C)
- If and , then there is , , such that forces over .
2.6. Definable Names
- (i)
- If Y belongs to (hence to ), then Y also belongs to
- (ii)
- If and Y belongs to (meaning in with arbitrary definability parameters in allowed) then there exists a name , , such that
- (I)
- iff ;
- (II)
- iff or ;
- (III)
- iff ;
- (IV)
- iff or ;
- (V)
- iff ;
- (VI)
- iff .
2.7. Collapse Forcing
3. Almost Disjoint Forcing, Uncountable Version
3.1. Introduction to almost Disjoint Forcing
- Let , the set of all constructible non-empty sequences s of ordinals , of length , called strings. We underline that , and , the empty string, does not belong to ;
- Let = all constructible -sequences of ordinals ; ;
- If then put ,a tree in , without terminal nodes;
- A set is dense iff , i. e. for any there is such that ;
- If then let . If is unbounded in then say that S covers f, otherwise S does not cover f.
- (i)
- If in then does not cover
- (ii)
- , hence
3.2. Product Almost Disjoint Forcing
- If then we define and
- If then define by , in the sense of Definition 3 in Section 3.1, for all .
- If U is an -system then is the -product of the sets , .
3.3. Structure of Product almost Disjoint Generic Extensions
- (i)
- (ii)
- If then the set is -generic over , hence if then does not cover
- (iii)
- If , is bounded, then
- (iv)
- All -cardinals are preserved in , and GCH holds in
- (i)
- All -cardinals are preserved in , so that for all
- (ii)
- GCH holds in
- (iii)
- If and , is bounded, then
- (iv)
- If and , then and .
4. The Forcing Notion and the Model
4.1. Systems, Definability Aspects
- An -system U is small, if each has cardinality in ;
- An -system U is disjoint if whenever ;
- If are -systems and for all , then V extends U, in symbol ;
- If is a sequence of -systems then the limit -system is defined by , for all .
4.2. Complete Sequences
- (*)
- If and is a closed unbounded set then there is such that .
- (†)
- If is a sequence of sets in and is a closed unbounded set then there is with .
- (i)
- The sequence is continuous, so that for all limit ordinals
- (ii)
- If then the “slice” is ;
- (iii)
- If then the “tail” is -complete, in the sense that for any set there is such that the -system -solvesD, i.e.,
- -
- either
- -
- or there is no -system with
- (iv)
- There is a recursive sequence of parameter free -formulas such that if and then iff .
- (a)
- , and
- (b)
- The -system -solves the set .
4.3. Preservation of the Completeness
4.4. Key Definability Engine
- (I)
- in ,
- (II)
- satisfies -CC in ,
- (III)
- is -closed and -distributive in .
- (i)
- is a cardinal in
- (ii)
- If then and holds, but
- (iii)
- If then and moreover there is no set in such that .
- (iv)
- It follows that in
- (v)
- If then the -th slice belongs to , where
- (vi)
- If , , and GCH holds in for all cardinals , then it holds in that for all
- (vii)
- Under the assumptions of (vi), it holds in that the set z as a whole belongs to .
4.5. We Specify
- -
- A -increasing sequence of -systems satisfying (i), (ii), (iii), (iv) of Theorem 6 for the chosen -cardinal ,
- -
- The limit -system ,
- -
- The basic forcing notion , and the subforcings , ,
4.6. The Model
- (i)
- is a set -generic over ,
- (ii)
- for all ordinals , in particular,
- (iii)
- If then and , whereas if then
- (iv)
- GCH holds;
- (v)
- Every constructible real belongs to ,
- (vi)
- If and then , and
- (vii)
- every real in is constructible.
5. Forcing Approximation
- either
- or
- and a is -definable in .
5.1. Language
- Assume that , . Then let be the set of all sets , , with in .
- for all atomic formulas,
- ,
- and ,
- Finally, .
- -
- Ordinals to substitute variables over ,
- -
- Names in to substitute variables over .
5.2. Forcing Approximation
- (F1)
- When writing , it will always be assumed that , , , , is a closed formula in .
- (F2)
- If , , , , and , then: iff in fact , and the same for the formulas and .
- (F3)
- If are as above, , , then: iff there exists a condition such that and .
- (F4)
- If are as above, then: iff and .
- (F5)
- If are as above, then iff there is such that .
- (F6)
- If are as above, then iff there exists a name such that .
- (F8)
- If are as in (F1), is a closed formula, , then iff there is no -system extending U, and no , , such that .
- (i)
- If , extends U, and , then ;
- (ii)
- If , , and , then fails.
5.3. Consequences for the Complete Forcing Notions
- (i)
- If and , , then , and accordingly,if and , then
- (ii)
- and contradict to each other.
5.4. Truth Lemma
6. Invariance
6.1. Hidden Invariance
6.2. The Invariance Theorem
6.3. Proof of Theorem 9 from the Invariance Theorem
6.4. The Invariance Theorem: Setup
- (A)
- a -system with , and a condition , , such that , but still holds by Lemma 22.
- (B)
- A bijection , , such that and .
- (C)
- A sequence of bijections , such that (see above), , and if then there is an ordinal such that .
6.5. Transformation
- (D)
- is a bijection and , and if then by (C).
- (E)
- for any -system U. The map is a bijection of onto itself and onto itself for any .
- (F)
- for any . The map is a -preserving bijection of onto .
- (G)
- If then is a -preserving bijection of onto .
- (H)
- If , , then the mapping is a bijection of onto and a bijection of -formulas onto -formulas.
6.6. Finalization
7. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kanovei, V.; Lyubetsky, V. A definable E0 class containing no definable elements. Arch. Math. Logic 2015, 54, 711–723. [Google Scholar] [CrossRef]
- Golshani, M.; Kanovei, V.; Lyubetsky, V. A Groszek—Laver pair of undistinguishable classes. Math. Logic Q. 2017, 63, 19–31. [Google Scholar] [CrossRef]
- Kanovei, V.; Lyubetsky, V. Definable classes at arbitrary projective levels. Ann. Pure Appl. Logic 2018, 169, 851–871. [Google Scholar] [CrossRef]
- Kanovei, V.; Lyubetsky, V. Models of set theory in which nonconstructible reals first appear at a given projective level. Mathematics 2020, 8, 910. [Google Scholar] [CrossRef]
- Kanovei, V.; Lyubetsky, V. On the problem of Harvey Friedman. Mathematics 2020, 8, 1477. [Google Scholar] [CrossRef]
- Hadamard, J.; Baire, R.; Lebesgue, H.; Borel, E. Cinq lettres sur la théorie des ensembles. Bull. Soc. Math. Fr. 1905, 33, 261–273. [Google Scholar] [CrossRef]
- Karagila, A. The Bristol model: An abyss called a Cohen reals. J. Math. Log. 2018, 18, 1850008. [Google Scholar] [CrossRef]
- Antos, C.; Friedman, S.D. Hyperclass forcing in Morse-Kelley class theory. J. Symb. Log. 2017, 82, 549–575. [Google Scholar] [CrossRef][Green Version]
- Antos, C.; Friedman, S.D.; Honzik, R.; Ternullo, C. (Eds.) The Hyperuniverse Project and Maximality; Birkhäuser: Cham, Switzerland, 2018; xi + 270p. [Google Scholar]
- Cummings, J.; Friedman, S.D.; Magidor, M.; Rinot, A.; Sinapova, D. Ordinal definable subsets of singular cardinals. Isr. J. Math. 2018, 226, 781–804. [Google Scholar] [CrossRef]
- Chan, W. Ordinal definability and combinatorics of equivalence relations. J. Math. Log. 2019, 19, 1950009. [Google Scholar] [CrossRef]
- Fischer, V.; Schrittesser, D. A Sacks indestructible co-analytic maximal eventually different family. Fundam. Math. 2020. [Google Scholar] [CrossRef]
- Enayat, A.; Kanovei, V. An unpublished theorem of Solovay on OD partitions of reals into two non-OD parts, revisited. J. Math. Log. 2020, 1–22. [Google Scholar] [CrossRef]
- Tarski, A. Der Wahrheitsbegriff in den formalisierten Sprachen. Studia Philos. 1935, 1, 261–401. [Google Scholar]
- Murawski, R. Undefinability of truth. The problem of priority: Tarski vs Gödel. Hist. Philos. Log. 1998, 19, 153–160. [Google Scholar] [CrossRef]
- Addison, J.W. Tarski’s theory of definability: Common themes in descriptive set theory, recursive function theory, classical pure logic, and finite-universe logic. Ann. Pure Appl. Logic 2004, 126, 77–92. [Google Scholar] [CrossRef]
- Tarski, A. Sur les ensembles définissables de nombres réels. I. Fundam. Math. 1931, 17, 210–239. [Google Scholar] [CrossRef]
- Tarski, A. A problem concerning the notion of definability. J. Symb. Log. 1948, 13, 107–111. [Google Scholar] [CrossRef]
- Gödel, K. The Consistency of the Continuum Hypothesis; Annals of Mathematics Studies, No. 3; Princeton University Press: Princeton, NJ, USA, 1940; p. 66. [Google Scholar]
- Mathias, A.R.D. Surrealist landscape with figures (a survey of recent results in set theory). Period. Math. Hung. 1979, 10, 109–175. [Google Scholar] [CrossRef]
- Friedman, H. One hundred and two problems in mathematical logic. J. Symb. Log. 1975, 40, 113–129. [Google Scholar] [CrossRef]
- Harrington, L. The Constructible Reals Can Be Anything. Preprint dated May 1974 with several addenda dated up to October 1975: (A) Models Where Separation Principles Fail, May 74; (B) Separation without Reduction, April 75; (C) The Constructible Reals Can Be (Almost) Anything, Part II, May 75. Available online: http://logic-library.berkeley.edu/catalog/detail/2135 (accessed on 9 December 2020).
- Jensen, R.B.; Solovay, R.M. Some applications of almost disjoint sets. In Math. Logic Found. Set Theory, Proc. Int. Colloqu., Jerusalem 1968; Studies in Logic and the Foundations of Mathematics; Bar-Hillel, Y., Ed.; North-Holland: Amsterdam, The Netherlands; London, UK, 1970; Volume 59, pp. 84–104. [Google Scholar]
- Hinman, P.G. Recursion-Theoretic Hierarchies; Perspectives in Mathematical Logic; Springer: Berlin/Heidelberg, Germany, 1978; x + 480p. [Google Scholar]
- Harrington, L. Long projective wellorderings. Ann. Math. Logic 1977, 12, 1–24. [Google Scholar] [CrossRef]
- Friedman, S.D. Constructibility and class forcing. In Handbook of Set Theory. In 3 Volumes; Springer: Dordrecht, The Netherlands, 2010; pp. 557–604. [Google Scholar]
- Friedman, S.D. Fine Structure and Class Forcing; De Gruyter Series in Logic and Its Applications; de Gruyter: Berlin, Germany, 2000; Volume 3, x + 221p. [Google Scholar]
- Kanovei, V.; Lyubetsky, V. Definable minimal collapse functions at arbitrary projective levels. J. Symb. Log. 2019, 84, 266–289. [Google Scholar] [CrossRef]
- Kanovei, V.; Lyubetsky, V. Non-uniformizable sets with countable cross-sections on a given level of the projective hierarchy. Fundam. Math. 2019, 245, 175–215. [Google Scholar] [CrossRef]
- Kanovei, V.; Lyubetsky, V. Models of set theory in which separation theorem fails. Izvestiya: Math. 2021, 85. to appear. [Google Scholar]
- Barwise, J. (Ed.) Handbook of Mathematical Logic; Studies in Logic and the Foundations of Mathematics; North-Holland: Amsterdam, The Netherlands, 1977; Volume 90, p. 1165. [Google Scholar]
- Jech, T. Set Theory; The Third Millennium Revised and Expanded Ed.; Springer: Berlin/Heidelberg, Germany, 2003; xiii + 769p. [Google Scholar]
- Addison, J.W. Some consequences of the axiom of constructibility. Fundam. Math. 1959, 46, 337–357. [Google Scholar] [CrossRef]
- Jensen, R.B.; Johnsbraten, H. A new construction of a non-constructible subset of ω. Fundam. Math. 1974, 81, 279–290. [Google Scholar] [CrossRef][Green Version]
- Kunen, K. Set Theory; Studies in Logic; College Publications: London, UK, 2011; Volume 34, viii + 401p. [Google Scholar]
- Shoenfield, J.R. Unramified forcing. In Axiomatic Set Theory. Proc. Sympos. Pure Math.; Scott, D.S., Ed.; AMS: Providence, RI, USA, 1971; Volume 13, Part 1; pp. 357–381. [Google Scholar]
- Kanovei, V. On the nonemptiness of classes in axiomatic set theory. Math. USSR Izv. 1978, 12, 507–535. [Google Scholar] [CrossRef]
- Jensen, R. Definable sets of minimal degree. In Math. Logic Found. Set Theory, Proc. Int. Colloqu., Jerusalem 1968; Studies in Logic and the Foundations of Mathematics; Bar-Hillel, Y., Ed.; North-Holland: Amsterdam, The Netherlands; London, UK, 1970; Volume 59, pp. 122–128. [Google Scholar]
- Friedman, S.D.; Gitman, V.; Kanovei, V. A model of second-order arithmetic satisfying AC but not DC. J. Math. Log. 2019, 19, 1850013. [Google Scholar] [CrossRef]
- Kanovei, V.; Lyubetsky, V. Counterexamples to countable-section uniformization and separation. Ann. Pure Appl. Logic 2016, 167, 262–283. [Google Scholar] [CrossRef]
- Abraham, U. A minimal model for ¬CH: Iteration of Jensen’s reals. Trans. Am. Math. Soc. 1984, 281, 657–674. [Google Scholar] [CrossRef][Green Version]
- Abraham, U. Minimal model of “ is countable” and definable reals. Adv. Math. 1985, 55, 75–89. [Google Scholar] [CrossRef][Green Version]
- Kanovei, V.; Lyubetsky, V. Non-uniformizable sets of second projective level with countable cross-sections in the form of Vitali classes. Izv. Math. 2018, 82, 61–90. [Google Scholar] [CrossRef]
- Groszek, M.; Jech, T. Generalized iteration of forcing. Trans. Amer. Math. Soc. 1991, 324, 1–26. [Google Scholar] [CrossRef]
- Groszek, M.; Laver, R. Finite groups of OD-conjugates. Period. Math. Hung. 1987, 18, 87–97. [Google Scholar] [CrossRef]
- Kanovei, V. On non-wellfounded iterations of the perfect set forcing. J. Symb. Log. 1999, 64, 551–574. [Google Scholar] [CrossRef]
- Versaci, M.; di Barba, P.; Morabito, F.C. Curvature-Dependent Electrostatic Field as a Principle for Modelling Membrane-Based MEMS Devices. A Review. Membranes 2020, 10, 361. [Google Scholar] [CrossRef]
- David, R. reals. Ann. Math. Logic 1982, 23, 121–125. [Google Scholar] [CrossRef]
- David, R. A very absolute real singleton. Ann. Math. Logic 1982, 23, 101–120. [Google Scholar] [CrossRef]
- Kanovei, V.; Lyubetsky, V. The full basis theorem does not imply analytic wellordering. Ann. Pure Appl. Logic 2020, Online. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanovei, V.; Lyubetsky, V. On the ‘Definability of Definable’ Problem of Alfred Tarski. Mathematics 2020, 8, 2214. https://doi.org/10.3390/math8122214
Kanovei V, Lyubetsky V. On the ‘Definability of Definable’ Problem of Alfred Tarski. Mathematics. 2020; 8(12):2214. https://doi.org/10.3390/math8122214
Chicago/Turabian StyleKanovei, Vladimir, and Vassily Lyubetsky. 2020. "On the ‘Definability of Definable’ Problem of Alfred Tarski" Mathematics 8, no. 12: 2214. https://doi.org/10.3390/math8122214
APA StyleKanovei, V., & Lyubetsky, V. (2020). On the ‘Definability of Definable’ Problem of Alfred Tarski. Mathematics, 8(12), 2214. https://doi.org/10.3390/math8122214





