On the ‘Definability of Definable’ Problem of Alfred Tarski ^†

Abstract

In this paper we prove that for any $m\ge 1$ there exists a generic extension of $\mathbf{L}$, the constructible universe, in which it is true that the set of all constructible reals (here subsets of $\omega$) is equal to the set ${\mathbf{D}}_{1m}$ of all reals definable by a parameter free type-theoretic formula with types bounded by m, and hence the Tarski ‘definability of definable’ sentence ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ (even in the form ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{21}$) holds for this particular m. This solves an old problem of Alfred Tarski (1948). Our methods, based on the almost-disjoint forcing of Jensen and Solovay, are significant modifications and further development of the methods presented in our two previous papers in this Journal.

1. Introduction

This paper continues our research project on the issues of definability in models of set theory, that was started in [1,2,3] among other papers, and most recently in [4,5] in this Journal. Questions of definability of mathematical objects were raised in the course of discussions on the foundations of mathematics, set theory, and the axiom of choice in the early twentieth century, such as, for instance, the famous discussion between Baire, Borel, Hadamard, and Lebesgue published in Sinq lettres [6]. Various aspects of definability in models of set theory have since remained the focus of work on the foundations of mathematics, see, for example, [7,8,9,10,11,12,13] among many important recent studies.

The topic of this paper goes back to the profound research by Alfred Tarski, who demonstrated in [14] that ‘being definable’ (in most general, unrestricted sense) is not a mathematically well-defined notion (see Murawski [15] on the history of this discovery and the role of Gödel, and Addison [16] on the modern perspective of the Tarski definability theory). More specificly, restricted notions of definability, in particular, type-theoretic definability, were considered by Tarski in [17] and later work in [18].

Definition 1

(Tarski). If $m,k<\omega$ then ${\mathbf{D}}_{km}$ is the set of all elements of order k, definable by a parameter free type-theoretic formula of order m.

Here elements of order 0 are just natural numbers (members of the set $\omega =\{0,1,2,\cdots \}$), elements of order 1 are sets of natural numbers (commonly called reals in modern set theory), and generally, elements of order $k+1$ ($k<\omega$) are arbitrary sets of elements of order k (see details in Section 2.1 below). The order of a type-theoretic formula is the largest order of all its quantified and free variables. The notion of definability is taken in the form:

$$x^k=\left\{y^{k-1} \mathrm{of} \mathrm{order} k-1:\phi \left(y^{k-1}\right)\right\},$$

(1)

where the upper index routinely denotes the order of a variable or element.

1.1. The Problem

Investigating the definability properties of sets ${\mathbf{D}}_{km}$, Tarski notes in [18] that ${\mathbf{D}}_{km}\in {\mathbf{D}}_{k+1,m+1}$. To prove this result, one can exploit the fact that the truth of all formulas of order m can be suitably expressed by a single formula of order $m+1$. Using such a formula, one easily gets ${\mathbf{D}}_{km}\in {\mathbf{D}}_{k+1,m+1}$. Then Tarski turns to the question whether a stronger sentence ${\mathbf{D}}_{km}\in {\mathbf{D}}_{k+1,m}$ holds. Tarski comes to the following conclusion (verbatim):

the solution of the problem is (trivially) positive if $k=0$; the solution is negative if $k\ge 2$; in the (perhaps most interesting) case $k=1$ the problem remains open.

The negative result for $k\ge 2$ (and $m\ge k-1$, to avoid trivialities) is obtained in [18] (page 110) essentially by virtue of the fact that countable ordinals admit a definable embedding into the set of all elements of order 2. This leaves:

$${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}(m\ge 1)$$

(2)

as a major open problem in [18].

Tarski notes in [18], with a reference to Gödel’s work on constructibility [19], that it seems:

very unlikely that an affirmative solution of the problem is possible.

Tarski does not elaborate on this point, but it is quite clear that the axiom of constructibility $\mathbf{V}=\mathbf{L}$ (and even a weaker hypothesis, see Lemma 2 below) implies ${\mathbf{D}}_{1m}\notin {\mathbf{D}}_{2m}$ for all $m\ge 1$, and hence no proof of ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ for even one single $m\ge 1$ (the “affirmative solution” in Tarski’s words), can be maintained in $\mathbf{ZFC}$. In other words, the hypothesis:

$${\mathbf{D}}_{1m}\notin {\mathbf{D}}_{2m} \mathrm{holds} \mathrm{for} \mathrm{all} m\ge 1$$

(the negative solution of (2) for all $m\ge 1$ simultaneously) does not contradict the $\mathbf{ZFC}$ axioms. The problem of consistency of the affirmative sentences ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ was left open in [18].

This paper is devoted to this problem of Alfred Tarski.

1.2. Further Reformulations and Harrington’s Statement

The problem emerged once again in the early years of forcing, especially in the case $m=1$ corresponding to analytic definability in second-order arithmetic. The early survey [20] by A. R. D. Mathias (the original typescript has been known to set theorists since 1968) contains Problem 3112, that requires finding a model of $\mathbf{ZFC}$ in which it is true that:

the set of analytically definable reals is analytically definable

that is, ${\mathbf{D}}_{11}\in {\mathbf{D}}_{21}$. Recall that reals in this context mean subsets of $\omega$. Another problem there, P 3110, suggests a sharper form of this statement, namely; find a model in which it is true that

analytically definable reals are precisely the constructible reals

that is, ${\mathbf{D}}_{11}=\mathcal{P}\left(\omega \right)\cap \mathbf{L}$. The set $\mathcal{P}\left(\omega \right)\cap \mathbf{L}$ of all constructible reals is (lightface) ${\Sigma }_2^1$, and hence ${\mathbf{D}}_{21}$, so that the equality ${\mathbf{D}}_{11}=\mathcal{P}\left(\omega \right)\cap \mathbf{L}$ implies ${\mathbf{D}}_{11}\in {\mathbf{D}}_{21}$, that is the case $m=1$ of the sentence (2).

Somewhat later, Problem 87 in Harvey Friedman’s survey One hundred and two problems in mathematical logic [21] requires to prove that for each n in the domain $2<n\le \omega$ there is a model of:

$$\mathbf{ZFC}+“\mathrm{the}\mathrm{constructible}\mathrm{reals}\mathrm{are}\mathrm{precisely}\mathrm{the}{\Delta }_n^1\mathrm{reals}”.$$

(3)

For $n\le 2$ this is definitely impossible by the Shoenfield absoluteness theorem. As ${\Delta }_{\omega }^1$ is the same as ${\mathbf{D}}_{11}$ = all analytically definable reals, the case $n=\omega$ in (3) is just a reformulation of ${\mathbf{D}}_{11}=\mathcal{P}\left(\omega \right)\cap \mathbf{L}$.

At the very end of [21], it is noted that Leo Harrington had solved problem (3) affirmatively. A similar remark, see in [20] (p. 166), a comment to P 3110. And indeed, Harrington’s handwritten notes [22] present the following major result quoted here verbatim:

Theorem 1

(Harrington [22] (p. 1)). There are models of $\mathbf{ZFC}$ in which the set of constructible reals is, respectively, exactly the following set of reals:

$${\Delta }_3^1,{\Delta }_4^1,\dots ,{\Delta }_{\omega }^1=projective,{\Delta }_n^m,1\le n\le \omega ,2\le m\le \omega .$$

We may note that ${\Delta }_{\omega }^1={\mathbf{D}}_{11}$ and generally ${\Delta }_{\omega }^m={\mathbf{D}}_{1m}$ for any $m\ge 2$ in the context of Theorem 1. On the other hand the set $\mathcal{P}\left(\omega \right)\cap \mathbf{L}$ of constructible reals is ${\Sigma }_2^1$, and hence ${\mathbf{D}}_{21}$. Therefore Theorem 1 implies the consistency of the affirmative sentences ${\mathbf{D}}_1\in {\mathbf{D}}_2$ and ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ for any particular value $m\ge 1$, and hence shows that the Tarski problems considered are independent of $\mathbf{ZFC}$.

Based on the almost-disjoint forcing tool of Jensen and Solovay [23], a sketch of a generic extension of $\mathbf{L}$, in which it is true that ${\omega }^{\omega }\cap \mathbf{L}={\Delta }_3^1$, follows in [22] (pp. 2–4). Then a few sentences are added on page 5 of [22], which explain, without much going into details, as how Harrington planned to get some other models claimed by the theorem, in particular, a model in which ${\omega }^{\omega }\cap \mathbf{L}={\Delta }_n^1$ holds for a given (arbitrary) natural index $n>3$, and a model in which ${\omega }^{\omega }\cap \mathbf{L}={\Delta }_{\omega }^1$, where ${\Delta }_{\omega }^1={\bigcup }_n{\Delta }_n^1={\mathbf{D}}_{11}$ (all analytically definable reals). This positively solves Problem 87 of [21], including the case $n=\omega$, of course. Different cases of higher order definability are briefly observed in [22] (p. 5) as well.

Yet, for all we know, no detailed proofs have ever emerged in Harrington’s published works. An article by Harrington, entitled “Consistency and independence results in descriptive set theory”, which apparently might have contained these results among others, was announced in the References list in Peter Hinman’s book [24] (p. 462) to appear in Ann. of Math., 1978, but in fact this or a similar article has never been published in Annals of Mathematics or any other journal. Some methods sketched in [22] were later used in [25], but with respect to different questions and only in relation to the definability classes of the 2nd and 3rd projective level.

1.3. The Main Theorem

The goal of this paper is to present a complete proof of the following part of Harrington’s statement in Theorem 1, related to the consistency of the Tarski sentence ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ and the equality ${\mathbf{D}}_{1m}=\mathcal{P}\left(\omega \right)\cap \mathbf{L}$, strengthened by extra claims (ii) and (iii). This is the main result of this paper.

Theorem 2.

Let $\mathbb{M}\ge 1$. There is a generic extension of $\mathbf{L}$ in which it is true that

(i)

${\mathbf{D}}_{1\mathbb{M}}=\mathcal{P}\left(\omega \right)\cap \mathbf{L}$, that is, constructible reals are precisely reals in ${\mathbf{D}}_{1\mathbb{M}}$ — in particular, ${\mathbf{D}}_{1\mathbb{M}}$ is a ${\Sigma }_2^1$ set, hence, ${\mathbf{D}}_{1\mathbb{M}}\in {\mathbf{D}}_{21}$, and even moreso, ${\mathbf{D}}_{1\mathbb{M}}\in {\mathbf{D}}_{2\mathbb{M}};$

(ii)

if $n\ne \mathbb{M}$ then ${\mathbf{D}}_{1n}\notin {\mathbf{D}}_{2n};$

(iii)

the general continuum hypothesis GCH holds.

Thus, for every particular $\mathbb{M}\ge 1$, there exists a generic extension of $\mathbf{L}$ in which the Tarski sentence ${\mathbf{D}}_{1\mathbb{M}}\in {\mathbf{D}}_{2\mathbb{M}}$ holds whereas ${\mathbf{D}}_{1n}\notin {\mathbf{D}}_{2n}$ for all other values $n\ne \mathbb{M}$. We recall that ${\mathbf{D}}_{1\mathbb{M}}\in {\mathbf{D}}_{2\mathbb{M}}$ fails in $\mathbf{L}$ itself for all $\mathbb{M}$, see above.

Corollary 1.

If $\mathbb{M}\ge 1$ then the sentence ${\mathbf{D}}_{1\mathbb{M}}\in {\mathbf{D}}_{2\mathbb{M}}$ is undecidable in $\mathbf{ZFC}$, even in the presence of $\forall n\ne \mathbb{M}({\mathbf{D}}_{1n}\notin {\mathbf{D}}_{2n})$.

This paper is dedicated to the proof of Theorem 2. This will be another application of the methods sketched by Harrington and developed in detail in our previous papers [4,5] in this Journal, but here modified and further developed for the purpose of a solution to the Tarski problem.

We may note that problems of construction of models of set theory in which this or another effect is obtained at a certain prescribed definability level (not necessarily the least possible one) are considered in modern set theory, see e.g., Problem 9 in [26] (Section 9) or Problem 11 in [27] (page 209). Some results of this type have recently been obtained in set theory, namely:

(A)

a model [3] in which, for a given $n\ge 3$, there exists a countable non-empty ${\Pi }_n^1$ set of reals, containing no OD element, while every countable ${\Sigma }_n^1$ set of reals contains only OD reals;

(B)

a model [28] in which, for a given $n\ge 2$, there is a ${\Pi }_n^1$ real singleton that effectively codes a cofinal map $\omega \to {\omega }_1^{\mathbf{L}}$, minimal over $\mathbf{L}$, while every ${\Sigma }_n^1$ real is constructible;

(C)

a model [29] in which, for a given $n\ge 2$, there exists a planar non-ROD-uniformizable lightface ${\Pi }_n^1$ set, all of whose vertical cross-sections are countable, whereas all boldface ${\Sigma }_n^1$ sets with countable cross-sections are ${\Delta }_{n+1}^1$-uniformizable;

(D)

a model [30] in which, for a given $n\ge 3$, the Separation principle fails for ${\Pi }_n^1$.

Theorem 2 of this paper naturally extends this research line.

1.4. Structure of the Proof

To define a model for Theorem 2, we employ the product of two forcing notions. The first forcing $\mathbb{C}$ is a Cohen-style collapse forcing that adjoins a generic collapse map $\zeta :\omega \stackrel{\mathrm{onto}}{⟶}\Xi =\mathcal{P}(\omega )\cap \mathbf{L}$, Section 2.7. The collapse is necessary since any model for Theorem 2 has to satisfy the inequality ${\omega }_1^{\mathbf{L}}<{\omega }_1$.

The second forcing notion has the form of the product ${\mathbb{P}}^{\mathbb{\Omega }}={\prod }_{n,i<\omega }{\mathbb{P}}^{\mathbb{\Omega }}(n,i)\in \mathbf{L}$, where each factor ${\mathbb{P}}^{\mathbb{\Omega }}(n,i)$ is an almost-disjoint type forcing determined by a set:

$${\mathbb{U}}^{\mathbb{\Omega }}(n,i)\in \mathbf{L},{\mathbb{U}}^{\mathbb{\Omega }}(n,i)\subseteq {\mathbf{Fun}}_{\mathbb{\Omega }}=\left({\mathbb{\Omega }}^{\mathbb{\Omega }}\right)\cap \mathbf{L},$$

dense in ${\mathbf{Fun}}_{\mathbb{\Omega }}$, where $\mathbb{\Omega }={\omega }_{\mathbb{M}}^{\mathbf{L}}$ and $\mathbb{M}\ge 1$ is the number we are dealing with in Theorem 2. This forcing ${\mathbb{P}}^{\mathbb{\Omega }}$ adjoins an according system of generic sets $S(n,i)\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}=\left({\mathbb{\Omega }}^{<\mathbb{\Omega }}\right)\cap \mathbf{L}$, such that:

(*)

if $f\in {\mathbf{Fun}}_{\mathbb{\Omega }}$ in $\mathbf{L}$ then $S(n,i)$ covers f (that is, $f\upharpoonright \xi \in S(n,i)$ for unbounded-many $\xi <\mathbb{\Omega }$) iff $f\notin {\mathbb{U}}^{\mathbb{\Omega }}(n,i)$ (Lemma 15).

Basically any system $U\in \mathbf{L}$ of dense sets $U(n,i)\subseteq {\mathbf{Fun}}_{\mathbb{\Omega }}$ defines a similar product forcing $\mathbf{P}\left[U\right]={\prod }_{n,i<\omega }P\left[U(n,i)\right]\in \mathbf{L}$ (see Section 3.2). Forcing notions of the form $\mathbf{P}\left[U\right]$ satisfy certain chain and distributivity conditions in $\mathbf{L}$ (Lemma 14), that imply some general properties of related generic extensions (Lemmas 15 and 16).

The key system ${\mathbb{U}}^{\mathbb{\Omega }}$ is defined in Section 4.4 (Definition 6, on the base of Theorem 6 in Section 4.2), in the form of componentwise union ${\mathbb{U}}^{\mathbb{\Omega }}={\bigvee }_{\alpha <{\mathbb{\Omega }}^{\oplus }}{\mathbb{U}}_{\alpha }^{\mathbb{\Omega }}$, i.e., ${\mathbb{U}}^{\mathbb{\Omega }}(n,i)={\bigcup }_{\alpha <{\mathbb{\Omega }}^{\oplus }}{\mathbb{U}}_{\alpha }^{\mathbb{\Omega }}(n,i)$ for all $n,i<\omega$, where ${\mathbb{\Omega }}^{\oplus }={\omega }_{\mathbb{M}+1}^{\mathbf{L}}$ is the $\mathbf{L}$-cardinal next to $\mathbb{\Omega }$, and the systems ${\mathbb{U}}_{\alpha }^{\mathbb{\Omega }}\in \mathbf{L}$ are:

-

Increasing, i.e., ${\mathbb{U}}_{\alpha }^{\mathbb{\Omega }}(n,i)\subseteq {\mathbb{U}}_{\gamma }^{\mathbb{\Omega }}(n,i)$ for all $\alpha <\gamma$ and $n,i<\omega$,

-

Small, i.e., $\mathtt{card}{\mathbb{U}}_{\alpha }^{\mathbb{\Omega }}(n,i)\le \mathbb{\Omega }$ in $\mathbf{L}$ for all $n,i<\omega$, and,

-

Disjoint, i.e., the components ${\mathbb{U}}_{\alpha }^{\mathbb{\Omega }}(n,i)$ are pairwise disjoint.

We apply a diamond-based argument in Section 4 to ensure that the resulting system ${\mathbb{U}}^{\mathbb{\Omega }}\in \mathbf{L}$ has its different slices ${\left\{{\mathbb{U}}^{\mathbb{\Omega }}(n,i)\right\}}_{i<\omega }$ ($n<\omega$) satisfying different definability and inner genericity requirements (Theorem 6 in Section 4.2), so that the descriptive complexity and the level of inner genericity (or completeness) of nth ‘slice’ tends to infinity with $n\to \infty$. This is a major novelty of the construction.

Then we consider the key product forcing notion ${\mathbb{P}}^{\mathbb{\Omega }}=\mathbf{P}\left[{\mathbb{U}}^{\mathbb{\Omega }}\right]={\prod }_{n,i<\omega }{\mathbb{P}}^{\mathbb{\Omega }}(n,i)$. We extend $\mathbf{L}$ by a collapse-generic map $\zeta :\omega \stackrel{\mathrm{onto}}{⟶}\mathcal{P}(\omega )\cap \mathbf{L}$ to $\mathbf{L}$, as above, and define the partial product ${\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{w}={\prod }_{⟨n,i⟩\in \mathit{w}}{\mathbb{P}}^{\mathbb{\Omega }}(n,i)\in \mathbf{L}\left[\zeta \right]$ as a forcing notion in $\mathbf{L}\left[\zeta \right]$, where:

$$\mathit{w}=\mathit{w}\left[\zeta \right]=\{⟨n,i⟩:n\in \omega \wedge i\in \zeta (n)\}.$$

Adjoining a $({\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{w})$-generic set G to $\mathbf{L}\left[\zeta \right]$, we get a model $\mathbf{L}[\zeta ,G]$ for Theorem 2. In particular, if $x=\zeta (n)\in \mathcal{P}(\omega )\cap \mathbf{L}$, then x is definable in $\mathbf{L}[\zeta ,G]$ by means of the equivalence:

$$i\in x⟺\exists S\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}\forall f\in {\mathbf{Fun}}_{\mathbb{\Omega }}\left(S\mathrm{covers}f\mathrm{iff}f\notin {\mathbb{U}}^{\mathbb{\Omega }}(n,i)\right),$$

(4)

in which the implication $⟹$ follows from (*) via $S=S(n,i)$ (note that $S(n,i)\in \mathbf{L}[\zeta ,G]$ since $⟨n,i⟩\in \mathit{w}$ in case $i\in x=\zeta (n)$), whereas the inverse implication $⟸$ is based on the completeness properties of the system ${\mathbb{U}}^{\mathbb{\Omega }}$. It also takes some effort to check that the right-hand side of (4) really defines a ${\mathbf{D}}_{1\mathbb{M}}$ relation in $\mathbf{L}[\zeta ,G]$; for that purpose Theorem 3 is proved beforehand in Section 2.3.

To prove that, conversely, every $x\in {\mathbf{D}}_{1\mathbb{M}}$ in $\mathbf{L}[\zeta ,G]$ belongs to $\mathbf{L}$, we introduce forcing approximations in Section 5, a forcing-like relation used to prove the elementary equivalence theorem. Its key advantage is the invariance under some transformations, including the permutations of the index set $\mathcal{I}$, see Section 6.5. The actual forcing notion ${\mathbb{P}}^{\mathbb{\Omega }}=\mathbf{P}\left[{\mathbb{U}}^{\mathbb{\Omega }}\right]$ is absolutely not invariant under permutations of $\mathcal{I}$, but the $\mathbb{M}$-completeness property, maintained through the inductive construction of ${\mathbb{U}}^{\mathbb{\Omega }}$ in $\mathbf{L}$, allows us to prove that the auxiliary forcing is in the same relation to the truth in ${\mathbb{P}}^{\mathbb{\Omega }}$-generic extensions, as the true ${\mathbb{P}}^{\mathbb{\Omega }}$-forcing relation (Theorem 10). We call this construction hidden invariance (see Section 6.1), and this is the other major novelty of this paper.

Finally, Section 6 presents the proof of the invariance theorem (Theorem 11), with the help of forcing approximations, and thereby completes the proof of Theorem 2.

The flowchart of the proof can be seen in Figure 1 on page 6.

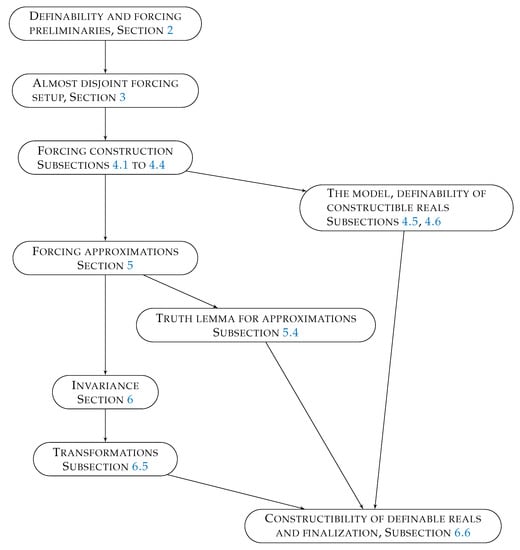
Figure 1. Flowchart of the proof of Theorem 2.

2. Preliminaries

This Section contains several definitions and results that will be very instrumental in the proof of Theorem 2.

2.1. Definability Issues

Beginning with the type-theoretic definability, we recall some details of Tarski’s constructions from [18]. The type-theoretic language deals with variables $x^k,y^k,\dots$ of orders $k<\omega$, and includes the Peano arithmetic language for order 0 and the atomic predicate ∈ of membership used as $x^k\in y^{k+1}$. The order of a formula $\phi$ is equal to the highest order of all variables in $\phi$. Variables of each order k can be substituted with elements of the corresponding iteration:

$${\mathcal{P}}^k(\omega )=\underset{k\mathrm{times}\mathrm{the}\mathrm{powerset}\mathrm{operation}\mathcal{P}(·)}{\underbrace{\mathcal{P}(\mathcal{P}(\dots \mathcal{P}(\omega )\dots ))}},\mathrm{the}\mathrm{set}\mathrm{of}\mathrm{all}\mathrm{elements}\mathrm{of}\mathrm{order}k$$

of the powerset operation. In particular, ${\mathcal{P}}^0(\omega )=\omega$ (natural numbers), ${\mathcal{P}}^1(\omega )=\mathcal{P}(\omega )$ (the reals), ${\mathcal{P}}^2(\omega )=\mathcal{P}(\mathcal{P}(\omega ))$ (sets of reals), and so on. Accordingly each quantifier $\exists x^k$, $\forall x^k$ in a type-theoretic formula is naturally relativized to ${\mathcal{P}}^k(\omega )$, and the truth of a closed type-theoretic formula (with or without parameters) is understood in the sense of such a relativization.

If $k,m<\omega$, $k\ge 1$, then, by Definition 1, ${\mathbf{D}}_{km}$ is the set of all $x^k\in {\mathcal{P}}^k(\omega )$, definable in the form:

$$x^k=\left\{y^{k-1}\in {\mathcal{P}}^{k-1}(\omega ):\phi (y^{k-1})\right\}$$

by a parameter free formula $\phi$ of order $\le m$; thus ${\mathbf{D}}_{km}\subseteq {\mathcal{P}}^k(\omega )$.

Remark 1.

We will occasionally extend the definition of ${\mathbf{D}}_{km}$ to binary relations, especially in the case $k=1$. Namely a set $X\subseteq {\mathcal{P}}^{k-1}(\omega )\times {\mathcal{P}}^{k-1}(\omega )$ belongs to ${\mathbf{D}}_{km}$ if it is definable by a parameter free formula of order $\le m$ with two free variables.

In matters of $\in$-definability, we refer to e.g., [31] (Part B, 5.4), or [32] (Chapter 13) on the Lévy hierarchy of ∈-formulas and definability classes ${\Sigma }_n^H$, ${\Pi }_n^H$, ${\Delta }_n^H$ for any transitive set H. In particular,

• ${\Sigma }_n^H$ = all sets $X\subseteq H$, definable in H by a parameter-free ${\Sigma }_n^{}$ formula;
• ${\Sigma }_n^{}(H)$ = all sets $X\subseteq H$, definable in H by a ${\Sigma }_n^{}$ formula with any sets in H as parameters.

Something like ${\Sigma }_n^H(x),x\in H$, means that only x is admitted as a parameter, while ${\Sigma }_n^H(P)$, where $P\subseteq H$, means that all $x\in P$ can be parameters. Collections like ${\Pi }_n^H,{\Pi }_n^H(x),{\Pi }_n^H(P)$ are defined similarly, and ${\Delta }_n^H={\Sigma }_n^H\cap {\Pi }_n^H$, etc. These definitions usually work with transitive sets of the form:

$$H=\mathrm{H}\varkappa =\{x:\mathtt{card}(\mathrm{TC}(x))<\varkappa \},\mathrm{where}\varkappa \mathrm{is}\mathrm{an}\mathrm{infinite}\mathrm{cardinal},$$

and $\mathrm{TC}$ is the transitive closure. In particular, $\mathbf{HC}=\mathrm{H}{\omega }_1$, all heredidarily-countable sets.

2.2. Constructibility Issues

As usual, $\mathbf{L}$ is the constructible universe, and ${<}_{\mathbf{L}}$ will denote the Gödel wellordering of $\mathbf{L}$. Let $\varkappa$ be an infinite regular cardinal. The following are well-known facts in the theory of constructibility, see e.g., [33] and Lemma 6.3 ff in [31] (Section B.5):

1°.

The set $\mathbf{H}\varkappa \cap \mathbf{L}$ belongs to ${\Sigma }_1^{\mathbf{H}\varkappa }$ and is equal to ${(\mathbf{H}\varkappa )}^{\mathbf{L}}={\mathbf{L}}_{\varkappa }$.

2°.

The restriction ${<}_{\mathbf{L}}\upharpoonright {(\mathbf{H}\varkappa )}^{\mathbf{L}}$ is a wellordering of ${(\mathbf{H}\varkappa )}^{\mathbf{L}}$ of length $\varkappa$ and a ${\Delta }_1^{{(\mathbf{H}\varkappa )}^{\mathbf{L}}}$ relation.

3°.

On the other hand, the set $\mathcal{P}(\omega )\cap \mathbf{L}$ and relation ${<}_{\mathbf{L}}\upharpoonright (\mathcal{P}(\omega )\cap \mathbf{L})$ belong to ${\Sigma }_2^1$ and to ${\mathbf{D}}_{21}$.

4°.

The map $x⟼\mathtt{pr}x=\left\{y:y{<}_{\mathbf{L}}x\right\}:{(\mathbf{H}\varkappa )}^{\mathbf{L}}\to {(\mathbf{H}\varkappa )}^{\mathbf{L}}$ is ${\Delta }_1^{{(\mathbf{H}\varkappa )}^{\mathbf{L}}}$ as well.

The last statement implies the following useful definability estimation.

5°.

Assume that $m\ge 1$ and $P\subseteq {(\mathbf{H}\varkappa )}^{\mathbf{L}}\times {(\mathbf{H}\varkappa )}^{\mathbf{L}}$ is ${\Delta }_m^{{(\mathbf{H}\varkappa )}^{\mathbf{L}}}$. If $x\in D=\left\{x\in {(\mathbf{H}\varkappa )}^{\mathbf{L}}:\exists yP(x,y)\right\}$, then let $y_x\in {(\mathbf{H}\varkappa )}^{\mathbf{L}}$ be the ${<}_{\mathbf{L}}$-least witness. Then $P^{\prime }=\{⟨x,y_x⟩:x\in D\}\subseteq P$ is ${\Delta }_m^{{(\mathbf{H}\varkappa )}^{\mathbf{L}}}$ as well.

Indeed $y=y_x$ is equivalent to $P(x,y)\wedge \forall z\in \mathtt{pr}y\neg P(x,z)$, where:

$$\begin{array}{ccc}\hfill \forall z\in \mathtt{pr}y\neg P(x,z)& ⟺& \exists Z\left(Z=\mathtt{pr}y\wedge \forall z\in Z\neg P(x,z)\right)\hfill \\ & ⟺& \forall Z\left(Z=\mathtt{pr}y⟹\forall z\in Z\neg P(x,z)\right),\hfill \end{array}$$

and the bounded quantifiers $\forall z\in Z$ do not influence the definability class.

We proceed with several easy and rather known lemmas.

Lemma 1.

Assume that $x,y\in \mathcal{P}(\omega )\cap \mathbf{L}$ and $y{<}_{\mathbf{L}}x$. Then $y\in {\Delta }_2^1(x)$, and hence if $y\in {\mathbf{D}}_{1n}$, $n\ge 1$, or $y\in {\mathbf{D}}_1$, then $x\in {\mathbf{D}}_{1n}$, resp., $x\in {\mathbf{D}}_1$ as well.

Proof. 

By the Shoenfield absoluteness, it suffices to prove that $y\in {\Delta }_2^1(x)$ is true in $\mathbf{L}$.

We argue in $\mathbf{L}$. Let $\varkappa ={\omega }_1$, so that $\mathbf{H}\varkappa ={(\mathbf{H}\varkappa )}^{\mathbf{L}}=\mathbf{HC}$ (hereditarily countable). The set:

$$P=\{⟨z,f⟩:z\subseteq \omega \wedge f:\omega \to \mathcal{P}(\omega )\wedge \mathtt{ran}f=\mathtt{pr}z\}$$

belongs to ${\Delta }_1^{\mathbf{HC}}$ by 4° since:

$$\begin{array}{ccc}\hfill \mathtt{ran}f=\mathtt{pr}z& ⟺& \exists u\left(u=\mathtt{pr}z\wedge \forall n(f(n)\in u)\wedge \forall z^{\prime }\in u\exists n(f(n)=z^{\prime })\right)\hfill \\ & ⟺& \forall u\left(u=\mathtt{pr}z⟹\forall n(f(n)\in u)\wedge \forall z^{\prime }\in u\exists n(f(n)=z^{\prime })\right).\hfill \end{array}$$

Let $f_z$ be the ${<}_{\mathbf{L}}$-least f such that $⟨z,f⟩\in P$; then $P^{\prime }=\{⟨z,f_z⟩:z\subseteq \omega \}$ is ${\Delta }_1^{\mathbf{HC}}$ by 5°. It follows that $f_x$ is ${\Delta }_1^{\mathbf{HC}}(x)$ (with x as the only parameter). Therefore, as $y{<}_{\mathbf{L}}x$, we have $y\in {\Delta }_1^{\mathbf{HC}}(x)$ because $y=f_x(n)$ for some n. It follows that $y\in {\Delta }_2^1(x)$. (See e.g., [34] (p. 281) on this translation result.) □

Remark 2

(Essentially Tarski [18]). If $n\ge 1$ and ${\omega }_1^{\mathbf{L}}={\omega }_1$ then ${\mathbf{D}}_{1n}\notin {\mathbf{D}}_{2n}$.

Proof. 

If ${\omega }_1^{\mathbf{L}}={\omega }_1$ then the set $Y=\mathcal{P}(\omega )\cap \mathbf{L}$ is uncountable. On the other hand $X={\mathbf{D}}_{1n}$ is countable, hence $Z=Y\setminus X\ne \varnothing$. Note that $Y\in {\mathbf{D}}_{21}$ by 3° above. It follows that if $X\in {\mathbf{D}}_{2n}$ then Z belongs to ${\mathbf{D}}_{2n}$, too, and then the ${<}_{\mathbf{L}}$-least element $z_0$ of the set Z belongs to ${\mathbf{D}}_{1n}$ because ${<}_{\mathbf{L}}$ is ${\mathbf{D}}_{21}$ on Y still by 3°. However $z_0\notin X={\mathbf{D}}_{1n}$ by construction. This is a contradiction. □

Lemma 2.

If $1\le n<m<\omega$ and ${\mathbf{D}}_{1m}\subseteq \mathbf{L}$, then ${\mathbf{D}}_{1n}\notin {\mathbf{D}}_{2n}$.

Proof. 

We have ${\mathbf{D}}_{1n}⫋{\mathbf{D}}_{1m}$ since $n<m$. Therefore ${\mathbf{D}}_{1n}⫋{\mathbf{D}}_{1m}\subseteq Y=\mathcal{P}(\omega )\cap \mathbf{L}$. If, to the contrary, ${\mathbf{D}}_{1n}\in {\mathbf{D}}_{2n}$, then the set $Y\setminus {\mathbf{D}}_{1n}$ belongs to ${\mathbf{D}}_{2n}$ as well since $Y\in {\mathbf{D}}_{21}$ by 3° above. We conclude that the ${<}_{\mathbf{L}}$-least element $y_0\in Y\setminus {\mathbf{D}}_{1n}$ belongs to ${\mathbf{D}}_{1n}$, because ${<}_{\mathbf{L}}$ is ${\mathbf{D}}_{21}$ on Y by 3°. This is a contradiction since $z_0\notin {\mathbf{D}}_{1n}$ by construction. □

2.3. Type-Theoretic Definability vs. $\in$-Definability

It occurs that the definability classes in sets of the form $\mathbf{H}\varkappa$ correspond to the Tarski definability classes, in the sense of the following theorem:

Theorem 3.

Assume that the generalized continuum hypothesis $2^{\vartheta }={\vartheta }^{+}$ holds for all infinite cardinals $\vartheta <{\omega }_{m-1}$. If $m\ge 1$ and $x\subseteq \omega$, then x is ${\mathbf{D}}_{1m}$ if x is $\in$-definable in $\mathbf{H}{\omega }_m$.

In case $m=1$ (then $\mathbf{H}{\omega }_m=\mathbf{H}{\omega }_1=\mathbf{HC}$ and the GCH premice is vacuous), this result was explicitly mentioned, in [34] (p. 281), a detailed proof see e.g., [32] (Lemma 25.25).

Proof. 

The GCH premice of the theorem is equivalent to ${\mathcal{P}}^m(\omega )\subseteq \mathbf{H}{\omega }_m$. This implies $⟹$: if $x\in {\mathbf{D}}_{1m}$ then x is surely $\in$-definable in $\mathbf{H}{\omega }_m$.

The inverse implication takes more effort. We have to somehow model the $\in$-structure of $\mathbf{H}{\omega }_m$ in ${\mathbf{D}}_{1m}$. For this purpose, if $k<\omega$ and $x,y\in {\mathcal{P}}^k(\omega )$ then define a quasi-pair $⟨x,y⟩{}^k\in {\mathcal{P}}^k(\omega )$ by induction as follows. If $k=0$, so that $x,y\in \omega$, then put $⟨x,y⟩{}^0=2^x·3^y\in \omega$. If $x,y\in {\mathcal{P}}^{k+1}(\omega )$ then put $⟨x,y⟩{}^{k+1}=\{⟨0,x^{\prime }⟩{}^k:x^{\prime }\in x\}\cup \{⟨1,y^{\prime }⟩{}^k:y^{\prime }\in y\}\in {\mathcal{P}}^{k+1}(\omega )$. Note that elements $0=\varnothing$ and $1=\{\varnothing \}$ belong to every type-theoretic level ${\mathcal{P}}^k(\omega )$. It can be easily established by induction that if $x,y,a,b\in {\mathcal{P}}^k(\omega )$ and $⟨x,y⟩{}^k=⟨a,b⟩{}^k$ then $x=a$ and $y=b$.

Following [32] (25.13), we associate, with each $r\in {\mathcal{P}}^m(\omega )$, a binary relation ${\mathsf{E}}_r$ defined so that:

$$x {\mathsf{E}}_r y\mathrm{iff}x,y\in M={\mathcal{P}}^{m-1}(\omega )\mathrm{and}⟨x,y⟩{}^{m-1}\in r.$$

on the set $M={\mathcal{P}}^{m-1}(\omega )$. Let ${\mathrm{WFE}}_0$ contain all sets $r\in {\mathcal{P}}^m(\omega )$ such that ${\mathsf{E}}_r$ is an extensional well-founded relation on $|r|=\left\{0\right\}\cup \{x\in M:\exists y\in M(x {\mathsf{E}}_r y\vee y {\mathsf{E}}_r x)\}$, with the additional property that 0 is the only top element of $|r|$, that is, $0 {\mathsf{E}}_r x$ holds for no $x\in |r|$. If $r\in {\mathrm{WFE}}_0$ then let ${\pi }_r$ be the unique 1-1 map defined on $|r|$ and satisfying ${\pi }_r(x)=\{{\pi }_r(y):y {\mathsf{E}}_r x\}$ for all $x\in |r|$ — the transitive collapse. We put $F(r)={\pi }_r(0)$.

Under our assumptions, F is a map from ${\mathrm{WFE}}_0$ onto $\mathbf{H}{\omega }_m$, $\in$-definable in $\mathbf{H}{\omega }_m$.

One easily proves that ${\mathrm{WFE}}_0$ belongs to ${\mathbf{D}}_{mm}$, that is, it is type-theoretically definable with quantifiers only over order levels $\le m$. Moreover the binary relations $\mathsf{EQ}$, $\mathsf{IN}$ defined on ${\mathrm{WFE}}_0$ by:

$$r \mathsf{EQ} q\mathrm{iff}F(r)=F(q),\mathrm{and}r \mathsf{IN} q\mathrm{iff}F(r)\in F(q),$$

belong to ${\mathbf{D}}_{mm}$ as well. Namely, let a bisimulation for $r,q\in {\mathrm{WFE}}_0$ be any binary relation $\mathsf{B}\subseteq |r|\times |q|$ satisfying $0 \mathsf{B} 0$ and, for all $x\in |r|$ and $y\in |q|$,

$$x \mathsf{B} y\mathrm{iff}\forall x^{\prime }\exists y^{\prime }(x^{\prime } {\mathsf{E}}_r x⟹y^{\prime } {\mathsf{E}}_q y\wedge x^{\prime } \mathsf{B} y^{\prime })\wedge \forall y^{\prime }\exists x^{\prime }(y^{\prime } {\mathsf{E}}_q y⟹x^{\prime } {\mathsf{E}}_r x\wedge x^{\prime } \mathsf{B} y^{\prime }).$$

Then, on the one hand, $F(r)=F(q)$ iff there exists a bisimulation for $r,q$ iff there exists $b\in {\mathcal{P}}^m(\omega )$ such that ${\mathsf{E}}_b$ is a bisimulation for $r,q$. On the other hand, we can express the property “${\mathsf{E}}_b$ is a bisimulation for $r,q$” by a type-theoretic formula with quantifiers only over orders $\le m$, by suitably replacing pairs $⟨·,·⟩$ with quasipairs $⟨·,·⟩{}^{m-1}$.

To treat $\mathsf{IN}$, we have to only change $0 \mathsf{B} 0$ above to $\exists y_0\in |q|(0 \mathsf{B} y_0\wedge y_0 {\mathsf{E}}_q 0)$.

Finally if $n<\omega$ then let $r_n=\{⟨i,j⟩{}^{m-1}:1\le i<j\le n\}\cup \{⟨i,0⟩{}^{m-1}:1\le i\le n\}$, so that $r_n\in {\mathrm{WFE}}_0$ and $F(r_n)=n$.

And now let $x=\{n<\omega :\mathbf{H}{\omega }_m\models \phi (n)\}\subseteq \omega$ be $\in$-definable in $\mathbf{H}{\omega }_m$ by a parameter free formula $\phi (·)$. Then we have $x=\{n<\omega :\Phi (r_n)\}$, where $\Phi$ is obtained from $\phi$ by substitution of $\mathsf{EQ}$ for = and $\mathsf{IN}$ for ∈ and relativization of all quantifiers to ${\mathrm{WFE}}_0$. This proves $x\in {\mathbf{D}}_{1m}$. □

2.4. Reduction to the Powerset Definability

Let ≼ be the wellordering of $\mathbf{Ord}\times \mathbf{Ord}$ defined so that $⟨\xi ,\eta ⟩\preccurlyeq ⟨{\xi }^{\prime },{\eta }^{\prime }⟩$ iff:

$$⟨\mathtt{max}\{\xi ,\eta \},\xi ,\eta ⟩{⩽}_{\mathrm{lex}}⟨\mathtt{max}\{{\xi }^{\prime },{\eta }^{\prime }\},{\xi }^{\prime },{\eta }^{\prime }⟩$$

lexicographically. Let $\mathrm{𝕡}:\mathbf{Ord}\times \mathbf{Ord}\stackrel{\mathrm{onto}}{⟶}\mathbf{Ord}$ be the order preserving map: $⟨\xi ,\eta ⟩\preccurlyeq ⟨{\xi }^{\prime },{\eta }^{\prime }⟩$ iff $\mathrm{𝕡}(\xi ,\eta )\le \mathrm{𝕡}({\xi }^{\prime },{\eta }^{\prime })$—the canonical pairing function. Let ${\mathrm{𝕡}}_1$ and ${\mathrm{𝕡}}_2$ be the inverse functions, so that $\alpha =\mathrm{𝕡}({\mathrm{𝕡}}_1(\alpha ),{\mathrm{𝕡}}_2(\alpha ))$ for all $\alpha$.

Lemma 3

(routine). If $\mathit{\Omega }$ is an infinite cardinal and $\kappa ={\mathit{\Omega }}^{+}$, then 𝕡 maps $\mathit{\Omega }\times \mathit{\Omega }$ onto $\mathit{\Omega }$ bijectively, and the restriction $\mathrm{𝕡}\upharpoonright (\mathit{\Omega }\times \mathit{\Omega })$ is constructible and ${\Delta }_1^{\mathbf{H}\kappa }$.

Now we prove another reduction-type definability theorem.

Theorem 4.

If $\mathit{\Omega }$ is a regular cardinal, $\varkappa ={\mathit{\Omega }}^{+}$, $X,Y\subseteq \omega$, and X is $\in$-definable in $\mathbf{H}\varkappa$ with Y as the only parameter, then X is $\in$-definable in the structure $⟨\mathcal{P}(\mathit{\Omega });\in ,\mathrm{𝕡}⟩$ with Y as the only parameter.

Proof (sketch). 

If $x\subseteq \mathit{\Omega }$ then let ${\mathsf{E}}_x^{\prime }=\{⟨\xi ,\eta ⟩:\xi ,\eta <\mathit{\Omega }\wedge \mathrm{𝕡}(\xi ,\eta )\in x\}$ be a binary relation on its domain $|x|=\mathtt{dom}{\mathsf{E}}_x^{\prime }\cup \mathtt{ran}{\mathsf{E}}_x^{\prime }$. Following the proof of Theorem 3, let ${\mathrm{WFE}}_0^{\prime }$ contain all sets $x\subseteq \mathit{\Omega }$ such that ${\mathsf{E}}_x^{\prime }$ is an extensional well-founded relation on $|x|$, with the additional property that $0\in |x|$ and 0 is the only top element of $|x|$, that is, $0 {\mathsf{E}}_x^{\prime } \xi$ holds for no $\xi \in |x|$. If $x\in {\mathrm{WFE}}_0^{\prime }$ then let ${\phi }_x$ be the unique 1-1 map defined on $|x|$ and satisfying ${\phi }_x(\xi )=\{{\phi }_x(\eta ):\eta {\mathsf{E}}_x^{\prime } \xi \}$ for all $\xi \in |x|$—the transitive collapse. We put $F^{\prime }(x)={\phi }_x(0)$; $F^{\prime }$ is a map from ${\mathrm{WFE}}_0^{\prime }$ onto $\mathbf{H}\varkappa$, $\in$-definable in $\mathbf{H}\varkappa$.

Both ${\mathrm{WFE}}_0^{\prime }$ and the binary relations ${\mathsf{EQ}}^{\prime }$, ${\mathsf{IN}}^{\prime }$ defined on ${\mathrm{WFE}}_0^{\prime }$ by:

$$x {\mathsf{EQ}}^{\prime } y\mathrm{iff}{F}^{\prime }(x)=F^{\prime }(y),\mathrm{and}x {\mathsf{IN}}^{\prime } y\mathrm{iff}{F}^{\prime }(x)\in F^{\prime }(y),$$

are $\in$-definable in $⟨\mathcal{P}(\mathit{\Omega });\in ,\mathrm{𝕡}⟩$ by the same bisimulation argument as in the proof of Theorem 3. Finally if $n<\omega$ then let $x_n=\{\mathrm{𝕡}(i,j):1\le i<j\le n\}\cup \{\mathrm{𝕡}(i,0):1\le i\le n\}$, so that $x_n\in {\mathrm{WFE}}_0^{\prime }$ and $F^{\prime }(x_n)=n$.

Now let $X=\{n<\omega :\mathbf{H}\varkappa \models \Phi (n,Y)\}\subseteq \omega$ be $\in$-definable in $\mathbf{H}\varkappa$ by a formula $\phi (·,Y)$. Then we have $X=\left\{n<\omega :{\Phi }^{\prime }(x_n)\right\}$, where ${\Phi }^{\prime }$ is obtained from $\Phi$ by the substitution of ${\mathsf{EQ}}^{\prime }$ for = and ${\mathsf{IN}}^{\prime }$ for ∈ and relativization of all quantifiers to ${\mathrm{WFE}}_0^{\prime }$. This proves the theorem. □

2.5. A Useful Result in Forcing Theory

We remind that, by [32] (Chapter 15), if $\varkappa$ is an infinite ordinal, then a forcing notion $P=⟨P;\le ⟩$:

• Is $\varkappa$-closed, if any $\le$-decreasing sequence ${\left\{p_{\alpha }\right\}}_{\alpha <\lambda }$ in P, of length $\lambda \le \varkappa$, has a lower bound in P;
• Is $\varkappa$-distributive, if the intersection of $\varkappa$-many open dense sets is open dense, and a set $D\subseteq P$ is open, iff $q⩽p\in D⟹q\in D$, and dense, iff for any $p\in P$ there is $q\in D$, $q⩽p$.
• Satisfies $\varkappa$-chain condition, or $\varkappa$-CC, if every antichain $A\subseteq P$ has cardinality strictly less than $\varkappa .$

We will make use of the following general result in forcing theory.

Lemma 4.

Assume that, in $\mathbf{L}$, $\vartheta <\mathbb{\Omega }={\vartheta }^{+}$ are regular infinite cardinals, and $Q,P\in \mathbf{L}$ are forcing notions, Q satisfies Ω-CC in $\mathbf{L}$, and P is ϑ-closed in $\mathbf{L}$. Assume that $⟨F,G⟩$ is a pair $(Q\times P)$-generic over $\mathbf{L}$. Then,

(i)

P remains ϑ-distributive in $\mathbf{L}\left[F\right]$,

(ii)

Ω is still a cardinal in $\mathbf{L}[F,G]$,

(iii)

Every set $X\in \mathbf{L}[F,G]$, $X\subseteq \mathbb{\Omega }$, bounded in Ω, belongs to $\mathbf{L}\left[F\right]$.

Proof. 

(i) Consider any sequence ${\left\{D_{\alpha }\right\}}_{\alpha <\vartheta }$ in $\mathbf{L}\left[F\right]$ of open dense sets $D_{\alpha }\subseteq P$. Prove that their intersection is dense. Let $\widehat{p}\in P$. Then $D=\{⟨\alpha ,p⟩:\alpha <\vartheta \wedge p\in D_{\alpha }\}$ belongs to $\mathbf{L}\left[F\right]$. Therefore there is a name $t\in \mathbf{L}$, $t\subseteq Q\times (\vartheta \times P)$, satisfying $D=t\left[F\right]$. Then $D_{\alpha }=t_{\alpha }\left[F\right]$ for all $\alpha$, where $t_{\alpha }=\{⟨q,p⟩:⟨q,⟨\alpha ,p⟩⟩\in t\}$. There exists a condition $q_0\in F$ which $Q$-forces

(A)

“$t_{\alpha }\left[\underline{F}\right]$ is open dense in P”

over $\mathbf{L}$ for every $\alpha <\vartheta$. We can w.l.o.g. assume that $1_Q$ forces (A), otherwise replace Q by $Q^{\prime }=\{q\in Q:q⩽q_0\}$. Under this assumption, we have the following:

(B)

If $\alpha <\vartheta$, $p\in P$, and $q\in Q$ then there exist $q^{\prime }\in Q$ and $p^{\prime }\in P$ such that $q^{\prime }⩽q$, $p^{\prime }⩽p$, and $q^{\prime }$$Q$-forces $p^{\prime }\in t_{\alpha }\left[\underline{F}\right]$ over $\mathbf{L}$.

Now we prove a stronger fact:

(C)

If $\gamma <\vartheta$ and $p\in P$, then there is $p^{\prime }\in P$, $p^{\prime }⩽p$, such that $1_Q$ forces $p^{\prime }\in t_{\gamma }\left[\underline{F}\right]$ over $\mathbf{L}$.

Indeed, arguing in $\mathbf{L}$, and using (B) and the assumption that P is $\vartheta$-closed, we can define a decreasing sequence ${\left\{p_{\alpha }\right\}}_{\alpha <\eta }$ of conditions in P, where $\eta <\mathbb{\Omega }$, and a sequence ${\left\{q_{\alpha }\right\}}_{\alpha <\eta }$ of conditions in Q, such that $q_0=q$, $q_{\alpha }$ is incompatible with $q_{\beta }$ whenever $\alpha \ne \beta$, and each $q_{\alpha }$ $Q$-forces $p_{\alpha +1}\in t_{\gamma }\left[\underline{F}\right]$. Note that the construction really has to stop at some $\eta <\mathbb{\Omega }$ otherwise we have an antichain in Q of cardinality $\mathbb{\Omega }$. Thus $A=\{q_{\alpha }:\alpha <\eta \}$ is a maximal antichain, and on the other hand, as P is $\vartheta$-closed and $\eta <\mathbb{\Omega }={\vartheta }^{+}$, there is a condition $p\in P$ satisfying $p⩽p_{\alpha }$ for all $\alpha <\eta$. Then every $q\in A$ $Q$-forces $p\in t_{\gamma }\left[\underline{F}\right]$ by construction, therefore, as A is a maximal antichain, q witnesses (C).

To accomplish the proof of (i), we define, using (C), a decreasing sequence ${\left\{p_{\gamma }\right\}}_{\gamma <\vartheta }\in \mathbf{L}$ of conditions in P, such that $p_0⩽\widehat{p}$ and, for any $\gamma <\vartheta$, $1_Q$ forces $p_{\gamma +1}\in t_{\gamma }\left[\underline{F}\right]$ over $\mathbf{L}$. Once again, there is a condition $p\in P$, $p⩽p_{\gamma }$ for all $\gamma$. Then $1_Q$ forces $p\in t_{\gamma }\left[\underline{F}\right]$ for all $\gamma$, hence $p\in {\bigcap }_{\gamma }{D}_{\gamma }$, as required.

Finally, as Q is $\mathbb{\Omega }$-CC in $\mathbf{L}$, $\mathbb{\Omega }$ remains a cardinal in $\mathbf{L}\left[F\right]$. Then, as P is $\vartheta$-distributive in $\mathbf{L}\left[F\right]$, we obtain (ii) and (iii) by standard arguments. □

2.6. Definable Names

Let $Q\in \mathbf{L}$ be any forcing notion. It is well known (see, e.g., Lemma 2.5 in Chapter B.4 of [31]) that if $F\subseteq Q$ is a $Q$-generic filter over $\mathbf{L}$, $X\in \mathbf{L}$, and $Y\in \mathbf{L}\left[F\right]$, $Y\subseteq X$, then there is a set $t\in \mathbf{L}$, $t\subseteq Q\times X$, such that:

$$Y=t\left[Q\right]:=\{x\in X:\exists q\in F(⟨q,x⟩\in t)\};$$

such a t is called a Q-name (for Y), whereas $t\left[G\right]$ is the $G$-valuation, or $G$-interpretation of t. There is a more comprehensive system of names and valuations, which involves all sets Y in generic extensions, not only those included in the groung model, see e.g., Chapter IV in [35], but it will not be used in this paper. The next theorem claims that in certain cases such a name t as above can be chosen of nearly the same definability level as the set Y itself.

Theorem 5.

Assume that $Q\in \mathbf{L}$ is any forcing, $F\subseteq Q$ is $Q$-generic over $\mathbf{L}$, $\varkappa >\omega$ is a cardinal in $\mathbf{L}\left[F\right]$ (hence, in $\mathbf{L}$, too), $n\ge 1$, $H={(\mathbf{H}\varkappa )}^{\mathbf{L}}$, $H\left[F\right]={(\mathbf{H}\varkappa )}^{\mathbf{L}\left[F\right]}$, and $Y\in \mathbf{L}\left[F\right]$, $Y\subseteq H$. Then,

(i)

If Y belongs to ${\Sigma }_n^H$ (hence to $\mathbf{L}$), then Y also belongs to ${\Sigma }_n^{H\left[F\right]};$

(ii)

If $Q\in H$ and Y belongs to ${\Sigma }_n^{}(H\left[F\right])$ (meaning ${\Sigma }_n^{}$ in $H\left[F\right]$ with arbitrary definability parameters in $H\left[F\right]$ allowed) then there exists a ${\Sigma }_n^{}(H)$ name $t\in \mathbf{L}$, $t\subseteq Q\times H$, such that $Y=t\left[F\right].$

Proof. 

To prove (i) note that $H=H\left[F\right]\cap \mathbf{L}$. But the formula “x is contructible” is ${\Sigma }_1^{}$ [31] (Part B, 5.4). It follows that H is ${\Sigma }_1^{H\left[F\right]}$. Now the result is clear: We formally relativize, to the ${\Sigma }_1^{H\left[F\right]}$ set H, all quantifiers in the ${\Sigma }_n^{}$ definition of Y in H, getting a ${\Sigma }_n^{}$ definition of Y in $H\left[F\right]$.

To prove (ii), assume that $Q\in H$. We utilize a more complex system of representation of sets in $\mathbf{L}\left[F\right]$, affecting all these sets, not just subsets of sets in $\mathbf{L}$. We take it from [36]. Inductively on the $\in$-rank $\mathtt{rk}(a)$, each set a is mapped to the set $K(a)=\{K(b):\exists q\in F(⟨q,b⟩\in a)\}$ (depends on F!). The next lemma continues the proof of Theorem 5.

Lemma 5. 

$H\left[F\right]=\{K(a):a\in H\}$.

Proof. 

From right to left, an elementary induction argument works. Prove it from left to right. Induction by the $\in$-rank $\mathtt{rk}(x)$, for each $x\in H\left[F\right]$ we define a set $a_x\in H$ such that $x=K(a_x)$. If $x=\varnothing$, then $a_x=\varnothing$ will do. Assume that $\mathtt{rk}(x)>0$ and $a_y$ is already defined for each $y\in x$. The set $A=\{a_y:y\in x\}\in L\left[F\right]$, $A\subseteq H$ has cardinality $<\varkappa$ in $L\left[F\right]$. Moreover, there is a set $B\in \mathbf{L}$, $B\subseteq H$, of cardinality $\le \varkappa$ in $\mathbf{L}$, such that $A\subseteq B$. (Indeed, $H\in \mathbf{L}$ has cardinality $\varkappa$ in $\mathbf{L}$. Let ${\left\{t_{\alpha }\right\}}_{\alpha <\varkappa }$ be a constructible enumeration of elements of H. As $\mathtt{card} A<\varkappa$ strictly, there is $\gamma <\varkappa$ such that $A\subseteq B=\{t_{\alpha }:\alpha <\gamma \}$. The set B is as required.)

According to the above, we have $A=\tau \left[F\right]$ for some $\tau \in \mathbf{L}$, $\tau \subseteq Q\times B$. Then $\tau \in H$. On the other hand, it is easy to check that $x=\{K(b):b\in A\}=K(\tau )$, that is, you can take $a_x=\tau$. This ends the proof of the lemma. □

In continuation of the proof of Theorem 5(ii), we introduce, following [36], the forcing relation $q⊩\phi$ (where $q\in Q$) by induction on the logical complexity of the formula $\phi$ (a closed formula with parameters in H); it corresponds to $H\left[F\right]$ as a Q-generic extension of H. Below ⩽ is the partial order on Q, and $q⩽q^{\prime }$ means that q is a stronger condition.

(I)

$q⊩a\in b$ iff $\exists ⟨q^{\prime },c⟩\in b(q⩽q^{\prime }\wedge q⊩a=c)$;

(II)

$q⊩a\ne b$   iff   $\exists ⟨q^{\prime },c⟩\in b(q⩽q^{\prime }\wedge q⊩c\notin a)$ or $\exists ⟨q^{\prime },c⟩\in a(q⩽q^{\prime }\wedge q⊩c\notin b)$;

(III)

$q⊩\neg \phi$   iff   $\neg \exists q^{\prime }(q^{\prime }⩽q\wedge q^{\prime }⊩\phi )$;

(IV)

$q⊩\phi \vee \psi$   iff   $q⊩\phi$ or $q⊩\psi$;

(V)

$q⊩\exists x\in b\phi (x)$   iff   $\exists ⟨q^{\prime },c⟩\in b(q⩽q^{\prime }\wedge q⊩\phi (c))$;

(VI)

$q⊩\exists x\phi (x)$   iff   $\exists c\in H(q⊩\phi (c))$.

This definition assumes that some logical connectives are expressed in a certain way via other connectives. For each parameter free formula $\phi (x_1,\dots ,x_k)$, define a set:

$$F_{\phi }=\{(q,a_1,\dots ,a_k):a_1,\dots ,a_k\in H\wedge q\in Q\wedge q⊩\phi (a_1,\dots ,a_k)\}.$$

Lemma 6. 

If $k>1$ and φ is a ${\Sigma }_k^{}$ formula, then $F_{\phi }$ is${\Sigma }_k^H(\left\{Q\right\})$ (Q is allowed as a sole parameter).

Proof. 

All quantifiers of definitions (I)–(V) are bounded either by the set $Q\in H$, or by a set of the form $Q\times a$, where still $a\in H$. Therefore it is not difficult to show that $F_{\phi }\in {\Sigma }_1^H$ for any bounded formula $\phi$. (The sole unbounded quantifier will express the existence of a full description of all subformulas of the form $a\in b$, $a=b$, that appear in accordance with (I)–(III).) Induction on k proves the result. □

The next lemma is similar to the Truth Lemma as in [36], so the proof is omitted.

Lemma 7. 

Let Φ be a closed formula with parameters in H, and ${\Phi }^{\prime }$ obtained from Φ so that each $a\in H$ is replaced by $K(a)$. Then ${\Phi }^{\prime }$ is true in $H\left[F\right]$ iff there exists $q\in F$ such that $q⊩\Phi$.

Let us finish the proof of Theorem 5(ii). Let $Y\in {\Sigma }_n^{}(H\left[F\right])$, $Y\subseteq H$. There is a parameter free ${\Sigma }_n^{}$ formula $\phi (·,·)$, and a parameter $y\in H\left[F\right]$, such that $X=\{x\in H:\phi (x,y)\mathrm{holds}\mathrm{in}H[F\left]\right\}$. For each $x\in H$, we define the set $\breve{x}\in H$ by induction, so that $\breve{\varnothing }=\varnothing$, and if $x\ne \varnothing$ then $\breve{x}=\{⟨q,\breve{z}⟩:q\in Q\wedge z\in x\}$. Then $K(\breve{x})=x$ for all x. It follows by Lemma 7 that:

$$X=\{x\in H:\exists q\in F(q⊩\phi (\breve{x},b))\}=t\left[F\right],$$

where $b\in H$ is such that $y=K(b)$ (exists by Lemma 5), whereas:

$$t=\{⟨q,x⟩:q\in Q\wedge x\in H\wedge q⊩\phi (\breve{x},b)\}.$$

Finally, note that the function $x⟼\breve{x}$ belongs to ${\Delta }_1^H(\left\{Q\right\})$. We conclude that $t\in {\Sigma }_n^{}(H)$ by Lemma 6, as required. This completes the proof of Theorem 5. □

2.7. Collapse Forcing

We conclude from Lemma 2 that the construction of any generic extension of $\mathbf{L}$, in which ${\mathbf{D}}_{1n}\in {\mathbf{D}}_{2n}$ holds for some $n\ge 1$, has to involve a collapse of ${\omega }_1^{\mathbf{L}}$ down to $\omega$, explicitly or implicitly. To set up such a collapse in a technically convenient form, we let $\Xi =\mathcal{P}(\omega )\cap \mathbf{L}$ be the set of all constructible sets $x\subseteq \omega$, and let $\mathbb{C}={\Xi }^{<\omega }$. Thus $\mathbb{C}\in \mathbf{L}$ is the ordinary Cohen-style collapse forcing that makes $\Xi$ (and ${\omega }_1^{\mathbf{L}}$ as well) countable in $\mathbb{C}$-generic extensions. The choice of $\Xi$ as the collapse domain, instead of ${\omega }_1^{\mathbf{L}}$, is made by technical reasons that will be clear below. Note that $\mathbb{C}$ adjoins generic maps $\zeta :\omega \stackrel{\mathrm{onto}}{⟶}\Xi$ to $\mathbf{L}$. A map $\zeta \in {\Xi }^{\omega }$ is $\mathbb{C}$-generic over $\mathbf{L}$ iff the set $G_{\zeta }=\{e\in \mathbb{C}:e\subset \zeta \}$ is $\mathbb{C}$-generic in the usual sense.

Lemma 8

(Routine). If $\zeta \in {\Xi }^{\omega }$ is $\mathbb{C}$-generic over $\mathbf{L}$ then ${\omega }_{\xi }^{\mathbf{L}\left[\zeta \right]}={\omega }_{\xi +1}^{\mathbf{L}}$ for all $\xi \in \mathbf{Ord}$.

The representation result, as in the beginning of Section 2.6, takes the following form: If $\zeta \in {\Xi }^{\omega }$ is $\mathbb{C}$-generic over $\mathbf{L}$, $X\in \mathbf{L}$, and $Y\in \mathbf{L}\left[\zeta \right]$, $Y\subseteq X$, then there is a set $t\in \mathbf{L}$, $t\subseteq \mathbb{C}\times X$, such that:

$$Y=t\left[\zeta \right]:=\{x\in X:\exists e\in G_{\zeta }(⟨e,x⟩\in t)\};$$

such a t is called a $\mathbb{C}$-name (for Y).

Theorem 5 is applicable for $Q=\mathbb{C}$ and any $\mathbf{L}$-cardinal $\varkappa \ge {\omega }_2^{\mathbf{L}}$, whereas if $\xi \in \mathbf{Ord}$, $\xi \ge 1$, then Lemma 4 is applicable for $Q=\mathbb{C}$, $\vartheta ={\omega }_{\xi }^{\mathbf{L}}$, $\mathbb{\Omega }={\omega }_{\xi +1}^{\mathbf{L}}$, and any forcing $P\in \mathbf{L}$, $\vartheta$-complete in $\mathbf{L}$.

3. Almost Disjoint Forcing, Uncountable Version

Here we introduce the main coding tool used in the proof of Theorem 2, an uncountable version of almost disjoint forcing of Jensen–Solovay [23].

3.1. Introduction to almost Disjoint Forcing

Definition 2.

Fix an uncountable successor $\mathbf{L}$-cardinal $\mathbb{\Omega }={\omega }_{\mu +1}^{\mathbf{L}}$. The value of Ω will be specified in Section 4.5 with respect to the integer $\mathbb{M}$ of Theorem 2, namely, $\mathbb{\Omega }={\omega }_{\mathbb{M}}^{\mathbf{L}}$, but until then we will view Ω as an arbitrary successor $\mathbf{L}$-cardinal.

We put ${\mathbb{\Omega }}^{\ominus }={\omega }_{\mu }^{\mathbf{L}}$ and ${\mathbb{\Omega }}^{\oplus }={\omega }_{\mu +2}^{\mathbf{L}}$. Here ${}^{\oplus }$, resp., ${}^{\ominus }$ mean the next, resp., previous $\mathbf{L}$-cardinal, which may not be true cardinals in generic extensions of $\mathbf{L}$.

We finally put:

$$\mathbb{H}={(\mathbf{H}{\mathbb{\Omega }}^{\oplus })}^{\mathbf{L}}=\{x\in \mathbf{L}:\mathtt{card}(\mathrm{TC}(x))<{\mathbb{\Omega }}^{\oplus }\mathrm{in}\mathbf{L}\}.$$

(5)

Moreover if $\mathbf{L}\left[G\right]$ is a generic extension of $\mathbf{L}$ then we define:

$$\mathbb{H}\left[G\right]={(\mathbf{H}{\mathbb{\Omega }}^{\oplus })}^{\mathbf{L}\left[G\right]}=\{x\in \mathbf{L}\left[G\right]:\mathtt{card}(\mathrm{TC}(x))<{\mathbb{\Omega }}^{\oplus }\mathrm{in}\mathbf{L}\left[G\right]\}.$$

(6)

provided ${\mathbb{\Omega }}^{\oplus }$ remains a cardinal in $\mathbf{L}\left[G\right]$.

• Let ${\mathbf{Seq}}_{\mathbb{\Omega }}=({\mathbb{\Omega }}^{<\mathbb{\Omega }}\setminus \{\Lambda \})\cap \mathbf{L}$, the set of all constructible non-empty sequences s of ordinals $<\mathbb{\Omega }$, of length $\mathtt{lh}s=\mathtt{dom}s<\mathbb{\Omega }$, called strings. We underline that ${\mathbf{Seq}}_{\mathbb{\Omega }}\in \mathbf{L}$, and $\Lambda$, the empty string, does not belong to ${\mathbf{Seq}}_{\mathbb{\Omega }}$;
• Let ${\mathbf{Fun}}_{\mathbb{\Omega }}={\mathbb{\Omega }}^{\mathbb{\Omega }}\cap \mathbf{L}$ = all constructible $\mathbb{\Omega }$-sequences of ordinals $<\mathbb{\Omega }$; ${\mathbf{Fun}}_{\mathbb{\Omega }}\in \mathbf{L}$;
• If $X\subseteq {\mathbf{Fun}}_{\mathbb{\Omega }}$ then put $X^{\vee }=\{f\upharpoonright \xi :f\in F_p\wedge 1\le \xi <\mathbb{\Omega }\}$,a tree in ${\mathbf{Seq}}_{\mathbb{\Omega }}$, without terminal nodes;
• A set $X\subseteq {\mathbf{Fun}}_{\mathbb{\Omega }}$ is dense iff $X^{\vee }={\mathbf{Seq}}_{\mathbb{\Omega }}$, i. e. for any $s\in {\mathbf{Seq}}_{\mathbb{\Omega }}$ there is $f\in X$ such that $s\subset f$;
• If $S\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }},f\in {\mathbf{Fun}}_{\mathbb{\Omega }}$ then let $S/f=\mathtt{sup}\{\xi <\mathbb{\Omega }:f\upharpoonright \xi \in S\}$. If $S/f$ is unbounded in $\mathbb{\Omega }$ then say that S covers f, otherwise S does not cover f.

Definition 3

(in $\mathbf{L}$). ${{}^{*}P}_{\mathbb{\Omega }}$ is the set of all pairs $p=⟨S_p;F_p⟩\in \mathbf{L}$ of sets $F_p\subseteq {\mathbf{Fun}}_{\mathbb{\Omega }}$, $S_p\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}$ of cardinality strictly less than Ω in $\mathbf{L}$. Elements of ${{}^{*}P}_{\mathbb{\Omega }}$ will be called (forcing) conditions.

If $p,q\in {{}^{*}P}_{\mathbb{\Omega }}$ then $p\wedge q=⟨S_p\cup S_q;F_p\cup F_q⟩$; a condition in ${{}^{*}P}_{\mathbb{\Omega }}$.

Let $p,q\in {{}^{*}P}_{\mathbb{\Omega }}$. Define $q⩽p$ (q is stronger as a forcing condition) iff $S_p\subseteq S_q,F_p\subseteq F_q$, and the difference $S_q\setminus S_p$ does not intersect $F_p^{\vee }$, that is, $S_q\cap F_p^{\vee }=S_p\cap F_p^{\vee }$. Here $F_p^{\vee }={(F_p)}^{\vee }$.

Lemma 9

(in $\mathbf{L}$). The sets ${\mathbf{Seq}}_{\mathbb{\Omega }}$, ${\mathbf{Fun}}_{\mathbb{\Omega }}$, ${{}^{*}P}_{\mathbb{\Omega }}$ belong to $\mathbf{L}$ and $\mathtt{card} ({\mathbf{Seq}}_{\mathbb{\Omega }})=\mathbb{\Omega }$ while $\mathtt{card} ({\mathbf{Fun}}_{\mathbb{\Omega }})=\mathtt{card} {{}^{*}P}_{\mathbb{\Omega }}={\mathbb{\Omega }}^{\oplus }$ in $\mathbf{L}$.

Clearly $q⩽p$ iff $S_p\subseteq S_q,F_p\subseteq F_q$, and $S_q\cap F_p^{\vee }=S_p\cap F_p^{\vee }$.

Lemma 10

(in $\mathbf{L}$). Conditions $p,q\in {{}^{*}P}_{\mathbb{\Omega }}$ are compatible in ${{}^{*}P}_{\mathbb{\Omega }}$ iff $1)$ $S_q\setminus S_p$ does not intersect $F_p^{\vee }$, and $2)$ $S_p\setminus S_q$ does not intersect $F_q^{\vee }$. Therefore any $p,q\in P^{*}$ are compatible in $P^{*}$ iff $p\wedge q⩽p$ and $p\wedge q⩽q$.

Proof. 

If (1), (2) hold then $p\wedge q⩽p$ and $p\wedge q⩽q$, thus $p,q$ are compatible. □

If $u\subseteq {\mathbf{Fun}}_{\mathbb{\Omega }}$ then put $P\left[u\right]=\{p\in {{}^{*}P}_{\mathbb{\Omega }}:F_p\subseteq u\}$. Thus if $u\in \mathbf{L}$ then $P\left[u\right]\in \mathbf{L}$.

Any conditions $p,q\in P\left[u\right]$ are compatible in $P\left[u\right]$ iff they are compatible in ${{}^{*}P}_{\mathbb{\Omega }}$ iff $p\wedge q=⟨S_p\cup S_q;F_p\cup F_q⟩\in P\left[u\right]$ satisfies both $(p\wedge q)⩽p$ and $(p\wedge q)⩽q$. Thus we say that conditions $p,q\in {{}^{*}P}_{\mathbb{\Omega }}$ are compatible (or incompatible) without an indication which set $P\left[u\right]$ containing $p,q$ is considered.

Lemma 11

(in $\mathbf{L}$). Let $\varnothing \ne u\subseteq {\mathbf{Fun}}_{\mathbb{\Omega }}$. Then it is true in $\mathbf{L}$ that $\mathtt{card}P\left[u\right]\le {\mathbb{\Omega }}^{\oplus }$, and the forcing notion $P\left[u\right]$ satisfies ${\mathbb{\Omega }}^{\oplus }$-CC, and is ${\mathbb{\Omega }}^{\ominus }$-closed, hence ${\mathbb{\Omega }}^{\ominus }$-distributive. Moreover $P\left[u\right]$ satisfies ${\mathbb{\Omega }}^{\oplus }$-CC in any generic extension $\mathbf{L}\left[H\right]$ of $\mathbf{L}$, in which ${\mathbb{\Omega }}^{\oplus }$ remains a cardinal.

Proof. 

The closed/distributive claim is obvious on the base of the cardinality restrictions in Definition 3. To prove the ${\mathbb{\Omega }}^{\oplus }$-CC claim, argue in $\mathbf{L}\left[H\right]$. If $p\ne q$ belong to an antichain $A\subseteq P\left[u\right]$ then $S_p\ne S_q$ by Lemma 10. Let $M=\{S_p:p\in {{}^{*}P}_{\mathbb{\Omega }}\}=$ all subsets $S\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}$, $S\in \mathbf{L}$, with $\mathtt{card}S<\mathbb{\Omega }$ in $\mathbf{L}$. Then M is a set of cardinality $\mathbb{\Omega }$ in $\mathbf{L}$, hence in $\mathbf{L}\left[H\right]$ as well. □

If $u\subseteq {\mathbf{Fun}}_{\mathbb{\Omega }}$ in $\mathbf{L}$, and $G\subseteq P\left[u\right]$ is a $P\left[u\right]$-generic set, then put $S_G={\bigcup }_{p\in G}{S}_p$; thus $S_G\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}$. The next lemma witnesses that forcing notions of the form $P\left[u\right]$ belong to the type of almost disjoint (AD, for brevity) forcing, invented in [23] (§ 5).

Lemma 12.

Suppose that, in $\mathbf{L}$, $u\subseteq {\mathbf{Fun}}_{\mathbb{\Omega }}$ is dense. Let $G\subseteq P\left[u\right]$ be a set $P\left[u\right]$-generic over $\mathbf{L}$. Then:

(i)

If $f\in {\mathbf{Fun}}_{\mathbb{\Omega }}$ in $\mathbf{L}$ then $f\in u⟺S_G$ does not cover $f;$

(ii)

$G=\{p\in P\left[u\right]:S_p\subseteq S_G\wedge (S_G\setminus S_p)\cap F_p^{\vee }=\varnothing \}$, hence $\mathbf{L}\left[G\right]=\mathbf{L}\left[S_G\right].$

Proof. 

(i) Let $f\in u$. The set $D_f=\{p\in P\left[u\right]:f\in F_p\}$ is dense in $P\left[u\right]$. (Let $q\in P\left[u\right]$. Define $p\in P\left[u\right]$ so that $S_p=S_q$ and $F_p=F_q\cup \left\{f\right\}$. Then $p\in D_f$ and $p⩽q$.) Therefore $D_f\cap G\ne \varnothing$. Pick any $p\in D_f\cap G$. Then $f\in F_p$. Now every $r\in G$ is compatible with p, and hence $S_r/f\subseteq S_p/f$ by Lemma 10. Thus $S_G/f=S_p/f$ is bounded in $\mathbb{\Omega }$. Let $f\notin u$. If $\xi <\mathbb{\Omega }$ then the set $D_{f\xi }=\{p\in P\left[u\right]:\mathtt{sup}(S_p/f)>\xi \}$ is dense in $P\left[u\right]$. (If $q\in P\left[u\right]$ then $\mathtt{card}(F_q^{\vee })<\mathbb{\Omega }$. As $f\notin u$, there is $\eta >\xi$, $\eta <\mathbb{\Omega }$, with $f\upharpoonright \eta \notin F_q^{\vee }$. Define p so that $F_p=F_q$ and $S_p=S_q\cup \left\{f\upharpoonright \eta \right\}$. Then $p\in D_{f\xi }$ and $p⩽q$.) Let $p\in D_{f\xi }\cap G$. Then $\mathtt{sup}(S_G/f)>\xi$. As $\xi <\mathbb{\Omega }$ is arbitrary, $S_G/f$ is unbounded.

(ii) Consider any $p\in P\left[u\right]$. Suppose $p\in G$. Then $S_p\subseteq S_G$. If there exists $s\in (S_G\setminus S_p)\cap F_p^{\vee }$ then by definition we have $s\in S_q$ for some $q\in G$. However, then $p,q$ are incompatible by Lemma 10, a contradiction. Now suppose $p\notin G$. Then there exists $q\in G$ incompatible with p. By Lemma 10, there are two cases. First, there exists $s\in (S_q\setminus S_p)\cap F_p^{\vee }$. Then $s\in S_G\setminus S_p$, so p is not compatible with $S_G$. Second, there exists $s\in (S_p\setminus S_q)\cap F_q^{\vee }$. Then any condition $r⩽q$ satisfies $s\notin S_r$. Therefore $s\notin S_G$, so $S_p⊈S_G$, and p is not compatible with $S_G$. □

3.2. Product Almost Disjoint Forcing

Arguing under the assumptions and notation of Definition 2, we consider $\mathcal{I}=\omega \times \omega$, the cartesian product, as the index set for a product forcing.

Definition 4

(in $\mathbf{L}$). ${{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ (note the boldface upright form) is the $\mathbf{L}$-product of $\mathcal{I}$ copies of ${{}^{*}P}_{\mathbb{\Omega }}$ (Definition 3 in Section 3.1), ordered componentwise: $p⩽q$ (p is stronger) iff $p(n,i)⩽q(n,i)$ in ${{}^{*}P}_{\mathbb{\Omega }}$ for all $n,i<\omega$.

That is, ${{}^{*}\mathbf{P}}_{\mathbb{\Omega }}\in \mathbf{L}$ and ${{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ consists of all maps $p\in \mathbf{L}$, $p:\mathcal{I}\to {{}^{*}P}_{\mathbb{\Omega }}$. If $p\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ then put ${\mathbf{F}}_p(n,i)=F_{p(n,i)}$ and ${\mathbf{S}}_p(n,i)=S_{p(n,i)}$ for all $n,i<\omega$, so that $p(n,i)=⟨{\mathbf{S}}_p(n,i);{\mathbf{F}}_p(n,i)⟩$, where ${\mathbf{S}}_p:\mathcal{I}\to {\mathcal{P}}_{<\mathbb{\Omega }}({\mathbf{Seq}}_{\mathbb{\Omega }})$ and ${\mathbf{F}}_p:\mathcal{I}\to {\mathcal{P}}_{<\mathbb{\Omega }}({\mathbf{Fun}}_{\mathbb{\Omega }})$ are arbitrary, and ${\mathcal{P}}_{<\mathbb{\Omega }}$ means all subsets of cardinality $<\mathbb{\Omega }$ strictly.

• Note that, unlike product almost-disjoint forcing notions developed in [4,5], ${{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ is not a finite-support product;
• If $p\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ then we define $|p|=\{⟨n,i⟩:p(n,i)\ne ⟨\varnothing ,\varnothing ⟩\}$ and

  $${\mathbf{F}}_p^{\vee }(n,i)=F_{p(n,i)}^{\vee }=\{f\upharpoonright \xi :f\in {\mathbf{F}}_p(n,i)\wedge 1\le \xi <\mathbb{\Omega }\};$$
• If $p,q\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ then define $p\wedge q\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ by $(p\wedge q)(n,i)=p(n,i)\wedge q(n,i)$, in the sense of Definition 3 in Section 3.1, for all $n,i<\omega$.

Lemma 13.

Conditions $p,q\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ are compatible in ${{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ iff $(p\wedge q)⩽p$ and $(p\wedge q)⩽q$.

Let an $\mathbb{\Omega }$-system be any map $U\in \mathbf{L}$, $U:\mathcal{I}\to \mathcal{P}({\mathbf{Fun}}_{\mathbb{\Omega }})$ such that each set $U(n,i)$ is empty or dense in ${\mathbf{Fun}}_{\mathbb{\Omega }}$. In this case, let $|U|=\{⟨n,i⟩:U(n,i)\ne \varnothing \}.$

• If U is an $\mathbb{\Omega }$-system then $\mathbf{P}\left[U\right]=\{p\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}:\forall ⟨n,i⟩\in |p|({\mathbf{F}}_p(n,i)\subseteq U(n,i))\}$ is the $\mathbf{L}$-product of the sets $P\left[U(n,i)\right]$, $n,i<\omega$.

Lemma 14

(in $\mathbf{L}$). Let U be an $\mathbb{\Omega }$-system. Then it is true in $\mathbf{L}$ that $\mathtt{card}\mathbf{P}\left[U\right]={\mathbb{\Omega }}^{\oplus }$, and the forcing notion $\mathbf{P}\left[U\right]$ is ${\mathbb{\Omega }}^{\ominus }$-closed, hence ${\mathbb{\Omega }}^{\ominus }$-distributive, and satisfies ${\mathbb{\Omega }}^{\oplus }$-CC, and the product $\mathbb{C}\times \mathbf{P}\left[U\right]$ satisfies ${\mathbb{\Omega }}^{\oplus }$-CC as well. Moreover $\mathbf{P}\left[U\right]$ satisfies ${\mathbb{\Omega }}^{\oplus }$-CC in any generic extension of $\mathbf{L}$ in which ${\mathbb{\Omega }}^{\oplus }$ remains a cardinal.

Proof. 

The closed/distributive claims follow from Lemma 11. To prove the antichain claim we observe that if $p,q\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ satisfy ${\mathbf{S}}_p={\mathbf{S}}_q$ then $p,q$ are compatible. However the set ${\Delta }_{\mathbf{S}}=\{{\mathbf{S}}_p:p\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}\}$ has cardinality $\le \mathbb{\Omega }<{\mathbb{\Omega }}^{\oplus }$ in $\mathbf{L}$ as it consists of all functions ${\mathbf{S}}_p:\mathcal{I}\to {\mathcal{P}}_{<\mathbb{\Omega }}({\mathbf{Seq}}_{\mathbb{\Omega }})$. To extend the result to the product $\mathbb{C}\times \mathbf{P}\left[U\right]$, note that $\mathtt{card}\mathbb{C}={\omega }_1^{\mathbf{L}}\le \mathbb{\Omega }$. □

Definition 5.

Suppose that $z\subseteq \mathcal{I}$. If $p\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ then define $p^{\prime }=p\upharpoonright z$ to be the usual restriction, so that $\mathtt{dom}(p\upharpoonright z)=z$ and $p^{\prime }(n,i)=p(n,i)$ for all $⟨n,i⟩\in z$. A special case: If $n,i<\omega$ then let $p{\upharpoonright }_{\ne ⟨n,i⟩}=p\upharpoonright z$, where $z=(\mathcal{I}\setminus \{⟨n,i⟩\})$. If U is an $\mathbb{\Omega }$-system then define $U\upharpoonright z$ to be the ordinary restriction as well. Furthermore, if $m<\omega$ then define:

$$\begin{array}{ccccc}\hfill p\upharpoonright {}^{<m}=p\upharpoonright z& \mathrm{and}& \hfill U\upharpoonright {}^{<m}=U\upharpoonright z,& \mathrm{where}& z=\{k:k<m\}\times \omega ,\hfill \\ \hfill p\upharpoonright {}^{\ge m}=p\upharpoonright z& \mathrm{and}& \hfill U\upharpoonright {}^{\ge m}=U\upharpoonright z,& \mathrm{where}& z=\{k:k\ge m\}\times \omega ,\hfill \\ \hfill p\upharpoonright {}^m=p\upharpoonright z& \mathrm{and}& \hfill U\upharpoonright {}^m=U\upharpoonright z,& \mathrm{where}& z=\left\{m\right\}\times \omega ,\hfill \end{array}$$

$Finally, if$Q ⊆ ^*P_Ω $then let$ Q ↾ z = {p ↾ z : p ∈ Q}; Q ↾ z ⊆^*P_Ω ↾ z. $This will be applied, e.g., in case$ Q = P[U], $where$ U ∈ L $is a \mathbb{\Omega }$-system, and then we get P[U] ↾ z = {p ↾ z : p ∈ P[U]}, P[U] ↾ _≠⟨n,i⟩, P[U] ↾ ^≥m, $etc$.

Remark 3.

Suppose that $z\in \mathbf{L}$ in Definition 5. If $p\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$, then $p\upharpoonright z$ can be identified with a condition $q\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ such that $q\upharpoonright z=p\upharpoonright z$ and $q(n,i)=⟨\varnothing ;\varnothing ⟩$ for all $⟨n,i⟩\in \mathcal{I}\setminus z$. For instance, this applies w.r.t. $p{\upharpoonright }_{\ne ⟨n,i⟩}$, $p\upharpoonright {}^{\ge m}$, $p\upharpoonright {}^{<m}$, $p\upharpoonright {}^m$.

With such an identification, we have ${{}^{*}\mathbf{P}}_{\mathbb{\Omega }}\upharpoonright z\subseteq {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$, and $Q\upharpoonright z\subseteq {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ for $Q\subseteq {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ (in case $z\in \mathbf{L}$).

However, if $z\notin \mathbf{L}$ then such an identification fails. This is a consequence of our deviation from the finite-support product approach taken in [4,5], which would not work in the setting of this paper.

The same applies for the restrictions $U\upharpoonright z$ of $\mathbb{\Omega }$-systems U.

3.3. Structure of Product almost Disjoint Generic Extensions

Arguing under the assumptions and notation of Definition 2, we let U be an $\mathbb{\Omega }$-system in $\mathbf{L}$. Consider $\mathbf{P}\left[U\right]$ as a forcing notion. We will study $\mathbf{P}\left[U\right]$-generic extensions $\mathbf{L}\left[G\right]$ of the ground universe $\mathbf{L}$. Define some elements of these extensions. Suppose that $G\subseteq \mathbf{P}\left[U\right]$ is a generic set. Let,

$${\mathbf{S}}_G(n,i)=S_{G(n,i)}={\bigcup }_{p\in G}{\mathbf{S}}_p(n,i)\mathrm{for}\mathrm{any}n,i<\omega ,$$

where $G(n,i)=\{p(n,i):p\in G\}\subseteq P\left[U(n,i)\right]$; thus ${\mathbf{S}}_G(n,i)\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}$ and $G\subseteq \mathbf{P}\left[U\right]$ splits into the family of sets $G(n,i),n,i<\omega$. This defines a sequence ${\overrightarrow{S}}_G={\left\{{\mathbf{S}}_G(n,i)\right\}}_{n,i<\omega }$ of subsets of ${\mathbf{Seq}}_{\mathbb{\Omega }}$.

If $z\subseteq \mathcal{I}$ then let $G\upharpoonright z=\{p\upharpoonright z:p\in G\}$.If $z\in \mathbf{L}$ then $G\upharpoonright z$ can be identified with $\{p\in G:|p|\subseteq z\}$.

Put $G{\upharpoonright }_{\ne ⟨n,i⟩}=\{p\in G:⟨n,i⟩\notin |p|\}=G\upharpoonright (\mathcal{I}\setminus \{⟨n,i⟩\})$.

Lemma 15.

Let U be an $\mathbb{\Omega }$-system in $\mathbf{L}$, and $G\subseteq \mathbf{P}\left[U\right]$ be a set $\mathbf{P}\left[U\right]$-generic over $\mathbf{L}$. Then:

(i)

$\mathbf{L}\left[G\right]=\mathbf{L}[{\overrightarrow{S}}_G];$

(ii)

If $n,i<\omega$ then the set $G(n,i)=\{p(n,i):p\in G\}\in \mathbf{L}\left[G\right]$ is $P\left[U(n,i)\right]$-generic over $\mathbf{L}$, hence if $f\in {\mathbf{Fun}}_{\mathbb{\Omega }}$ then $f\in U(n,i)⟺{\mathbf{S}}_G(n,i)$ does not cover $f;$

(iii)

If $X\in \mathbf{L}\left[G\right]$, $X\subseteq \mathbb{\Omega }$ is bounded, then $X\in \mathbf{L};$

(iv)

All $\mathbf{L}$-cardinals are preserved in $\mathbf{L}\left[G\right]$, and GCH holds in $\mathbf{L}\left[G\right].$

Proof. 

To prove (i) apply Lemma 12(ii).

The genericity in (ii) holds by the product forcing theorem, then use Lemma 12(i).

Claim (iii) follows from the ${\mathbb{\Omega }}^{\ominus }$-closure claim of Lemma 14.

(iv) We conclude from (iii) that all $\mathbf{L}$-cardinals $\le \mathbb{\Omega }$ remain cardinals in $\mathbf{L}\left[G\right]$, and GCH holds for all $\mathbf{L}$-cardinals $<\mathbb{\Omega }$ strictly. It follows from the ${\mathbb{\Omega }}^{\oplus }$-CC claim of Lemma 14 that all $\mathbf{L}$-cardinals $\ge {\mathbb{\Omega }}^{\oplus }$ remain cardinals in $\mathbf{L}\left[G\right]$, and since $\mathtt{card}\mathbf{P}\left[U\right]\le {\mathbb{\Omega }}^{\oplus }$ in $\mathbf{L}$, GCH holds for all of them in $\mathbf{L}\left[G\right]$. And finally we still have $exp(\mathbb{\Omega })={\mathbb{\Omega }}^{\oplus }$ in $\mathbf{L}\left[G\right]$ since by (i) the model $\mathbf{L}\left[G\right]$ is an extension of $\mathbf{L}$ by adjoining a subset of $\mathbb{\Omega }$ obtained by a suitable wrapping of ${\overrightarrow{S}}_G$. □

The next lemma is useful in dealing with combined $(\mathbb{C}\times \mathbf{P}[U])$-generic extensions $\mathbf{L}[\zeta ,G]$ of $\mathbf{L}$, where, by the product forcing theorem, $\zeta \in {\Xi }^{\omega }$ is $\mathbb{C}$-generic over $\mathbf{L}$ and G is $\mathbf{P}\left[U\right]$-generic over $\mathbf{L}\left[\zeta \right]$, or equivalently, G is $\mathbf{P}\left[U\right]$-generic over $\mathbf{L}$ and $\zeta$ is $\mathbb{C}$-generic over $\mathbf{L}\left[G\right]$.

Lemma 16.

Let U be an $\mathbb{\Omega }$-system in $\mathbf{L}$, and a pair $⟨\zeta ,G⟩$ is $(\mathbb{C}\times \mathbf{P}[U])$-generic over $\mathbf{L}$. Then:

(i)

All $\mathbf{L}\left[\zeta \right]$-cardinals are preserved in $\mathbf{L}[\zeta ,G]$, so that ${\omega }_{\xi }^{\mathbf{L}[\zeta ,G]}={\omega }_{\xi }^{\mathbf{L}\left[\zeta \right]}={\omega }_{\xi +1}^{\mathbf{L}}$ for all $\xi \ge 1;$

(ii)

GCH holds in $\mathbf{L}[\zeta ,G];$

(iii)

If $\mathbb{\Omega }\ge {\omega }_2^{\mathbf{L}}$ and $X\in \mathbf{L}[\zeta ,G]$, $X\subseteq \mathbb{\Omega }$ is bounded, then $X\in \mathbf{L}\left[\zeta \right];$

(iv)

If $1\le k<\omega$ and ${\omega }_k^{\mathbf{L}}<\mathbb{\Omega }$, then ${(\mathbf{H}\mathbb{\Omega })}^{\mathbf{L}[\zeta ,G]}={(\mathbf{H}\mathbb{\Omega })}^{\mathbf{L}\left[\zeta \right]}$ and ${\mathcal{P}}^k(\omega )\cap \mathbf{L}[\zeta ,G]={\mathcal{P}}^k(\omega )\cap \mathbf{L}\left[\zeta \right]$.

Note that Claims (iii), (iv) are not applicable in case $\mathbb{\Omega }={\omega }_1^{\mathbf{L}}$.

Proof. 

To prove (i), (ii) recall that all $\mathbf{L}$-cardinals remain cardinals in $\mathbf{L}\left[G\right]$, and GCH holds in $\mathbf{L}\left[G\right]$, by Lemma 15(iv). It remains to note that $\zeta$ is $\mathbb{C}$-generic over $\mathbf{L}\left[G\right]$ and make use of Lemma 8. To prove (iii) apply Lemma 4 with $\vartheta ={\mathbb{\Omega }}^{\ominus }$, $P=\mathbf{P}\left[U\right]$, $Q=\mathbb{C}$. Note that $\mathtt{card}\mathbb{C}={\omega }_1^{\mathbf{L}}\le {\mathbb{\Omega }}^{\ominus }$ in case $\mathbb{\Omega }\ge {\omega }_2^{\mathbf{L}}$.

Finally Claim (iv) is a routine corollary of (i)–(iii). □

4. The Forcing Notion and the Model

In this Section, we prove Theorem 2 on the base of another result, Theorem 8, see Remark 4 on page 23. The proof of Theorem 8 will follow in the remainder of the paper. The structure of the extension will be presented in Section 4.6, after the definition of the forcing notion involved in Section 4.5. Recall that the $\mathbf{L}$-cardinals:

$${\mathbb{\Omega }}^{\ominus }={\omega }_{\mu }^{\mathbf{L}}<\mathbb{\Omega }={\omega }_{\mu +1}^{\mathbf{L}}<{\mathbb{\Omega }}^{\oplus }={\omega }_{\mu +2}^{\mathbf{L}}$$

were introduced by Definition 2 on page 13. They remain to be fixed until Section 4.5, where their value will be specified in terms of the number $\mathbb{M}\ge 1$ we are dealing with in Theorem 2.

4.1. Systems, Definability Aspects

We argue in $\mathbf{L}$ under the assumptions and notation of Definition 2 on page 13.

In continuation of our notation related to $\mathbb{\Omega }$-systems in Section 3.2, define the following.

• An $\mathbb{\Omega }$-system U is small, if each $U(n,i)$ has cardinality $\le \mathbb{\Omega }$ in $\mathbf{L}$;
• An $\mathbb{\Omega }$-system U is disjoint if $U(n,i)\cap U(k,j)=\varnothing$ whenever $⟨n,i⟩\ne ⟨k,j⟩$;
• If $U,V$ are $\mathbb{\Omega }$-systems and $U(n,i)\subseteq V(n,i)$ for all $n,i$, then V extends U, in symbol $U\preccurlyeq V$;
• If ${\left\{U_{\xi }\right\}}_{\xi <\lambda }$ is a sequence of $\mathbb{\Omega }$-systems then the limit $\mathbb{\Omega }$-system $U={\bigvee }_{\xi <\lambda }{U}_{\xi }$ is defined by $U(n,i)={\bigcup }_{\xi <\lambda }{U}_{\xi }(n,i)$, for all $n,i$.

Let ${\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ (disjoint systems) be the set of all disjoint $\mathbb{\Omega }$-systems, and let ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ (small disjoint systems) be the set of all small disjoint $\mathbb{\Omega }$-systems $U\in {\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$.

Define ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}=\{U\upharpoonright {}^{\ge m}:U\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\}$, and similarly ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{<m}$ etc. by Definition 5.

The sets ${\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$, ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$, ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}$, ${\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{<m}$ etc., and the order relation ≼, belong to $\mathbf{L}$, of course. Recall that, by (5),

$$\mathbb{H}={(\mathbf{H}{\mathbb{\Omega }}^{\oplus })}^{\mathbf{L}}=\{x\in \mathbf{L}:\mathtt{card}(\mathrm{TC}(x))\le \mathbb{\Omega }\mathrm{in}\mathbf{L}\}.$$

Lemma 17

(in $\mathbf{L}$). The following sets belong to ${\Delta }_1^{\mathbb{H}}(\left\{\mathbb{\Omega }\right\})$ and to ${\Delta }_3^{\mathbb{H}}:$ $\left\{\mathbb{\Omega }\right\}$, $\left\{{\mathbf{Seq}}_{\mathbb{\Omega }}\right\}$, ${\mathbf{Fun}}_{\mathbb{\Omega }}$, ${{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$, ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$, ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}$, ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{<m}$, the set $\{⟨U,p⟩:U\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\wedge p\in \mathbf{P}\left[U\right]\}$, the relation ≼.

Proof. 

All these sets have rather straightforward ${\Delta }_1^{\mathbb{H}}(\left\{\mathbb{\Omega }\right\})$ definitions, with $\mathbb{\Omega }\in \mathbb{H}$ as the only parameter. To eliminate $\mathbb{\Omega }$, it suffices to prove that $\left\{\mathbb{\Omega }\right\}\in {\Delta }_3^{\mathbb{H}}$. Note first of all that “$\vartheta$ is a cardinal (initial ordinal)” is a ${\Pi }_1^{}$ formula:

$$\vartheta \in \mathbf{Ord}\wedge \forall \alpha <\vartheta \forall f(f:\alpha \to \vartheta ⟹\mathtt{ran}f\ne \vartheta ).$$

On the other hand, $\mathbb{\Omega }$ is the largest cardinal in $\mathbb{H}$, hence it holds in $\mathbb{H}$ that:

$$\vartheta =\mathbb{\Omega }⟺\forall \varkappa (\varkappa \mathrm{is}\mathrm{a}\mathrm{cardinal}⟹\varkappa \le \mathbb{\Omega }).$$

We conclude that $\left\{\mathbb{\Omega }\right\}\in {\Pi }_2^{\mathbb{H}}\subseteq {\Delta }_3^{\mathbb{H}}$. Finally, the conversion ${\Delta }_1^{\mathbb{H}}(\left\{\mathbb{\Omega }\right\})\to {\Delta }_3^{\mathbb{H}}$ is routine. □

4.2. Complete Sequences

We prove a major theorem (Theorem 6) in this Subsection. It deals with $\preccurlyeq$-increasing transfinite sequences in ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$, satisfying some genericity/definability requirements. This is similar to some constructions in [4] and especially in [5] (Theorem 3). Yet there is a principal difference. Here the notion of extension ≼ is just the componentwise set theoretic extension, unlike [4,5], and originally [23], where the extension method was designed so that increments had to be finitewise Cohen-style generic over associated transitive models of a certain fragment of $\mathbf{ZFC}$. Here the only restriction is that extensions have to obey the disjointness condition as defined in Section 4.1. In other words, if $U\preccurlyeq V$ are $\mathbb{\Omega }$-systems in ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$, then, beside $U(n,i)\subseteq V(n,i)$, the increments $\Delta (n,i)=V(n,i)\setminus U(n,i)$ have to be pairwise disjoint and each $\Delta (n,i)$ to be disjoint with the union ${\bigcup }_{⟨k,j⟩\ne ⟨n,i⟩}U(k,j)$.

Such a simplification is made possible here largely because the definability classes of the form ${\mathbf{D}}_{1m}$ depend only on the highest quantifier order and do not depend on the number and type of the quantifiers involved in the definition of the set considered—unlike e.g., [5], where we dealt with the definability classes ${\Delta }_n^1$, which obviously depend on the number of the quantifiers involved.

We begin with an auxiliary lemma.

Recall that, by (5), $\mathbb{H}={(\mathbf{H}{\mathbb{\Omega }}^{\oplus })}^{\mathbf{L}}=\{x\in \mathbf{L}:\mathtt{card}(\mathrm{TC}(x))\le \mathbb{\Omega }\mathrm{in}\mathbf{L}\}={\mathbf{L}}_{{\mathbb{\Omega }}^{\oplus }}.$

Lemma 18

(in $\mathbf{L}$). Under the assumptions and notation of Definition 2, for any $\alpha <{\mathbb{\Omega }}^{\oplus }$ there exist $m_{\alpha }<\omega$, $t_{\alpha }\in \mathbb{H}$, and $U^{\alpha }\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ such that the sequences ${\left\{m_{\alpha }\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}$, ${\left\{t_{\alpha }\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}$, ${\left\{U^{\alpha }\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}$ belong to ${\Delta }_3^{\mathbb{H}}$ and, if $m<\omega$, $t\in \mathbb{H}$, and ${\left\{U_{\alpha }\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}$ is a $\preccurlyeq$-increasing continuous sequence of $\mathbb{\Omega }$-systems in ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$, then any closed unbounded set $C\subseteq {\mathbb{\Omega }}^{\oplus }$ contains an ordinal $\alpha \in C$ such that $m=m_{\alpha },t=t_{\alpha },U_{\alpha }=U^{\alpha }$.

Proof. 

We argue in $\mathbf{L}$, that is, under the assumption of $\mathbf{V}=\mathbf{L}$, the axiom of constructibility. It is known that the diamond principle ${◊}_{\varkappa }$ holds in $\mathbf{L}$ for any regular cardinal $\varkappa$, in particular, for $\varkappa ={\mathbb{\Omega }}^{\oplus }$, see, e.g., Theorem 13.21 and page 442 in [32]. The principle ${◊}_{\varkappa }$ asserts that there is a sequence ${\left\{S_{\alpha }\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}\in \mathbf{L}$ of sets $S_{\alpha }\subseteq \alpha$, of definability class ${\Delta }_1^{\mathbb{H}}$, and such that:

(*)

If $X\subseteq {\mathbb{\Omega }}^{\oplus }$ and $C\subseteq {\mathbb{\Omega }}^{\oplus }$ is a closed unbounded set then there is $\alpha \in C$ such that $X\cap \alpha =S_{\alpha }$.

Let $h:{\mathbb{\Omega }}^{\oplus }\stackrel{\mathrm{onto}}{⟶}\mathbb{H}$ be any ${\Delta }_1^{\mathbb{H}}$ bijection. Put $Y_{\alpha }=\{h(\xi ):\xi \in S_{\alpha }\}$. Clearly ${\left\{Y_{\alpha }\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}$ is still a ${\Delta }_1^{\mathbb{H}}$ sequence. Moreover the following is true:

(†)

If ${\left\{B_{\alpha }\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}$ is a sequence of sets in $\mathbb{H}$ and $C\subseteq {\mathbb{\Omega }}^{\oplus }$ is a closed unbounded set then there is $\alpha \in C$ with ${\left\{B_{\xi }\right\}}_{\xi <\alpha }=Y_{\alpha }$.

Using the sets $Y_{\alpha }$, we accomplish the proof of the lemma as follows. Assume that $\alpha <{\mathbb{\Omega }}^{\oplus }$. If $Y_{\alpha }$ is a sequence of the form ${\left\{y_{\xi }\right\}}_{\xi <\alpha }$, such that each $y_{\xi }$ is a triple $⟨m,t,U_{\xi }^{\alpha }⟩$, where both $m\in \omega$ and $t\in \mathbb{H}$ do not depend on $\xi$ whereas $U_{\xi }^{\alpha }\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ for each $\xi$ and ${\left\{U_{\xi }^{\alpha }\right\}}_{\xi <\alpha }$ is a $\preccurlyeq$-increasing and continuous sequence, then put $m_{\alpha }=m,t_{\alpha }=t$, and $U^{\alpha }={\bigvee }_{\xi <\alpha }{U}_{\xi }^{\alpha }$. Otherwise put $m_{\alpha }=t_{\alpha }=0$ and let $U^{\alpha }$ be the null $\mathbb{\Omega }$-system, that is, $U^{\alpha }(n,i)=\varnothing$ for all $n,i$. It follows from (†) (plus a routine analysis of definability based on Lemma 17) that this construction leads to the result required. □

Theorem 6

(in $\mathbf{L}$). Under the assumptions and notation of Definition 2, there is a $\preccurlyeq$-increasing sequence ${\left\{{\mathbb{U}}_{\alpha }\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}$ of $\mathbb{\Omega }$-systems in ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$, such that:

(i)

The sequence is continuous, so that ${\mathbb{U}}_{\lambda }={\bigvee }_{\alpha <\lambda }{\mathbb{U}}_{\alpha }$ for all limit ordinals $\lambda <{\mathbb{\Omega }}^{\oplus };$

(ii)

If $n<\omega$ then the “slice” ${\left\{{\mathbb{U}}_{\alpha }\upharpoonright {}^n\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}$ is ${\Delta }_{n+4}^{\mathbb{H}}$;

(iii)

If $m<\omega$ then the “tail” ${\left\{{\mathbb{U}}_{\alpha }\upharpoonright {}^{\ge m}\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}$ is $(m+3)$-complete, in the sense that for any ${\Sigma }_{m+3}^{}(\mathbb{H})$ set $D\subseteq {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}$ there is $\xi <{\mathbb{\Omega }}^{\oplus }$ such that the $\mathbb{\Omega }$-system ${\mathbb{U}}_{\xi }\upharpoonright {}^{\ge m}$$m$-solvesD, i.e.,

-

either ${\mathbb{U}}_{\xi }\upharpoonright {}^{\ge m}\in D;$

-

or there is no $\mathbb{\Omega }$-system $U\in D$ with ${\mathbb{U}}_{\xi }\upharpoonright {}^{\ge m}\preccurlyeq U;$

(iv)

There is a recursive sequence of parameter free $\in$-formulas ${\chi }_n(\alpha ,x)$ such that if $\alpha <{\mathbb{\Omega }}^{\oplus }$ and $x\in \mathbb{H}$ then $\mathbb{H}\models {\chi }_n(\alpha ,x)$ iff $x={\mathbb{U}}_{\alpha }\upharpoonright {}^n$.

Here the “slice” $U\upharpoonright {}^n$ of a system U is essentially equal to the “column” ${\left\{U(n,i)\right\}}_{i<\omega }$ of the whole “matrix” $U={\left\{U(n,i)\right\}}_{n,i<\omega }$, while the “tail” $U\upharpoonright {}^{\ge m}$ can be viewed in the union of all columns to the right of m inclusively, see Definition 5.

Proof. 

We argue in $\mathbf{L}$. One of the difficulties here is that we have to account for different levels of genericity and completeness for different slices of the construction. To cope with this issue, we make use of Lemma 18. Let us fix the sequences of terms $m_{\alpha },t_{\alpha },U^{\alpha }$ such as in the lemma.

Let ${<}_{\mathbf{L}}$ be Gödel’s wellordering of $\mathbf{L}$, as in Section 2.2.

For any $m<\omega$, let ${\Theta }_m\subseteq \mathbb{H}\times \mathbb{H}$ be a fixed universal ${\Sigma }_{m+3}^{\mathbb{H}}$ set, that is, ${\Theta }_m$ itself is ${\Sigma }_{m+3}^{\mathbb{H}}$, and if $X\subseteq \mathbb{H}$ is ${\Sigma }_{m+3}^{}(\mathbb{H})$ (parameters in $\mathbb{H}$ allowed), then there is $t\in \mathbb{H}$ such that $X=\{x:⟨t,x⟩\in {\Theta }_m\}$. If $m<\omega$ and $\alpha <{\mathbb{\Omega }}^{\oplus }$, then let $U^{m\alpha }$ be the ${<}_{\mathbf{L}}$-least $\mathbb{\Omega }$-system in ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ satisfying $U^m\preccurlyeq U^{m\alpha }$ and:

(a)

$U^{m\alpha }\upharpoonright {}^{<m}=U^{\alpha }\upharpoonright {}^{<m}$, and

(b)

The $\mathbb{\Omega }$-system $U^{m\alpha }\upharpoonright {}^{\ge m}$ $m$-solves the set $D_{\alpha }=\{V\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}:⟨t_{\alpha },V⟩\in {\Theta }_m\}$.

Making use of 5° of Section 2.2, we conclude that the sequence ${\left\{U^{m\alpha }\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}$ is ${\Delta }_{m+4}^{\mathbb{H}}$.

Now we define a sequence of $\mathbb{\Omega }$-systems ${\mathbb{U}}_{\xi }$, as required by Theorem 6, by induction.

Put ${\mathbb{U}}_0(n,i)=\varnothing$ for all $n,i$.

If $\lambda <{\mathbb{\Omega }}^{\oplus }$ is the limit then by (i) define ${\mathbb{U}}_{\lambda }={\bigvee }_{\alpha <\lambda }{\mathbb{U}}_{\alpha }$.

Suppose that a $\mathbb{\Omega }$-system ${\mathbb{U}}_{\alpha }$ is defined, and the goal is to define the next one ${\mathbb{U}}_{\alpha +1}$. Fix $n,i$ and define the components ${\mathbb{U}}_{\alpha +1}(n,i)$. Note that this definition will depend on the components ${\mathbb{U}}_{\alpha }(n,i)$ (with the same $n,i$) only, but not on the $\mathbb{\Omega }$-system ${\mathbb{U}}_{\alpha }$ as a whole.

If it is true that:

$$m_{\alpha }\le n\mathrm{and}{\mathbb{U}}_{\alpha }(n,i)=U^{\alpha }(n,i)$$

(7)

(where $U^{\alpha }$ is the $\mathbb{\Omega }$-system given by Lemma 18), then put $m=m_{\alpha }$ and ${\mathbb{U}}_{\alpha +1}(n,i)=U^{m\alpha }(n,i)$. Otherwise, i.e., if (7) fails, just keep it with ${\mathbb{U}}_{\alpha +1}(n,i)={\mathbb{U}}_{\alpha }(n,i)$.

We assert that this inductive construction of $\mathbb{\Omega }$-systems ${\mathbb{U}}_{\alpha }$ leads to Theorem 6.

Requirement (i) of the theorem is satisfied by construction.

The definability requirement (ii) of the theorem is subject to routine verification on the base of Lemma 17, which we leave to the reader.

To prove (iii), fix a number m and a ${\Sigma }_{m+3}^{}(\mathbb{H})$ set $D\subseteq {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}$. We have to find an index $\xi <{\mathbb{\Omega }}^{\oplus }$ such that the $\mathbb{\Omega }$-system ${\mathbb{U}}_{\xi }\upharpoonright {}^{\ge m}$$m$-solves D. There is an element $t\in \mathbb{H}$ satisfying:

$$D=\{V\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}:⟨t,V⟩\in {\Theta }_m\},$$

where ${\Theta }_m$ is the universal set as above. Pick, by Lemma 18, an ordinal $\alpha <{\mathbb{\Omega }}^{\oplus }$ satisfying $m=m_{\alpha },t=t_{\alpha },{\mathbb{U}}_{\alpha }=U^{\alpha }$. Then (7) holds for all $n\ge m$, and hence by definition we have ${\mathbb{U}}_{\alpha +1}\upharpoonright {}^{\ge m}=U^{m\alpha }\upharpoonright {}^{\ge m}$. Therefore the $\mathbb{\Omega }$-system ${\mathbb{U}}_{\alpha +1}\upharpoonright {}^{\ge m}$ $m$-solves the set D by (b), as required.

(iv) Coming back to the choice of universal sets ${\Theta }_m$ in (b), it can be w.l.o.g. assumed that there is a recursive sequence of parameter free $\in$-formulas ${\vartheta }_n(t,x)$ such that each ${\vartheta }_n$ is a ${\Sigma }_{n+3}^{}$ formula and ${\Theta }_m=\{⟨t,x⟩\in \mathbb{H}:\mathbb{H}\models {\vartheta }_n(t,x)\}$. This routinely leads to $\in$-formulas ${\chi }_n(\alpha ,x)$ required. It can be observed that in fact each ${\chi }_n$ is a ${\Sigma }_{n+4}^{}$ formula (not important and will not be used).

This completes the proof of Theorem 6. □

4.3. Preservation of the Completeness

The next lemma says that the completeness property (iii) of Theorem 6, of the sequence ${\left\{{\mathbb{U}}_{\xi }\right\}}_{\xi <{\mathbb{\Omega }}^{\oplus }}$, still holds, to some extent, in rather mild generic extensions of $\mathbf{L}$.

Lemma 19.

Under the assumptions and notation of Definition 2, suppose that ${\left\{{\mathbb{U}}_{\alpha }\right\}}_{\alpha <{\mathbb{\Omega }}^{\oplus }}\in \mathbf{L}$ is a $\preccurlyeq$-increasing sequence of $\mathbb{\Omega }$-systems in ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ satisfying (i)–(iv) of Theorem 6.

Let $Q\in \mathbf{L}$ be a forcing notion with $\mathtt{card}Q\le \mathbb{\Omega }$ in $\mathbf{L}$, e.g., $Q=\mathbb{C}$. Let $F\subseteq Q$ be a set $Q$-generic over $\mathbf{L}$.

Assume that $m<\omega$, $\delta <{\mathbb{\Omega }}^{\oplus }$, and a set $D\in \mathbf{L}\left[F\right]$, $D\subseteq {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}$, belongs to ${\Sigma }_{m+3}^{}(\mathbb{H}\left[F\right])$, and is open in ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}$ so that any extension of a $\mathbb{\Omega }$-system $U\in D$ in ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}$ belongs to D itself.

Then there is an ordinal α, $\delta \le \alpha <{\mathbb{\Omega }}^{\oplus }$, such that ${\mathbb{U}}_{\alpha }\upharpoonright {}^{\ge m}$$m$-solvesD, as in Theorem 6(iii).

We recall that $\mathbb{H}={(\mathbf{H}{\mathbb{\Omega }}^{\oplus })}^{\mathbf{L}}$ and $\mathbb{H}\left[F\right]={(\mathbf{H}{\mathbb{\Omega }}^{\oplus })}^{\mathbf{L}\left[F\right]}$ by (5), (6).

Proof. 

As obviously ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}\subseteq \mathbb{H}$, we conclude by Theorem 5(ii) that there is a ${\Sigma }_{m+3}^{}(\mathbb{H})$ name $t\in \mathbf{L}$, $t\subseteq Q\times \mathbb{H}$, such that $D=t\left[F\right]$.

We argue in $\mathbf{L}$. If $q\in Q$, $U\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}$, and there is such a condition $h\in Q$ that $h⩽q$ (meaning h is stronger) and $⟨h,U⟩\in t$, then write $A(q,U)$. If $b\in Q$ then we define:

$$D(b)=\{U\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge m}:\exists q\in Q(q⩽b\wedge A(q,U))\}.$$

Each of the sets $D(b)\subseteq \mathbb{H}$ belongs to ${\Sigma }_{m+3}^{}(\mathbb{H})$ by virtue of Lemma 17 and the choice of t. Therefore, by the choice of the sequence of $\mathbb{\Omega }$-systems, for every $b\in Q$ there is an ordinal $\alpha (b)$, $\delta <\alpha (b)<{\mathbb{\Omega }}^{\oplus }$, such that the $\mathbb{\Omega }$-system ${\mathbb{U}}_{\alpha (b)}\upharpoonright {}^{\ge m}$ $m$-solves the set $D(b)$.

Note that $\delta ={sup}_{b\in Q}\alpha (b)<{\mathbb{\Omega }}^{\oplus }$ by the cardinality argument.

We claim that the $\mathbb{\Omega }$-system ${\mathbb{U}}_{\delta }\upharpoonright {}^{\ge m}$ $m$-solves D. It suffices to prove that if a $\mathbb{\Omega }$-system $U\in D$ extends ${\mathbb{U}}_{\delta }\upharpoonright {}^{\ge m}$, then the $\mathbb{\Omega }$-system ${\mathbb{U}}_{\delta }\upharpoonright {}^{\ge m}$ itself belongs to D. Moreover, as D is open, it suffices to find $b\in Q$, satisfying ${\mathbb{U}}_{\alpha (b)}\upharpoonright {}^{\ge m}\in D$.

We argue in $\mathbf{L}$. Consider the set $B=\{b\in Q:{\mathbb{U}}_{\alpha (b)}\upharpoonright {}^{\ge m}\in D(b)\}$. If $b\in B$ then pick a particular $q=q(b)\in Q$ such that $q⩽b$ and $A(q,{\mathbb{U}}_{\alpha (b)}\upharpoonright {}^{\ge m})$ holds. If $b\in Q\setminus B$ then put $q(b)=b$. The set $Q^{\prime }=\{q(b):b\in Q\}$ is dense in Q. It follows that there is $b\in Q^{\prime }\cap F$. On the other hand, as $U\in D$, there is a condition $h\in Q$ with $⟨h,U⟩\in t$.

Then there exists some $q\in F$ satisfying $q⩽h$ and $q⩽h(b)⩽b$. This implies $U\in D(b)$. It follows, by the choice of $\alpha (b)$, that ${\mathbb{U}}_{\alpha (b)}\upharpoonright {}^{\ge m}\in D(b)$, too. However then $b\in B$, and hence we have $A(q(b),{\mathbb{U}}_{\alpha (b)}\upharpoonright {}^{\ge m})$. By definition there is a condition $h^{\prime }\in Q$ with $q(b)⩽h^{\prime }$, such that $⟨h^{\prime },{\mathbb{U}}_{\alpha (b)}\upharpoonright {}^{\ge m}⟩\in t.$ However $h^{\prime }\in F$ (since $f(b)\in F$). We conclude that ${\mathbb{U}}_{\delta }\upharpoonright {}^{\ge m}\in D$, as required. □

4.4. Key Definability Engine

We argue under the assumptions and notation of Definition 2 on page 13. In particular, a successor $\mathbf{L}$-cardinal $\mathbb{\Omega }>\omega$ is fixed. We make the following arrangements.

Definition 6

(in $\mathbf{L}$). We fix a $\preccurlyeq$-increasing sequence of $\mathbb{\Omega }$-systems ${\left\{{\mathbb{U}}_{\xi }^{\mathbb{\Omega }}\right\}}_{\xi <{\mathbb{\Omega }}^{\oplus }}$ satisfying conditions (i)–(iv) of Theorem 6 for the particular $\mathbf{L}$-cardinal Ω introduced by Definition 2.

We define the limit $\mathbb{\Omega }$-system ${\mathbb{U}}^{\mathbb{\Omega }}={\bigvee }_{\xi <{\mathbb{\Omega }}^{\oplus }}{\mathbb{U}}_{\xi }^{\mathbb{\Omega }}$, the basic forcing notion ${\mathbb{P}}^{\mathbb{\Omega }}=\mathbf{P}\left[{\mathbb{U}}^{\mathbb{\Omega }}\right]$, and the subforcings ${\mathbb{P}}_{\gamma }^{\mathbb{\Omega }}=\mathbf{P}\left[{\mathbb{U}}_{\gamma }^{\mathbb{\Omega }}\right]$, $\gamma <{\mathbb{\Omega }}^{\oplus }$.

Define restrictions ${\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright z$, $G\upharpoonright z$ ($z\subseteq \mathcal{I}$, $G\subseteq {\mathbb{P}}^{\mathbb{\Omega }}$), ${\mathbb{P}}^{\mathbb{\Omega }}{\upharpoonright }_{\ne ⟨n,i⟩}$ etc. as in Section 3.2.

Thus by construction ${\mathbb{P}}^{\mathbb{\Omega }}\in \mathbf{L}$ is the $\mathbf{L}$-product of sets ${\mathbb{P}}^{\mathbb{\Omega }}(n,i)=P\left[{\mathbb{U}}^{\mathbb{\Omega }}(n,i)\right],n,i\in \omega$. Lemma 14 implies some cardinal characterictics of ${\mathbb{P}}^{\mathbb{\Omega }}$, namely:

(I)

$\mathtt{card}{\mathbb{P}}^{\mathbb{\Omega }}={\mathbb{\Omega }}^{\oplus }$ in $\mathbf{L}$,

(II)

${\mathbb{P}}^{\mathbb{\Omega }}$ satisfies ${\mathbb{\Omega }}^{\oplus }$-CC in $\mathbf{L}$,

(III)

${\mathbb{P}}^{\mathbb{\Omega }}$ is ${\mathbb{\Omega }}^{\ominus }$-closed and ${\mathbb{\Omega }}^{\ominus }$-distributive in $\mathbf{L}$.

Corollary 2.

${\mathbb{P}}^{\mathbb{\Omega }}$ does not adjoin new reals to $\mathbf{L}$.

Proof. 

The result follows from (III) because ${\mathbb{\Omega }}^{\ominus }\ge \omega$ by Definition 2. □

As for definability, the set ${\mathbb{U}}^{\mathbb{\Omega }}$ is not parameter free definable in $\mathbb{H}={(\mathbf{H}{\mathbb{\Omega }}^{\oplus })}^{\mathbf{L}}$, yet its slices are:

Lemma 20

(in $\mathbf{L}$). Let $n<\omega$. Then the set ${\mathbb{U}}^{\mathbb{\Omega }}\upharpoonright {}^n=\{⟨i,f⟩:f\in {\mathbb{U}}^{\mathbb{\Omega }}(n,i)\}$ belongs to ${\Sigma }_{n+4}^{\mathbb{H}}$. In addition there is a recursive sequence of parameter free $\in$-formulas ${\mathit{u}}_n(i,f)$ such that, for any $n<\omega$, if $i<\omega$ and $f\in {\mathbf{Fun}}_{\mathbb{\Omega }}$ then $f\in {\mathbb{U}}^{\mathbb{\Omega }}(n,i)$ iff $\mathbb{H}\models {\mathit{u}}_n(i,f)$.

Proof. 

To prove the first claim, apply (ii) of Theorem 6. To prove the additional claim define:

$${\mathit{u}}_n(i,f):=\exists \alpha \exists x\left({\chi }_n(\alpha ,x)\wedge f\in x(n,i)\right),$$

where ${\chi }_n$ are formulas given by (iv) of Theorem 6. □

We further let formulas ${\mathbb{\Gamma }}_{ni}^{\mathbb{\Omega }}$ ($n,i\in \omega$) be defined as follows:

$${\mathbb{\Gamma }}_{ni}^{\mathbb{\Omega }}(S):{=}_{\mathrm{def}}S\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}\wedge \forall f\in {\mathbf{Fun}}_{\mathbb{\Omega }}\left(f\in {\mathbb{U}}^{\mathbb{\Omega }}(n,i)⟺S\mathrm{does}\mathrm{not}\mathrm{cover}f\right).$$

The next theorem shows that any real in $\mathbf{L}$ and even in some generic extensions of $\mathbf{L}$ can be made parameter free definable in appropriate subextensions of ${\mathbb{P}}^{\mathbb{\Omega }}$-generic extensions, basically by means of the formulas ${\mathbb{\Gamma }}_{ni}^{\mathbb{\Omega }}(S)$. We prove this result in a rather general form, which includes the case of a forcing notion $Q=\mathbb{C}$, actually used in this paper, as just a particular case. The proof of the particular case $Q=\mathbb{C}$ would not be any simpler though.

Theorem 7.

Assume that $Q\in \mathbf{L}$ is a forcing notion, $\mathtt{card}Q\le \mathbb{\Omega }$ in $\mathbf{L}$, a pair $⟨W,G⟩$ is $(Q\times {\mathbb{P}}^{\mathbb{\Omega }})$-generic over $\mathbf{L}$, $Y\in \mathbf{L}\left[W\right]$, and $z\in \mathbf{L}\left[Y\right],z\subseteq \mathcal{I}=\omega \times \omega$. Then,

(i)

${\mathbb{\Omega }}^{\oplus }$ is a cardinal in $\mathbf{L}[Y,G];$

(ii)

If $⟨n,i⟩\in z$ then $S_G(n,i)\in \mathbf{L}\left[G\upharpoonright z\right]$ and ${\mathbb{\Gamma }}_{ni}^{\mathbb{\Omega }}(S_G(n,i))$ holds, but

(iii)

If $⟨n,i⟩\in \mathcal{I}\setminus z$ then $S_G(n,i)\notin \mathbf{L}[Y,G\upharpoonright z];$ and moreover there is no set $S\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}$ in $\mathbf{L}[Y,G\upharpoonright z]$ such that ${\mathbb{\Gamma }}_{ni}^{\mathbb{\Omega }}(S)$.

(iv)

It follows that $z=\{⟨n,i⟩:\exists S\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}{\mathbb{\Gamma }}_{ni}^{\mathbb{\Omega }}(S)\}$ in $\mathbf{L}[Y,G\upharpoonright z];$

(v)

If $n<\omega$ then the $n$-th slice ${(z)}_n=\{i:⟨n,i⟩\in z\}$ belongs to ${\Sigma }_{n+6}^{\mathbb{T}}$, where $\mathbb{T}=\mathbb{H}[Y,G\upharpoonright z]={(\mathbf{H}{\mathbb{\Omega }}^{\oplus })}^{\mathbf{L}[Y,G\upharpoonright z]};$

(vi)

If $1\le \ell <\omega$, ${\mathbb{\Omega }}^{\oplus }={\omega }_{\ell }^{\mathbf{L}[Y,G\upharpoonright z]}$, and GCH holds in $\mathbf{L}[Y,G\upharpoonright z]$ for all cardinals ${\omega }_k,k<\ell -1$, then it holds in $\mathbf{L}[Y,G\upharpoonright z]$ that ${(z)}_n\in {\mathbf{D}}_{1\ell }$ for all $n<\omega ;$

(vii)

Under the assumptions of (vi), it holds in $\mathbf{L}[Y,G\upharpoonright z]$ that the set z as a whole belongs to ${\mathbf{D}}_{1,\ell +1}$.

Proof. 

(i) ${\mathbb{\Omega }}^{\oplus }$ remains a cardinal in $\mathbf{L}\left[G\right]$ by Lemma 15(iv), hence Q still satisfies $\mathtt{card}Q<{\mathbb{\Omega }}^{\oplus }$ in $\mathbf{L}\left[G\right]$. As W is $Q$-generic over $\mathbf{L}\left[G\right]$, ${\mathbb{\Omega }}^{\oplus }$ remains a cardinal in $\mathbf{L}[W,G]$ and in $\mathbf{L}[Y,G]\subseteq \mathbf{L}[W,G]$.

(ii) If $⟨n,i⟩\in z$ then by construction:

$$G(n,i):=\{p(n,i):p\in G\}=\{p^{\prime }(n,i):p^{\prime }\in G\upharpoonright z\}\in \mathbf{L}\left[G\upharpoonright z\right],$$

and hence $S_G(n,i)\in \mathbf{L}\left[G\upharpoonright z\right]$ as well. Now ${\mathbb{\Gamma }}_{ni}^{\mathbb{\Omega }}(S_G(n,i))$ follows from Lemma 15(ii).

(iii) We w.l.o.g. assume that $z=\mathcal{I}\setminus \{⟨n,i⟩\}$ and $Y=W$. Then ${\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright z={\mathbb{P}}^{\mathbb{\Omega }}{\upharpoonright }_{\ne ⟨n,i⟩}$ can be identified with $\{p\in {\mathbb{P}}^{\mathbb{\Omega }}:p(n,i)=⟨\varnothing ,\varnothing ⟩\}$, see Remark 3. Suppose towards the contrary that $S\in \mathbf{L}[W,G{\upharpoonright }_{\ne ⟨n,i⟩}]=\mathbf{L}\left[W\right]\left[G{\upharpoonright }_{\ne ⟨n,i⟩}\right]$ satisfies ${\mathbb{\Gamma }}_{ni}^{\mathbb{\Omega }}(S)$. There is a name $\tau \in \mathbf{L}\left[W\right]$, $\tau \subseteq {\mathbb{P}}^{\mathbb{\Omega }}{\upharpoonright }_{\ne ⟨n,i⟩}\times {\mathbf{Seq}}_{\mathbb{\Omega }}$, such that:

$$S=\tau \left[G{\upharpoonright }_{\ne ⟨n,i⟩}\right]:=\{s\in {\mathbf{Seq}}_{\mathbb{\Omega }}:\exists p\in G{\upharpoonright }_{\ne ⟨n,i⟩}(⟨p,s⟩\in \tau )\}.$$

The forcing ${\mathbb{P}}^{\mathbb{\Omega }}$ remains ${\mathbb{\Omega }}^{\oplus }$-CC in $\mathbf{L}\left[W\right]$ by Lemma 14. This allows us to w.l.o.g. assume that $\mathtt{card}\tau <{\mathbb{\Omega }}^{\oplus }$ in $\mathbf{L}\left[W\right]$, and then $\tau \in \mathbb{H}\left[W\right]={(\mathbf{H}{\mathbb{\Omega }}^{\oplus })}^{\mathbf{L}\left[W\right]}$.

There is a condition $p_0\in G$ which $({\mathbb{P}}^{\mathbb{\Omega }}{\upharpoonright }_{\ne ⟨n,i⟩})$-forces ${\mathbb{\Gamma }}_{ni}(\tau \left[\underline{G}{\upharpoonright }_{\ne ⟨n,i⟩}\right])$ over $\mathbf{L}\left[W\right]$. If $s\in {\mathbf{Seq}}_{\mathbb{\Omega }}$ then put $A_s=\{p:⟨p,s⟩\in \tau \}$; $A_s\subseteq {\mathbb{P}}^{\mathbb{\Omega }}{\upharpoonright }_{\ne ⟨n,i⟩}$.

We argue in $\mathbf{L}$. As $\mathtt{card}\tau <{\mathbb{\Omega }}^{\oplus }$, there is an ordinal $\gamma <{\mathbb{\Omega }}^{\oplus }$ such that $\tau \subseteq ({\mathbb{P}}_{\gamma }^{\mathbb{\Omega }}{\upharpoonright }_{\ne ⟨n,i⟩})\times {\mathbf{Seq}}_{\mathbb{\Omega }}$ and $p_0\in {\mathbb{P}}_{\gamma }^{\mathbb{\Omega }}{\upharpoonright }_{\ne ⟨n,i⟩}$. Consider the set D of all $\mathbb{\Omega }$-systems $U\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ extending ${\mathbb{U}}_{\gamma }^{\mathbb{\Omega }}$ and such that there exists a condition $p^{\prime }\in \mathbf{P}\left[U\right]{\upharpoonright }_{\ne ⟨n,i⟩}$, $p^{\prime }⩽p_0$, an element $f\in U{}^{\complement }(n,i)={\bigcup }_{⟨k,j⟩\ne ⟨n,i⟩}U(k,j)$, and an ordinal $\mu <\mathbb{\Omega }$, such that $p^{\prime }$ contradicts to every $p\in {\bigcup }_{\mu \le \alpha <\mathbb{\Omega }}{A}_{f\upharpoonright \alpha }$. Then D is ${\Delta }_3^{\mathbb{H}}$ by Lemma 17 (and Theorem 5(i), to transfer the definability properties from $\mathbb{H}$ to $\mathbb{H}\left[W\right]$), with $\tau \in \mathbb{H}\left[W\right]$ as a parameter. Therefore, by Lemma 19, there is an ordinal $\eta <{\mathbb{\Omega }}^{\oplus }$ such that the pair ${\mathbb{U}}_{\eta }^{\mathbb{\Omega }}$ $0$-solves D as in Theorem 6(iii). We have two cases.

Case 1: ${\mathbb{U}}_{\eta }^{\mathbb{\Omega }}\in D$. Let this be witnessed by $p^{\prime },f,\mu$ as indicated. Then $f\in ({\mathbb{U}}_{\eta }^{\mathbb{\Omega }}){}^{\complement }(n,i)$, therefore $f\notin {\mathbb{U}}^{\mathbb{\Omega }}(n,i)$. By definition ${\mathbb{U}}_{\gamma }^{\mathbb{\Omega }}\preccurlyeq {\mathbb{U}}_{\eta }^{\mathbb{\Omega }}$, hence $\gamma \le \eta$. Furthermore, if $s=f\upharpoonright \xi$, $\mu \le \xi <{\omega }_1$, then the condition $p^{\prime }$ $({\mathbb{P}}^{\mathbb{\Omega }}{\upharpoonright }_{\ne ⟨n,i⟩})$-forces $s\notin \tau \left[\underline{G}{\upharpoonright }_{\ne ⟨n,i⟩}\right]$ over $\mathbf{L}\left[W\right]$. We conclude that $p^{\prime }$ forces $\tau \left[\underline{G}\right]/f<\mu <\mathbb{\Omega }$ over $\mathbf{L}\left[W\right]$. Note that $p_0$ forces $\tau \left[\underline{G}{\upharpoonright }_{\ne ⟨n,i⟩}\right]/f=\mathbb{\Omega }$ because $f\notin \mathbb{U}(n,i)$. However $p^{\prime }⩽p_0$. This is a contradiction.

Case 2: There is no $\mathbb{\Omega }$-system $U\in D$ extending ${\mathbb{U}}_{\eta }^{\mathbb{\Omega }}$. We can assume that $\gamma \le \eta$, since if $\eta <\gamma$ then the $\mathbb{\Omega }$-system ${\mathbb{U}}_{\gamma }^{\mathbb{\Omega }}$ has the same property. Easily there exists $\delta ,\eta <\delta <{\omega }_1$, such that ${\mathbb{U}}_{\delta }^{\mathbb{\Omega }}(n,i)\setminus {\mathbb{U}}_{\eta }^{\mathbb{\Omega }}(n,i)\ne \varnothing$. (To prove this claim note that the set $D^{\prime }$ of all $\mathbb{\Omega }$-systems $U\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ satisfying $U(n,i)\setminus {\mathbb{U}}_{\eta }^{\mathbb{\Omega }}(n,i)\ne \varnothing$ is dense in ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ therefore, any U that $0$-solves $D^{\prime }$ belongs to $D^{\prime }$.)

Take any $f\in {\mathbb{U}}_{\delta }^{\mathbb{\Omega }}(n,i)\setminus {\mathbb{U}}_{\eta }^{\mathbb{\Omega }}(n,i)$. Then $f\in {\mathbb{U}}^{\mathbb{\Omega }}(n,i)$, and hence $p_0$ forces $\tau \left[\underline{G}\right]/f<\mathbb{\Omega }$ over $\mathbf{L}\left[W\right]$ by the choice of $p_0$. It follows that there exists a condition $p^{\prime }\in {\mathbb{P}}^{\mathbb{\Omega }}{\upharpoonright }_{\ne ⟨n,i⟩}$, $p^{\prime }⩽p_0$, and an ordinal $\mu <{\omega }_1$, such that for any $\alpha \ge \mu$, $p^{\prime }$ forces $s\notin \tau \left[\underline{G}{\upharpoonright }_{\ne ⟨n,i⟩}\right]$ over $\mathbf{L}\left[W\right]$, where $s=f\upharpoonright \alpha$. Thus $p^{\prime }$ contradicts to each condition $p\in {\bigcup }_{\mu \le \alpha <\mathbb{\Omega }}{A}_{f\upharpoonright \alpha }$. We may w.l.o.g. assume that $p^{\prime }\in {\mathbb{P}}_{\delta }^{\mathbb{\Omega }}{\upharpoonright }_{\ne ⟨n,i⟩}$ (otherwise increase $\delta$ appropriately). Under these assumptions, define a $\mathbb{\Omega }$-system U so that:

$$U(n,i)={\mathbb{U}}_{\delta }^{\mathbb{\Omega }}(n,i)\setminus \left\{f\right\},U(n,i+1)={\mathbb{U}}_{\delta }^{\mathbb{\Omega }}(n,i+1)\cup \left\{f\right\},$$

and $U(k,j)={\mathbb{U}}_{\delta }^{\mathbb{\Omega }}(k,j)$ for all pairs of indices $⟨k,j⟩$ other than $⟨n,i⟩$ and $⟨n,i+1⟩$. Obviously U extends ${\mathbb{U}}_{\eta }^{\mathbb{\Omega }}$, and $p^{\prime }\in \mathbf{P}\left[U\right]$. Therefore $U\in D$. But this contradicts the Case 2 hypothesis.

Claim (iv) is an immediate corollary of (ii) and (iii).

To prove (v), note that (*) ${(z)}_n=\{i:\exists S\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}{\mathbb{\Gamma }}_{ni}^{\mathbb{\Omega }}(S)\}$ by (iv). However with n fixed the relation $f\in {\mathbb{U}}^{\mathbb{\Omega }}(n,i)$ with $i,f$ as arguments is ${\Sigma }_{n+4}^{\mathbb{H}}$ by Lemma 20, hence ${\Sigma }_{n+4}^{\mathbb{T}}$ by Theorem 5(i). Now ${(z)}_n\in {\Sigma }_{n+6}^{\mathbb{T}}$ follows by (*).

To prove (vi), make use of (v) and Theorem 3.

Let us finally prove (vii). Detalizing the proof of (v) and (vi) on the base of formulas ${\mathit{u}}_n(f,i)$ of Lemma 20, we obtain a recursive sequence of parameter free $\in$-formulas ${\phi }_n(i)$ such that if $n,i<\omega$ then $i\in {(z)}_n$ iff $\mathbb{T}\models {\phi }_n(i)$. The proof of Theorem 3 is obviously effective enough to obtain another recursive sequence of parameter free type-theoretic formulas ${\psi }_n(i)$ of order $\le \ell$ such that it holds in $\mathbf{L}[Y,G\upharpoonright z]$ that: $i\in {(z)}_n$ iff ${\psi }_n(i)$, that is, $z=\left\{⟨n,i⟩:{\psi }_n(i)\right\}$.

However it is known that the truth of formulas of order $\le \ell$ can be uniformly expressed by a suitable formula of order $\ell +1$, see e.g., [18]. In other words, there is a parameter free type theoretic formula $\Psi (n,i)$ of order $\le \ell +1$ such that it holds in $\mathbf{L}[Y,G\upharpoonright z]$ that: $i\in {(z)}_n$ iff $\Psi (n,i)$, that is, $z=\{⟨n,i⟩:\Psi (n,i)\}$. We conclude that z is definable in $\mathbf{L}[Y,G\upharpoonright z]$ by a type-theoretic formula of order $\le \ell +1$. In other words, $z\in {\mathbf{D}}_{1,\ell +1}$ in $\mathbf{L}[Y,G\upharpoonright z]$, as required. □

4.5. We Specify $\mathbb{\Omega }$

We come back to Theorem 2. Now it is time to specify the value of the $\mathbf{L}$-cardinal $\mathbb{\Omega }$, so far left rather arbitrary by Definition 2 on page 13.

Definition 7

(in $\mathbf{L}$). Recall that $1\le \mathbb{M}<\omega$ is a number considered in Theorem 2.

We let $\mathbb{\Omega }={\omega }_{\mathbb{M}}^{\mathbf{L}}$, and accordingly define ${\mathbb{\Omega }}^{\ominus }={\omega }_{\mathbb{M}-1}^{\mathbf{L}}$, ${\mathbb{\Omega }}^{\oplus }={\omega }_{\mathbb{M}+1}^{\mathbf{L}}$,

$$\mathbb{H}={(\mathbf{H}{\mathbb{\Omega }}^{\oplus })}^{\mathbf{L}}={(\mathbf{H}{\omega }_{\mathbb{M}+1}^{\mathbf{L}})}^{\mathbf{L}}=\{x\in \mathbf{L}:\mathtt{card}(\mathrm{TC}(x))<{\omega }_{\mathbb{M}+1}^{\mathbf{L}}\mathrm{in}\mathbf{L}\}$$

by Definition 2. Applying Definition 6 with $\mathbb{\Omega }={\omega }_{\mathbb{M}}^{\mathbf{L}}$, we accordingly fix:

-

A $\preccurlyeq$-increasing sequence of $\mathbb{\Omega }$-systems ${\left\{{\mathbb{U}}_{\xi }^{\mathbb{\Omega }}\right\}}_{\xi <{\mathbb{\Omega }}^{\oplus }}$ satisfying (i), (ii), (iii), (iv) of Theorem 6 for the chosen $\mathbf{L}$-cardinal $\mathbb{\Omega }={\omega }_{\mathbb{M}}^{\mathbf{L}}$,

-

The limit $\mathbb{\Omega }$-system ${\mathbb{U}}^{\mathbb{\Omega }}={\bigvee }_{\xi <{\mathbb{\Omega }}^{\oplus }}{\mathbb{U}}_{\xi }^{\mathbb{\Omega }}$,

-

The basic forcing notion ${\mathbb{P}}^{\mathbb{\Omega }}=\mathbf{P}\left[{\mathbb{U}}^{\mathbb{\Omega }}\right]$, and the subforcings ${\mathbb{P}}_{\gamma }^{\mathbb{\Omega }}=\mathbf{P}\left[{\mathbb{U}}_{\gamma }^{\mathbb{\Omega }}\right]$, $\gamma <{\mathbb{\Omega }}^{\oplus }$,

and define restrictions ${\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright z$ ($z\subseteq \mathcal{I}$), ${\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright {}^{\ge n}$, ${\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright {}^{<n}$, ${\mathbb{P}}^{\mathbb{\Omega }}{\upharpoonright }_{\ne ⟨n,i⟩}$ etc. as in Section 3.2.

4.6. The Model

To prove Theorem 2 we make use of a certain submodel of a $(\mathbb{C}\times {\mathbb{P}}^{\mathbb{\Omega }})$-generic extension of $\mathbf{L}$. First of all, if $g:\omega \to \mathcal{P}(\omega )$ is any function then we put:

$$\mathit{w}\left[g\right]=\{⟨k,j⟩:k<\omega \wedge j\in g(k)\}.$$

(8)

Now consider a pair $⟨\zeta ,G⟩$, $(\mathbb{C}\times {\mathbb{P}}^{\mathbb{\Omega }})$-generic over $\mathbf{L}$. Thus $\zeta :\omega \stackrel{\mathrm{onto}}{⟶}\Xi$ is a generic collapse function, while the set $G\subseteq {\mathbb{P}}^{\mathbb{\Omega }}$ is ${\mathbb{P}}^{\mathbb{\Omega }}$-generic over $\mathbf{L}\left[\zeta \right]$. The set:

$$\mathit{w}\left[\zeta \right]=\{⟨k,j⟩:k<\omega \wedge j\in \zeta (k)\}\subseteq \mathcal{I}=\omega \times \omega$$

(9)

obviously belongs to the model $\mathbf{L}\left[\zeta \right]=\mathbf{L}\left[\mathit{w}\right[\zeta \left]\right]$, but not to $\mathbf{L}$. Therefore the restrictions ${\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{w}\left[\zeta \right]$, $G\upharpoonright \mathit{w}\left[\zeta \right]$ in the next theorem have to be understood in the sense of Definition 5 on page 15, ignoring Remark 3 since, definitely $\mathit{w}\left[\zeta \right]\notin \mathbf{L}$. Thus ${\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{w}\left[\zeta \right]$ is a forcing notion in $\mathbf{L}\left[\zeta \right]$, not in $\mathbf{L}$.

The following theorem describes the structure of such generic models.

Theorem 8.

Under the assumptions of Definition 7, let a pair $⟨\zeta ,G⟩$ be $(\mathbb{C}\times {\mathbb{P}}^{\mathbb{\Omega }})$-generic over $\mathbf{L}$. Then:

(i)

$G\upharpoonright \mathit{w}\left[\zeta \right]$ is a set $({\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{w}\left[\zeta \right])$-generic over $\mathbf{L}\left[\zeta \right]$,

(ii)

${\omega }_{\gamma }^{\mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]}={\omega }_{1+\gamma }^{\mathbf{L}}$ for all ordinals $\gamma \ge 1$, in particular, ${\mathbb{\Omega }}^{\oplus }={\omega }_{\mathbb{M}}^{\mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]};$

and it is true in the model $\mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]$ that

(iii)

If $\mathbb{M}\ge 2$ then $\mathbb{\Omega }={\omega }_{\mathbb{M}-1}$ and ${\mathbb{\Omega }}^{\oplus }={\mathbb{\Omega }}^{+}={\omega }_{\mathbb{M}}$, whereas if $\mathbb{M}=1$ then $\omega <\mathbb{\Omega }={\mathbb{\Omega }}^{\oplus }={\omega }_1;$

(iv)

GCH holds;

(v)

Every constructible real belongs to ${\mathbf{D}}_{1\mathbb{M}}$,

(vi)

If $1\le m<\omega$ and $m\ne \mathbb{M}$ then ${\mathbf{D}}_{1m}\notin {\mathbf{D}}_{2m}$, and

(vii)

every real in ${\mathbf{D}}_{1\mathbb{M}}$ is constructible.

Remark 4.

Theorem 8 implies Theorem 2 via the model $\mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]$, of course. As for Theorem 8 itself, its proof follows below in this paper. Claims (i)–(vi) will be established right now, and Claim (vii) is accomplished in Section 6.6, based on the substantial work in Section 5 and Section 6.

Proof 

(Claims (i)–(vi) of Theorem 8). To prove that $G\upharpoonright \mathit{w}\left[\zeta \right]$ is $({\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{w}\left[\zeta \right])$-generic over $\mathbf{L}\left[\zeta \right]$, note that $G\subseteq {\mathbb{P}}^{\mathbb{\Omega }}$ is ${\mathbb{P}}^{\mathbb{\Omega }}$-generic over $\mathbf{L}\left[\zeta \right]$ by the product forcing theorem w.r.t. the product $\mathbb{C}\times {\mathbb{P}}^{\mathbb{\Omega }}$. However ${\mathbb{P}}^{\mathbb{\Omega }}$ can be naturally identified with the product $({\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{w}\left[\zeta \right])\times ({\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright z)$ in $\mathbf{L}\left[\zeta \right]$, where $z=\mathcal{I}\setminus \mathit{w}\left[\zeta \right]$. This implies the result by another application of the product forcing theorem.

To establish (ii), (iii), and (iv), it suffices to apply Lemma 16, as $\mathbf{L}\left[\zeta \right]\subseteq \mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]\subseteq \mathbf{L}[\zeta ,G]$.

To prove Claim (v), let $x\in \mathbf{L},x\subseteq \omega$. By the genericity of $\zeta$, there is a number $n_0<\omega$ such that $x=\zeta (n_0)$. Then, for any i, we have $⟨n_0,i⟩\in \mathit{w}\left[\zeta \right]$ iff $i\in x$. By Theorem 7(vi) (with $Q=\mathbb{C}$, $z=\mathit{w}\left[\zeta \right]$, $Y=\zeta$, $\ell =\mathbb{M}$), it is true in $\mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]$ that x belongs to ${\mathbf{D}}_{1\mathbb{M}}$, as required.

To prove Claim (vi), assume that $1\le m<\omega$ and $m\ne \mathbb{M}$; we have to show that ${\mathbf{D}}_{1m}\notin {\mathbf{D}}_{2m}$ in $\mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]$. We have two cases.

Case 1: $m>\mathbb{M}$. Consider the set $z=\mathit{w}\left[\zeta \right]$ defined by (9) in Section 4.6. By definition $z\subseteq \omega \times \omega$, $z\in \mathbf{L}\left[\zeta \right]$. It follows from Theorem 7(vii) (with $Q=\mathbb{C}$, $z=\mathit{w}\left[\zeta \right]$, $Y=\zeta$, $\ell =\mathbb{M}$), that $z\in {\mathbf{D}}_{1,\mathbb{M}+1}$, hence $z\in {\mathbf{D}}_{1,\mathbb{M}+1}$ as $\mathbb{M}+1\le m$. Now suppose to the contrary that ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ in $\mathbf{L}[\zeta ,G\upharpoonright z]$. As ${\omega }_1^{\mathbf{L}\left[z\right]}={\omega }_1^{\mathbf{L}[\zeta ,G\upharpoonright z]}={\omega }_2^{\mathbf{L}}$, there exist real $x\in \mathbf{L}\left[z\right]$, $x\subseteq \omega$, which do not belong to ${\mathbf{D}}_{1m}$; let $x_0$ be the least of them in the sense of the Gödel well ordering of $\mathbf{L}\left[z\right]$. Then $x_0$ itself belongs to ${\mathbf{D}}_{1m}$ by 5° of Section 2.2, since so does z by the above, which is a contradiction.

Case 2: $1\le m<\mathbb{M}$. It suffices to apply Lemma 2 on page 8 because $m<\mathbb{M}$ and ${\mathbf{D}}_{1\mathbb{M}}=\mathcal{P}(\omega )\cap \mathbf{L}$ holds in $\mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]$ by Claims (v) and (vii). We may note that this short argument refers to Claim (vii) that will be conclusively established only in Section 6.6.

An independent proof is as follows. If $1\le m<\mathbb{M}$, then $\mathbb{M}\ge 2$, and hence Theorem 8(iii) implies:

$${\mathcal{P}}^m(\omega )\cap \mathbf{L}\left[\zeta \right]={\mathcal{P}}^m(\omega )\cap \mathbf{L}[\zeta ,G\upharpoonright w]={\mathcal{P}}^m(\omega )\cap \mathbf{L}[\zeta ,G].$$

We conclude that the sets ${\mathbf{D}}_{1m}$ and ${\mathbf{D}}_{2m}$ are the same in these models, and hence it suffices to prove that ${\mathbf{D}}_{1m}\notin {\mathbf{D}}_{2m}$ in the $\mathbb{C}$-generic extension $\mathbf{L}\left[\zeta \right]$. Now we apply the fact that collapse forcing notions similar to $\mathbb{C}$ are homogeneous enough for any parameter free formula either be forced by every condition, or be negated by every condition. In our case, it follows that ${({\mathbf{D}}_{1m})}^{\mathbf{L}\left[\zeta \right]}\in \mathbf{L}$ and ${({\mathbf{D}}_{1m})}^{\mathbf{L}\left[\zeta \right]}$ is countable in $\mathbf{L}$. Therefore if, to the contrary, ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ in $\mathbf{L}\left[\zeta \right]$, then taking the Gödel-least $x\in (\mathcal{P}(\omega )\cap \mathbf{L})\setminus {\mathbf{D}}_{1m}$ in $\mathbf{L}\left[\zeta \right]$, we routinely get $x\in {\mathbf{D}}_{1m}$ in $\mathbf{L}\left[\zeta \right]$ via 5° of Section 2.2, with a contradiction.

This completes the proof of Claims (i)–(vi) of Theorem 8. □

5. Forcing Approximation

We argue under the assumptions and notation of Definition 7 on page 22.

Beginning here a lengthy proof of Claim (vii) of Theorem 8, our plan will be to establish the following, somewhat unexpected result. Recall that, by Theorem 8(ii), it is true in $\mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]$ that $\mathbb{\Omega }={\omega }_{\mathbb{M}-1}$ and ${\mathbb{\Omega }}^{\oplus }={\mathbb{\Omega }}^{+}={\omega }_{\mathbb{M}}$ in case $\mathbb{M}\ge 2$, whereas $\omega <\mathbb{\Omega }={\mathbb{\Omega }}^{\oplus }={\omega }_1$ in case $\mathbb{M}=1$.

Theorem 9.

Assume that a pair $⟨\zeta ,G⟩$ is $(\mathbb{C}\times {\mathbb{P}}^{\mathbb{\Omega }})$-generic over $\mathbf{L}$, and $a\in \mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]$, $a\subseteq \omega$, and it is true in $\mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]$ that:

either 

$\mathbb{M}\ge 2$ and a is $\in$-definable in $⟨\mathcal{P}(\mathbb{\Omega });\in ,\mathrm{𝕡}⟩$ (see Section 2.4);

or 

$\mathbb{M}=1$ and a is $\in$-definable in $⟨\mathcal{P}(\omega );\in ⟩$.

Then $a\in \mathbf{L}\left[G\right]$.

Remark 5.

Theorem 9 implies Claim (vii) of Theorem 8.

Indeed, arguing in $\mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]$, suppose that $a\subseteq \omega$, $a\in {\mathbf{D}}_{1\mathbb{M}}$. If $\mathbb{M}=1$ then we immediately have the “or” case of Theorem 9. Thus suppose that $\mathbb{M}\ge 2$. Theorem 3 is applicable by Theorem 8(iv), therefore x is $\in$-definable in $\mathbf{H}{\omega }_{\mathbb{M}}$, that is, in $\mathbf{H}{\mathbb{\Omega }}^{\oplus }$ by Theorem 8(iii). Then Theorem 4 is applicable as well, and hence we have the “either” case of Theorem 9. We conclude that $a\in \mathbf{L}\left[G\right]$ by Theorem 9. However, by Lemma 14, the forcing notion $\mathbb{P}$ is ${\mathbb{\Omega }}^{\ominus }$-closed in $\mathbf{L}$, and this property is sufficient for $\mathbb{P}$-generic sets not to add new subsets of ω, so $a\in \mathbf{L}$, as required by (vii) of Theorem 8.

Thus Theorem 9 completes the proof of Theorem 8 as a whole because other claims of Theorem 8 have been already established, see Section 4.6.

To prove Theorem 9, we are going to define a forcing-like relation ${}^{}\mathrm{forc}{}_{}^{}$ similar to approximate forcing relations considered in [4,5], and earlier in [3] and some other papers on the base of forcing notions not of an almost-disjoint type. Then we exploit certain symmetries of objects related to ${}^{}\mathrm{forc}{}_{}^{}$.

Definition 8.

Extending Definition 7 on page 22, let us fix a pair $⟨\zeta ,\mathbf{G}⟩$, $(\mathbb{C}\times {\mathbb{P}}^{\mathbb{\Omega }})$-generic over $\mathbf{L}$ for the remainder of the text. We consider generic extensions:

$$\mathbf{L}\left[\zeta \right]\subseteq \mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{w}\left[\zeta \right]]\subseteq \mathbf{L}[\zeta ,\mathbf{G}].$$

We shall assume that $\mathbb{M}\ge 2$ (the “either” case of Theorem 9). The “or” case $\mathbb{M}=1$ is pretty similar: Ω is changed to ω during the course of the proof.

5.1. Language

We argue under the assumptions and notation of Definitions 7 and 8.

• Assume that $z\in \mathbf{L}\left[\zeta \right]$, $z\subseteq \mathcal{I}=\omega \times \omega$. Then let ${\mathbf{Nam}}_{\zeta }^z\in \mathbf{L}\left[\zeta \right]$ be the set of all sets $\tau \in \mathbf{L}\left[\zeta \right]$, $\tau \subseteq ({{}^{*}\mathbf{P}}_{\mathbb{\Omega }}\upharpoonright z)\times \mathbb{\Omega }$, with $\mathtt{card}\tau <{\mathbb{\Omega }}^{\oplus }$ in $\mathbf{L}\left[\zeta \right]$.

Note that ${{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$, a bigger forcing notion, is used instead of ${\mathbb{P}}^{\mathbb{\Omega }}$ in this definition. One of the advantages is that ${{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ is $\in$-definable in $\mathbb{H}$ by Lemma 17.

If $\tau \in {\mathbf{Nam}}_{\zeta }^z$ and $G\subseteq {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}\upharpoonright z$ then put $\tau \left[G\right]=\{\alpha <\mathbb{\Omega }:\exists p\in G(⟨p,\alpha ⟩\in \tau )\}$.

Lemma 21.

$\mathcal{P}(\mathbb{\Omega })\cap \mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]=\{\tau \left[\mathbf{G}\upharpoonright \mathit{w}\right[\zeta \left]\right]:\tau \in {\mathbf{Nam}}_{\zeta }^{\mathit{w}\left[\zeta \right]}\}$.

Proof. 

Let $X\in \mathbf{L}[\zeta ,G\upharpoonright \mathit{w}\left[\zeta \right]]$, $X\subseteq \mathbb{\Omega }$. The set $\mathbf{G}\upharpoonright \mathit{w}\left[\zeta \right]$ is $({\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{w}\left[\zeta \right])$-generic over $\mathbf{L}\left[\zeta \right]$ by the product forcing theory. Therefore, by a well-known property of generic extensions (see, e.g., [32]), there is a name $t\in \mathbf{L}\left[\zeta \right]$, $t\subseteq ({\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{w}\left[\zeta \right])\times \mathbb{\Omega }$, such that $X=t\left[\mathbf{G}\upharpoonright \mathit{w}\right[\zeta \left]\right]$. To reduce t to a name $\tau$ with the same property, satisfying $\mathtt{card}\tau <{\mathbb{\Omega }}^{\oplus }$, apply Lemma 14. □

Now, arguing in $\mathbf{L}\left[\zeta \right]$, we introduce a language that will help us to study analytic definability in the generic extensions considered. We argue under the assumptions and notation of Definition 8.

Let $\mathcal{L}$ be the 2nd order language, with variables $\alpha ,\beta ,\dots$, assumed to vary over ordinals $<\mathbb{\Omega }$, and $X,Y,\dots$, varying over the subsets of $\mathbb{\Omega }$. Atomic formulas of the following types are allowed:

$$\alpha <\beta ,\alpha =\beta ,\alpha \in X,\mathrm{𝕡}(\alpha ,\beta )=\gamma .$$

(See Section 2.4 on 𝕡.) Only the connectives ∧ and ¬ and quantifiers $\exists \alpha$ and $\exists X$ are allowed, the other connectives and $\forall$ are treated as shortcuts, and, to reduce the number of cases, the equality $X=Y$ will be treated as a shortcut for $\forall \alpha (\alpha \in X⟺\alpha \in Y)$.

The complexity $\#(\phi )$ of an $\mathcal{L}$-formula $\phi$ is defined by induction so that:

• $\#(\phi )=0$ for all atomic formulas,
• $\#(\phi \wedge \psi )=max\{\#(\phi ),\#(\psi )\}$,
• $\#(\exists \alpha \phi (\alpha ))=\#(\phi (\alpha ))$ and $\#(\exists X\phi (X))=\#(\phi (X))$,
• Finally, $\#(\neg \phi )=\#(\phi )+1$.

Note that the complexity of quantifier-free formulas can be as high as one wants.

If $z\in \mathbf{L}\left[\zeta \right]$, $z\subseteq \omega \times \omega$, then let $\mathcal{L}(z)$ be the extension of $\mathcal{L}$ by:

-

Ordinals $\alpha <\mathbb{\Omega }$ to substitute variables over $\mathbb{\Omega }$,

-

Names in ${\mathbf{Nam}}_{\zeta }^z$ to substitute variables $X,Y,\dots$ over $\mathcal{P}(\mathbb{\Omega })$.

If $G\subseteq {{}^{*}\mathbf{P}}_{\mathbb{M}}\upharpoonright z$, then the valuation $\phi \left[G\right]$ of such a formula $\phi$ is defined by substitution of $\tau \left[G\right]$ for any name $\tau \in {\mathbf{Nam}}_{\zeta }^z$ that occurs in $\phi$, and relativizing each quantifier $\exists \alpha$ or $\exists X$ to resp. $\mathbb{\Omega }$, $\mathcal{P}(\mathbb{\Omega })$. Thus $\phi \left[G\right]$ is a formula of $\mathcal{L}$ with parameters in $\mathcal{P}(\mathbb{\Omega })\cap \mathbf{L}[\zeta ,G]$ and quantifiers relativized as above, that is, to $\mathbb{\Omega }$ and to $\mathcal{P}(\mathbb{\Omega })$, and $\phi \left[G\right]$ can contain 𝕡 interpreted as $\mathrm{𝕡}\upharpoonright (\mathbb{\Omega }\times \mathbb{\Omega })$. (See Section 2.4 on 𝕡.)

5.2. Forcing Approximation

We still argue under the assumptions and notation of Definitions 7 and 8.

Our next goal is to define, in $\mathbf{L}\left[\zeta \right]$, a forcing-style relation $p {\mathbf{forc}}_U^z\phi$. In case $z=\mathit{w}\left[\zeta \right]$ and $U={\mathbb{U}}^{\mathbb{\Omega }}$, the relation ${\mathbf{forc}}_U^z$ will be compatible with the truth in the model $\mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{w}\left[\zeta \right]]=\mathbf{L}\left[\zeta \right]\left[\mathbf{G}\upharpoonright \mathit{w}\right[\zeta \left]\right]$, viewed as a $({\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{w}\left[\zeta \right])$-generic extension of $\mathbf{L}\left[\zeta \right]$. But, perhaps unlike the true forcing relation associated with ${\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{w}\left[\zeta \right]$, the relation ${\mathbf{forc}}_U^z$ will be invariant under certain transformations.

The definition goes on in $\mathbf{L}\left[\zeta \right]$ by induction on the complexity of $\phi$.

(F1)

When writing $p {\mathbf{forc}}_U^z\phi$, it will always be assumed that $U\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$, $z\in \mathbf{L}\left[\zeta \right]$, $z\subseteq \omega \times \omega$, $p\in \mathbf{P}\left[U\right]\upharpoonright z$, $\phi$ is a closed formula in ${\mathcal{L}}_z$.

(F2)

If $U\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$, $z\in \mathbf{L}\left[\zeta \right]$, $z\subseteq \omega \times \omega$, $p\in \mathbf{P}\left[U\right]\upharpoonright z$, and $\alpha ,\beta ,\gamma <\mathbb{\Omega }$, then: $p {\mathbf{forc}}_U^z\alpha +\beta =\gamma$ iff in fact $x^0+y^0=z^0$, and the same for the formulas $\alpha +\beta =\gamma$ and $\mathrm{𝕡}(\alpha ,\beta )=\gamma$.

(F3)

If $U,p,z$ are as above, $\alpha <\mathbb{\Omega }$, $Y\in {\mathbf{Nam}}_{\zeta }^z$, then: $p {\mathbf{forc}}_U^z\alpha \in Y$ iff there exists a condition $q\in \mathbf{P}\left[U\right]\upharpoonright z$ such that $⟨q,\alpha ⟩\in Y$ and $p⩽q$.

(F4)

If $U,p,z$ are as above, then: $p {\mathbf{forc}}_U^z(\phi \wedge \psi )$ iff $p {\mathbf{forc}}_U^z\phi$ and $p {\mathbf{forc}}_U^z\psi$.

(F5)

If $U,p,z$ are as above, then $p {\mathbf{forc}}_U^z\exists \alpha \phi (\alpha )$ iff there is $\alpha <\mathbb{\Omega }$ such that $p {\mathbf{forc}}_U^z\phi (\alpha )$.

(F6)

If $U,p,z$ are as above, then $p {\mathbf{forc}}_U^z\exists Y\phi (Y)$ iff there exists a name $\tau \in {\mathbf{Nam}}_{\zeta }^z$ such that $p {\mathbf{forc}}_U^z\phi (Y)$.

We precede the last item with another definition. If $n<\omega$ then let $\mathbf{s}\mathbf{D}\mathbf{S}\left[n\right]$ be the set of all $\mathbb{\Omega }$-systems $U\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ such that $U\upharpoonright {}^{<n}={\mathbb{U}}_{\xi }^{\mathbb{\Omega }}\upharpoonright {}^{<n}$ for some $\xi <{\mathbb{\Omega }}^{\oplus }$. Thus $\mathbf{s}\mathbf{D}\mathbf{S}={\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$.

(F8)

If $U,p,z$ are as in (F1), $\phi$ is a closed ${\mathcal{L}}_z$ formula, $n=\#(\phi )$, then $p {\mathbf{forc}}_U^z\neg \phi$ iff there is no $\mathbb{\Omega }$-system $U^{\prime }\in \mathbf{s}\mathbf{D}\mathbf{S}\left[n\right]$ extending U, and no $q\in \mathbf{P}\left[U^{\prime }\right]\upharpoonright z$, $q⩽p$, such that $q {\mathbf{forc}}_{U^{\prime }}^z\phi$.

Lemma 22

(in $\mathbf{L}\left[\zeta \right]$). Let $U,p,z,\phi$ satisfy (F1) above. Then:

(i)

If $p {\mathbf{forc}}_U^z\phi$, $U^{\prime }\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ extends U, and $q\in \mathbf{P}\left[U^{\prime }\right]\upharpoonright z,q⩽p$, then $q {\mathbf{forc}}_{U^{\prime }}^z\phi$;

(ii)

If $U\in \mathbf{s}\mathbf{D}\mathbf{S}\left[n\right]$, $\#(\phi )\le n$, and $p {\mathbf{forc}}_U^z\phi$, then $p {\mathbf{forc}}_U^z\neg \phi$ fails.

Proof. 

The proof of (i) by straightforward induction is elementary. As for (ii), make use of (F8). □

Now let us evaluate the complexity of the relation ${\mathbf{forc}}_{}^{}$. Given a parameter free $\mathcal{L}$-formula $\phi (\alpha ,\beta ,\dots ,X,Y,\dots )$ with any set of free variables allowed in $\mathcal{L}$, we define, in $\mathbf{L}\left[\zeta \right]$, the set:

$$\begin{array}{ccc}\mathbf{Forc}(\phi )\hfill & =& \{⟨z,U,p,\alpha ,\beta ,\dots ,{\tau }_X,{\tau }_Y,\dots ⟩:U\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\wedge z\subseteq \omega \times \omega \hfill \\ & & \wedge p\in \mathbf{P}\left[U\right]\upharpoonright z\wedge \alpha ,\beta ,\cdots <\mathbb{\Omega }\wedge {\tau }_X,{\tau }_Y,\cdots \in {\mathbf{Nam}}_{\zeta }^z\hfill \\ & & \wedge p {\mathbf{forc}}_U^z \phi (\alpha ,\beta ,\dots ,{\tau }_X,{\tau }_Y,\dots ) \}.\hfill \end{array}$$

Lemma 23

(in $\mathbf{L}\left[\zeta \right]$). If φ is a parameter free $\mathcal{L}$-formula and $n=\#(\phi )$, then $\mathbf{Forc}(\phi )$ is ${\Sigma }_{n+3}^{\mathbb{H}\left[\zeta \right]}$.

Proof. 

The set ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ is ${\Delta }_3^{\mathbb{H}}$ by Lemma 17, and hence ${\Delta }_3^{\mathbb{H}\left[\zeta \right]}$ as well by Theorem 5(i) in Section 2.6. The relations $p\in \mathbf{P}\left[U\right]\upharpoonright z,\alpha <\mathbb{\Omega },\tau \in {\mathbf{Nam}}_{\zeta }^z,$ with arguments resp. $p,U,z;\alpha ;\tau ,z$, are routinely checked to be ${\Delta }_3^{\mathbb{H}\left[\zeta \right]}$, too. (Note that bounded quantifiers preserve ${\Delta }_3^{\mathbb{H}\left[\zeta \right]}$.) After this remark, prove the lemma by induction on the structure of $\phi$.

The case of atomic formulas of type (F2) is immediately clear. (The pairing function $\mathrm{𝕡}\upharpoonright (\mathbb{\Omega }\times \mathbb{\Omega })$ in (F2) is ${\Delta }_1^{\mathbb{H}}$ by Lemma 3.) The result for atomic formulas of type (F3) amounts to the formula $\exists q\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}\upharpoonright z(⟨q,\alpha ⟩\in Y\wedge p⩽q)$, which is ${\Sigma }_3^{\mathbb{H}\left[\zeta \right]}$ by the above. The step (F4) amounts to the intersection of two sets is quite obvious. And so are steps (F5) and (F6) (a $\exists$-quantification on the top of a given ${\Sigma }_{\#(\phi )+3}^{\mathbb{H}\left[\zeta \right]}$).

To carry out the step (F8), note that $\mathbf{s}\mathbf{D}\mathbf{S}\left[n\right]$ is ${\Sigma }_{n+3}^{\mathbb{H}}$ by Lemma 20, therefore ${\Sigma }_{n+3}^{\mathbb{H}\left[\zeta \right]}$ by Theorem 5(i) in Section 2.6. This if $\mathbf{Forc}(\phi )$ is ${\Sigma }_{n+3}^{\mathbb{H}\left[\zeta \right]}$ then $\mathbf{Forc}(\neg \phi )$ is ${\Pi }_{n+3}^{\mathbb{H}\left[\zeta \right]}$, hence ${\Sigma }_{n+4}^{\mathbb{H}\left[\zeta \right]}$, as required. □

5.3. Consequences for the Complete Forcing Notions

We continue to argue under the assumptions and notation of Definitions 7 on page 22 and 8 on page 25. Coming back to the sequence of $\mathbb{\Omega }$-systems ${\mathbb{U}}_{\xi }^{\mathbb{\Omega }}\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ given by Definition 7, we note that every $\mathbb{\Omega }$-system ${\mathbb{U}}_{\xi }^{\mathbb{\Omega }}$ belongs to ${\bigcap }_m\mathbf{s}\mathbf{D}\mathbf{S}\left[m\right]$.

Let ${\displaystyle \mathbf{forc}{}_{\xi }^z}$ be ${\mathbf{forc}}_{{\mathbb{U}}_{\xi }^{\mathbb{\Omega }}}^z$, and let $p{\displaystyle \mathbf{forc}{}_{\infty }^z}\phi$ mean: $\exists \xi <{\mathbb{\Omega }}^{\oplus }(p{\displaystyle \mathbf{forc}{}_{\xi }^z}\phi )$. Note that $p{\displaystyle \mathbf{forc}{}_{\xi }^z}\phi$ implies $p\in {\mathbb{P}}_{\xi }^{\mathbb{\Omega }}\upharpoonright z$, whereas $p{\displaystyle \mathbf{forc}{}_{\infty }^z}\phi$ implies $p\in {\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright z$. Lemma 22 takes the following form:

Lemma 24

(in $\mathbf{L}\left[\zeta \right]$). Assume that $z\subseteq \omega \times \omega$, φ is a closed ${\mathcal{L}}_z$ formula, $p\in {\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright z$. Then:

(i)

If $p{\displaystyle \mathbf{forc}{}_{\xi }^z}\phi$ and $\xi \le \eta <{\mathbb{\Omega }}^{\oplus }$, $q\in {\mathbb{P}}_{\eta }^{\mathbb{\Omega }}\upharpoonright z,q⩽p$, then $q{\displaystyle \mathbf{forc}{}_{\eta }^z}\phi$, and accordingly,

if $p{\displaystyle \mathbf{forc}{}_{\infty }^z}\phi$ and $q\in {\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright z,q⩽p$, then $q{\displaystyle \mathbf{forc}{}_{\infty }^z}\phi ;$

(ii)

$p{\displaystyle \mathbf{forc}{}_{\infty }^z}\phi$ and $p{\displaystyle \mathbf{forc}{}_{\infty }^z}\neg \phi$ contradict to each other.

The following result will be very important.

Lemma 25

(in $\mathbf{L}\left[\zeta \right]$). If $z\subseteq \omega \times \omega$, φ is a closed ${\mathcal{L}}_z$ formula, $p\in {\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright z$, then there is a condition $q\in {\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright z,q⩽p$, such that either $q{\displaystyle \mathbf{forc}{}_{\infty }^z}\phi$, or $q{\displaystyle \mathbf{forc}{}_{\infty }^z}\neg \phi$.

Proof. 

Let $n=\#(\phi )$. There is an ordinal $\eta <{\mathbb{\Omega }}^{\oplus }$ such that $p\in {\mathbb{P}}_{\eta }^{\mathbb{\Omega }}\upharpoonright z$. Consider the set D of all $\mathbb{\Omega }$-systems $U^{\prime }\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge n}$ such that there is a $\mathbb{\Omega }$-system $U\in \mathbf{s}\mathbf{D}\mathbf{S}\left[n\right]$ that extends ${\mathbb{U}}_{\eta }^{\mathbb{\Omega }}$ and satisfies $U\upharpoonright {}^{\ge n}=U^{\prime }$, and there is also a condition $q\in \mathbf{P}\left[U\right]\upharpoonright z$, $q⩽p$, satisfying $q {\mathbf{forc}}_U^z\phi$. The set D belongs to ${\Sigma }_{n+3}^{}(\mathbb{H}\left[\zeta \right])$ (with ${\mathbb{U}}_{\eta }^{\mathbb{\Omega }},{\mathbb{V}}_{\eta }^{\mathbb{\Omega }},p$ as definability parameters) by Lemma 23. Therefore by Lemma 19 there is an ordinal $\xi ,\eta \le \xi <{\mathbb{\Omega }}^{\oplus }$, such that the $\mathbb{\Omega }$-system ${\mathbb{U}}_{\xi }^{\mathbb{\Omega }}\upharpoonright {}^{\ge n}$ n-solves D. We have two cases.

Case 1: ${\mathbb{U}}_{\zeta }^{\mathbb{\Omega }}\upharpoonright {}^{\ge m}\in D$. Then there exist: a $\mathbb{\Omega }$-system $U\in \mathbf{s}\mathbf{D}\mathbf{S}\left[n\right]$ extending ${\mathbb{U}}_{\eta }^{\mathbb{\Omega }}$ and satisfying $U\upharpoonright {}^{\ge n}={\mathbb{U}}_{\zeta }^{\mathbb{\Omega }}\upharpoonright {}^{\ge n}$, and a condition $q\in \mathbf{P}\left[U\right]\upharpoonright z$, $q⩽p$, with $q {\mathbf{forc}}_U^z\phi$. By definition there is an ordinal $\vartheta <{\mathbb{\Omega }}^{\oplus }$ such that $U\upharpoonright {}^{<n}={\mathbb{U}}_{\vartheta }^{\mathbb{\Omega }}\upharpoonright {}^{<n}$. Now let $\mu =\mathtt{max}\{\xi ,\vartheta \}$. Then $U\preccurlyeq {\mathbb{U}}_{\mu }^{\mathbb{\Omega }}$, hence $q{\displaystyle \mathbf{forc}{}_{\mu }^z}\phi$ and $q{\displaystyle \mathbf{forc}{}_{\infty }^z}\phi$.

Case 2: There is no $\mathbb{\Omega }$-system $U\in D$ that extends ${\mathbb{U}}_{\xi }^{\mathbb{\Omega }}\upharpoonright {}^{\ge n}$. Prove that $p{\displaystyle \mathbf{forc}{}_{\xi }^z}\neg \phi$. Suppose towards the contrary that this fails. Then, by (F8) in Section 5.2, there exists a $\mathbb{\Omega }$-system $U\in \mathbf{s}\mathbf{D}\mathbf{S}\left[n\right]$ extending ${\mathbb{U}}_{\xi }^{\mathbb{\Omega }}$, and a condition $q\in \mathbf{P}\left[U\right],q⩽p$, such that $q {\mathbf{forc}}_U^z\phi$. Define $U^{\prime }=U\upharpoonright {}^{\ge n}$. Then by definition the $\mathbb{\Omega }$-system $U^{\prime }$ belongs to ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}\upharpoonright {}^{\ge n}$, and moreover the $\mathbb{\Omega }$-system U witnesses that $U^{\prime }\in D$. But this contradicts the Case 2 assumption. □

5.4. Truth Lemma

According to the next theorem (“the truth lemma”), the truth in the generic extensions considered is connected in the usual way with the relation ${\displaystyle \mathbf{forc}{}_{\infty }^{}}$. We continue to argue under the assumptions and notation of Definitions 7 on page 22 and 8 on page 25.

Theorem 10.

Assume that $\mathit{z}=\mathit{w}\left[\zeta \right]$ and φ is a ${\mathcal{L}}_{\mathit{z}}$-formula. Then $\phi \left[\mathbf{G}\upharpoonright \mathit{z}\right]$ is true in $\mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{z}]$ iff there is a condition $p\in \mathbf{G}\upharpoonright \mathit{z}$ such that $p{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\phi$.

Proof. 

We proceed by induction. Suppose that $\phi$ is an atomic formula of type (F3) of Section 5.2. (The case of formulas as in (F2) is pretty elementary.) To prove the implication $⟸$, assume that $p\in \mathbf{G}\upharpoonright \mathit{z}$ and $p{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\alpha \in \tau$, where $\alpha <\mathbb{\Omega }$ and $\tau \in {\mathbf{Nam}}_{\zeta }^{\mathit{z}}$. Then by definition ((F3) in Section 5.2) there exists a condition $q\in {\mathbb{P}}^{\mathbb{\Omega }}\upharpoonright \mathit{z}$ satisfying $p⩽q$ and $⟨q,\alpha ⟩\in \tau$. There are conditions $p^{\prime },q^{\prime }\in {\mathbb{P}}^{\mathbb{\Omega }}$ such that $p=p^{\prime }\upharpoonright \mathit{z}$ and $q=q^{\prime }\upharpoonright \mathit{z}$, but not necessarily $p^{\prime }⩽q^{\prime }$. We only know that $p^{\prime }(n,i)⩽q^{\prime }(n,i)$ for all $⟨n,i⟩\in \mathit{z}$. Therefore $\mathit{z}\subseteq Z=\{⟨n,i⟩:p^{\prime }(n,i)⩽q^{\prime }(n,i)\}$. The set Z belongs to $\mathbf{L}$ since so do $p^{\prime },q^{\prime }$ as elements of ${\mathbb{P}}^{\mathbb{\Omega }}\in \mathbf{L}$ (whereas about $\mathit{z}$ we only assert that $\mathit{z}\in \mathbf{L}\left[\zeta \right]$). Therefore a condition $q^{″}\in {\mathbb{P}}^{\mathbb{\Omega }}$ can be defined by:

$$q^{″}(n,i)=\left\{\begin{array}{ccc}\hfill q(n,i),& \mathrm{in}\mathrm{case}& ⟨n,i⟩\in Z,\hfill \\ \hfill p(n,i),& \mathrm{in}\mathrm{case}& ⟨n,i⟩\notin Z,\hfill \end{array}\right.$$

and we still have $q^{″}\upharpoonright \mathit{z}=q^{\prime }\upharpoonright \mathit{z}$ and $p^{\prime }⩽q^{″}$. It follows that $q^{″}\in \mathbf{G}$ by genericity, hence $q^{″}\upharpoonright \mathit{z}=q^{\prime }\upharpoonright \mathit{z}\in \mathbf{G}\upharpoonright \mathit{z}$. But then $\alpha \in \tau \left[\mathbf{G}\upharpoonright \mathit{z}\right]$, as required.

To prove the converse, assume that $\alpha \in \tau \left[\mathbf{G}\upharpoonright \mathit{z}\right]$. There exists a condition $p\in \mathbf{G}\upharpoonright \mathit{z}$ such that $⟨q,\alpha ⟩\in \tau$, and we have $p{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\alpha \in \tau$, as required.

Rather simple inductive steps (F4), (F5) of Section 5.2 are left for the reader.

Let us carry out step (F6). Let $\phi :=\exists X\psi (X)$. Suppose that $p\in \mathbf{G}\upharpoonright \mathit{z}$ and $p{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\phi$. By definition there exists a name $\tau \in {\mathbf{Nam}}_{\zeta }^{\mathit{z}}$ such that $p{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\psi (\tau )$. The formula $\psi (\tau )\left[\mathbf{G}\upharpoonright \mathit{z}\right]$ is then true in $\mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{z}]$ by the inductive hypothesis. But $\psi (\tau )\left[\mathbf{G}\upharpoonright \mathit{z}\right]$ coincides with $\psi \left[\mathbf{G}\upharpoonright \mathit{z}\right](Y)$, where $Y=\tau \left[\mathbf{G}\upharpoonright \mathit{z}\right]\in \mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{z}]$, $Y\subseteq \mathbb{\Omega }$. We conclude that $\exists X\psi (X)\left[\mathbf{G}\upharpoonright \mathit{z}\right]$ is true in $\mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{z}]$, as required.

To prove the converse, let $\phi \left[\mathbf{G}\upharpoonright \mathit{z}\right]$, that is, $\exists X\psi (X)\left[\mathbf{G}\upharpoonright \mathit{z}\right]$, be true in $\mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{z}]$. As X is relativized to $\mathcal{P}(\mathbb{\Omega })$, there is a set $X\in \mathcal{P}(\mathbb{\Omega })$ in $\mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{z}]$ satisfying $\phi (X)\left[\mathbf{G}\upharpoonright \mathit{z}\right]$ in $\mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{z}]$. By Lemma 21, there is a name $\tau \in {\mathbf{Nam}}_{\zeta }^z$ with $X=\tau \left[\mathbf{G}\upharpoonright \mathit{z}\right]$, so $\psi (\tau )\left[\mathbf{G}\upharpoonright \mathit{z}\right]$ holds in $\mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{z}]$. The inductive hypothesis implies that some $p\in \mathbf{G}\upharpoonright \mathit{z}$ satisfies $p{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\psi (\tau )$, hence $p{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\phi$, as required.

Finally, let us carry out step (F8), which is somewhat less trivial. Prove the lemma for a ${\mathcal{L}}_{\mathit{z}}$ formula $\neg \phi$, assuming that the result holds for $\phi$. If $\neg \phi \left[\mathbf{G}\upharpoonright \mathit{z}\right]$ is false in $\mathbf{L}[\zeta ,\mathbf{G}]$ then $\phi \left[\mathbf{G}\upharpoonright \mathit{z}\right]$ is true. Thus by the inductive hypothesis, there is a condition $p\in \mathbf{G}\upharpoonright \mathit{z}$ such that $p{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\phi$. Then $q{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\neg \phi$ for any $q\in \mathbf{G}\upharpoonright \mathit{z}$ is impossible by Lemma 24 above.

Conversely suppose that $p{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\neg \phi$ holds for no $p\in \mathbf{G}\upharpoonright \mathit{z}$. Then by Lemma 25 there exists $q\in \mathbf{G}\upharpoonright \mathit{z}$ such that $q{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\phi$. It follows that $\phi \left[\mathbf{G}\upharpoonright \mathit{z}\right]$ is true by the inductive hypothesis, therefore $\phi \left[\mathbf{G}\upharpoonright \mathit{z}\right]$ is false. □

6. Invariance

The goal of this section is to prove Theorem 9 on page 24, and thereby accomplish the proof of Theorem 8, and the proof of Theorem 2 (the main theorem) itself. The proof makes use of the relation ${}^{}\mathrm{forc}{}_{}^{}$ introduced in Section 5, and exploits certain symmetries in ${}^{}\mathrm{forc}{}_{}^{}$, investigated in Section 6.5.

6.1. Hidden Invariance

Theorem 9 belongs to a wide group of results on the structure of generic models which assert that such-and-such elements of a given generic extension belong to a smaller and/or better shaped extension. One of possible methods to prove such results is to exploit the homogeneity of the forcing notion considered, or in different words, its invariance w.r.t. a sufficiently large system of order-preserving transformations. In particular, for a straightforward proof of Theorem 11 below, which is our key technical step in the proof of Theorem 9, the invariance of the forcing notion ${\mathbb{P}}^{\mathbb{\Omega }}$ under permutations of indices in $\mathcal{I}=\omega \times \omega$ (to permute areas $\mathit{z}$ and $\widehat{\mathit{z}}$) would be naturally required, whereas ${\mathbb{P}}^{\mathbb{\Omega }}$ is definitely not invariant w.r.t. permutations.

On the other hand, the auxiliary forcing relation $\mathbf{forc}$ is invariant w.r.t. permutations. Theorem 10 in Section 5.4 conveniently binds the relation $\mathbf{forc}$ with the truth in ${\mathbb{P}}^{\mathbb{\Omega }}$-generic extensions by means of a forcing-style association. This principal association was based on the $\mathbb{M}$-completeness property (Definition 7 on page 22 and Theorem 6). Basically it occurs that some transformations, that is, permutations, are hidden in construction of ${\mathbb{P}}^{\mathbb{\Omega }}$, so that they do not act explicitly, but their influence is preserved and can be recovered via the relation $\mathbf{forc}$.

This method of hidden invariance, that is, invariance properties (of an auxiliary forcing-type relation like $\mathbf{forc}$) hidden in ${\mathbb{P}}^{\mathbb{\Omega }}$ by a suitable generic-style construction of ${\mathbb{P}}^{\mathbb{\Omega }}$, was introduced in Harrington’s notes [22] in in the context of the almost disjoint forcing (in a somewhat different terminology from what is used here). It was introduced independently by one of the authors in [37] in the context of the Sacks forcing and its Jensen’s modification in [38]; see e.g., [3,28,39] for further research in this direction based on product and iterated versions of the Sacks and Jensen forcing earlier studied in detail in [40,41,42,43,44,45,46,47].

6.2. The Invariance Theorem

We still argue under the assumptions and notation of Definitions 7 on page 22 and 8 on page 25.

Let $\Pi$ be the group of all finite permutations of $\omega$, that is, all bijections $\pi :\omega \stackrel{\mathrm{onto}}{⟶}\omega$ since the set $|\pi |=\{k:\pi (k)\ne k\}$ is finite. If $m<\omega$ then the subgroup ${\Pi }_m$ consists of all $\pi \in \Pi$ satisfying $\pi (k)=k$ for all $k<m$. If $\pi \in \Pi$, and $z\subseteq \omega \times \omega$ then put $\pi z=\{⟨\pi (n),i⟩:⟨n,i⟩\in z\}$.

If in addition $g:\omega \to \Xi$ then define $\pi g:\omega \to \Xi$ by $\pi g(\pi (n))=g(n)$, all n.

Similarly if $e\in \mathbb{C}$ and $|\pi |\subseteq \mathtt{lh}e$, then define $e^{\prime }=\pi e\in \mathbb{C}$ such that $\mathtt{lh}{e}^{\prime }=\mathtt{lh}e$ and $e^{\prime }(\pi (n))=e(n)$ for all $n<\mathtt{lh}e$. The following is the invariance theorem.

Theorem 11

(in $\mathbf{L}\left[\zeta \right]$). Assume that $\mathit{z}=\mathit{w}\left[\zeta \right]$, $\pi \in {\Pi }_m$, ${\mathit{z}}^{\prime }=\pi \mathit{z}$, φ is a closed parameter free formula of ${\mathcal{L}}_{\mathit{z}}$, $\#(\phi )\le m$, and $p_0\in {\mathbb{P}}^{\mathbb{\Omega }}$. Then $p_0\upharpoonright \mathit{z}{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\neg \phi$ iff $p_0\upharpoonright {\mathit{z}}^{\prime }{\displaystyle \mathbf{forc}{}_{\infty }^{{\mathit{z}}^{\prime }}}\neg \phi$.

A lengthy proof of Theorem 11 follows below in this Section.

6.3. Proof of Theorem 9 from the Invariance Theorem

Under the assumptions of Theorem 9, consider an arbitrary set $a\in \mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{w}\left[\zeta \right]]$, $a\subseteq \omega$, and assume that $\mathbb{M}\ge 2$ (see Definition 8) and it is true in $\mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{w}\left[\zeta \right]]$ that a is parameter free definable in $⟨\mathcal{P}(\mathbb{\Omega });\in ,\mathrm{𝕡}⟩$, i.e., $a=\{j<\omega :\neg \phi (j)\}$, where $\phi (·)$ is a parameter free ${\mathcal{L}}_{\mathit{z}}$-formula. Let $m=\#(\phi )$ and $\mathit{w}=\mathit{w}\left[\zeta \right]$. The goal is to prove that $a\in \mathbf{L}\left[\mathbf{G}\right]$. This is based on the next lemma.

Lemma 26.

The set $T=\{⟨p,j⟩:p\in {\mathbb{P}}^{\mathbb{\Omega }}\wedge p\upharpoonright \mathit{w}{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{w}}}\neg \phi (j)\}$ belongs to $\mathbf{L}$.

Proof. 

Note that, by Lemma 23, the set:

$$K=\{⟨z,p,j⟩:p\in {\mathbb{P}}^{\mathbb{\Omega }}\wedge z\in \mathbf{L}\left[\zeta \right]\wedge z\subseteq \omega \times \omega \wedge j<\omega \wedge p\upharpoonright z{\displaystyle \mathbf{forc}{}_{\infty }^z}\neg \phi (j)\}$$

is definable in $\mathbf{L}\left[\zeta \right]$ by a formula with sets in $\mathbf{L}$ as parameters, say $K=\{⟨z,p,j⟩:\vartheta (z,p,j,S)\}$ in $\mathbf{L}\left[\zeta \right]$, where $S\in \mathbf{L}$ is a sole parameter. Recall that $\zeta \in {\Xi }^{\omega }$ is $\mathbb{C}$-generic over $\mathbf{L}$, and $\mathit{w}=\mathit{w}\left[\zeta \right]=\{⟨n,j⟩:j\in \zeta (n)\}$. Let $\breve{\zeta }$ be a canonical $\mathbb{C}$-name for $\zeta$, and ⊩ be the $\mathbb{C}$-forcing relation over $\mathbf{L}$. We claim that:

$$\vartheta (\mathit{w},p,j,S)\mathrm{holds}\mathrm{in}\mathbf{L}\left[\zeta \right]\mathrm{iff}\zeta \upharpoonright m⊩\vartheta (\mathit{w}\left[\breve{\zeta }\right],p,j,S);$$

(10)

$\zeta \upharpoonright m$ belongs to $\mathbb{C}$, of course. The direction $⟸$ is obvious.

To establish $⟹$, assume that the right-hand side fails. Then there is a condition $e_0\in \mathbb{C}$ such that $\zeta \upharpoonright m\subseteq e_0$ and $e_0⊩\neg \vartheta (\mathit{w}\left[\breve{\zeta }\right],p,j,S)$. We note that the set:

$$D=\{e\in \mathbb{C}:\zeta \upharpoonright m\subseteq e\wedge \exists \pi \in {\Pi }_m(|\pi |\subseteq \mathtt{dom}e\wedge e_0\subseteq \pi e)\}$$

is dense in $\mathbb{C}$ over $\zeta \upharpoonright m$. Therefore, by the genericity of $\zeta$, there exists a number $k>m$ such that $e=\zeta \upharpoonright k\in D$. Accordingly, there is a permutation $\pi \in {\Pi }_m$ satisfying $|\pi |\subseteq k$ and $e_0\subseteq \pi e$.

We put ${\zeta }^{\prime }=\pi \zeta$; this is still a $\mathbb{C}$-generic element of ${\Xi }^{\omega }$, with $\mathbf{L}\left[{\zeta }^{\prime }\right]=\mathbf{L}\left[\zeta \right]$ since $\pi \in \mathbf{L}$, and we have $e_0\subseteq \pi e\subset {\zeta }^{\prime }$. It follows, by the choice of $e_0$, that $\vartheta (\mathit{w}\left[{\zeta }^{\prime }\right],p,j,S)$ fails in $\mathbf{L}\left[{\zeta }^{\prime }\right]=\mathbf{L}\left[\zeta \right]$, and hence $⟨\mathit{w}\left[{\zeta }^{\prime }\right],p,j⟩\notin K$ by the choice of $\vartheta$. However $\mathit{w}\left[{\zeta }^{\prime }\right]=\pi ·\mathit{w}\left[\zeta \right]=\pi \mathit{w}$, thus we have $⟨\pi \mathit{w},p,j⟩\notin K$.

We conclude that $p\upharpoonright \pi \mathit{w}{\displaystyle \mathbf{forc}{}_{\infty }^{\pi \mathit{w}}}\neg \phi (j)$ fails by the definition of K. Therefore $p\upharpoonright \mathit{w}{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{w}}}\neg \phi (j)$ fails as well by Theorem 11, so we have $⟨\mathit{w},p,j⟩\notin K$, and hence $\vartheta (\mathit{w},p,j,S)$ fails in $\mathbf{L}\left[{\zeta }^{\prime }\right]=\mathbf{L}\left[\zeta \right]$, as required. This completes the proof of (10). Now, coming back to the lemma, we deduce the equality $T=\{⟨p,j⟩\in \mathbf{L}:\zeta \upharpoonright m⊩\vartheta (\mathit{w}\left[\breve{\zeta }\right],p,j,S)\}$ from (10). This implies $T\in \mathbf{L}$. □

It remains to notice that, by Theorem 10,

$$\begin{array}{ccccc}j\in a& ⟺& \mathbf{L}[\zeta ,\mathbf{G}\upharpoonright \mathit{w}\left[\zeta \right]]\models \neg \phi (j)& ⟺& \exists p\in \mathbf{G}\upharpoonright \mathit{w}(p{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{w}}}\neg \phi (j))\hfill \\ & & & ⟺& \exists p\in \mathbf{G}(p\upharpoonright \mathit{w}{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{w}}}\neg \phi (j)).\hfill \end{array}$$

Therefore $j\in a⟺\exists p\in \mathbf{G}(⟨p,j⟩\in T)$. But $T\in \mathbf{L}$ by Lemma 26. We conclude that $a\in \mathbf{L}\left[\mathbf{G}\right]$, as required.

This completes the proof of Theorem 9 from Theorem 11.

6.4. The Invariance Theorem: Setup

We still argue under the assumptions and notation of Definitions 7 on page 22 and 8 on page 25.

Here we begin the proof of Theorem 11. It will be completed in Section 6.6.

We fix m, $\pi \in {\Pi }_m$, $p_0$, $\mathit{z}=\mathit{w}\left[\zeta \right]$, $\widehat{\mathit{z}}=\pi \mathit{z}$, and $\phi$ with $\#(\phi )\le m$, as in Theorem 11. Suppose towards the contrary that $p_0\upharpoonright \widehat{\mathit{z}}{\displaystyle \mathbf{forc}{}_{\infty }^{\widehat{\mathit{z}}}}\neg \phi$, but $p_0\upharpoonright \mathit{z}{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\neg \phi$ fails. By definition there is an ordinal $\mu <{\mathbb{\Omega }}^{\oplus }$ such that $p_0\upharpoonright \widehat{\mathit{z}}{\displaystyle \mathbf{forc}{}_{\mu }^{\widehat{\mathit{z}}}}\neg \phi$, but $p_0\upharpoonright \mathit{z}{\displaystyle \mathbf{forc}{}_{\mu }^{\mathit{z}}}\neg \phi$ fails. Then we have:

(A)

a $\mathbb{\Omega }$-system $U^1\in \mathbf{s}\mathbf{D}\mathbf{S}\left[m\right]$ with ${\mathbb{U}}_{\mu }^{\mathbb{\Omega }}\preccurlyeq U^1$, and a condition $p_1\in \mathbf{P}\left[U^1\right]$, $p_1⩽p_0$, such that $p_1\upharpoonright \mathit{z}{\mathbf{forc}}_{U^1}^{\mathit{z}}\phi$, but $p_1\upharpoonright \widehat{\mathit{z}}{\mathbf{forc}}_{U^1}^{\widehat{\mathit{z}}}\neg \phi$ still holds by Lemma 22.

We now recall that any condition $p\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ is a map $p\in \mathbf{L}$, defined on $\mathcal{I}=\omega \times \omega$, and each value $p(n,i)=⟨{\mathbf{S}}_p(n,i);{\mathbf{F}}_p(n,i)⟩$ is a pair of a set ${\mathbf{S}}_p(n,i)\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}$ and ${\mathbf{F}}_p(n,i)\subseteq {\mathbf{Fun}}_{\mathbb{\Omega }}$, with $\mathtt{card}({\mathbf{S}}_p(n,i)\cup {\mathbf{F}}_p(n,i))<\mathbb{\Omega }$ strictly, in $\mathbf{L}$. We define the support:

$$||p||=\bigcup _{n,i<\omega }||p|{|}_{ni},\mathrm{where}||p|{|}_{ni}=\{s(0):s\in {\mathbf{S}}_p(n,i)\}\cup \{f(0):f\in {\mathbf{F}}_p(n,i)\};$$

then $||p||\in \mathbf{L}$, $||p||\subseteq \mathbb{\Omega }$, and $\mathtt{card}||p||<\mathbb{\Omega }$ strictly, so that $||p||$ is a bounded subset of $\mathbb{\Omega }$. In particular, $||p_1||$ is a bounded subset of $\mathbb{\Omega }$ in $\mathbf{L}$. Therefore there is:

(B)

A bijection $b\in \mathbf{L}$, $b:\mathbb{\Omega }\stackrel{\mathrm{onto}}{⟶}\mathbb{\Omega }$, such that $||p_1||\cap (b^{″}||p_1||)=\varnothing$ and $b=b^{-1}$.

Furthermore, as $U^1\in \mathbf{s}\mathbf{D}\mathbf{S}\left[m\right]$, the $\mathbb{\Omega }$-system $U^1$ is $\mathbb{\Omega }$-size, and hence the set $J={\bigcup }_{n,i<\omega }{U}^1(n,i)\in \mathbf{L}$ satisfies $\mathtt{card}J\le \mathbb{\Omega }$ in $\mathbf{L}$. It follows that there exists:

(C)

A sequence ${\left\{F_{\alpha }\right\}}_{\alpha <\mathbb{\Omega }}\in \mathbf{L}$ of bijections $F_{\alpha }:\mathbb{\Omega }\stackrel{\mathrm{onto}}{⟶}\mathbb{\Omega }$, such that $F_0=b$ (see above), $F_{\alpha }={F_{\alpha }}^{-1}$, and if $f,g\in J$ then there is an ordinal $\alpha <\mathbb{\Omega }$ such that $f(\alpha )\ne F_{\alpha }(g(\alpha ))$.

6.5. Transformation

In continuation of the proof of Theorem 11, we now define an automorphism acting on several different domains in $\mathbf{L}$. It will be based on $\pi$ and $F_{\alpha }$ of Section 6.4 and its action will be denoted by $\widehat{\phantom{x}}$. Along the way we will formulate properties (D)–(H) of the automorphism, a routine check of which is left to the reader.

We argue under the assumptions and notation of Definitions 7 on page 22 and 8 on page 25.

If $\alpha \le \mathbb{\Omega }$ and $f:\alpha \to \mathbb{\Omega }$ then $\widehat{f}:\alpha \to \mathbb{\Omega }$ is defined by $\widehat{f}(\gamma )=F_{\gamma }(f(\gamma ))$ for all $\gamma <\alpha$. In particular, $\widehat{f}(0)=F_0(f(0))=b(f(0))$. This defines $\widehat{s}\in {\mathbf{Seq}}_{\mathbb{\Omega }}$ and $\widehat{f}\in {\mathbf{Fun}}_{\mathbb{\Omega }}$ for all $s\in {\mathbf{Seq}}_{\mathbb{\Omega }}$ and $f\in {\mathbf{Fun}}_{\mathbb{\Omega }}$.

(D)

$f⟼\widehat{f}$ is a bijection ${\mathbf{Seq}}_{\mathbb{\Omega }}\stackrel{\mathrm{onto}}{⟶}{\mathbf{Seq}}_{\mathbb{\Omega }}$ and ${\mathbf{Fun}}_{\mathbb{\Omega }}\stackrel{\mathrm{onto}}{⟶}{\mathbf{Fun}}_{\mathbb{\Omega }}$, and if $f,g\in J={\bigcup }_{n,i<\omega }{U}^1(n,i)$ then $\widehat{f}\ne g$ by (C).

If $u\subseteq {\mathbf{Fun}}_{\mathbb{\Omega }}$ then let $\widehat{u}=\{\widehat{f}:f\in u\}$. If $S\subseteq {\mathbf{Seq}}_{\mathbb{\Omega }}$ then let $\widehat{S}=\{\widehat{s}:s\in S\}$.

If U is a $\mathbb{\Omega }$-system then define a $\mathbb{\Omega }$-system $\widehat{U}$, such that:

$$\begin{array}{ccccc}\hfill \widehat{U}(n,i)& =& U(n,i),\hfill & \mathrm{in}\mathrm{case}& n<m;\hfill \\ \hfill \widehat{U}(\pi (n),i)& =& \widehat{U(n,i)}=\{\widehat{f}:f\in U(n,i)\},\hfill & \mathrm{in}\mathrm{case}& n\ge m.\hfill \end{array}$$

If $p\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ then let $\widehat{p}\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ be defined so that:

$$\begin{array}{ccccc}\hfill \widehat{p}(n,i)& =& p(n,i),\hfill & \mathrm{in}\mathrm{case}& n<m;\hfill \\ \hfill \widehat{p}(\pi (n),i)& =& ⟨\widehat{{\mathbf{S}}_p(n,i)};\widehat{{\mathbf{F}}_p(n,i)}⟩,\hfill & \mathrm{in}\mathrm{case}& n\ge m;\hfill \end{array}$$

where $\widehat{{\mathbf{S}}_p(n,i)}=\{\widehat{s}:s\in {\mathbf{S}}_p(n,i)\}$ and $\widehat{{\mathbf{F}}_p(n,i)}=\{\widehat{s}:s\in {\mathbf{F}}_p(n,i)\}$ by the above. These are consistent definitions because $\pi \in {\Pi }_m$.

(E)

$\widehat{U}\upharpoonright {}^{<m}=U\upharpoonright {}^{<m}$ for any $\mathbb{\Omega }$-system U. The map $U⟼\widehat{U}$ is a bijection of ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$ onto itself and $\mathbf{s}\mathbf{D}\mathbf{S}\left[k\right]$ onto itself for any $k\le m$.

(F)

$\widehat{p}\upharpoonright {}^{<m}=p\upharpoonright {}^{<m}$ for any $p\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$. The map $p⟼\widehat{p}$ is a $⩽$-preserving bijection of $\mathbf{P}\left[U\right]$ onto $\mathbf{P}\left[\widehat{U}\right]$.

If in addition $z\subseteq \omega \times \omega$ (not necessarily $z\in \mathbf{L}$), then if conditions $p,q\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ satisfy $p\upharpoonright z=q\upharpoonright z$, then easily $\widehat{p}\upharpoonright \widehat{z}=\widehat{q}\upharpoonright \widehat{z}$, where $\widehat{z}=\pi ·z=\{⟨\pi (n),i⟩:⟨n,i⟩\in z\}$. This allows us to define $\widehat{r}=\widehat{p}\upharpoonright \widehat{z}$ for every $r\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}\upharpoonright z$, where $p\in {{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$ is any condition satisfying $r=p\upharpoonright z$.

(G)

If $z\subseteq \omega \times \omega$ then $p⟼\widehat{p}$ is a $⩽$-preserving bijection of $\mathbf{P}\left[U\right]\upharpoonright z$ onto $\mathbf{P}\left[\widehat{U}\right]\upharpoonright \widehat{z}$.

If $z\subseteq \omega \times \omega$ and $\tau \in {\mathbf{Nam}}_{\zeta }^z$ (see Section 5.1) then we define $\widehat{\tau }=\{⟨\widehat{p},\alpha ⟩:⟨p,\alpha ⟩\in \tau \}$, and accordingly if $\phi$ is a ${\mathcal{L}}_z$-formula then $\widehat{\phi }$ is obtained by substituting $\widehat{\tau }$ for each name $\tau$ in $\phi$.

(H)

If $z\subseteq \omega \times \omega$, $z\in \mathbf{L}\left[\zeta \right]$, then the mapping $\tau ⟼\widehat{\tau }$ is a bijection of ${\mathbf{Nam}}_{\zeta }^z$ onto ${\mathbf{Nam}}_{\zeta }^{\widehat{z}}$ and a bijection of ${\mathcal{L}}_z$-formulas onto ${\mathcal{L}}_{\widehat{z}}$-formulas.

Remark 6.

The action of $\widehat{\phantom{x}}$ is idempotent, so that e.g., $\widehat{\widehat{f}}=f$ for any $f\in {\mathbf{Fun}}_{\mathbb{\Omega }}$ etc. This is because we require that $b^{-1}=b$ and $F_{\alpha }^{-1}=F_{\alpha }$ for all $\alpha <\mathbb{\Omega }$.

The action of $\widehat{\phantom{x}}$ is constructible on ${\mathbf{Seq}}_{\mathbb{\Omega }}$, ${\mathbf{Fun}}_{\mathbb{\Omega }}$, $\mathbb{\Omega }$-systems, ${{}^{*}\mathbf{P}}_{\mathbb{\Omega }}$, since both π and the sequence of maps $F_{\alpha }$ belong to $\mathbf{L}$ by (B), (C).

If $z\in \mathbf{L}\left[\zeta \right]$ then the action of $\widehat{\phantom{x}}$ on ${{}^{*}\mathbf{P}}_{\mathbb{\Omega }}\upharpoonright z$ and names in ${\mathbf{Nam}}_{\zeta }^z$ belongs to $\mathbf{L}\left[\zeta \right]$, since the extra parameter $z\in \mathbf{L}\left[\zeta \right]$ does not necessarily belong to $\mathbf{L}$.

It is not unusual that transformations of a forcing notion considered lead to this or another invariance. The next lemma is exactly of this type.

Lemma 27

(in $\mathbf{L}\left[\zeta \right]$). Assume that $U\in {\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$, $\mathit{z}=\mathit{w}\left[\zeta \right]$, $\pi \in {\Pi }_m$, $\widehat{\mathit{z}}=\pi \mathit{z}$, $p\in \mathbf{P}\left[U\right]\upharpoonright \mathit{z}$, and φ is a closed formula of ${\mathcal{L}}_{\mathit{z}}$, $\#(\phi )\le m+1$. Then $p {\mathbf{forc}}_U^{\mathit{z}}\Phi$ iff $\widehat{p}{\mathbf{forc}}_{\widehat{U}}^{\widehat{\mathit{z}}}\widehat{\Phi }$.

Proof. 

We argue by induction on the structure of $\Phi$. Routine cases of atomic formulas (F2) and steps (F4) and (F5) of Section 5.2 by means of (D)–(H) are left to the reader. Thus we concentrate on atomic formulas of type (F3) and steps (F6) and (F8) in Section 5.2. In all cases we take care of only one direction of the equivalence of the lemma, as the other direction is entirely similar via Remark 6 just above.

Formulas of type (F3). Let $\Phi$ be $\alpha \in \tau$, where $\alpha <\mathbb{\Omega }$ and $\tau \in {\mathbf{Nam}}_{\zeta }^z$. Assume that $p {\mathbf{forc}}_U^{\mathit{z}}\alpha \in \tau$. Then by definition there is a condition $q\in \mathbf{P}\left[U\right]\upharpoonright \mathit{z}$ such that $p⩽q$ and $⟨q,\alpha ⟩\in \tau$. Then $\widehat{q}$ and $\widehat{p}$ belong to $\mathbf{P}\left[\widehat{U}\right]\upharpoonright \widehat{\mathit{z}}$, $\widehat{p}⩽\widehat{q}$, and $⟨\widehat{q},\alpha ⟩\in \widehat{\tau }$, so we have $\widehat{p} {\mathbf{forc}}_{\widehat{U}}^{\widehat{\mathit{z}}}\alpha \in \widehat{\tau }$, as required.

Step (F6). Let $\Phi :=\exists X\Psi (X)$. Suppose that $p {\mathbf{forc}}_U^{\mathit{z}}\Phi$. By definition there exists a name $\tau \in {\mathbf{Nam}}_{\zeta }^z$ such that $p{\displaystyle \mathbf{forc}{}_{\infty }^{\mathit{z}}}\Psi (\tau )$, Then we have $\widehat{p} {\mathbf{forc}}_{\widehat{U}}^{\widehat{\mathit{z}}}\widehat{\Psi (\tau )}$ by the inductive hypothesis. But $\widehat{\Psi (\tau )}$ coincides with $\widehat{\Psi }(\widehat{\tau })$, where $\widehat{\tau }\in {\mathbf{Nam}}_{\zeta }^{\widehat{\mathit{z}}}$ by (H) above. We conclude that $\widehat{p} {\mathbf{forc}}_{\widehat{U}}^{\widehat{\mathit{z}}}\exists X\widehat{\Psi (X)}$, that is, $\widehat{p} {\mathbf{forc}}_{\widehat{U}}^{\widehat{\mathit{z}}}\widehat{\Phi }$, as required.

Step (F8). Prove the lemma for a ${\mathcal{L}}_{\mathit{z}}$ formula $\Phi :=\neg \Psi$, assuming that the result holds for $\Psi$. Note that $\#(\Phi )⩽m+1$, hence $\#(\Psi )⩽m$. Suppose that $p{\mathbf{forc}}_U^{\mathit{z}}\neg \Psi$ fails. By definition there is a $\mathbb{\Omega }$-system $U^{\prime }\in \mathbf{s}\mathbf{D}\mathbf{S}\left[m\right]$ extending $U^{\prime }$, and a condition $q\in \mathbf{P}\left[U^{\prime }\right]\upharpoonright \mathit{z}$, $q⩽p$, such that $q {\mathbf{forc}}_{U^{\prime }}^{\mathit{z}} \Psi$. Then $\widehat{q} {\mathbf{forc}}_{\widehat{U^{\prime }}}^{\widehat{\mathit{z}}}\widehat{\Psi }$ by the inductive hypothesis. Yet $\widehat{U^{\prime }}$ belongs to ${\mathbf{s}\mathbf{D}\mathbf{S}}_{\mathbb{\Omega }}$, extends $\widehat{U}$, and satisfies $\widehat{U^{\prime }}\upharpoonright {}^{<m}=U^{\prime }\upharpoonright {}^{<m}$ by (E), hence belonging even to $\mathbf{s}\mathbf{D}\mathbf{S}\left[m\right]$ by the choice of $U^{\prime }$, and in addition $\widehat{q}\in \mathbf{P}\left[\widehat{U^{\prime }}\right]\upharpoonright \widehat{\mathit{z}}$ and $\widehat{q}⩽\widehat{p}$ by (F). We conclude, by definition, that $\widehat{p} {\mathbf{forc}}_{\widehat{U}}^{\widehat{\mathit{z}}}\neg \widehat{\Psi }$ fails too, as required. □

6.6. Finalization

We continue to argue under the assumptions and notation of Definitions 6 on page 20 and 8 on page 25. The goal of this Section is to accomplish the proof of Theorem 11 in Section 6.2 that was started in Section 6.4. We return to objects introduced in (A), (B), (C) of Section 6.2.

Let $q_1=p_1\upharpoonright \mathit{z}$, so that $q_1\in \mathbf{P}\left[U^1\right]\upharpoonright \mathit{z}$ and $q_1 {\mathbf{forc}}_{U^1}^{\mathit{z}}\phi$ by (A). We have:

$$\widehat{U^1}\in \mathbf{s}\mathbf{D}\mathbf{S}\left[m\right]\wedge \widehat{p_1}\in \mathbf{P}\left[\widehat{U^1}\right]\wedge \widehat{q_1}=\widehat{p_1}\upharpoonright \widehat{\mathit{z}}\in \mathbf{P}\left[\widehat{U^1}\right]\upharpoonright \widehat{\mathit{z}}\wedge \widehat{q_1} {\mathbf{forc}}_{\widehat{U^1}}^{\widehat{\mathit{z}}}\phi$$

(11)

by Lemma 27. (Here $\phi$, as a parameter free formula, coincides with $\widehat{\phi }$.) Let a $\mathbb{\Omega }$-system U be defined by $U(n,i)=U^1(n,i)\cup \widehat{U^1}(n,i).$

Lemma 28.

The $\mathbb{\Omega }$-system U belongs to $\mathbf{s}\mathbf{D}\mathbf{S}\left[m\right]$ and extends both $U^1$ and $\widehat{U^1}$.

Conditions $p_1$ and $\widehat{p_1}$ belong to $\mathbf{P}\left[U\right]$ and are compatible in $\mathbf{P}\left[U\right]$.

Proof (Lemma). 

It follows by (D) (last claim) that U is a disjoint $\mathbb{\Omega }$-system. It follows by (E) that $U\upharpoonright {}^{<m}=U^1\upharpoonright {}^{<m}=\widehat{U^1}\upharpoonright {}^{<m}$. Therefore U belongs to $\mathbf{s}\mathbf{D}\mathbf{S}\left[m\right]$ because so does $U^1$.

To prove compatibility, it suffices to check that if $n,i<\omega$ then either $p_1(n,i)=\widehat{p_1}(n,i)$ or $||p_1|{|}_{ni}\cap ||\widehat{p_1}|{|}_{ni}=\varnothing$. If $n<m$ then we have the ‘either’ case because by definition $p_1\upharpoonright {}^{<m}=\widehat{p_1}\upharpoonright {}^{<m}$. Suppose that $n\ge m$. Let $k={\pi }^{-1}(n)$; thus still $k\ge m$ (as $\pi \in {\Pi }_m$), $n=\pi (k)$, and $\widehat{p_1}(n,i)=⟨\widehat{{\mathbf{S}}_p(k,i)};\widehat{{\mathbf{F}}_p(k,i)}⟩$. It follows that $||\widehat{p_1}|{|}_{ni}$ is the $F_0$-image, hence the b-image of the set $||p_1|{|}_{ki}$. However $||p_1|{|}_{ki}\cup ||p_1|{|}_{ni}\subseteq ||p_1||$. We conclude that $||p_1|{|}_{ni}\cap ||\widehat{p_1}|{|}_{ni}=\varnothing$ by Claim (B) of Section 6.4, as required. □

To finalize the proof of Theorem 11, let, by Lemma 28, $r\in \mathbf{P}\left[U\right]\upharpoonright \widehat{\mathit{z}}$ satisfy both $r⩽p_1\upharpoonright \widehat{\mathit{z}}$ and $r⩽\widehat{p_1}\upharpoonright \widehat{\mathit{z}}=\widehat{q_1}$. However $\widehat{q_1} {\mathbf{forc}}_{\widehat{U^1}}^{\widehat{\mathit{z}}}\phi$ by (11). We conclude that $r {\mathbf{forc}}_U^{\widehat{\mathit{z}}}\phi$ by Lemma 28 and Lemma 22. On the other hand, $p_1\upharpoonright \widehat{\mathit{z}} {\mathbf{forc}}_{U^1}^{\widehat{\mathit{z}}}\neg \phi$ by (A) of Section 6.4, therefore we have $r {\mathbf{forc}}_U^{\widehat{\mathit{z}}}\neg \phi$. It remains to remind that $\#(\phi )\le m$ and $U\in \mathbf{s}\mathbf{D}\mathbf{S}\left[m\right]$ by Lemma 28—and we still get a contradiction by Lemma 22(ii). The contradiction completes the proof of Theorem 11.

Finalization.

Theorem 11 just proved implies Theorem 9, see Section 6.3.

Theorem 9 ends the proof of Theorem 8 of Section 4.6, see Remark 5 on page 24.

This completes the proof of Theorem 2, the main result of this paper, see Remark 4 on page 23.

7. Conclusions and Discussion

In this study, the method of almost-disjoint forcing was employed to the problem of getting a model of $\mathbf{ZFC}$ in which the set ${\mathbf{D}}_{1m}$ of all reals, definable by a parameter free type-theoretic formula with the highest quantifier order not exceeding a given natural number $\mathbb{M}\ge 1$, belongs to ${\mathbf{D}}_{2\mathbb{M}}$, that is, it is itself definable by a formula of the same quantifier order. Moreover, we have ${\mathbf{D}}_{1\mathbb{M}}=\mathbf{L}\cap \mathbb{R}$ in the model, that is, the set ${\mathbf{D}}_{1\mathbb{M}}$ is equal to the set of all Gödel-constructible reals.

The problem of getting a model for ${\mathbf{D}}_{1\mathbb{M}}\in {\mathbf{D}}_{2\mathbb{M}}$ was posed in Alfred Tarski’s article [18]. Its particular case $\mathbb{M}=1$ (analytical definability), that is, the problem of getting models for ${\mathbf{D}}_{11}\in {\mathbf{D}}_{21}$, or stronger, ${\mathbf{D}}_{11}=\mathbf{L}\cap \mathbb{R}$, has been known since the early years of forcing, see e.g., problem 87 in Harvey Friedman’s survey [21], and problems 3110, 3111, and 3112 in another early survey [20] by A. Mathias. As mentioned in [20,21], the particular case $\mathbb{M}=1$ was solved by Leo Harrington, and a sketch of the proof, related to a model for ${\Delta }_3^1=\mathbf{L}\cap \mathbb{R}$, can be found in Harrington’s handwritten notes [22]. Our paper presents a full proof of the comprehensive result (Theorem 2) that finally solves the Tarski problem.

From this study, it is concluded that the hidden invariance technique (as outlined in Section 6.1) allows one to solve the problem by providing a generic extension of $\mathbf{L}$ in which the constructible reals are precisely the ${\mathbf{D}}_{1\mathbb{M}}$ reals, for a chosen value $\mathbb{M}\ge 1$. The hidden invariance technique has also been applied in recent papers [3,4,5,28] for the problem of getting a set theoretic structure of this or another kind at a preselected projective level. We finish with a short list of related problems.

1. If $x\subseteq \omega$ then let ${\mathbf{D}}_{pm}(x)$ be the set of all objects of order p, definable by a formula with x as the only parameter, whose all quantified variables are over orders $\le m$. (Compare to Definition 1 on page 2.) One may be interested in getting a model for:

$$\forall x\subseteq \omega ({\mathbf{D}}_{1m}(x)\in {\mathbf{D}}_{2m}(x),\mathrm{or}\mathrm{stronger},{\mathbf{D}}_{1m}(x)=\mathcal{P}(\omega )\cap \mathbf{L}).$$

(12)

This is somewhat similar to Problem 87${}^{\prime }$ in [21]: Find a model of:

$$\mathrm{ZFC}+“\mathrm{for}\mathrm{any}\mathrm{reals}x,y,\mathrm{we}\mathrm{have}:x\in \mathbf{L}\left[y\right]⟹x\mathrm{is}{\Delta }_3^1\mathrm{in}y”.$$

(13)

Problem (13) was known in the early years of forcing, see, e.g., problem 3111 in [20] or (3) in [23] (Section 6.1). Problem (13) was positively solved by René David [48,49], where the question is attributed to Harrington. The proof makes use of a tool known as David’s trick, see S. D. Friedman [27] (Chapters 6, 8).

So far it is unknown whether the result of David [48] generalizes to higher projective classes ${\Delta }_n^1$, $n\ge 4$, or ${\Delta }_{\omega }^1$, whether it can be strengthened towards $⟺$ instead of $⟹$, and whether it can lead to an even partial solution of (12). This is a very interesting and perhaps difficult question.

2. Coming back to Harvey Friedman’s ${\Delta }_n^1$ problem of getting a model for the sentence:

$$\mathrm{the}\mathrm{set}{d}_n=\mathcal{P}(\omega )\cap {\Delta }_n^1\mathrm{is}\mathrm{equal}\mathrm{to}\mathcal{P}(\omega )\cap \mathbf{L},$$

(14)

(Section 1.2), it is clear that, unlike ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$, if (14) holds for some $n\ge 3$ then it definitely fails for any $n^{\prime }\ne n$. But we can try to weaken (14) to just:

$$d_n\in {\Pi }_n^1,$$

(15)

and then ask whether there is a generic extension of $\mathbf{L}$ satisfying $\forall n(d_n\in {\Pi }_n^1)$. It holds by rather routine estimations that $d_1\in {\Pi }_1^1\setminus {\Sigma }_1^1$, $d_2\in {\Sigma }_2^1\setminus {\Pi }_2^1$, and if all reals are constructible then $d_n\in {\Sigma }_n^1\setminus {\Pi }_n^1$ for all $n\ge 3$ as well, so ${\Pi }_n^1$ looks rather suitable in (15).

3. Recall that Theorem 2 implies the consistency of ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ for each particular $m\ge 1$.

But what about the consistency of the sentence “${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ holds for all $m\ge 1$”? Perhaps a method developed in [50] can be useful to solve this problem.

4. It would be interesting to define a generic extension of $\mathbf{L}$ in which, for instance, ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ holds for all even $m\ge 1$ but fails for all odd $m\ge 1$, or vice versa.

Lemma 2 on page 8 presents a possible difficulty: If we have ${\mathbf{D}}_{1n}\in {\mathbf{D}}_{2n}$ for some $n\ge 1$ by means of the equality ${\mathbf{D}}_{1n}=\mathcal{P}(\omega )\cap \mathbf{L}$, then ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ definitely fails for all $m<n$.

5. Another question considered by Tarski in [18] is related to the sets ${\mathbf{D}}_k={\bigcup }_m{\mathbf{D}}_{km}$(all elements of order k, definable by a formula of any order). Tarski proves that ${\mathbf{D}}_k\notin {\mathbf{D}}_{k+1}$ for all $k\ge 2$, and leaves open the question whether ${\mathbf{D}}_1\in {\mathbf{D}}_2$. Similarly to the problem ${\mathbf{D}}_{1m}\in {\mathbf{D}}_{2m}$ in Section 1.1, the negative answer ${\mathbf{D}}_1\notin {\mathbf{D}}_2$ follows from the axiom of constructibility $\mathbf{V}=\mathbf{L}$, and hence is consistent with $\mathbf{ZFC}$.

Prove the consistency of the sentences ${\mathbf{D}}_1\in {\mathbf{D}}_2$ and ${\mathbf{D}}_1=\mathcal{P}(\omega )\cap \mathbf{L}$.