Meta-Analysis with Few Studies and Binary Data: A Bayesian Model Averaging Approach

Abstract

In meta-analysis, the existence of between-sample heterogeneity introduces model uncertainty, which must be incorporated into the inference. We argue that an alternative way to measure this heterogeneity is by clustering the samples and then determining the posterior probability of the cluster models. The meta-inference is obtained as a mixture of all the meta-inferences for the cluster models, where the mixing distribution is the posterior model probabilities. When there are few studies, the number of cluster configurations is manageable, and the meta-inferences can be drawn with BMA techniques. Although this topic has been relatively neglected in the meta-analysis literature, the inference thus obtained accurately reflects the cluster structure of the samples used. In this paper, illustrative examples are given and analysed, using real binary data.

1. Introduction

Statistical methods for meta-analysis have been widely applied in many research areas and are of particular importance in healthcare studies. When randomised controlled clinical trials (or studies) are made of a medical treatment for patients with a given disease and heterogeneous samples are compiled, a meta-analysis may be conducted to determine what can fairly be concluded about the fundamental question addressed in each such study, i.e., the effectiveness of the treatment. This parameter is usually estimated on the basis of a prior estimate of the between-study variation, for which purposes random-effects meta-analysis techniques are employed. Thus, meta-analysis addresses the problem of drawing inferences concerning the treatment effect based on k samples. Between-sample heterogeneity introduces additional uncertainty into the process, namely that of model uncertainty. Rücker et al. [1] commented that statistical heterogeneity and small study effects are major issues affecting the validity of meta-analysis. Heterogeneity is difficult to estimate if few studies are considered, and the resulting model uncertainty might lead to misleading results being obtained. In this paper, we define heterogeneity as the statistical variation found in the collected effect size data, which has to be assessed after the studies have been pooled [1].

According to Sutton and Abrams [2], the Bayesian random-effects model for meta-analyses is given by:

$$\begin{array}{c}\hfill x_i\sim \mathcal{N}({\theta }_i,{\tau }_i),i=1,\dots ,k\\ \hfill {\theta }_i\sim \mathcal{N}(\theta ,\tau ),\\ \hfill \theta \sim [-,-]\tau \sim [-,-],\end{array}$$

(1)

where for each study $i\in \{1,\dots ,k\},$ the observed effect $x_i$ is assumed to be normally distributed with mean parameter ${\theta }_i$ (the treatment effectiveness conditional on study i) and variance ${\tau }_i$. Similarly, $\theta$ represents the unconditional treatment effectiveness, i.e., the pooled effect size; $\tau$ is its variance; and $[-,-]$ indicates a prior density to be assigned. When the effectiveness is measured by a discrete 0–1 random variable, the above hierarchical normal model is typically applied to the logit transformation of the data $log\left(x_i/(n_i-x_i)\right)$ with the reparametrisation $log\left({\theta }_i/(1-{\theta }_i)\right)$ [3,4,5,6,7,8]. If the samples contain zeros, a fixed data continuity correction is applied, and a logit approximation is then used. However, this practice has been criticised by Sweeting et al. [9], who proposed an alternative empirical data correction. Furthermore, small studies present more heterogeneity than large ones [10]. Recently, Weber et al. (2020) [11] recommended that zero-cell corrections should be avoided due to the poor performance of their statistical properties. Obviously, continuity corrections are not the only way to proceed. A number of meta-analysis methods based, e.g., on binomial models were proposed in [12] and the references therein.

In the meta-analysis literature, determining statistical heterogeneity mainly consists of either estimating the between-study variation, characterised as the variance, or heterogeneity parameter, or otherwise testing the null hypothesis that the true treatment effects across studies are identical $H_0:{\theta }_1={\theta }_2=\dots ={\theta }_k=\theta$ [8,13]. A measure of evidence for heterogeneity is obtained by means of the Q test, a chi-squared test with $k-1$ degrees of freedom, first defined by Cochran [14]. Alternatively, and in order to overcome the dependence on the number of studies considered for the meta-analysis, which is the case with the Q test, Higgings and Thompson [15] proposed the dimensionless $I^2$ index, which describes the percentage of variation across studies that is due to heterogeneity rather than chance. Mittlböck and Heinzl [16] compared these two relative measures of heterogeneity jointly with the index ${\displaystyle H_M^2=\frac{Q}{k-1}-1,}$ through an intensive simulation study. Basically, $I^2$ and $H_M^2$ have similar properties, although $H_M^2$ is preferred when few studies are considered. As shown in [16], the number of studies affects the power of the heterogeneity test and the heterogeneity measures $I^2$, but not $H_M^2$.

It is well known that all tests of heterogeneity have relatively little power to detect heterogeneity when data are sparse and/or when meta-analyses are based on a small number of studies [1,9,15,17]. These situations are very common in daily practice, for instance with respect to rare or orphan diseases, where zero values are often observed in both the trial and the treatment arms considered.

Statistical heterogeneity is a characteristic of the studies that compose a meta-analysis and can be present at different levels of intensity, ranging from homogeneity to heterogeneity. There are also many intermediate situations that should be considered in order to correctly estimate the quantities of interest. Higgins et al. [18] proposed a tentative naive categorisation of values for $I^2$, relating values of $25\%$, $50\%$ and $75\%$ with low, moderate and high levels of heterogeneity, respectively, and considering a significant degree of heterogeneity to be present when $I^2>50\%.$

In the present analysis, we address the question from a different standpoint, arguing that between-sample heterogeneity is a clustering problem and that model uncertainty can be incorporated into the inference using a Bayesian procedure. Under this procedure, the posterior probabilities of the cluster models are computed, and the meta-inference is then obtained as a mixture of the meta-inferences obtained for the cluster models, using the posterior model probabilities as a mixing distribution. Another point of difference is that most previous studies analysed between-study heterogeneity for a quantity of interest in the comparison of two treatments, such as the mean difference, relative risk or odds ratio. In our proposal, the configuration of between-study heterogeneity is analysed for each treatment separately, which allows the heterogeneity structure to differ between the experimental treatment and the control.

The proposed methodology is known as Bayesian model averaging and has recently begun to be used in meta-analyses. For instance, Bayesian meta-analyses modelling averages over fixed and random effect models were considered in Gronau et al. [19] and Scheibehenne et al. [20].

1.1. A Motivating Example

Günhan et al. [12] suggested the use of weakly informative priors for the treatment effect parameter of a Bayesian meta-analysis model, to be applied in a paediatric transplant dataset. In the present study, and for illustrative purposes, we focus on a dataset corresponding to renal post-transplant lymphoproliferative diseases (PTLD). The results obtained are shown in Table 1.

Table 1. Data on post-transplant lymphoproliferative diseases (PTLD) in Günhan et al.

Trial	Treatment
	Control		Experimental
	Events	Total	Events	Total
Schuller et al. (${\mathit{x}}_1$)	0	12	0	18
Ganschow et al. (${\mathit{x}}_2$)	0	54	1	54
Spada et al. (${\mathit{x}}_3$)	1	36	1	36

In this respect, Crins et al. [21] conducted Cochrane’s Q test and found no evidence of heterogeneity between the trials. Moreover, Günhan et al. obtained low values for the estimated heterogeneity parameter under weakly informative or vague priors and maximum likelihood estimation. However, the structure of the partition clustering induced by the PTLD dataset in Table 1 shown in Figure 1 indicates that different forms of inter-trial variability could be present.

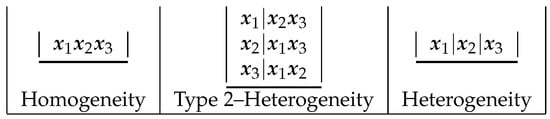
Figure 1. Clustering structure and different heterogeneity structures in the Günhan et al. dataset.

There are $\left|\mathcal{M}\right|=5$ possible partitions (models or heterogeneity configurations), and for each of the cluster classes, there are $1,3,1$ partitions, respectively. Thus, the selection of any one model (homogeneity, for example) among the five that are possible may ignore the uncertainty underlying model selection and misrepresent the uncertainty concerning the quantities of interest. In view of these considerations, we believe that Bayesian model averaging (BMA) is an appropriate means of accounting for model uncertainty and, thus, heterogeneity. Expectations and quantities of interest are obtained by weighted averages over the set of models, rather than by selecting a single model and drawing inferences as if it were the true model.

For each of the treatments considered (control and experimental), Table 2 shows the (posterior) probabilities of each of the five models induced by the clustering applied to the data in this example. These posterior probabilities constitute the weights to be used for averaging the set of models. Their expressions are given in Section 3. As an example, let us observe the control treatment. The case of homogeneity has the highest posterior probability of being true, 0.39. However, this option does not consider the remaining heterogeneity structures and therefore would result in misleading inferences being drawn, by rejecting all other possible models, which constitute a combined probability of 0.61. The same reasoning is applicable to the experimental treatment.

Table 2. Cluster models and their posterior probabilities.

Cluster Model	Posterior Probabilities
	Control	Experimental
$M_1$: Homogeneity $\left\{{\mathit{x}}_1{\mathit{x}}_2{\mathit{x}}_3\right\}$	0.39	0.45
$M_2$: Heterogeneity $\{\left\{{\mathit{x}}_1\right\},\left\{{\mathit{x}}_2\right\},\left\{{\mathit{x}}_3\right\}\}$	0.29	0.25
$M_3:\{\left\{{\mathit{x}}_1\right\},\left\{{\mathit{x}}_2{\mathit{x}}_3\right\}\}$	0.09	0.11
$M_4:\{\left\{{\mathit{x}}_2\right\},\left\{{\mathit{x}}_1{\mathit{x}}_3\right\}\}$	0.10	0.09
$M_5:\{\left\{{\mathit{x}}_3\right\},\left\{{\mathit{x}}_1{\mathit{x}}_2\right\}\}$	0.13	0.10

The BMA approach to meta-analysis involves averaging over all the possible models when making inferences about the quantities of interest. For example, for the dataset considered in this case study, if $\theta$ is the treatment effect under the control treatment, its posterior distribution, for the data given, is:

$$\pi \left(\theta \right|\mathrm{data})=\sum _{m=1}^{\left|\mathcal{M}\right|}\pi \left(\theta \right|M_m,\mathrm{data})Pr\left(M_m|\mathrm{data}\right),$$

(2)

i.e., the average of the posterior distributions under each of the models (“type of heterogeneity”) considered, weighted by its posterior model probability. For instance, the posterior mean for $\theta$ is a weighted average of the posterior means in each model:

$$\mathbb{E}\left(\theta |\mathrm{data}\right)=\sum _{m=1}^{\left|\mathcal{M}\right|}\mathbb{E}\left(\theta |M_m,\mathrm{data}\right)Pr\left(M_m|\mathrm{data}\right),$$

(3)

where the posterior probability for model $M_m$ can be obtained by:

$$Pr\left(M_m|\mathrm{data}\right)=\frac{Pr\left(M_m\right)Pr\left(\mathrm{data}|M_m\right)}{{\sum }_{m=1}^{\left|\mathcal{M}\right|}Pr\left(M_m\right)Pr\left(\mathrm{data}|M_m\right)},m=1,\dots ,\left|\mathcal{M}\right|,$$

(4)

where:

$$Pr\left(\mathrm{data}|M_m\right)=\int Pr\left(\mathrm{data}|{\theta }_m,M_m\right)Pr\left({\theta }_m|M_m\right)d{\theta }_m,$$

(5)

is the integrated likelihood of the model $M_m$, ${\theta }_m$ is the vector of the parameters of model $M_m$, $Pr\left({\theta }_m|M_m\right)$ is the prior density of ${\theta }_m$ under model $M_m,$$Pr\left(\mathrm{data}|{\theta }_m,M_m\right)$ is the likelihood and $Pr\left(M_m\right)$ is the prior probability of model $M_m.$ All probabilities are implicitly conditional on $\mathcal{M},$ the set of all models being considered, where $\left|\mathcal{M}\right|$ represents its cardinal.

1.2. Summary

The rest of this paper is organised as follows. The binomial Bayesian models and the conditional distributions linking the experimental parameters ${\theta }_i$ and the meta-parameter $\theta$ are presented in Section 2, where the Bayesian procedure for clustering the samples and the likelihood of the meta-parameter are also given. The Bayesian model averaging procedure for estimating the meta-parameters is described in Section 3. Three illustrative examples are provided in the following section, with real datasets. Finally, Section 5 summarises the main conclusions drawn and presents some concluding remarks.

2. The Bayesian Binomial Model

Assume a meta-analysis involves k studies that provide k independent discrete samples with the binomial distribution $\{\mathrm{Bin}\left(x_i\right|n_i,{\theta }_i),i=1,\dots ,k\}$, where ${\theta }_i$ represents the treatment effectiveness, $n_i$ the number of patients and $x_i$ the number of successful treatments, conditional on the study i. Assume, moreover, that the prior information on the conditional treatment effectiveness ${\theta }_i$ is weak. Accordingly, the uniform prior $\mathrm{Unif}\left({\theta }_i\right|0,1)$ is used in a context where the data contain zeros [22,23]. Therefore, for $i=1,\dots ,k$, we consider the Bayesian sampling models:

$$M_i:\left\{\mathrm{Bin}\left(x_i\right|n_i,{\theta }_i),\pi \left({\theta }_i\right)={\mathbf{1}}_{(0,1)}\left({\theta }_i\right)\right\},$$

(6)

where:

$$\mathrm{Bin}\left(x_i\right|n_i,{\theta }_i)=Pr\left(x_i\right|n_i,{\theta }_i)=\left({\displaystyle \genfrac{}{}{0pt}{}{n_i}{x_i}}\right){\theta }_i^{x_i}{(1-{\theta }_i)}^{n_i-x_i},x_i=0,1,\dots ,n_i,$$

(7)

and ${\mathbf{1}}_A$ is the indicator function. The value of one is assigned to all elements of A, and zero elsewhere. In this analysis, it is convenient to consider a $0-1$ latent variable x, the meta-variable, which is defined as the result obtained when a treatment with meta-effectiveness $\theta$ is applied to a patient in a virtual study, which is not affected by between-study variability. The distribution of this meta-variable x is of the same type as that of $x_i$, and hence, we have the Bernoulli meta-model $\mathrm{Ber}\left(x\right|\theta )$, where the meta-parameter $\theta$ represents the true (unconditional) treatment effect. This meta-model gives a precise meaning to the meta-parameter $\theta$. The objective Bayesian meta-model M is then given by:

$$M:\left\{Pr\left(x\right|\theta )={\theta }^x{(1-\theta )}^{1-x},\pi \left(\theta \right)={\mathbf{1}}_{(0,1)}\left(\theta \right)\right\}.$$

(8)

The Bayesian meta-analysis is then based on the posterior distribution of the parameter $\theta ,$ which is given by:

$$\pi \left(\theta \right|\mathit{x})\propto f({\mathit{x}}_1,\dots ,{\mathit{x}}_k|\theta )\pi \left(\theta \right),0<\theta <1,$$

(9)

where ${\mathit{x}}_i=(x_i,n_i),i=1,\dots ,k.$ The likelihood function in (9) cannot be obtained with the information on sample ${\mathit{x}}_i$ on study i, which is related to ${\theta }_i$, but not to $\theta$. Therefore, further steps are required to derive an appropriate likelihood function for $\theta$:

• A distribution $\pi \left({\theta }_i\right|\theta )$ is needed to link the experimental parameters ${\theta }_i$ and the meta-parameter $\theta .$ This linking distribution must ensure there is coherence between the conditional and marginal distributions of the experimental parameter and the meta-parameter. Mathematically, this requires that the corresponding bivariate distribution belong to the class of bivariate distributions with given marginals.
• It is clear that the likelihood of $\theta$ strongly depends on the cluster structure of the samples. Therefore, before formulating the likelihood of $\theta$ for the samples ${\mathit{x}}_i,i=1,\dots ,k$, we must address the important question of whether k, the dimension of the model, can be reduced by clustering homogeneous samples.
• In other words, each cluster model indicates a different heterogeneity structure of the sampling model for $\mathit{x}$, and the posterior probability informs us about the uncertainty for this structure. For the data $\mathit{x}=({\mathit{x}}_1,\dots ,{\mathit{x}}_k),$ we need to obtain the likelihood of $\theta$ conditional on a given cluster model. Finally, the likelihood of $\theta$ for the data $\mathit{x}$ is obtained as a mixture of the above conditional likelihood functions.

We now proceed step-by-step.

2.1. Linking the Experimental Parameters with the Meta-Parameter

A conditional distribution $\pi \left({\theta }_i\right|\theta )$, i.e., the linking distribution, is chosen to represent the likelihood of $\theta$ for the available samples. To ensure that this conditional distribution is compatible with the marginal priors $\pi \left({\theta }_i\right)$ and $\pi \left(\theta \right)$ given in (6) and (8), the bivariate distribution $\pi ({\theta }_i,\theta )=\pi \left({\theta }_i\right|\theta )\pi \left(\theta \right)$ must satisfy the integral equations:

$${\int }_0^1\pi ({\theta }_i,\theta )d{\theta }_i=\pi \left(\theta \right)\mathrm{and}{\int }_0^1\pi ({\theta }_i,\theta )d\theta =\pi \left({\theta }_i\right).$$

(10)

Following Moreno et al. [24], we consider the conditional intrinsic linking distributions $\{{\pi }^I\left({\theta }_i\right|\theta ,t),t=1,2,\dots \}$ obtained by comparing model M with model $M_i$, which presents interesting properties as a linking distribution. For any positive integer t, the intrinsic method gives the conditional intrinsic prior as the following mixture of Beta distributions,

$${\pi }^I\left({\theta }_i\right|\theta )=\sum _{z=0}^t\mathrm{Bin}\left(z\right|t,\theta )\times \mathrm{Beta}\left({\theta }_i\right|z+1,t-z+1).$$

(11)

From (11), we obtain:

$$\mathbb{E}\left({\theta }_i\right|\theta )=\frac{1+t\theta }{2+t},\mathrm{and}\mathbb{V}\left({\theta }_i\right|\theta )=\frac{(1+t)(1-2t\theta (\theta -1\left)\right)}{{(2+t)}^2(3+t)},$$

and hence, the hyperparameter t indicates how strongly the conditional distribution ${\pi }^I\left({\theta }_i\right|\theta )$ concentrates mass around $\theta$. In practice, hyperparameter t is fixed. Hence, for the sake of simplicity in notation, we refer to the linking distribution $\pi \left({\theta }_i\right|\theta )$ rather than $\pi ({\theta }_i,|\theta ,t)$.

The bidimensional prior ${\pi }^I({\theta }_i,\theta )={\pi }^I\left({\theta }_i\right|\theta ){\mathbf{1}}_{(0,1)}\left(\theta \right)$ satisfies Equation (10) for any t, and therefore, the linking class of intrinsic distributions and the Bayesian models (6) and (8) are coherent. In the following, we assume that ${\theta }_i,i=1,\dots ,k$, are conditional independent given $\theta$. Therefore, the linking distribution of ${\theta }_1,\dots ,{\theta }_k$ conditional on $\theta$ is given by:

$${\pi }^I({\theta }_1,\dots ,{\theta }_k|\theta )=\prod _{i=1}^k{\pi }^I\left({\theta }_i\right|\theta ).$$

(12)

Finally, observe that the proposed linking intrinsic distribution of ${\theta }_i$, conditional on $\theta$, does not require the use of the logit transformation for the sparse data as is the case with standard random-effect models.

2.2. Clustering the Experimental Samples

Following Moreno et al. [25], we first define what is meant by cluster. The samples ${\mathit{x}}_i$ and ${\mathit{x}}_j,$ $i\ne j$, from $f\left(x\right|{\theta }_i)$ and $f\left(x\right|{\theta }_j),$ respectively, are said to be in the same cluster if ${\theta }_i={\theta }_j.$ The between-study heterogeneity is then determined by the number of clusters and by the location of the samples ${\mathit{x}}_1,\dots ,{\mathit{x}}_k$ within these clusters. The posterior distribution of the clusters is needed in order to draw inferences from these quantities.

To cluster the samples, we adopt the product partition model approach proposed by Barry and Hartigan [26], together with a Bayesian model selection procedure based on Bayes factors for the intrinsic priors for the model parameters and on hierarchical uniform priors for the cluster models.

Following Casella et al. [27], we employ the following notations and expressions in the meta-analysis conducted. For a given p, we define a partition of the samples into p clusters by the vector ${\mathbf{r}}_p=(r_1,\dots ,r_k)$, where $r_i,i=1,\dots ,k$, is an integer between one and p denoting the cluster to which ${\mathit{x}}_i$ is assigned. For example, for $k=3$ as in Figure 1, the possible $\mathbf{r}$ vectors are shown in Table 3.

Table 3. Different cluster configurations in a meta-analysis with $k=3$ trials.

r	Cluster Model (Heterogeneity Structure)
$(1,1,1)$	${\theta }_1={\theta }_2={\theta }_3$ (homogeneity)
$(1,2,2)$	${\theta }_2={\theta }_3$ (type 2–heterogeneity)
$(1,2,1)$	${\theta }_1={\theta }_3$(type 2–heterogeneity)
$(1,1,2)$	${\theta }_1={\theta }_2$ (type 2–heterogeneity)
$(1,2,3)$	all $\theta$s are different (heterogeneity)

2.3. The Likelihood of $\theta$

From (7), given a partition ${\mathbf{r}}_p=(r_1,\dots ,r_k)$, the sampling distribution of $\mathit{x}=({\mathit{x}}_1,\dots ,{\mathit{x}}_k)$ is:

$$f\left(\mathit{x}\right|p,{\mathbf{r}}_p,{\mathbf{\theta }}_p)=\prod _{j=1}^p\left({\displaystyle \genfrac{}{}{0pt}{}{m_j}{s_j}}\right){\theta }_j^{s_j}{(1-{\theta }_j)}^{m_j-s_j},$$

(13)

where ${\mathbf{\theta }}_p=({\theta }_{r_1},\dots ,{\theta }_{r_k})$ is an unknown parameter of dimension p and the component ${\theta }_j$ in (13) corresponds to $r_i=j$, $m_j={\sum }_{i:r_i=j}{n}_i$ and $s_j={\sum }_{i:r_i=j}{x}_i$.

For example, the cluster model given by the heterogeneity structure $(1,2,2)$ in Table 3 has the sampling distribution:

$$\left({\displaystyle \genfrac{}{}{0pt}{}{n_1}{x_1}}\right){\theta }_1^{x_1}{(1-{\theta }_1)}^{n_1-x_1}\left({\displaystyle \genfrac{}{}{0pt}{}{n_2+n_3}{x_2+x_3}}\right){\theta }_2^{x_2+x_3}{(1-{\theta }_2)}^{(n_2+n_3)-(x_2+x_3)}.$$

The heterogeneity partition ${\mathbf{r}}_k=(1,2,\dots ,k)$ has the corresponding likelihood function given by:

$$f\left(\mathit{x}\right|k,{\mathbf{r}}_k,{\mathbf{\theta }}_k)=\prod _{i=1}^k\left({\displaystyle \genfrac{}{}{0pt}{}{n_i}{x_i}}\right){\theta }_i^{x_i}{(1-{\theta }_i)}^{n_i-x_i}.$$

Now, following Moreno et al. [25], integrating out ${\mathbf{\theta }}_p$ with the intrinsic prior ${\displaystyle \pi \left({\mathbf{\theta }}_p\right|p,{\mathbf{r}}_p)=\int {\pi }^I({\theta }_1,\dots ,{\theta }_p|\theta ){\mathbf{1}}_{(0,1)}\left(\theta \right)d\theta }$, we obtain the likelihood of $\theta$, conditional on the cluster model $(p,{\mathbf{r}}_{\mathbf{p}}).$ After some algebra and using the assistance Wolfram Mathematica, the likelihood of $\theta$, conditional on the cluster model $(p,{\mathbf{r}}_{\mathbf{p}})$, is given by:

$$\begin{array}{ccc}\hfill f(\mathit{x}|p,{\mathbf{r}}_p,\theta )& =& \prod _{j=1}^p{\int }_0^{1}f(\mathit{x}|p,{\mathbf{r}}_p,\mathbf{\theta }{}_p)\pi \left({\theta }_j\right|\theta )d{\theta }_j\hfill \\ & =& {(1+t)}^p{(1-\theta )}^{tp}\prod _{j=1}^p\frac{\Gamma (s_j+1)\Gamma (m_j+t-s_j+1)}{\Gamma (m_j+t+2)}{}_3{F}_2({\mathbf{a}}_j,{\mathbf{b}}_j,\frac{\theta }{\theta -1}),\hfill \end{array}$$

(14)

where ${}_3{F}_2(\mathbf{v},\mathbf{w},z)$ denotes the generalised hypergeometric function with argument z and vector parameters $\mathbf{v}$ and $\mathbf{w}$ of dimensions two and three, respectively, ${\mathbf{a}}_j=(-t,-t,s_j+1)$ and ${\mathbf{b}}_j=(1,-m_j-t+s_j).$

To derive the necessary likelihood function of $\theta$, we then integrate out (14) with respect to a discrete prior on $(p,{\mathbf{r}}_p).$ As recommended by Moreno et al., an appropriate uniform hierarchical prior is used, in which each factorised prior is uniform.

$$\pi (p,{\mathbf{r}}_p)=\pi \left(p\right|{\mathbf{r}}_p)\pi \left(p\right)=\frac{k_1!·\dots ·k_p!}{k!}\frac{{\prod }_{i=1}^k\left({\sum }_{j=1}^p\mathbf{1}(k_j=i)\right)!}{b(k,p)}\frac{1}{k}.$$

(15)

For example, for the cluster configuration $(1,2,2)$ in Table 3, the uniform hierarchical prior is:

$${\displaystyle \pi (2,(1,2,2))=\frac{1!2!}{3!}·\frac{1!}{1}·\frac{1}{3}=\frac{1}{9}.}$$

The complexity in this task lies in knowing how many elements are in each heterogeneity subclass. According to Casella et al. [27], who presented a comprehensive description of these calculations, the first product factor in (15) corresponds to the inverse of the multinomial factor, where $k_1\le k_2\le \dots \le k_p$ are integers assigned to cluster $1,\dots ,p$ such that $k_1+\dots +k_p=k.$ The second product factor takes into account the redundancies in the number of samples $k_1,\dots ,k_p$, and $b(k,p)$ is the number of these possible sizes of $k_j$ that satisfy the recursive equation $b(k,p)=b(k-1,p-1)+b(k-p,p),1\le p\le k$ with $b(k,1)=b(k,k)=1.$ For each value given for k and $p,$ this number is readily obtained with the Mathematica package PartitionFunctionP. The third factor corresponds to the discrete uniform distribution of the number of studies in the meta-analysis.

Finally, from (14) and (15), the (unconditional) likelihood of $\theta$ for the data $\mathit{x}$ is given by:

$$f\left(\mathit{x}\right|\theta )=\sum _{p=1}^k\left(\sum _{{\mathbf{r}}_p}f\left(\mathit{x}\right|p,{\mathbf{r}}_p,\theta )\pi (p,{\mathbf{r}}_p)\right).$$

(16)

3. Bayesian Model Averaging in the Meta-Analysis

As mentioned in Section 1, the BMA approach to meta-analysis requires us to average all possible models (heterogeneity structures) when making inferences on $\theta$. In this case, the posterior probabilities in (4) correspond to those of any heterogeneity structure given by a pair $(p,{\mathbf{r}}_p)$, which is represented by:

$$Pr(p,{\mathbf{r}}_p|\mathit{x})=\frac{m_{{\mathbf{r}}_p}\left(\mathit{x}\right|p,{\mathbf{r}}_p)\pi (p,{\mathbf{r}}_p)}{{\sum }_{p=1}^k\left({\sum }_{{\mathbf{r}}_p}{m}_{{\mathbf{r}}_p}\left(\mathit{x}\right|p,{\mathbf{r}}_p)\pi (p,{\mathbf{r}}_p)\right)},$$

(17)

where ${\displaystyle m_{{\mathbf{r}}_p}\left(\mathit{x}\right|p,{\mathbf{r}}_p)=\int f\left(\mathit{x}\right|p,{\mathbf{r}}_p,{\mathit{\theta }}_p)\pi \left({\mathit{\theta }}_p\right|p,{\mathbf{r}}_p)d{\mathit{\theta }}_p}$ is the marginal of the data $\mathit{x}$ conditional on model $(p,{\mathbf{r}}_p),$ with $f\left(\mathit{x}\right|p,{\mathbf{r}}_p,{\mathit{\theta }}_p)$ and $\pi \left({\mathit{\theta }}_p\right|p,{\mathbf{r}}_p)$ as in (13) and (15), respectively. These posterior model probabilities $Pr(p,{\mathbf{r}}_p|\mathit{x})$ are the weights for the meta inference.

The posterior distribution in (2) becomes:

$$\pi \left(\theta \right|\mathit{x})=\sum _{{\mathbf{r}}_p}\pi \left(\theta \right|\mathit{x},p,{\mathbf{r}}_p)Pr(p,{\mathbf{r}}_p),$$

(18)

where, since as in (8) $\pi \left(\theta \right)={\mathbf{1}}_{(0,1)}\left(\theta \right),$

$$\pi \left(\theta \right|\mathit{x},p,{\mathbf{r}}_p)=\frac{f\left(\mathit{x}\right|p,{\mathbf{r}}_p,\theta )}{{\int }_0^{1}f\left(\mathit{x}\right|p,{\mathbf{r}}_p,\theta )d\theta },0<\theta <1.$$

(19)

The posterior distribution in (18) is computed numerically over the parametric space $\Theta =(0,1)$ using Wolfram Mathematica, which has a huge library of ready-to-use functions and, moreover, provides a simple code. Furthermore, once the posterior distribution has been obtained, the command ProbabilityDistribution can be used to generate any sample of the posterior distribution of the parameter of interest and its transforms, as shown in the examples given in Section 4.

4. Illustrations

To illustrate the arguments developed in the preceding section, we now analyse two real datasets. For these case studies, we assume that $t=48,$ indicating that the intrinsic link distribution concentrates a considerable mass of probability around $\theta .$ Other values of t have also been used, and the results obtained are very robust. The Mathematica code for the case study datasets is available from the authors upon request.

4.1. Motivating Example Revisited

Returning to the dataset considered in Section 1, from Table 2, observe that we have different posterior probabilities for the cluster structures and thus for the Bayesian model average of the true treatment effect under treatment (T) or control (C), ${\theta }_T$ and ${\theta }_C$. All the measures of interest can be obtained from the BMA posterior distribution in (18). Table 4 shows the posterior summaries of the PTLD rate for both cases (mean and highest density interval (HDI)).

Table 4. Posterior PTLD rates $\mathbb{E}\left(\theta \right|\mathit{x})$ under control and experimental treatments. HDI, highest density interval; RR, risks ratio.

Control		Treatment
$\mathbb{E}\left({\theta }_C\right|\mathit{x})$	$95\%$ HDI	$\mathbb{E}\left({\theta }_T\right|\mathit{x})$	$95\%$ HDI
0.030	(0, 0.109)	0.038	(0, 0.127)
log(RR)
$\mathbb{E}(log(\mathrm{RR}\left)\right|\mathit{x})$		$95\%$ HDI
0.26		(–3.27, 3.91)

Figure 2 (left panel) shows the BMA posterior density of ${\theta }_C$ and ${\theta }_T$ given by (18). It is apparent that the posterior density of $\theta$ under the experimental treatment is slightly shifted towards higher PTLD rates with respect to the control treatment. Observe, moreover, that the sparsity of the data yields reverse J-shaped posterior distributions with a mode at $\theta =0.$

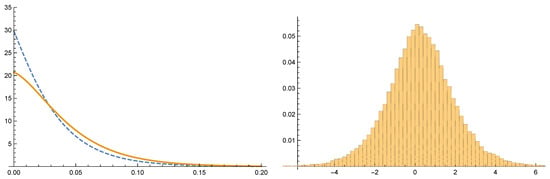
Figure 2. (Left) BMA posterior density of the meta-parameters ${\theta }_C$ (dashed line) and ${\theta }_T$ (continuous line). (Right) Posterior distribution of the logRR.

On the other hand, since we have an explicit expression for the posterior distribution of ${\theta }_C$ and ${\theta }_T$ from (18), it is straightforward to simulate these independent distributions. The usual parameters of interest, such as the risks ratio or the odds ratio and their log, are obtained immediately using the corresponding transform of the above-simulated values. Figure 2 (right panel) shows the posterior distribution of the log risks ratio (RR), where the (posterior) probability $Pr(log(RR)>0|\mathit{x})=Pr(RR>1\left|\mathit{x}\right)=0.57.$

For comparison, Table 5 shows the estimations of the risk and odds ratio from Crins et al. [21] and from Günhan et al. [12], together with those from our BMA approach.

Table 5. Estimated risks and odds ratios in the motivating example (revisited).

Quantity	Crins et al. [21]	BMA
	& Günhan et al. [12]
Risks ratio	$1.60$	1.30
	($95\%$ HDI 0.22–29.96)	($95\%$ HDI 0.04–44.66)
Odds ratio	1.98	1.32
	($95\%$ HDI 0.20–25.18)	($95\%$ HDI 0.038–49.899)

These estimated values show some differences from those obtained by Crins et al. and Günhan et al. Although Crins et al. asserted that there is no evidence for between-trial heterogeneity for PTLD outcomes, this conclusion does not follow from Table 2. Certainly, the homogeneity model has the largest posterior probability, for both treatment options, but a large proportion of the uncertainty accumulated in the remaining heterogeneity structures must be considered, in line with the BMA approach. This, together with the very small number of informative studies conducted in this respect, no more than three, accounts for the wider intervals obtained by the BMA procedure.

4.2. Another Case with Few and Double-Zero Studies

The dataset in Table 6 is extracted from Cosmi et al. [28] and corresponds to the comparison of total mortality in four studies ($k=4$) of patients treated with ticlopidine (T) versus oral anticoagulation for coronary stenting (C). Cosmi et al. found no evidence of heterogeneity, and $I^2$ was estimated at $0.0\%.$ This fact occurs frequently for meta-analyses with a small number of studies [29]. Furthermore, the Q test for this situation possesses a very low power [30]. As a consequence, we have little information on homogeneity (heterogeneity) either way.

Table 6. Data in Cosmi et al.

Study	Treatment		Control
	Events	Total	Events	Total
FANTASTIC (${\mathit{x}}_1$)	2	243	4	230
ISAR (${\mathit{x}}_2$)	1	257	2	260
MATTIS (${\mathit{x}}_3$)	3	177	2	173
STARS (${\mathit{x}}_4$)	0	546	0	550

In this case, there are 15 models. These are all averaged in the BMA posterior distributions, but for simplicity, the top cluster models (posterior probability greater than 0.05) for both treatments are shown in Table 7. The homogeneity cluster model is the best model for the control treatment, but only has a 0.221 mass of probability, while the remaining probability is distributed among the other 14 models. The outcome is similar for the experimental treatment, for which the best option is now the heterogeneity cluster model. Obviously, these between-study variabilities should be considered in any meta-analysis.

Table 7. Top cluster models in Cosmi et al.

Treatment		Control
Cluster Model	Post. Prob.	Cluster Model	Post. Prob.
$\left\{{\mathit{x}}_1\right\}\left\{{\mathit{x}}_2\right\}\left\{{\mathit{x}}_3\right\}\left\{{\mathit{x}}_4\right\}$	0.303	$\left\{{\mathit{x}}_1{\mathit{x}}_2{\mathit{x}}_3{\mathit{x}}_4\right\}$	0.221
$\left\{{\mathit{x}}_1{\mathit{x}}_2{\mathit{x}}_3{\mathit{x}}_4\right\}$	0.124	$\left\{{\mathit{x}}_1\right\}\left\{{\mathit{x}}_2\right\}\left\{{\mathit{x}}_3\right\}\left\{{\mathit{x}}_4\right\}$	0.216
$\left\{{\mathit{x}}_1{\mathit{x}}_2{\mathit{x}}_3\right\}$$\left\{{\mathit{x}}_4\right\}$	0.115	$\left\{{\mathit{x}}_1{\mathit{x}}_3\right\}$$\left\{{\mathit{x}}_2{\mathit{x}}_4\right\}$	0.122
$\left\{{\mathit{x}}_1\right\}$$\left\{{\mathit{x}}_2{\mathit{x}}_3\right\}$$\left\{{\mathit{x}}_4\right\}$	0.094	$\left\{{\mathit{x}}_1\right\}$$\left\{{\mathit{x}}_2{\mathit{x}}_4\right\}$$\left\{{\mathit{x}}_3\right\}$	0.079
$\left\{{\mathit{x}}_1{\mathit{x}}_3\right\}$$\left\{{\mathit{x}}_2\right\}$$\left\{{\mathit{x}}_4\right\}$	0.085	$\left\{{\mathit{x}}_1{\mathit{x}}_2\right\}$$\left\{{\mathit{x}}_3\right\}$$\left\{{\mathit{x}}_4\right\}$	0.073
$\left\{{\mathit{x}}_1{\mathit{x}}_3\right\}$$\left\{{\mathit{x}}_2\right\}{\mathit{x}}_4\}$	0.072	$\left\{{\mathit{x}}_1{\mathit{x}}_2{\mathit{x}}_4\right\}$$\left\{{\mathit{x}}_3\right\}$	0.068
$\left\{{\mathit{x}}_1{\mathit{x}}_2\right\}$$\left\{{\mathit{x}}_3\right\}$$\left\{{\mathit{x}}_4\right\}$	0.069	$\left\{{\mathit{x}}_1{\mathit{x}}_2{\mathit{x}}_3\right\}$$\left\{{\mathit{x}}_4\right\}$	0.060
the rest	<0.05	$\left\{{\mathit{x}}_1{\mathit{x}}_3\right\}$$\left\{{\mathit{x}}_2\right\}$$\left\{{\mathit{x}}_4\right\}$	0.051
		the rest	<0.05

Cosmi et al. used the Mantel-Haenszel method under random-effects to estimate the risks ratio, for which a value of 0.73 ($95\%$ CI 0.25–2.18) was obtained. The main conclusion derived from these data was that ticlopidine plus aspirin versus oral anticoagulation did not affect all-cause mortality. Using the proposed BMA approach, a risks ratio of 0.959 is obtained, which is in line with the value reported by Cosmi et al. However, once again, a realistic and larger interval becomes apparent when all of the uncertainty is managed via the BMA perspective ($95\%$ HDI 0.02–41.86).

5. Conclusions

The question of statistical heterogeneity in a meta-analysis based on a relatively small number of studies is important and has been addressed by Friede et al. [17], IntHout et al. [10] and Pateras et al. [31], among many others. Moreover, if zero events occur in these small trials, the challenge is multiplied. There has been much debate about the presence of significant between-study heterogeneity in these cases, and it has been reported that the misuse of continuity correction procedures can lead to incorrect inferences being drawn [9]. In this respect, Veroniki et al. [32] catalogued various methods for estimating between-study heterogeneity. The examples given in the present paper also show that the usual measures employed to determine the presence or otherwise of heterogeneity, $I^2$ and $\tau$, may not consider all the scenarios contained in the meta-analysis, and therefore, it is currently recommended to accompany the $I^2$ statistic and the estimate of $\tau$ with a confidence interval. Such a confidence interval will be very wide, especially in the case of a small number of effect sizes in a meta-analysis.

The Bayesian model averaging that we propose is an intuitively attractive approach to the problem of accounting for heterogeneity uncertainty, even in meta-analyses with zero events. This method involves averaging all the heterogeneity structures (models) obtained by clustering the observed sample when making inferences about the true treatment effect. The number of models (types of heterogeneity) considered in BMA rises in line with the number k of studies, according to Bell’s number [27]. However, this number is easily manageable for the case of few studies (2 for $k=2,$ 5 for $k=3$, 15 for $k=4$, and 52 for the limit case $k=5$), and therefore, the computation of the posterior probabilities of each model and the derivation of the posterior BMA distribution of the parameter of interest are immediate and computationally feasible. In this respect, Rhodes et al. [33] conducted an extensive review of the Cochrane Database of Systematic Reviews (CDSR), developed in Davey et al. [34], and pointed out that: “Of 22453 meta-analyses from CDSR, containing at least two studies, just under $75\%$ contained five or fewer studies”. We recommend our method when the meta-analysis has 10 or fewer studies.

The clustering procedure considered takes into account all uncertainty in the heterogeneity structures. This fact has important consequences for treatment comparison, due to the likelihood of $\theta$ being different for each heterogeneity configuration.

On the other hand, observed heterogeneity could be a starting point to investigate sources of heterogeneity. In this paper, every potential cluster model is estimated. However, this might also be a starting point to investigate sources of heterogeneity before the simple model averaging takes place.

From these considerations, we conclude that the BMA procedure proposed is not only more compelling in a conceptual sense, but also provides novel probabilistic clustering methods that are capable of resolving challenging meta-analysis scenarios, in which there are few studies and sparse data.