Correlated Functional Models with Derivative Information for Modeling Microfading Spectrometry Data on Rock Art Paintings

Abstract

Rock art paintings present high sensitivity to light, and an exhaustive evaluation of the potential color degradation effects is essential for further conservation and preservation actions on these rock art systems. Microfading spectrometry (MFS) is a technique that provides time series of stochastic observations that represent color fading over time at the measured points on the surface under study. In this work, a reliable and robust modeling framework for a short and greatly fluctuating observation dataset collected over the surfaces of rock art paintings located on the walls of Cova Remigia in Ares del Maestrat, Castellón, Spain, is presented. The model is based on a spatially correlated spline-based time series model that takes into account prior information in the form of model derivatives to guarantee monotonicity and long-term saturation for predictions of new color fading estimates at unobserved locations on the surface. The correlation among the (spatially located) time series is modeled by defining Gaussian process (GP) priors over the spline coefficients across time series. The goal is to obtain a complete spatio-temporal mapping of color fading estimates for the study area, which results in very important and useful information that will potentially serve to create better policies and guidelines for heritage preservation and sustainable rock art cultural tourism.

1. Introduction

Prehistoric rock art paintings (see, for example, Figure 1, left plot) are exposed to environmental elements that can accelerate their degradation, increasing the risk of losing such valuable cultural assets from past societies. The study and documentation of potential damages to these rock art systems are essential for their conservation and preservation [1,2,3], and it is a priority for cultural and research organizations, scientists and government agencies. The present research is focused on the paintings located in Cova Remigia open-air rock art shelter in Castellón (Spain), which is part of the Spanish Levantine rock art paintings of the Mediterranean basin on the Iberian Peninsula declared World Heritage by UNESCO in 1998. There is still a lack of knowledge about their conservation status and how rock art is deteriorating [4,5,6].

Rock art paintings are prone to different types of weathering, not only due to human activity but mainly through natural weathering processes [7,8]. Particularly, paintings of Levantine environments such as Cova Remigia are at risk, threatened by warming temperatures, higher seasonal variable precipitation and increased wind speeds. Furthermore, long and intense exposure to sunlight has adverse effects on these open-air shelters due to thermal and photochemical degradation of the historic materials, and changes in the spectral properties (color) of the materials are one of the main effects. Heating from insolation results in rapid temperature variations on the rock surface relative to its interior causing physical failure. In addition, photochemical degradation of pigments has also been observed. This is a surface effect, and the degree of color change depends on the chemical composition of the pigment [4,9].

This study is focused on the study and documentation of the degree of color-changing/fading of paintings, patinas and host rock due to the effects of insolation. Materials with higher light sensitivity usually experience rapid color changes during the early stages of light exposure, followed by slower rates after maximum fading has occurred; the total disappearance of the substance that produces the color (chromophore) occurs at this second stage of the fading [10,11,12,13]. For these reasons, fading cannot decrease with time and it is expected to stabilize in the long term. Materials can show different times to saturation depending on their physicochemical properties and concentrations of chromophores [3].

Microfading spectrometry (MFS) is a method for assessing the stability to light irradiation of cultural heritage objects. This method allows for real-time monitoring of spectral changes of a cultural heritage object by undertaking in situ lightfastness measurements on the surface under study [14,15]. MFS provides for each measured point on the surface of a rock art painting a time series of observations that represents potential color fading over time given exposure to light [16]. Hence, microfading measurements can be seen as observations of an underlying spatio-temporal stochastic process.

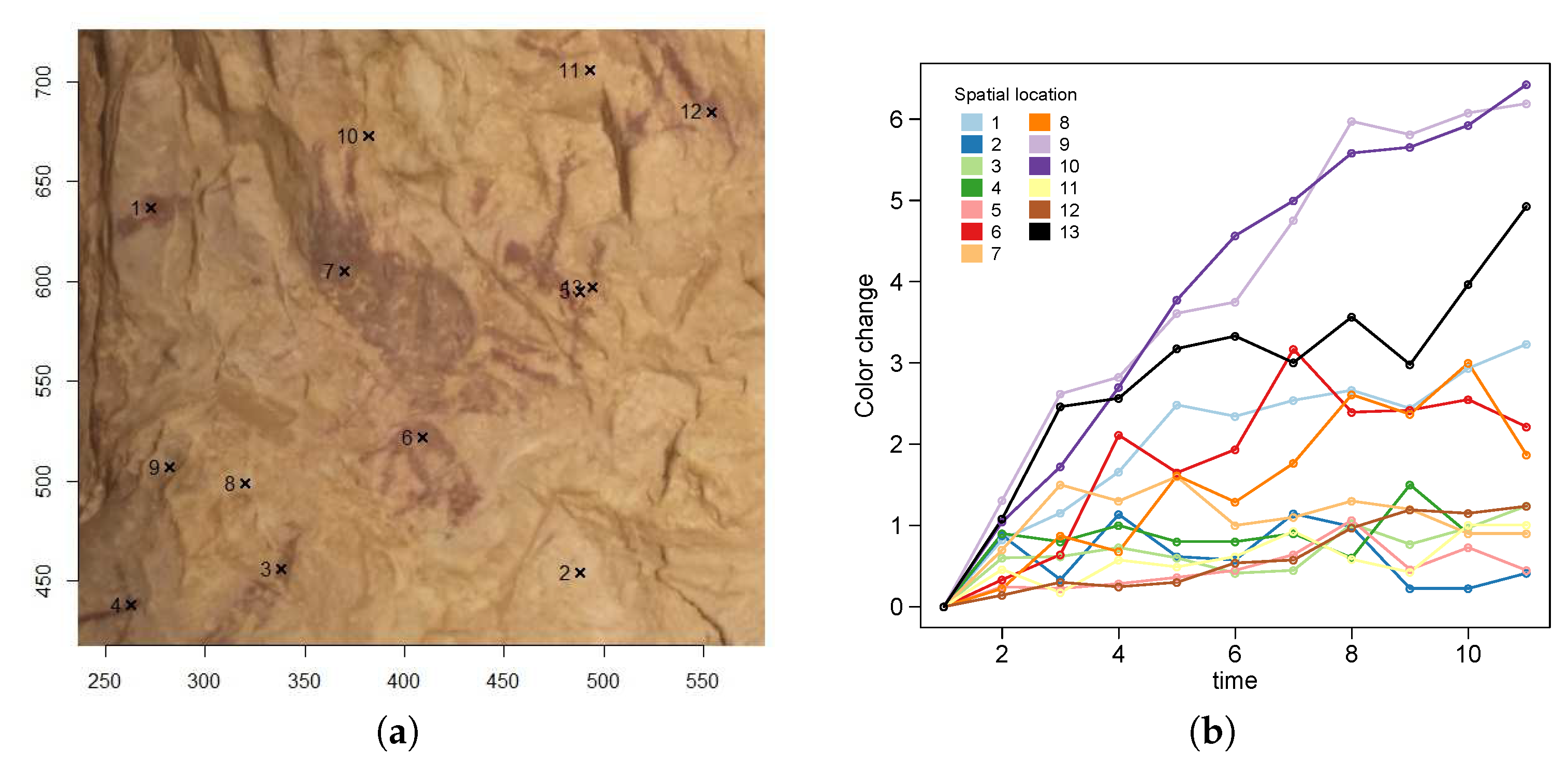
The microfading instrument is very sensitive to movement and glossy surface effects, causing extremely large fluctuations in the measurements. Furthermore, they can be easily contaminated by changes in the lighting conditions when the measurements are performed in outside environments. These large fluctuations and possible systematic noise effects in the observations can lead to models that do not satisfy those properties of non-decreasing monotonicity and long-term stabilization of color fading over time. Thus, it is recommended to include additional information in the models in order to meet these properties and to ensure reliable properties for color fading estimates in new unobserved locations. Existing lightfastness studies on these systems have been limited to analyzing a few measured points on the surfaces of the rock art paintings because these measurements are largely time-consuming and difficult to materialize under harsh conditions (Figure 1, right plot).

Hence, in this paper a reliable modeling framework for a short and greatly fluctuating observation dataset is proposed, aiming at extending the analysis of color fading at locations on the surfaces of rock art paintings where no observations are available. The model is based on spatially correlated time series functions with the consideration of additional information on the derivatives of the functions aiming at ensuring the functions are monotonically non-decreasing and saturated in the long term. A complete map of potential color fading estimates for the entire surface under study and over time offers important and useful information in order to achieve further successful conservation actions and policies. Although color fading is only one of the potentially damaging effects on the surfaces of rock art paintings, color fading is an important effect to control.

Information of potential color fading estimates, alone or in conjunction with the evaluation of other potential damaging factors, will help to develop conservation policies. A comprehensive evaluation of the state of preservation of rock art paintings together with a risk assessment plan that considers their potential damage due to exposure to environmental elements will serve to better allocate resources and devise a plan of heritage conservation tasks for these rock art systems. The research will also allow creating policies and guidelines for sustainable rock art cultural tourism, guaranteeing the conservation and preservation of this enormous patrimonial legacy for the enjoyment of present and future generations and at the same time creating further economic benefits in the region and community. Once the key elements that affect the long-term conservation of the rock art paintings are well understood, the next step is to consider the economic factors that drive tourism and increase the public interest in this geographical area. This is an enormous challenge, as rock art is of evident contemporary cultural and social value, but at the same time it can be difficult to create sustainable tourism businesses centered around these sites. This makes good understanding and documentation of the potential damages on these systems an essential matter.

The rest of the paper is structured as follows. In Section 2, a brief bibliographic review of correlated functional models and monotonic approximations is done. Section 3 states the proposed modeling methodology in detail. Section 4 describes the case study and the available data set. Section 5 and Section 6 focus on the modeling and inference formulation, respectively. Section 7 describes model checking and model selection procedures. Section 8 analyzes and evaluates the fit of the model and describes the results of applying the model to the data set. Section 9 briefly discusses the conducted research and results in relation to the applied field. Section 10 presents brief conclusions of the work.

2. Background Methods

Functional data usually refer to independent realizations of a functional random variable that take values in a continuous space. Time series of observations (e.g., color-fading time series) might be the most common case of functional data in 1D, but spatially distributed observations can also be seen as functional data in a 2D space and spatio-temporal observations in a 3D space. In order to construct a model useful for making predictions of new functional data as a function of new values of the variables in the input space, the process must be considered as an structured process with dependence among observations.

Correlated functional models consider the observed functional data as non-independent functions. A popular approach for correlated space-time functional data consists of three-way (spatial, 2D, and temporal, 1D) penalized spline models [17] with different basis constructions based on Kronecker products [18,19] or additive basis components [20]. Aguilera, et al. [21] proposed a mixture of a functional regression model for functional response and a penalized spline spatial regression. However, in general, these models have large numbers of parameters.

Another interesting approach consists of considering the space-time structured observations as stochastic realizations of a Gaussian process (GP) prior with a spatio-temporal covariance function. GPs [22,23] are natural and flexible non-parametric prior models for D-dimensional (e.g., space and time) functions with multivariate predictors (input variables) in each dimension. In a separable form, the space-time covariance function is made of two independent processes, space and time [24]. In a non-separable form, the covariance function models space–time interaction [25,26]. The drawback of GP models is their expensive computational demand in covariance matrix inversion that is in general a $O\left({\left(NT\right)}^3\right)$ operation, with N being the number of spatial locations, with coordinates $(S_x,S_y)$, and T being the number of time points.

A geostatistical approach for spatio-temporal data is the kriging approach for 1D-functional data [27], in which the 1D-functional data are a time series. The spatial correlation of the time series is modeled in the covariance function. The dimension of the covariance matrix is $N\times N$ and the matrix inversion is an $O\left(N^3\right)$ operation. Although this approach requires less computational effort than the spatio-temporal GPs, it has the drawback of having less flexible spatio-temporal structure since the same spatial structure is defined for all time series. A related approach can be found in [28], where the spatial correlation between the time series is modeled by defining GPs with a spatial covariance function across the time series functional coefficients. This construction allows for modeling different spatial structures for the different orders of the coefficients.

Inducing monotonicity or gradient to functions can be expressed in terms of the derivative of the function, as either the sign of a derivative for monotonicity or the value of a derivative for gradients. As differentiation is a linear operator, the derivatives of both semiparametric models and GP models can be used as additional observations jointly with the regular observations in order to force the function to fit these properties [29,30]. Riihimäki and Vehtari [31] used a GP model and the information of its derivative process to induce monotonicity on the functions using virtual observations of the sign of the derivatives. It is known that there are practical issues with this approach of inducing monotonicity through virtual observations, since the posterior distributions of the functions depend on the number of the inducing points; when the number of points is too large, the posteriors tend to be overly smoothed. This over-smoothing effect appears to be particularly significant when using GPs as compared to splines. However, if the function is smooth, this problem can be avoided in practice by choosing only a few inducing points ([32], Chapter 4). In [33] the authors used the same idea of using virtual observations to include constraints concerning the derivative of the functions in deep probabilistic models.

On the other hand, monotonicity in semiparametric models can be forced by construction. Shively, et al. [30] proposes two approaches to obtain monotonic functions, the first using a modified characterization of the smooth monotone functions proposed in [34] that allows for unconstrained estimation, and the second using constrained prior distributions for the regression coefficients to ensure monotonicity. Brezger and Steiner [35] induces monotonicity on semiparametric and non-parametric models by imposing the restriction that the regression coefficients are ordered, sometimes also known as isotonic regression. These constraints are imposed by specifying truncated prior distributions in order to reject the undesired draws for the parameters in the MCMC sampling. Reich, et al. [36] used a similar approach: imposing order to the regression parameters by means of reparameterizing and constraining these parameters with application to a quantile regression model. Regarding imposing monotonicity by construction in non-parametric GP prior models, this becomes more difficult. Generic GP prior models do not restrict the function values to be monotonically increasing or decreasing with respect to input variables. Recently, Andersen, et al. [37] proposed a monotonic model based on applying a non-linear transformation of a GP and then using Hilbert space methods to approximate the model to make the inference tractable [38].

3. Proposed Methodology

In this study, a specific application with the aim of modeling and predicting color fading time series at new unobserved spatial locations on the surfaces of rock art paintings was carried out. The main motivation of this study is to construct a model that exploits the correlation structure of the data in order to extend the analysis and make useful predictions, in the scenario of a short set of sampling observations, as in the case of microfading measurements on rock art paintings. In fact, in the present csae study, only 13 measured locations on the surface were collected. A spatially correlated time series model with information of the derivative process is proposed, and the spatial correlation among time series and their derivatives is established by defining multivariate GPs over the spline coefficients across the time series. A GP is a natural way to evaluate the covariance structure of the data and use it to make useful generalizations. This approach of combining spline functions for the temporal dimension and multivariate GPs to spatially correlate the spline coefficients is an original spatio-temporal approach, seldom implemented in practice (a related but simpler approach can be found in [28]) that, as discussed in Section 6, is flexible and can reasonably consider different covariance structures, with different complexities between space and knots.

The color-fading time series are modeled as penalized cubic-spline functions. The derivative of a semiparametric model such as a spline model is still a linear model and can be used as an additional observation together with actual observations, thereby encoding derivative information of the functions into the modeling. Derivative observations of both the sign and the values of the partial derivatives are used to induce (non-decreasing) monotonicity and long-term saturation of color fading (long term color fading [3]), respectively, as a function of time. In order to force the functions to be zero at the starting points of every time series, observations with the absence of noise are used at these points. A thorough illustration of the implementation of both zero and first order modeling constraints to control the values of the function and the dynamics (monotonicity and gradients) of the function, respectively, in a full Bayesian framework, was carried out. Monotonicity through virtual observations in Bayesian GPs was originally proposed by Riihimäki and Vehtari [31], and in this work, this idea is used on spline functions.

Color fading is mainly related to physicochemical properties of the measured surface. Physicochemical data for all the points on the surface as inputs to predict new curves are hard to obtain. Instead, image color values can be used as surrogate input variables to construct and evaluate the correlation, since these image color variables are known to be related to the physicochemical properties of the imaged material [39]. A multivariate covariance function in a GP allows modeling trichromatic image color variables jointly with spatial distances as inputs to evaluate the covariance structure of the data.

For model evaluation and comparison, the same model but without derivative information was also fitted. Cross-validation procedures were conducted (see Section 7) to compute the posterior predictive checks, the expected log predictive density and the mean square predictive errors in order to do model checking and selection and evaluate the predictive performance.

4. Case Study and Data Description

Microfade testing allows for real-time monitoring of spectral changes of a small area (diameter of 0.5 mm) of a cultural heritage object by exposing it to light. This method was developed by Whitmore and others [14,15] and has been extensively used to study the lightfastness of cultural objects [40,41,42]. In this practical case, we sought to evaluate and document the degree of color fading over time and space on rock art paintings located in Cova Remigia rock-shelter (in Ares del Maestrat, Castellón, Spain) caused by direct solar irradiation. This site is particularly interesting because there are hundreds of tiny (cm-level) rock art figures. These have been drawn using black and red pigments (and white), instead of red like the rest of rock art caves, which makes Cova Remigia particularly important in the overall context. There is still a lack of knowledge about their conservation status and how the rock art is deteriorating. The current study analyzes photostability and potential color change, which has important implications for Cova Remigia, since it describes the paintings and explains their long-term degradation under future environmental conditions.

MFS testing at each measured point on the surface gives rise to a time series that represents color fading over time. Color fading can be described in terms of CIE color differences ${\Delta }{E}_{ab}^{*}$ [39]. The microfading measurements have a duration of 10 min. The sampling frequency will be once per minute, such that the resulting time series will consist of 11 time points ($T=11$), represented by the time input variable $\mathit{t}=\{t_l=l:l=1,2,\cdots ,T\}$. Since these measurements are largely time-consuming and difficult to materialize, especially in these rock art systems, the MFS dataset available only consisted of 13 observed locations on the surface ($N=13$). Figure 2-left shows their pixel locations on a color image of the study area; each location incorporates color fading time series of observations (Figure 2, right plot).

The number of available input variables to evaluate the covariance between spatial locations is 5 ($D=5$), which are the three image color variables per spatial location i ($i=1,2,\cdots ,N$): hue ($H_i$), saturation ($S_i$) and intensity ($I_i$), and the two spatial coordinates ${S_x}_i$ and ${S_y}_i$.

Table 1. Summary statistics of the input variables.

	H	S	I	${\mathit{S}}_{\mathit{x}}$	${\mathit{S}}_{\mathit{y}}$
Mean	5.255	9.704	5.155	3.549	4.969
Std. Dev.	1.0	1.0	1.0	0.732	0.674
1st Qu.	4.359	9.042	4.603	2.910	4.387
3rd Qu.	5.913	10.273	5.772	4.187	5.551

contains summary statistics for these input variables, which have been rescaled by dividing by their standard deviations. Spatial coordinates ${\mathit{S}}_{\mathit{x}}$ and ${\mathit{S}}_{\mathit{y}}$ were divided by their common standard deviation.

Each time series is modeled as a spline-based function. The order or number of knots K of the spline functions is set to 3 and placed uniformly through the time points variable. Due to the large fluctuations present in the measurements conducted on these rock art systems and the limited sample data set, some modeling issues can arise, such as not starting at zero, not being monotonically non-decreasing or not stabilizing in the long term as a function of time, which are properties assumed for the color fading curves, as discussed above. Most of the rock art painting systems analyzed so far show stabilization at or before the 10-minute MFS monitoring measurements.

Therefore, the functions must be constrained to be zero at observations in subset $B=\left\{\right(l,i):l=1\}$ of starting points of every time series, that is, the predicted time series must start at zero. Subset $E=\left\{\right(l,i):l=11\}$ contains the ending points of every time series, the functions will be constrained to reach a stabilization as a function of time. The functions are guaranteed to be monotonically non-decreasing as a function of time when the partial derivative is non-negative. Virtual points for monotonicity will be appropriately placed at two time points of every time series, denoted by subset $F=\left\{\right(l,i):l\in \{7,10\left\}\right\}$ of observation indices. The use of only two virtual points in every time series will probably be enough to ensure monotonicity in expectation for the entire time series, since the time series functions to be learned are expected to be smooth. Additionally, only two virtual points to prevent posterior functions from being overly smoothed are used, as commented on in the previous Section 2, even though this is known not to affect splines severely ([32], Chapter 4).

The actual equivalency of the exposure time used in MFS in years depends on the hours and intensity of sunlight that affects the paintings on a changing daily basis. Without proper monitoring of light, this equivalency is difficult to obtain, so this aspect of the research is not considered in the current study.

5. Spatially Correlated Time-Series Model with Derivative Information

5.1. Observational Model

We consider a continuous stochastic process based on time series observed at spatial locations on a surface. Thus, $y_{li}$ denotes the l-th value of the time series at the ith spatial location, with $l=1,2,\cdots ,T$ representing the time points and $i=1,2,\cdots ,N$ representing the spatial locations. We adopt the model $y_{li}=f_{li}+{ϵ}_{li}$, where $f_{li}$ is the value of the latent function $f_i:\mathrm{I}\mathrm{R}\to \mathrm{I}\mathrm{R}$ evaluated at the time input value $t_l$, i.e., $f_{li}=f_i\left(t_l\right)$, and ${ϵ}_{li}\sim \mathcal{N}(0,{\sigma }^2)$ is the Gaussian noise. The latent function $f_i(·)$ underlies the time series of noisy observations for the ith spatial location. Let $\mathit{y}\in {\mathrm{I}\mathrm{R}}^{T\times N}$ and $\mathit{f}\in {\mathrm{I}\mathrm{R}}^{T\times N}$ be the matrices of spatio-temporal noisy observations and latent function values, respectively.

5.2. Penalized Spline Time-Series Functions

We consider a penalized thin-plate cubic-spline function for modeling the latent function of each time series of the spatio-temporal data. It is worth noting that quadratic-splines may be sufficient as the observed color fading curves seem quite smooth. However, cubic-splines have been implemented in this paper for generality and modeling flexibility. In particular, penalized thin-plate splines as presented by Crainiceanu, et al. [43] have been used, which are semiparametric regression models [17,44].

Firstly, it is assumed that latent function $f_i(·)$ is a thin-plate cubic-spline function:

$$f_i\left(t_l\right)={\beta }_{1i}+{\beta }_{2i}{t}_l+\sum _{k=1}^K{Z}_{lk}{u}_{ki}={\mathit{H}}_{l·}{\mathit{\beta }}_{·i}+{\mathit{Z}}_{l·}{\mathit{u}}_{·i},$$

(1)

where ${\mathit{H}}_{l·}=(1,t_l)$ is the row-vector of linear function values of the lth time point, ${\mathit{\beta }}_{·i}={({\beta }_{1i},{\beta }_{2i})}^{\top }$ is the column-vector of linear coefficients for the ith time series, ${\mathit{Z}}_{l·}=(Z_{l1},\cdots ,Z_{lK})\in {\mathrm{I}\mathrm{R}}^K$ is the row-vector of cubic-spline function values of the lth time point, and ${\mathit{u}}_{·i}={(u_{1i},\cdots ,u_{Ki})}^{\top }\in {\mathrm{I}\mathrm{R}}^K$ is the column-vector of spline coefficients for the ith time series, with K the order of the spline function and number of knots. The kth element of the vector ${\mathit{Z}}_{l·}$ of cubic-spline function values is

$$\begin{array}{cc}\hfill Z_{lk}& =\varphi (t_l,{\kappa }_k)=\hfill \\ \hfill & \frac{1}{4}\left({({\kappa }_k-0.5)}^2-\frac{1}{12}\right)\left({(t_l-0.5)}^2-\frac{1}{12}\right)-\frac{1}{24}\left({\left(|t_l-{\kappa }_k|-0.5\right)}^4-\frac{1}{2}{\left(|t_l-{\kappa }_k|-0.5\right)}^2\right),\hfill \end{array}$$

(2)

which is the one-dimensional cubic-spline function $\varphi$ [45] evaluated at the lth time point and the pre-fixed knot ${\kappa }_k$ corresponding to the kth spline component, with $k=1,2,\cdots ,K$.

Next, the penalized representation of the thin-plate spline function in Equation (1) is derived. A more detailed explanation of this approach can be found in Crainiceanu, et al. [43]. In order to derive the penalized representation, let first formulate the complete latent model for the time series of observations at spatial location i:

$${\mathit{y}}_{·i}={\mathit{f}}_{·i}+{\mathit{ϵ}}_{·i}=H{\mathit{\beta }}_{·i}+Z{\mathit{u}}_{·i}+{\mathit{ϵ}}_{·i},$$

where ${\mathit{y}}_{·i}={(y_{1i},\cdots ,y_{Ti})}^{\top }\in {\mathrm{I}\mathrm{R}}^T$ and ${\mathit{f}}_{·i}={(f_{1i},\cdots ,f_{Ti})}^{\top }\in {\mathrm{I}\mathrm{R}}^T$ are the column-vectors of noisy observations and latent function values, respectively, for spatial location i, where latent function value $f_{li}$ is the value of the latent function $f_i(·)$ evaluated at the time input value $t_l$, i.e., $f_{li}=f_i\left(t_l\right)$. $H\in {\mathrm{I}\mathrm{R}}^{T\times 2}$ denotes the matrix of linear function values with l-th row ${\mathit{H}}_{l·}$, $Z\in {\mathrm{I}\mathrm{R}}^{T\times K}$ denotes the matrix of cubic-spline function values with lth row ${\mathit{Z}}_{l·}$, and ${\mathit{ϵ}}_{·i}\sim \mathcal{N}(0,{\sigma }^2)$ is the Gaussian noise term. To perform the penalization of the function in order to avoid overfitting at location i, the following term can be minimized:

$$\frac{1}{{\sigma }^2}\left|\right|{\mathit{y}}_{·i}-H{\mathit{\beta }}_{·i}-Z{\mathit{u}}_{·i}{\left|\right|}^2+\frac{1}{{\sigma }_u^2}{\mathit{u}}_{·i}^{\top }{\Omega }{\mathit{u}}_{·i},$$

in which the covariance of vector ${\mathit{u}}_{·i}$ is $cov\left({\mathit{u}}_{·i}\right)={\sigma }_u^2{{\Omega }}^{-1}$, the covariance of the residuals ${\mathit{ϵ}}_{·i}$ is $cov\left({\mathit{ϵ}}_{·i}\right)={\sigma }^{2}I$ (with I the identity matrix), and ${\Omega }\in {\mathrm{I}\mathrm{R}}^{K\times K}$ is the matrix of penalization with an element $(q,k)$:

$$\begin{array}{cc}\hfill {{\Omega }}_{qk}& =\varphi ({\kappa }_q,{\kappa }_k)=\hfill \\ \hfill & \frac{1}{4}\left({({\kappa }_k-0.5)}^2-\frac{1}{12}\right)\left({({\kappa }_q-0.5)}^2-\frac{1}{12}\right)-\frac{1}{24}\left({\left(|{\kappa }_q-{\kappa }_k|-0.5\right)}^4-\frac{1}{2}{\left(|{\kappa }_q-{\kappa }_k|-0.5\right)}^2\right),\hfill \end{array}$$

(3)

that is, the cubic-spline function $\varphi$ evaluated at every pair of the pre-fixed knots ${\kappa }_q$ and ${\kappa }_k$, corresponding to the qth and kth spline component, respectively, with $q,k=1,\cdots ,K$.

When reparametrization ${\mathit{u}}_{·i}={{\Omega }}^{-1/2}{\mathit{b}}_{·i}$ is used, an equivalent model representation of the penalized thin-plate splines is obtained in the form of linear mixed models [46]:

$${\mathit{y}}_{·i}={\mathit{f}}_{·i}+{\mathit{ϵ}}_{·i}=H{\mathit{\beta }}_{·i}+Z{{\Omega }}^{-1/2}{\mathit{b}}_{·i}+{\mathit{ϵ}}_{·i},$$

where the covariance of the vector of spline coefficients ${\mathit{b}}_{·i}\in {\mathrm{I}\mathrm{R}}^K$ is now $cov\left({\mathit{b}}_{·i}\right)={\sigma }_b^{2}I$.

As a result, the latent function $f_i(·)$ can be represented as penalized thin-plate cubic splines in the form of linear mixed models:

$$f_i\left(t_l\right)={\mathit{H}}_{l·}{\mathit{\beta }}_{·i}+{\mathit{Z}}_{l·}{{\Omega }}^{-1/2}{\mathit{b}}_{·i},$$

(4)

where ${\mathit{b}}_{·i}={(b_{1i},\cdots ,b_{Ki})}^{\top }\in {\mathrm{I}\mathrm{R}}^K$ is the column-vector of penalized spline coefficients for the ith time series.

In practice, the inverse of the square root of the matrix ${\Omega }$ is often computed as ${{\Omega }}^{-1/2}=U{D}^{-1/2}{V}^{\top }$, where $UD{V}^{\top }$ is the singular value decomposition of the matrix ${\Omega }$, where D is the rectangular diagonal matrix with the singular values, U and V are the matrices with the left-singular vectors and the right-singular vectors of ${\Omega }$, respectively.

The matrix $\mathit{f}=[{\mathit{f}}_{·1}{\mathit{f}}_{·2}\cdots {\mathit{f}}_{·N}]\in {\mathrm{I}\mathrm{R}}^{T\times N}$ of spatio-temporal latent function values can be expressed as:

$$\begin{array}{c}\hfill \mathit{f}=H\mathit{\beta }+Z{{\Omega }}^{-\frac{1}{2}}\mathit{b},\end{array}$$

where $\mathit{\beta }\in {\mathrm{I}\mathrm{R}}^{2\times N}$ is the matrix of linear coefficients with ith column ${\mathit{\beta }}_{·i}$, $\mathit{b}=[{\mathit{b}}_{·1}{\mathit{b}}_{·2}\cdots {\mathit{b}}_{·N}]\in {\mathrm{I}\mathrm{R}}^{K\times N}$ is the matrix of spline coefficients with ith column ${\mathit{b}}_{·i}$.

5.3. Spatially Correlating the Penalized Spline Time-Series Functions

In order to establish a correlation structure among time series, the matrix of spline coefficients $\mathit{b}\in {\mathrm{I}\mathrm{R}}^{K\times N}$ is considered as a realization of a continuous stochastic process, and a GP prior model with a two-dimensional (with K knots and N space points) covariance function can be defined on them.

To simplify the covariance structure and the computational requirements of inverting the Gram matrix of the covariance function when performing inference on GPs, a null covariance between the spline coefficients associated with a different order in the model can be considered, which is equivalent to defining K independent GP prior distributions, one for each kth row ${\mathit{b}}_{k·}=(b_{k1},\cdots ,b_{kN})\in {\mathrm{I}\mathrm{R}}^N$ of matrix $\mathit{b}$, such that

$$\begin{array}{c}\hfill {\mathit{b}}_{k·}\sim \mathcal{GP}\left(0,{\alpha }_k{C}_k(\mathit{x},{\mathit{\rho }}_k)\right),\end{array}$$

for $k=1,2,\cdots ,K$. $C_k$ is the covariance function for vector of coefficients ${\mathit{b}}_{k·}$, which is a function of matrix of inputs $\mathit{x}=[{\mathit{x}}_{·1}{\mathit{x}}_{·2}\cdots {\mathit{x}}_{·N}]\in {\mathrm{I}\mathrm{R}}^{5\times N}$, with ith column ${\mathit{x}}_{·i}={(H_i,S_i,I_i,S_{x_i},S_{y_i})}^{\top }\in {\mathrm{I}\mathrm{R}}^5$ containing the input values for the ith spatial location as described in Section 4, and vector of length-scale parameters ${\mathit{\rho }}_k=({\rho }_{1k},\cdots ,{\rho }_{5k})\in {\mathrm{I}\mathrm{R}}^5$ for vector ${\mathit{b}}_{k·}$. Hyperparameter ${\alpha }_k$ is the marginal variance of the GP which controls the overall scale or magnitude of the range of values of vector ${\mathit{b}}_{k·}$. Thus, specific covariance structure for each kth vector of spline coefficients ${\mathit{b}}_{k·}$ can be specified.

Furthermore, in this work the covariance structure is simplified even more by considering the same prior spatial structure for every vector of spline coefficients ${\mathit{b}}_{k·}$, i.e.,

$$\begin{array}{c}\hfill {\mathit{b}}_{k·}\sim \mathcal{GP}\left(0,{\alpha }_{k}C(\mathit{x},\mathit{\rho })\right),\end{array}$$

and C is a common covariance function for every vector of coefficients ${\mathit{b}}_{k·}$, which is a function of matrix of inputs $\mathit{x}$ and length-scales $\mathit{\rho }=({\rho }_1,\cdots ,{\rho }_5)$. Saying that ${\mathit{b}}_{k·}$ follows a GP prior distribution of zero mean (a generic mean function can also be used) and covariance function C and marginal variance ${\alpha }_k$, is equivalent to saying that ${\mathit{b}}_{k·}$ is normally distributed with zero mean and covariance matrix ${{\Sigma }}_k\in {\mathrm{I}\mathrm{R}}^{N\times N}$,

$$\begin{array}{c}\hfill {\mathit{b}}_{k·}\sim \mathcal{N}\left(\mathit{0},{{\Sigma }}_k\right),\end{array}$$

(5)

where an element $(i,j)$ of ${{\Sigma }}_k$ is given by

$$\begin{array}{c}\hfill {{\Sigma }}_{k_{(i,j)}}={\alpha }_{k}C({\mathit{x}}_{·i},{\mathit{x}}_{·j},\mathit{\rho }),\end{array}$$

with $i,j=1,2,\cdots ,N$, and $C({\mathit{x}}_{·i},{\mathit{x}}_{·j},\mathit{\rho })$ represents the covariance function evaluated at the specific i-th and j-th spatial locations. A squared exponential covariance function (see Rasmussen and Williams [23] for a review of covariance functions for GPs) is considered:

$$\begin{array}{c}\hfill C({\mathit{x}}_{·i},{\mathit{x}}_{·j},\mathit{\rho })=exp\left(-\frac{1}{2}\sum _{d=1}^5\frac{1}{{\rho }_d^2}{({\mathit{x}}_{di}^{}-{\mathit{x}}_{dj}^{})}^2\right),\end{array}$$

where $x_{di}$ and $x_{dj}$ are the values of the d-th input variable at the i-th and j-th spatial locations, respectively. Length-scale parameters ${\rho }_1$, ${\rho }_2$ and ${\rho }_3$ correspond to the input variables $\mathit{H}$, $\mathit{S}$ and $\mathit{I}$, respectively. The spatial coordinates input variables ${\mathit{S}}_{\mathit{x}}$ and ${\mathit{S}}_{\mathit{y}}$ are sharing the length-scale parameter (${\rho }_4={\rho }_5$), so that the covariance function depends on the (Euclidean) distance between spatial coordinates. Hyperparameter ${\rho }_d$ controls the smoothness of the function for ${\mathit{b}}_{k·}$ in the dimension of the d-th input variable. The use of a multidimensional length-scale basically makes the isotropic covariance function non-isotropic. The squared exponential covariance function is a stationary function with respect to the input variables. Stationarity in covariance is a reasonable assumption for the current application. In applications where non-stationarity is desirable, valid non-stationary covariance functions for GPs can also be used (see [23] for a complete review of covariance functions for GPs).

5.4. Derivative of the Penalized Spline Time-Series Functions

The derivative function $f_i^{\prime }:\mathrm{I}\mathrm{R}\to \mathrm{I}\mathrm{R}$ of penalized cubic-spline function $f_i(·)$ in Equation (4) with respect to the time input variable takes the form:

$$f_i^{\prime }\left(t_l\right)=\frac{\partial f_i\left(t_l\right)}{\partial t_l}={\mathit{\beta }}_{2i}+\frac{\partial {\mathit{Z}}_{l·}}{\partial t_l}{{\Omega }}^{-\frac{1}{2}}{\mathit{b}}_{·i},$$

(6)

where $\frac{\partial {\mathit{Z}}_{l·}}{\partial t_l}=(\frac{\partial Z_{l1}}{\partial t_l},\cdots ,\frac{\partial Z_{lK}}{\partial t_l})\in {\mathrm{I}\mathrm{R}}^K$ is the row-vector of derivative cubic-spline values at time $t_l$, and an element $\frac{\partial Z_{lk}}{\partial t_l}$ is the partial derivative of the cubic spline function $Z_{lk}$ in Equation (2) with respect to the time input variable:

$$\begin{array}{cc}\hfill \frac{\partial Z_{lk}}{\partial t_l}& =\frac{\varphi (t_l,{\kappa }_k)}{\partial t_l}=\hfill \\ \hfill & \frac{1}{4}\left({({\kappa }_k-0.5)}^2-\frac{1}{12}\right)2(t_l-0.5)-\frac{1}{24}\left(4{\left(|t_l-{\kappa }_k|-0.5\right)}^3-\left(|t_l-{\kappa }_k|-0.5\right)\right).\hfill \end{array}$$

(7)

5.5. A Zero-Order Constraint for Time-Series to Start at Zero

In order to force predicted time series functions to start at zero, a zero-order constraint can be specified by using a Dirac Delta function $\delta (·)$ as the observational model for the observations in subset $B=\left\{\right(l,i):l=1\}$ of starting points of every time series:

$$\begin{array}{c}\hfill p\left({\mathit{y}}_B\right|{\mathit{f}}_B)=\prod _{(l,i)\in B}\delta (y_{li}-f_i\left(t_l\right)),\end{array}$$

with

$${\mathit{y}}_B=\{0:(l,i)\in B\}$$

(8)

denoting the subset of observations in subset B of points. The rest of observations, i.e., observations $\mathit{y}$ in subset $A=\left\{\right(l,i):l>1\}$ of points and denoted by

$${\mathit{y}}_A=\{y_{li}:(l,i)\in A\},$$

(9)

are considered to be contaminated with Gaussian noise so that:

$$p\left({\mathit{y}}_A\right|{\mathit{f}}_A,{\sigma }^2)=\prod _{(l,i)\in A}\mathcal{N}\left(y_{li}\right|f_i\left(t_l\right),{\sigma }^2).$$

In the previous equations, ${\mathit{f}}_B$ and ${\mathit{f}}_A$ denote the function values $f_i\left(t_l\right)$ in Equation (4) in subsets B and A of points, respectively.

5.6. A First-Order Derivative Constraint for Time-Series

In order to impose a saturation constraint for long-term stabilization of the time series, a set of virtual observations $m_{li}$ of the value of the partial derivative of the function with respect to the time input variable ($m_{li}=\frac{\partial f_{li}}{\partial t_l}$) equal to zero can be considered:

$$\mathit{m}=\{0:(l,i)\in E\},$$

(10)

where $E=\left\{\right(l,i):l=11\}$ is the subset of ending points of every time series to induce saturation of the function (as explained in Section 4). The Dirac Delta function $\delta (·)$ can also be used as an observational model for these observations,

$$\begin{array}{c}\hfill p\left(\mathit{m}\right|{\mathit{f}}_E^{\prime })=\prod _{(l,i)\in E}\delta (m_{li}-f_i^{\prime }\left(t_l\right)),\end{array}$$

where ${\mathit{f}}_E^{\prime }$ denotes the partial derivative function values $f_i^{\prime }\left(t_l\right)$ in Equation (6) in the subset E of points.

5.7. Monotonicity Constraint for the Time-Series

The function is guaranteed to be non-decreasing as a function of time when the partial derivative is non-negative. This constraint can be specified by using a set of virtual observations $z_{li}$ of the sign of the partial derivative of the function with respect to the time input variable ($z_{li}=sign(\frac{\partial f_{li}}{\partial t_l})$) equal to one:

$$\mathit{z}=\{1:(l,i)\in F\},$$

(11)

where $F=\left\{\right(l,i):l=\{7,10\left\}\right\}$ is the subset of desired points where to induce monotonicity (as explained in Section 4). The probit function ${\Phi }:\mathrm{I}\mathrm{R}\to (0,1)$ can be used as an observation model for the signs of the partial derivatives [31],

$$p\left(\mathit{z}\right|{\mathit{f}}_F^{\prime })=\prod _{(l,i)\in F}{\Phi }\left(z_{li}·f_i^{\prime }\left(t_l\right)·\frac{1}{v}\right),$$

where ${\mathit{f}}_F^{\prime }$ denotes the partial derivative values $f_i^{\prime }\left(t_l\right)$ in Equation (6) in the subset F of points. Function ${\Phi }(·)$ is the standard Normal cumulative distribution function and $v>0$ is a parameter controlling the strictness of the constraint. When v approaches zero ($v\to 0$), the function ${\Phi }$ approaches a step function. Setting $v={10}^{-4}$ seems a reasonable value for this study.

5.8. Likelihood Function

The joint likelihood of regular observations $\mathit{y}=({\mathit{y}}_A,{\mathit{y}}_B)$ (Equations (9) and (8)), derivative value observations $\mathit{m}$ (Equation (10)) and derivative sign observations $\mathit{z}$ (Equation (11)), given the parameters $\mathit{\beta }$, $\mathit{b}$ and $\sigma$ is:

$$\begin{array}{cc}\hfill & p(\mathit{y},\mathit{m},\mathit{z}|\mathit{\beta },\mathit{b},\sigma )=p\left({\mathit{y}}_A\right|{\mathit{f}}_A)p\left({\mathit{y}}_B\right|{\mathit{f}}_B)p\left(\mathit{z}\right|{\mathit{f}}_F^{\prime })p\left(\mathit{m}\right|{\mathit{f}}_E^{\prime })=\hfill \\ \hfill & \left(\prod _{l,i\in A}\mathcal{N}\left(y_{li}\right|f_i\left(t_l\right),{\sigma }^2)\right)\left(\prod _{l,i\in B}\delta \left(y_{li}-f_i\left(t_l\right)\right)\right)\left(\prod _{l,i\in F}{\Phi }\left(z_{li}·f_i^{\prime }\left(t_l\right)·\frac{1}{v}\right)\right)\left(\prod _{l,i\in E}\delta \left(m_{li}-f_i^{\prime }\left(t_l\right)\right)\right).\hfill \end{array}$$

(12)

5.9. Posterior and Predictive Distributions

The posterior joint distribution of parameters given the data, which is proportional to the product of the likelihood and priors, is:

$$\begin{array}{c}\hfill p(\mathit{\beta },\mathit{b},\sigma |\mathit{y},\mathit{m},\mathit{z})\propto p(\mathit{y},\mathit{m},\mathit{z}|\mathit{\beta },\mathit{b},\sigma )p\left(\mathit{\beta }\right)p\left(\mathit{b}\right|\alpha ,\mathit{\rho }\left)p\right(\alpha \left)p\right(\mathit{\rho }\left)p\right(\sigma ),\end{array}$$

where $p(\mathit{y},\mathit{m},\mathit{z}|\mathit{\beta },\mathit{b},\sigma )$ is the likelihood of the model in Equation (12) and $p\left(\mathit{b}\right|\alpha ,\mathit{\rho })={\prod }_{k=1}^K\mathcal{N}\left({\mathit{b}}_{k·}|0,{{\Sigma }}_k\right)$ is the GP prior to the spline coefficients $\mathit{b}$ (Equation (5)). We set normal prior distributions for the linear coefficients $\mathit{\beta }$, $p\left(\mathit{\beta }\right)=\mathcal{N}\left(\alpha \right|0,10I)$ and positive half-normal prior distributions for the hyperparameters $\alpha$, $p\left(\alpha \right)={\mathcal{N}}^{+}\left(\alpha \right|0,10)$ and $\sigma$, $p\left(\sigma \right)={\mathcal{N}}^{+}\left(\sigma \right|0,10)$; and gamma distributions for the hyperparameters $\mathit{\rho }$ and $p\left({\rho }_d\right)=Gamma\left({\rho }_d\right|1,0.1)$ for all d. These correspond to weakly informative prior distributions based on prior knowledge about the magnitude of the parameters.

The joint predictive distribution of new output values $\tilde{\mathit{y}}$ and ${\tilde{\mathit{y}}}^{\prime }$ for a new sequence of input values ${\mathit{x}}^{*}$ can be computed by integrating out over the posterior distribution:

$$\begin{array}{c}\hfill p(\tilde{\mathit{y}},\tilde{\mathit{m}},\tilde{\mathit{z}}|\mathit{y},\mathit{m},\mathit{z})=\int p(\tilde{\mathit{y}},\tilde{\mathit{m}},\tilde{\mathit{z}}|\mathit{\beta },\mathit{b},\sigma )p(\mathit{\beta },\mathit{b},\sigma |\mathit{y},\mathit{m},\mathit{z})\mathrm{d}\mathit{\beta }\mathrm{d}\mathit{b}\mathrm{d}\sigma .\end{array}$$

6. Bayesian Inference

The posterior distributions of interest $p(\mathit{f},\sigma |\mathit{y},\mathit{m},\mathit{z})$ and $p(\mathit{\beta },\mathit{b},\sigma |\mathit{y},\mathit{m},\mathit{z})$ are in general not available in closed form. Hence, to estimate both the parameter posterior distribution and the posterior predictive distribution for this model, simulation methods and distributional [47] or numerical [48,49] approximation methods must be used. Simulation methods based on the Markov chain Monte Carlo (MCMC) [50], and more recently, the Hamiltonian Monte Carlo (HMC) [51], are general sampling methods to obtain samples from the joint posterior distribution. In this study, HMC methods are used to make inferences about the posterior and predictive distributions. Using sampling methods such as HMC, the covariance matrix must be inverted at every step of the sampler.

When computing the posterior distribution, the main computational demands come from the need of inverting the Gram matrix of the covariance function, usually through Cholesky factorization, of the hyperparameters in the GP prior defined over the spline coefficients $\mathit{b}$. The proposed model considers the same prior spatial covariance structure for every vector of spline coefficients ${\mathit{b}}_{·k}$ associated with a different order k of the spline functions. This requires $O\left(N^3\right)$ computations due to the covariance matrix inversion, where N denotes the number of observed spatial locations.

In general, the computational requirements to invert the covariance matrix in the proposed spatially correlated time series model framework is substantially reduced compared to using a full spatio-temporal GP model framework. The spatially correlated time series model framework, where a complete covariance structure among spline coefficients is considered, requires $O\left({\left(NK\right)}^3\right)$ operations in the covariance matrix inversion, whereas a spatio-temporal GP requires $O\left({\left(NT\right)}^3\right)$. Notice that the number of knots K in spline-based models is usually much lower than the number of time points T (i.e., $K\ll T$). Furthermore, it is meaningful, in the proposed splines-based model framework, to consider different covariance structures, with different complexities, between space and knots. In case a null covariance is considered between spline coefficients associated with different spline knots, the computational cost of the correlated spline model becomes $O\left(N^{3}K\right)$. Furthermore, if the same prior spatial structure is considered for the spline coefficients associated with different spline knots, as implemented in the current work, the computational cost of the proposed model becomes $O\left(N^3\right)$.

For a large N and T for which the covariance matrix inversion is computationally intractable, sparse [52] or basis functions [53] approximations for GPs can be used. A recently developed reduced-rank approximate GP based on Hilbert space methods was developed by Solin and Särkkä [38] and its practical implementation investigated by Riutort-Mayol, et al. [54]. For even larger datasets, where iterative simulation algorithms are too slow, modal and distributional approximation methods can be efficient alternatives.

7. Model Checking, Predictive Performance and Model Selection

Typical methods for checking normality and trends on the fitted residuals can be used to assess the model. Additionally, other criteria—in order to guarantee good model performance and ensure that the model is compatible with the data—are the posterior predictive checks, the expected log predictive density and the mean square predictive errors, which can be computed following cross-validation procedures.

The posterior predictive checks, which are also known as the leave-one-out probability integral transformation (LOO-PIT), can be used to assess whether the model predictive distributions are calibrated, that is, they are describing the model predictive uncertainty well. In case of a good calibration of predictive distribution, LOO-PIT values are uniformly distributed. They are based on computing the probability of a predictive value ${\tilde{y}}_{il}$ to be lower than or equal to its corresponding actual observation $y_{il}$ that has not taken part in fitting the model [47,55]:

$${\text{LOO-PIT}}_{(l,i)\in \mathfrak{D}}=P({\tilde{y}}_{li}\le y_{li}),$$

where $\mathfrak{D}$ denotes the subset of observation indices of new predictions in the cross-validation; and $\left|\mathfrak{D}\right|$ is its cardinality; $y_{li}$ denotes the actual observation at point $(l,i)$ that does not take part in fitting the model; ${\tilde{y}}_{li}$ denotes the predicted value from the model at point $(l,i)$. Using simulation methods for inference, the calculation of the probability that a predicted value is less than observed in the LOO-PIT is straightforward through the collection of simulations.

From the models having well-calibrated predictive distributions, we would prefer the most certain one, which can be assessed using mean square predictive error (MSE) or even better using the expected log posterior predictive density (ELPD). The MSE evaluates, by averaging over all checking observations, how far new data are from the model by using the distance (error) between the actual observation $y_i$ and the predictive mean ${\tilde{y}}_{li}$:

$$\mathrm{MSE}=\frac{1}{\left|\mathfrak{D}\right|}\sum _{(l,i)\in \mathfrak{D}}{(y_{li}-{\tilde{y}}_{li})}^2.$$

Additionally, the ELPD evaluates, by averaging over all checking observations, how far new data are from the model while taking the posterior uncertainties into account. It is based on the log-density of new data given the model [56,57]:

$$\mathrm{ELPD}=\frac{1}{\left|\mathfrak{D}\right|}\sum _{(l,i)\in \mathfrak{D}}ln\left(p\left(y_{li}\right|{\mathit{y}}_{-\mathfrak{D}})\right),$$

where ${\mathit{y}}_{-\mathfrak{D}}$ denotes the dataset without the subset $\mathfrak{D}$ of observations, ${\mathit{y}}_{-\mathfrak{D}}=\{y_{li}:(l,i)\notin \mathfrak{D}\}$.

Following a leave one out cross-validation (denoted as loo-cv) scheme, the subset $\mathfrak{D}$ of observation indices will be just a single observation $(l,i)$, $\mathfrak{D}=\left\{\right(l,i\left)\right\}$. The LOO-PIT, ELPD, and MSE will be computed following the loo-cv scheme. The LOO-PIT will essentially be useful for model checking, assessing that the model is compatible with the data. The ELPD and MSE will evaluate the predictive accuracy of individual observations.

The end goal of this work is to predict complete color-fading time series at new unobserved locations. In order to do that, a leave one location out cross-validation (denoted as lolo-cv) scheme can be performed, where the subset of observation indices $\mathfrak{D}$ will be a complete time series of a specific spatial location i, $\mathfrak{D}=\left\{\right(l,i):l\in \{1,\cdots ,T\left\}\right\}$. The statistics ELPD and MSE will be computed following the lolo-cv scheme. Plots of predicted new time series superimposed to their corresponding actual observations will be shown in order to visually evaluate the predictive performance. Model selection can be done by comparing the predictive performance between models using the ELPD and MSE statistics. The best model is the one that maximizes the ELPD and/or minimizes the MSE.

8. Experimental Results

The posterior and predictive distributions have been estimated using HMC sampling methods [51] using the Stan software [58]. Three simulation chains with different initial values have been launched. The convergence of the simulation chains was evaluated by the split-Rhat convergence diagnostic and the effective sample size of the chains [47,59]. A value of 1 in the split-Rhat convergence statistic indicates good mixing of simulated chains. Traditionally accepted good value for split-Rhat would be between 1 and 1.1. However, a more strict range has also been suggested [59] recently. In our case and for both models, a split-Rhat value lower than 1.05 has been obtained for all parameter simulation chains.

8.1. Posterior Distributions of Hyperparameters

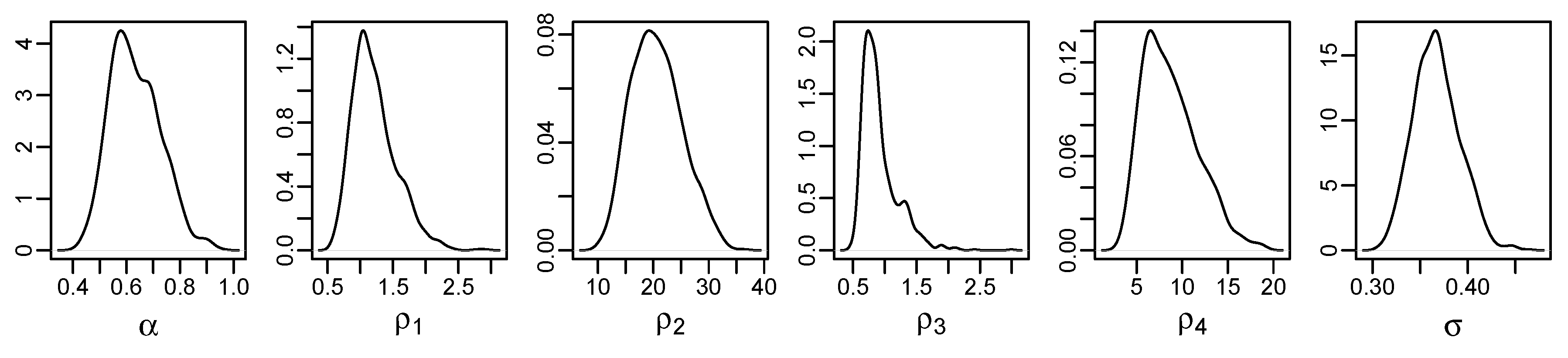
Figure 3 depicts the estimated posterior marginal distributions of the hyperparameters: length-scales $\mathit{\rho }$ associated with the input variables, overall magnitude $\alpha$ of the GP prior for the spline coefficients and observation noise $\sigma$ of the model. Their mode estimates are shown in

Table 2. Estimated posterior modes of the hyperparameters.

Length-Scale of Spatial Input Variables					Marginal Magnitude of GP Prior for Coefficients b	Obs. Noise
$\mathit{H}$	$\mathit{S}$	$\mathit{I}$	${\mathit{S}}_{\mathit{x}}$	${\mathit{S}}_{\mathit{y}}$
${\rho }_1$	${\rho }_2$	${\rho }_3$	${\rho }_4$	${\rho }_5$	$\alpha$	$\sigma$
1.10	20.0	0.85	7.9		0.58	0.38

.

Input variables were previously re-scaled (standardized). The length-scale parameters control how the covariance function changes on the difference between the values of the different input variables between locations. Large values indicate a slow decay of the covariance function as the difference between the input values increases and small values indicate a fast decay. The length-scale parameters ${\rho }_1$ and ${\rho }_3$, corresponding to variables $\mathit{H}$ and $\mathit{I}$, respectively, are relatively small. This indicates that the rate of decay of the correlation is moderately high. Therefore, variations in input variables $\mathit{H}$ and $\mathit{I}$ imply a quick decrease in the correlations towards zero. Variables $\mathit{S}$, ${\mathit{S}}_{\mathit{x}}$, and ${\mathit{S}}_{\mathit{y}}$ have larger length-scales. Notice that variables ${\mathit{S}}_{\mathit{x}}$ and ${\mathit{S}}_{\mathit{y}}$ share the same length-scale (${\rho }_4={\rho }_5$), so that the covariance function depends on the Euclidean distance between spatial coordinates. This indicates that the covariance function depends on $\mathit{S}$ and the Euclidean spatial distance in a smoother way.

8.2. Model Checking and Selection

Figure 4 shows the frequency histograms of the posterior predictive checks (LOO-PIT) by following the loo-cv scheme for both models, with and without derivatives. Both histograms are close to uniform distribution, which means the model predictions are well-calibrated.

Table 3. ELPD and MSE for both models, with and without derivative information, computed by the two cross-validation schemes, loo-cv and lolo-cv.

		with Derivative Information	without Derivative Information
loo-cv	ELPD	−0.61	−0.78
	MSE	0.13	0.14
lolo-cv	ELPD	−16.40	−33.39
	MSE	3.09	4.42

shows the ELPD and MSE statistics computed by following the two different cross-validation schemes, loo-cv and lolo-cv, for both models, with and without derivatives. The MSE for the model with derivatives is lower than the model without derivatives in the lolo-cv scheme. Furthermore, when the uncertainty is taken into account in the evaluation with the ELPD statistic, the improvement of using derivatives is even considerably larger in both cross-validation scenarios. Therefore, the results of these statistics confirm that the model with derivatives is closer to new data, either in terms of the expected log-density or the mean error.

8.3. Posterior and Predicted Time-Series Functions

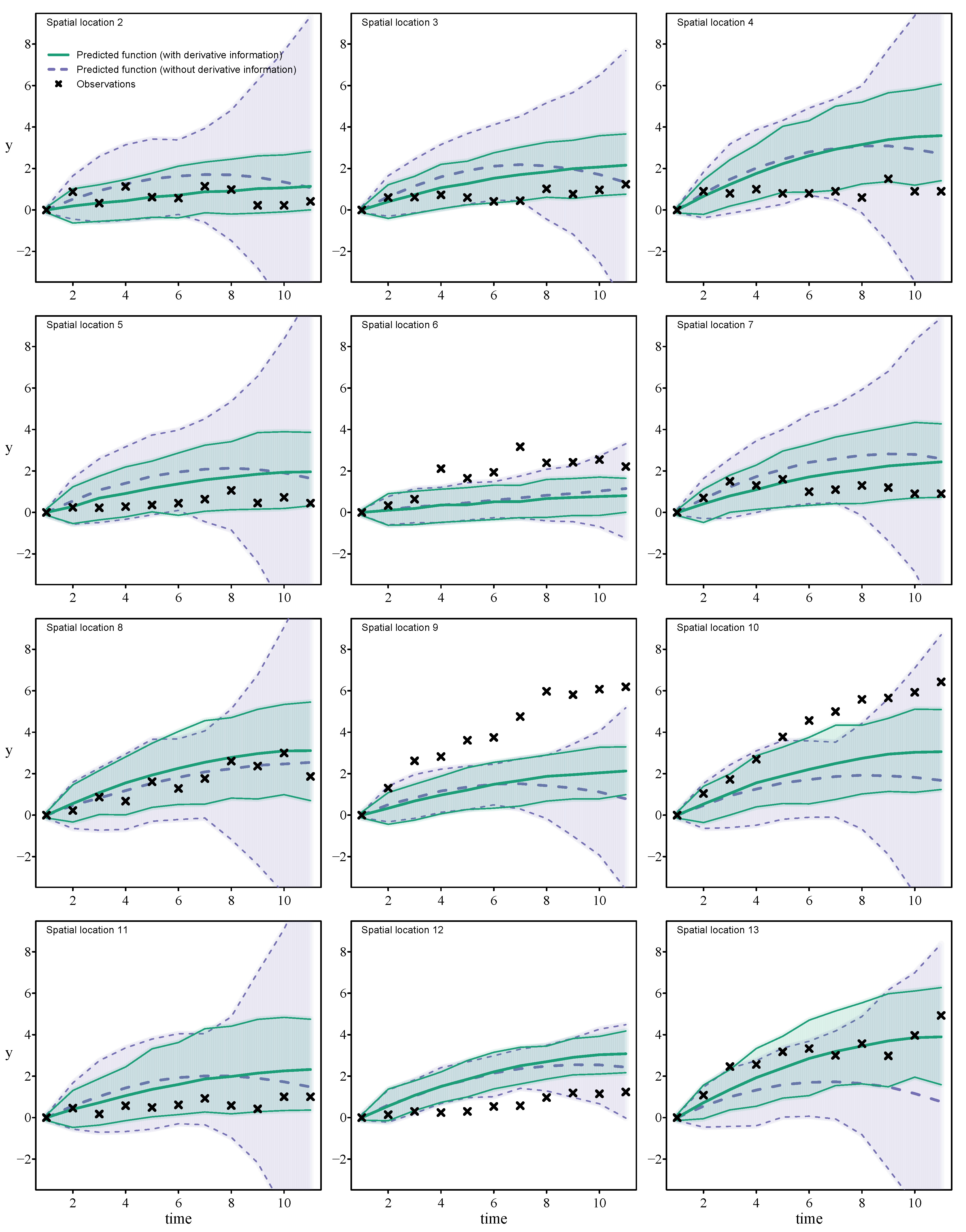
Figure 5 shows the means and 95% pointwise credible intervals of predictive distributions, $p\left(\tilde{\mathit{y}}\right|\mathit{y},\mathit{m},\mathit{z})$, evaluated over the sampling input space and plotted as a function of time (time series) for specific spatial locations and superimposed to the actual observations $\mathit{y}$. Additionally, the means of the predictive distribution of the model without the inclusion of the derivatives, $p\left(\tilde{\mathit{y}}\right|\mathit{y})$, are also plotted for comparison.

The lolo-cv scheme, based on leaving a whole time series out of the training data, has been carried out in order to evaluate the prediction performance of complete new time series at new locations. Figure 6 shows the predicted time series at left-out locations (predictive distributions at left-out input locations and time points) following the lolo-cv scheme with derivative constraints, $p\left({\tilde{\mathit{y}}}_{·i}\right|{\mathit{y}}_{·-i},{\mathit{m}}_{·-i},{\mathit{z}}_{·-i})$, and without them, $p\left({\tilde{\mathit{y}}}_{·i}\right|{\mathit{y}}_{·-i})$, the consideration of derivatives. Here, ${\mathit{y}}_{·-i}$, ${\mathit{m}}_{·-i}$ and ${\mathit{z}}_{·-i}$ denote the sets of observations $\mathit{y}$, $\mathit{m}$ and $\mathit{z}$ without those observations corresponding to time series i. The actual data of predicted time series ${\mathit{y}}_{·i}$ in the loo-cv scheme are also plotted to visually evaluate the predictions. Closer predictions to the actual data, narrower predictive intervals (especially at the last part of the time series functions) and good shapes of the functions for the model with derivatives can be appreciated, as monotonicity and saturation constraints improve and reduce the credible intervals of the predictions (Figure 6). The accuracy in mean and uncertainty of new predicted time series was evaluated by the MSE and ELPD in Table 3.

It is worth mentioning that the use of an observation model with the absence of noise at the starting time points, $\{y_{li}=0:l=1\}$, forces the predicted time series to be zero at those starting points (Figure 5 and Figure 6).

Inducing monotonicity by means of virtual observations of the sign of the partial derivatives at two time points, $\{sign\left(\frac{\partial f_{li}}{\partial t_l}\right)=1:l\in \{7,10\}\}$, has been sufficient to achieve monotonicity throughout the time series (Figure 5 and Figure 6), preventing an overly smoothing effect on the posterior functions due to using many virtual points for monotonicity, as indicated in Riutort-Mayol [32], Chapter 4. In the same way, the consideration of additional observations of the value of the partial derivative equal to zero at the last time points, $\{\frac{\partial f_{li}}{\partial t_l}=0:l=11\}$, induced a stationary state at the end of the time series.

Monotonicity and long term saturation properties of the curves were not assured when using the models without derivative information (Figure 5 and Figure 6). Hence, the proposed model with derivative information yields a better fit and predictions for dynamics of the functions, improving their interpretability. In this sense, the analysis of the color fading curves using a model without derivative information could not be done properly because the temporal degradation, especially at the last time points, is unrealistic.

Prediction sensitivity due to the short set of data available has been found. Figure 6 shows poor predictive performance in some spatial locations when compared to the observed data. This is due to the high sensitivity of the model to leaving some data out since the dataset is scarce.

8.4. A Continuous Map of Color Fading Estimates

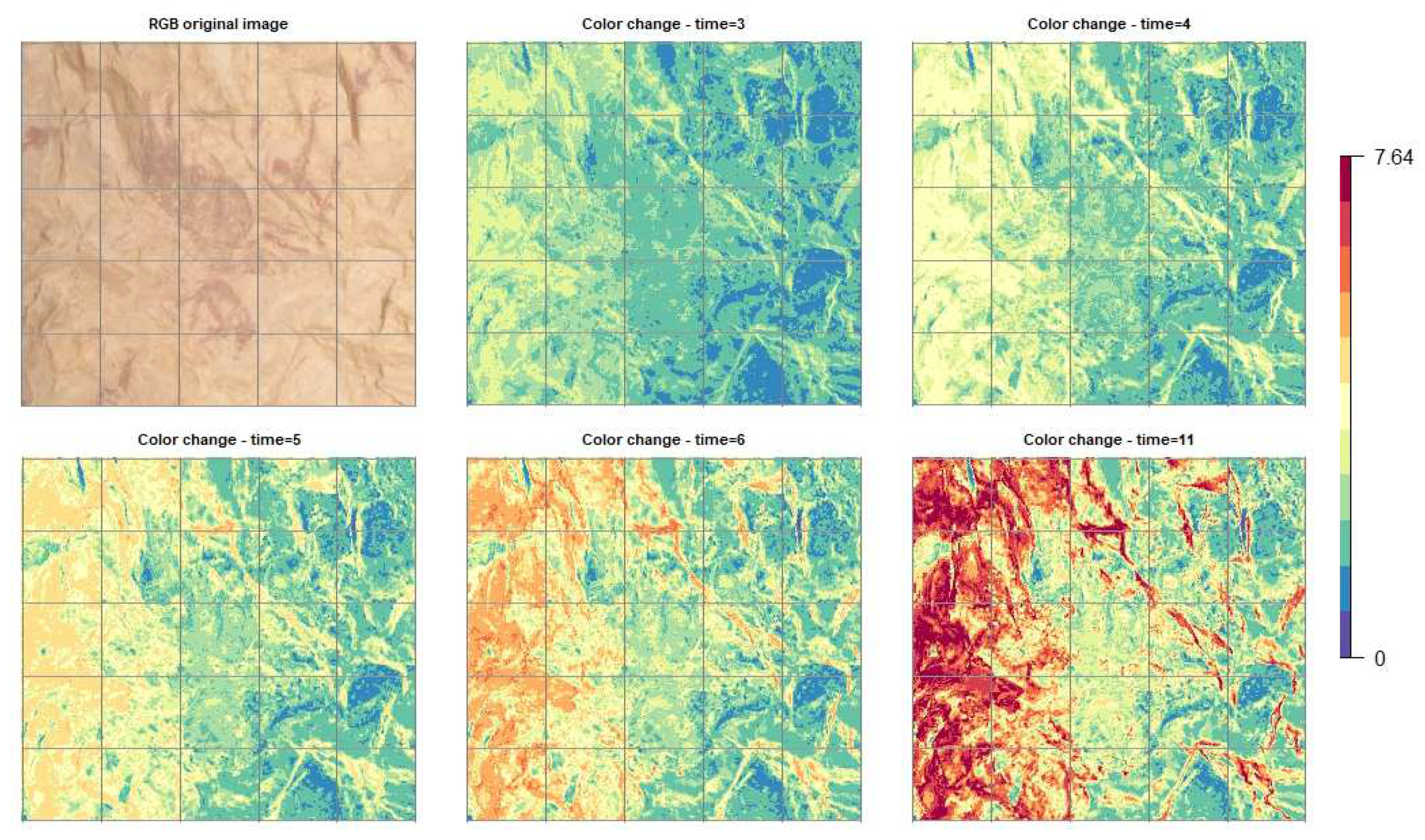
In order to make spatial continuous maps of color fading estimates, predictions of color fading time series, $p\left({\tilde{\mathit{y}}}_{·j}\right|\mathit{y},\mathit{m},\mathit{z})$, have been computed for all the spatial pixel locations j of the rock art painting image (Figure 2). In Figure 7 six images representing the spatial distributions and the evolutions over time of those color fading estimates are shown. The images correspond to the time points $t_3=3$, $t_4=4$, $t_5=5$, $t_6=6$ and $t_{11}=11$, respectively.

The spatial distribution over time of color fading values seems to be quite unvarying. This was expected, since the time series adjusted in the different locations have similar patterns—smooth, monotonically increasing and tending to saturate in the long term, and the same prior spatial covariance structure was specified through the time dimension. Color fading values, especially when they are low values, like in this case (the maximum is 7.64), are not worth being converted to the RGB color space and plotted as an image, because the color changes will be not visible in an RGB image. The best way is plotting color ${\Delta }{E}_{ab}^{*}$ values (Figure 7). The science of colorimetry argues that ${\Delta }{E}_{ab}^{*}$ values higher than approximately 3.5 would be perceptible for the human eye looking at the real object [39].

The actual equivalency of the time points variable used in microfading measurements in years depends on the hours and intensity of sunlight that affects the paintings on a changing daily basis. Without proper monitoring of light, this equivalency is difficult to obtain. Although this aspect of the research was not considered in the current study, future work will include an evaluation of the location and geographical orientation of the paintings together with long-term monitoring of light and UV radiation to estimate the dose acting upon the paintings in years.

9. Discussion

The preservation of rock art paintings has been an important research topic over the last decades. Research has shown that there is a need for developing and testing new methods for assessing the state of preservation of materials and their potential degradation due to exposure to environmental factors. Studies on rock art have traditionally focus on the one hand, on the documentation, understanding and interpretation of the themes depicted by ancient civilizations [60,61,62,63], and on the other hand, on the preservation of paintings and petroglyphs [2,64,65]. Due to the complexity of materials found in rock art paintings, a combination of analytical techniques is often needed to provide a comprehensive identification of the pigment, substrate systems at a particular site [66]. At the elemental analysis level, the use of scanning electron microscopy coupled with energy dispersive X-ray analysis (SEM-EDX) and X-ray fluorescence (XRF) spectrometry has been essential for enhancing the current understanding of these materials, as can be seen from various studies conducted on several rock art sites from Valencia, Spain [67,68,69]. In some cases, inductively coupled plasma—mass spectrometry (ICPMS) has been employed for elemental analysis due to its enhanced sensitivity and the possibility of conducting semi-quantitative analysis; this can be seen for example in two separate studies conducted in Spain [67] and Australia [70]. Most researchers agree that to provide a more accurate identification of the mineral content of rock art, molecular techniques must be used in conjunction with elemental analysis. For example, quantitative mineral analysis provided by X-ray diffractometry (XRD) has been used to differentiate the various forms of minerals. For example, Beck, et al. [71] employed XRD to differentiate crystalline structures of manganese oxide after conducting in situ analysis of rock art paintings in the cave of Rouffignac, France. Similarly, Aura Tortosa, et al. [67] identified the presence of either hematite or goethite in samples from Coves de Santa Maira in Spain. Moreover, advances in infrared and Raman spectroscopies have enhanced the possibilities of pigment and binder identification in rock art at the molecular level. A comprehensive review article by Bersani and Lottici [72] provides an overview of the use of Raman spectroscopy to identify pigments found in rock art sites around the globe. An example of the use of infrared spectroscopy to characterize binding media employed in Australian rock art can be found in the work by Horn [73].

Nevertheless, a multi-technique approach has been recognized as the most adequate as a single technique does not usually provides all the information required [74]. In addition to identifying the materials present in rock art, more recent studies have dealt with degradation aspects of materials. For example, studies have been conducted in sites in Argentina [75], Ethiopia [76], and France [77] using some of the techniques indicated above. Although it is generally believed that rock art pigments are not very light sensitive, some studies have demonstrated that exposure to sunlight can have damaging effects on them due to thermal and photochemical degradation, and spectral (color) changes of the materials are one of its main effects [4,9]. Studies dealing with the use of MFS testing to evaluate the photostability of pigments found in rock art are very limited. To the best of the authors’ knowledge, there is only one similar microfading study available in which the author tested samples from the Mogao Grottoes in China [78]. MFS testing results are complementary to other chemical characterization studies of pigments previously conducted on related sites [79] and to earlier integral documentation work using 2D and 3D digital techniques [62]. However, the objective of the present study was to evaluate the performance of the technique in situ to later generate a series of degradation maps by an innovative mathematical treatment of MFS curves in this field, which is based on a probabilistic model with correlation structure and the inclusion of constraints on the MFS curves to model their monotonic behavior and find their saturation plateau. A reliable and accurate extrapolation of the color change curves was carried out to estimate the potential color degradation that may occur simultaneously in different zones of the paintings with the aim of producing degradation maps that take into account the relative degradation factors calculated for the different colored areas. These degradation maps provide a novel insight in the documentation and analysis of potential degradation of the materials.

The color change estimates are based on standardized color spaces, as this permits the visualization of color/substrate systems over a period of time. These calculations over the microfading data extrapolation map can be used to produce digital renderings of problematic zones throughout the rock art paintings. The original images representing the current state of preservation of the rock art paintings are later retouched to simulate a future state using computer imaging software. These simulations can be used to identify areas more prone to degradation in the context of the whole object with the aim of creating and developing a preservation strategy for the paintings. During the development of such a strategy, several important parameters need to be taken into account, including the position of the sun at different times of the year and its connection with the irradiation of rock art paintings and sunlight levels reaching the shelter walls. The virtual images obtained through the proposed method are useful for communicating and discussing with cultural heritage professionals and site managers about the potential detrimental effects that sunlight can have on rock art paintings. These discussions are essential for developing a preservation strategy, which takes into consideration the acceptable level of change in these valuable objects. These actions have a direct impact on rock art tourism as they serve to increase the public awareness about human and natural degradation issues in prehistoric rock art sites.

The development of a preservation strategy is possible once the degree of damage caused by direct sunlight is estimated, understood and visualized. Preventive conservation measures aimed at minimizing the effects of direct sunlight on rock art paintings may include, for example, ways of minimizing and controlling total exposure on the paintings, preparing schedules for covering sensitive objects during the times of the year when the rate of potential damage is higher, and building artificial barriers and/or shelters in the form of walls (permanent or removable) or directly applying conservation materials to act as barriers between the sunlight and the painted surfaces [80]. For paintings exhibiting a very poor state of preservation, only remedial measures are possible, including either removal of endangered rock-paintings where protection cannot be guaranteed (non-recommended policy because it is against solid ICOMOS conservation and restauration doctrines) or creating virtual models of the paintings to be used and shared by museums (state-of-the-art trend).

Careful documentation, testing, mathematical modeling and visualization of long-term changes have significant practical implications for geoarchaeology, conservation, preservation and heritage studies. The results from the present study provide a valuable social resource to raise awareness about the importance of preserving rock art among stakeholders and members of the public, local communities and future generations. Archaeologists and cultural heritage documentation specialists were initially concerned with the use of MFS testing on actual rock art paintings [3]. However, the present study has provided answers to the questions formulated by researchers currently involved in the study of rock art paintings. Microfading is an adequate application tool to study the long-term behavior of rock/pigment systems exposed to sunlight radiation. For this reason, a multidisciplinary approach, which includes mathematical modeling of microfading data along with virtual visualization of paintings, can enhance the documentation of these sites by offering a new dimension in terms of ageing processes and photostability of their colored systems.

10. Conclusions

Color is an important aspect of the documentation and conservation of historical assets such as prehistoric rock art paintings. Therefore, the knowledge of the potential color degradation on these systems is crucial for eventual safeguarding and conservation. MFS measurements are difficult and lengthy to materialize, especially in these rock art systems, so an interpolation procedure to make accurate predictions for other locations on the surface in a scenario with a small sample dataset is important. Furthermore, these measurements in these systems show large fluctuations, so the consideration of constraints in the modeling to overcome possible modeling issues that may arise due to these large fluctuations is highly encouraged.

A reliable model for a dataset with small and large fluctuations based on spatially correlated time series has been formulated, in which the regular process is jointly modeled with the derivative process. Modeling the derivative process allows us to include model constraints related to the derivative of the functions in order to fit the desired properties of the color fading curves and minimize the effects of large fluctuations in the original observations. Furthermore, taking into account these first-order constraints has been demonstrated to be beneficial, either in terms of predictive performance or application-specific interpretability. Predictive capacity (as measured by MSE and ELPD) is considerably better with the model with derivative constraints compared to the model without them. However, high sensitivity of the models to leaving some data out has been found due to the small size of the data set.

GPs have been used to spatially correlate the spline time series by correlating their splines coefficients. A multivariate covariance function in a GP has allowed the usage of many predictors to evaluate the spatial covariance structure of the data. In this sense, the color space variables and the spatial distance in the covariance function have been included, and the colorimetric variables demonstrated being useful to correlate MFS data. The contribution of the spatial positions to this covariance structure has been found to matter; consequently, often and widely used traditional spatial or spatio-temporal models may detect a useful correlation structure in the data. Furthermore, GPs are one of the most natural ways to evaluate the covariance structure and make useful generalizations of the data, and this approach of combining spline functions for the temporal dimension and multivariate GPs to spatially correlate the spline coefficients is an original spatio-temporal approach, seldom implemented in practice.

Multivariate covariance metrics and zero and first-order constraints might be very hard to implement outside of a Bayesian framework and GP models. A GP is flexible enough and allowed us to properly model this complex covariance structure of the time series dependent on different input covariates. The Bayesian framework has allowed us to jointly use normally distributed observations with probit distributed observations of the sign of the partial derivatives, allowing us to fulfill the determinants of the behavior of the functions. A useful and comprehensive implementation of derivative constraints for spline functions and in a Bayesian framework has been illustrated in this work. Furthermore, the computational requirements of inverting the Gram matrix of the covariance function to compute the posterior distribution in the proposed spatially correlated time series model framework have been reduced substantially compared to using a spatio-temporal GP framework, since $K\left(\mathrm{knots}\right)\ll T(\mathrm{time}\mathrm{points})$. Finally, it is possible to consider other covariance structures for the relationship between space and knots. Even so, given the large number of points at which predictions must be made, the computational burden is large, in particular given that HMC algorithms are being used. To speed up computation, distributional or numerical approximation methods can be faster alternatives. In relation to this, a future line of research will be to use an approximate method for Bayesian inference that could speed up computation, making it easier to apply the methodology on several other rock art sites.

To conclude, a Bayesian statistical model with the considerations of constraints and multivariate GPs to spatially correlate the color fading curves is a significant advancement in the applied field, useful for making accurate predictions and ensuring good properties for the color fading estimates. Research shows that reliable evolution maps of color fading estimates can be elaborated by means of using the proposed model with derivative information in comparison to the model without derivative information. Furthermore, from a social and economic standpoint, these research results will help to improve the allocation of resources and conservation strategies by taking into account the possible degradation of this important and unique group of prehistoric rock art paintings over time. This will also be useful information, alone or in conjunction with the evaluations of other environmental damaging factors, with which to create better policies for heritage preservation and sustainable archaeological cultural tourism.