Cavitation Model Calibration Using Machine Learning Assisted Workflow
Abstract
1. Introduction
2. CFD Setup
2.1. Governing Equations
2.2. Cavitation Model
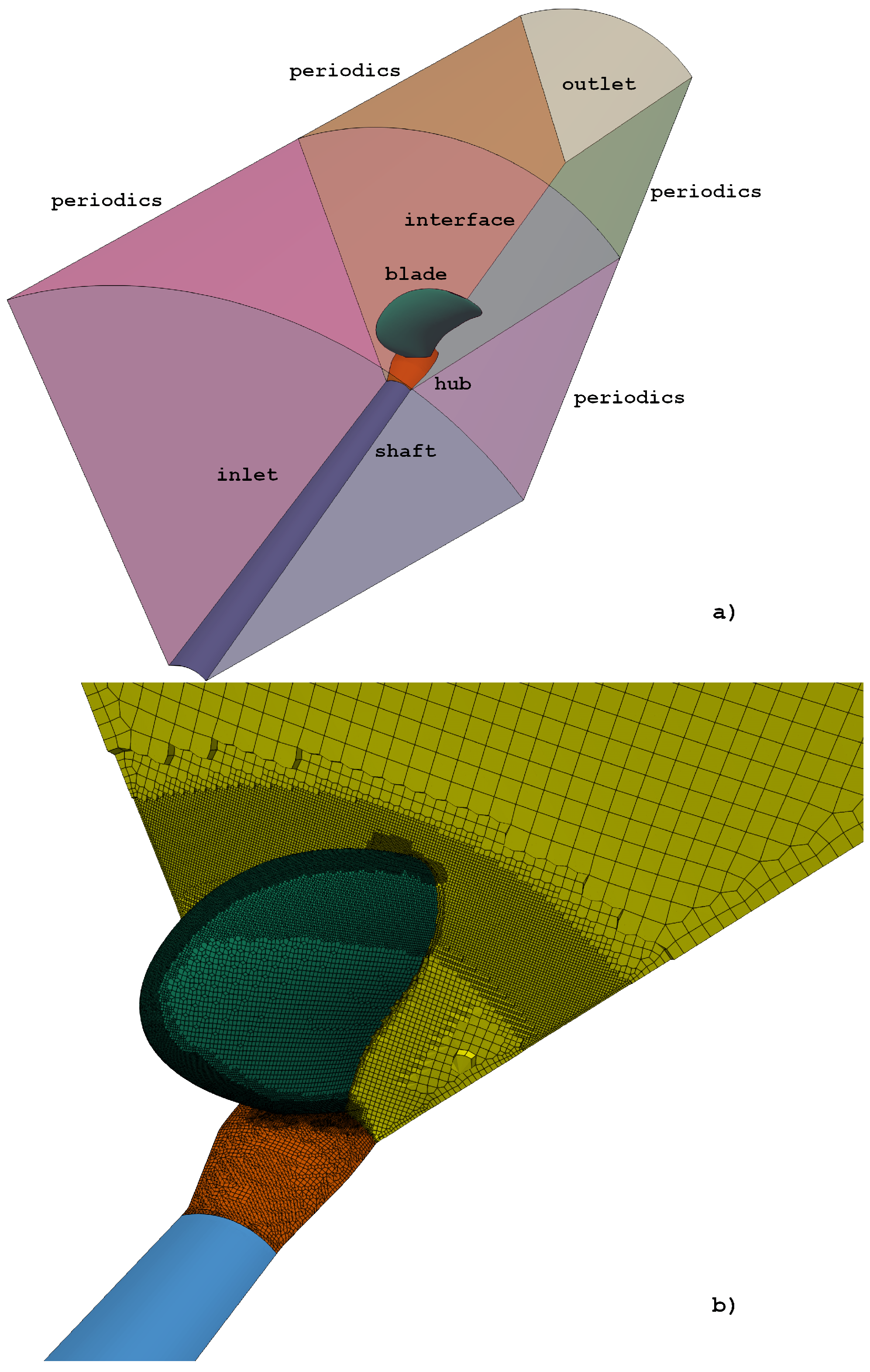
2.3. Geometry and Computational Domain
2.4. Numerical Setup
2.5. Grid Convergence
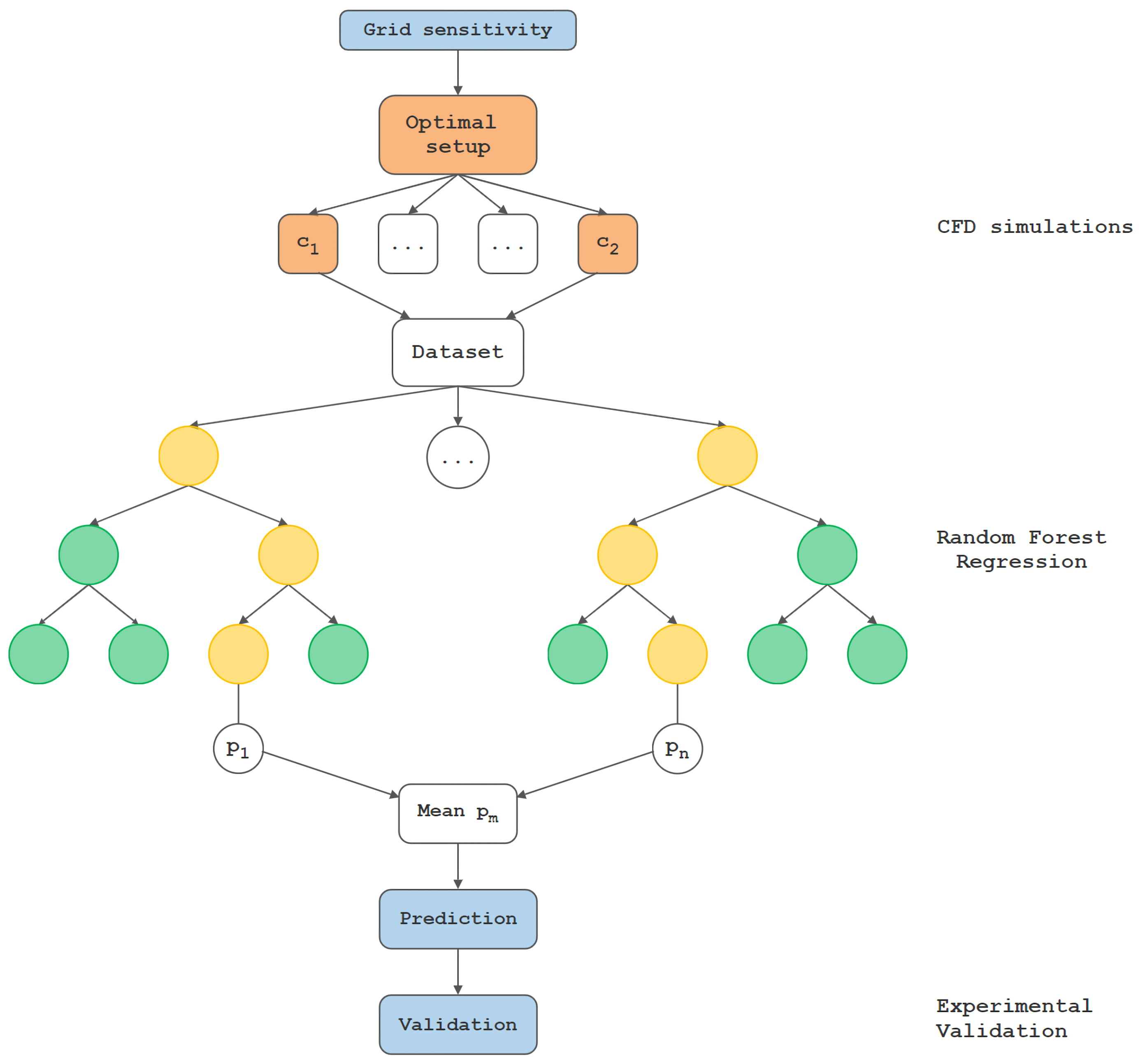
3. Machine Learning Assisted Workflow
3.1. Challenges in Cavitation Analysis
3.2. ML Algorithm and Generalized Workflow
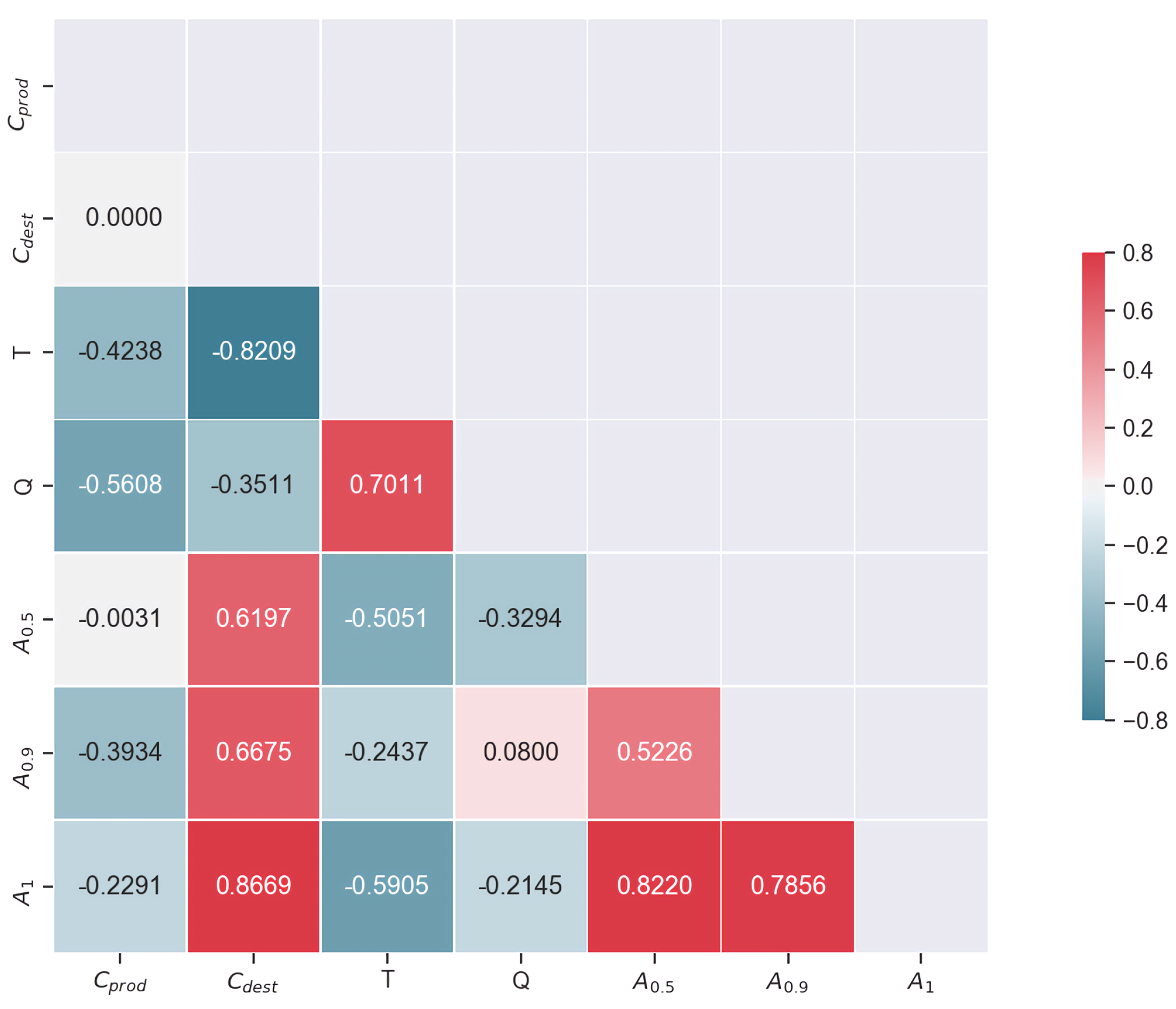
3.3. Data Analysis and Random Forest Regression
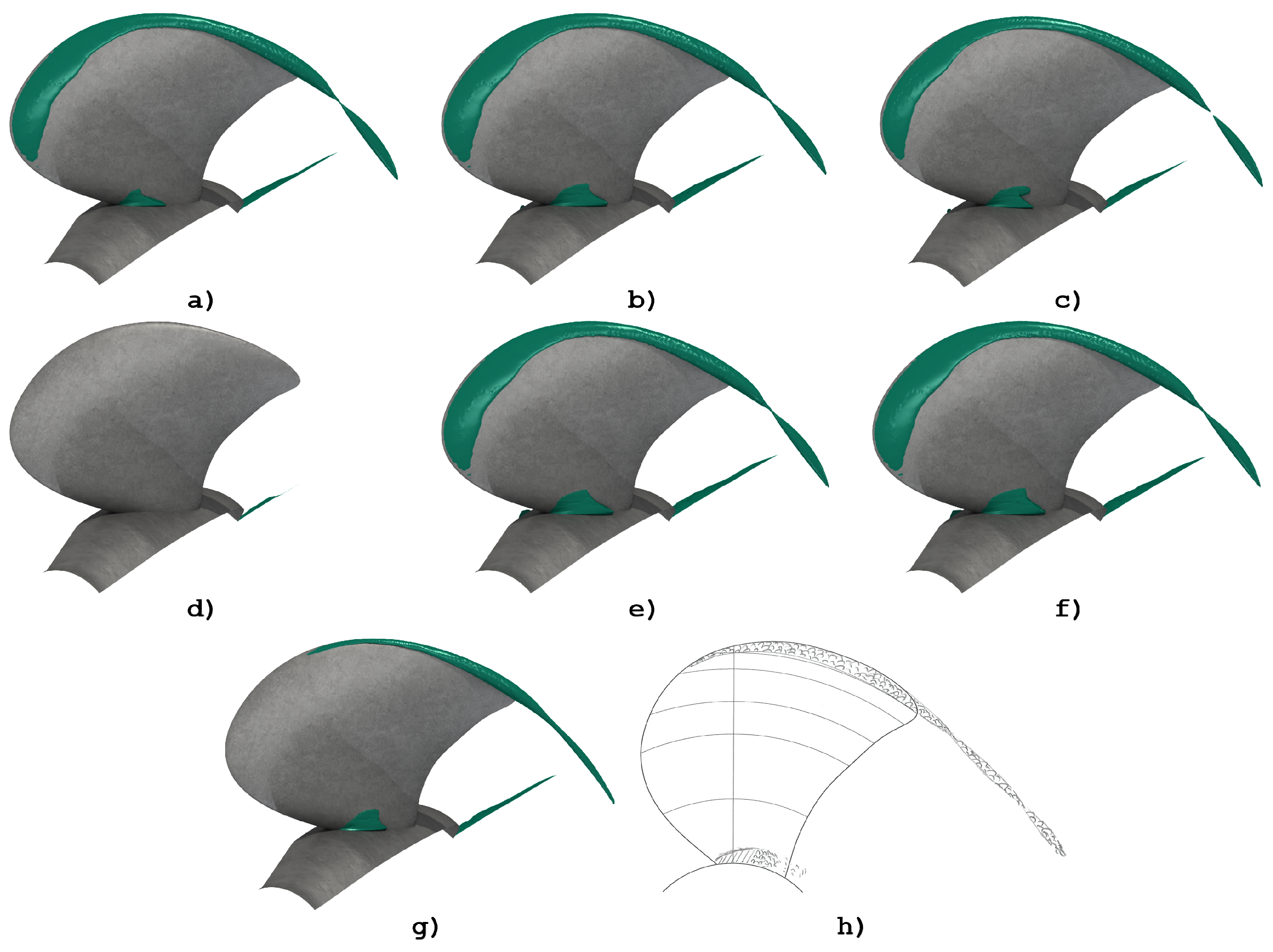
4. Predictions and Validity
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bertetta, D.; Brizzolara, S.; Gaggero, S.; Viviani, M.; Savio, L. CPP propeller cavitation and noise optimization at different pitches with panel code and validation by cavitation tunnel measurements. Ocean Eng. 2012, 53, 177–195. [Google Scholar] [CrossRef]
- Gaggero, S.; Tani, G.; Villa, D.; Viviani, M.; Ausonio, P.; Travi, P.; Bizzarri, G.; Serra, F. Efficient and multi-objective cavitating propeller optimization: An application to a high-speed craft. Appl. Ocean Res. 2017, 64, 31–57. [Google Scholar] [CrossRef]
- Kubota, A.; Kato, H.; Yamaguchi, H. A new modelling of cavitating flows: A numerical study of unsteady cavitation on a hydrofoil section. J. Fluid Mech. 1992, 240, 59–96. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Chyczewski, T.S.; Stinebring, D.; Gibeling, H.; Govindan, T. Multi-phase CFD analysis of natural and ventilated cavitation about submerged bodies. In Proceedings of the 3rd ASME-JSME Joint Fluids Engineering Conference, San Francisco, CA, USA, 18–23 July 1999. [Google Scholar]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–3 June 2004; Volume 152. [Google Scholar]
- Schnerr, G.H.; Sauer, J. Physical and numerical modeling of unsteady cavitation dynamics. In Proceedings of the Fourth International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001; Volume 1. [Google Scholar]
- Gaggero, S.; Tani, G.; Viviani, M.; Conti, F. A study on the numerical prediction of propellers cavitating tip vortex. Ocean Eng. 2014, 92, 137–161. [Google Scholar] [CrossRef]
- Lidtke, A.K.; Humphrey, V.F.; Turnock, S.R. Feasibility study into a computational approach for marine propeller noise and cavitation modelling. Ocean Eng. 2016, 120, 152–159. [Google Scholar] [CrossRef]
- Gaggero, S.; Villa, D. Steady cavitating propeller performance by using OpenFOAM, StarCCM+ and a boundary element method. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2017, 231, 411–440. [Google Scholar] [CrossRef]
- Viitanen, V.; Siikonen, T.; Sánchez-Caja, A. Cavitation on Model-and Full-Scale Marine Propellers: Steady And Transient Viscous Flow Simulations At Different Reynolds Numbers. J. Mar. Sci. Eng. 2020, 8, 141. [Google Scholar] [CrossRef]
- Roohi, E.; Pendar, M.R.; Rahimi, A. Simulation of three-dimensional cavitation behind a disk using various turbulence and mass transfer models. Appl. Math. Model. 2016, 40, 542–564. [Google Scholar] [CrossRef]
- Medvitz, R.B.; Kunz, R.F.; Boger, D.A.; Lindau, J.W.; Yocum, A.M.; Pauley, L.L. Performance analysis of cavitating flow in centrifugal pumps using multiphase CFD. J. Fluids Eng. 2002, 124, 377–383. [Google Scholar] [CrossRef]
- Lindau, J.W.; Boger, D.A.; Medvitz, R.B.; Kunz, R.F. Propeller cavitation breakdown analysis. J. Fluids Eng. 2005, 127, 995. [Google Scholar] [CrossRef]
- Bensow, R.E.; Bark, G. Implicit LES predictions of the cavitating flow on a propeller. J. Fluids Eng. 2010, 132, 041302. [Google Scholar] [CrossRef]
- Lu, N.X.; Bensow, R.E.; Bark, G. Large eddy simulation of cavitation development on highly skewed propellers. J. Mar. Sci. Technol. 2014, 19, 197–214. [Google Scholar] [CrossRef]
- Morgut, M.; Nobile, E.; Biluš, I. Comparison of mass transfer models for the numerical prediction of sheet cavitation around a hydrofoil. Int. J. Multiph. Flow 2011, 37, 620–626. [Google Scholar] [CrossRef]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Wu, J.; Utturkar, Y.; Shyy, W. Assessment of modeling strategies for cavitating flow around a hydrofoil. In Proceedings of the Fifth International Symposium on Cavitation, Osaka, Japan, 1–4 November 2003; pp. 1–5. [Google Scholar]
- Johansen, S.T.; Wu, J.; Shyy, W. Filter-based unsteady RANS computations. Int. J. Heat Fluid Flow 2004, 25, 10–21. [Google Scholar] [CrossRef]
- Coutier-Delgosha, O.; Reboud, J.; Delannoy, Y. Numerical simulation of the unsteady behaviour of cavitating flows. Int. J. Numer. Methods Fluids 2003, 42, 527–548. [Google Scholar]
- Coutier-Delgosha, O.; Fortes-Patella, R.; Reboud, J.L. Evaluation of the turbulence model influence on the numerical simulations of unsteady cavitation. J. Fluids Eng. 2003, 125, 38–45. [Google Scholar] [CrossRef]
- Coutier-Delgosha, O.; Deniset, F.; Astolfi, J.A.; Leroux, J.B. Numerical prediction of cavitating flow on a two-dimensional symmetrical hydrofoil and comparison to experiments. J. Fluids Eng. 2007, 129, 279–292. [Google Scholar] [CrossRef]
- Kunz, R.F.; Lindau, J.W.; Kaday, T.A.; Peltier, L.J. Unsteady RANS and detached eddy simulations of cavitating flow over a hydrofoil. In Proceedings of the Fifth International Symposium on Cavitation, Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Bensow, R.E. Simulation of the unsteady cavitation on the Delft Twist11 foil using RANS, DES and LES. In Proceedings of the Second International Symposium on Marine Propulsors, Hamburg, German, 15–17 June 2011. [Google Scholar]
- Shi, W.; Zhang, G.; Zhang, D. Evaluation of turbulence models for the numerical prediction of transient cavitation around a hydrofoil. IOP Conf. Ser. Mater. Sci. Eng. 2013, 52, 062013. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.; Wu, Y.; Peng, X.; Duan, Y. Numerical analysis of unsteady cavitating turbulent flow and shedding horse-shoe vortex structure around a twisted hydrofoil. Int. J. Multiph. Flow 2013, 51, 33–43. [Google Scholar] [CrossRef]
- Kadivar, E.; el Moctar, O.; Javadi, K. Investigation of the effect of cavitation passive control on the dynamics of unsteady cloud cavitation. Appl. Math. Model. 2018, 64, 333–356. [Google Scholar] [CrossRef]
- Kadivar, E.; Timoshevskiy, M.V.; Pervunin, K.S.; el Moctar, O. Experimental and numerical study of the cavitation surge passive control around a semi-circular leading-edge flat plate. J. Mar. Sci. Technol. 2019, 25, 1–4. [Google Scholar] [CrossRef]
- SVA Team. PPTC smp’11 Workshop. 2011. Available online: https://www.sva-potsdam.de/pptc-smp11-workshop/ (accessed on 18 July 2020).
- The OpenFOAM Foundation. OpenFOAM User Guide. 2016. Available online: https://www.openfoam.org (accessed on 18 July 2020).
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Roache, P.J. Verification and Validation in Computational Science and Engineering; Hermosa Publisher: Socorro, NM, USA, 1998; Volume 895. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Quinlan, R. C4.5. In Programs for Machine Learning; Morgan Kaufmann Publishers: Burlington, MA, USA, 1993. [Google Scholar]
- Hothorn, T.; Hornik, K.; Zeileis, A. Unbiased recursive partitioning: A conditional inference framework. J. Comput. Graph. Stat. 2006, 15, 651–674. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Botchkarev, A. Performance metrics (error measures) in machine learning regression, forecasting and prognostics: Properties and typology. arXiv 2018, arXiv:1809.03006. [Google Scholar]
- Vaz, G.; Hally, D.; Huuva, T.; Bulten, N.; Muller, P.; Becchi, P.; Herrer, J.L.; Whitworth, S.; Macé, R.; Korsström, A. Cavitating flow calculations for the E779A propeller in open water and behind conditions: Code comparison and solution validation. In Proceedings of the Fourth International Symposium on Marine Propulsors SMP, Austin, TX, USA, 31 May–4 June 2015; Volume 15, pp. 344–360. [Google Scholar]
- Zhou, H.; Xiang, M.; Okolo, P.N.; Wu, Z.; Bennett, G.J.; Zhang, W. An efficient calibration approach for cavitation model constants based on OpenFOAM platform. J. Mar. Sci. Technol. 2019, 24, 1043–1056. [Google Scholar] [CrossRef]
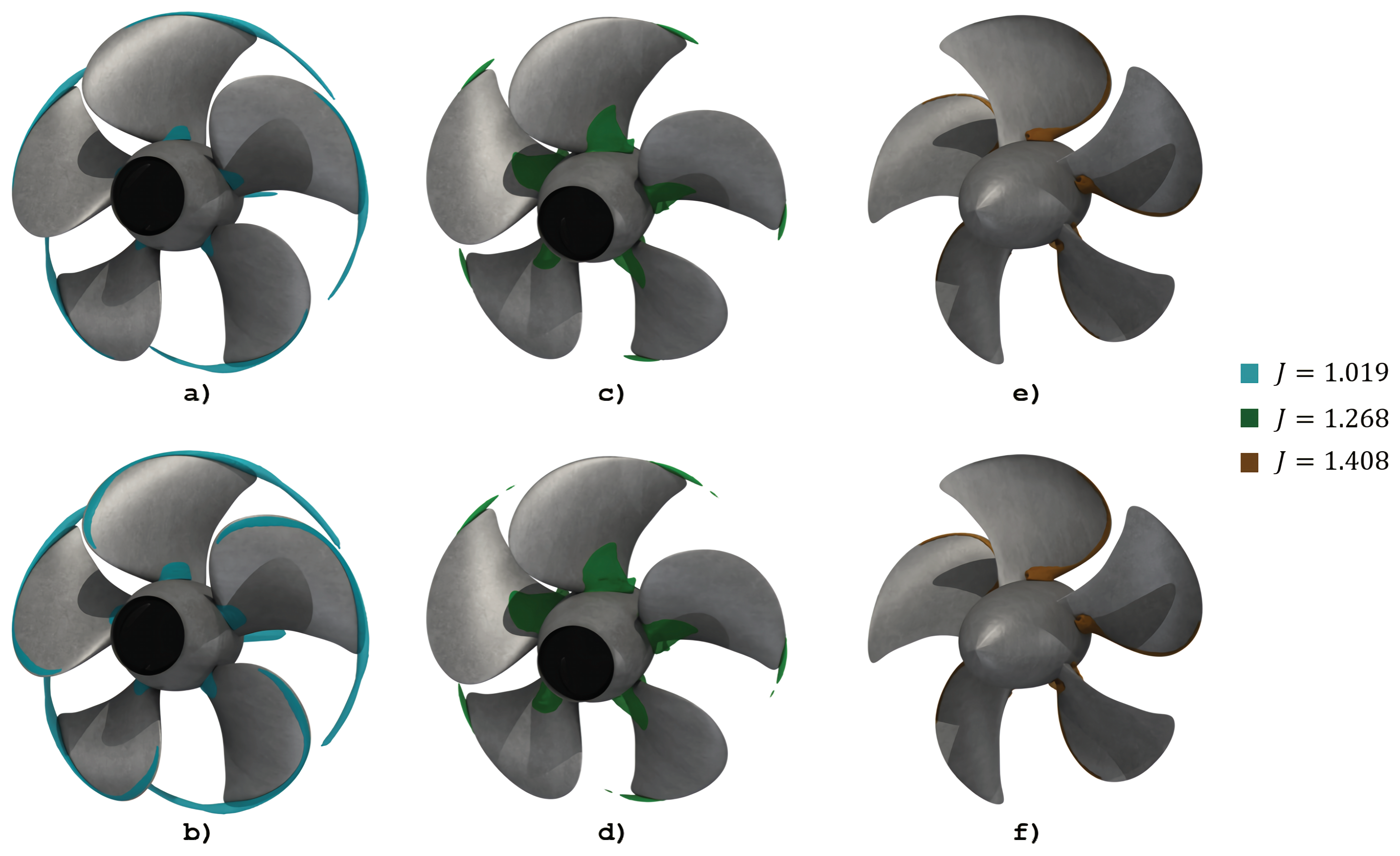
| Propeller diameter [m] | 0.250 |
| Pitch ratio at | 1.635 |
| Chord length at [m] | 0.104 |
| Skew [] | 18.837 |
| Hub ratio | 0.300 |
| Number of blades | 5 |
| Rotation | right |
| Field | Inlet | Outlet | Blades / Hub | Shaft |
|---|---|---|---|---|
| u | fixedValue | zeroGradient | movingWallVelocity | noSlip |
| prgh | zeroGradient | prghPressure | fixedFluxPressure | fixedFluxPressure |
| alpha | fixedValue | zeroGradient | zeroGradient | zeroGradient |
| calculated | calculated | nutkWallFunction | nutkWallFunction | |
| k | fixedValue | zeroGradient | kqRWallFunction | kqRWallFunction |
| fixedValue | zeroGradient | omegaWallFunction | omegaWallFunction |
| Mesh | Coarse | Medium | Fine |
|---|---|---|---|
| Grid Size | |||
| Max. Cell Size (m) | |||
| Grid Refinement ratio | - | 1.231 | 1.300 |
| Relative Error (%) | - | 0.983 | 0.758 |
| GCI (%) | - | 2.175 | 1.244 |
| Performance Metrics | MAE | RMSE | MAPE |
|---|---|---|---|
| Training Set (80%) | 0.1558 | 0.1982 | 0.2852 |
| Test Set (20%) | 0.1583 | 0.2085 | 0.2966 |
| Reference | ||
|---|---|---|
| Bensow et al. [15] | 20,000 | 1000 |
| Morgut et al. [17] | 455 | 4100 |
| Kunz et al. [4] | 100 | 100 |
| Kunz et al. [5] | 0.2 | 0.2 |
| Vaz et al. [40] | 10,000 | 500 |
| Zhou et al. [41] | 4328 | 3323 |
| Predicted | 172 | 5 |
| Case | (N) | (N) | (N) | (Nm) | (Nm) | (Nm) |
|---|---|---|---|---|---|---|
| 908.70 | 921.13 | 932.49 | 58.98 | 58.94 | 59.64 | |
| 502.08 | 483.27 | 500.69 | 38.38 | 37.20 | 38.28 | |
| 331.94 | 332.94 | 320.24 | 29.80 | 29.17 | 29.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sikirica, A.; Čarija, Z.; Lučin, I.; Grbčić, L.; Kranjčević, L. Cavitation Model Calibration Using Machine Learning Assisted Workflow. Mathematics 2020, 8, 2107. https://doi.org/10.3390/math8122107
Sikirica A, Čarija Z, Lučin I, Grbčić L, Kranjčević L. Cavitation Model Calibration Using Machine Learning Assisted Workflow. Mathematics. 2020; 8(12):2107. https://doi.org/10.3390/math8122107
Chicago/Turabian StyleSikirica, Ante, Zoran Čarija, Ivana Lučin, Luka Grbčić, and Lado Kranjčević. 2020. "Cavitation Model Calibration Using Machine Learning Assisted Workflow" Mathematics 8, no. 12: 2107. https://doi.org/10.3390/math8122107
APA StyleSikirica, A., Čarija, Z., Lučin, I., Grbčić, L., & Kranjčević, L. (2020). Cavitation Model Calibration Using Machine Learning Assisted Workflow. Mathematics, 8(12), 2107. https://doi.org/10.3390/math8122107





