Figure 1.
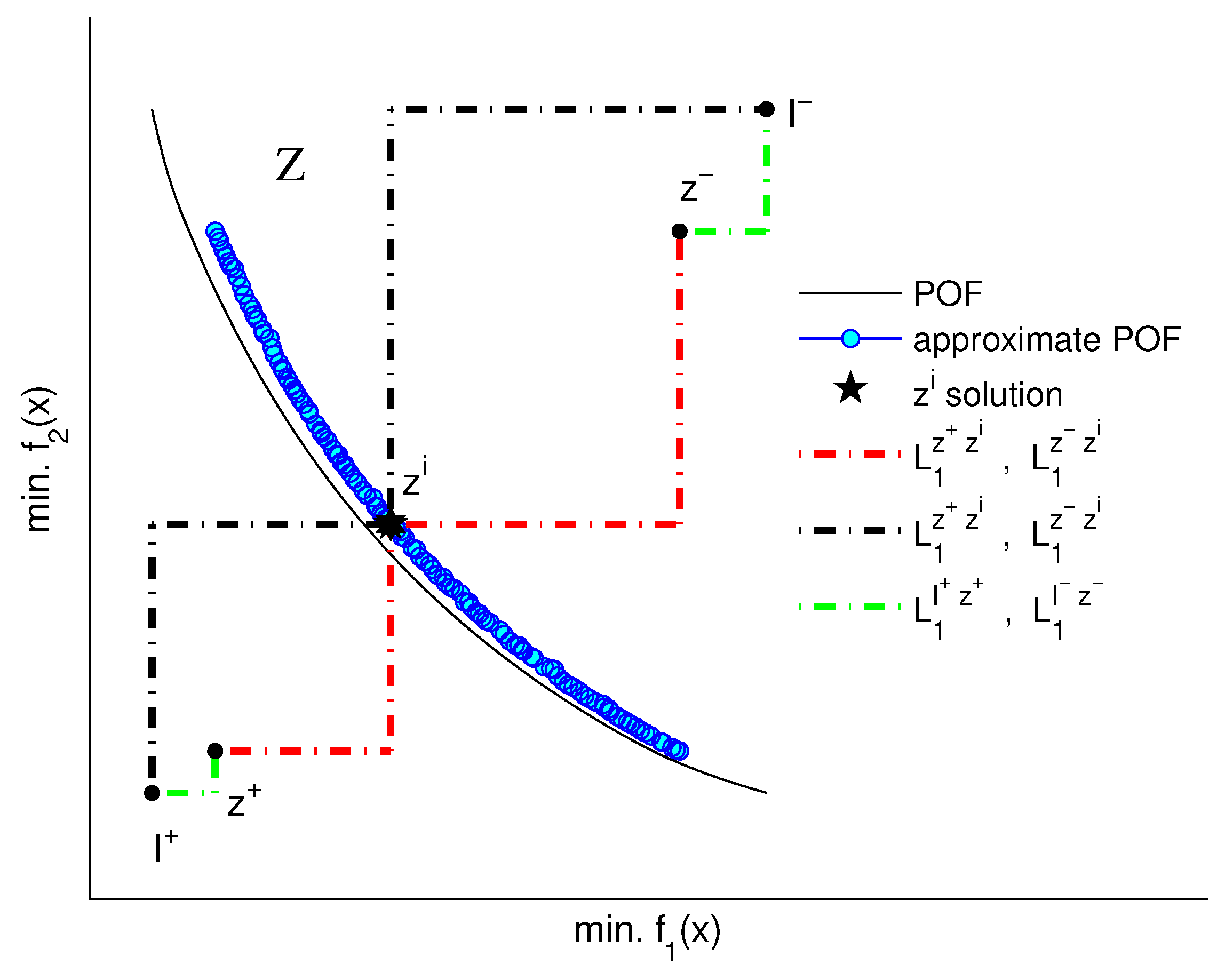
Feasible solution set Z in the objectives space, the ideal and nadir solutions, the approximate ideal and nadir solutions and distances.
Figure 1.
Feasible solution set Z in the objectives space, the ideal and nadir solutions, the approximate ideal and nadir solutions and distances.
Figure 2.
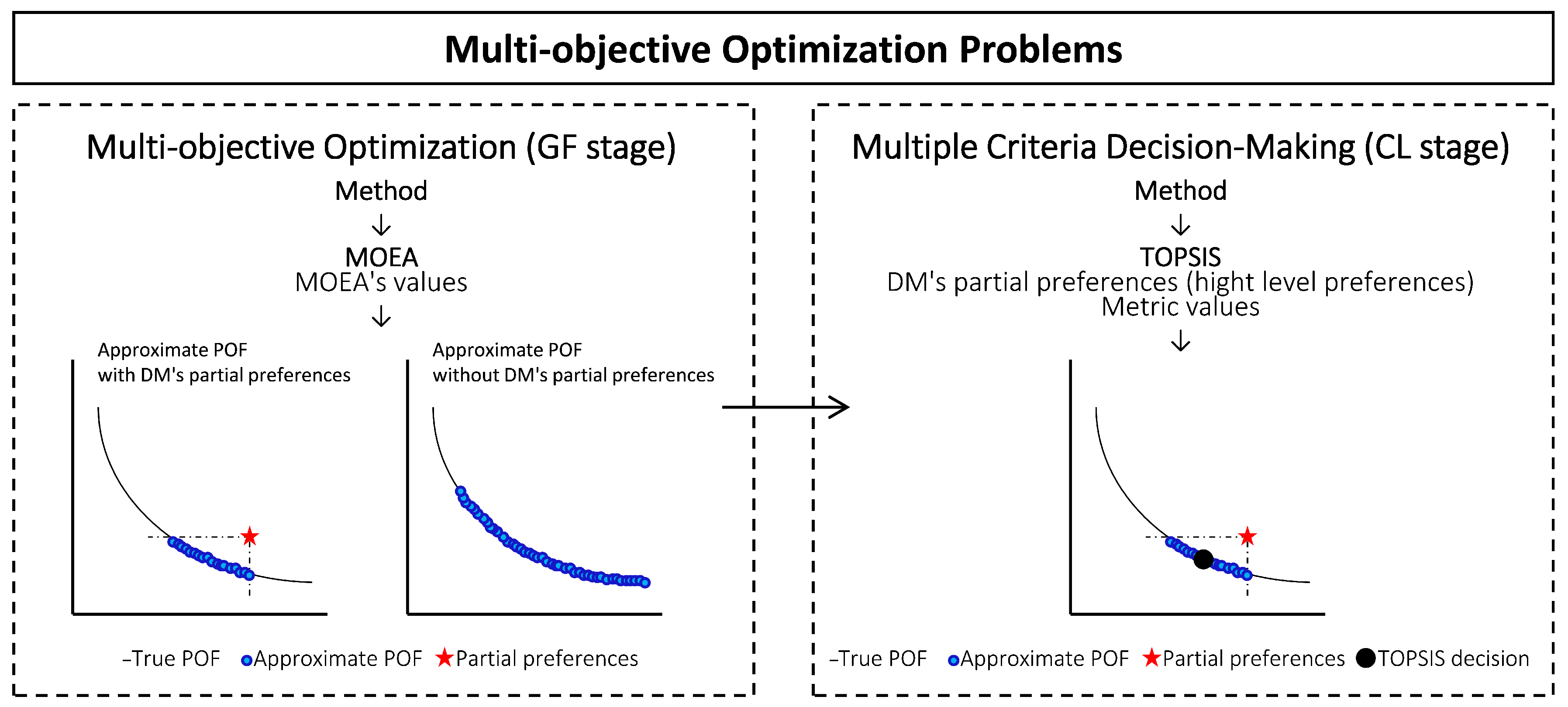
Proposed two-stage MOO and MCDM methodology.
Figure 2.
Proposed two-stage MOO and MCDM methodology.
Figure 3.
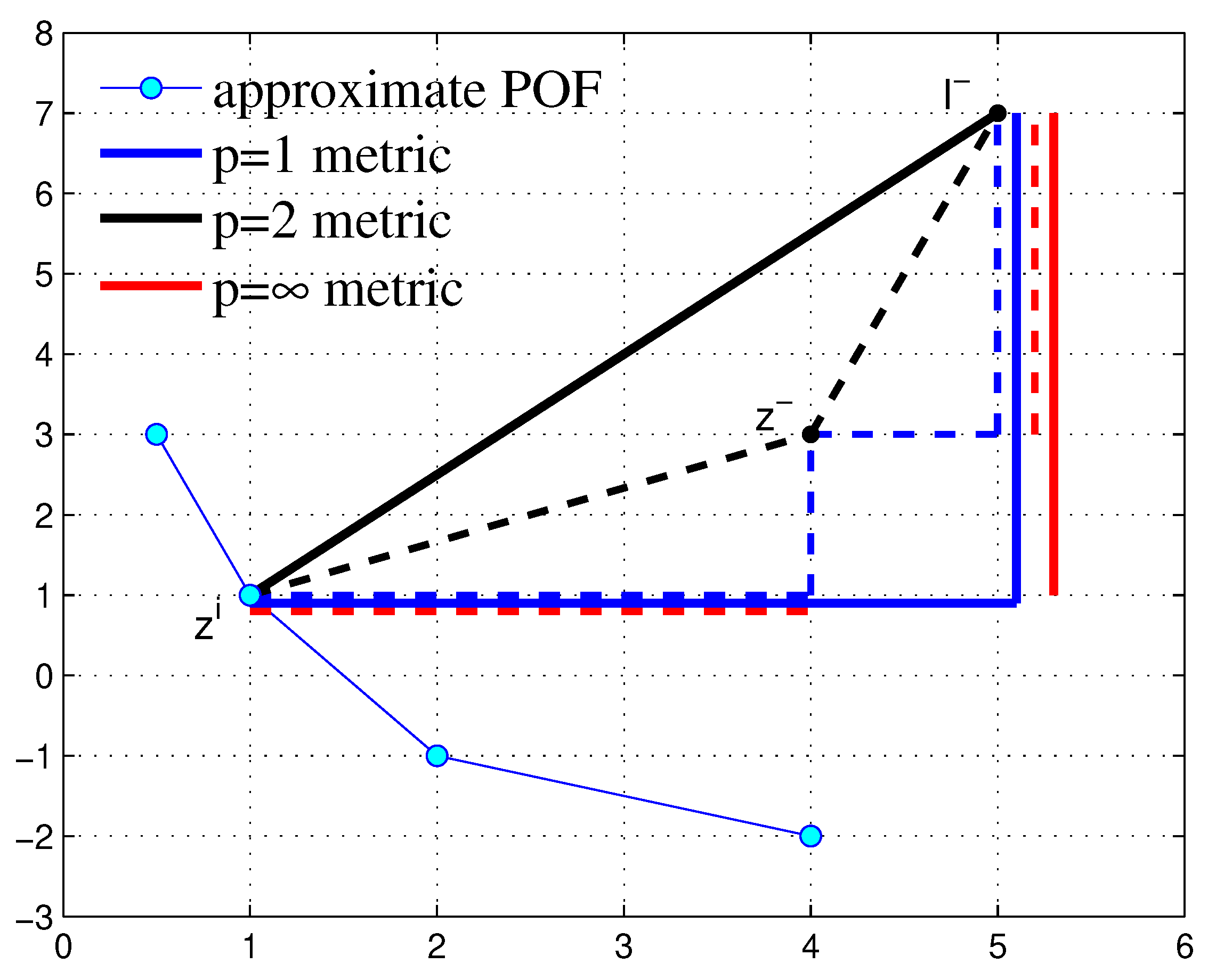
Distances , and with ∞ metric.
Figure 3.
Distances , and with ∞ metric.
Figure 4.
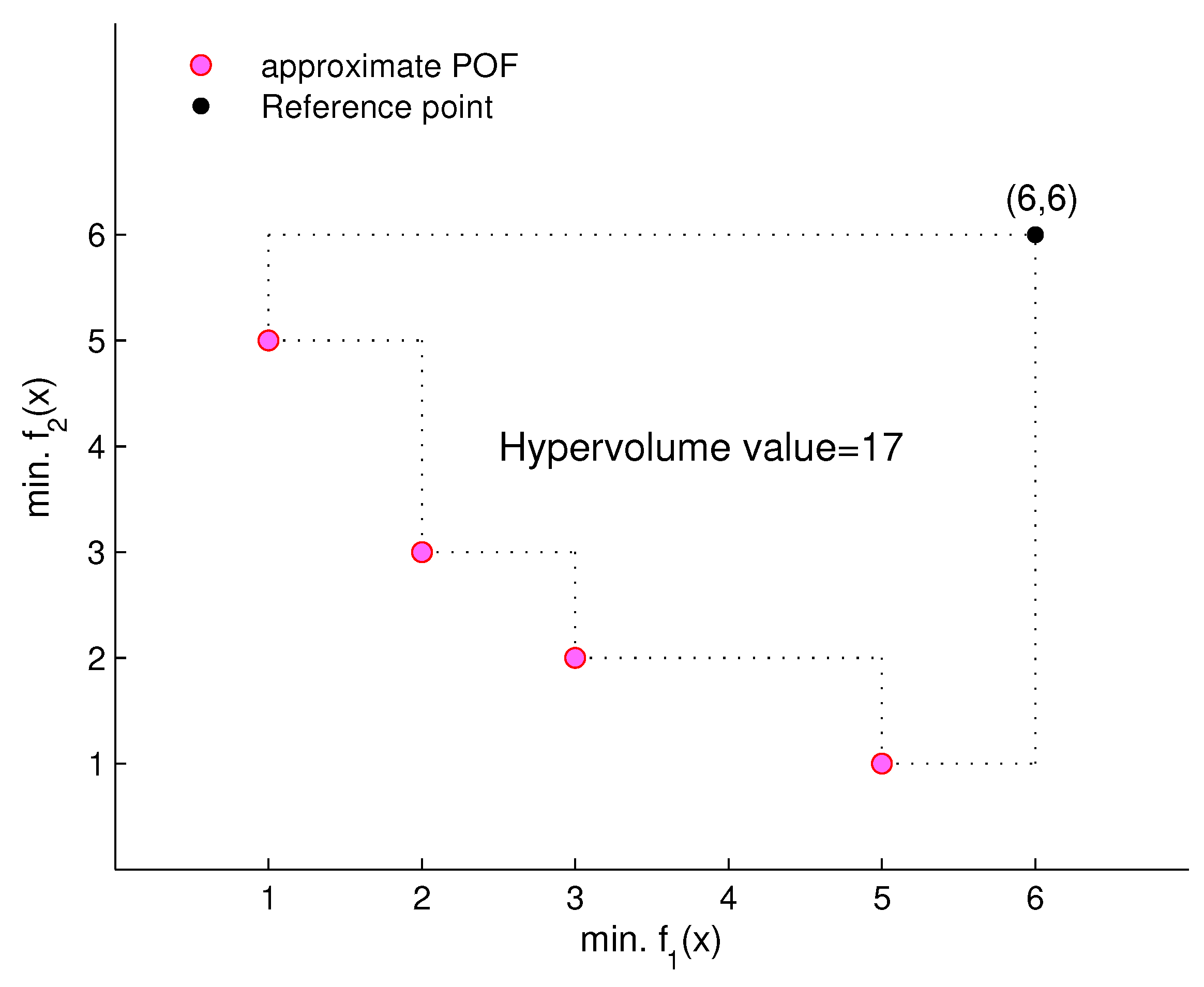
Evaluation of the hypervolume value with respect to the given reference point (6,6) on a two-objective minimization problem; larger hypervolume values indicate better quality of the approximate POF.
Figure 4.
Evaluation of the hypervolume value with respect to the given reference point (6,6) on a two-objective minimization problem; larger hypervolume values indicate better quality of the approximate POF.
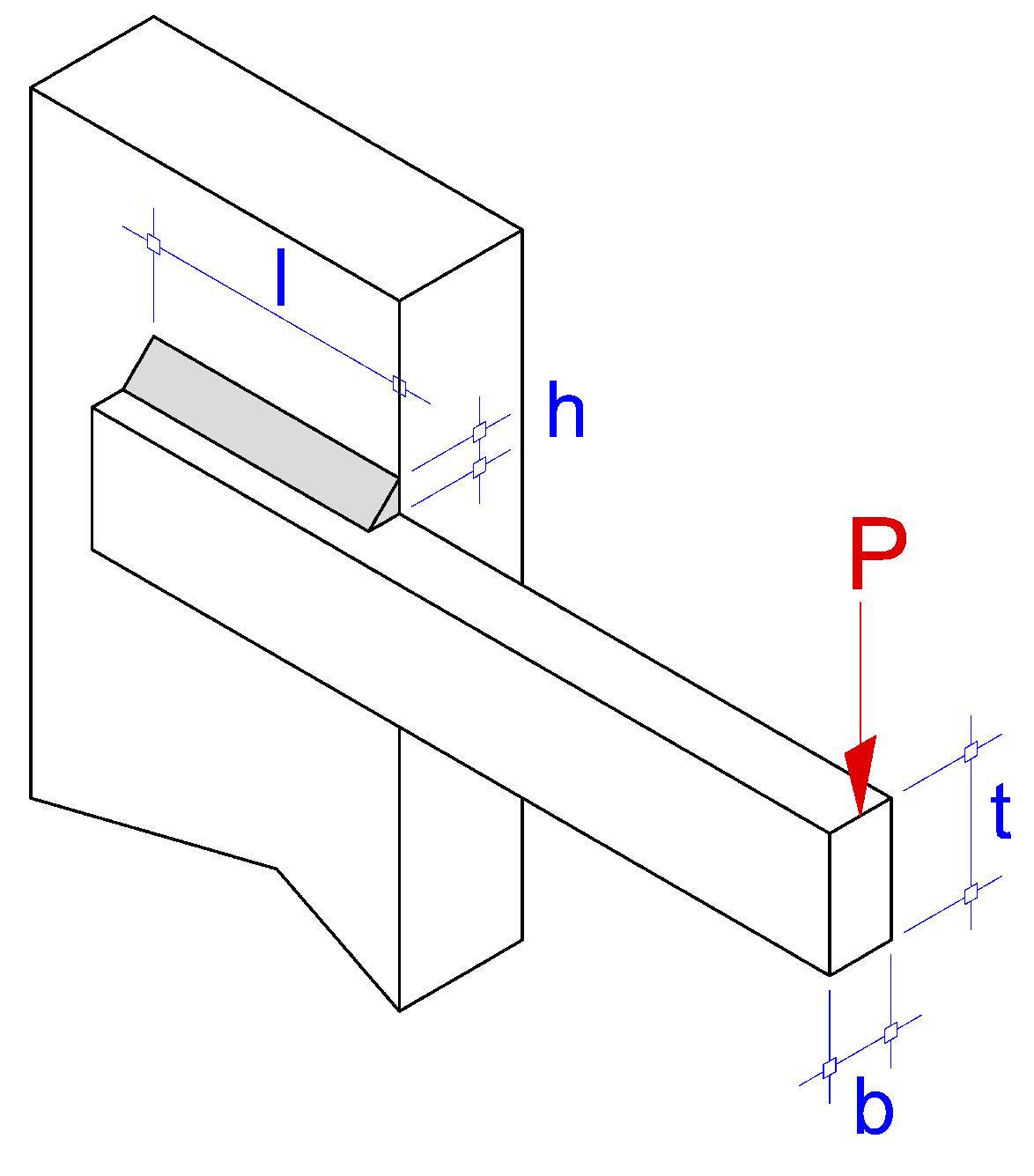
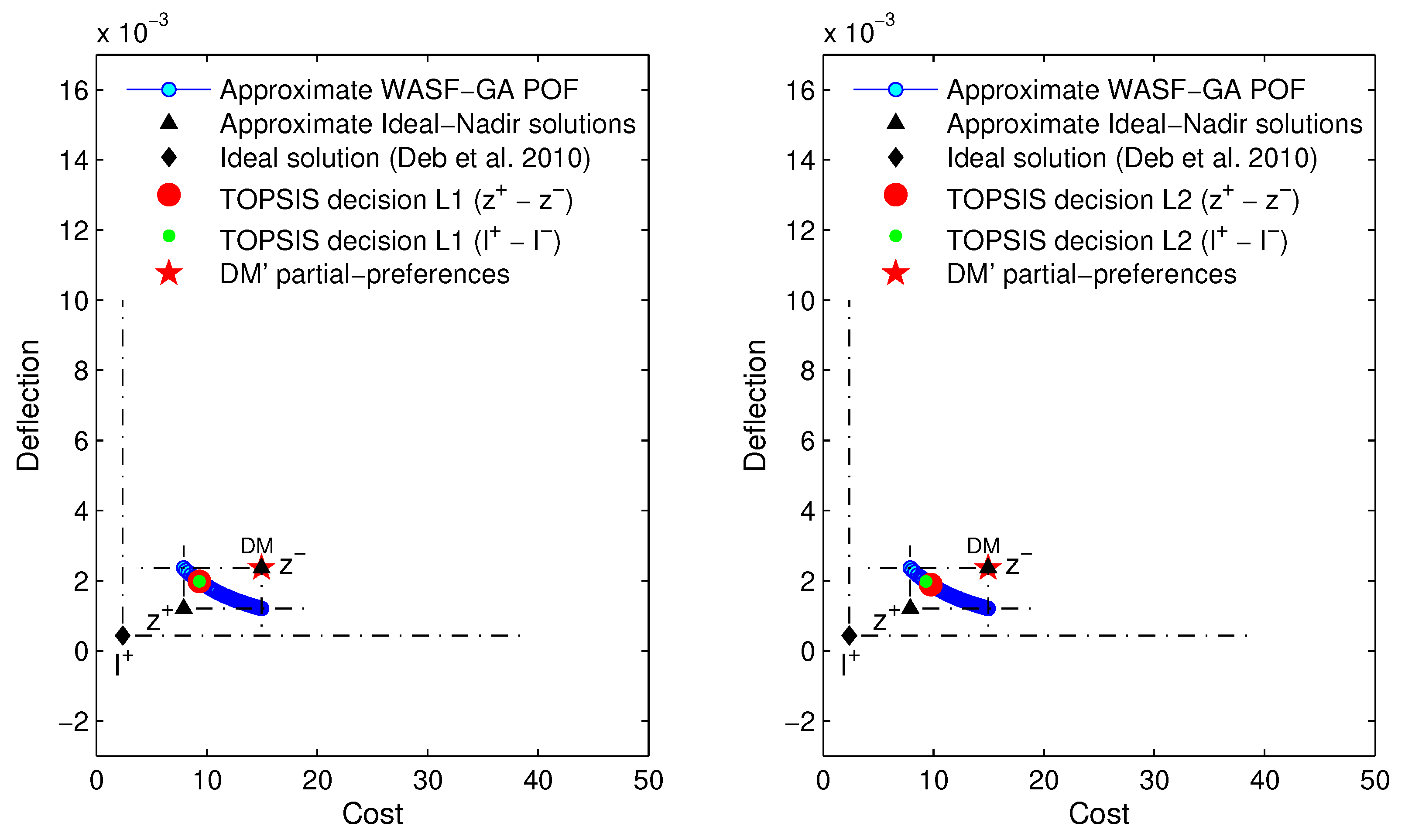
Figure 5.
Welded beam design problem.
Figure 5.
Welded beam design problem.
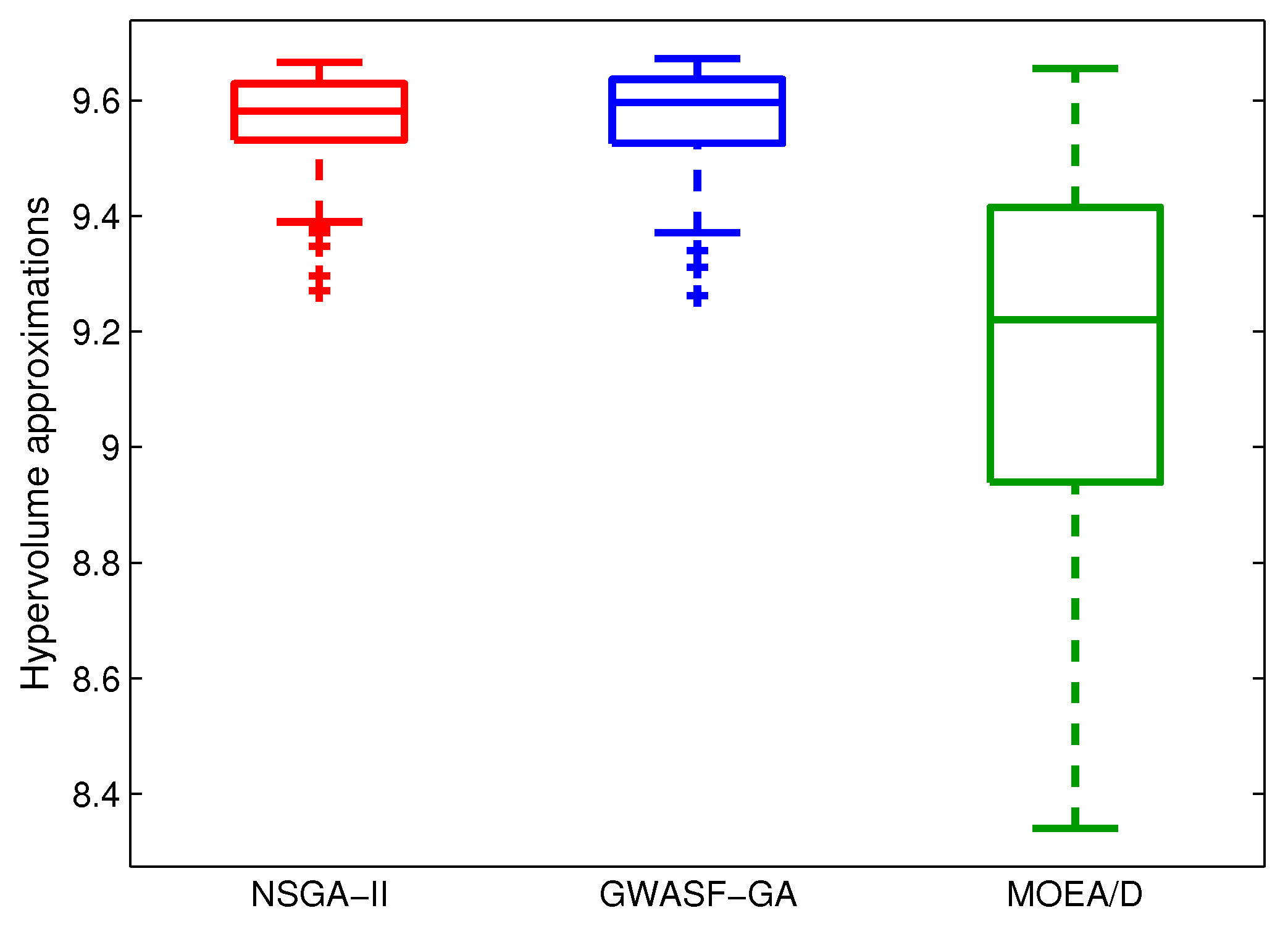
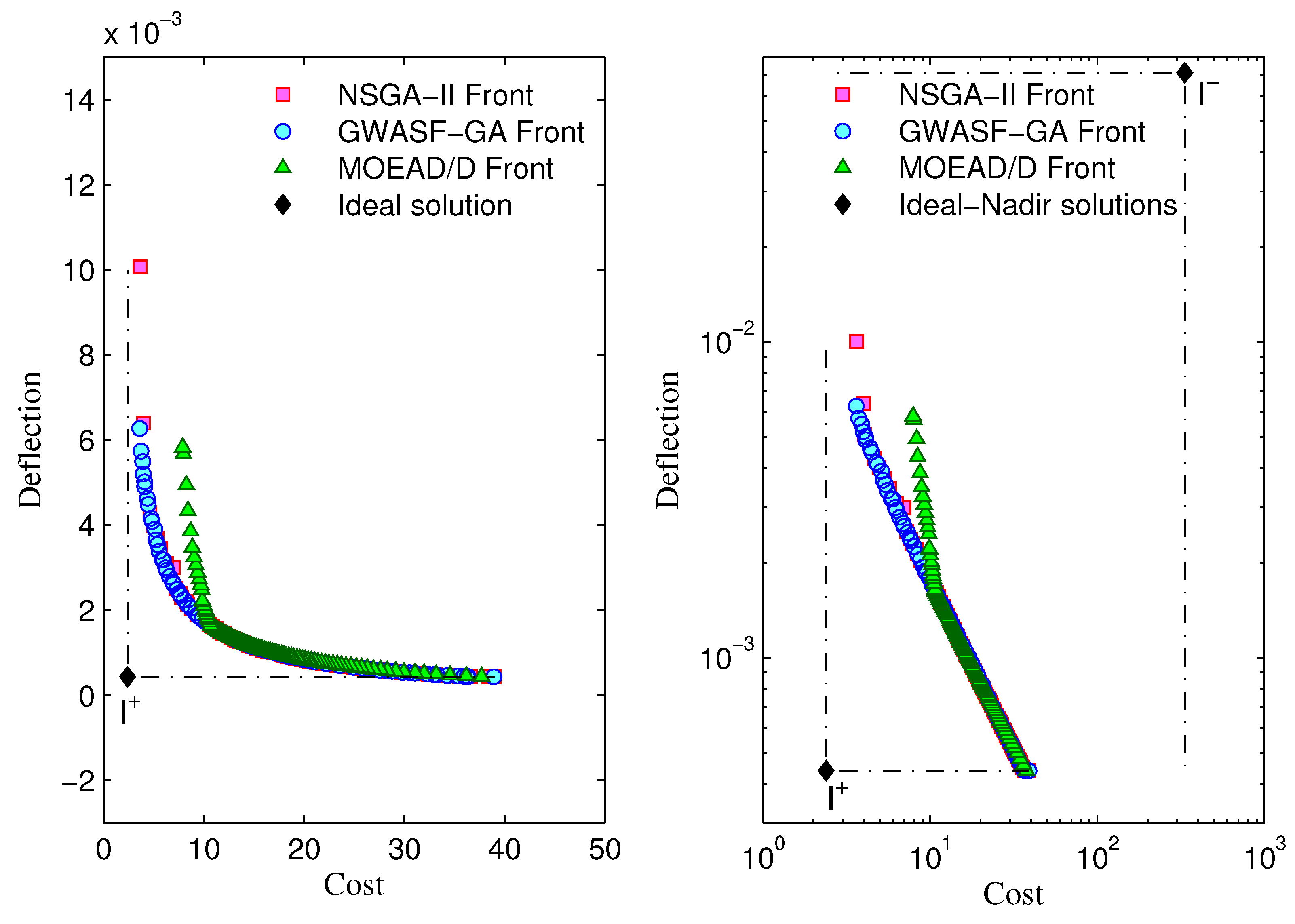
Figure 6.
Box-plots based on the hypervolume metric for NSGA-II, GWASF-GA and MOEA/D ().
Figure 6.
Box-plots based on the hypervolume metric for NSGA-II, GWASF-GA and MOEA/D ().
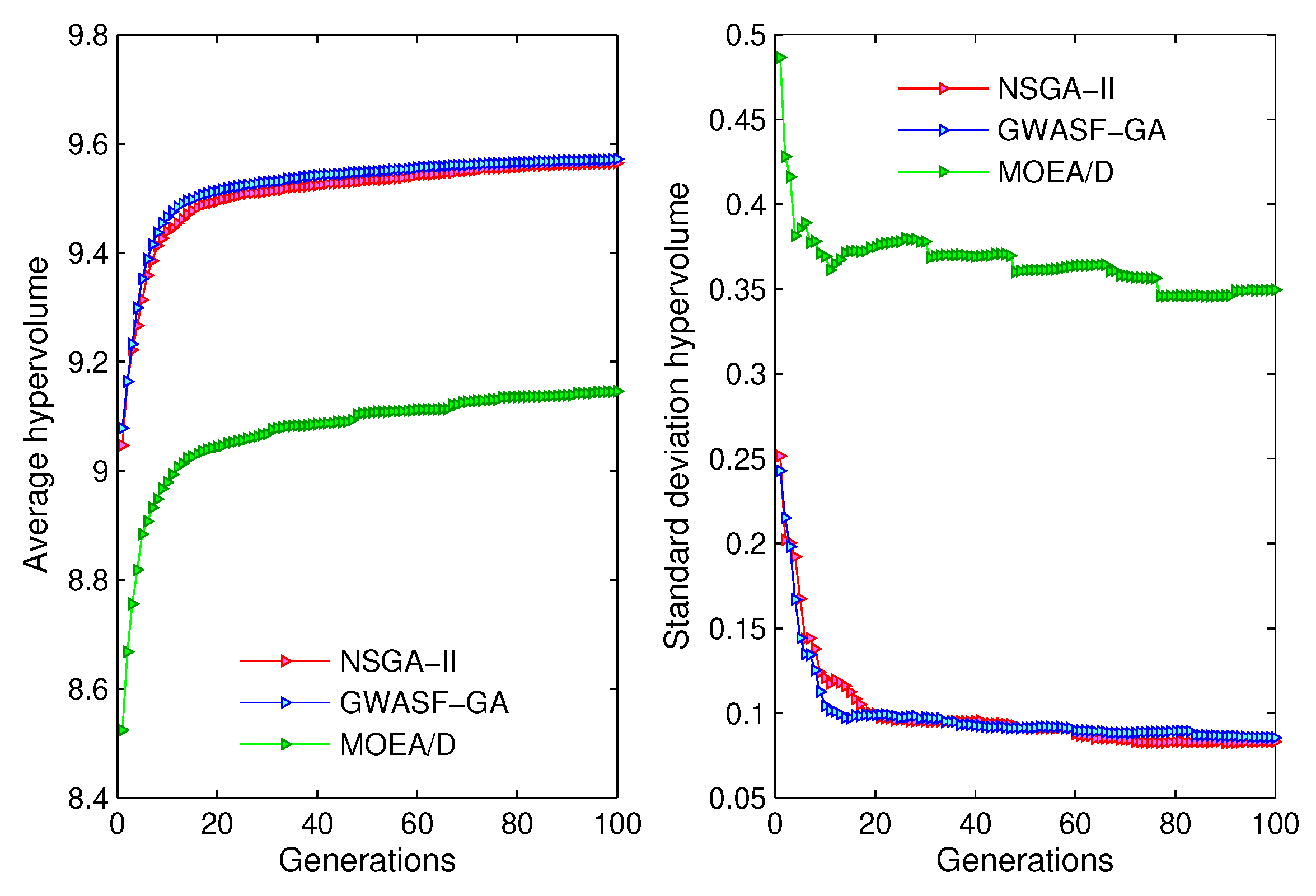
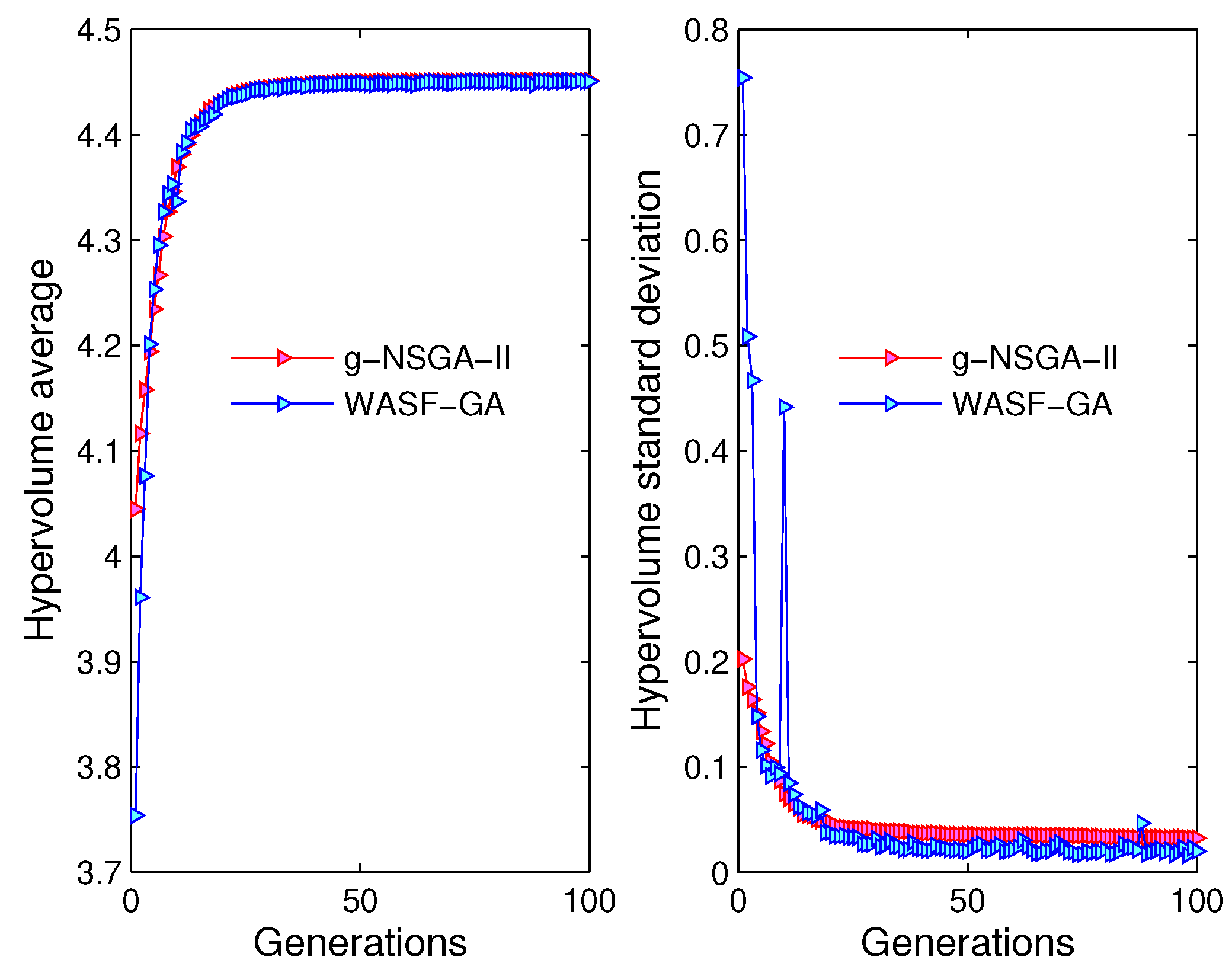
Figure 7.
Evolution of the average hypervolume (left); and evolution of the standard deviation hypervolume (right) for NSGA-II, GWASF-GA and MOEA/D ().
Figure 7.
Evolution of the average hypervolume (left); and evolution of the standard deviation hypervolume (right) for NSGA-II, GWASF-GA and MOEA/D ().
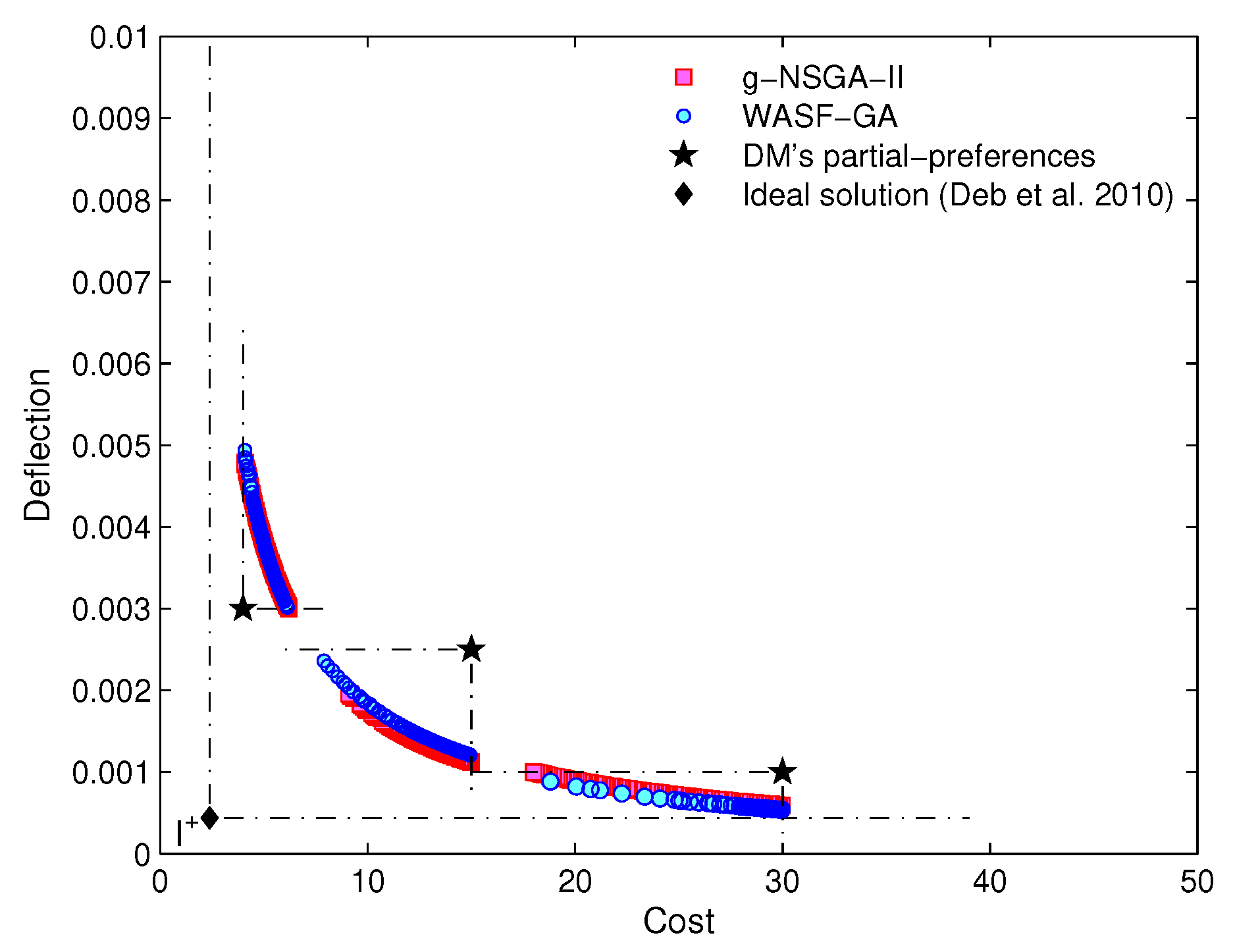
Figure 8.
DM’s partial-preferences and and the respective approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs for g-NSGA-II and WASF-GA ().
Figure 8.
DM’s partial-preferences and and the respective approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs for g-NSGA-II and WASF-GA ().
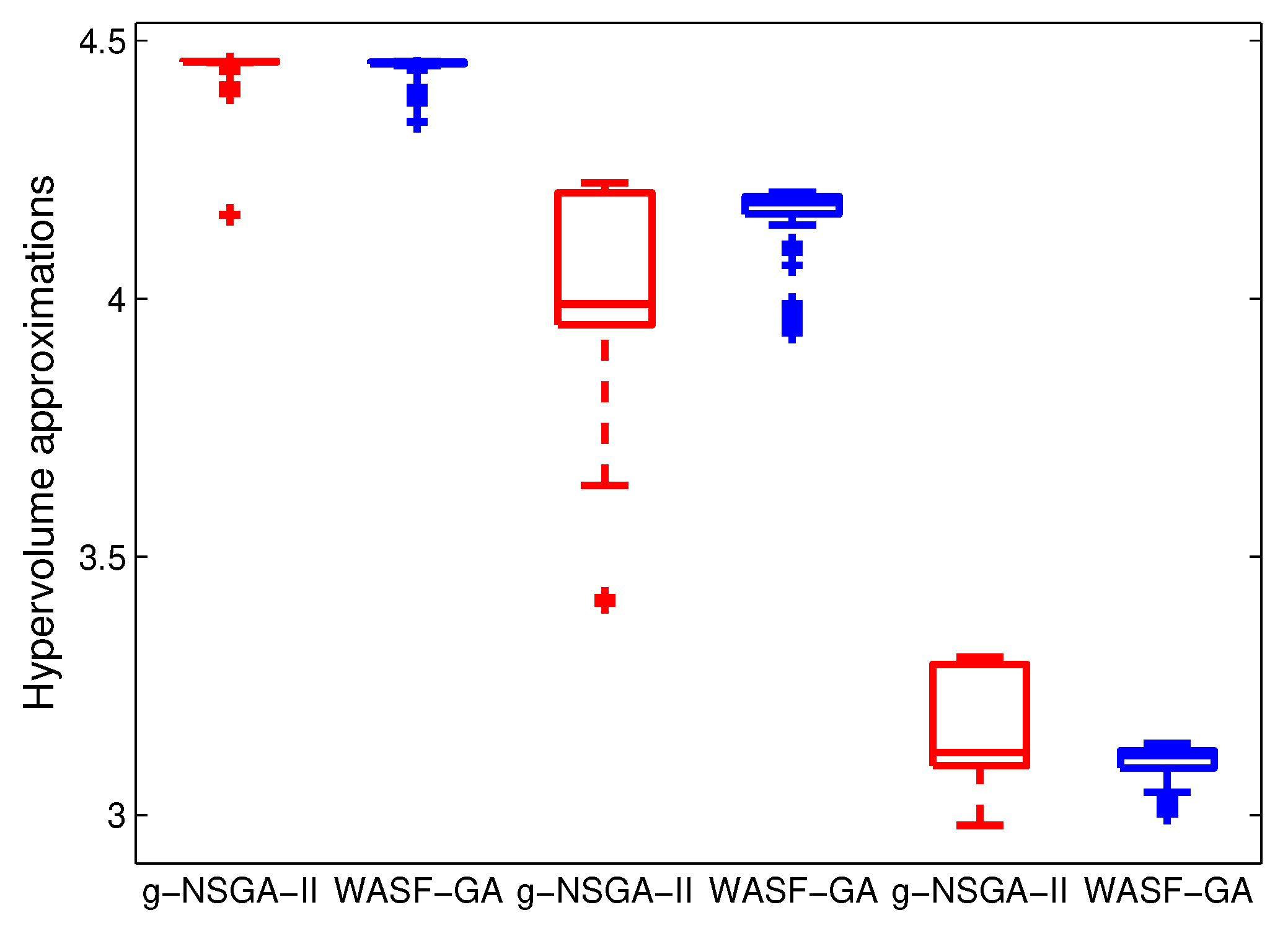
Figure 9.
Box-plots based on the hypervolume metrics (left), (middle) and (right) for g-NSGA-II and WASF-GA ().
Figure 9.
Box-plots based on the hypervolume metrics (left), (middle) and (right) for g-NSGA-II and WASF-GA ().
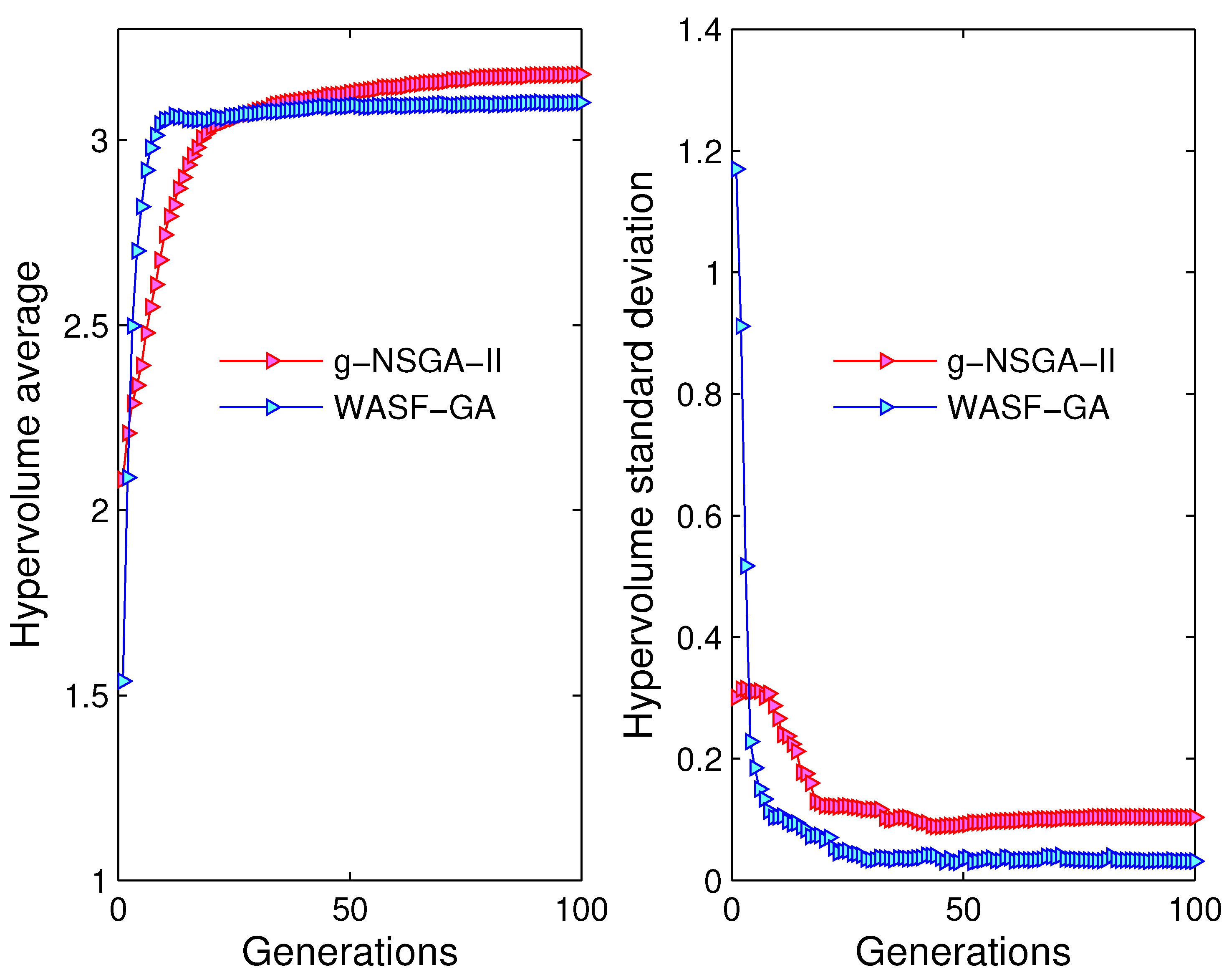
Figure 10.
Evolution of the average hypervolume (left); and evolution of the standard deviation hypervolume (right) for g-NSGA-II, WASF-GA, DM’s partial-preferences ().
Figure 10.
Evolution of the average hypervolume (left); and evolution of the standard deviation hypervolume (right) for g-NSGA-II, WASF-GA, DM’s partial-preferences ().
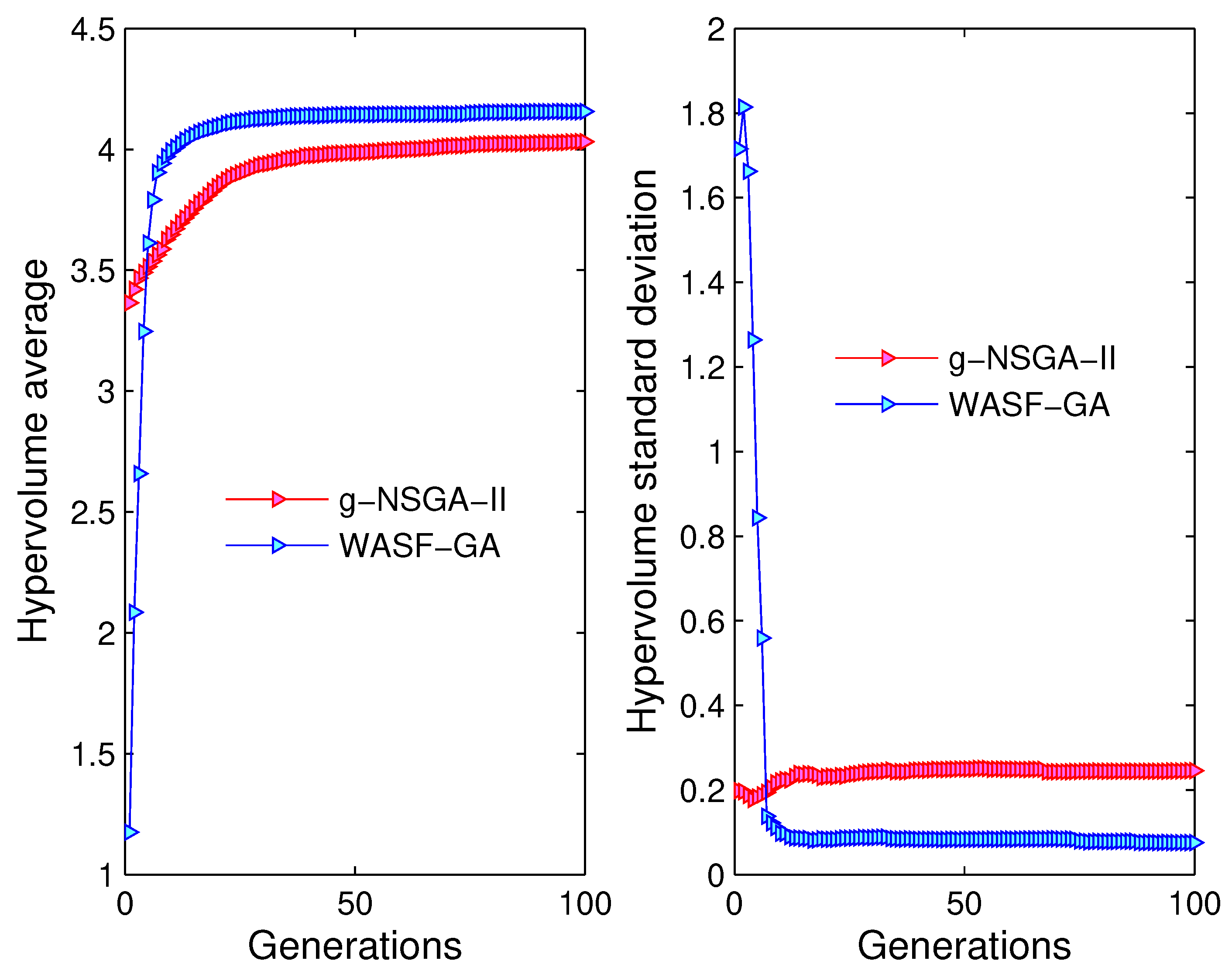
Figure 11.
Evolution of the average hypervolume (left); and evolution of the standard deviation hypervolume (right) for g-NSGA-II, WASF-GA, DM’s partial-preferences ().
Figure 11.
Evolution of the average hypervolume (left); and evolution of the standard deviation hypervolume (right) for g-NSGA-II, WASF-GA, DM’s partial-preferences ().
Figure 12.
Evolution of the average hypervolume (left); and evolution of the standard deviation hypervolume (right) for g-NSGA-II, WASF-GA, DM’s partial-preferences ().
Figure 12.
Evolution of the average hypervolume (left); and evolution of the standard deviation hypervolume (right) for g-NSGA-II, WASF-GA, DM’s partial-preferences ().
Figure 13.
Approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs (left); and the same data drawn with logarithmic scale (right) for NSGA-II, GWASF-GA and MOEA/D ().
Figure 13.
Approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs (left); and the same data drawn with logarithmic scale (right) for NSGA-II, GWASF-GA and MOEA/D ().
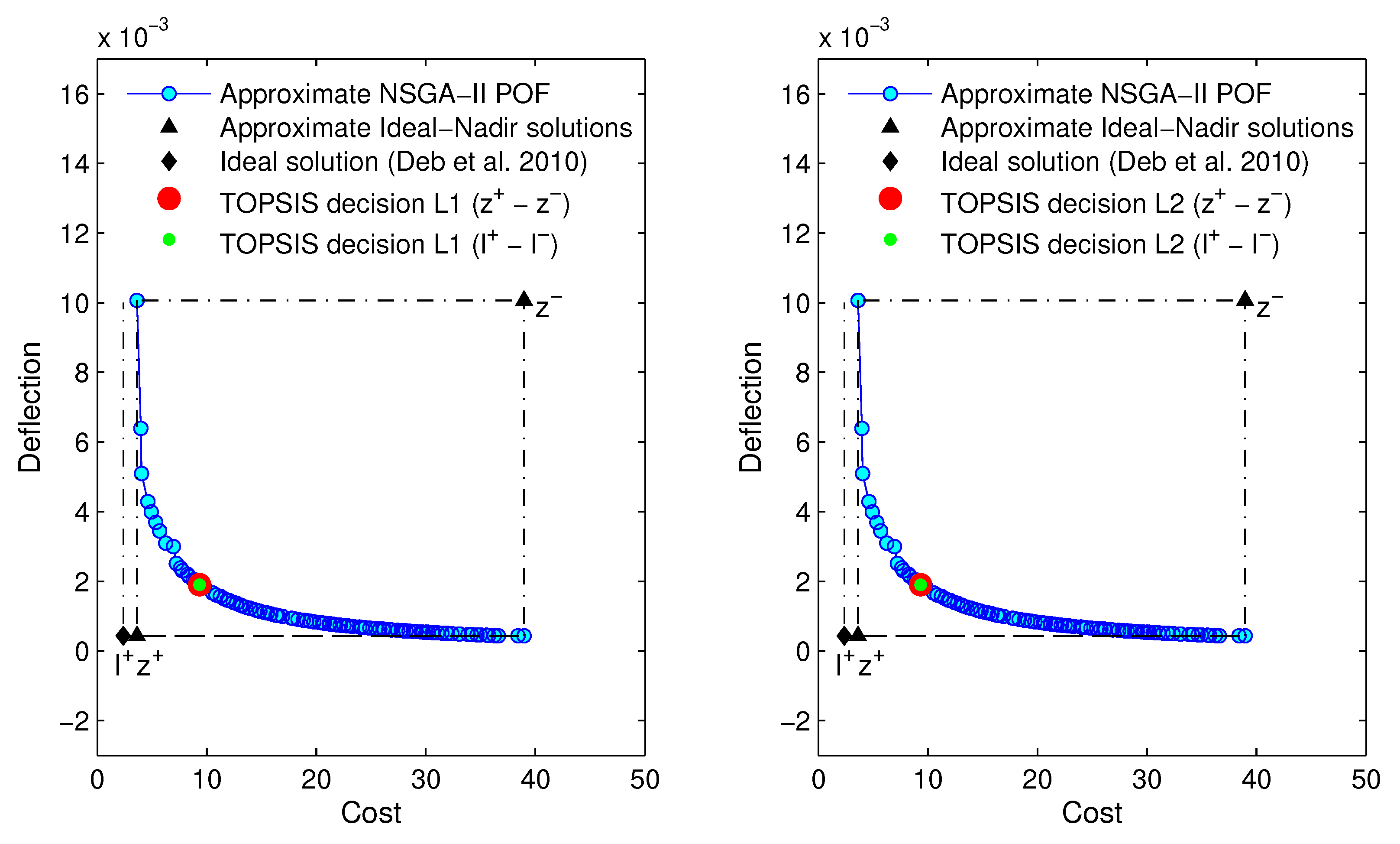
Figure 14.
TOPSIS decision with (left) and (right) metrics on the approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs for NSGA-II ().
Figure 14.
TOPSIS decision with (left) and (right) metrics on the approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs for NSGA-II ().
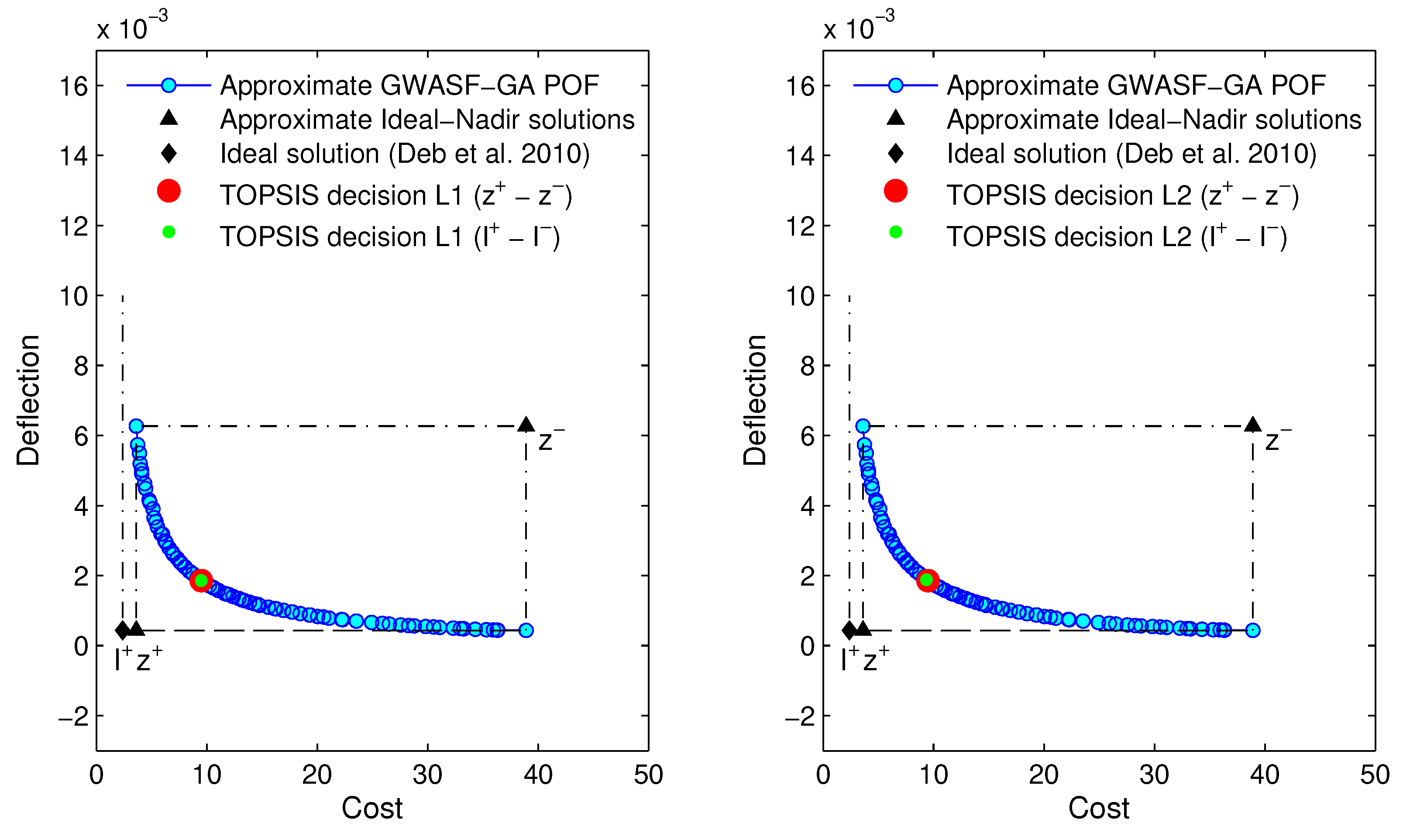
Figure 15.
TOPSIS decision with (left) and (right) metrics on the approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs for GWASF-GA ().
Figure 15.
TOPSIS decision with (left) and (right) metrics on the approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs for GWASF-GA ().
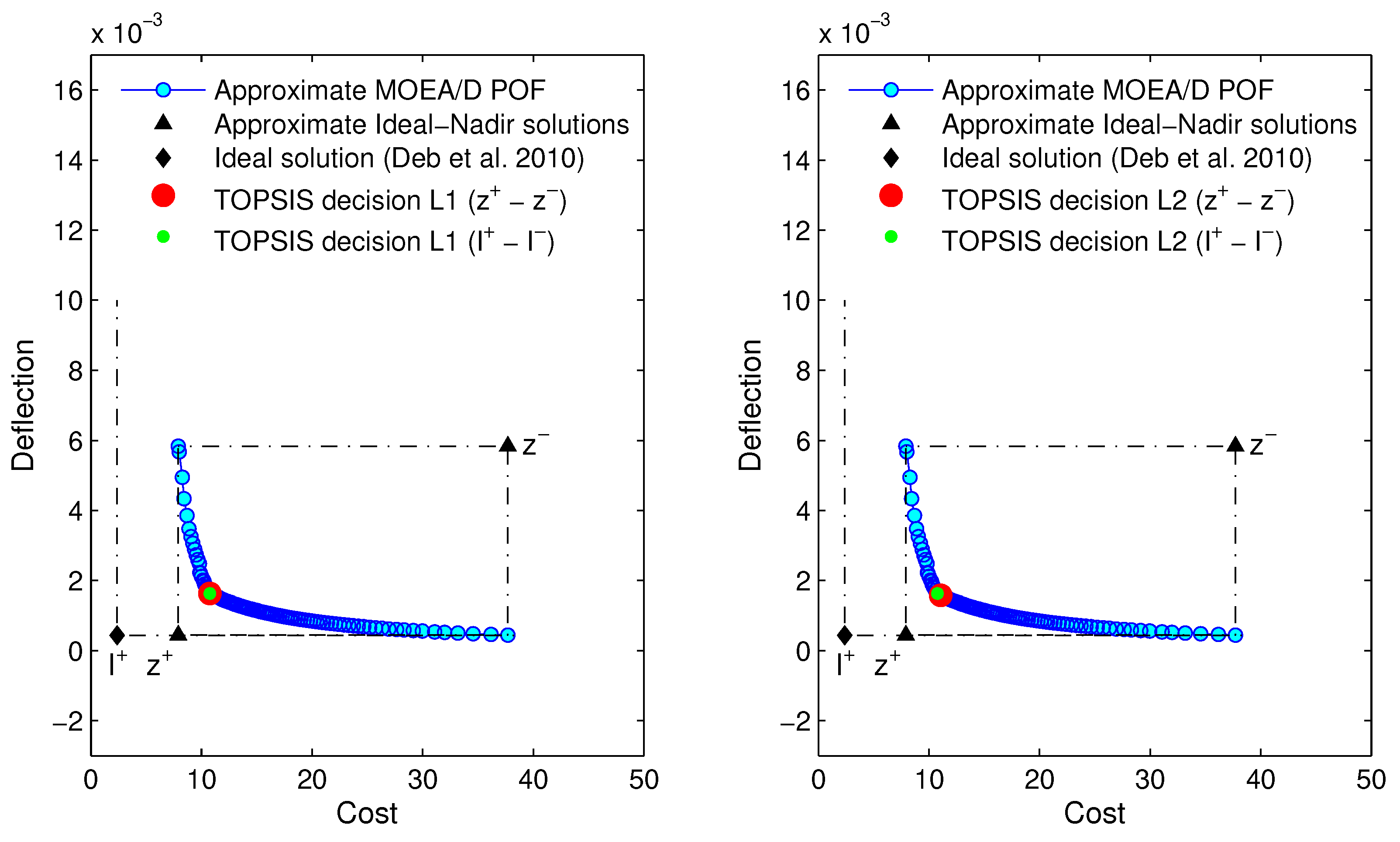
Figure 16.
TOPSIS decision with (left) and (right) metrics on the approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs for MOEA/D ().
Figure 16.
TOPSIS decision with (left) and (right) metrics on the approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs for MOEA/D ().
Figure 17.
TOPSIS decision with (left) and (right) metrics on the approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs for WASF-GA, DM’s partial-preferences () ().
Figure 17.
TOPSIS decision with (left) and (right) metrics on the approximate POF with the hypervolume indicator closest to the average value of hypervolume after 100 runs for WASF-GA, DM’s partial-preferences () ().
Figure 18.
TOPSIS decision with (top) and (bottom) metrics and ELECTRE I decision on the approximate POF achieved in a random run for NSGA-II ().
Figure 18.
TOPSIS decision with (top) and (bottom) metrics and ELECTRE I decision on the approximate POF achieved in a random run for NSGA-II ().
Table 1.
Comparison and statistical results of the mean, standard deviation values (upper), and the best and worst hypervolume values (lower), respectively, for NSGA-II, GWASF-GA and MOEA/D, over 100 runs.
Table 1.
Comparison and statistical results of the mean, standard deviation values (upper), and the best and worst hypervolume values (lower), respectively, for NSGA-II, GWASF-GA and MOEA/D, over 100 runs.
| | | |
|---|
| NSGA-II | 9.4734–0.1142 | 9.5643–0.0830 |
| | 9.6612–9.2145 | 9.6658–9.2703 |
| GWASF-GA | 9.5067–0.1166 | 9.5717–0.0854 |
| | 9.6653–9.1825 | 9.6721–9.2619 |
| MOEA/D | 9.1202–0.3977 | 9.1455–0.3495 |
| | 9.6594–7.7837 | 9.6549–8.3405 |
Table 2.
Comparison and statistical results of the best objective cost, mean and standard deviation, respectively, found by different MOEAs (NA, not available).
Table 2.
Comparison and statistical results of the best objective cost, mean and standard deviation, respectively, found by different MOEAs (NA, not available).
| Algorithms | NFEs | Best | Mean | Std. Dev. |
|---|
| NSGA-II [58] | 10,000 | 2.7900 | NA | NA |
| paϵ-ODEMO [59] | 15000 | 2.8959 | NA | NA |
| MOWCA [60] | 15,000 | 2.5325 | NA | NA |
| M20-CSA [52] | 12,000 | 7.9669 | NA | NA |
| MOCCSA [52] | 12,000 | 13.6193 | NA | NA |
| MOCSA [52] | 12,000 | 3.6842 | NA | NA |
| NSGA-II Present study | 5000 | 2.5279 | 4.5480 | 1.2005 |
| NSGA-II Present study | 10,000 | 2.5257 | 3.6236 | 0.8807 |
| GWASF-GA Present study | 5000 | 2.5313 | 4.231306 | 1.2324 |
| GWASF-GA Present study | 10,000 | 2.4553 | 3.5657 | 0.9138 |
| MOEA/D Present study | 5000 | 2.5835 | 8.0708 | 4.0780 |
| MOEA/D Present study | 10,000 | 2.6263 | 7.8712 | 3.5982 |
Table 3.
Comparison and statistical results of the mean, standard deviation values (upper), and the best and worst hypervolume values (lower), respectively, for three different DM’s partial-preferences and for g-NSGA-II and WASF-GA.
Table 3.
Comparison and statistical results of the mean, standard deviation values (upper), and the best and worst hypervolume values (lower), respectively, for three different DM’s partial-preferences and for g-NSGA-II and WASF-GA.
| | | | | | | |
|---|
| | | | |
| g- NSGA-II | 4.420–0.079 | 4.451–0.032 | 3.833–0.297 | 3.988–0.264 | 3.059–0.293 | 3.177–0.103 |
| | 4.459–3.936 | 4.460–4.162 | 4.221–3.410 | 4.224–3.411 | 3.306–1.978 | 3.306–2.980 |
| WASF-GA | 4.382–0.135 | 4.450–0.020 | 4.085–0.116 | 4.156–0.075 | 3.065–0.050 | 3.101–0.031 |
| | 4.459–3.843 | 4.459–4.342 | 4.204–3.645 | 4.206–3.933 | 3.136–2.898 | 3.139–3.002 |
Table 4.
TOPSIS ranking results with metric for NSGA-II, GWASF-GA and MOEA/D ().
Table 4.
TOPSIS ranking results with metric for NSGA-II, GWASF-GA and MOEA/D ().
| NSGA-II | Cost | Deflection | | | | Rank | Rank |
| | 9.3441 | 0.0019 | 0.0190 | 0.1023 | 0.8436 | 1 | 1 |
| | 8.7703 | 0.0020 | 0.0190 | 0.1022 | 0.8431 | 2 | 2 |
| | 10.520 | 0.0017 | 0.0191 | 0.1022 | 0.8428 | 3 | 3 |
| | 8.3866 | 0.0021 | 0.0192 | 0.1020 | 0.8418 | 4 | 4 |
| | 10.854 | 0.0016 | 0.0192 | 0.1020 | 0.8418 | 5 | 5 |
| | 9.7900 | 0.0018 | 0.0192 | 0.1020 | 0.8416 | 6 | 6 |
| | 8.9661 | 0.0020 | 0.0193 | 0.1019 | 0.8406 | 7 | 7 |
| | 8.2575 | 0.0022 | 0.0194 | 0.1018 | 0.8398 | 8 | 8 |
| NSGA-II | Cost | Deflection | | | | Rank | Rank |
| | 9.3441 | 0.0019 | 0.0208 | 0.9792 | 0.9792 | 1 | 1 |
| | 8.7703 | 0.0020 | 0.0209 | 0.9791 | 0.9791 | 2 | 2 |
| | 10.520 | 0.0017 | 0.0209 | 0.9791 | 0.9791 | 3 | 3 |
| | 8.3866 | 0.0021 | 0.0211 | 0.9789 | 0.9789 | 4 | 4 |
| | 10.854 | 0.0016 | 0.0211 | 0.9789 | 0.9789 | 5 | 5 |
| | 9.7900 | 0.0018 | 0.0211 | 0.9789 | 0.9789 | 6 | 6 |
| | 8.9661 | 0.0020 | 0.0212 | 0.9788 | 0.9788 | 7 | 7 |
| | 8.2575 | 0.0022 | 0.0213 | 0.9787 | 0.9787 | 8 | 8 |
| GWASF-GA | Cost | Deflection | | | | Rank | Rank |
| | 9.4910 | 0.0019 | 0.0189 | 0.0755 | 0.8002 | 1 | 1 |
| | 9.3520 | 0.0019 | 0.0189 | 0.0755 | 0.8002 | 2 | 2 |
| | 9.3810 | 0.0019 | 0.0189 | 0.0755 | 0.7999 | 3 | 3 |
| | 9.8331 | 0.0018 | 0.0189 | 0.0755 | 0.7993 | 4 | 4 |
| | 9.1265 | 0.0019 | 0.0189 | 0.0755 | 0.7993 | 5 | 5 |
| | 10.220 | 0.0017 | 0.0190 | 0.0754 | 0.7991 | 6 | 6 |
| | 10.521 | 0.0017 | 0.0191 | 0.0753 | 0.7980 | 7 | 7 |
| | 10.515 | 0.0017 | 0.0191 | 0.0753 | 0.7978 | 8 | 8 |
| GWASF-GA | Cost | Deflection | | | | Rank | Rank |
| | 9.4910 | 0.0019 | 0.0207 | 0.9793 | 0.9793 | 1 | 1 |
| | 9.3520 | 0.0019 | 0.0207 | 0.9793 | 0.9793 | 2 | 2 |
| | 9.3810 | 0.0019 | 0.0207 | 0.9793 | 0.9793 | 3 | 3 |
| | 9.8331 | 0.0018 | 0.0208 | 0.9792 | 0.9792 | 4 | 4 |
| | 9.1265 | 0.0019 | 0.0208 | 0.9792 | 0.9792 | 5 | 5 |
| | 10.220 | 0.0017 | 0.0208 | 0.9792 | 0.9792 | 6 | 6 |
| | 10.521 | 0.0017 | 0.0209 | 0.9791 | 0.9791 | 7 | 7 |
| | 10.515 | 0.0017 | 0.0209 | 0.9791 | 0.9791 | 8 | 8 |
| MOEA/D | Cost | Deflection | | | | Rank | Rank |
| | 10.754 | 0.0016 | 0.0127 | 0.0703 | 0.8471 | 1 | 1 |
| | 10.913 | 0.0016 | 0.0128 | 0.0703 | 0.8464 | 2 | 2 |
| | 10.689 | 0.0017 | 0.0128 | 0.0702 | 0.8462 | 3 | 3 |
| | 11.059 | 0.0016 | 0.0128 | 0.0702 | 0.8457 | 4 | 4 |
| | 11.236 | 0.0016 | 0.0129 | 0.0701 | 0.8446 | 5 | 5 |
| | 11.384 | 0.0015 | 0.0130 | 0.0701 | 0.8439 | 6 | 6 |
| | 11.571 | 0.0015 | 0.0131 | 0.0699 | 0.8423 | 7 | 7 |
| | 10.575 | 0.0017 | 0.0131 | 0.0699 | 0.8422 | 8 | 8 |
| MOEA/D | Cost | Deflection | | | | Rank | Rank |
| | 10.754 | 0.0016 | 0.0210 | 0.9790 | 0.9790 | 1 | 1 |
| | 10.913 | 0.0016 | 0.0211 | 0.9789 | 0.9789 | 2 | 2 |
| | 10.689 | 0.0017 | 0.0211 | 0.9789 | 0.9789 | 3 | 3 |
| | 11.059 | 0.0016 | 0.0211 | 0.9789 | 0.9789 | 4 | 4 |
| | 11.236 | 0.0016 | 0.0212 | 0.9788 | 0.9787 | 5 | 5 |
| | 11.384 | 0.0015 | 0.0213 | 0.9787 | 0.9787 | 6 | 6 |
| | 11.571 | 0.0015 | 0.0214 | 0.9786 | 0.9786 | 7 | 7 |
| | 10.575 | 0.0017 | 0.0214 | 0.9786 | 0.9786 | 8 | 8 |
Table 5.
TOPSIS ranking results with metric for NSGA-II, GWASF-GA and MOEA/D ().
Table 5.
TOPSIS ranking results with metric for NSGA-II, GWASF-GA and MOEA/D ().
| NSGA-II | Cost | Deflection | | | | Rank | Rank |
| | 9.3441 | 0.0019 | 0.0190 | 0.1031 | 0.8441 | 1 | 1 |
| | 10.520 | 0.0017 | 0.0191 | 0.1035 | 0.8439 | 2 | 4 |
| | 9.7900 | 0.0018 | 0.0192 | 0.1030 | 0.8428 | 3 | 3 |
| | 10.854 | 0.0016 | 0.0194 | 0.1035 | 0.8424 | 4 | 7 |
| | 8.7703 | 0.0020 | 0.0193 | 0.1028 | 0.8416 | 5 | 2 |
| | 8.9661 | 0.0020 | 0.0196 | 0.1025 | 0.8396 | 6 | 5 |
| | 11.246 | 0.0016 | 0.0198 | 0.1034 | 0.8394 | 7 | 10 |
| | 8.3866 | 0.0021 | 0.0198 | 0.1025 | 0.8383 | 8 | 6 |
| NSGA-II | Cost | Deflection | | | | Rank | Rank |
| | 9.3441 | 0.0019 | 0.0208 | 0.9792 | 0.9792 | 1 | 1 |
| | 8.7703 | 0.0020 | 0.0210 | 0.9791 | 0.9790 | 2 | 5 |
| | 9.7900 | 0.0018 | 0.0211 | 0.9789 | 0.9789 | 3 | 3 |
| | 10.520 | 0.0017 | 0.0213 | 0.9791 | 0.9788 | 4 | 2 |
| | 8.9661 | 0.0020 | 0.0212 | 0.9788 | 0.9788 | 5 | 6 |
| | 8.3866 | 0.0021 | 0.0213 | 0.9789 | 0.9787 | 6 | 8 |
| | 10.854 | 0.0016 | 0.0215 | 0.9789 | 0.9785 | 7 | 4 |
| | 8.2575 | 0.0022 | 0.0216 | 0.9787 | 0.9784 | 8 | 11 |
| GWASF-GA | Cost | Deflection | | | | Rank | Rank |
| | 9.4910 | 0.0019 | 0.0189 | 0.0767 | 0.8023 | 1 | 2 |
| | 9.3520 | 0.0019 | 0.0189 | 0.0768 | 0.8022 | 2 | 1 |
| | 9.3810 | 0.0019 | 0.0189 | 0.0767 | 0.8020 | 3 | 3 |
| | 9.8331 | 0.0018 | 0.0189 | 0.0765 | 0.8014 | 4 | 5 |
| | 9.1265 | 0.0019 | 0.0191 | 0.0768 | 0.8010 | 5 | 4 |
| | 10.220 | 0.0017 | 0.0190 | 0.0763 | 0.8006 | 6 | 6 |
| | 10.521 | 0.0017 | 0.0192 | 0.0760 | 0.7988 | 7 | 9 |
| | 10.515 | 0.0017 | 0.0192 | 0.0760 | 0.7987 | 8 | 10 |
| GWASF-GA | Cost | Deflection | | | | Rank | Rank |
| | 9.3520 | 0.0019 | 0.0207 | 0.9793 | 0.9793 | 1 | 2 |
| | 9.4910 | 0.0019 | 0.0207 | 0.9793 | 0.9793 | 2 | 1 |
| | 9.3810 | 0.0019 | 0.0207 | 0.9793 | 0.9793 | 3 | 3 |
| | 9.1265 | 0.0019 | 0.0208 | 0.9792 | 0.9792 | 4 | 5 |
| | 9.8331 | 0.0018 | 0.0209 | 0.9792 | 0.9791 | 5 | 4 |
| | 10.220 | 0.0017 | 0.0210 | 0.9792 | 0.9790 | 6 | 6 |
| | 8.7400 | 0.0020 | 0.0210 | 0.9791 | 0.9790 | 7 | 9 |
| | 8.4192 | 0.0021 | 0.0212 | 0.9790 | 0.9788 | 8 | 11 |
| MOEA/D | Cost | Deflection | | | | Rank | Rank |
| | 11.059 | 0.0016 | 0.0132 | 0.0709 | 0.8429 | 1 | 5 |
| | 11.236 | 0.0016 | 0.0132 | 0.0708 | 0.8428 | 2 | 7 |
| | 11.384 | 0.0015 | 0.0132 | 0.0707 | 0.8427 | 3 | 9 |
| | 10.913 | 0.0016 | 0.0133 | 0.0711 | 0.8426 | 4 | 3 |
| | 10.754 | 0.0016 | 0.0133 | 0.0712 | 0.8422 | 5 | 1 |
| | 11.571 | 0.0015 | 0.0132 | 0.0705 | 0.8418 | 6 | 11 |
| | 11.724 | 0.0015 | 0.0133 | 0.0704 | 0.8415 | 7 | 12 |
| | 11.874 | 0.0015 | 0.0133 | 0.0703 | 0.8410 | 8 | 13 |
| MOEA/D | Cost | Deflection | | | | Rank | Rank |
| | 10.754 | 0.0016 | 0.0214 | 0.9790 | 0.9786 | 1 | 5 |
| | 10.689 | 0.0017 | 0.0215 | 0.9789 | 0.9785 | 2 | 9 |
| | 10.913 | 0.0016 | 0.0216 | 0.9789 | 0.9784 | 3 | 4 |
| | 10.575 | 0.0017 | 0.0217 | 0.9786 | 0.9783 | 4 | 14 |
| | 11.059 | 0.0016 | 0.0217 | 0.9789 | 0.9783 | 5 | 1 |
| | 10.469 | 0.0018 | 0.0219 | 0.9783 | 0.9781 | 6 | 18 |
| | 11.236 | 0.0016 | 0.0219 | 0.9788 | 0.9781 | 7 | 2 |
| | 10.387 | 0.0018 | 0.0220 | 0.9782 | 0.9780 | 8 | 21 |
Table 6.
TOPSIS ranking results with metric for WASF-GA, DM’s partial-preferences (15, 0.0025) ().
Table 6.
TOPSIS ranking results with metric for WASF-GA, DM’s partial-preferences (15, 0.0025) ().
| WASF-GA | Cost | Deflection | | | | Rank | Rank |
| | 9.3174 | 0.0020 | 0.0076 | 0.0112 | 0.5954 | 1 | 1 |
| | 9.7537 | 0.0019 | 0.0076 | 0.0112 | 0.5954 | 2 | 2 |
| | 9.8696 | 0.0019 | 0.0076 | 0.0112 | 0.5947 | 3 | 3 |
| | 9.1067 | 0.0020 | 0.0076 | 0.0111 | 0.5943 | 4 | 4 |
| | 9.6178 | 0.0019 | 0.0076 | 0.0111 | 0.5935 | 5 | 5 |
| | 10.224 | 0.0018 | 0.0077 | 0.0111 | 0.5919 | 6 | 6 |
| | 8.9470 | 0.0021 | 0.0077 | 0.0111 | 0.5911 | 7 | 7 |
| | 10.314 | 0.0018 | 0.0077 | 0.0112 | 0.5909 | 8 | 8 |
| WASF-GA | Cost | Deflection | | | | Rank | Rank |
| | 9.3174 | 0.0020 | 0.0213 | 0.9787 | 0.9787 | 1 | 1 |
| | 9.7537 | 0.0019 | 0.0213 | 0.9787 | 0.9787 | 2 | 2 |
| | 9.8696 | 0.0019 | 0.0214 | 0.9786 | 0.9786 | 3 | 3 |
| | 9.1067 | 0.0020 | 0.0214 | 0.9786 | 0.9786 | 4 | 4 |
| | 9.6178 | 0.0019 | 0.0214 | 0.9786 | 0.9786 | 5 | 5 |
| | 10.224 | 0.0018 | 0.0214 | 0.9786 | 0.9786 | 6 | 6 |
| | 8.9470 | 0.0021 | 0.0214 | 0.9786 | 0.9786 | 7 | 7 |
| | 10.314 | 0.0018 | 0.0214 | 0.9786 | 0.9786 | 8 | 8 |
Table 7.
TOPSIS ranking results with metric for WASF-GA, DM’s partial-preferences () ().
Table 7.
TOPSIS ranking results with metric for WASF-GA, DM’s partial-preferences () ().
| WASF-GA | Cost | Deflection | | | | Rank | Rank |
| | 9.7537 | 0.0019 | 0.0078 | 0.0120 | 0.6054 | 1 | 2 |
| | 9.8696 | 0.0019 | 0.0078 | 0.0119 | 0.6048 | 2 | 5 |
| | 9.6178 | 0.0019 | 0.0080 | 0.0122 | 0.6035 | 3 | 3 |
| | 9.3174 | 0.0020 | 0.0083 | 0.0126 | 0.6034 | 4 | 1 |
| | 9.1067 | 0.0020 | 0.0086 | 0.0129 | 0.6034 | 5 | 4 |
| | 10.224 | 0.0018 | 0.0077 | 0.0115 | 0.6004 | 6 | 7 |
| | 10.118 | 0.0018 | 0.0078 | 0.0116 | 0.5986 | 7 | 9 |
| | 10.314 | 0.0018 | 0.0077 | 0.0115 | 0.5985 | 8 | 10 |
| WASF-GA | Cost | Deflection | | | | Rank | Rank |
| | 9.3174 | 0.0020 | 0.0213 | 0.9787 | 0.9787 | 1 | 4 |
| | 9.7537 | 0.0019 | 0.0214 | 0.9787 | 0.9786 | 2 | 1 |
| | 9.6178 | 0.0019 | 0.0214 | 0.9786 | 0.9786 | 3 | 3 |
| | 9.1067 | 0.0020 | 0.0214 | 0.9786 | 0.9786 | 4 | 5 |
| | 9.8696 | 0.0019 | 0.0214 | 0.9786 | 0.9786 | 5 | 2 |
| | 8.9470 | 0.0021 | 0.0215 | 0.9786 | 0.9785 | 6 | 9 |
| | 10.224 | 0.0018 | 0.0215 | 0.9786 | 0.9785 | 7 | 6 |
| | 8.8117 | 0.0021 | 0.0215 | 0.9786 | 0.9785 | 8 | 10 |
Table 8.
TOPSIS ranking results with metric for NSGA-II.
Table 8.
TOPSIS ranking results with metric for NSGA-II.
| NSGA-II | Cost | Deflection | Stress | | | | Rank | Rank |
| | 23.7093 | 0.0007 | 1596.7010 | 0.0281 | 0.2655 | 0.9043 | 1 | 1 |
| | 28.0821 | 0.0006 | 1338.5632 | 0.0290 | 0.2646 | 0.9013 | 2 | 2 |
| | 19.1353 | 0.0009 | 2007.9248 | 0.0291 | 0.2645 | 0.9010 | 3 | 3 |
| | 22.9850 | 0.0008 | 1734.4095 | 0.0294 | 0.2642 | 0.9000 | 4 | 4 |
| | 26.5692 | 0.0007 | 1476.5583 | 0.0295 | 0.2641 | 0.8997 | 5 | 5 |
| | 26.1854 | 0.0007 | 1507.1893 | 0.0295 | 0.2641 | 0.8996 | 6 | 6 |
| | 17.2381 | 0.0010 | 2235.0525 | 0.0302 | 0.2634 | 0.8971 | 7 | 7 |
| | 30.7015 | 0.0006 | 1260.3816 | 0.0306 | 0.2630 | 0.8957 | 8 | 8 |
| NSGA-II | Cost | Deflection | Stress | | | | Rank | Rank |
| | 23.7093 | 0.0007 | 1596.7010 | 0.0291 | 0.9609 | 0.9706 | 1 | 1 |
| | 28.0821 | 0.0006 | 1338.5632 | 0.0300 | 0.9600 | 0.9697 | 2 | 2 |
| | 19.1353 | 0.0009 | 2007.9248 | 0.0301 | 0.9599 | 0.9696 | 3 | 3 |
| | 22.9850 | 0.0008 | 1734.4095 | 0.0304 | 0.9596 | 0.9693 | 4 | 4 |
| | 26.5692 | 0.0007 | 1476.5583 | 0.0305 | 0.9595 | 0.9692 | 5 | 5 |
| | 26.1854 | 0.0007 | 1507.1893 | 0.0305 | 0.9595 | 0.9692 | 6 | 6 |
| | 17.2381 | 0.0010 | 2235.0525 | 0.0312 | 0.9588 | 0.9684 | 7 | 7 |
| | 30.7015 | 0.0006 | 1260.3816 | 0.0317 | 0.9583 | 0.9680 | 8 | 8 |
Table 9.
TOPSIS ranking results with metric for NSGA-II.
Table 9.
TOPSIS ranking results with metric for NSGA-II.
| NSGA-II | Cost | Deflection | Stress | | | | Rank | Rank |
| | 19.1353 | 0.0009 | 2007.9248 | 0.0339 | 0.3584 | 0.9137 | 1 | 1 |
| | 17.2381 | 0.0010 | 2235.0525 | 0.0344 | 0.3541 | 0.9115 | 2 | 2 |
| | 23.7093 | 0.0007 | 1596.7010 | 0.0371 | 0.3660 | 0.9080 | 3 | 6 |
| | 22.9850 | 0.0008 | 1734.4095 | 0.0369 | 0.3633 | 0.9077 | 4 | 4 |
| | 21.7416 | 0.0009 | 1948.9974 | 0.0370 | 0.3590 | 0.9065 | 5 | 5 |
| | 17.1718 | 0.0011 | 2418.4668 | 0.0371 | 0.3505 | 0.9044 | 6 | 3 |
| | 15.0645 | 0.0011 | 2599.6250 | 0.0379 | 0.3472 | 0.9017 | 7 | 7 |
| | 26.1854 | 0.0007 | 1507.1893 | 0.0407 | 0.3675 | 0.9003 | 8 | 8 |
| NSGA-II | Cost | Deflection | Stress | | | | Rank | Rank |
| | 19.1353 | 0.0009 | 2007.9248 | 0.0353 | 0.9649 | 0.9647 | 1 | 1 |
| | 17.2381 | 0.0010 | 2235.0525 | 0.0357 | 0.9637 | 0.9643 | 2 | 1 |
| | 17.1718 | 0.0011 | 2418.4668 | 0.0382 | 0.9613 | 0.9617 | 3 | 6 |
| | 22.9850 | 0.0008 | 1734.4095 | 0.0386 | 0.9647 | 0.9615 | 4 | 4 |
| | 21.7416 | 0.0009 | 1948.9974 | 0.0386 | 0.9628 | 0.9615 | 5 | 5 |
| | 23.7093 | 0.0007 | 1596.7010 | 0.0388 | 0.9661 | 0.9614 | 6 | 3 |
| | 15.0645 | 0.0011 | 2599.6250 | 0.0388 | 0.9610 | 0.9611 | 7 | 7 |
| | 26.1854 | 0.0007 | 1507.1893 | 0.0425 | 0.9648 | 0.9578 | 8 | 8 |
Table 10.
Aggregate dominance matrix ( = 0.1, = 0.9).
Table 10.
Aggregate dominance matrix ( = 0.1, = 0.9).
| Solutions | |
|---|
| 1 | 00000000000000000000000000000000000000000000000000 |
| 2 | 00000000000000000000000000000000000000000000000000 |
| 3 | 11000000000000000000000000000000000000000000000000 |
| 4 | 11000000000000000000000000000000000000000000000000 |
| 5 | 11110000000000000000000000000000000000000000000000 |
| 6 | 11111000000000000000000000000000000000000000000000 |
| 7 | 11111100000000000000000000000000000000000000000001 |
| 8 | 11111110000000000000000000000000000000000000000001 |
| 9 | 11111111000000000000000000000000000000000000000011 |
| 10 | 11111111100000000000000000000000000000000000000011 |
| 11 | 11111111110000000000000000000000000000000000000111 |
| 12 | 11111111110000000000000000000000000000000000000111 |
| 13 | 11111111111100000000000000000000000000000000000111 |
| 14 | 11111111111110000000000000000000000000000000000111 |
| 15 | 11111111111111000000000000000000000000000000001111 |
| 16 | 11111111111111100000000000000000000000000000011111 |
| 17 | 11111111111111110000000000000000000000000000111111 |
| 18 | 11111111111111111000000000000000000000000001111111 |
| 19 | 11111111111111111100000000000000000000000011111111 |
| 20 | 11111111111111111110000000000000000000000111111111 |
| 21 | 11111111111111111111000000000000000000000111111111 |
| 22 | 11111111111111111111100000000000000000001111111111 |
| 23 | 11111111111111111111110000000000000000001111111111 |
| 24 | 11111111111111111111111000000000000000111111111111 |
| 25 | 11111111111111111111111100000000000000111111111111 |
| 26 | 11111111111111111111111110000000000000111111111111 |
| 27 | 11111111111111111111111111000000000011111111111111 |
| 28 | 11111111111111111111111111100000000011111111111111 |
| 29 | 11111111111111111111111111110000000111111111111111 |
| 30 | 11111111111111111111111111111010000111111111111111 |
| 31 | 11111111111111111111111111110000000111111111111111 |
| 32 | 11111111111111111111111111111110001111111111111111 |
| 33 | 11111111111111111111111111111111011111111111111111 |
| 34 | 11111111111111111111111111111111001111111111111111 |
| 35 | 11111111111111111111111111100000000111111111111111 |
| 36 | 11111111111111111111111110000000000011111111111111 |
| 37 | 11111111111111111111111000000000000001111111111111 |
| 38 | 11111111111111111111110000000000000000111111111111 |
| 39 | 11111111111111111110000000000000000000001111111111 |
| 40 | 11111111111111111111000000000000000000101111111111 |
| 41 | 11111111111111111100000000000000000000000111111111 |
| 42 | 11111111111111000000000000000000000000000011111111 |
| 43 | 11111111111100000000000000000000000000000001111111 |
| 44 | 11111111111100000000000000000000000000000000111111 |
| 45 | 11111111000000000000000000000000000000000000011111 |
| 46 | 11111111000000000000000000000000000000000000001111 |
| 47 | 11111110000000000000000000000000000000000000000111 |
| 48 | 11111100000000000000000000000000000000000000000011 |
| 49 | 11000000000000000000000000000000000000000000000001 |
| 50 | 00000000000000000000000000000000000000000000000000 |
Table 11.
Sensitivity analysis to variations in the thresholds and .
Table 11.
Sensitivity analysis to variations in the thresholds and .
| | Solutions |
|---|
| 0.1 | 0.9 | 33 |
| 0.2 | 0.8 | 33–34 |
| 0.33 | 0.67 | 28–29–33–34 |
Table 12.
Results for the TOPSIS and ELECTRE I methods.
Table 12.
Results for the TOPSIS and ELECTRE I methods.
| | Cost | Deflection | Normal Stress |
|---|
| TOPSIS decision | 23.709299 | 0.000696 | 1596.701050 |
| ELECTRE I decision | 9.226740 | 0.001943 | 4446.901367 |