A New Kumaraswamy Generalized Family of Distributions with Properties, Applications, and Bivariate Extension
Abstract
1. Introduction
- (i)
- ,
- (ii)
- is differentiable and monotonically non-decreasing, and
- (iii)
- and .
- (i)
- Constructing new and novel G-families as a function of a cdf, , is a difficult task in these days. A few pioneer G-families were developed in the literature considering viz. exponentiated-G with power parameter (LA1 and LA2) (Gupta et al. [3]) [], beta-G (Eugene et al. [4]) [], ZBgamma-G (Zografos and Balakrishnan [7]) [], odd log-logistic-G (Gleaton and Lynch [5]) [], RBgamma-G (Ristic and Balakrishnan [10]) [], log-odd logistic-G (Torabi and Montazeri [22]) [], Gumbel-X (Al-Aqtash et al. [23]) [], Weibull-X (T-X approach) and Weibull-X (Ahmad et al. [24]) [] are the pioneer works. Other G-families either non-composite (alone based on well-established parent model) or composite (mixture of two G-families) and compounded G-families are the extensions or modifications of the above described pioneer G-families. For example, the generator , where was pioneered by (Eugene et al. [4]) for defining the beta-G family, and later this generator was adopted by (Cordeiro and de-Castro [8]; Alexander et al. [9]; Rezaei et al. [15]) for defining the Kw-G, Mc-G and TL-G families, respectively. Similarly, the odd generator (where ) was suggested by (Gleaton and Lynch, [5]) for proposing the odd log-logistic-G family, and it was adopted by (Bourguignon et al. [12]; Torabi and Montazeri [25]; Tahir et al. [13]; Silva et al. [26]; Cordeiro et al. [27]; Alizadeh et al. [28]; Cordeiro et al. [29]; Hassan et al. [30]; Hassan and Nassr [31]; Maiti and Pramanik [32]); El-Morshedy and Eliwa [33], Alizadeh et al. [34]; El-Morshedy et al. [35]; Eliwa et al. [36] for defining the odd Weibull-G, odd gamma-G, odd generalized-exponential-G, odd Lindley-G, odd Burr-G, odd power-Cauchy-G, odd half-Cauchy, odd additive Weibull-G, odd power-Lindley-G, odd Xgamma-G, odd flexible Weibull-H, odd log-logistic Lindley-G, odd Chen generator and exponentiated odd Chen-G, respectively, among others.
- (ii)
- The proposed extension of the Kumaraswamy-G model is based on a new generator for instead of the only existing generator for which the beta-G, Kw-G, Mc-G and TL-G classes were developed so far.
- (iii)
- The proposed generator seems little complicated in comparison to earlier well-established generator for the unit interval but it has the ability to produce better estimates and goodness-of-fit (GoF) tests results that can make it distinguishable and attractive for applied researchers (as evident from the results in Section 5 and Section 7).
- (iv)
- For most of the families and models, if the cdf is in closed form, then the quantile function (qf) can be straightforward to obtain. In some families and models, where the qf is based on some special functions such as beta, gamma, and others, then the qfs can only be determined by using power series. In our case, the cdf of the family is in closed form but the qf can be obtained only numerically.
2. The NKw-G Family
3. Properties of the NKw-G Family
3.1. Quantile Function
- (i)
- Set ;
- (ii)
- Find numerically in using any Newton-Raphson algorithm;
- (iii)
- Solving numerically for x in yields the qf of X.
3.2. Asymptotics
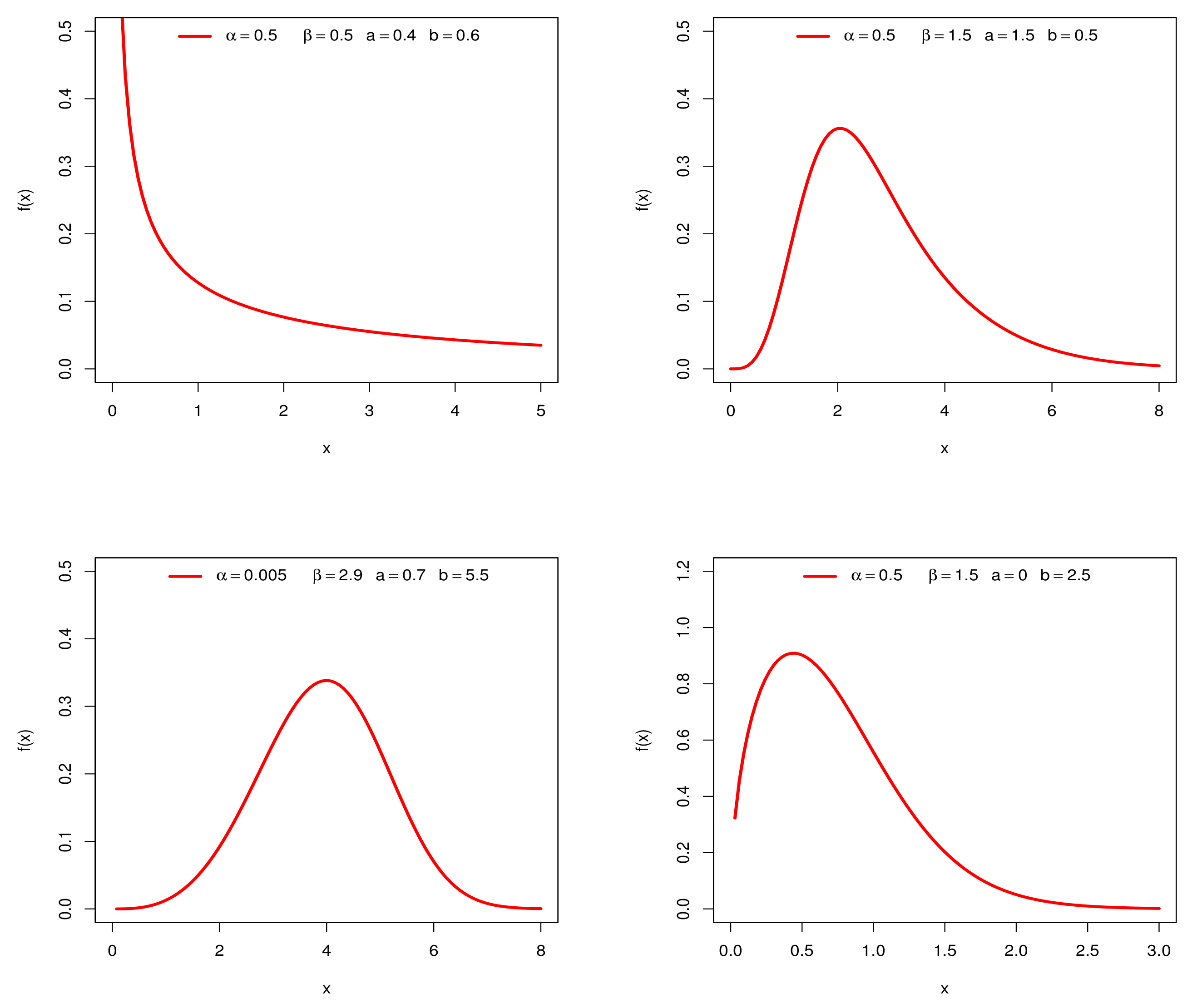
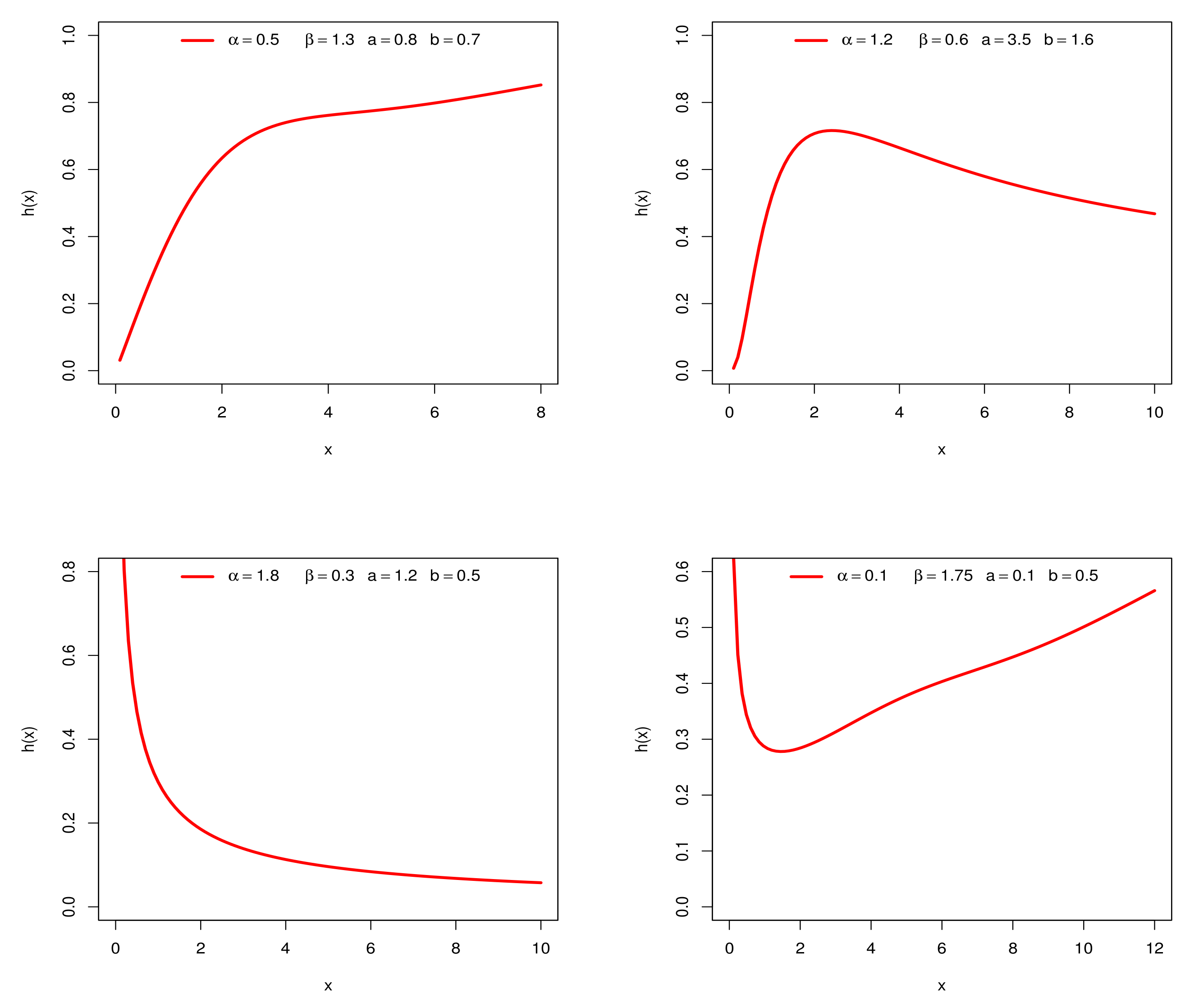
3.3. Analytic Shapes of the Density and Hazard Rate Function
3.4. Linear Representation of the NKw-G Density
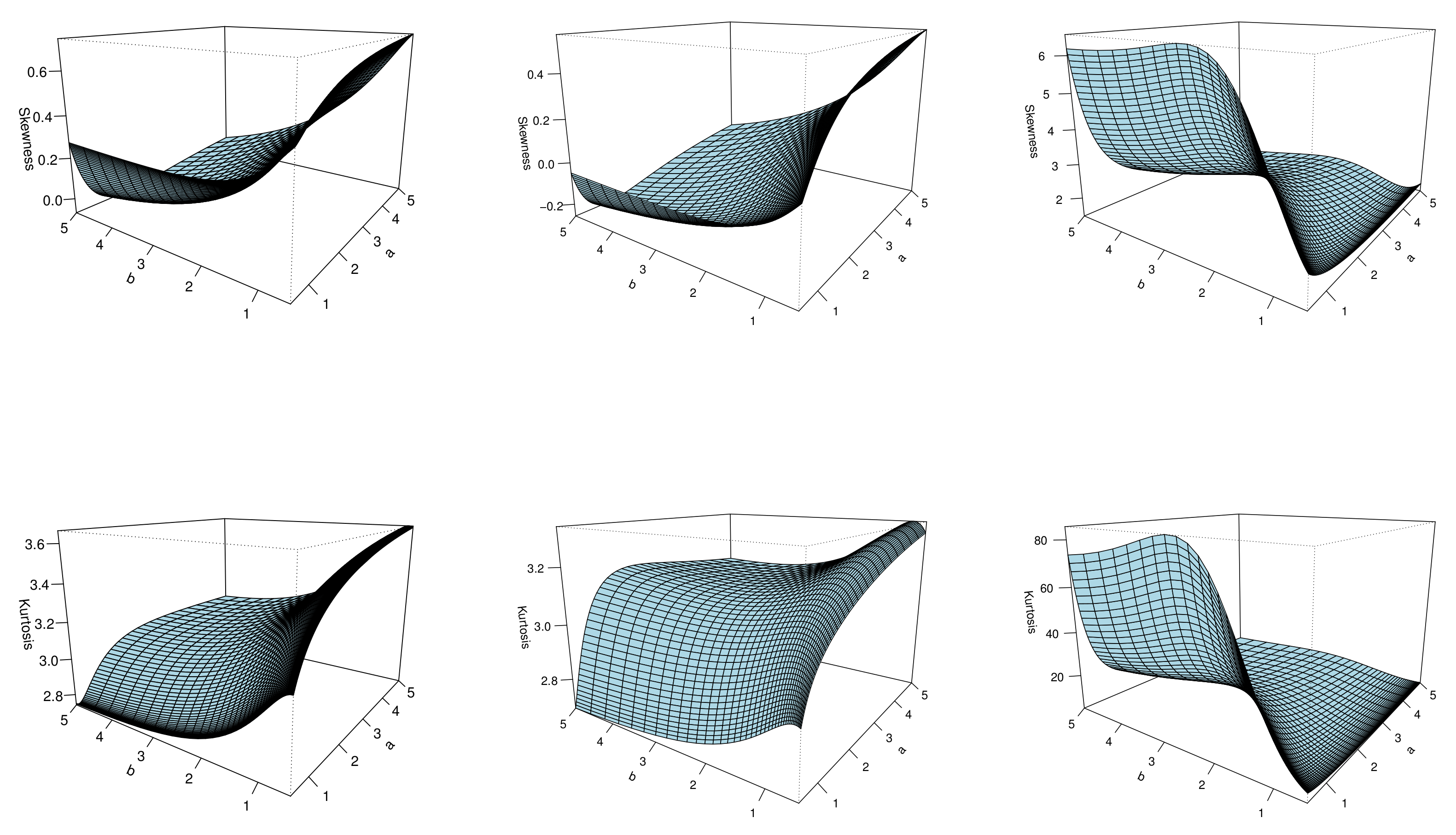
3.5. Mathematical Properties
3.6. Estimation
4. The NKwW Distribution
4.1. Linear Representation
4.2. Properties
4.3. Quantile Function and Simulation Study
- Set n, , , a, b and initial value .
- Generate U ∼Uniform.
- If , (, very small tolerance limit), then store as a variate from the NKwW() distribution.
- If , then, set and go to step 3.
- Repeat steps (2)–(5) n times to generate .
4.4. Estimation
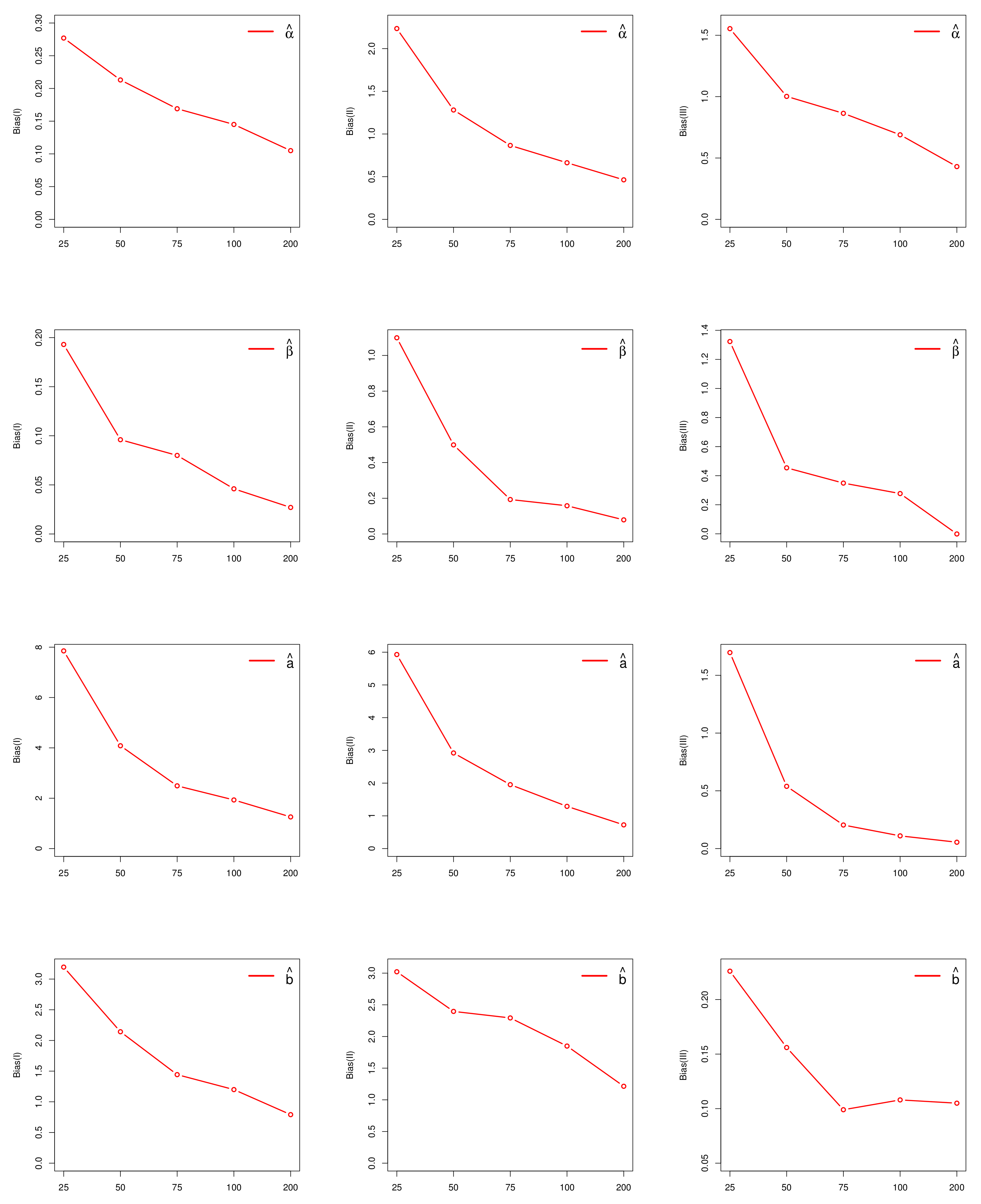
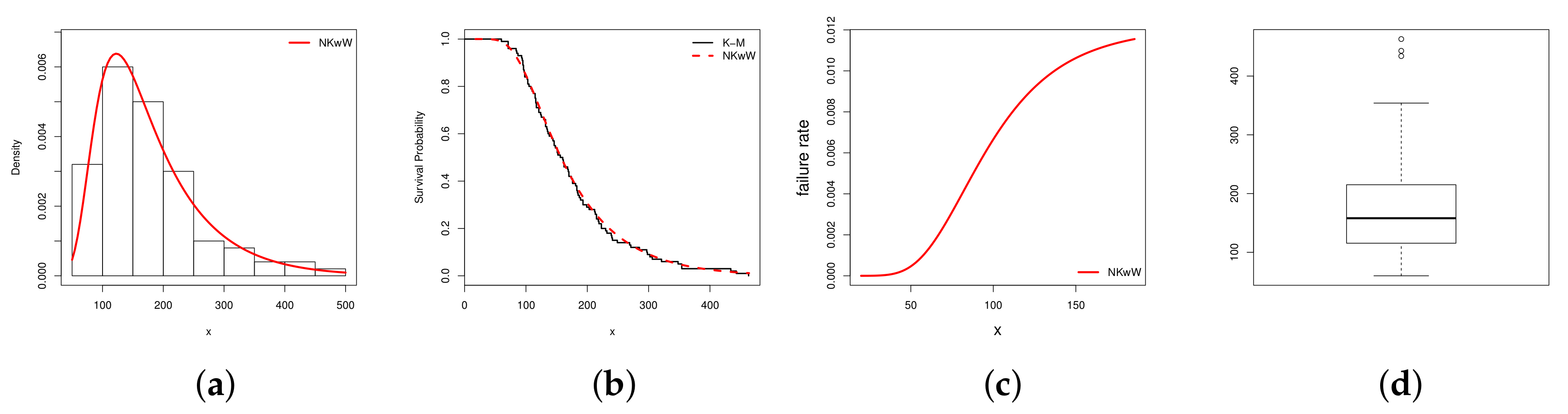
5. Empirical Illustrations of NKwW Model
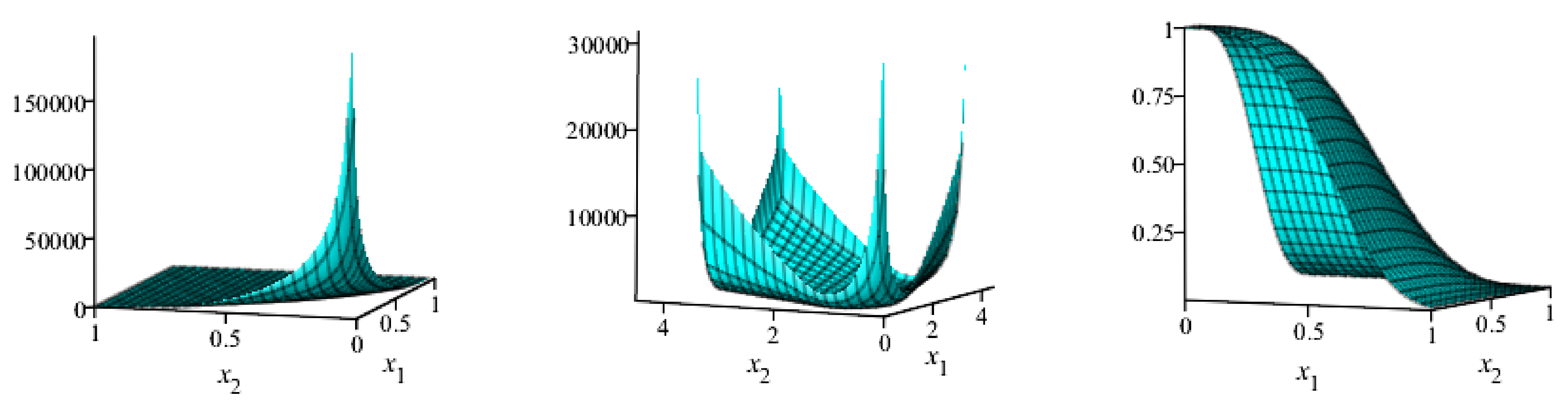
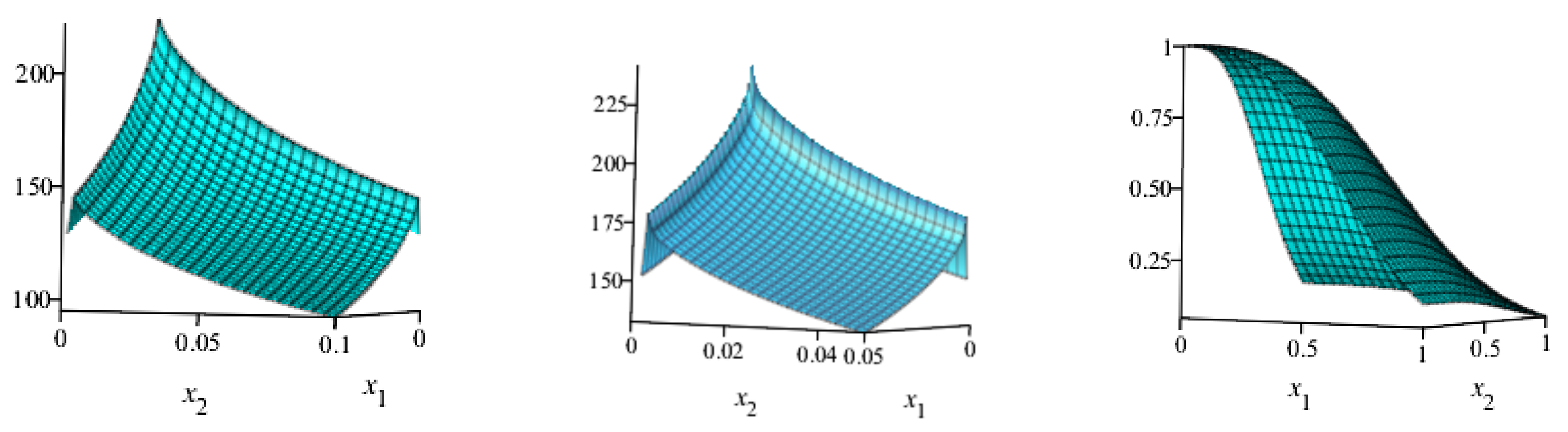
6. Bivariate New Kumaraswamy G-Family
The MLE for the BvNKw-G Family
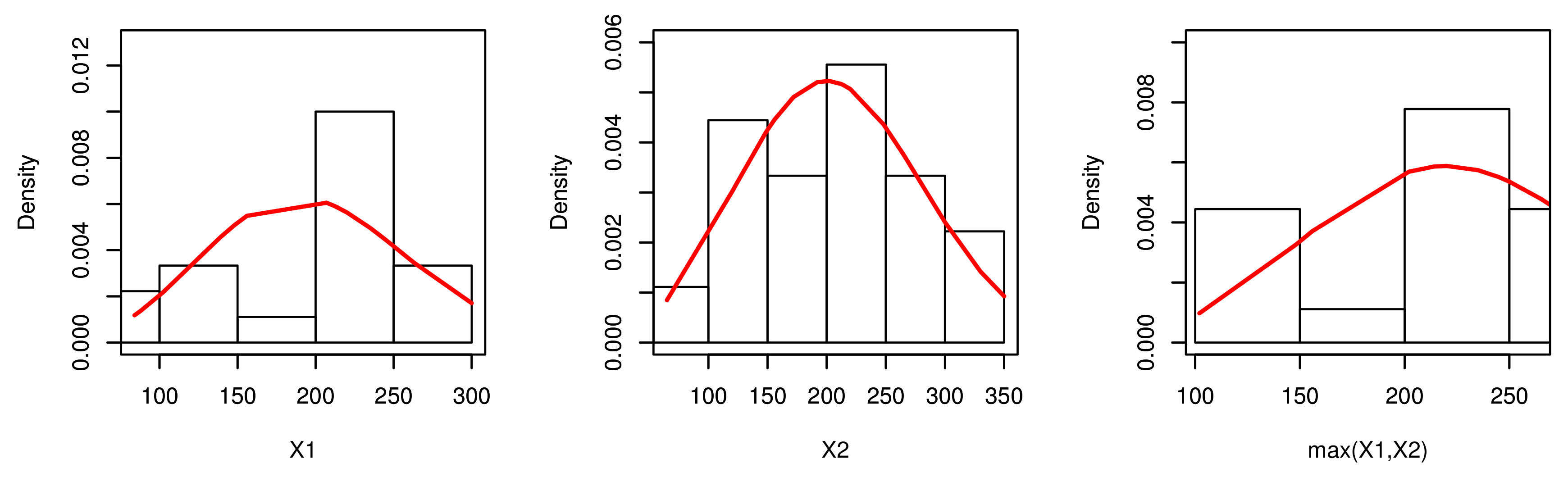
7. Empirical Illustrations of BvNKwW Model Through Motors Data
8. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Marshall, A.W.; Olkin, I. A new method for adding parameters to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Gupta, R.C.; Gupta, P.L.; Gupta, R.D. Modeling failure time data by Lehman alternatives. Commun. Stat. Theory Methods 1998, 27, 887–904. [Google Scholar] [CrossRef]
- Eugene, N.; Lee, C.; Famoye, F. Beta-normal distribution and its applications. Commun. Stat. Theory Methods 2002, 31, 497–512. [Google Scholar] [CrossRef]
- Gleaton, J.U.; Lynch, J.D. Properties of generalized log-logistic families of lifetime distributions. J. Prob. Stat. Sci. 2006, 4, 51–64. [Google Scholar]
- Shaw, W.T.; Buckley, I.R. The alchemy of probability distributions: Beyond Gram-Charlier expansions, and a skew-kurtotic-normal distribution from a rank transmutation map. arXiv 2009, arXiv:0901.0434. [Google Scholar]
- Zografos, K.; Balakrishnan, N. On families of beta- and generalized gamma generated distributions and associated inference. Stat. Methodol. 2009, 6, 344–362. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; de-Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2011, 81, 883–898. [Google Scholar] [CrossRef]
- Alexander, C.; Cordeiro, G.M.; Ortega, E.M.M.; Sarabia, J.M. Generalized beta-generated distributions. Comput. Stat. Data Anal. 2012, 56, 1880–1897. [Google Scholar] [CrossRef]
- Ristić, M.M.; Balakrishnan, N. The gamma-exponentiated exponential distribution. J. Stat. Comput. Simul. 2012, 82, 1191–1206. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.M.; Cunha, D.C.C. The exponentiated generalized class of distributions. J. Data Sci. 2013, 11, 1–27. [Google Scholar]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull-G family of probability distributions. J. Data Sci. 2014, 12, 53–68. [Google Scholar]
- Tahir, M.H.; Cordeiro, G.M.; Alizadeh, M.; Mansoor, M.; Zubair, M.; Hamedani, G.G. The odd generalized exponential family of distributions with applications. J. Stat. Distrib. App. 2015, 2. [Google Scholar] [CrossRef]
- Tahir, M.H.; Cordeiro, G.M.; Alizadeh, M.; Mansoor, M.; Zubair, M. The logistic-X family of distributions and its applications. Commun. Stat. Theory Methods 2016, 45, 7326–7349. [Google Scholar] [CrossRef]
- Rezaei, S.; Sadr, B.B.; Alizadeh, M.; Nadarajah, S. Topp-Leone generated family of distributions: Properties and applications. Commun. Stat. Theory Methods 2017, 46, 2893–2909. [Google Scholar] [CrossRef]
- Tahir, M.H.; Nadarajah, S. Parameter induction in continuous univariate distributions: Well-established G families. An. Acad. Bras. Ciênc 2015, 87, 539–568. [Google Scholar] [CrossRef]
- Tahir, M.H.; Cordeiro, G.M. Compounding of distributions: A survey and new generalized classes. J. Stat. Distrib. App. 2016, 3. [Google Scholar] [CrossRef]
- Kumaraswamy, P. Generalized probability density function for double bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Lai, C.D.; Xie, M.; Murthy, D.N.P. A modified Weibull distribution. IEEE Trans. Reliab. 2003, 52, 33–37. [Google Scholar] [CrossRef]
- Bebbington, M.; Lai, C.D.; Zitikis, R. A flexible Weibull extension. Reliab. Eng. Syst. Saf. 2007, 92, 719–726. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Famoye, F.; Lee, C. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Torabi, H.; Montazeri, N.H. The logistic-uniform distribution and its application. Commun. Stat. Simul. Comput. 2014, 43, 2551–2569. [Google Scholar] [CrossRef]
- Al-Aqtash, R.; Lee, C.; Famoye, F. Gumbel-Weibull distribution: Properties and applications. J. Mod. Appl. Stat. Methods 2014, 13, 201–225. [Google Scholar] [CrossRef]
- Ahmad, Z.; Elgarhy, M.; Hamedani, G.G. A new Weibull-X family of distributions: Properties, characterizations and applications. J. Stat. Distrib. Appl. 2018, 5. [Google Scholar] [CrossRef]
- Torabi, H.; Montazeri, N.H. The gamma-uniform distribution and its application. Kybernetika 2012, 48, 16–30. [Google Scholar]
- Silva, F.S.; Percontini, A.; de-Brito, E.; Ramos, M.W.; Venancio, R.; Cordeiro, G.M. The odd Lindley-G family of distribution. Austrian J. Stat. 2017, 46, 65–87. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Alizadeh, M.; Ramires, T.G.; Ortega, E.M.M. The generalized odd half-Cauchy family of distributions: Properties and applications. Commun. Stat. Theory Methods 2018, 46, 5685–5705. [Google Scholar] [CrossRef]
- Alizadeh, M.; Altun, E.; Cordeiro, G.M.; Rasekhi, M. The odd power-Cauchy family of distributions: Properties, regression models and applications. J. Stat. Comput. Simul. 2018, 88, 785–807. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Yousof, H.M.; Ramires, T.G.; Ortega, E.M.M. The Burr XII system of densities: Properties, regression model and applications. J. Stat. Comput. Simul. 2017, 88, 432–456. [Google Scholar] [CrossRef]
- Hassan, A.S.; Hemeda, S.E.; Maiti, S.S.; Pramanik, S. The generalized additive Weibull-G family of distributions. Int. J. Stat. Prob. 2017, 6, 65–83. [Google Scholar] [CrossRef]
- Hassan, A.S.; Nassr, S.G. Power Lindley-G family of distributions. Ann. Data Sci. 2019, 6, 189–210. [Google Scholar] [CrossRef]
- Maiti, S.S.; Pramanik, S. A generalized Xgamma generator family of distributions. arXiv 2009, arXiv:1805.03892. [Google Scholar]
- El-Morshedy, M.; Eliwa, M.S. The odd flexible Weibull-H family of distributions: Properties and estimation with applications to complete and upper record data. Filomat 2019, 33, 2635–2652. [Google Scholar] [CrossRef]
- Alizadeh, M.; Afify, A.Z.; Eliwa, M.S.; Ali, S. The odd log-logistic Lindley-G family of distributions: Properties, Bayesian and non-Bayesian estimation with applications. Comput. Stat. 2020, 35, 281–308. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.S.; Afify, A.Z. The odd Chen generator of distributions: Properties and estimation methods with applications in medicine and engineering. J. Natl. Sci. Found. Sri Lanka 2020, 48, 113–130. [Google Scholar]
- Eliwa, M.S.; El-Morshedy, M.; Ali, S. Exponentiated odd Chen-G family of distributions: Statistical properties, Bayesian and non-Bayesian estimation with applications. J. Appl. Stat. 2020. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.M.; Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Frankl. Inst. 2010, 347, 1399–1429. [Google Scholar] [CrossRef]
- Lee, C.; Famoye, F.; Olumolade, O. Beta-Weibull distribution: Some properties and applications to censored data. J. Mod. Appl. Stat. Methods 2007, 6, 173–186. [Google Scholar] [CrossRef]
- Oguntunde, P.E.; Odetunmibi, O.A.; Adejum, A.O. On the exponentiated generalized Weibull distribution: A generalization of the Weibull distribution. Indian J. Sci. Technol. 2015, 8, 1–7. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Hashimoto, E.M.; Ortega, E.M.M. The McDonald Weibull model. Statistics 2012, 48, 256–278. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Aristizábal, W.D.; Suárez, D.M.; Lozano, S. The gamma modified Weibull distribution. Chil. J. Stat. 2011, 6, 37–48. [Google Scholar]
- Da-Cruz, J.N.; Ortega, E.M.M.; Cordeiro, G.M. The log-odd log-logistic Weibull regression model: Modelling, estimation, influential diagnostics and residual analysis. J. Stat. Comput. Simul. 2016, 86, 1516–1538. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Al-Hussaini, E.K.; Al-Jarallah, R.A. Marshall-Olkin extended Weibull distribution and its application to censored data. J. Appl. Stat. 2005, 32, 1025–1034. [Google Scholar] [CrossRef]
- Khan, M.S.; King, R.; Hudson, I.L. Transmuted Weibull distribution: Properties and estimation. Commun. Stat. Theory Methods 2017, 46, 5394–5418. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Res. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Asgharzadeh, A.; Bakouch, H.S.; Habibi, M. A generalized binomial exponential 2 distribution: Modeling and applications to hydrologic events. J. Appl. Stat. 2017, 44, 2368–2387. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A multivariate exponential model. J. Am. Stat. Assoc. 1967, 62, 30–44. [Google Scholar] [CrossRef]
- Sarhan, A.M.; Balakrishnan, N. A new class of bivariate distributions and its mixture. J. Multivar. Anal. 2007, 98, 1508–1527. [Google Scholar] [CrossRef][Green Version]
- Kundu, D.; Dey, A.K. Estimating the parameters of the Marshall-Olkin bivariate Weibull distribution by EM algorithm. Comput. Stat. Data Anal. 2009, 53, 956–965. [Google Scholar] [CrossRef]
- El-Gohary, A.; El-Bassiouny, A.H.; El-Morshedy, M. Bivariate exponentiated modified Weibull extension distribution. J. Stat. Appl. Prob. 2016, 5, 67–78. [Google Scholar] [CrossRef]
- Muhammed, H.Z. Bivariate inverse Weibull distribution. J. Stat. Comput. Simul. 2016, 86, 2335–2345. [Google Scholar] [CrossRef]
- El-Bassiouny, A.H.; EL-Damcese, M.; Abdelfattah, M.; Eliwa, M.S. Bivariate exponentaited generalized Weibull-Gompertz distribution. J. Appl. Probab. Stat. 2016, 11, 25–46. [Google Scholar]
- Ghosh, I.; Hamedani, G.G. On the Ristic-Balakrishnan distribution: Bivariate extension and characterizations. J. Stat. Theory Pract. 2018, 12, 436–449. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Alhussain, Z.A.; Atta, D.; Almetwally, E.M.; Eliwa, M.S. Bivariate Burr X generator of distributions: Properties and estimation methods with applications to complete and type-II censored samples. Mathematics 2020, 8, 264. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.S.; El-Gohary, A.; Khalil, A.A. Bivariate exponentiated discrete Weibull distribution: Statistical properties, estimation, simulation and applications. Math. Sci. 2020, 1–14. [Google Scholar] [CrossRef]
- Eliwa, M.S.; Alhussain, Z.A.; Ahmed, E.A.; Salah, M.M.; Ahmed, H.H.; El-Morshedy, M. Bivariate Gompertz generator of distributions: Statistical properties and estimation with application to model football data. J. Natl. Sci. Found. 2020, 48, 54–72. [Google Scholar] [CrossRef]
- Eliwa, M.S.; El-Morshedy, M. Bivariate Gumbel-G family of distributions: Statistical properties, Bayesian and non-Bayesian estimation with application. Ann. Data Sci. 2019, 6, 39–60. [Google Scholar] [CrossRef]
- Gijbels, I.; Omelka, M.; Pesta, M.; Veraverbeke, N. Score tests for covariate effects in conditional copulas. J. Multivar. Anal. 2017, 159, 111–133. [Google Scholar] [CrossRef]
- Husková, M.; Maciak, M. Discontinuities in robust nonparametric regression with alpha-mixing dependence. J. Nonparametr. Stat. 2017, 29, 447–475. [Google Scholar] [CrossRef]
- Relia Softś, R.; Staff, D. Using QALT models to analyze system configurations with load sharing. Reliab. Edge 2002, 3, 1–4. Available online: http://www.reliasoft.com/pubs/reliabilityedge_4q2002.pdf (accessed on 9 January 2020).



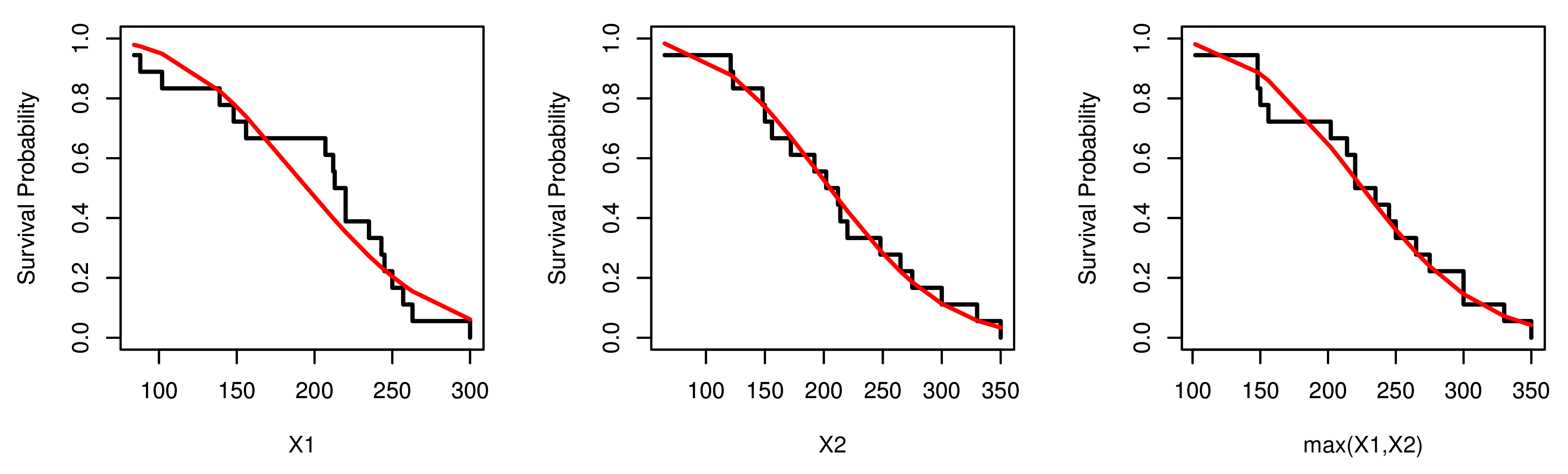
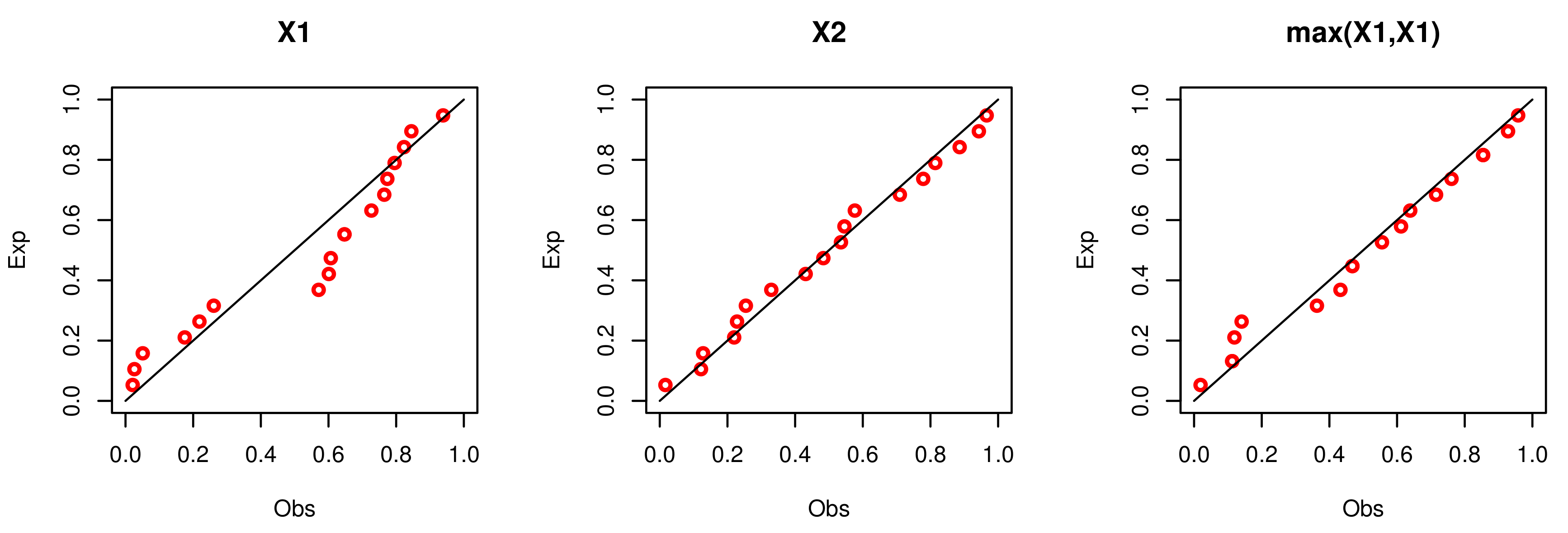
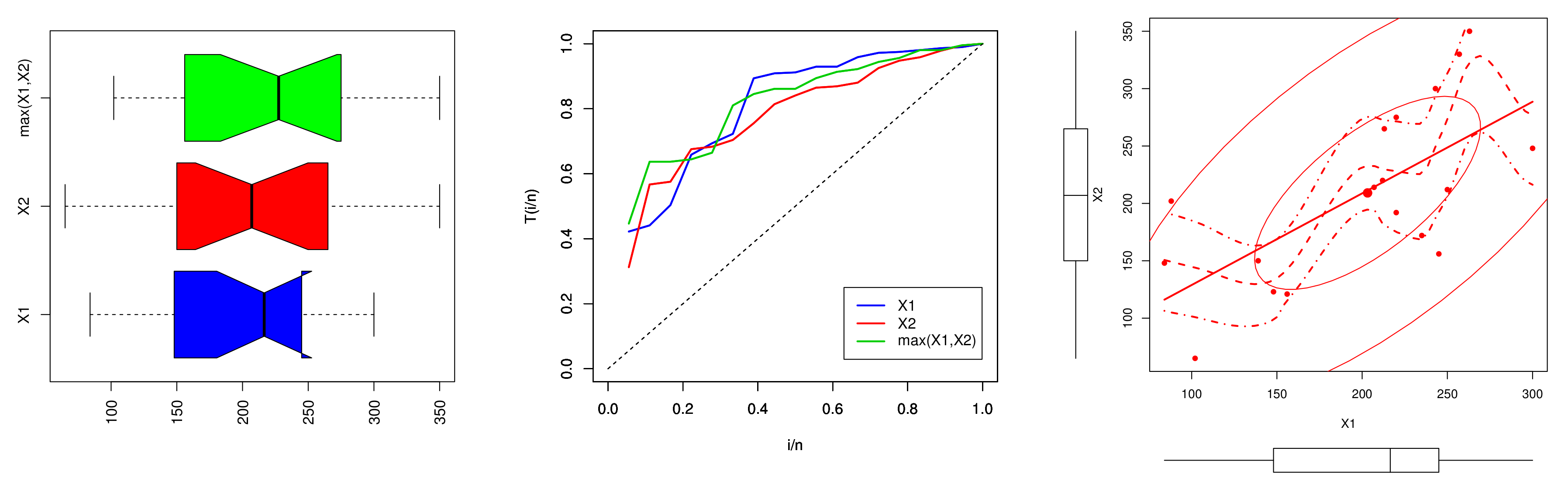
| Distribution | a | b | |||
|---|---|---|---|---|---|
| NKwW | 0.0089 | 1.1514 | 5.0192 | 0.5054 | – |
| (0.0023) | (0.0730) | (1.6716) | (0.1807) | – | |
| KwW | 0.0160 | 1.3962 | 5.7590 | 0.3381 | – |
| (0.0027) | (0.2113) | (1.9264) | (0.1554) | – | |
| BW | 0.0219 | 0.7969 | 13.2183 | 1.2340 | – |
| (0.0076) | (0.1903) | (5.1706) | (0.9787) | – | |
| EGW | 0.0086 | 0.9045 | 2.0898 | 10.5512 | – |
| (0.0022) | (0.1288) | (0.6257) | (4.4416) | – | |
| McW | 0.0132 | 1.2859 | 1.7925 | 0.5887 | 2.5824 |
| (0.0032) | (0.2544) | (0.6126) | (0.3831) | (0.9474) | |
| GaW | 1.1306 | 0.5469 | 17.6158 | – | – |
| (0.0496) | (0.0154) | (1.4970) | – | – | |
| OLLW | 0.0045 | 1.0313 | 2.4836 | – | – |
| (0.0003) | (0.1759) | (0.4532) | – | – | |
| MOW | 0.0032 | 3.4739 | – | – | 0.1039 |
| (0.0002) | (0.3436) | – | – | (0.0489) | |
| TrW | 0.0043 | 2.4549 | – | – | 0.6144 |
| (0.0003) | (0.1755) | – | – | (0.2078) | |
| W | 0.0050 | 2.2745 | – | – | – |
| (0.0002) | (0.1629) | – | – | – |
| Distribution | a | b | |||
|---|---|---|---|---|---|
| NKwW | 0.1742 | 0.9887 | 59.0160 | 0.2183 | – |
| (0.0316) | (0.0619) | (0.4024) | (0.0585) | – | |
| KwW | 0.1609 | 1.0252 | 54.7825 | 0.2041 | – |
| (0.0153) | (0.0276) | (0.1358) | (0.0382) | – | |
| BW | 0.1320 | 1.1080 | 23.0602 | 0.1940 | – |
| (0.0073) | (0.0068) | (8.7941) | (0.0324) | – | |
| EGW | 0.0090 | 0.7774 | 5.5966 | 10.5493 | – |
| (0.0041) | (0.1370) | (2.0458) | (5.6821) | – | |
| McW | 0.1608 | 1.0049 | 14.5078 | 0.2210 | 2.5180 |
| (0.0340) | (0.0466) | (9.8227) | (0.0757) | (0.0895) | |
| GaW | 4.6144 | 0.4983 | 14.7225 | – | – |
| (0.1518) | (0.0217) | (1.7239) | – | – | |
| OLLW | 0.0154 | 0.9508 | 2.3925 | – | – |
| (0.0021) | (0.3378) | (0.9487) | – | – | |
| MOW | 0.0065 | 3.3556 | – | – | 0.0145 |
| (0.0014) | (0.4292) | – | – | (0.0146) | |
| TrW | 0.0137 | 1.9476 | – | – | 0.7003 |
| (0.0016) | (0.1941) | – | – | (0.2483) | |
| W | 0.0171 | 1.7719 | – | – | – |
| (0.0015) | (0.1776) | – | – | – |
| K-S | ||||||||
|---|---|---|---|---|---|---|---|---|
| Distribution | AIC | BIC | HQIC | K-S | P-Value | |||
| NKwW | 565.2337 | 1138.4670 | 1148.8880 | 1142.6850 | 0.1722 | 0.0207 | 0.0454 | 0.9863 |
| KwW | 566.6253 | 1141.2510 | 1151.6710 | 1145.4680 | 0.3678 | 0.0477 | 0.0572 | 0.8987 |
| BW | 566.2292 | 1140.4580 | 1150.8790 | 1144.6760 | 0.3149 | 0.0411 | 0.0489 | 0.9707 |
| EGW | 566.2248 | 1140.4500 | 1150.8700 | 1144.6670 | 0.3266 | 0.0427 | 0.0487 | 0.9718 |
| McW | 567.4362 | 1144.8720 | 1157.8980 | 1150.1440 | 0.4868 | 0.0655 | 0.0596 | 0.8695 |
| GaW | 567.2618 | 1140.5240 | 1148.3390 | 1143.6870 | 0.5071 | 0.0689 | 0.0547 | 0.9257 |
| OLLW | 569.6909 | 1145.3820 | 1153.1970 | 1148.5450 | 0.6649 | 0.0932 | 0.0807 | 0.5335 |
| MOW | 568.4818 | 1142.9640 | 1150.7790 | 1146.1270 | 0.6431 | 0.0866 | 0.0595 | 0.8713 |
| TrW | 573.7855 | 1153.5710 | 1161.3870 | 1156.7340 | 1.4659 | 0.2183 | 0.0872 | 0.4321 |
| W | 576.1180 | 1156.2360 | 1161.4460 | 1158.3450 | 1.8275 | 0.2767 | 0.0936 | 0.3450 |
| K-S | ||||||||
|---|---|---|---|---|---|---|---|---|
| Distribution | AIC | BIC | HQIC | K-S | P-Value | |||
| NKwW | 215.1742 | 438.3485 | 445.8333 | 441.1770 | 0.2003 | 0.0277 | 0.0776 | 0.9346 |
| KwW | 215.5195 | 439.0389 | 446.5238 | 441.8675 | 0.2495 | 0.0347 | 0.0834 | 0.8924 |
| BW | 216.1573 | 440.3147 | 447.7995 | 443.1432 | 0.3387 | 0.0477 | 0.0973 | 0.7538 |
| EGW | 218.1801 | 444.3601 | 451.8449 | 447.1887 | 0.6147 | 0.0913 | 0.0973 | 0.7543 |
| McW | 215.7566 | 441.5132 | 450.8692 | 445.0489 | 0.2699 | 0.0374 | 0.0837 | 0.8895 |
| GaW | 219.4700 | 444.9401 | 450.5537 | 447.0615 | 0.8278 | 0.1250 | 0.1176 | 0.5203 |
| OLLW | 220.4104 | 446.8208 | 452.4344 | 448.9422 | 0.9051 | 0.1388 | 0.0934 | 0.7966 |
| MOW | 218.2594 | 442.5187 | 448.1323 | 444.6401 | 0.5773 | 0.0868 | 0.0791 | 0.9247 |
| TrW | 224.0997 | 454.1994 | 459.8130 | 456.3208 | 1.5006 | 0.2372 | 0.1291 | 0.4001 |
| W | 225.7065 | 455.4131 | 459.1555 | 456.8273 | 1.7286 | 0.2765 | 0.1399 | 0.3048 |
| Model | −L | K-S | P-Value | −L | K-S | P-Value | −L | K-S | P-Value |
| NKwW | |||||||||
| Model | |||||||
|---|---|---|---|---|---|---|---|
| Statistic | BvNKwW | BvGPW | BvEW | BvW | BvGEx | BvEx | BvGLFR |
| − | |||||||
| − | |||||||
| 1.5591 | 30.1381 | 0.2004 | 2.4541 | 0.0023 | 0.4171 | ||
| − | |||||||
| − | |||||||
| − | − | − | − | − | − | ||
| − | − | − | − | − | − | ||
| AIC | |||||||
| CAIC | |||||||
| BIC | |||||||
| HQIC | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tahir, M.H.; Hussain, M.A.; Cordeiro, G.M.; El-Morshedy, M.; Eliwa, M.S. A New Kumaraswamy Generalized Family of Distributions with Properties, Applications, and Bivariate Extension. Mathematics 2020, 8, 1989. https://doi.org/10.3390/math8111989
Tahir MH, Hussain MA, Cordeiro GM, El-Morshedy M, Eliwa MS. A New Kumaraswamy Generalized Family of Distributions with Properties, Applications, and Bivariate Extension. Mathematics. 2020; 8(11):1989. https://doi.org/10.3390/math8111989
Chicago/Turabian StyleTahir, Muhammad H., Muhammad Adnan Hussain, Gauss M. Cordeiro, M. El-Morshedy, and M. S. Eliwa. 2020. "A New Kumaraswamy Generalized Family of Distributions with Properties, Applications, and Bivariate Extension" Mathematics 8, no. 11: 1989. https://doi.org/10.3390/math8111989
APA StyleTahir, M. H., Hussain, M. A., Cordeiro, G. M., El-Morshedy, M., & Eliwa, M. S. (2020). A New Kumaraswamy Generalized Family of Distributions with Properties, Applications, and Bivariate Extension. Mathematics, 8(11), 1989. https://doi.org/10.3390/math8111989









