Series Expansion and Fourth-Order Global Padé Approximation for a Rough Heston Solution
Abstract
1. Introduction
2. The Rough Heston Model
2.1. The Model
2.2. Characteristic Function of the Rough Heston Model
3. Analytical Approximation
3.1. Preliminaries
3.2. Laplace–Adomian-Decomposition Method
4. The Fractional Adams–Bashforth–Moulton Method and Series Expansion Solutions for the Fractional Riccati Equation
4.1. The Fractional Adams–Bashforth–Moulton
4.2. Expansions for the Solution of the Fractional Riccati Equation
4.2.1. Small Time Series Expansion
4.2.2. Large Time Series Expansion
5. The Global Padé Approximation
5.1. Definition
5.2. Approximation Errors
5.3. Third-Order Global Padé Approximant
5.4. Fourth-Order Global Padé Approximant
5.4.1. Fourth-Order Approximant
5.4.2. Fourth-Order Approximant
5.4.3. Fourth-Order Approximant
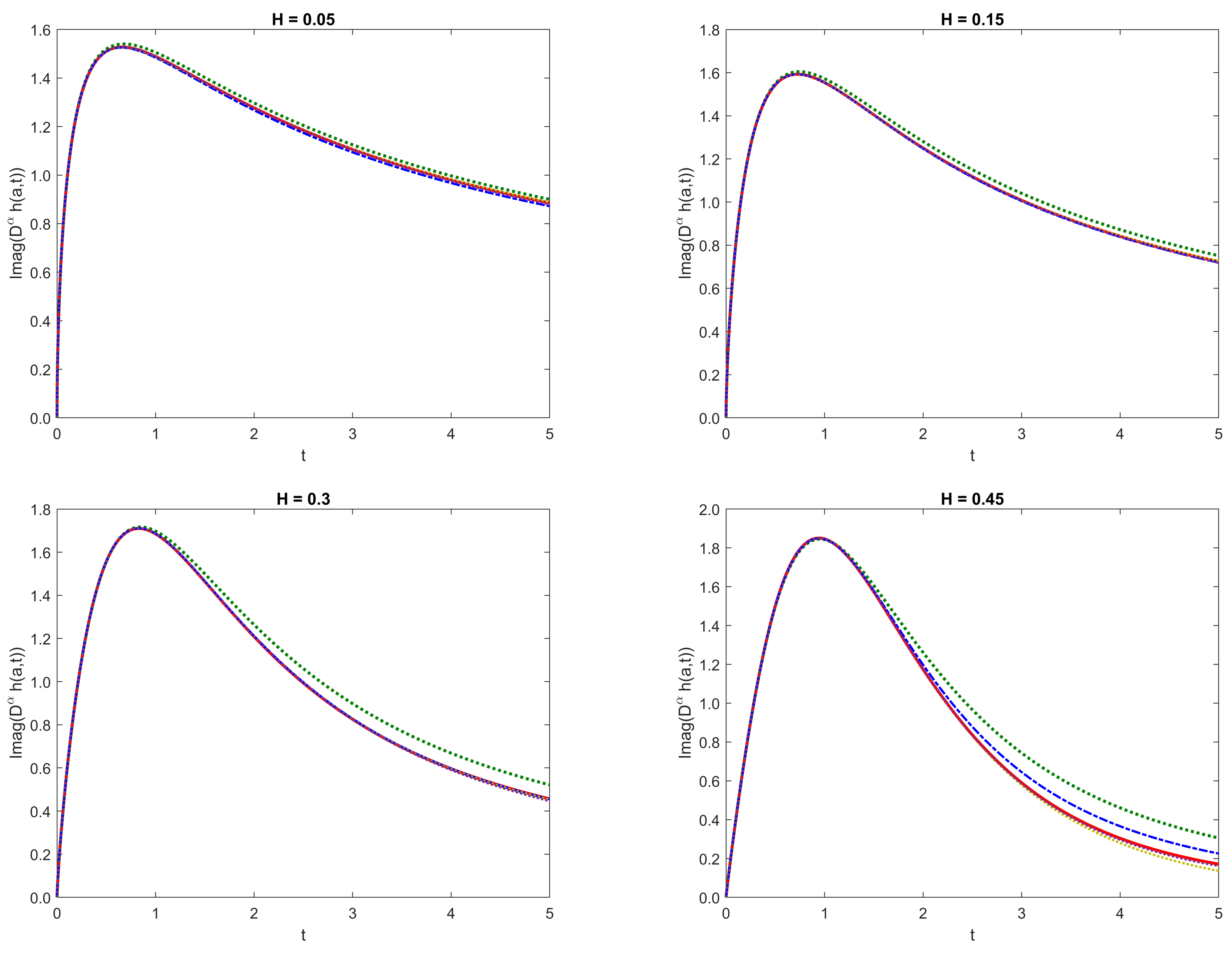
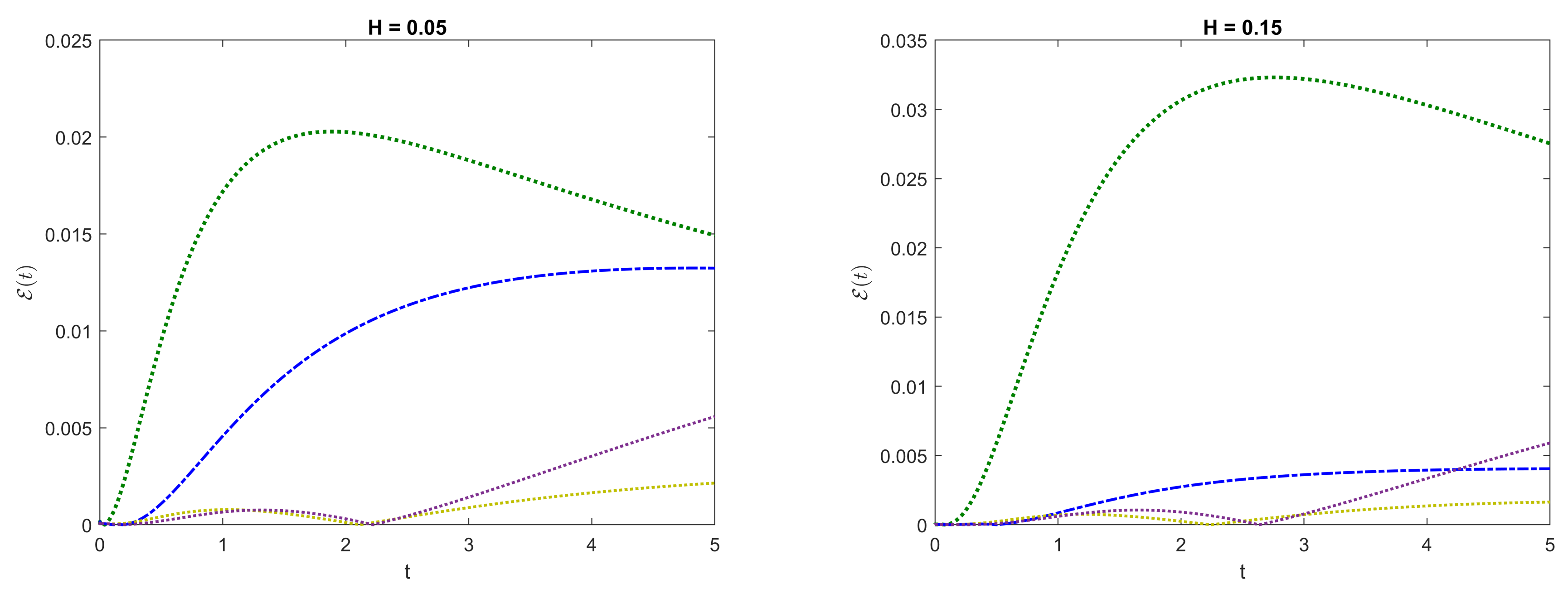
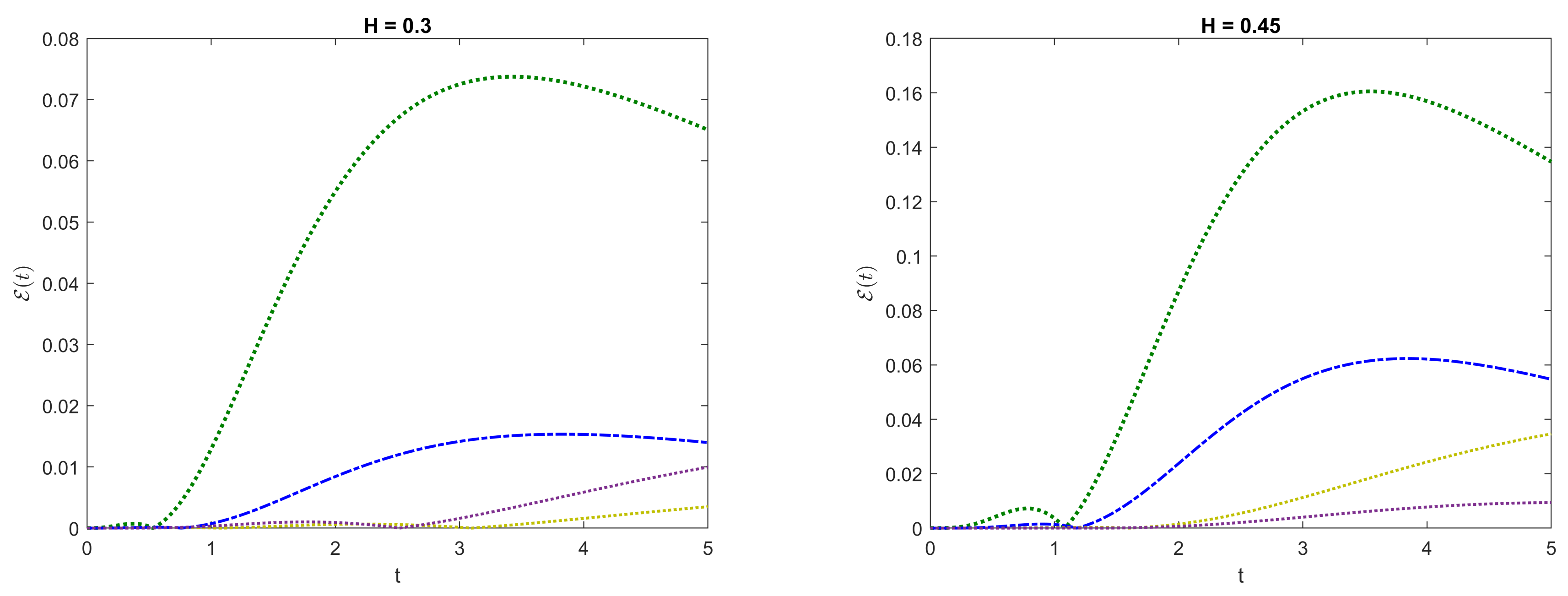
6. Numerical Experiments
6.1. Comparisons of Methods on the Fractional Riccati Equation
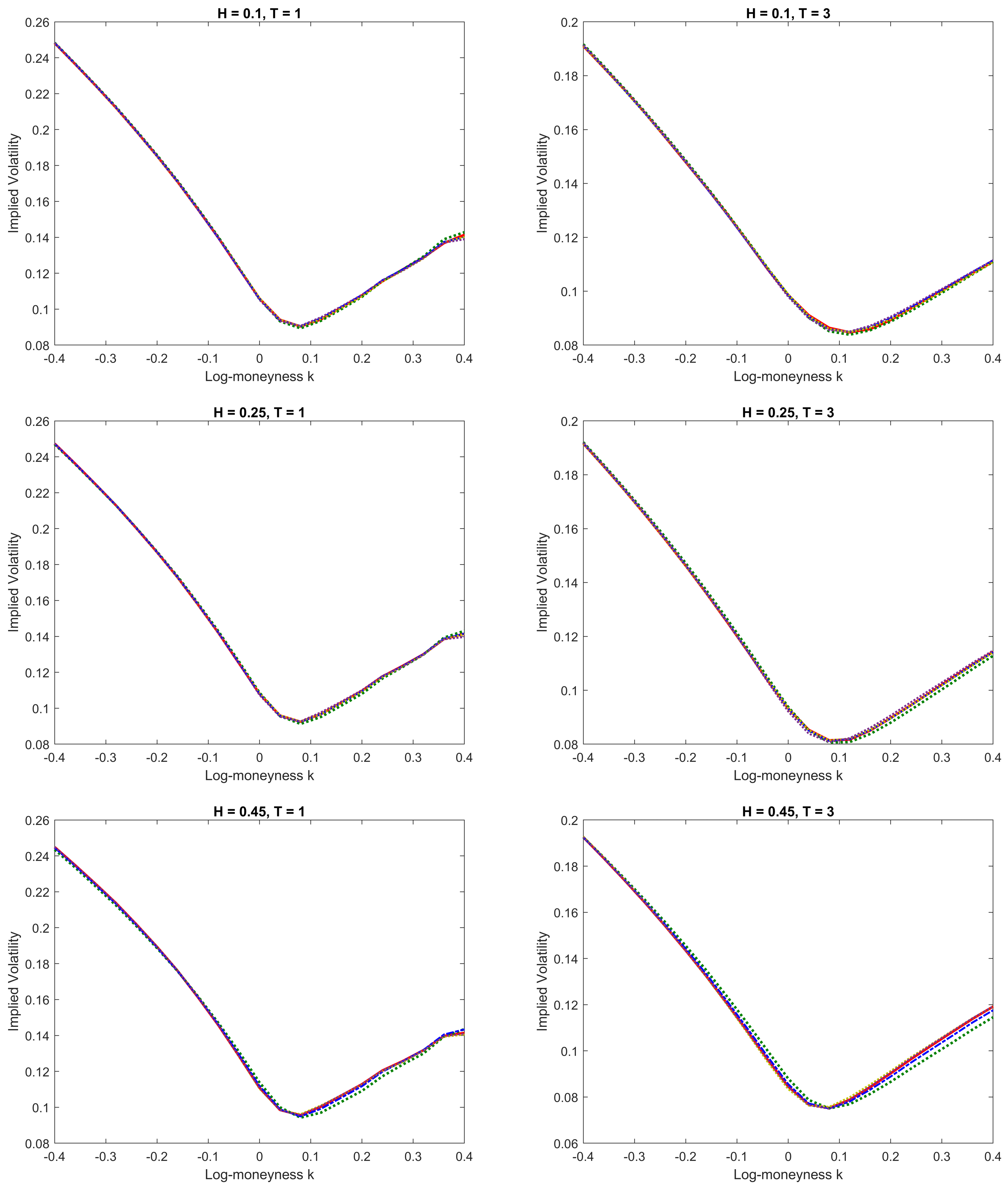
6.2. Option Pricing
7. Summary and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| fBm | Fractional Brownian motion |
| BSS | Hybrid Brownian semistationary method |
| LADM | Laplace–Adomian-decomposition method |
| GPadé | Gatheral’s third-order Global Padé approximant |
Appendix A. Riemann–Liouville Fractional Calculus
Appendix B. The Laplace–Adomian-Decomposition Method on the Fractional Riccati Equation
- Step 1: We apply the Laplace transform to the both sides of the fractional Riccati Equation (6); then we can obtain the following equation:From Equation (7), we can simplify the equation toA further simplification gives us
- Step 2: Let . The traditional Adomian decomposition method assumes that the solution is an infinite series:and the square of the solution is decomposed aswhere are the Adomian polynomials and can be computed using methods stated from [59,60]. The Adomian polynomials can be computed by the formulaAs for , the first 12 Adomian polynomials are computed by [31] as
- Step 3: By substituting Equations (A6) and (A7) from Step 2 into Equation (A5), we obtain the following:By matching both sides of Equation (A10) as in the usual Adomian decomposition method, we getFinally, we use the inverse Laplace transform on Equations (A11)–(A14) to obtain the terms . With the help of Lemma 1, we can obtain asSubsequently, is computed as follows:By performing an inverse Laplace transform on Equation (A12) and utilizing Lemma 2, we obtain as follows.We repeat the process by letting , and then performing an inverse Laplace transform on in Equation (A13). Similarly, we use Lemma 2 to obtain asRepeat the process to obtain , and finally we have the following expansion:
- Step 4: For our purpose of study, from Equation (4), we substitute the following , and to Equation (A19). Let the series expansion of to be in the form ofFinally, the first five coefficients are
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Merton, R.C. Option pricing when underlying stock returns are discontinuous. J. Financ. Econ. 1976, 3, 125–144. [Google Scholar] [CrossRef]
- Hull, J.; White, A. The pricing of options on assets with stochastic volatilities. J. Financ. 1987, 42, 281–300. [Google Scholar] [CrossRef]
- Heston, S.L. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef]
- Renault, E.; Touzi, N. Option hedging and implied volatilities in a stochastic volatility model 1. Math. Financ. 1996, 6, 279–302. [Google Scholar] [CrossRef]
- Lee, R.W. Implied volatility: Statics, dynamics, and probabilistic interpretation. In Recent Advances in Applied Probability; Springer: Berlin, Germany, 2005; pp. 241–268. [Google Scholar]
- Lewis, A.L. Option Valuation under Stochastic Volatility II; Finance Press: Newport Beach, CA, USA, 2009. [Google Scholar]
- Medvedev, A.; Scaillet, O. Approximation and calibration of short-term implied volatilities under jump-diffusion stochastic volatility. Rev. Financ. Stud. 2007, 20, 427–459. [Google Scholar] [CrossRef]
- Bates, D.S. Jumps and stochastic volatility: Exchange rate processes implicit in deutsche mark options. Rev. Financ. Stud. 1996, 9, 69–107. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Comte, F.; Renault, E. Long memory in continuous-time stochastic volatility models. Math. Financ. 1998, 8, 291–323. [Google Scholar] [CrossRef]
- Cheridito, P. Mixed fractional Brownian motion. Bernoulli 2001, 7, 913–934. [Google Scholar] [CrossRef]
- Gatheral, J.; Jaisson, T.; Rosenbaum, M. Volatility is rough. Quant. Financ. 2018, 18, 933–949. [Google Scholar] [CrossRef]
- Fukasawa, M. Asymptotic analysis for stochastic volatility: Martingale expansion. Financ. Stoch. 2011, 15, 635–654. [Google Scholar] [CrossRef]
- Alòs, E.; León, J.A.; Vives, J. On the short-time behavior of the implied volatility for jump-diffusion models with stochastic volatility. Financ. Stoch. 2007, 11, 571–589. [Google Scholar] [CrossRef]
- Bayer, C.; Friz, P.; Gatheral, J. Pricing under rough volatility. Quant. Financ. 2016, 16, 887–904. [Google Scholar] [CrossRef]
- El Euch, O.; Rosenbaum, M. The characteristic function of rough Heston models. Math. Financ. 2019, 29, 3–38. [Google Scholar] [CrossRef]
- El Euch, O.; Fukasawa, M.; Rosenbaum, M. The microstructural foundations of leverage effect and rough volatility. Financ. Stoch. 2018, 22, 241–280. [Google Scholar] [CrossRef]
- Gatheral, J.; Radoicic, R. Rational approximation of the rough Heston solution. Int. J. Theor. Appl. Financ. 2019, 22, 1950010. [Google Scholar] [CrossRef]
- Bennedsen, M.; Lunde, A.; Pakkanen, M.S. Hybrid scheme for Brownian semistationary processes. Financ. Stoch. 2017, 21, 931–965. [Google Scholar] [CrossRef]
- McCrickerd, R.; Pakkanen, M.S. Turbocharging Monte Carlo pricing for the rough Bergomi model. Quant. Financ. 2018, 18, 1877–1886. [Google Scholar] [CrossRef]
- Abi Jaber, E.; El Euch, O. Multifactor Approximation of Rough Volatility Models. SIAM J. Financ. Math. 2019, 10, 309–349. [Google Scholar] [CrossRef]
- Abi Jaber, E. Lifting the Heston model. Quant. Financ. 2019, 19, 1995–2013. [Google Scholar] [CrossRef]
- El Euch, O.; Gatheral, J.; Rosenbaum, M. Roughening Heston. 2018. Available online: https://ssrn.com/abstract=3116887 (accessed on 25 March 2019).
- Callegaro, G.; Grasselli, M.; Pages, G. Rough but not so tough: Fast hybrid schemes for fractional Riccati equations. arXiv 2018, arXiv:1805.12587. [Google Scholar]
- Odibat, Z.; Momani, S. Application of variational iteration method to nonlinear differential equations of fractional order. Int. J. Nonlinear Sci. Numer. Simul. 2006, 7, 27–34. [Google Scholar] [CrossRef]
- Momani, S.; Shawagfeh, N. Decomposition method for solving fractional Riccati differential equations. Appl. Math. Comput. 2006, 182, 1083–1092. [Google Scholar] [CrossRef]
- Cang, J.; Tan, Y.; Xu, H.; Liao, S.J. Series solutions of non-linear Riccati differential equations with fractional order. Chaos Solitons Fractals 2009, 40, 1–9. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. Modified homotopy perturbation method: Application to quadratic Riccati differential equation of fractional order. Chaos Solitons Fractals 2008, 36, 167–174. [Google Scholar] [CrossRef]
- Khan, N.A.; Ara, A.; Khan, N.A. Fractional-order Riccati differential equation: Analytical approximation and numerical results. Adv. Differ. Equ. 2013, 185. [Google Scholar] [CrossRef]
- Tsai, P.-Y.; Chen, C.-K. An approximate analytic solution of the nonlinear Riccati differential equation. J. Frankl. Inst. 2010, 347, 1850–1862. [Google Scholar] [CrossRef]
- Jafari, H.; Tajadodi, H.; Matikolai, S.H. Homotopy perturbation pade technique for solving fractional Riccati differential equations. Int. J. Nonlinear Sci. Numer. Simul. 2010, 11, 271–276. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Khan, J.A.; Qureshi, I.M. A new stochastic approach for solution of Riccati differential equation of fractional order. Ann. Math. Artif. Intell. 2010, 60, 229–250. [Google Scholar] [CrossRef]
- Merino, R.; Vives, J. A generic decomposition formula for pricing vanilla options under stochastic volatility models. Int. J. Stoch. Anal. 2015, 3, 125–144. [Google Scholar] [CrossRef]
- Alòs, E. A decomposition formula for option prices in the Heston model and applications to option pricing approximation. Quant. Financ. 2012, 20, 13–27. [Google Scholar] [CrossRef]
- Alós, E.; Yang, Y. A Closed-Form Option Pricing Approximation Formula for a Fractional Heston Model. Economics Working Papers. 2014. Available online: https://econ-papers.upf.edu/papers/1446.pdf (accessed on 1 September 2020).
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Carr, P.; Madan, D. Option valuation using the fast Fourier transform. J. Comput. Financ. 1999, 2, 61–73. [Google Scholar] [CrossRef]
- Lewis, A.L. A Simple Option Formula for General Jump-Diffusion and Other Exponential Lévy Processes. 2001. Available online: https://ssrn.com/abstract=282110 (accessed on 15 February 2020).
- Thompson, I.J. Coupled reaction channels calculations in nuclear physics. Comput. Phys. Rep. 1988, 7, 167–212. [Google Scholar] [CrossRef]
- Rakityansky, S.; Sofianos, S.; Elander, N. Pade approximation of the S-matrix as a way of locating quantum resonances and bound states. J. Phys. A Math. Theor. 2007, 40, 14857. [Google Scholar] [CrossRef]
- Lanti, E.; Dominski, J.; Brunner, S.; McMillan, B.; Villard, L. Padé Approximation of the adiabatic electron contribution to the gyrokinetic quasi-neutrality equation in the ORB5 code. In Proceedings of the Joint Varenna-Lausanne International Workshop on the Theory of Fusion Plasmas, Varenna, Italy, 29 August–2 September 2016; IOP Publishing: Bristol, UK, 2016; Volume 775, p. 012006. [Google Scholar]
- Baker, G.A.; Graves-Morris, P. Padé Approximants; Cambridge University Press: Cambridge, UK, 1996; Volume 59. [Google Scholar]
- Lubinsky, D.S. Rogers-Ramanujan and the Baker-Gammel-Wills (padé) conjecture. Ann. Math. 2003, 157, 847–889. [Google Scholar] [CrossRef]
- Lubinsky, D.S. Reflections on the Baker–Gammel–Wills (Padé) Conjecture. In Analytic Number Theory, Approximation Theory, and Special Functions; Springer: Berlin, Germany, 2014; pp. 561–571. [Google Scholar]
- Jeng, S.W.; Kilicman, A. Fractional Riccati Equation and Its Applications to Rough Heston Model Using Numerical Methods. Symmetry 2020, 12, 959. [Google Scholar] [CrossRef]
- Winitzki, S. Uniform approximations for transcendental functions. In International Conference on Computational Science and Its Applications; Springer: Berlin, Germany, 2003; pp. 780–789. [Google Scholar]
- Abassy, T.A.; El-Tawil, M.A.; El-Zoheiry, H. Exact solutions of some nonlinear partial differential equations using the variational iteration method linked with laplace transforms and the padé technique. Comput. Math. Appl. 2007, 54, 940–954. [Google Scholar] [CrossRef][Green Version]
- Dehghan, M.; Hamidi, A.; Shakourifar, M. The solution of coupled Burgers’ equations using Adomian–Pade technique. Appl. Math. Comput. 2007, 189, 1034–1047. [Google Scholar] [CrossRef]
- Atkinson, C.; Osseiran, A. Rational solutions for the time-fractional diffusion equation. SIAM J. Appl. Math. 2011, 71, 92–106. [Google Scholar] [CrossRef]
- Zeng, C.; Chen, Y.Q. Global Padé approximations of the generalized Mittag-Leffler function and its inverse. Fract. Calc. Appl. Anal. 2015, 18, 1492–1506. [Google Scholar] [CrossRef]
- Starovoitov, A.P.; Starovoitova, N.A. Padé approximants of the Mittag-Leffler functions. Sb. Math. 2007, 198, 1011. [Google Scholar] [CrossRef]
- Sarumi, I.O.; Furati, K.M.; Khaliq, A.Q. Highly Accurate Global Padé Approximations of Generalized Mittag–Leffler Function and Its Inverse. J. Sci. Comput. 2020, 82, 46. [Google Scholar] [CrossRef]
- Alos, E.; Gatheral, J.; Radoičić, R. Exponentiation of conditional expectations under stochastic volatility. Quant. Financ. 2020, 20, 13–27. [Google Scholar] [CrossRef]
- El Euch, O.; Rosenbaum, M. Perfect hedging in rough Heston models. Ann. Appl. Probab. 2018, 28, 3813–3856. [Google Scholar] [CrossRef]
- Gatheral, J. The Volatility Surface: A Practitioner’s Guide; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 357. [Google Scholar]
- Podlubny, I. The Laplace transform method for linear differential equations of the fractional order. arXiv 1997, arXiv:funct-an/9710005. [Google Scholar]
- Schiff, J.L. The Laplace Transform: Theory and Applications; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Biazar, J.; Pourabd, M. A Maple program for computing Adomian polynomials. Int. Math. Forum 2006, 1, 1919–1924. [Google Scholar] [CrossRef]
- Biazar, J.; Shaof, S. A simple algorithm for calculating Adomian polynomials. Int. J. Contemp. Math. Sci. 2007, 2, 975–982. [Google Scholar] [CrossRef]
- Diethelm, K.; Freed, A.D. The FracPECE Subroutine for the Numerical Solution of Differential Equations of Fractional Order. Semantic Scholar. 1999. Available online: https://static.aminer.org/pdf/PDF/000/243/047/numerical_approaches_to_the_solution_of_some_fractional_differential_equations.pdf (accessed on 15 May 2020).
- Diethelm, K.; Freed, A.D. On the solution of nonlinear fractional-order differential equations used in the modeling of viscoplasticity. In Scientific Computing in Chemical Engineering II; Springer: Berlin/Heidelberg, Germany, 1999; pp. 217–224. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D.; Luchko, Y. Algorithms for the fractional calculus: A selection of numerical methods. Comput. Methods Appl. Mech. Eng. 2005, 194, 743–773. [Google Scholar] [CrossRef]
- Dumitru, B.; Kai, D.; Enrico, S. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012; Volume 3. [Google Scholar]
- Li, C.; Tao, C. On the fractional Adams method. Comput. Math. Appl. 2009, 58, 1573–1588. [Google Scholar] [CrossRef]
| GPadé [19] | ||||
|---|---|---|---|---|
| 0.0283 | 0.0132 | 0.0022 | 0.0056 | |
| 0.0252 | 0.0080 | 0.0019 | 0.0057 | |
| 0.0323 | 0.0040 | 0.0016 | 0.0059 | |
| 0.0423 | 0.0008 | 0.0013 | 0.0065 | |
| 0.0737 | 0.0153 | 0.0035 | 0.0100 | |
| 0.1605 | 0.0623 | 0.0346 | 0.0094 | |
| 0.1946 | 0.0838 | 0.0469 | 0.0155 |
| GPadé [19] | ||||
|---|---|---|---|---|
| 0.6240 | 0.2568 | 0.2400 | 0.4816 | |
| 0.7663 | 0.0712 | 0.1179 | 0.3834 | |
| 1.7917 | 0.6308 | 0.2651 | 0.1009 | |
| 0.5802 | 0.2874 | 0.2232 | 0.5417 | |
| 1.0778 | 0.1257 | 0.1124 | 0.5995 | |
| 2.6452 | 0.9404 | 0.5356 | 0.1566 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeng, S.W.; Kilicman, A. Series Expansion and Fourth-Order Global Padé Approximation for a Rough Heston Solution. Mathematics 2020, 8, 1968. https://doi.org/10.3390/math8111968
Jeng SW, Kilicman A. Series Expansion and Fourth-Order Global Padé Approximation for a Rough Heston Solution. Mathematics. 2020; 8(11):1968. https://doi.org/10.3390/math8111968
Chicago/Turabian StyleJeng, Siow Woon, and Adem Kilicman. 2020. "Series Expansion and Fourth-Order Global Padé Approximation for a Rough Heston Solution" Mathematics 8, no. 11: 1968. https://doi.org/10.3390/math8111968
APA StyleJeng, S. W., & Kilicman, A. (2020). Series Expansion and Fourth-Order Global Padé Approximation for a Rough Heston Solution. Mathematics, 8(11), 1968. https://doi.org/10.3390/math8111968