Free Interfaces at the Tips of the Cilia in the One-Dimensional Periciliary Layer
Abstract
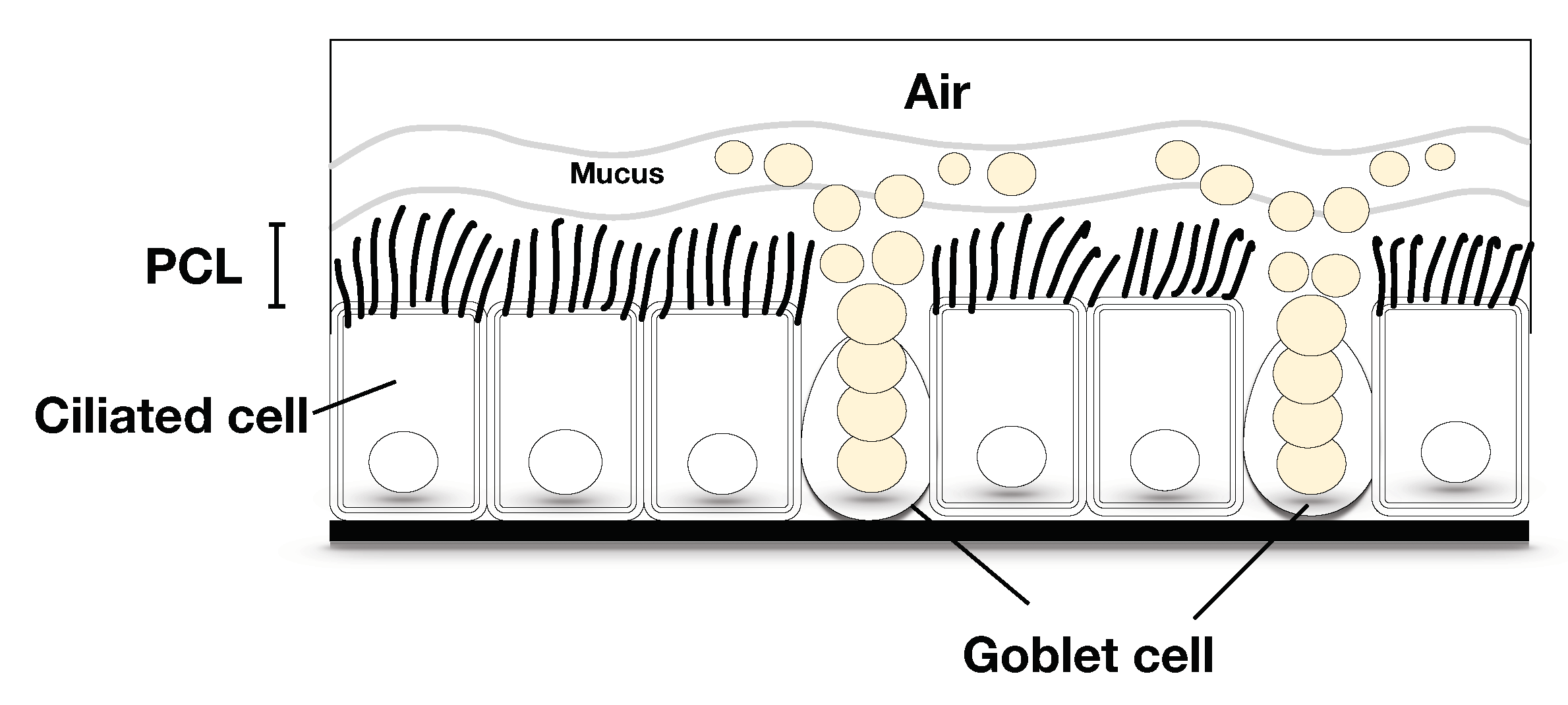
1. Introduction
2. Mathematical Model
3. Boundary Immobilization Technique
4. Model Discretization
5. Numerical Validation
6. Numerical Results
7. Conclusions
- To avoid the numerical grid adjustment for every change in the the angle , we adopted the boundary immobilization technique to the mathematical model;
- The one-dimensional isotropic finite element method was applied to the Brinkman equation and a finite different scheme was employed to the Stefan problem to calculate the numerical solutions;
- The numerical results were verified by comparing them with an exact solution with a fixed boundary condition at when . The results converge to the exact solution, where the -norm errors are provided in Table 1;
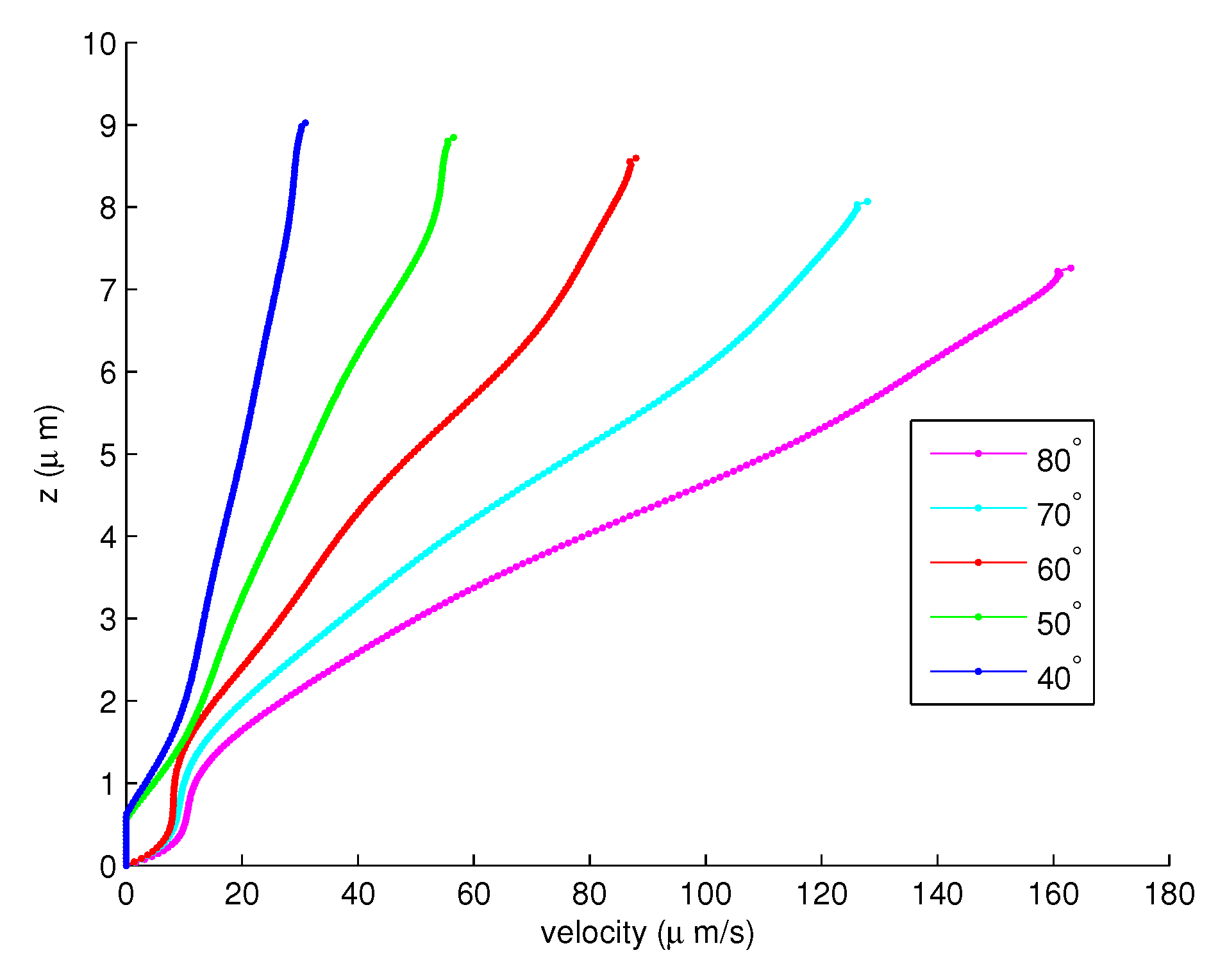
- The numerical results of each angle are provided in Figure 6, Figure 7 and Figure 8 for the forward stroke from the angles to . Even if the velocity of the cilia is highest at (Figure 5 in [41]), the highest velocity of the PCL fluid is found at . That is, the velocities of the PCL fluid increase from the starting angle and decrease from the angles to ;
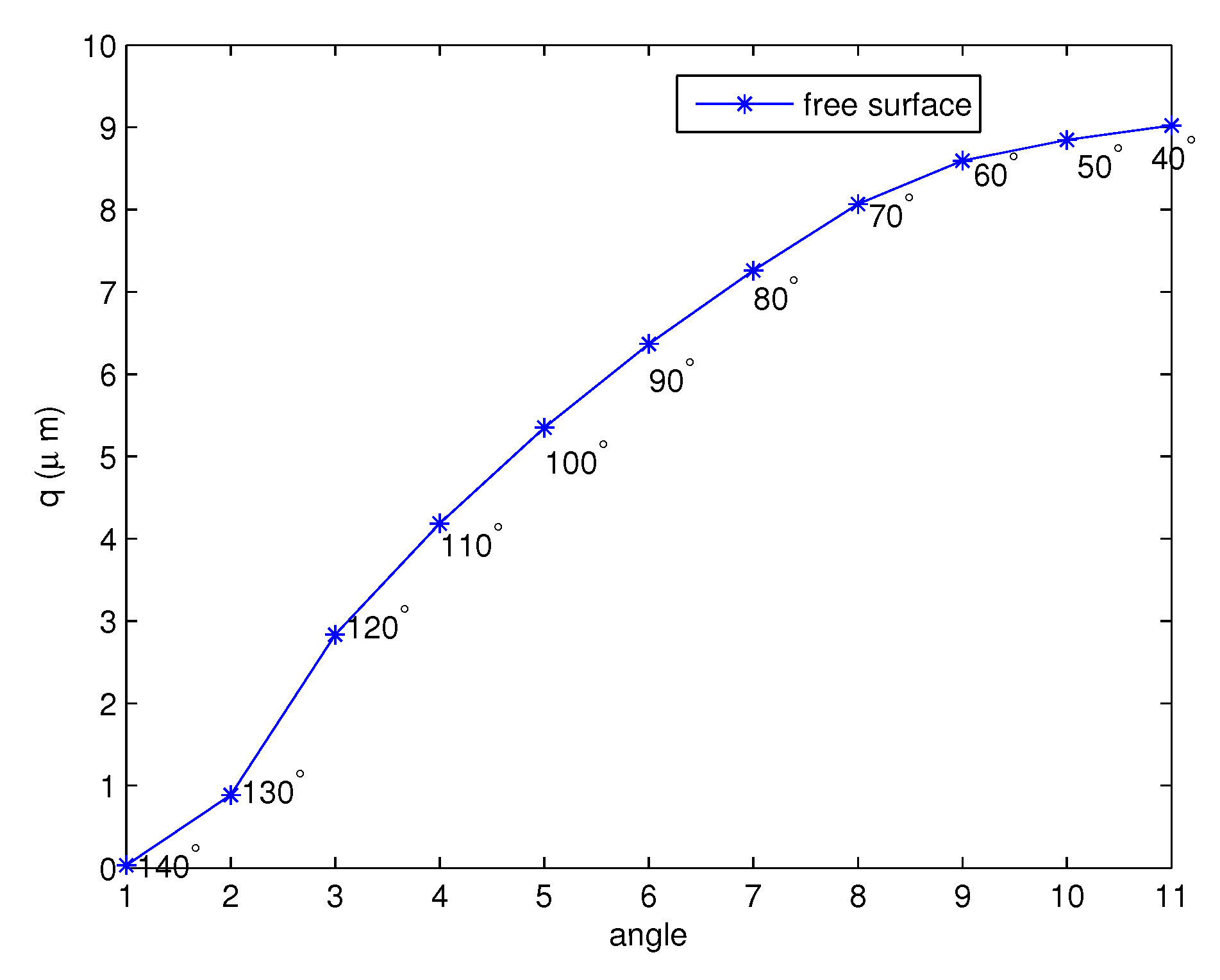
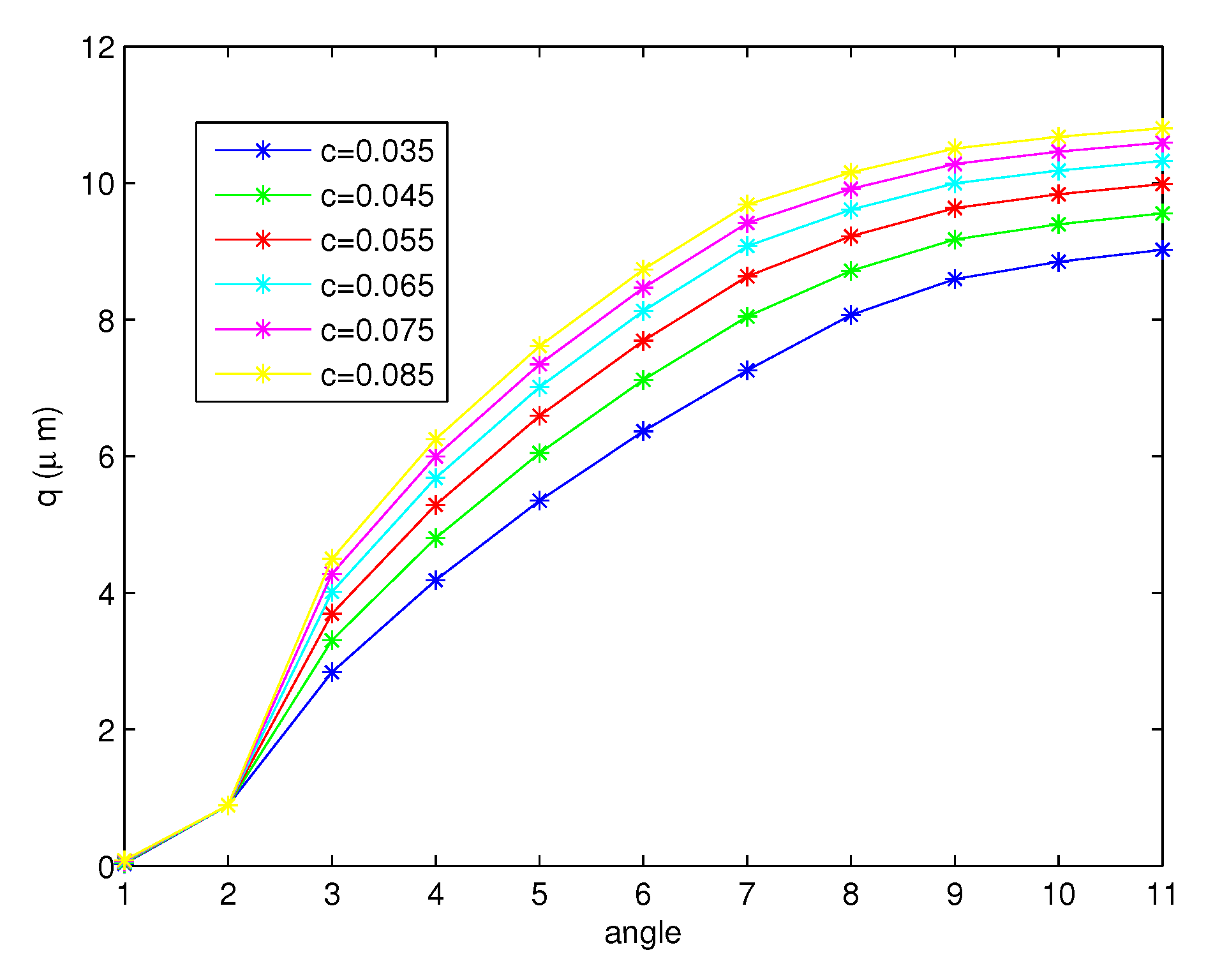
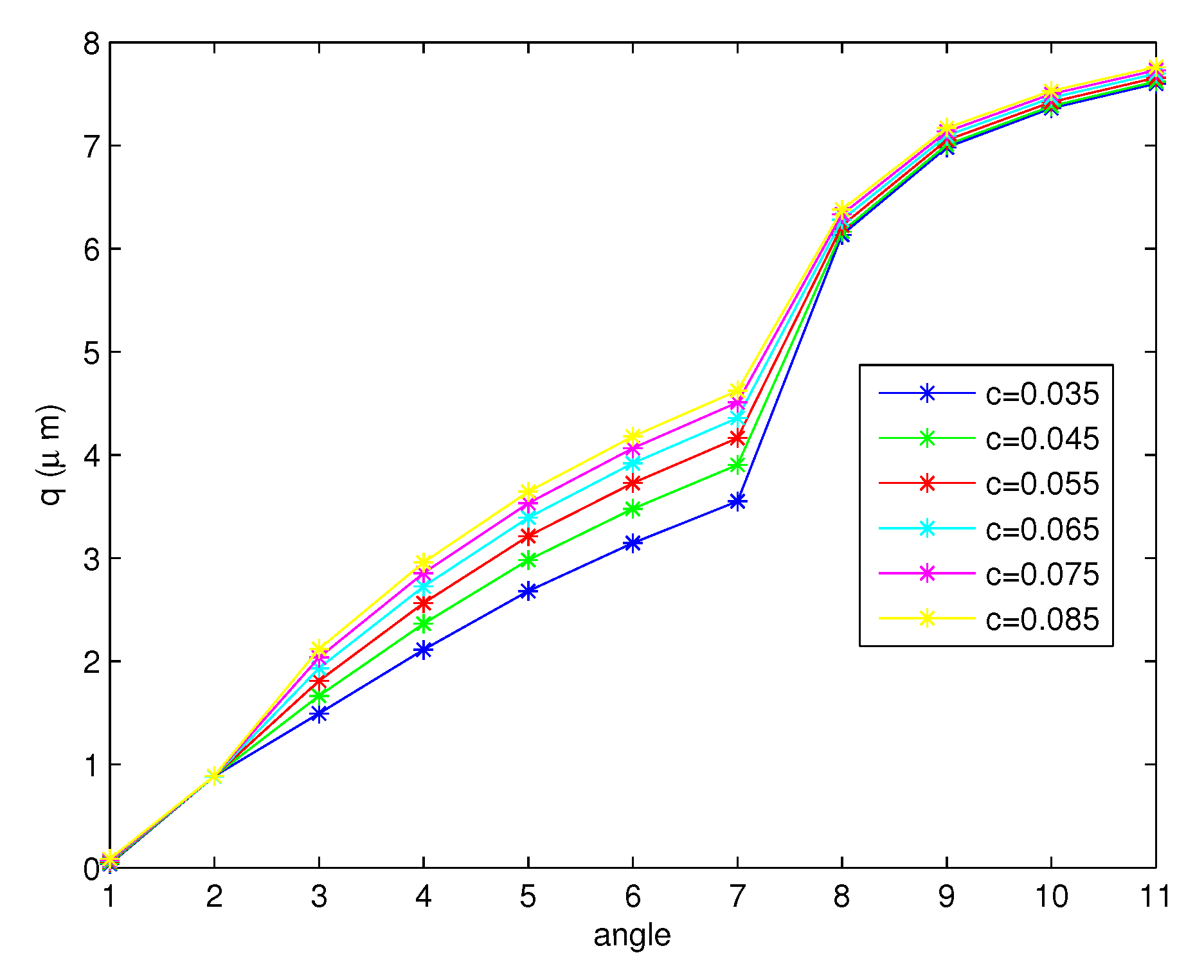
- The free surfaces due to the movement of cilia are shown in Figure 10, Figure 11 and Figure 12. We discovered that the height of the surface increases for the full forward stroke although the velocities of the PCL fluid increase in the first half of the effective stroke and decrease for the second half. Moreover, we found that the initial value c does not change the shape of the free surface, but the different functions r cause the change in the shape of the surface as illustrated in Figure 11 and Figure 12;
- To the author’s knowledge, no experimental data in the literature provide the shape of the free surface, only the average value is given. The numerical results were compared with the available experimental data. For the non-CF tissues, the average heights of the PCL from our results and the experimental data were and m, respectively. The difference between and is , which is small. This is one of the justifications that shows that our mathematical model is suitable for this problem.
Funding
Acknowledgments
Conflicts of Interest
References
- Blake, J.R.; Winet, H. On the Mechanics of muco-ciliary transport. Biorheology 1980, 17, 125–134. [Google Scholar] [CrossRef]
- Fulford, G.R.; Blake, J.R. Muco-ciliary Transport in the Lung. J. Theor. Biol. 1986, 121, 381–402. [Google Scholar] [CrossRef]
- Sleigh, M.A. Adaptations of Ciliary Systems for the Propulsion of Water and Mucus. Comp. Biochem. Physiol. 1989, 94A, 359–364. [Google Scholar] [CrossRef]
- Hofmann, W.; Asgharian, B. Comparison of Mucociliary Clearance Velocities in Human and Rat Lungs for Extrapolation Modeling. Ann. Occup. Hyg. 2002, 46 (Suppl. 1), 323–325. [Google Scholar]
- Smith, D.J.; Gaffney, E.A.; Blake, J.R. A Viscoelastic Traction Layer Model of Muco-Ciliary Transport. Bull. Math. Biol. 2007, 69, 289–327. [Google Scholar] [CrossRef][Green Version]
- Smith, D.J.; Gaffney, E.A.; Blake, J.R. Modelling Mucociliary Clearance. Respir. Physiol. Neurobiol. 2008, 163, 178–188. [Google Scholar] [CrossRef] [PubMed]
- Sears, P.R.; Davis, W.; Chua, M.; Sheehan, K. Mucociliary Interactions and Mucus Dynamics in Ciliated Human Bronchial Epithelial Cell Cultures. Am. J. Physiol. Lung Cell. Mol. Physiol. 2010, 301, L181–L186. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lee, W.L.; Jayathilake, P.G.; Tan, Z.; Le, D.V.; Lee, H.P.; Khoo, B.C. Muco-Ciliary Transport: Effect of Mucus Viscosity, Cilia Beat Frequency and Cilia Density. Comput. Fluids 2011, 49, 214–221. [Google Scholar] [CrossRef]
- Sears, P.R.; Thompson, K.; Knowles, M.R.; Davis, C.W. Human Airway Ciliary Dynamics. Am. J. Physiol. Lung Cell. Mol. Physiol. 2012, 304, L170–L183. [Google Scholar] [CrossRef] [PubMed]
- Brawley, W. Health Check: What You Need to Know about Mucus and Phlegm. Available online: http://theconversation.com/health-check-what-you-need-to-know-about-mucus-and-phlegm-33192 (accessed on 5 July 2017).
- Chilvers, M.; O’Callaghan, C. Analysis of Ciliary Beat Pattern and Beat Frequency using Digital High Speed Imaging: Comparison with the Photomultiplier and Photodiode Methods. Thorax 2000, 55, 314–317. [Google Scholar] [CrossRef] [PubMed]
- Vanaki, S.M.; Holmes, D.; Jayathilake, P.G.; Brown, R. Three-Dimensional Numerical Analysis of Periciliary Liquid Layer: Ciliary Abnormalities in Respiratory Diseases. Appl. Sci. 2019, 9, 4033. [Google Scholar] [CrossRef]
- Lima, R.; Imai, Y.; Ishikawa, T.; Cano, V. Visualization and Simulation of Complex Flows in Biomedical Engineering; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Gueron, S.; Liron, N. Ciliary Motion Modeling, and Dynamic Multicilia Interactions. Biophys. J. 1992, 63, 1045–1058. [Google Scholar] [CrossRef]
- Gueron, S.; Liron, N. Simulations of 3-dimensional Ciliary Beats and Cilia Interactions. Biophys. J. 1993, 65, 499–507. [Google Scholar] [CrossRef]
- Gueron, S.; Levit-Gurevich, K. Computation of the Internal Forces in Cilia: Application to Ciliary Motion, the Effects of Viscosity, and Cilia Interaction. Biophys. J. 1998, 74, 1658–1676. [Google Scholar] [CrossRef]
- Gueron, S.; Levit-Gurevich, K. Energetic Considerations of Ciliary Beating and the Advantage of Metachronal Coordination. Proc. Natl. Acad. Sci. USA 1999, 96, 12240–12245. [Google Scholar] [CrossRef] [PubMed]
- Peterson, M.A. Geometry of Ciliary Dynamics. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2009, 80, 011923. [Google Scholar] [CrossRef]
- Lindermann, C.B. A Model of Flagellar and Ciliary Functioning which Uses the Forces Transverse to the Axoneme as the Regulator of Dynein Activation. Cell Motil Cytoskelet. 1994, 29, 141–154. [Google Scholar] [CrossRef]
- Hines, M.; Blum, J.J. Three-Dimensional Mechanics of Eukaryotic Flagella. Biophys. J. 1983, 41, 67–79. [Google Scholar] [CrossRef]
- Den Toonder, J.M.J.; Onck, P.R. Artificial Cilia; RSC Publishing: London, UK, 2013. [Google Scholar]
- Shavit, U.; Bar-Yosef, G.; Rosenzweig, R. Modified Brinkman Equation for a Free Flow Problem at the Interface of Porous Surfaces: The Cantor-Taylor Brush Configuration Case. Water Resour. Res. 2002, 38, 1320. [Google Scholar] [CrossRef]
- Liou, W.W.; Lu, M.H. Rough-wall layer modeling using the Brinkman equation. J. Turbul. 2009, 10. [Google Scholar] [CrossRef]
- Cortez, R.; Cummins, B.; Leiderman, K.; Varela, D. Computation of Three-Dimensional Brinkman Flows Using Regularized methods. J. Comput. Phys. 2010, 229. [Google Scholar] [CrossRef]
- Morandotti, M. Self-Propelled Micro-Swimmers in a Brinkman Fluid. J. Biol. Dyn. 2010, 6, 88–103. [Google Scholar] [CrossRef]
- Skrzypacz, P.; Wei, D. Solvability of the Brinkman-Forchheimer-Darcy Equation. J. Appl. Math. 2017, 2017, 7305230. [Google Scholar] [CrossRef]
- Ashgriz, N.; Poo, J. FLAIR: Flux Line-Segment Model for Advection and Interface Reconstruction. J. Comput. Phys. 1991, 93, 449–468. [Google Scholar] [CrossRef]
- Youngs, D. Time-Dependent Multi-Material Flow with Large Distortion. Numer. Method Fluid Dyn. 1982, 53, 63–85. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Mashayek, F.; Ashgriz, N. A Hybrid Finite?ElementÐVolume-of-Fluid Method for Simulating Free Surface Flows and Interfaces. Int. J. Numer. Methods Fluids 1995, 20. [Google Scholar] [CrossRef]
- Stefan, J. Uber die theorie der eisbidung inbesondee uber die eisbindung im polarmeere. Ann. Phys. U Chem. 1891, 42, 269–286. [Google Scholar] [CrossRef]
- Kutluay, S.; Bahadir, A.R.; Özdes, A. The Numerical Solution of One-Phase Classical Stefan Problem. J. Comput. Appl. Math. 1997, 81, 135–144. [Google Scholar] [CrossRef]
- Tilley, A.E.; Walters, M.S.; Shaykhiev, R.; Crystal, R.G. Cilia Dysfunction in Lung Disease. Annu. Rev. Physiol. 2015, 77, 379–406. [Google Scholar] [CrossRef]
- Bennethum, L.S. Multiscale, Hybrid Mixture Theory for Swelling Systems with Interfaces; Lecture Note; University of Colorado: Denver, CO, USA, August 2007. [Google Scholar]
- Bennethum, L.S.; Cushman, J.H. Multiphase, Hybrid Mixture Theory for Swelling Systems—I: Balance Laws. Int. J. Eng. Sci. 1996, 34, 125–145. [Google Scholar] [CrossRef]
- Cushman, J.H.; Bennethum, L.S.; Hu, B.X. A Primer on Upscaling Tools for Porous Media. Adv. Water Resour. 2002, 25, 1043–1067. [Google Scholar] [CrossRef]
- Weinstein, T.F. Three-Phase Hybrid Mixture Theory for Swelling Drug Delivery Systems. Ph.D. Thesis, University of Colorado, Denver, CO, USA, 2005. [Google Scholar]
- Wuttanachamsri, K.; Schreyer, L. Derivation of Fluid Flow due to a Moving Solid in a Porous Medium Framework. arXiv 2020. submitted. [Google Scholar]
- Poopra, S.; Wuttanachamsri, K. The Velocity of PCL Fluid in Human Lungs with Beaver and Joseph Boundary Condition by Using Asymptotic Expansion Method. Mathematics 2019, 7, 567. [Google Scholar] [CrossRef]
- Kwon, Y.W.; Bang, H. The Finite Element Method Using MATLAB; CRC Press LLC: Boca Raton, FL, USA, 1997. [Google Scholar]
- Wuttanachamsri, K.; Schreyer, L. Effects of Cilia Movement on Fluid Velocity: II Numerical Solutions over a Fixed Domain. Transp. Porous Media 2020, 134, 471–489. [Google Scholar] [CrossRef]
- Kammi, C.; Jeangdee, T.; Poohuttum, N.; Wuttanachamsri, K. The Finite Element Method of Stokes-Brinkman Equations for One-Dimensional Domain. In A Special Problem for the Degree of Bachelor of Science, Dapartment of Mathematics; KMITL: Bangkok, Thailand, 2017. [Google Scholar]
- Chamsri, K.; Bennethum, L.S. Permeability of Fluid Flow through a Periodic Array of Cylinders. Appl. Math. Model. 2015, 39, 244–254. [Google Scholar] [CrossRef]
- Matsui, H.; Grubb, B.; Tarran, R.; Randell, S.; Gatzy, J.; Davis, C.; Boucher, R. Evidence for Periciliary Liquid Layer Depletion, Not Abnormal Ion Composition, in the Pathogenesis of Cystic Fibrosis Airways Disease. Cell 1998, 95, 1005–1015. [Google Scholar] [CrossRef]
- Griesenbach, U.; Soussi, S.; Larsen, M.B.; Casamayor, I.; Dewar, A.; Regamey, N.; Bush, A.; Shah, P.L.; Davies, J.C.; Alton, E.W.F.W. Quantification of Periciliary Fluid Height in Human Airway Biopsies Is Feasible, but Not Suitable as a Biomarker. Am. J. Respir. Cell Mol. Biol. 2011, 44, 309–315. [Google Scholar] [CrossRef]


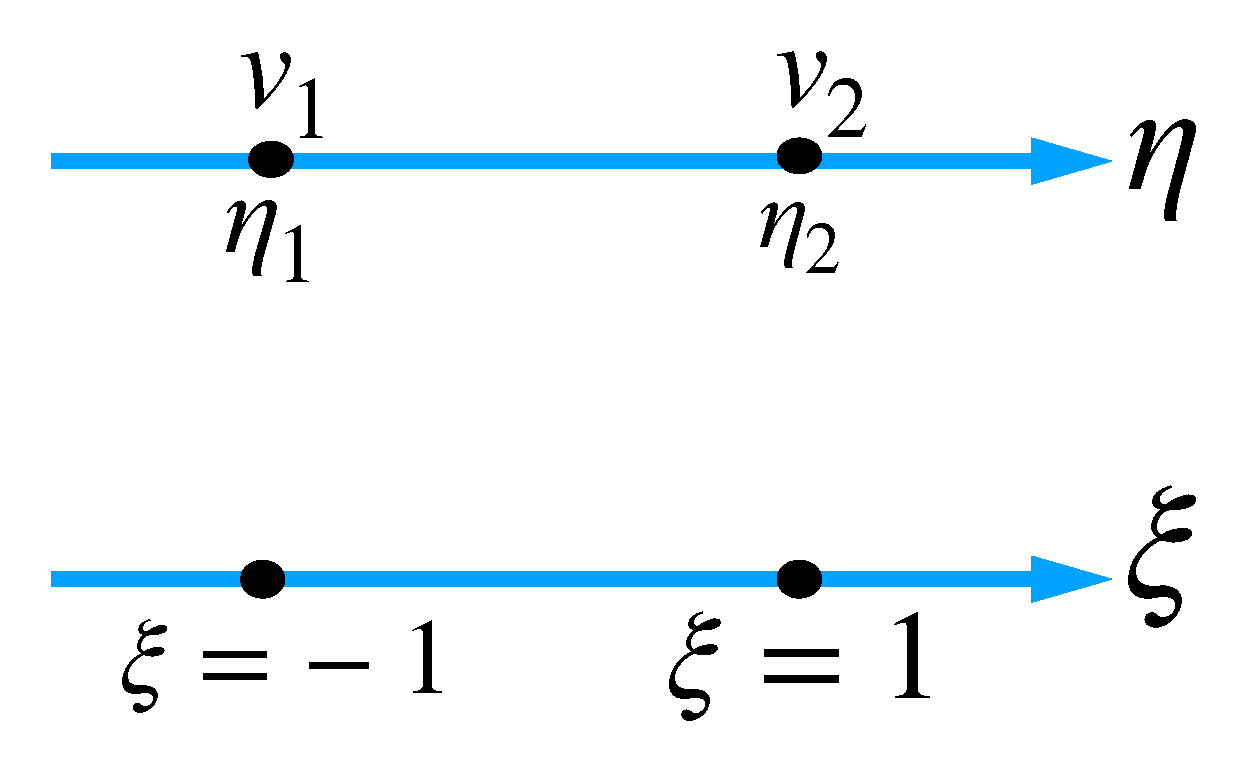




| Number of Nodes along z-Axis | -Norm Errors |
|---|---|
| 10 | 4.0837 |
| 20 | 1.3711 |
| 100 | 0.1184 |
| 400 | 0.0148 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wuttanachamsri, K. Free Interfaces at the Tips of the Cilia in the One-Dimensional Periciliary Layer. Mathematics 2020, 8, 1961. https://doi.org/10.3390/math8111961
Wuttanachamsri K. Free Interfaces at the Tips of the Cilia in the One-Dimensional Periciliary Layer. Mathematics. 2020; 8(11):1961. https://doi.org/10.3390/math8111961
Chicago/Turabian StyleWuttanachamsri, Kanognudge. 2020. "Free Interfaces at the Tips of the Cilia in the One-Dimensional Periciliary Layer" Mathematics 8, no. 11: 1961. https://doi.org/10.3390/math8111961
APA StyleWuttanachamsri, K. (2020). Free Interfaces at the Tips of the Cilia in the One-Dimensional Periciliary Layer. Mathematics, 8(11), 1961. https://doi.org/10.3390/math8111961




