Quasi-Probability Husimi-Distribution Information and Squeezing in a Qubit System Interacting with a Two-Mode Parametric Amplifier Cavity
Abstract
1. Introduction
2. Physical Model
3. Husimi Distribution (HD)
3.1. Husimi Function
3.2. Wehrl Entropy
4. Squeezing Phenomenon
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Mohamed, A.-B.A. Quantum correlation of correlated two qubits interacting with a thermal field. Phys. Scr. 2012, 85, 055013. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7. [Google Scholar] [CrossRef]
- Pljonkin, A.P. Vulnerability of the Synchronization Process in the Quantum Key Distribution System. Int. J. Cloud Appl. Comput. 2019, 9, 50. [Google Scholar] [CrossRef]
- Pljonkin, A.; Rumyantsev, K.; Singh, P.K. Synchronization in Quantum Key Distribution Systems. Cryptography 2017, 1, 18. [Google Scholar] [CrossRef]
- Puigibert, M.l.G.; Askarani, M.F.; Davidson, J.H.; Verma, V.B.; Shaw, M.D.; Nam, S.W.; Lutz, T.; Amaral, G.C.; Oblak, D.; Tittel, W. Nonclassical Effects Based on Husimi Distributions in Two Open Cavities Linked by an Optical Waveguide. Phys. Rev. Res. A 2020, 2, 013039. [Google Scholar] [CrossRef]
- Sete, E.A.; Eleuch, H. High-efficiency quantum state transfer and quantum memory using a mechanical oscillator. Phys. Rev. A 2015, 91, 032309. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef]
- Bennett, C.H.; DiVincenzo, D.P. Quantum information and computation. Nature 2000, 404, 247. [Google Scholar] [CrossRef]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Shannon, C.E.; Weaver, W. Mathematical Theory of Communication; Urbana University Press: Chicago, IL, USA, 1949. [Google Scholar]
- Obada, A.-S.F.; Hessian, H.A.; Mohamed, A.-B.A. Effects of a phase-damping cavity on entanglement and purity loss in two-qubit system. Opt. Commun. 2008, 281, 5189. [Google Scholar] [CrossRef]
- Husimi, K. Some properties of the Husimi function. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264. [Google Scholar]
- Yazdanpanah, N.; Tavassoly, M.K.; Juárez-Amaro, R.; Moya-Cessa, H.M. Reconstruction of quasiprobability distribution functions of the cavity field considering field and atomic decays. Opt. Commun. 2017, 400, 69. [Google Scholar] [CrossRef]
- Miller, C.A.; Hilsenbeck, J.; Risken, H. Asymptotic approximations for the Q function in the Jaynes-Cummings model. Phys. Rev. A 1992, 46, 4323. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Coherence and information dynamics of a Λ-type three-level atom interacting with a damped cavity field. Eur. Phys. J. Plus 2017, 132, 75. [Google Scholar] [CrossRef]
- Hessian, H.A.; Mohamed, A.-B.A. Quasi-Probability Distribution Functions for a Single Trapped Ion Interacting with a Mixed Laser Field. Laser Phys. 2008, 18, 1217–1223. [Google Scholar] [CrossRef]
- Furusawa, A.; Sørensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional Quantum Teleportation. Science 1998, 282, 706. [Google Scholar] [CrossRef]
- Sorensen, A.; Molmer, K. Spin-Spin Interaction and Spin Squeezing in an Optical Lattice. Phys. Lett. A 1999, 83, 2274. [Google Scholar] [CrossRef]
- Flouris, K.; Jimenez, M.M.; Debus, J.-D.; Herrmann, H.J. Landau levels in wrinkled and rippled graphene sheets. Phys. Rev. B 2018, 98, 155419. [Google Scholar] [CrossRef]
- Jabri, H.; Eleuch, H. Quantum fluctuations inside a microcavity with a pair of quantum wells: Linear regime. JOSA B 2018, 35, 2317. [Google Scholar] [CrossRef]
- Qasymeh, M.; Eleuch, H. Quantum microwave-to-optical conversion in electrically driven multilayer graphene. Opt. Express 2019, 27, 5945. [Google Scholar] [CrossRef]
- Fang, M.F.; Zhou, P.; Swain, S. Entropy squeezing of an atom with a k-photon in the Jaynes-Cummings model. J. Mod. Opt 2000, 47, 1043. [Google Scholar] [CrossRef]
- Wineland, D.J.; Bollinger, J.J.; Itano, W.M.; Heinzen, D.J. Squeezed atomic states and projection noise in spectroscopy. Phys. Rev. A 1994, 50, 67. [Google Scholar] [CrossRef]
- Hillery, M. Quantum cryptography with squeezed states. Phys. Rev. A 2000, 61, 022309. [Google Scholar] [CrossRef]
- Sete, E.A.; Eleuch, H.; Das, S. Semiconductor cavity QED with squeezed light: Nonlinear regime. Phys. Rev. A 2011, 84, 053817. [Google Scholar] [CrossRef]
- Korbicz, J.K.; Gühne, O.; Lewenstein, M.; Häffner, H.; Roos, C.; Blatt, R. Generalized spin-squeezing inequalities in N-qubit systems: Theory and experiment. Phys. Rev. A 2006, 74, 052319. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H.; Obada, A.-S.F. Quantum effects in two-qubit systems interacting with two-mode fields: Dissipation and dipole-dipole interplay effects. Results Phys. 2020, 17, 103019. [Google Scholar] [CrossRef]
- Yu, M.; Fang, M. Steady and optimal entropy squeezing of a two-level atom with quantum-jump-based feedback and classical driving in a dissipative cavity. Quantum Inf. Process. 2016, 15, 4175. [Google Scholar] [CrossRef]
- Liu, X.-J.; Luo, A.; Peng, Z.-H.; Jia, C.-X.; Jiang, C.-L.; Zhou, B.-J. Generation and Preparation of the Sustained Optimal Entropy Squeezing State of a Motional Atom Inside Vacuum Cavity. Int. J. Theor. Phys. 2018, 57, 138. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Abdalla, M.S.; Khalil, E.M. Statistical properties of two-mode parametric amplifier interacting with a single atom. Physica A 2004, 336, 433. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Ahmed, M.M.A.; Faramawy, F.K.; Khalil, E.M. Entropy and entanglement of the nonlinear Jaynes-Cummings model. Chin. J. Phys. 2004, 42, 79. [Google Scholar]
- Golkar, S.; Tavassoly, M.K. Atomic motion and dipole–dipole effects on the stability of atom-atom entanglement in Markovian/non-Markovian reservoir. Mod. Phys. Lett. 2019, 34, 1950077. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A. Non-local correlations via Wigner Yanase skew information in two SC-qubit having mutual interaction under phase decoherence. Eur. Phys. J. D 2017, 71, 261. [Google Scholar] [CrossRef]
- Eberly, J.H.; Narozhny, N.B.; Mondragon, J.J.S. Periodic Spontaneous Collapse and Revival in a Simple Quantum Model. Phys. Rev. Lett. 1980, 44, 1323. [Google Scholar] [CrossRef]
- Brune, M.; Raimond, J.M.; Goy, P.; Davidovich, L.; Haroche, S. Realization of a two-photon maser oscillator. Phys. Rev. Lett. 1987, 59, 1899. [Google Scholar] [CrossRef]
- Louisell, W.H. Coupled Mode and Parametric Electronics; Wiley: New York, NY, USA, 1960. [Google Scholar]
- Kumar, S.; Mehta, C.L. Theory of the interaction of a single-mode radiation field with N two-level atoms. II. Time evolution of the statistics of the system. Phys. Rev. A 1981, 24, 1460. [Google Scholar] [CrossRef]
- Kuang, L.M.; Tong, Z.Y.; Oyang, Z.W.; Zeng, H.S. Decoherence in two Bose-Einstein condensates. Phys. Rev. A 2000, 61, 013608. [Google Scholar] [CrossRef]
- Mohamed, A.-B.; Eleuch, H. Non-classical effects in cavity QED containing a nonlinear optical medium and a quantum well: Entanglement and non-Gaussanity. Eur. Phys. J. D 2015, 69, 191. [Google Scholar] [CrossRef]
- Redwan, A.; Abdel-Aty, A.-H.; Zidan, N.; El-Shahat, T. Dynamics of the entanglement and teleportation of thermal state of a spin chain with multiple interactions. Chaos 2019, 29, 013138. [Google Scholar] [CrossRef]
- Abdalla, M.S.; Obada, A.S.-F.; Khalil, E.M.; Mohamed, A.-B.A. Wehrl entropy information and purity of a SC charge qubit interacting with a lossy cavity field. Solid State Commun. 2014, 184, 56. [Google Scholar] [CrossRef]
- Milburn, G.J. Intrinsic decoherence in quantum mechanics. Phys. Rev. A 1991, 44, 5401. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A. Pairwise quantum correlations of a three-qubit XY chain with phase decoherence. Quantum Inf. Process. 2013, 12, 1141. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A. Bipartite non-classical correlations for a lossy two connected qubit-cavity systems: Trace distance discord and Bell’s non-locality. Quantum Inf. Process. 2018, 17, 96. [Google Scholar] [CrossRef]
- Courty, J.-M.; Spälter, S.; König, F.; Sizmann, A.; Leuchs, G. Noise-free quantum-nondemolition measurement using optical solitons. Phys. Rev. A 1998, 58, 1501. [Google Scholar] [CrossRef]
- Barut, A.O.; Girardello, L. New coherent states associated with non-compact groups. Commun. Math. Phys. 1971, 21, 41. [Google Scholar] [CrossRef]
- Vieira, V.R.; Sacramento, P.D. Generalized Phase-Space Representatives of Spin-J Operators in Terms of Bloch Coherent States. Ann. Phys. 1995, 242, 188. [Google Scholar] [CrossRef]
- Zyczkowski, K. Localization of Eigenstates & Mean Wehrl Entropy. Physica E 2001, 9, 583. [Google Scholar]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Quasi-probability information in a coupled two-qubit system interacting non-linearly with a coherent cavity under intrinsic decoherence. Sci. Rep. 2020, 10, 13240. [Google Scholar] [CrossRef]
- Van Enk, S.J.; Kimble, H.J. Quantum Information Processing in Cavity-QED. Quant. Inform. Comput. 2002, 2, 1. [Google Scholar]
- Obada, A.-S.F.; Mohamed, A.-B.A. Erasing information and purity of a quantum dot via its spontaneous decay. Solid State Commun. 2011, 151, 1824. [Google Scholar] [CrossRef]
- Sanchez-Ruis, J. Improved bounds in the entropic uncertainty and certainty relations for complementary observables. Phys. Lett. A 1995, 201, 125. [Google Scholar] [CrossRef]
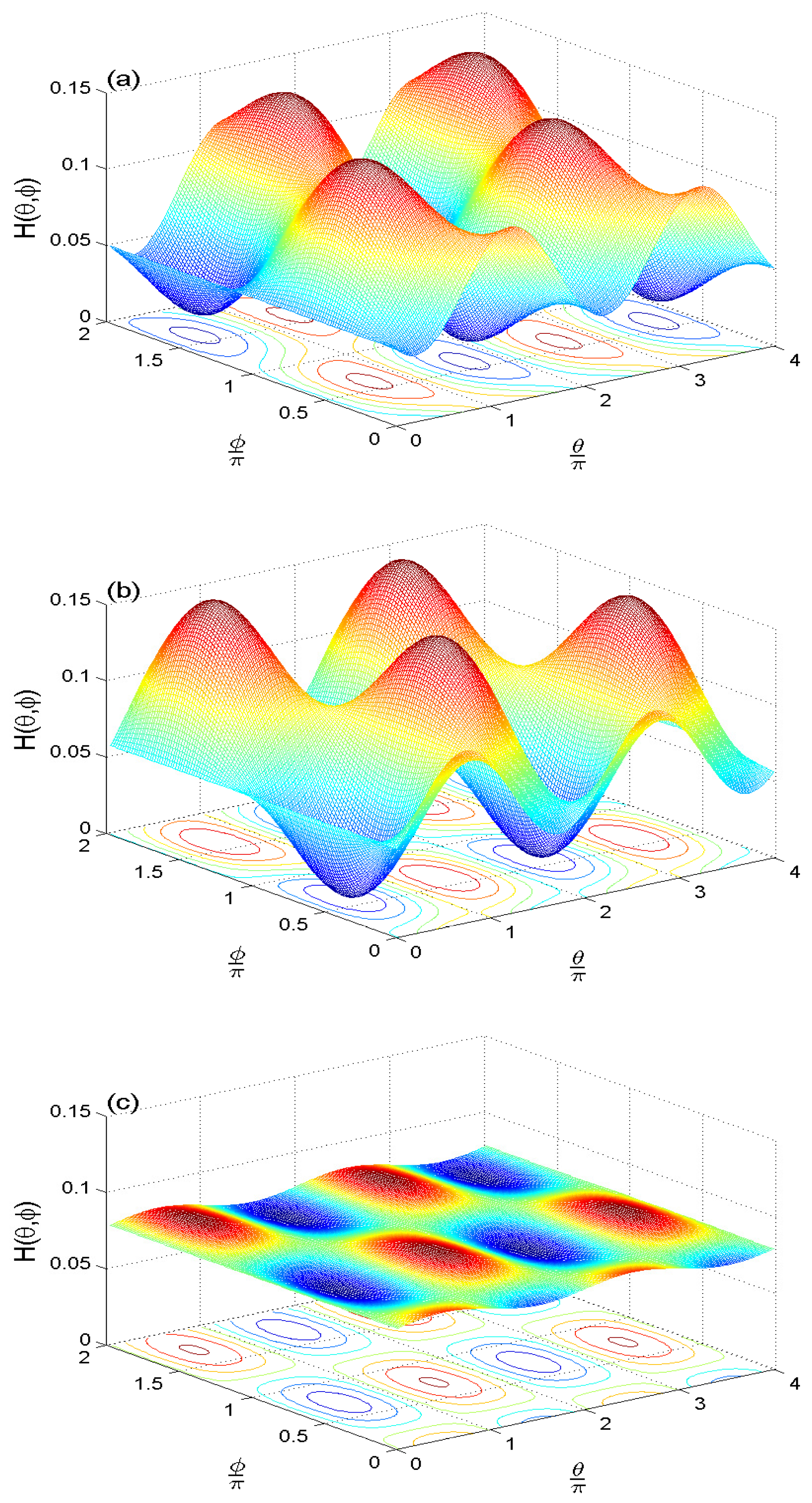
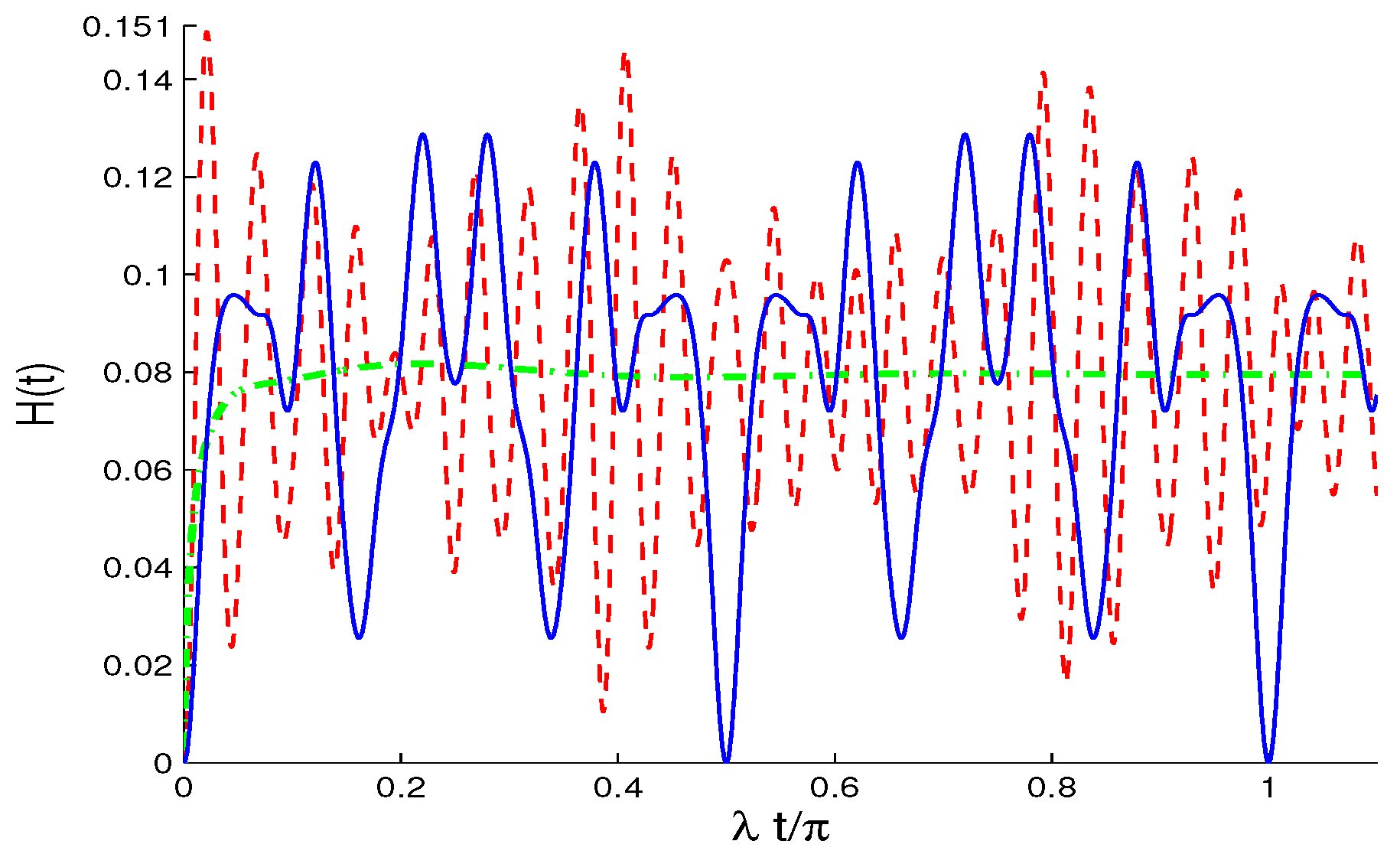
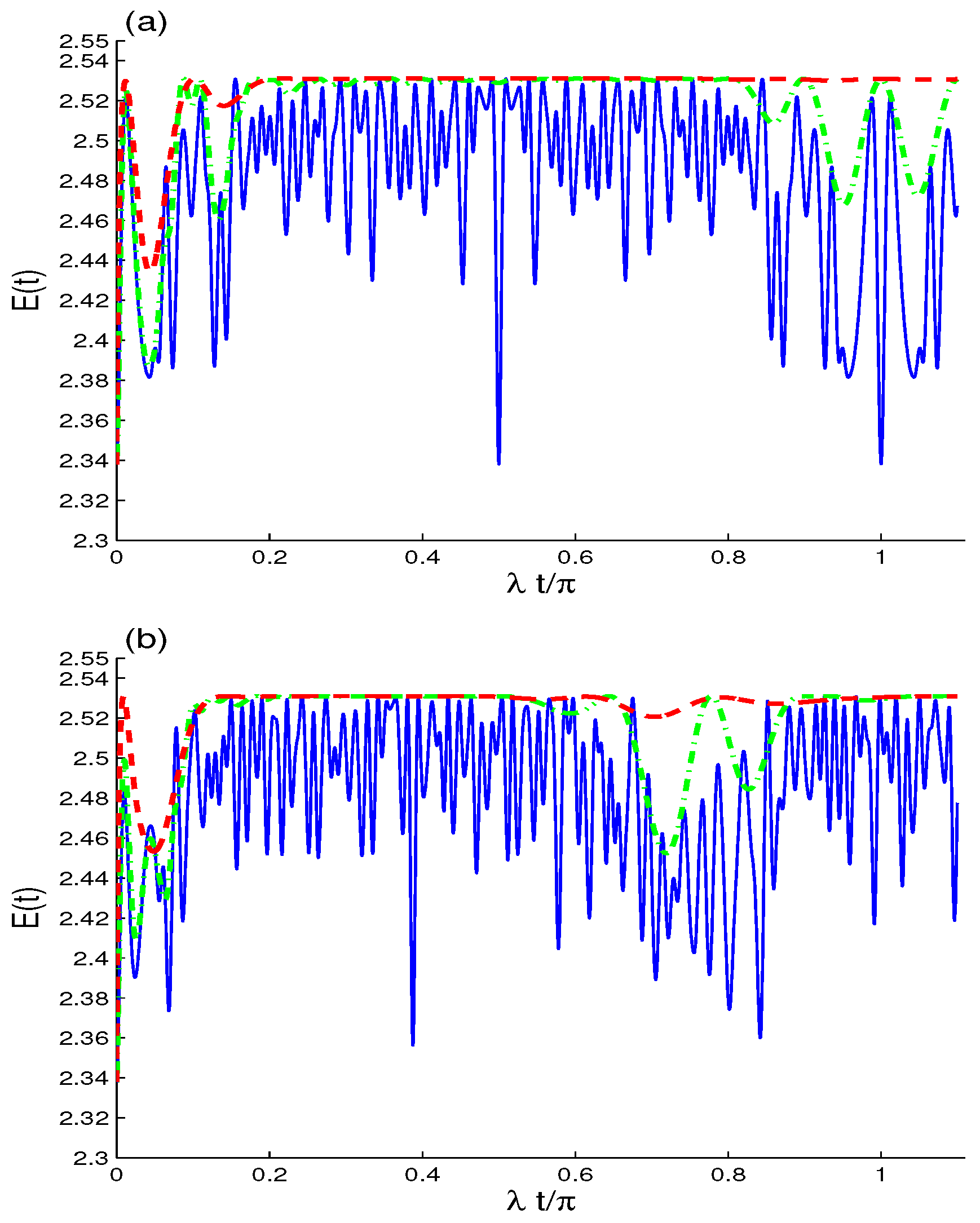
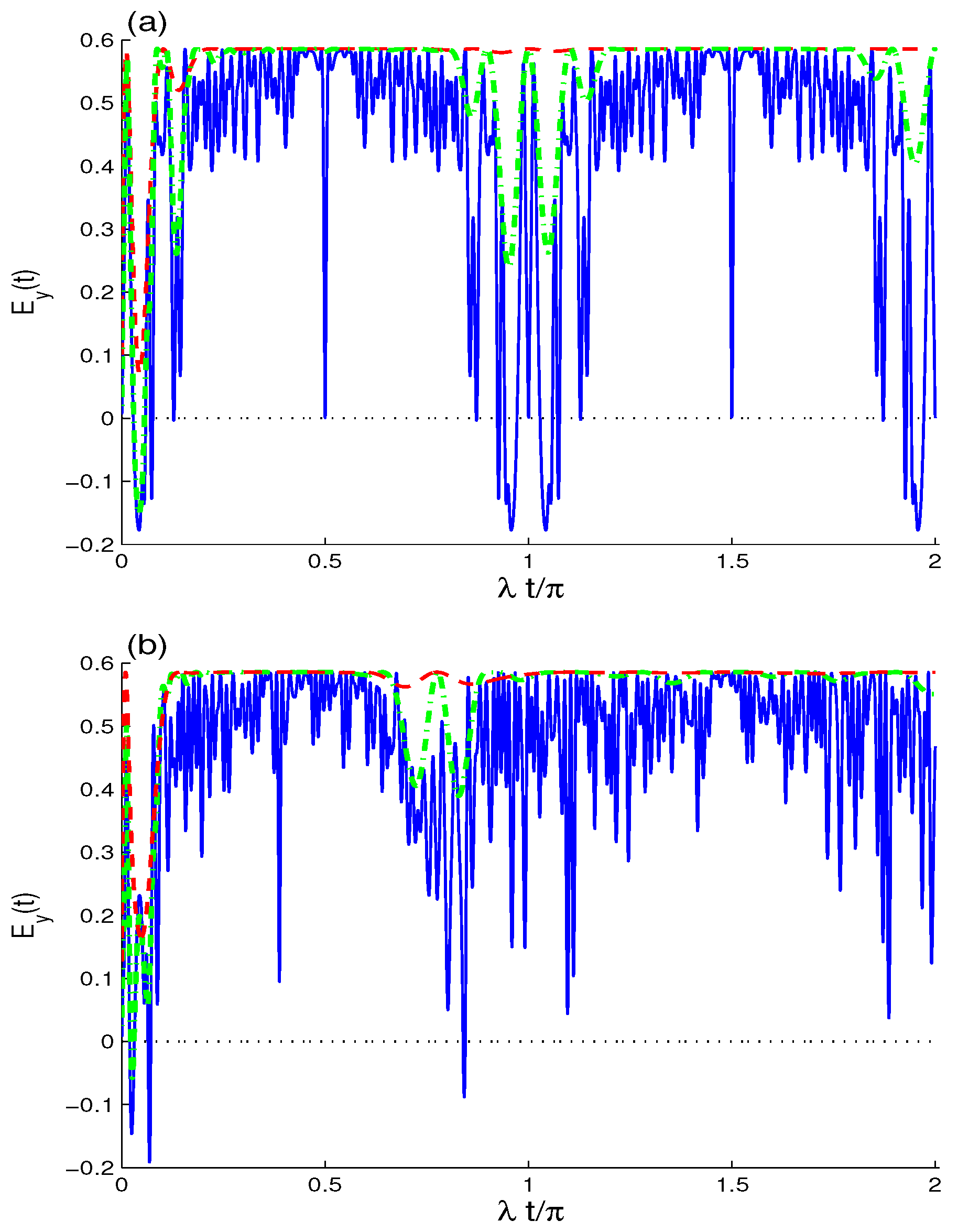
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalil, E.M.; Mohamed, A.-B.A.; Obada, A.-S.F.; Eleuch, H. Quasi-Probability Husimi-Distribution Information and Squeezing in a Qubit System Interacting with a Two-Mode Parametric Amplifier Cavity. Mathematics 2020, 8, 1830. https://doi.org/10.3390/math8101830
Khalil EM, Mohamed A-BA, Obada A-SF, Eleuch H. Quasi-Probability Husimi-Distribution Information and Squeezing in a Qubit System Interacting with a Two-Mode Parametric Amplifier Cavity. Mathematics. 2020; 8(10):1830. https://doi.org/10.3390/math8101830
Chicago/Turabian StyleKhalil, Eied. M., Abdel-Baset. A. Mohamed, Abdel-Shafy F. Obada, and Hichem Eleuch. 2020. "Quasi-Probability Husimi-Distribution Information and Squeezing in a Qubit System Interacting with a Two-Mode Parametric Amplifier Cavity" Mathematics 8, no. 10: 1830. https://doi.org/10.3390/math8101830
APA StyleKhalil, E. M., Mohamed, A.-B. A., Obada, A.-S. F., & Eleuch, H. (2020). Quasi-Probability Husimi-Distribution Information and Squeezing in a Qubit System Interacting with a Two-Mode Parametric Amplifier Cavity. Mathematics, 8(10), 1830. https://doi.org/10.3390/math8101830




