Abstract
Life in today’s world is characterized by complexity and rapid change. Twenty-first century skills and especially mathematical understanding are supposed to crucially contribute to meeting the demands of our world since mathematics offers strategies to structure or simplify complex problems. An open question is which teaching practices are appropriate to provide all students with such skills and to broaden the participation of underprivileged students. The present article explores these aspects by focusing on complex tasks, a practice that can be considered highly accepted in the context of mathematics education all over the world. We will concentrate on the perspective of the German mathematics education community as the foundation of our considerations. Based on an analytical investigation of mathematical literacy and twenty-first century skills (such as creativity, critical thinking, or problem-solving), we will address central ideas and characteristics of complex mathematical tasks. To complement the analytical approach, we will illustrate their characteristics as well as possible intersections with twenty-first century skills by presenting an elementary school teaching experiment. Finally, we will critically discuss the potentials and pitfalls of complex mathematical tasks from an abstract perspective and conclude by debating practical consequences for organizing mathematical learning-teaching-processes.
1. Introduction
Modern society in the twenty-first century is characterized by complexity and rapid change. The problems we encounter in daily life are increasingly diverse and demand a variety of problem-solving skills. Moreover, the twenty-first century world is “characterized by numbers, numerically based arguments and data represented and misrepresented in a number of different ways” [1] (p. 8). This got more obvious than ever in the corona crisis of 2020, when the Daily News offered a variety of diagrams (with a linear or logarithmic scale) as well as infection, mortality, and recovery rates.
Making sense of this increasingly complex world and dealing with its challenges require a variety of tools, skills, and approaches. Mathematical understanding can crucially contribute to meeting the demands of our world today since mathematics offers strategies to structure or simplify complex problems, especially if we see mathematics as a way of “solving problems in an adaptive, not arbitrary, and coherent fashion” [2] (p. xiii). Providing students with opportunities to acquire those skills and tools is a basic goal of mathematics education and the core meaning of mathematical literacy.
In that way, mathematics education has to enable students to solve their real-life problems and to participate as critical, responsible, and active future citizens of society [3]. This, in turn, requires learning with understanding and not simply practicing and using a series of techniques over and over again [2]. The concept of mathematical literacy aims at such learning with understanding and the flexibility in putting mathematics to use in novel intra- or extra-mathematical contexts and situations. Furthermore, the concept is associated with education for the general public rather than with specialized academic training for a selected target group [4]. If we are serious about pursuing mathematical literacy for all students, practices and activities have to be found that (a) enable students at different levels to engage with a certain mathematical concept and (b) promote the acquisition of a variety of skills and knowledge.
Within the realm of mathematics education, it is, in particular, mathematical complexity that is considered an approach to enable rich mathematical activities for all children as one common subject. In Germany, such activities have gained popularity especially in the last decade. One reason for this development is the declared strive for an inclusive society and inclusive school settings and the perceived diversification of society and, therefore, of the students. While the number of publications and materials promoting this kind of teaching and learning mathematics has grown rapidly in the last years, there is a lack of academic discussion on their potentials and limitations. The aim of this paper is to address this gap. We will start with an investigation of mathematical literacy and twenty-first century skills, followed by an analysis of the core idea of complex tasks (and similar concepts). On that basis, we will give insight into a teaching experiment from grades 3 and 4 (students aged 8 to 11) that shows how mathematical substance can serve as a common ground for all students to promote equitable teaching in mathematics classrooms. We argue that dynamic and potential-orientated teaching practices (rather than calculus- or deficit-oriented processes) can motivate students both to engage with mathematics profoundly and to acquire critical twenty-first century skills. Finally, we will discuss the potentials and pitfalls of such teaching practices from an analytical point of view.
2. Mathematical Literacy and Twenty-First Century Skills
The term mathematical literacy first occurred in 1944 in the US [4]. Therefore, it is neither a new concept nor specifically related to the twenty-first century. Nevertheless, since the concept was first used as a framework for TIMSS (Trends in International Mathematics and Science Study) in 1994 and later also for PISA (Programme for International Student Assessment), it gained momentum within the field of mathematics education, especially in the last 25 years. Niss and Jablonka state that “meanings and usages associated with the notion of mathematical literacy and its relatives have not yet reached a stage of universally accepted conceptual clarification nor of general agreement about their place and role” [4] (p. 395). However, some aspects can be identified as basic assumptions or commonalities in the different interpretations of the notion of mathematical literacy (and related concepts). On the one hand, they do have in common the endeavor to challenge the image of learning mathematics as solely knowing facts and rules and mastering procedures by rote. Instead, mathematics educators stress abilities and skills of using mathematics flexibly. On the other hand, mathematical literacy is associated with a certain generality, inclusiveness, social justice, and democratic participation: basic mathematics education needs to be ensured for as many students as possible, which allows individuals to make sense of, participate in, and contribute to the world they live in. Niss and Jablonka state that considering combined phrases, such as statistical literacy or computer literacy, the addition of literacy may suggest some level of critical understanding [4]. Therefore, even though a generally accepted definition or description is still missing, there is at least a consensus on the main ideas.
Compared to mathematical literacy, the notion of twenty-first century skills is even less a universally accepted concept. The general meaning behind the term is literally a set of abilities supposed to be needed to navigate in the current times. Attempts of determining those abilities have been made from different perspectives, such as governments, educators, or businesses. Depending on the perspective, differences can be found in the main focus of conceptualizing twenty-first century skills. An idea that can be identified in many relevant documents is the fostering of skills that are seen to be relevant to succeed in and to meet the demands of the labor market in the so-called information age. Which skills are exactly seen as relevant often stays vague.
According to Ärlebäck and Albarracín, no consensus has yet been reached, although there are numerous attempts in the literature trying to establish and to specify a set of skills and knowledge. Additionally, even the notions used vary between contexts [5]. Maaß et al. make us aware that stakeholders from different sectors “are emphasizing the urgent need to identify and improve the competencies young people will require to meet the demands of their futures” [6] (p. 870). These competencies have been identified as lifelong learning competencies, key competencies, or twenty-first century skills. The different notions show great commonalities and illustrate the lack of a widely accepted concept. Binkley et al. analyzed twelve twenty-first century skills frameworks from different countries and identified ten skills grouped into four broad categories (Table 1) [7].

Table 1.
Twenty-first century skills [7] (p. 36 italics in original).
Maaß et al. state that there is no definitive catalog of so-called twenty-first century competencies but conclude from the comparison of different conceptualization: “Thus, adaptable and flexible critical thinking and reasoning, the capacity to search for and interpret information, to communicate and collaborate with others within the contexts of cultural, and social and ethical obligations, are key aspects of twenty-first century skills” [6] (p. 874). To summarize the current state of research, although there is no commonly used framework, certain core skills can be detected in all conceptualizations.
Comparing the two concepts (mathematical literacy and twenty-first century skills), intersections become apparent as well as differences in the general assumptions. A rather obvious difference is the focus of mathematical literacy on mathematical skills and competencies based on mathematical means, while twenty-first century skills are rather subject independent. Mathematics education, however, can contribute essentially to preparing students for the society of the future, especially due to the position of mathematics in a digitized society. Therefore, Gravemeijer et al. argue that twenty-first century skills should be adopted as goals of mathematics education [8]. Rizki and Priatna even argue that mathematical literacy is regarded as a twenty-first century skill [9]. They conclude from a literature review that mathematical literacy is one of the components needed to construct the twenty-first century skills.
According to the Curriculum and Assessment Policy Statement on Mathematical Literacy of South Africa, “competencies developed through Mathematical Literacy allow individuals to participate in and contribute to the twenty-first century world” [1] (p. 8). Thus, strong interrelationships become apparent. Mathematical literacy appears as a necessary basis for developing twenty-first century skills. This does not indicate any order or hierarchy regarding mathematics education. Rather, we argue that fostering mathematical literacy in school can contribute largely to the development of twenty-first century skills.
However, as the definitions of mathematical literacy and twenty-first century skills change over time and context and they are not fixed frameworks, it is hardly possible to determine their relation exactly. Taking the historic development into account, it can be argued that mathematical literacy is rather used as a (flexible) concept to meet the demands of respective times, while twenty-first century skills relate specifically to the actual circumstances of today’s world. Another difference we perceive in the focus of both concepts is that twenty-first century skills rather relate to requirements of coping with daily life and working life issues. Although this includes citizenship, social, and cultural responsibility, the orientation of mathematical literacy on democratic participation and inclusiveness seems less relevant in the frameworks of twenty-first century skills. Especially, the inclusive approach of mathematics education that can be identified in conceptualizations of mathematical literacy (i.e., a concept of mathematics education enabling all students to acquire mathematically relevant skills) is not a dominant factor in twenty-first century skills.
To conclude, both mathematical literacy and twenty-first century skills are rather vague notions. While the official PISA 2018 Mathematics Framework entails at least a frequently and internationally cited definition, there is not yet such a reference point for twenty-first century skills [10]. A common core of both notions seems to be the capacity to employ mathematics in a variety of contexts which requires a certain flexibility, creativity, as well as problem-solving skills. This includes the assumption that not only content knowledge is of relevance but also a range of skills and competencies (usually expressed in the form of verbs) ought to be applied.
As often suggested e.g., [6] and as we state in the very first sentence of this article, the twenty-first century is particularly characterized by complexity and rapid change. The role of education is to provide students and future citizens with knowledge, skills, and abilities to cope with the demands of the micro and macro worlds they live in. If we assume that growing complexity and rapid change are essential characteristics of the world today and the near future, we have to find ways in mathematics education (i.e., methods, tasks, circumstances, etc.) to prepare students adequately. Maaß et al. state as well that there is considerable acceptance of the need to develop the skills of young people in preparation for all aspects of twenty-first century life but that there is currently limited practical advice to teachers about how to promote these capabilities [6]. We argue that complex mathematical tasks might be one tool for that purpose.
3. Central Ideas and Characteristics of Complex Mathematical Tasks
The ways to implement complexity in mathematics education are diverse and to relate to methods or learning arrangements, especially to task design. In contrast to common isolated and constrained tasks that allow only certain solutions and predetermined approaches, complex and substantial mathematical activities ensure a certain degree of openness and freedom. Therefore, complex tasks are tightly associated with open problems.
In an article of 1995, Silver identified a growth of interest in the use of open problems, in particular to increase problem-solving activities in mathematics education [11]. Especially in the late 1990s and the early 2000s, the number of research papers increased internationally as well as in Germany. This upturn within the academic discourse has not endured until today. However, we interpret this development not as a decrease of interest in open tasks but rather as a shift to an axiomatic imperative within the mathematics education discourse.
In spite of this development, it can still be observed that many teachers (at least in Germany) continue to reflect a subjective picture of mathematical teaching-learning processes following traditional calculus-oriented views e.g., [12] and that open learning arrangements are integrated into mathematics classrooms rather sporadically e.g., [13] This might be due to beliefs of teachers about learning mathematics that have been developed within their professional biographies or due to a lack of empirical evidence on the benefits of exploratory and active learning (in summary, e.g., [14]). The claimed advantage of open problems is that they are supposed to allow more individuality in the learning process, for example in terms of ways of solution, the use of manipulatives, kinds of notation, problems to solve, or further questions emerging from a given one e.g., [15]. Silver emphasized differences in the meaning of open problems in the discipline of mathematics and the context of mathematical pedagogy [11]. He described different varieties of open problems by referring to possible meanings of openness: with respect to the solution method, regarding the interpretation of the problem or its plausible solutions, or such kind of openness that invite other problems as a natural follow-up to the given problem [11]. Greefrath makes us aware that the terms open tasks and open problems are not used consistently within the literature and that some authors even distinguish between both terms [16].
It is not only the kind of openness but also the degree of openness that can vary. According to Greefrath, different researchers have provided classifications of open tasks which mainly categorize the tasks in terms of clarity of the starting point, the target state, and the transformation (that transfers the starting point into the target state) [16]. The more these aspects are vague, the more open is the task. It needs to be stressed that open tasks are not to be equated with realistic tasks or word problems. Open tasks can certainly be drawn from real-world contexts but can also be purely mathematic.
The implementation of open tasks is expected to enable a more student-centered teaching as they imply inquiry-based and problem-centered learning. This kind of mathematics education requires students to solve problems, to handle mathematical structures, or to regard real-life contexts by “mathematical eyes”. Therefore, open tasks are supposed to promote fundamental mathematical experiences. Silver argues that “open problems and their associated processes are central to the discipline of mathematics and the nature of mathematical thinking both as it occurs within mathematics itself and as it occurs in the application of mathematics to solve applied problems” [11] (p. 67). Additionally, student-centered teaching approaches entail a constructivist perspective, assuming that understanding is based on students’ both exploratory and active learning.
While there is no fixed definition of complex tasks, in our understanding, they imply different kinds of openness and are in that way complex. Openness is given in terms of the solution method, plausible solutions, the profundity, the use of materials and visualization tools, or the creation of follow-up problems. This requires a certain degree of mathematical substance. Although complex tasks imply a certain openness, they are not necessarily the same as open tasks. According to the different categorizations of open tasks, complex tasks are different from tasks that are simply lacking a clear instruction or certain information. Complex tasks imply openness in a variety of ways by simultaneously offering a low threshold, so that all students can access the task, without being overwhelmed. The complexity is rather given by a rich mathematical substance that offers potential for individually guided activities with options of going more into depths or of working on follow-up problems. Therefore, according to Krauthausen, complex is not necessarily the same as complicated [17]. On the contrary, it is especially the mathematical substance that enables “a personal access at a certain point for the individual student” [17] (p. 331), while not all students have to master all details of the content. The individual way of working on one big task, which is the same starting point for the whole class, offers a natural potential for interaction and exchange among the students. The presentation of a solution is therefore not an end in itself or an explanation for those who have not solved the task themselves successfully.
Following this understanding, complex tasks broadly correspond to the concept of open-ended math activities (Australia, see [18]), so-called low floor, high ceiling tasks (Canada/USA, see, e.g., [19,20]) or learning environments (Germany, see, e.g., [21]). These concepts share the idea that the task is accessible to all students and can be solved in different ways. Additionally, the mathematical problems should be challenging but accessible to a much broader spectrum of students than typical exercises. The problem, the working process, and the exchange among the students are of primary importance, while the answer or solution is rather subordinate. Therefore, such tasks aim at a rich mathematical discourse among the students. The extra dimension wide walls might extend the concept of low floor, high ceiling to avoid the impression that there is only a single path from floor to ceiling.
According to Gadanidis and Hughes, who call those learning activities big math ideas, the low mathematical floor allows students to engage even with minimal mathematical knowledge [19]. The high mathematical ceiling offers opportunities to extend their mathematical thinking even to concepts and relationships beyond their grade level. In this way, the different ideas and concepts have in common that they are suitable for diverse mathematics classrooms, i.e., students with different needs, at different levels, with different ways of thinking, and individual resources within one classroom.
In Germany, the general approach behind complex tasks or learning environments is labeled natural differentiation and gained popularity in the last two decades, especially due to approaches that enable (a content-related) participation for all students. The meaning of natural refers to holistic and complex problems that offer by nature various levels of demands and “naturally allow to develop a momentum of their own, giving room for the inherent dynamism of the topic” [17] (italics added). Even though there is no unambiguous and fixed definition of what natural differentiation encompasses, complexity is a constitutive feature. Complexity refers to a holistic and rich mathematical substance, which allows for a large spectrum of discoveries as well as profound mathematical insights. Students, therefore, have the opportunity to discover structures and patterns themselves that form the necessary basis for understanding the nature of mathematics. This argument complements the assumption of Silver that working on open problems is central to the discipline of mathematics and the nature of mathematical thinking [11]. Additionally, the holistic nature facilitates access for learners with different capabilities, which is in line with the idea of low floors.
A second significant feature of natural differentiation, which closely relates to the first, is that all students work on the same task or problem. Therefore, this way of arranging mathematics classrooms is opposed to strictly individualized learning where every student gets his or her own tasks and materials to work on. While strictly individualized classroom arrangements allow for a learning that is tailored to the single student to the maximum, it simultaneously runs danger to neglect social learning and the negotiation of mathematical meaning. Social learning, on the other side, is reliant on communication and requires that several students engage with the same content [17]. One common task for the whole group, as it is the case with complex tasks, ensures interaction. As the approaches and solutions to complex tasks are likely to differ within the class, the presentation of the students’ work goes beyond a sole verbalization. A rich discussion about mathematics can only be initiated by a variety of students’ findings. In addition, the interaction and exchange among students not only promote content-related knowledge but also contributes to the development of process-related competencies such as mathematical reasoning; communicating in, with, and about mathematics; or representing mathematics [22].
In sum, task-related complexity can promote the acquisition of various skills, strategies, and (mental) approaches that are necessary to deal with larger, more challenging issues [23]. In that way, implementing complex tasks in the mathematics classroom appears promising to prepare all students for the challenges of their future lives and, therefore, to promote the development of twenty-first century skills. Empirical research, however, especially with longitudinal designs, is still a desideratum. In the following, we will at least provide empirical insight into how complex tasks can be implemented in the classroom and what effects can be observed when doing so.
4. Impressions of a Teaching Experiment—Cube Buildings as an Example of a Complex Task
In this section, we will present impressions of a teaching experiment conducted by applying cube buildings as an example of a complex task (for further examples of complex tasks, see, e.g., [24,25]). The main objective of this chapter is to illustrate the idea of how natural differentiation can arise from the subject-specific substance. Furthermore, in addition to the theoretical considerations of the previous sections, we will review the impressions of the teaching experiment to discuss intersections of necessary skills as for mathematical literacy and twenty-first century skills. Afterward, we will extend the impressions to an abstract perspective.
4.1. Backgrounds: From Polycubes to Cube Buildings
One example of complex tasks offers a well-known research question on cube buildings (among others [26]), a specific variation of polycubes: such a cube building is a structure consisting of connected cubes (). The polycubes’ sequence of the first ten cubes is 1, 1, 2, 8, 29, 166, 1023, 6922, 48311, and 346,543 (http://oeis.org/A000162, 08/13/2020; see also, e.g., [27]). Figure 1 shows the 8 tetracubes as an example.
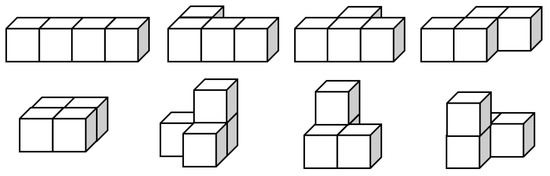
Figure 1.
Tetracubes.
In mathematics teaching, especially for younger students, orientation and positioning are usually taken into account additionally, i.e., (1) mirror images of polycube structures are regarded as different and (2) rotated, but otherwise, identical polycube structures are regarded as different. Furthermore, it is considered that not all polycubes can be actively explored without the help of auxiliary materials, e.g., by fixing a wooden cube that would actually fall with glue (for example, if a polycube forming an “L” would be turned by 180°, the wooden cube forming the “nose” would fall). If those restricting rules are applied, the term cube building is used. Usually, the rules of constructing cube buildings are formulated in a child-friendly manner for implementing them in classrooms (e.g., “Cube buildings are combinations of cubes in which the edges and surfaces of each cube adjoin those of others that stand on a surface”). Figure 2 exemplarily shows the cube buildings that can be formed by four cubes.
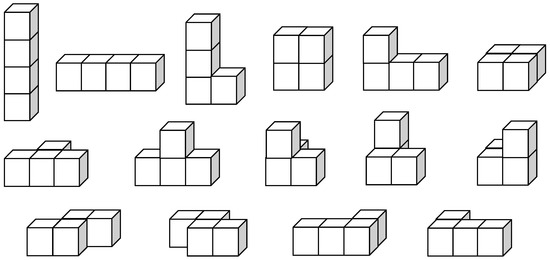
Figure 2.
Cube buildings consisting of four cubes.
A question for a complex task could be “How many cube buildings can you build with 2, 3, 4, 5, ... cubes?” (e.g., [28]). This complex question combines aspects of spatial perception such as orientation in space, imagining and dealing with spatial configurations, two- and three-dimensional representations of buildings, or creating and reconstructing building plans with easily accessible number explorations. For primary school children, it makes sense to limit the research assignment to the exploration of the numbers of possible cube buildings that can be built from two, three, or four cubes. Searching for all cube buildings consisting of five cubes becomes rather complex compared to those consisting of four cubes. Of course, this has to be understood in the sense of a fundamentum plus additum, as the exploration of higher numbers of cube buildings should always be open to interested students [29].
These research questions open up a complex task in terms of the criteria subsumed in the third section, because
- usually, the students are familiar with cubes from their daily environment and access through skills ranging from spatial imagination to haptic building is possible, which creates a high motivational potential;
- the rules for constructing cube buildings as well as the research question are easy to understand, so that the task has a low barrier of understanding; the possibility of haptic access has a constructive effect as well;
- the mathematical substance is extraordinarily large and allows for different approaches and representations; it suggests a search for general patterns, structures or strategies, and abstractions in the sense of polycubes; and
- beyond polycubes, there are more possibilities of natural follow-ups for the given problems, e.g., investigating surfaces and volumes of cube buildings or exploring sequences of figures of cube buildings.
4.2. Methodology of the Teaching Experiment
We have conducted the task “How many cube buildings can you build with 2, 3, or 4 cubes?” several times in regular mathematics lessons in different classrooms of grades 3 and 4 (students aged 8 to 11). The main intention was to explore which discoveries, solutions, or strategies are found with elementary school children who have different individual backgrounds and how those aspects are mutually enriching. The report of case examples below is based on analyses of the student’s productions as well as on thought analyses based on observations or notes from an open observation protocol, in which discoveries, solutions, or strategies, sometimes even entire quotations of the students were documented.
All teaching experiments followed a standardized schedule: A fifteen-minute introduction to the problem took place in a circle of seats using large cubes as visual aids to create a common basis of understanding for the subsequent research phase. In addition, the students made various assumptions about the number of cube buildings for given numbers of cubes to awaken their individual desire for exploring and proofing. The introduction was followed by a research phase of 60 min. In addition to the openness of the task in terms of the mathematical substance, there was a parallel openness with regard to the classroom arrangement: students were free to work alone or with others, and they could choose the material, the level of representation, as well as the type of documentation. A worksheet included the rules of how to construct cube buildings as well as the research question. For students who had difficulties with accessing the content, a second optional worksheet offered possible ideas for the notation in the form of building plans. Furthermore, another optional worksheet provided follow-up research impulses for particularly interested or high-achieving students (including the question, “How many cube buildings can you build with 5 or more cubes?”). In a final fifteen-minute discussion, the students presented their results and discussed their discoveries, solutions, and strategies.
4.3. Case Examples from the Teaching Experiment
The students made very different assumptions about the numbers of cube buildings with two, three, or four cubes; some of them, for example, called very small numbers like only four possible cube buildings with four cubes, but other students thought of well over a hundred and more cube buildings with four cubes. Examining their assumptions had a highly challenging character, awakened the students’ need for proof, and initiated numerous activities ranging from the pure construction of all possible cube buildings to a certain number of cubes to more complex formal representations with construction plans, ranging from pure trial and error to systematic strategies. In the following, we look at examples of activities conducted by children with very different backgrounds (the description of the students’ backgrounds is based on information from their mathematics teacher). Then, we abstract the potentials and pitfalls of complex tasks from these concrete examples.
Sebastian (All students’ names are rendered anonymous; personal data which have any identifying factors were removed), a student with attested special educational needs related to learning in general, drew the possible cube buildings of both one and two cubes by hand. He explained (all quotes are translated from German): “With a single cube, there is only one building, you do not put anything else on it. With two cubes, there are only two different cube buildings because the cubes either stand on top of each other or next to each other. With three cubes, you have to think more because the cubes also turn the around corner”. He illustrated his considerations by perspective drawings (without foreshortening the diagonal edges; Figure 3 left). Afterward, he began to build possible cube buildings from three cubes with wooden cubes (Figure 3 right).
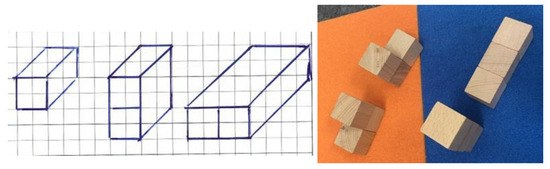
Figure 3.
Sebastian’s approaches with one and two cubes (left) and with three cubes (right).
Toni, an “average” achiever, and Claudia, a low achieving student, worked together. At first, they did not understand the construction rules of cube buildings well and they concentrated on repeating them in detail. Afterward, the number of possible cube buildings with one or two cubes was immediately clear to them, so they began their exploration with three cubes. They followed the same strategy as Sebastian, by building all possible cube buildings made of three cubes with wooden cubes. The strategy of completely building all possible cube buildings to a certain number of cubes was chosen by many children regardless of their individual backgrounds, even with higher numbers of cubes. Clara, for example, who was attested a visual impairment, worked together with Franz and Ali (all three students are considered at least average achievers). The enactive approach, the tactile access to different cube buildings, was very productive, especially for Clara. Initially, each of the students worked alone on the research impulse to build all the cube buildings with four cubes. Then, they talked about their results and their strategies for finding all the cube buildings made of four cubes (Figure 4). What they had in common was that they first developed the sticks, then the angles, and finally special shapes such as a “pistol”.

Figure 4.
Clara’s, Ali’s, and Franz’s cube buildings with four cubes.
Maria, a student who is assessed to have a very high mathematical potential, worked together with Dimitri, a student who tends to achieve less than average. Following Maria’s suggestion, they completely dispensed enactive approaches or iconic representations; they used construction plans to systematically discover all possible cube buildings with one, two, three, or four cubes (Figure 5), i.e., they turned to a formal-symbolic representation since the building plans correspond to a ground-plan perspective. It is made up of squares, which indicate how many cubes are stacked on top of each other in each position.
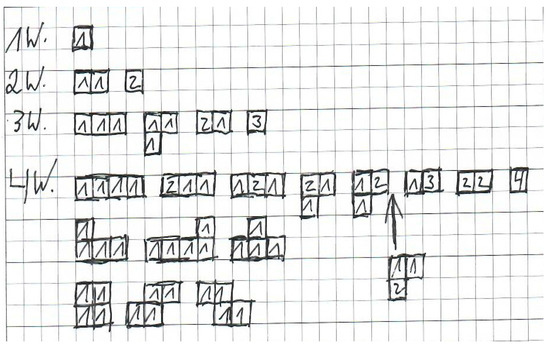
Figure 5.
Maria’s and Dimitri’s construction plans.
Later, Maria started working with Peter, who is also considered to have huge mathematical potential. Maria had noticed that cube buildings are a very specific consideration of more general cube figures and argued: “But it does not have to be at all that the cubes are only at the bottom. It can happen that the cubes would fall, but then, there would still be surface to surface and edge to edge”. Together with Peter, she sketched her ideas for a cube building with three cubes (Figure 6).
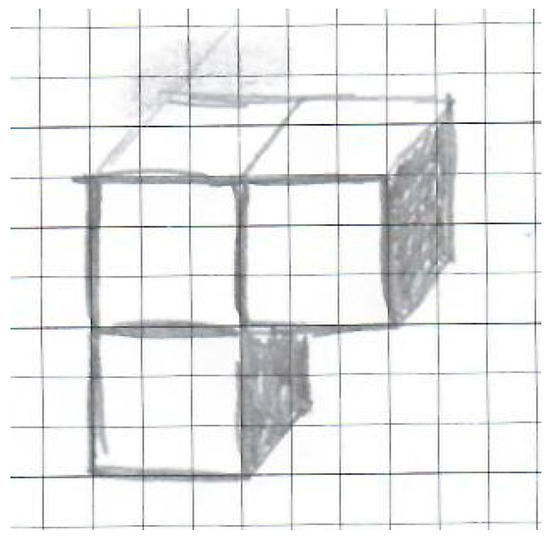
Figure 6.
Maria’s and Peter’s illustration of a polycube.
Peter said: “But you can look at it very differently because the tower of three cubes and the stick are actually the same!” Although Maria and Peter did not have enough time to think their thoughts through to the end during the mathematics lesson, they decided to talk about it later.
In the final presentation phases of the teaching experiments, different students, pairs, or small groups presented their results and procedures. More important than the rating as right or wrong were the arguments of the students, which led to complex discussions on whether, for example, all cube buildings had actually been found with a certain number of cubes; for instance, Dimitri argued: “We are sure that we have found all the cube buildings with four cubes. We first sketched all those that were on four boxes, then all those on three boxes, then all on two, then on one, and we tried every possibility we could think of.” Maria also initiated a discussion on whether rotations or floating cubes should be allowed, which also invited other students to critically reflect on the viability of the construction rules of cube buildings.
4.4. A Transverse Perspective and Interim Conclusion
The case examples demonstrate a wide range of possible discoveries and approaches. All students found access to the activity, alone, in pairs, or groups. The mutual exchange and the presentation at the end of the activity enhanced the learning of all. Especially, the necessity to argue why they found all possible cube buildings made the students find ways to present their solutions. Additionally, they communicated in, with, and about mathematics and learned to reason mathematically. They made use of different manipulatives and ways of representing mathematical entities.
Abstracting the experiences from the teaching experiments, we draw tentative conclusions with regard to the contribution of complex tasks to the development of twenty-first century skills. As a conceptual structure for those conclusions, we use the categorization of twenty-first century skills of Binkley et al. as it represents a summarizing framework of the concepts of different countries.
- It is important that the research impulse is very easy to understand and, therefore, that it allows all students to learn and to participate. The case examples of the teaching experiment show that the students approach the research impulse in different ways, with different materials, and in a different mathematical depth (comparing for example Sebastian’s and Maria’s approaches). Regarding twenty-first century skills in the sense of Binkley et al. [7], we recognize intersections to the component of Ways of thinking, especially to (mathematical) problem-solving.
- Reasoning and communication skills provide the foundation for authentic joint learning. Those competencies are an important component of educational standards in Germany [30] as well as in the international context. Accordingly, process-related competencies open up paths that imply both participation and the importance of diversity for mathematical teaching-learning processes (compare for example the approaches of Sebastian and Dimitri). As for twenty-first century skills, this is linked to critical thinking as part of the skill group ways of thinking. Additionally, there are intersections to the component ways of working, in particular to communication and collaboration (for example, due to manifold discussions about viable strategies or solutions in order to find all cube buildings with a certain number of cubes).
- Furthermore, we find links to the component of living in the world, more precisely to personal and social responsibility, since the task on cube buildings focused on mutual support as well as participation, and thus, it avoids any kind of exclusion from learning mathematics.
- At first glance, with regard to content-specific learning objectives, however, the picture is rather vague, perhaps even diffuse. For example, looking at German educational standards for primary education [30], numerous references for a curricular classification of cube buildings can be found in the category space and shape. One example is the ability to orientate oneself in space (having spatial imagination; recognizing, describing, and using spatial relationships, such as configurations, paths, plans, or views; and relating two- and three-dimensional representations of buildings to one another). Another reference can be found in abilities to recognize, name, and represent geometric figures (for example, making and examining models of spatial objects or planar figures, such as building, laying, or connecting and drawings with auxiliaries or freehand drawings). The strength of this vagueness may lie in an individual determination of learning objectives and in an immanent stimulation to the zone of proximate development in the sense of Vygotsky in a setting which nevertheless allows joint learning [31]. Regarding twenty-first century skills, we recognize mainly intersections to the component of ways of thinking, more precisely to a learning to learn (due to the open and broad nature of complex tasks).
Of course, the intersections do not pretend to be comprehensive, but they can be used as examples to show how contributions to twenty-first century skills can be made in mathematics lessons applying complex tasks. The component tools for working has not been addressed yet; we do not consider it to be excluded but rather as an always inherent component. How and which of the tools available in the mathematics classroom are used, however, can vary from individual to individual (Sebastian, for example, created his own visualizations; Maria and Dimitri may have already known or they may have researched construction plans for cube buildings; Maria might have conducted an internet search on polycubes together with Peter after the teaching experiment; and maybe other students might access constructing cube buildings or polycubes applying a dynamic geometry software).
The teaching experiment presented focused on grades 3 and 4. Therefore, the impressions are limited to elementary schools. Nevertheless, the task on cube buildings is suitable for higher grades as well. This even applies to mathematically more experienced people: for example, we use the task in the context of teacher education. We have observed how student teachers as well as in-service-teachers work intensively on cube buildings, trying to figure out patterns and discussing vividly about possible numbers of cube buildings. The extension of cube buildings to polycubes offers additional potential for discoveries and intensive mathematical discourse also on a higher level.
5. Discussion Polycubes: Potentials and Limitations of Complex Mathematical Tasks
With regard to living in the modern world, various skills are needed to meet the challenges of the society, everyday life, and the labor market (in this paper, conceptualized as twenty-first century skills). Education and in particular mathematics education have to prepare students for those challenges. While there is no definite answer to how this is realized, certain tools and methods have to be discussed as suitable. In this contribution, we argue that complex tasks have the potential to contribute to that goal and additionally to promote equitable teaching in mathematics classrooms.
As for intersections of mathematical literacy and twenty-first century skills, based on both the theoretical considerations and impressions of the teaching experiment, we will extend the impressions of skills focused on complex tasks to an abstract perspective in order to discuss their (in our view, most important) potentials and pitfalls in such a context; mainly, our considerations will be structured according to the framework of Binkley et al. [7]. We separate our consideration according to the partial- and subcomponents prototypically, but of course, there are various overlaps.
5.1. Potentials
Regarding ways of thinking as one component of twenty-first century skills, the construction and implementation of complex tasks offer potentials for realizing broadly accepted postulates regarding the mathematical teaching-learning-process. In the sense of the subcomponent creativity and innovation, complex tasks demand for non-routine ways of solution and divergent thinking, especially in order to ask new questions (as a sign of mathematical creativity; see e.g., [32]) or to present follow-up problems arising from a given problem [15]. It is obvious that there are many references to the subcomponents problem-solving (i.e., to deal with problems when no direct solution method is readily applicable or available [5]) and decision making (for example, regarding the solution to be chosen, regarding the auxiliaries to be used, as well as regarding the solution’s representation or depiction). Reflections on the prospects of a chosen strategy as well as on the viability of the argumentation of oneself or others show possible contributions to critical thinking. Finally, the holistic character of complex tasks can support learning to learn, since working on complex tasks enables individual, constructivist, and inquiry-based learning. Thus, complex mathematical tasks seem to be one element to organize the teaching and learning of mathematics as a social practice with individual constructions.
With regard to the component ways of working, it is, in particular, the diversity of possible approaches, solutions, and representations that is beneficial for fostering twenty-first century skills: as for the subcomponent communication, discussions of different approaches are to be mentioned here as well as discussions about the sustainability or also about the aesthetics of argumentation (in which, in the sense of mathematical literacy, corresponding process-related competencies are mirrored). Regarding collaboration (teamwork), complex tasks open up a wide range of possibilities for social exchange and cooperation beyond the discussion of results, especially when the natural differentiation induced by the mathematical substance is combined with methodological, social, and democratic openness [33].
Regarding the category living in the world, complex tasks offer potentials for authentic joint learning in such a way that the diversity of ideas, approaches, and solutions becomes a benefit and learning resource for the whole group. Thus, the implementation of complex tasks can contribute to the social goal of acclaiming diversity and, therefore, becoming an inclusive society since decategorizations are attainable and open task activities call for a focus on the potentials of both individuals and the group rather than concentrating on their deficits (subcomponent personal and social responsibility). Associated with that aspect, complex tasks (and, therefore, mathematics education) can contribute to developing skills and attitudes in relation to the subcomponent citizenship—local and global. Finally, solving complex tasks enables students to experience the nature of mathematical working (e.g., making and proving assumptions or dealing with mathematical structures) [11,34] and, thus, contributes to the ability to look at the world with mathematical eyes, which is related to the subcomponent life and career.
5.2. Limitations and Pitfalls
Beyond questions of intentions, as promising as activities in the frame of complex tasks might sound, they also provide space for misunderstandings and pitfalls. For instance, regarding the skill group ways of thinking as one component of twenty-first century skills, we want to stress that openness is not to be equated with arbitrariness. Although students have freedom and autonomy to choose their own path on how to deal with tasks, not every approach necessarily leads to a learning with understanding. Additionally, we have to acknowledge the limits of complex tasks, avoiding the impression of providing an overall solution for all problems in the teaching and learning of mathematics. First, not all mathematics lessons can be arranged appropriately around complex tasks and inquiry-based learning, as certain knowledge, such as mathematical notions, cannot be “discovered” and, therefore, require other classroom settings. Another problem not solved yet evolves due to contradictions in our educational systems and educational policy. On the one hand, current national and international teaching guidelines require a learning environment that respects the different needs, skills, and capabilities of the students and is adapted accordingly. On the other hand, in tests, examinations, and other forms of assessment, traditionally all students have to solve the same tasks and are measured against the same standards. While individual learning processes are highly encouraged, individual assessment is not yet realized. Therefore, as long as educational systems are built around grades and degrees and have selective functions, the demands for inclusive mathematics education and for respecting diversity necessarily provoke contradictions.
The development of abilities and attitudes contained in the category ways of working strongly depends on the atmosphere, routines, and rituals within a classroom as well as on the individual objectives of a teacher. Especially, the elaboration of skills relevant for communication and collaboration requires a respectful culture of social interaction that has to be established by the teacher. When teachers focus more on the individual attainment of students or on a classroom atmosphere that is dominantly characterized by competition or disrespect, the implementation of complex tasks in the mathematics classroom will not result in a communicative and collaborative working process. It is, in particular, the teacher’s responsibility to create an environment that accentuates collaboration and communication.
As for the category living in the world, with regard to inclusive mathematics education as one fragment of inclusive education and the goal of an inclusive society in general, there might be doubts in terms of the suitability of complex task for all students (that are hardly addressed in the literature) and the question if it is really possible to support society’s goals by single learning arrangements in the sense of contributions to the subcomponents personal and social responsibility and citizenship. In the last years, complex tasks have been discussed to be adequate for inclusive settings as every student can work on his or her own level and with his or her own strategies, using or not using support. The present article argues in that way as well. However, we want to question if complex tasks can really satisfy this high demand and meet all the challenges mentioned above. Indeed, we have to ask if any classroom setting is able to suit this demand and to provoke mathematical learning and understanding for all children. This question, or we should rather say this objection, is of special relevance for inclusive classrooms, where the diversity among the students is notably and intentionally high. Without questioning the general idea of inclusive education, it remains an open question how far, for example, students with severe impairments will learn mathematics with understanding and participate meaningfully in the mathematical activity. Also, other students might have difficulties, for example coping with the openness and degree of freedom. In recent research, we find a vivid discussion about the needs of low achieving students or students with learning impairments. While Scherer and Wittmann argue that inquiry-based learning is suitable and beneficial also for students with severe learning impairments [35,36], other studies show lower effectiveness of open learning arrangements for low achieving, socially disadvantaged students [37]. While both statements are not necessarily contradictory, the argument of Grünke might be valid also for the implementation of complex tasks [37]. Grünke argues that students with learning difficulties struggle with structuring, planning, organizing, and strategically acting. Confronting those students with open learning arrangements, where exactly those skills are required, may lead to overstraining demands and, therefore, to negative experiences with learning (mathematics). It might be argued that this objection does not apply to complex tasks, as they start with a simple question with a low threshold. However, this reveals a need for further and expanded research studying the suitability of complex tasks for students with different needs and abilities. In any case, on the side of the teacher, it requires sensibility and fundamental knowledge about the mathematical learning process to support students appropriately without guiding them too much. A study of Höveler, investigating the learning process of students in learning environments, revealed that, in the lessons under analysis, not all students made progress [21]. As one result of the study, the author states that the learning progress depends on various factors. For example, a general attitude among the group that the interaction with others is helpful for their own learning seems to be necessary. Additionally, Höveler points out that it is, in particular, the teacher’s practice how to implement such tasks, that is essential for the learning process of the students: his or her way of arranging the whole activity, of developing a certain attitude on the side of the students, of creating a respectful atmosphere, or of setting stimulating impulses [21].
5.3. Summary and Outlook
We conclude that, apart from the chances and opportunities that complex tasks offer, there is a variety of pitfalls and limits that must be reflected on in research and teaching practice. Despite those limitations and pitfalls, we want to take up the argumentation of Krauthausen to motivate teachers and teacher educators to implement complex tasks in the mathematics classrooms:
This may startle teachers at first or make them skeptical—especially with respect to low achievers who (in traditional differentiation) have been fostered by applying the principle of small and smallest steps and the principle of isolated difficulties. But holistic and complex problems naturally allow to develop a momentum of their own, giving room for the inherent dynamism of the topic.[17] (p. 19)
Similar to the concrete example considered in the teaching experiment, in our opinion, no universal statement can be made about the gain or limitations of solving complex tasks for the skills from the category tools for working, since their use can greatly vary from one individual to another, from one task to another, or from one teaching context to another (think of curricular differences in the use of, for example, spreadsheet software or dynamic geometry software). However, from our point of view, those skills should always be promoted in modern mathematics education, enhancing information literacy (e.g., doing research on mathematical facts) and ICT literacy (handling software)—not only when dealing with complex tasks but also fundamentally within mathematical teaching-learning processes in school.
In addition to the question of how complex tasks might contribute to the students’ development of twenty-first century skills, the teaching process must be taken into consideration: For the teacher, it requires a certain sensitivity to support students without directing them too much. This also applies to helping students who do not immediately find access or refuse to engage with open activities, especially when they are predominantly used to narrow, simplified tasks. According to Krauthausen, the teacher’s responsibility requires specific professional skills: Even an autonomously learning and high-performing student needs support when he or she meets the zone of his or her proximal development [17,31]. The teacher is responsible for leading a child to individual limits, and he or she must offer impulses to push those limits more and more forwards. Delving into mathematical structures of the learning content in that sense does not happen automatically, rather a well-considered encouragement is necessary. Therefore, Krauthausen emphasizes that the design and implementation of activities complying with natural differentiation are specifically a teacher’s responsibility and “cannot be delegated to elementary students, as some questionable teaching methods may suggest” [17] (p. 331). The demands put upon teachers are various and contain both subject-specific and pedagogical content knowledge [38].
6. Concluding Remarks
Against the background of the challenges of the modern, rapidly changing world, the discussion about the potentials and limitations of complex tasks highlighted some aspects being particularly significant from our point of view. Of course, complex tasks provide nothing more than one way to teach (and learn) mathematics. Additionally, it is only one approach to organize diversity. A large spectrum of different methods has to be considered, always scrutinizing the intentions of a learning situation
- in terms of the relationships within a group focusing on participative, communicative, and collaborative learning;
- in terms of the individual focusing on personalized learning with regard to different individual needs and potentials.
As we argued in this paper, implementing complex tasks in the mathematics classroom has the potential to create a setting considering both levels. At the same time, our line of argumentation only represents selected aspects and seeks to be complemented by other contributions. In the literature, as far as we have recognized, potentials and limitations of complex tasks have been explored primarily on the basis of philosophical-conceptual considerations and experiences. The empirical investigation of their benefits and boundaries rather continues to be a desideratum. Although intervention studies in a pre-post-design (which seem to be most popular in recent approaches of studying benefits of mathematical formats) may provide a possible technique, they seem not to be sufficient for the investigation of long-lasting effects or complex phenomena like students’ thinking. We suggest mixed-methods-designs, for example, a triangulation of contrasting case studies and impressions from participating class observations (as indicated by our teaching experiment on cube buildings) and/or longitudinal studies since their holistic perspective seems to be more appropriate to meet the challenges to study the impacts of solving complex tasks for mathematical literacy as well as twenty-first century skills and, thus, for living in a complex modern world. Additionally, our teaching experiments are to be complemented by studies which implement complex tasks in higher grades. In particular with regard to mathematical literacy and twenty-first century skills, mathematics education in elementary school sets the cornerstones of mathematical understanding and creates the basis for a rich mathematical discourse. Secondary schools have the important role to build on those cornerstones and to carry inquiry-based mathematical learning activities forward.
However, we want to stress that even the best tasks (complex or not) will not be able to prepare students completely to master the challenges of our world today and to develop all mathematically relevant twenty-first century skills. The design and implementation of complex tasks in mathematics classrooms can only be one part. Every school subject as well as the classroom culture has to contribute to this very fundamental role of schooling in its own way. Nevertheless, complex tasks might be suitable to gain fundamental mathematical experiences, to learn mathematics with understanding, and to perceive mathematics as a social practice. It requires more fundamental theoretical and empirical research to confirm (or to refute) those assumptions.
We want to add that, apart from the design of complex tasks, also the way of implementing them in the mathematics classroom is of great importance. The exchange among the students and the mutual presentation at the end of the activity stimulates mathematical reasoning and ways of representing. This description corresponds to the idea of “mathematics as an evolving social practice that is constituted by, and does not exist apart from, the constructive activities of individuals” [39] (p. 28).
Additionally, we want to stress that the different concepts in different countries do not necessarily share the same understanding and assumptions of such complex tasks. Surprisingly, there is rather little discussion in the recent German discourse. Optimistic and practical contributions, including best practice examples, outweigh an academic discussion about advantages and disadvantages, potentials, and limitations of complex tasks. Therefore, from our point of view, it needs more of the latter, taking this contribution as a starting point.
Author Contributions
Conceptualization, N.B. and R.B.; Formal analysis, N.B. and R.B.; Writing—original draft, N.B. and R.B.; Writing—review & editing, N.B. and R.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We gratefully acknowledge Timo Dexel and Anna-Maria Schmitz for their review of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Department of Basic Education. Mathematical literacy—Curriculum and Assessment Policy Statement Grades 10–12. Available online: https://bit.ly/33wZpfX (accessed on 4 August 2020).
- Nunes, T.; Bryant, P. Learning and Teaching Mathematics: An International Perspective; Psychology Press: East Sussex, UK, 1997; ISBN 978-086-377-455-3. [Google Scholar]
- Sachdeva, S. Students’ Experiences of Learner Autonomy in Mathematics Classes. In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education, Utrecht, The Netherlands, 6–10 February 2019; Available online: https://hal.archives-ouvertes.fr/hal-02421636/document (accessed on 4 August 2020).
- Niss, M.; Jablonka, E. Mathematical literacy. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 391–396. ISBN 978-94-007-4978-8. [Google Scholar]
- Ärlebäck, J.B.; Albarracín, L. The use and potential of Fermi problems in the STEM disciplines to support the development of twenty-first century competencies. ZDM 2019, 6, 979–990. [Google Scholar] [CrossRef]
- Maaß, K.; Geiger, V.; Ariza, M.R.; Goos, M. The Role of Mathematics in interdisciplinary STEM education. ZDM 2019, 51, 869–884. [Google Scholar] [CrossRef]
- Binkley, M.; Erstad, O.; Herman, J.; Raizen, S.; Ripley, M.; Miller-Ricci, M.; Rumble, M. Defining twenty–first century skills. In Assessment and Teaching of Twenty-First Century Skills; Griffin, P., McGaw, B., Care, E., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 17–66. ISBN 978-94-017-9394-0. [Google Scholar]
- Gravemeijer, K.; Stephan, M.; Julie, C.; Lin, F.L.; Ohtani, M. What mathematics education may prepare students for the society of the future? IJSME 2017, 15, 105–123. [Google Scholar] [CrossRef]
- Rizki, L.M.; Priatna, N. Mathematical literacy as the twenty-first century skill. JPCS 2019, 1157, 1–5. [Google Scholar] [CrossRef]
- PISA. PISA 2018 Assessment and Analytical Framework; OECD Publishing: Paris, France, 2019; pp. 73–95. ISBN 978-92-64-47759-9. [Google Scholar]
- Silver, E.A. The nature and use of open problems in mathematics education: Mathematical and pedagogical perspectives. ZDM 1995, 27, 67–72. [Google Scholar]
- Wittmann, G.; Levin, A. Elementarmathematisches und mathematikdidaktisches Wissen. In AnschlussM. Anschlussfähigkeit mathematikdidaktischer Überzeugungen und Praktiken von ErzieherInnen und GrundschullehrerInnen; Wittmann, G., Levin, A., Bönig, D., Eds.; Waxmann: Münster, Germany, 2016; pp. 150–151. ISBN 978-3-8309-3156-0. [Google Scholar]
- Bruder, R.; Linneweber-Lammerskitten, H.; Reibold, J. Individualisieren und Differenzieren. In Handbuch der Mathematikdidaktik; Bruder, R., Hefendehl-Hebeker, L., Schmidt-Thieme, B., Weigand, H.-G., Eds.; Springer Spektrum: Heidelberg, Germany, 2015; pp. 513–537. ISBN 978-3-642-35118-1. [Google Scholar]
- Kollosche, D. Entdeckendes Lernen auf dem Prüfstand. MNU J. 2020, 4, 282–286. [Google Scholar]
- Scherer, P.; Krauthausen, G. Natural Differentiation in Mathematics—The NaDiMa project. In Panama Cursusboek 28 Waardevol Reken-Wiskundeonderwijs—Kenmerken van Kwaliteit; van Zanten, M., Ed.; Panama/Freudenthal Instituut: Utrecht, The Netherlands, 2010; pp. 33–57. [Google Scholar]
- Greefrath, G. Offene Aufgaben mit Realitätsbezug. Eine Übersicht mit Beispielen und erste Ergebnisse aus Fallstudien. J. Math Didakt 2004, 27, 16–38. [Google Scholar]
- Krauthausen, G. Natural Differentiation—An Approach to Cope with Heterogeneity. In Invited Lectures from the 13th International Congress on Mathematical Education; Kaiser, G., Forgasz, H., Graven, M., Kuzniak, A., Simmt, E., Xu, B., Eds.; Springer: Cham, Switzerland, 2018; pp. 325–341. ISBN 978-3-319-72169-9. [Google Scholar]
- Sullivan, P.; Lilburn, P. Open-Ended Maths Activities. Using ‘Good’ Questions to Enhance Learning in Mathematics, rev. ed.; Oxford University Press: Oxford, UK, 2017; ISBN 978-0-1903-0403-4. [Google Scholar]
- Gadanidis, G.; Hughes, J. Performing big math ideas across the grades. TCM 2011, 17, 486–496. [Google Scholar]
- Boaler, J. Mathematical Mindsets: Unleashing Students’ Potential through Creative Math, Inspiring Messages and Innovative Teaching; Jossey-Bass: San Francisco, CA, USA, 2016; ISBN 978-0-470-89452-1. [Google Scholar]
- Höveler, K. Learning Environments in Inclusive Mathematics Classrooms. In Inclusive Mathematics Education; Kollosche, D., Marcone, R., Knigge, M., Penteado, M., Skovsmose, O., Eds.; Springer: Cham, Switzerland, 2019; pp. 87–105. ISBN 978-3-030-11517-3. [Google Scholar]
- Scherer, P. Natural differentiation in the teaching of mathematics to children starting school. SAJCE 2013, 3, 100–116. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. In Handbook for Research on Mathematics Teaching and Learning; Grouws, D., Ed.; MacMillan: New York, NY, USA, 1992; pp. 334–370. ISBN 978-1-59311-598-2. [Google Scholar]
- Findell, C.; Gavin, C.; Greenes, C.; Sheffield, L.J. Awesome Math Problems for Creative Thinking; Creative Publications: Chicago, IL, USA, 2000. [Google Scholar]
- Nolte, M.; Pamperien, K. Challenging problems in a regular classroom setting and in a special foster programme. ZDM 2017, 49, 121–136. [Google Scholar] [CrossRef]
- Radatz, H.; Rickmeyer, K. Handbuch für den Geometrieunterricht an Grundschulen; Schroedel: Hannover, Germany, 1991; ISBN 978-3-5073-4040-4. [Google Scholar]
- Rouse Ball, W.W.; Coxeter, H.S.M. Mathematical Recreations and Essays, 13th ed.; Dover: New York, NY, USA, 1987; ISBN 978-0-486-25357-2. [Google Scholar]
- Franke, M.; Reinhold, S. Didaktik der Geometrie in der Grundschule, 3rd ed.; Springer: Heidelberg, Germany, 2016; ISBN 978-3-662-47265-1. [Google Scholar]
- Benölken, R.; Berlinger, N.; Veber, M. Würfelgebäude. In Alle Zusammen! Offene, Substanzielle Problemfelder als Gestaltungsbaustein für Inklusiven Mathematikunterricht; Benölken, R., Berlinger, N., Veber, M., Eds.; WTM: Münster, Germany, 2018; pp. 161–172. ISBN 978-3-95987-091-7. [Google Scholar]
- Kultusministerkonferenz. Bildungsstandards im Fach Mathematik für den Primarbereich (Jahrgangsstufe 4). In Proceedings of the Beschlüsse der Kultusministerkonferenz, Germany, 15 October 2004. Available online: https://www.kmk.org/fileadmin/Dateien/veroeffentlichungen_beschluesse/2004/2004_10_15-Bildungsstandards-Mathe-Primar.pdf (accessed on 9 September 2020).
- Vygotsky, L.S. Mind in Society: The Development of Higher Psychological Processes; Harvard University Press: Cambridge, MA, USA, 1978; ISBN 978-0-674-57629-2. [Google Scholar]
- Sriraman, B. The characteristics of mathematical creativity. ZDM 2004, 41, 13–27. [Google Scholar] [CrossRef]
- Benölken, R.; Veber, M.; Berlinger, N. Gestaltung fachlich fundierter Lehr-Lern-Settings für alle ohne Ausschluss. In Alle Zusammen! Offene, Substanzielle Problemfelder als Gestaltungsbaustein für Inklusiven Mathematikunterricht; Benölken, R., Berlinger, N., Veber, M., Eds.; WTM: Münster, Germany, 2018; pp. 1–15. ISBN 978-3-95987-091-7. [Google Scholar]
- Davis, P.J.; Hersh, R. The Mathematical Experience, study ed.; Birkhäuser: Basel, Switzerland, 2012; ISBN 978-0-8176-8294-1. [Google Scholar]
- Scherer, P. Fördern durch Fordern—Aktiv-entdeckendes Lernen und Produktives Üben im Mathematikunterricht der Schule für Lernbehinderte. ZfH 1994, 11, 761–773. [Google Scholar]
- Wittmann, E.C. Aktiv-entdeckendes und soziales Lernen im Arithmetikunterricht. In Mit Kindern Rechnen; Wittmann, E.C., Müller, G.N., Eds.; Arbeitskreis Grundschule: Frankfurt am Main, Germany, 1995; pp. 10–41. ISBN 978-3-9300-2454-4. [Google Scholar]
- Grünke, M. Richtig fördern-aber wie? Zeitnah 2007, 52, 9–23. [Google Scholar]
- Wittmann, E.C. Developing mathematics education in a systemic process. In Proceedings of the Ninth International Congress on Mathematical Education; Fujita, H., Hashimoto, Y., Hodgson, B.R., Yee Lee, P., Lerman, S., Sawada, T., Eds.; Kluwer Academic Publishers: Norwell, MA, USA, 2004; pp. 73–90. ISBN 978-1-4020-7910-8. [Google Scholar]
- Cobb, P.; Yackel, E.; Wood, T. A Constructivist Alternative to the Representational View of Mind in Mathematics Education. JRME 1992, 23, 2–33. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).