The Exact Solution of the Falling Body Problem in Three-Dimensions: Comparative Study
Abstract
1. Introduction
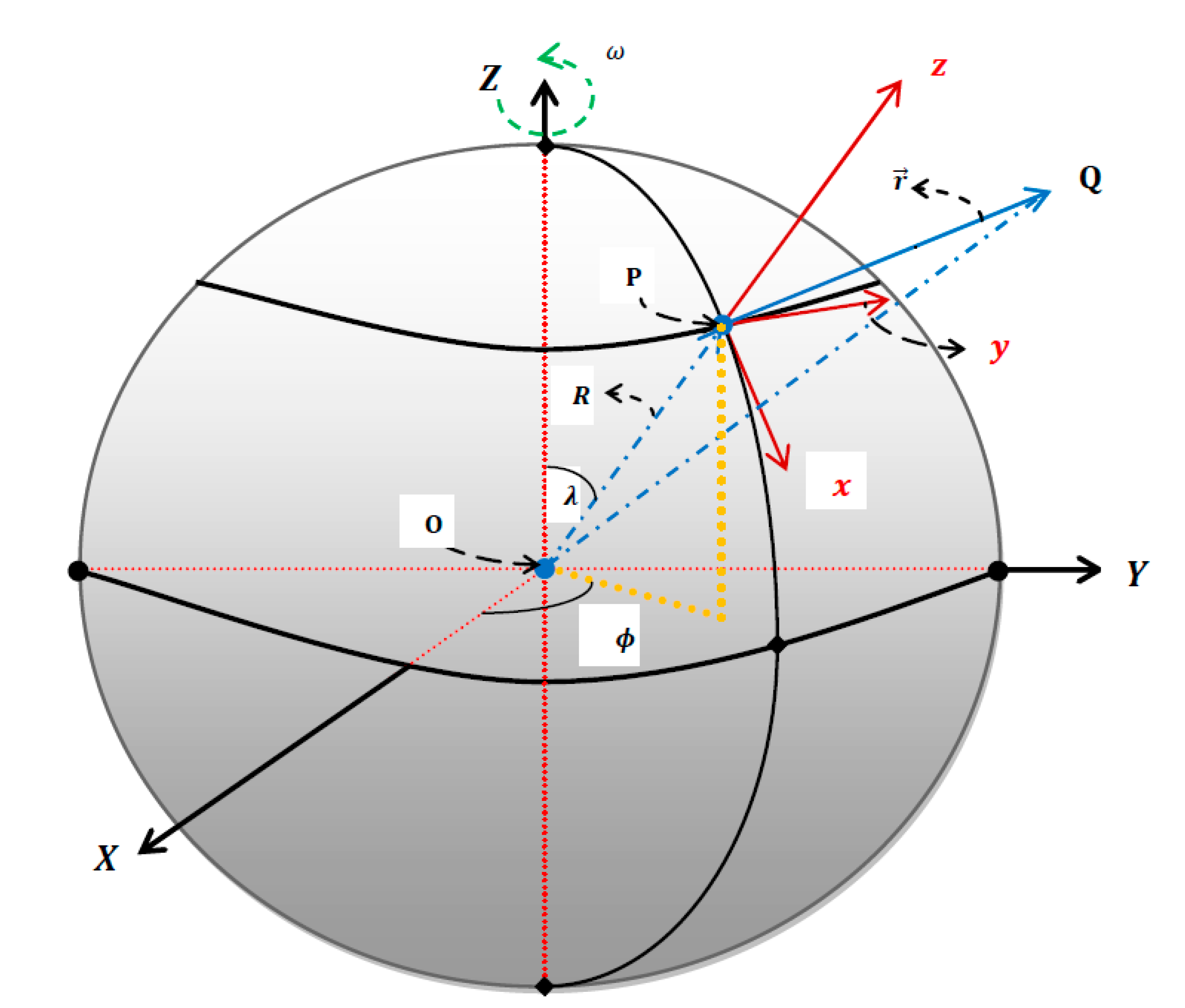
2. The Exact Solution
3. Coordinates and Characteristics of the Falling Point
3.1. Coordinates of the Falling Point
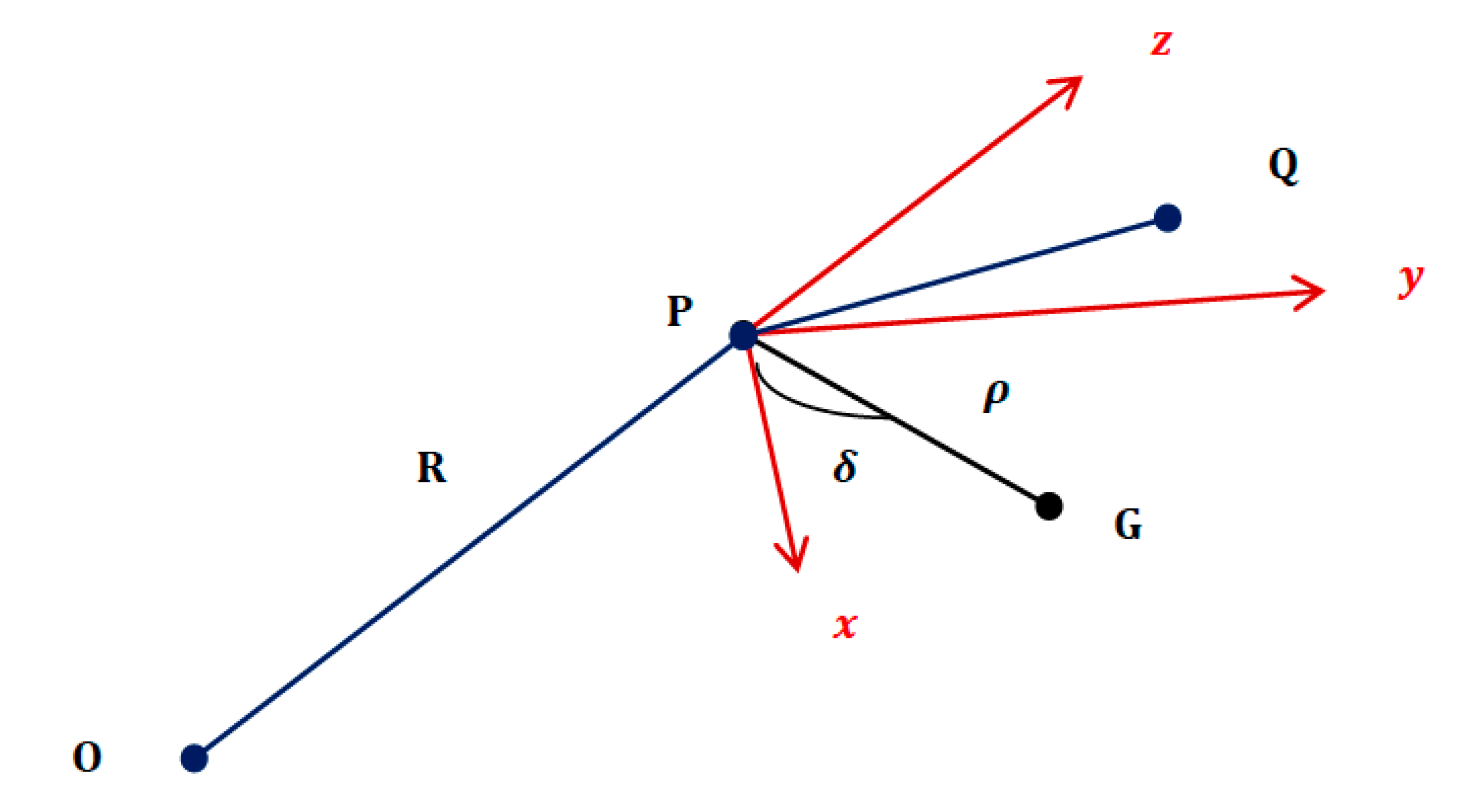
3.2. Characteristics of the Falling Point
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Laplace Transform and Its Properties
Appendix B
Appendix B.1. Special Cases
Appendix B.1.1. (North Pole)
Appendix B.1.2. (South Pole)
Appendix B.1.3. (Equator)
Appendix C
Appendix C.1. Coordinates of the Falling Point at Special Cases
Appendix C.1.1. (North Pole)
Appendix C.1.2. (South Pole)
Appendix C.1.3. (Equator)
References
- Kwok, S.F. A falling body problem through the air in view of the fractional derivative approach. Phys. A Stat. Mech. Appl. 2005, 350, 199–206. [Google Scholar]
- Garcia, J.J.R.; Calderon, M.G.; Ortiz, J.M.; Baleanu, D.; de Santiago, C.S.V. Motion of a particle in a resisting medium using fractional calculus approach. Proc. Rom. Acad. A 2013, 14, 42–47. [Google Scholar]
- Ebaid, A.; Masaedeh, B.; Machado, J.A.T. A New Fractional Model for the Falling Body Problem. Chin. Phys. Lett. 2017, 34, 20201. [Google Scholar] [CrossRef]
- Hayen, J.C. Projectile motion in a resistant medium: Part I: Exact solution and properties. Int. J. Non-linear Mech. 2003, 38, 357–369. [Google Scholar] [CrossRef]
- Hayen, J.C. Projectile motion in a resistant medium Part II: Approximate solution and estimates. Int. J. Non-linear Mech. 2003, 38, 371–380. [Google Scholar] [CrossRef]
- Weinacht, P.; Cooper, G.R.; Newell, J.F. Analytical Prediction of Trajectories for High-Velocity Direct-Fire Munitions; Technical report ARL-TR-3567; US Army Research Laboratory: Aberdeen Proving Ground, MD, USA, 2005. [Google Scholar]
- Yabushita, K.; Yamashita, M.; Tsuboi, K. An analytic solution of projectile motion with the quadratic resistance law using the homotopy analysis method. J. Phys. A Math. Theor. 2007, 40, 8403–8416. [Google Scholar] [CrossRef]
- Benacka, J. Solution to projectile motion with quadratic drag and graphing the trajectory in spreadsheets. Int. J. Math. Educ. Sci. Technol. 2010, 41, 373–378. [Google Scholar] [CrossRef]
- Benacka, J. On high-altitude projectile motion. Can. J. Phys. 2011, 89, 1003–1008. [Google Scholar] [CrossRef]
- Ebaid, A. Analysis of projectile motion in view of fractional calculus. Appl. Math. Model. 2011, 35, 1231–1239. [Google Scholar] [CrossRef]
- Rosales, J.J.; Guía, M.; Gómez, F.; Aguilar, F.; Martinez, J. Two dimensional fractional projectile motion in a resisting medium. Open Phys. 2014, 12, 517–520. [Google Scholar] [CrossRef]
- Ahmad, B.; Batarfi, H.; Nieto, J.J.; Otero-Zarraquiños, Ó.; Shammakh, W. Projectile motion via Riemann-Liouville calculus. Adv. Differ. Equ. 2015, 2015, 1231. [Google Scholar] [CrossRef]
- Alharbi, F.M.; Baleanu, D.; Ebaid, A. Physical properties of the projectile motion using the conformable derivative. Chin. J. Phys. 2019, 58, 18–28. [Google Scholar] [CrossRef]
- Ebaid, A.; El-Zahar, E.R.; Aljohani, A.; Salah, B.; Krid, M.; Machado, J.T. Analysis of the two-dimensional fractional projectile motion in view of the experimental data. Nonlinear Dyn. 2019, 97, 1711–1720. [Google Scholar] [CrossRef]
- Seddek, L.; Ebaid, A.; Aljohani, A.; Machado, J.A.T.; Baleanu, D. Re-Evaluating the Classical Falling Body Problem. Mathematics 2020, 8, 553. [Google Scholar] [CrossRef]
- Spiegel, M.R. Schaum’s Outline of Theory and Problems of Theoretical Mechanics; McGraw Hill: New York, NY, USA, 1967. [Google Scholar]
- Poisson, E. Advanced Mechanics; Lecture Notes; Department of Physics, University of Guelph: Guelph, ON, Canada, 2008. [Google Scholar]
- NASA Science. Solar System Exploration. Available online: https://solarsystem.nasa.gov/planets/overview/ (accessed on 27 September 2020).
- Spiegel, M.R. Laplac Transforms; McGraw Hill: New York, NY, USA, 1965. [Google Scholar]
| Case | (Radian) | Cartesian Coordinates of the Release Point Q | (S) | ||||
|---|---|---|---|---|---|---|---|
| Exact (Present) | Approximate [15] | Error | |||||
| 1 | 10 | 10 | 10 | 45.1949 | 45.1754 | 0.0195 | |
| 2 | 20 | 20 | 20 | 63.9154 | 63.8877 | 0.0277 | |
| 3 | 30 | 30 | 30 | 78.2803 | 78.2461 | 0.0342 | |
| 4 | 40 | 40 | 40 | 90.3905 | 90.3508 | 0.0397 | |
| 5 | 50 | 50 | 50 | 101.0598 | 101.0153 | 0.0445 | |
| 6 | 10 | 10 | 10 | 45.2145 | 45.1754 | 0.0391 | |
| 7 | 20 | 20 | 20 | 63.9431 | 63.8877 | 0.0554 | |
| 8 | 30 | 30 | 30 | 78.3143 | 78.2461 | 0.0682 | |
| 9 | 40 | 40 | 40 | 90.4299 | 90.3508 | 0.0791 | |
| 10 | 50 | 50 | 50 | 101.1040 | 101.0153 | 0.0887 | |
| 11 | 10 | 10 | 10 | 45.2340 | 45.1754 | 0.0586 | |
| 12 | 20 | 20 | 20 | 63.9708 | 63.8877 | 0.0831 | |
| 13 | 30 | 30 | 30 | 78.3483 | 78.2461 | 0.1022 | |
| 14 | 40 | 40 | 40 | 90.4692 | 90.3508 | 0.1184 | |
| 15 | 50 | 50 | 50 | 101.1480 | 101.0153 | 0.1327 | |
| 16 | 10 | 10 | 10 | 45.2535 | 45.1754 | 0.0781 | |
| 17 | 20 | 20 | 20 | 63.9984 | 63.8877 | 0.1107 | |
| 18 | 30 | 30 | 30 | 78.3820 | 78.2461 | 0.1359 | |
| 19 | 40 | 40 | 40 | 90.5082 | 90.3508 | 0.1574 | |
| 20 | 50 | 50 | 50 | 101.1916 | 101.0153 | 0.1763 | |
| Case | (Radian) | Cartesian Coordinates of the Release Point Q | Error of Cartesian Coordinates of G | Error of Polar Coordinates of G | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 10 | 10 | 10 | 0.0541 | 0.0538 | 0.0763 | 1.1819 |
| 2 | 0 | 20 | 20 | 20 | 0.2165 | 0.2152 | 0.3053 | 3.3429 |
| 3 | 0 | 30 | 30 | 30 | 0.4875 | 0.4838 | 0.6868 | 6.1413 |
| 4 | 0 | 40 | 40 | 40 | 0.8672 | 0.8596 | 1.2211 | 9.4550 |
| 5 | 0 | 50 | 50 | 50 | 1.3557 | 1.3425 | 1.9079 | 13.2137 |
| 6 | 10 | 10 | 10 | 0.2152 | 0.0541 | 0.0763 | 1.1819 | |
| 7 | 20 | 20 | 20 | 0.4838 | 0.2165 | 0.3053 | 3.3429 | |
| 8 | 30 | 30 | 30 | 0.8596 | 0.4875 | 0.6868 | 6.1413 | |
| 9 | 40 | 40 | 40 | 1.3425 | 0.8672 | 1.2211 | 9.4550 | |
| 10 | 50 | 50 | 50 | 0.2152 | 1.3557 | 1.9079 | 13.2137 | |
| Case | (Radian) | Cartesian Coordinates of the Release Point Q | Error of Cartesian Coordinates of G | |||
|---|---|---|---|---|---|---|
| 1 | 10 | 10 | 10 | 14.9922 | 0.0303 | |
| 2 | 20 | 20 | 20 | 30.1361 | 0.1487 | |
| 3 | 30 | 30 | 30 | 45.4317 | 0.3619 | |
| 4 | 40 | 40 | 40 | 60.8793 | 0.6722 | |
| 5 | 50 | 50 | 50 | 76.4789 | 1.0808 | |
| 6 | 10 | 10 | 10 | 17.3067 | 0.0407 | |
| 7 | 20 | 20 | 20 | 34.7489 | 0.1782 | |
| 8 | 30 | 30 | 30 | 52.3271 | 0.4166 | |
| 9 | 40 | 40 | 40 | 70.0412 | 0.7570 | |
| 10 | 50 | 50 | 50 | 87.8912 | 1.2004 | |
| 11 | 10 | 10 | 10 | 14.9911 | 0.0623 | |
| 12 | 20 | 20 | 20 | 30.0799 | 0.2398 | |
| 13 | 30 | 30 | 30 | 45.2667 | 0.5302 | |
| 14 | 40 | 40 | 40 | 60.5515 | 0.9327 | |
| 15 | 50 | 50 | 50 | 75.9343 | 1.4469 | |
| 16 | 10 | 10 | 10 | 4.8873 × 10−8 | 21.9937 | |
| 17 | 20 | 20 | 20 | 3.9099 × 10−7 | 62.2715 | |
| 18 | 30 | 30 | 30 | 1.3196 × 10−6 | 114.4901 | |
| 19 | 40 | 40 | 40 | 3.1280 × 10−6 | 176.3861 | |
| 20 | 50 | 50 | 50 | 6.1094 × 106 | 246.6514 | |
| Planet | Ratio of Acceleration Due to Gravity [Earth = 1] | Acceleration Due to Gravity [m/s2] | Radius (km) | Rotation Period (in Earth Days) | Angular Velocity [s−1] |
|---|---|---|---|---|---|
| Mercury | 0.38 | 3.7278 | 2439 | 58.65 | 1.24 × 10−6 |
| Venus | 0.9 | 8.829 | 6052 | 243 | 2.99 × 10−7 |
| Earth | 1 | 9.80 | 6378 | 1.00 | 7.27 × 10−5 |
| Mars | 0.38 | 3.7278 | 3394 | 1.03 | 7.10 × 10−5 |
| Jupiter | 2.64 | 25.8984 | 71,400 | 0.41 | 1.80 × 10−4 |
| Saturn | 0.93 | 9.1233 | 60,000 | 0.44 | 1.70 × 10−4 |
| Uranus | 0.89 | 8.7309 | 25,559 | 0.72 | 1.0 × 10−4 |
| Neptune | 1.12 | 10.9872 | 24,764 | 0.72 | 1.0 × 10−4 |
| Planet | Errors of Falling Time (T) [S] | ||
|---|---|---|---|
| Mercury | 0.000022 | 0.02334 | 0.00103 |
| Venus | 0.000020 | 0.00714 | 0.00003 |
| Earth | 0.044593 | 76.48 | 1.08084 |
| Mars | 0.098546 | 104.25 | 2.80507 |
| Jupiter | 0.707271 | 1982.68 | 7.62458 |
| Saturn | 2.586710 | 4332.41 | 29.9594 |
| Uranus | 0.396289 | 642.56 | 0.43672 |
| Neptune | 0.271695 | 493.98 | 0.01481 |
| Planet | Errors of Falling Time (T) [S] | ||
|---|---|---|---|
| Mercury | 0.00004 | 0.02637 | 0.00103 |
| Venus | 0.00001 | 0.00153 | 0.00003 |
| Earth | 0.08874 | 87.8912 | 1.20038 |
| Mars | 0.19522 | 119.268 | 3.06653 |
| Jupiter | 1.43850 | 2341.8 | 3.25094 |
| Saturn | 5.37170 | 5262.61 | 16.1197 |
| Uranus | 0.79587 | 746.424 | 0.99274 |
| Neptune | 0.54491 | 572.814 | 0.99814 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebaid, A.; Alharbi, W.; Aljoufi, M.D.; El-Zahar, E.R. The Exact Solution of the Falling Body Problem in Three-Dimensions: Comparative Study. Mathematics 2020, 8, 1726. https://doi.org/10.3390/math8101726
Ebaid A, Alharbi W, Aljoufi MD, El-Zahar ER. The Exact Solution of the Falling Body Problem in Three-Dimensions: Comparative Study. Mathematics. 2020; 8(10):1726. https://doi.org/10.3390/math8101726
Chicago/Turabian StyleEbaid, Abdelhalim, Weam Alharbi, Mona D. Aljoufi, and Essam R. El-Zahar. 2020. "The Exact Solution of the Falling Body Problem in Three-Dimensions: Comparative Study" Mathematics 8, no. 10: 1726. https://doi.org/10.3390/math8101726
APA StyleEbaid, A., Alharbi, W., Aljoufi, M. D., & El-Zahar, E. R. (2020). The Exact Solution of the Falling Body Problem in Three-Dimensions: Comparative Study. Mathematics, 8(10), 1726. https://doi.org/10.3390/math8101726






