A Case Study of a Lesson on the Sample Mean for Prospective Mathematics Teachers
Abstract
1. Introduction
- What are the students’ misconceptions regarding the sample mean that are revealed when the exploratory lesson is performed?
- What do students gain through the exploratory lesson that implements Keller’s ARCS model of motivational design theory?
2. Theoretical Background
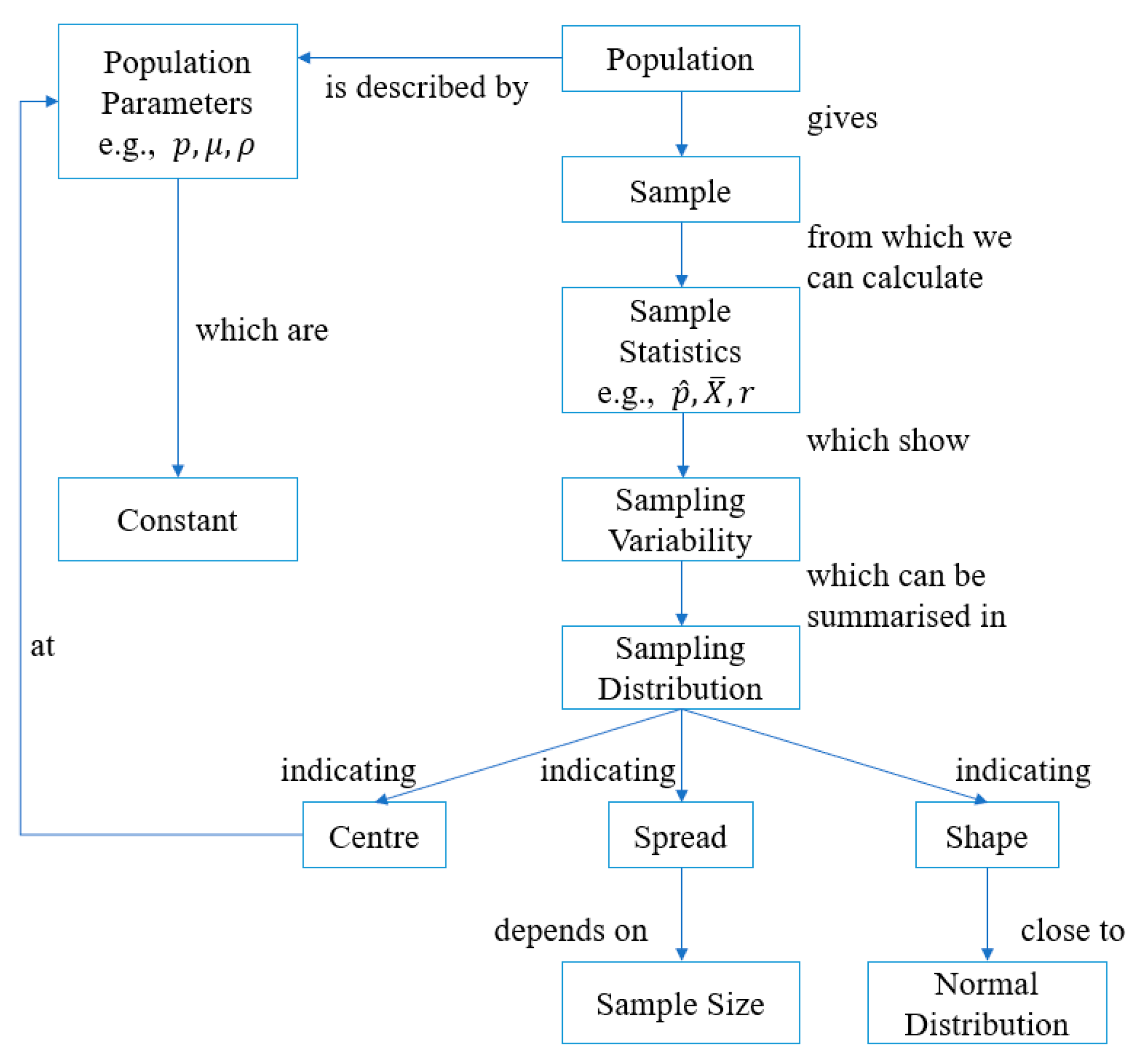
2.1. Key Concepts Concerning the Sample Mean and the Sampling Distribution
2.2. Keller’s ARCS Model of Motivational Design Theory
- The motivation for learning is defined in a way to enable the teachers to observe actual changes by their measures.
- The motivation for learning is defined in a way that can be easily understood by other teachers or class designers.
- The motivation for learning enables the teachers to manipulate the motivation for learning.
3. Methodology
3.1. Participants and Context
3.2. Data Collection
3.2.1. Learning Hierarchy for Sample Mean and Sampling Distribution
3.2.2. Design of Exploratory Lesson Using Strategies of Keller’s ARCS Model
4. Findings
4.1. Identifying the Misconceptions of Prospective Teachers
4.1.1. Misconceptions about the Population in the Dice-Rolling Exploration
“In this rolling-a-dice exploration, can you describe what the population is and what its distribution looks like?”
4.1.2. Misconception about the Sample Size in the Dice-Rolling Exploration
“What do you think the sample size is in this rolling-a-dice exploration?”
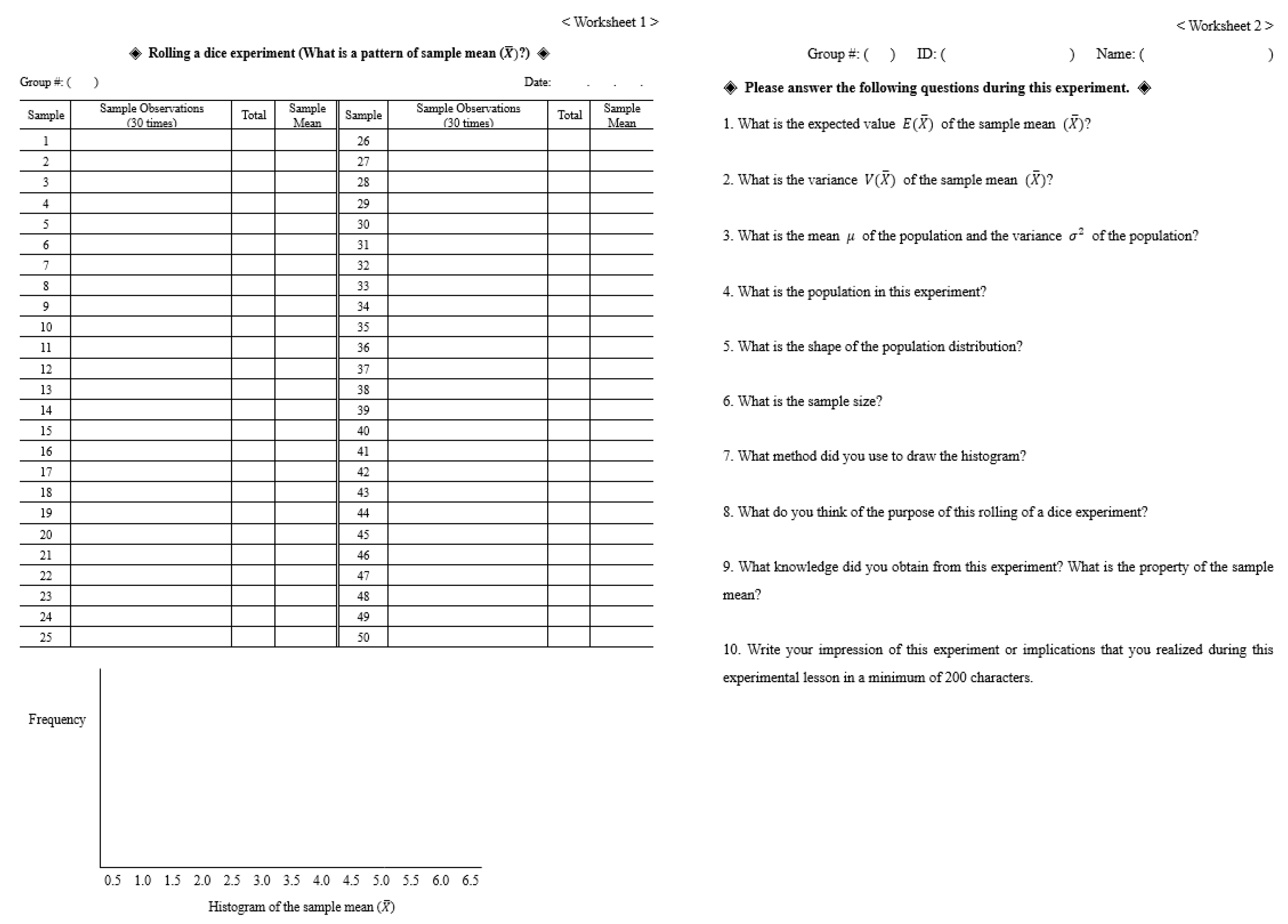
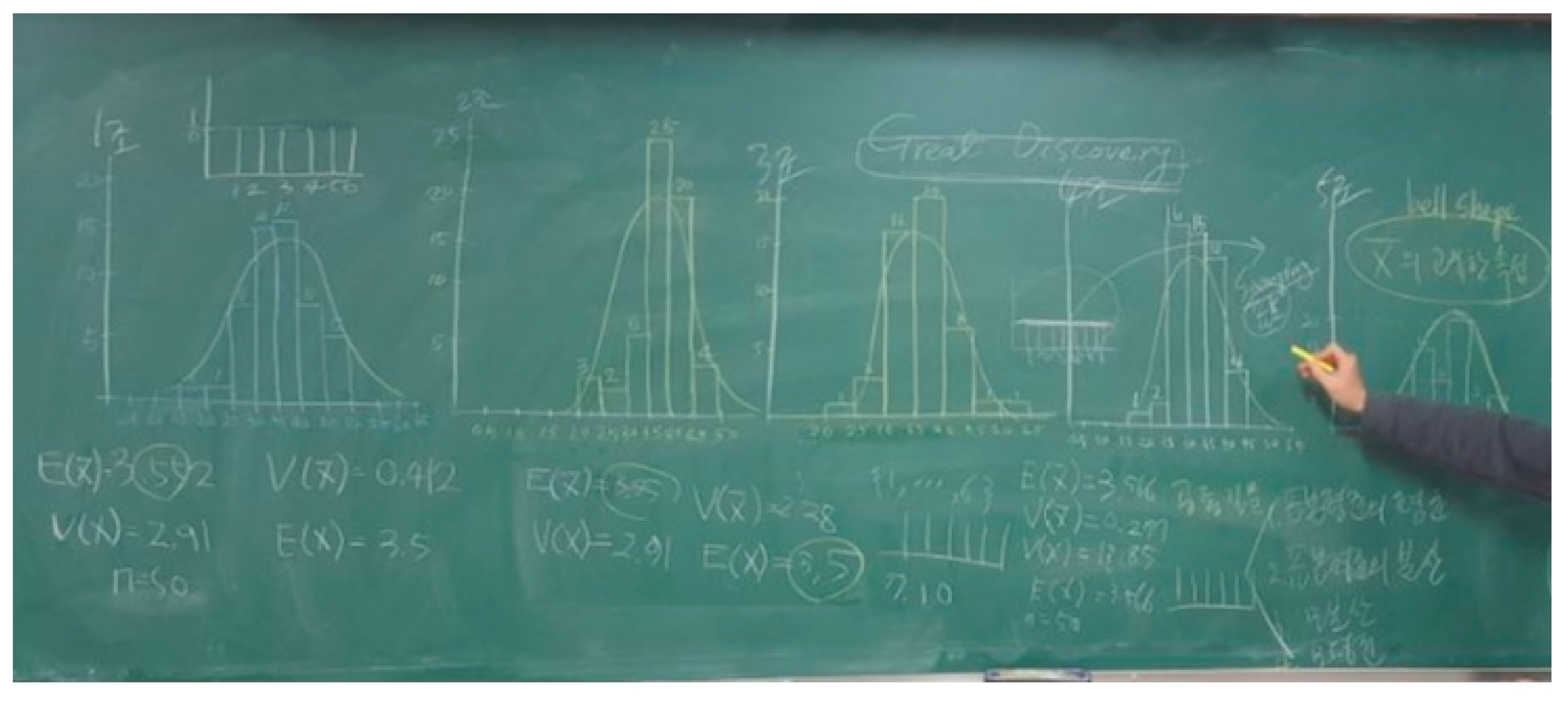
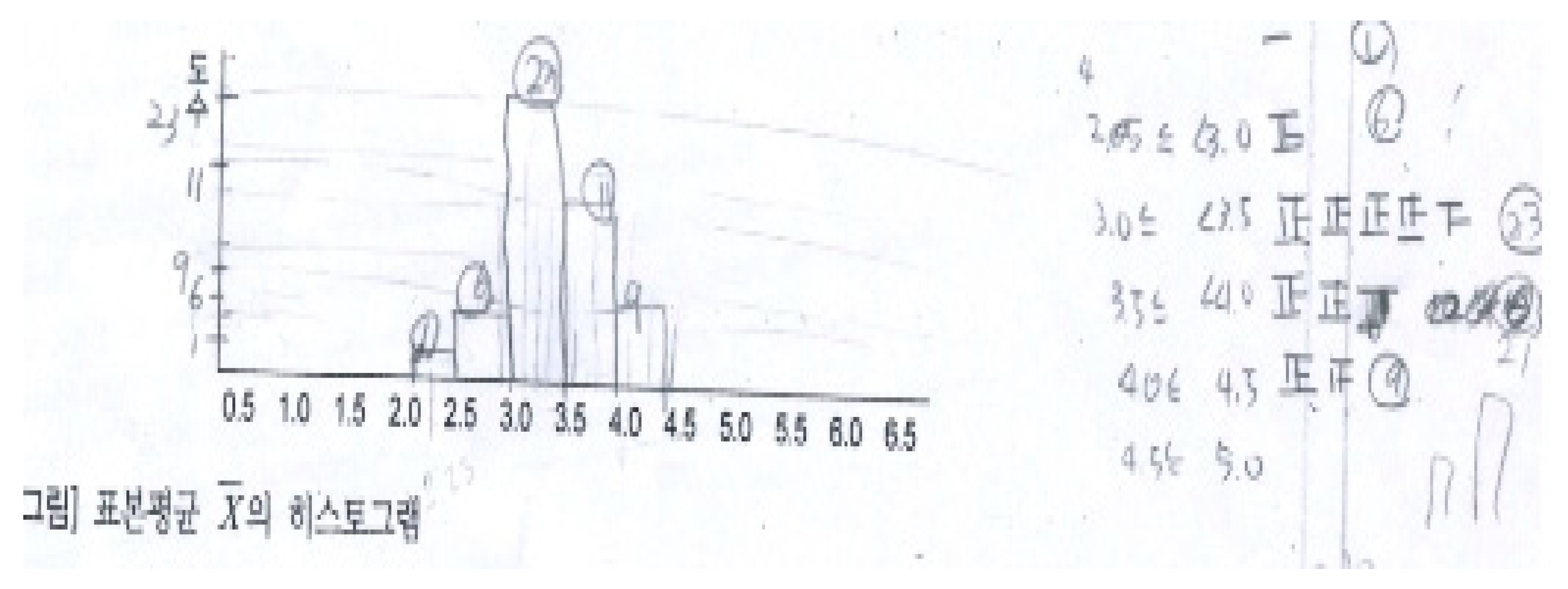
4.2. An Anecdote about Discovering the Property of Sample Mean Distribution
5. Discussion
Funding
Conflicts of Interest
References
- Garfield, J. The challenge of developing statistical reasoning. J. Stat. Educ. 2002, 10, 1–12. [Google Scholar] [CrossRef]
- Lipson, K. The role of the sampling distribution in understanding statistical inference. Math. Educ. Res. J. 2003, 15, 270–287. [Google Scholar] [CrossRef]
- Mills, J. Using computer simulation methods to teach statistics: A review of the literature. J. Stat. Educ. 2002, 10, 1–20. [Google Scholar]
- Williams, A.M. Student’s Understanding of the Significance Level Concepts. In Statistical Education-Expanding the Network Proceedings of the 5th International Conference on Teaching Statistics, Singapore, 21–26 June 1998; Pereira-Mendoza, L., Kea, L.S., Kee, T.W., Wong, W., Eds.; International Statistics Institute: Voorburg, The Netherlands, 1998; Volume 2, pp. 743–749. [Google Scholar]
- Lipson, K. The Role of the Sampling Distribution in Developing Understanding of the Statistical Inference. Ph.D. Thesis, Swinburne University of Technology, Melbourne, Australia, 2000. [Google Scholar]
- Moore, D.S.; McCabe, G.P. Introduction to the Practice of Statistics, 3rd ed.; W. H. Freeman and Company: New York, NY, USA, 1999. [Google Scholar]
- Ben-Zvi, D.; Garfield, J. Statistical literacy, reasoning, and thinking: Goals, definitions, and challenges. In The Challenge of Developing Statistical Literacy, Reasoning and Thinking; Ben-Zvi, D., Garfield, J., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; pp. 3–15. [Google Scholar]
- Chance, B.; delMas, R.C.; Garfield, J. Reasoning about sampling distributions. In The Challenge of Developing Statistical Literacy, Reasoning and Thinking; Ben-Zvi, D., Garfield, J., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; pp. 295–323. [Google Scholar]
- Lipson, K. The Role of Computer Based Technology in Developing Understanding of the Sampling Distribution. In Developing a Statistically Literate Society Proceedings of the 6th International Conference on Teaching Statistics, Capetown, South Africa, 7–12 July 2002; Phillips, B., Ed.; International Statistics Institute: Voorburg, The Netherlands, 2002; pp. 1–6. [Google Scholar]
- Shaughnessy, J.M. Research in probability and statistics: Reflections and directions. In Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics; Grouws, D.A., Ed.; Macmillan: New York, NY, USA, 1992; pp. 465–494. [Google Scholar]
- Sotos, A.E.C.; Vanhoof, S.; Van den Noortgate, W.; Onghena, P. Students’ misconceptions of statistical inference: A review of the empirical evidence from research on statistics education. Educ. Res. Rev. 2007, 2, 98–113. [Google Scholar] [CrossRef]
- Yu, C.; Behrens, J.T.; Anthony, S. Identification of misconceptions in the central limit theorem and related concepts and evaluation of computer media as a remedial tool. In ERIC Document Reproduction Service No. 395 989; ERIC: New Orleans, LA, USA, 1995; pp. 1–15. [Google Scholar]
- Simon, J.L. What some puzzling problems teach about the theory of simulation and the use of resampling. Am. Stat. 1994, 48, 290–293. [Google Scholar]
- Saldanha, L.A.; Thompson, P.W. Students’ Reasoning about Sampling Distributions and Statistical Inference. In Proceedings of the Twenty-Third Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Snowbird, UT, USA, 18–21 October 2001; Speiser, R., Maher, C., Charles, W., Eds.; ERIC Clearinghouse: Columbus, OH, USA, 2001; Volume 1, pp. 449–454. [Google Scholar]
- Hancock, S.A.; Rummerfield, W. Simulation methods for teaching sampling distributions: Should hands-on activities precede the computer? J. Stat. Educ. 2020, 28, 9–17. [Google Scholar] [CrossRef]
- Keller, J.M. The use of the ARCS model of motivation in teacher training. In Aspects of Educational Technology; Trott, K.S.A.J., Ed.; Kogan Page: London, UK, 1984; Volume 17, pp. 140–145. [Google Scholar]
- Wong, H.K.; Wong, R.T. The First Days of School: How to Be an Effective Teacher; Harry K Wong Publishing Company: Sunnyvale, CA, USA, 2009. [Google Scholar]
- Agresti, A.; Finlay, B. Statistical Methods for the Social Sciences, 4th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Garfield, J.; delMas, R.C.; Chance, B. Tools for Teaching and Assessing Statistical Inference. 2002. Available online: http://www.gen.umn.edu/faculty_staff/delmas/stat_tools/index.html (accessed on 23 April 2003).
- Keller, J.M. The arcs model of motivational design. In Motivational Design for Learning and Performance; Springer: Boston, MA, USA, 2010; pp. 43–74. [Google Scholar]
- Keller, J.M.; Song, S.H. Charming Instruction Design; Kyoukkwahaksa: Seoul, Korea, 1999. [Google Scholar]
- Zerbolio, D.J., Jr. A ‘bag of tricks’ for teaching about sampling distributions. Teach. Psychol. 1989, 16, 207–209. [Google Scholar] [CrossRef]
- Hodgson, T. The Effects of Hands-on Activities on Students’ Understanding of Selected Statistical Concepts. In Proceedings of the Eighteenth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Panama City, FL, USA, 12–15 October 1996; Jakubowski, E., Watkins, D., Biske, H., Eds.; ERIC Clearinghouse for Science, Mathematics, and Environmental Education: Columbus, OH, USA, 1996; Volume 1, pp. 241–246. [Google Scholar]
- Dyck, J.L.; Gee, N.R. A sweet way to teach students about the sampling distribution of the mean. Teach. Psychol. 1998, 25, 192–195. [Google Scholar] [CrossRef]
- Harradine, A.; Batanero, C.; Rossman, A. Students and teachers’ knowledge of sampling and inference. In Teaching Statistics in School Mathematics-Challenges for Teaching and Teacher Education; Batanero, C., Burrill, G., Reading, C., Eds.; Springer: Dordrecht, The Netherlands, 2011; Volume 14, pp. 235–246. [Google Scholar]

| Prior Knowledge for Learning the Sampling Distribution |
|---|
| The concept of variability, random variables, and variance |
| The concept of central tendency and dispersion or spread |
| The concept of distribution: normal, skewed, uniform, and bimodal |
| Being able to read and interpret graphical displays of quantitative data and describe the overall pattern of variation |
| Properties of normal distribution |
| Probability related to density curve and area |
| The concept of sampling |
| The concept of random samples |
| The relationship between a sample statistic and a population parameter |
| A sampling distribution of sample means (based on quantitative data) is a distribution of all possible sample means (statistics) for a given sample size randomly sampled from a population with mean and standard deviation . It is a probability distribution for the sample mean. |
| The sampling distribution for means has the same mean as the population. |
| As the sample size () gets larger, the variability of the sample means gets smaller (a statement, a visual recognition, and predicting what will happen or how the next picture will differ). |
| Standard error of the mean is a measure of variability of sample statistic values. |
| The building block of a sampling distribution is a sample statistic. |
| Some values of statistics are more or less likely than others to be drawn from a particular population. |
| The normal approximation applies in some situations but not others. |
| If the normal approximation applies, then the empirical rule can be applied to make statements about how often the sample statistic will fall within, say, 2 standard deviations of the mean. |
| Different sample sizes lead to different probabilities for the same statistic value (know how sample size affects the probability of different outcomes for a statistic). |
| Sampling distributions tend to have the shape of a normal distribution rather than the shape of the population distribution, even for small samples. |
| As sample sizes get very large, all sampling distributions for means look alike (i.e., have the same shape) regardless of the population from which they are drawn. |
| Averages are more normal and less variable than individual observations. |
| Be able to distinguish between a distribution of observations in one sample and a distribution of statistics (sample means) from many samples (sample size greater than 1) that have been randomly selected. |
| Believe sampling distribution should look like the population (for sample size ). |
| Think sampling distribution should look more like the population as the sample size increases (generalizes expectations for a single sample of observed values to a sampling distribution). |
| Predict that sampling distributions for small and large sample sizes have the same variability. |
| Believe sampling distributions for large samples have more variability. |
| Do not understand that a sampling distribution is a distribution of sample statistics. |
| Confuse one sample (real data) with all possible samples (in distribution) or potential samples. |
| Pay attention to the wrong things, for example, heights of histogram bars. |
| Think the mean of a positive skewed distribution will be greater than the mean of the sampling distribution for samples taken from this population. |
| Major Categories | Strategies | Descriptions |
|---|---|---|
| Attention | Perceptual arousal (A1) | Use audiovisual materials such as animations, illustrations, diagrams, graphs, sound, and glitter effects that generate the students’ curiosity and emotions. |
| Inquiry arousal (A2) | Engage students in a problem-solving experiential situation to pose or create their own questions, carry out exploratory activities, and solve problems. | |
| Variability (A3) | Modify the components of the class, adopt different approaches to class management, and mix a variety of activities such as practice, quizzes, presentations, and class discussions to sustain the students’ attention. | |
| Relevance | Goal orientation (R1) | Set achievable goals and have the students perceive usefulness of the new knowledge to them. |
| Motive matching (R2) | Ensure that the lesson matches with the students’ learning styles and personal motive structures. | |
| Familiarity (R3) | Use examples, terminologies, or concepts related to the students’ preexisting beliefs, prior knowledge, experience, or values. | |
| Confidence | Learning requirements (C1) | Present clearly the performance requirements for successful learning and the criteria for evaluation to the students. |
| Success opportunities (C2) | Provide challenging tasks and have the students experience successes in the learning or practicing process. | |
| Personal control (C3) | Provide opportunities for students to control their learning and give feedback to support their personal endeavors and skills. | |
| Satisfaction | Natural consequences (S1) | Provide the learners with opportunities to acquire and apply new skills and knowledge to maintain their intrinsic enjoyment in learning. |
| Positive consequences (S2) | Provide positive verbal feedback or appropriate external reward such as incentives, trophies, and special privileges to students. Do not reward the students’ incorrect responses. | |
| Equity (S3) | Ensure that course purpose, expectations, and outcomes are consistent with initial presentations and that consistent standards for measuring students’ academic achievements are maintained. |
| Propositions |
|---|
| Samples are selected from populations. |
| Populations (distributions) are described by parameters. |
| Parameters are constant in value. |
| Samples are described by statistics. |
| Statistics are variable quantities. |
| The distribution of a sample statistics is known as a sampling distribution. |
| The sampling distribution of the sample statistic is approximately normal. |
| The sampling distribution of the sample statistic is characterized by shape, center, spread. |
| The spread of the sampling distribution is related to the sample size. |
| The sampling distribution is centered at the population parameter. |
| Lesson Stages | Activities | Concepts for Sampling Distribution | Keller’s Strategies of ARCS |
|---|---|---|---|
| Introduction | Types of mean Types of distribution | Population Sample Sample statistics Sample mean | A2 Inquiry arousal |
| Exploration | Rolling a dice exploration Worksheet | Sampling Sample mean Sampling variability Sampling distribution | A3 Variability R2 Motive Matching R3 Familiarity C1 Learning requirements C3 Personal control |
| Development | Presentation and discussion Question and answer | Center, Spread, Shape Normal distribution Central limit theorem | C2 Success opportunities S1 Natural consequences |
| Ending | Summary | Correction of misconceptions Confirmation of central limit theorem | S1 Natural consequences |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S. A Case Study of a Lesson on the Sample Mean for Prospective Mathematics Teachers. Mathematics 2020, 8, 1706. https://doi.org/10.3390/math8101706
Kim S. A Case Study of a Lesson on the Sample Mean for Prospective Mathematics Teachers. Mathematics. 2020; 8(10):1706. https://doi.org/10.3390/math8101706
Chicago/Turabian StyleKim, Somin. 2020. "A Case Study of a Lesson on the Sample Mean for Prospective Mathematics Teachers" Mathematics 8, no. 10: 1706. https://doi.org/10.3390/math8101706
APA StyleKim, S. (2020). A Case Study of a Lesson on the Sample Mean for Prospective Mathematics Teachers. Mathematics, 8(10), 1706. https://doi.org/10.3390/math8101706




