Exploring a Convection–Diffusion–Reaction Model of the Propagation of Forest Fires: Computation of Risk Maps for Heterogeneous Environments
Abstract
1. Introduction
2. Summary of the Mathematical Model
3. Numerical Method
4. Numerical Results
4.1. Preliminaries
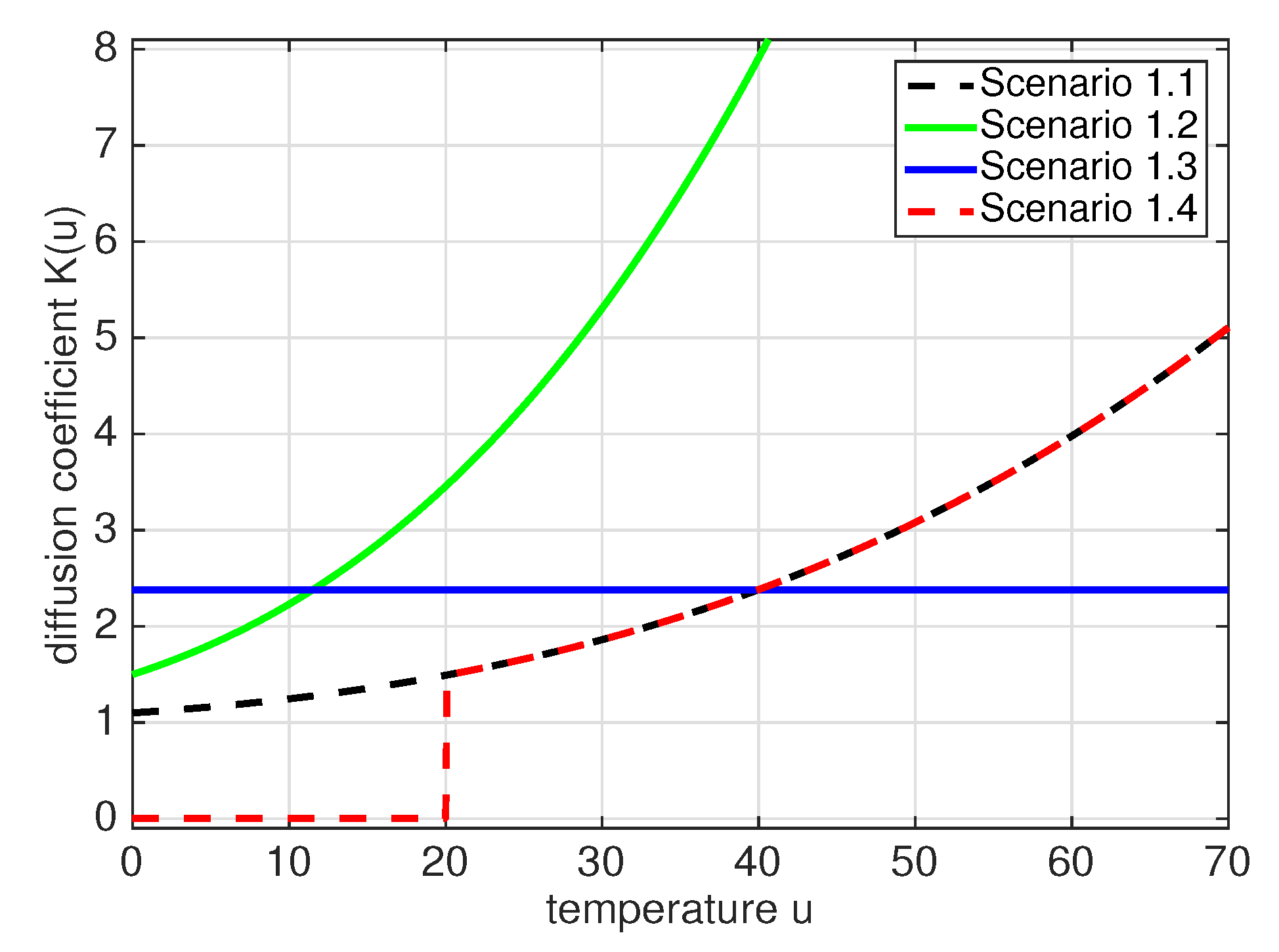
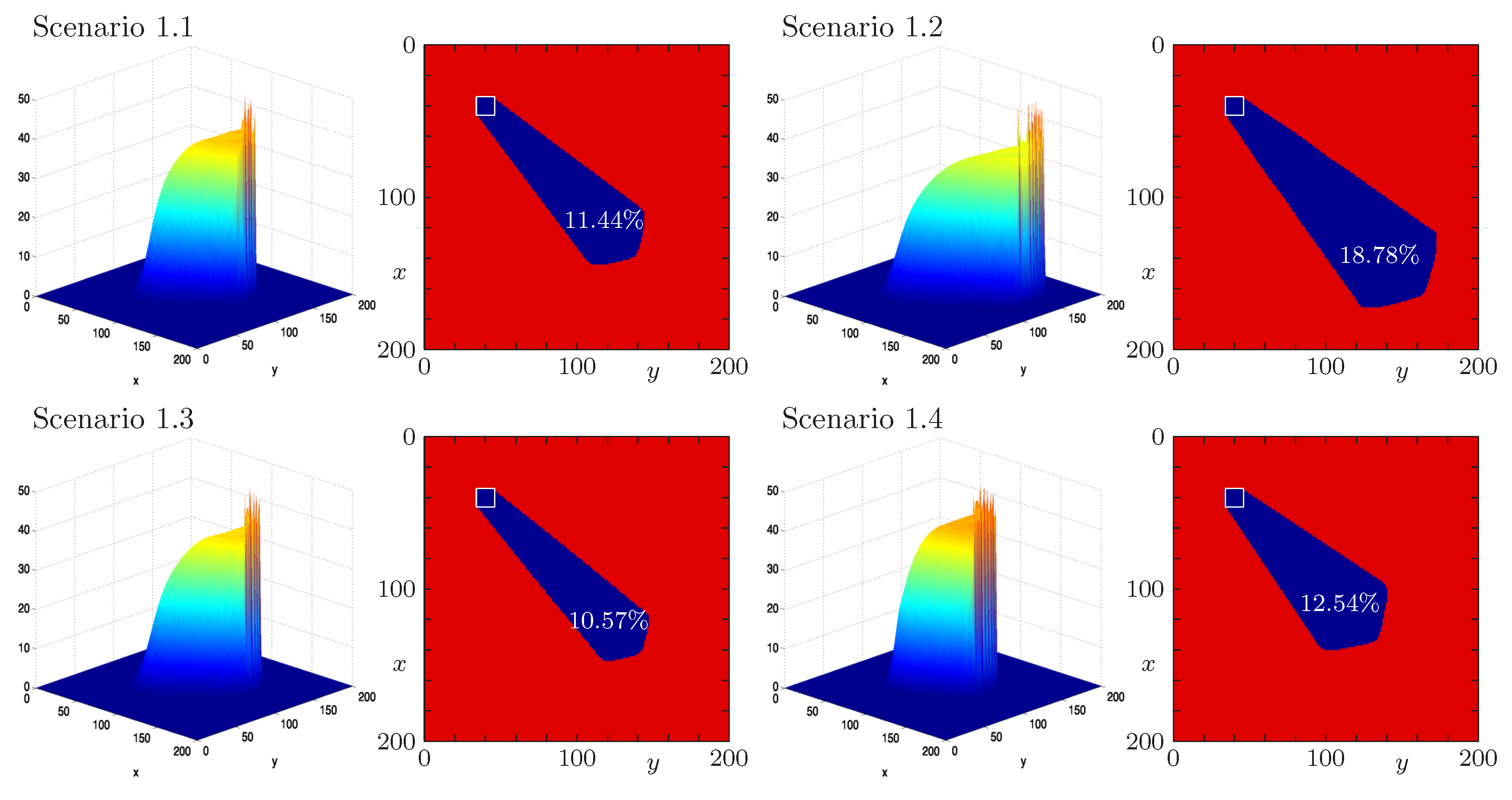
4.2. Scenarios 1.1 to 1.4: Numerical Experiments with Various Diffusion Coefficients
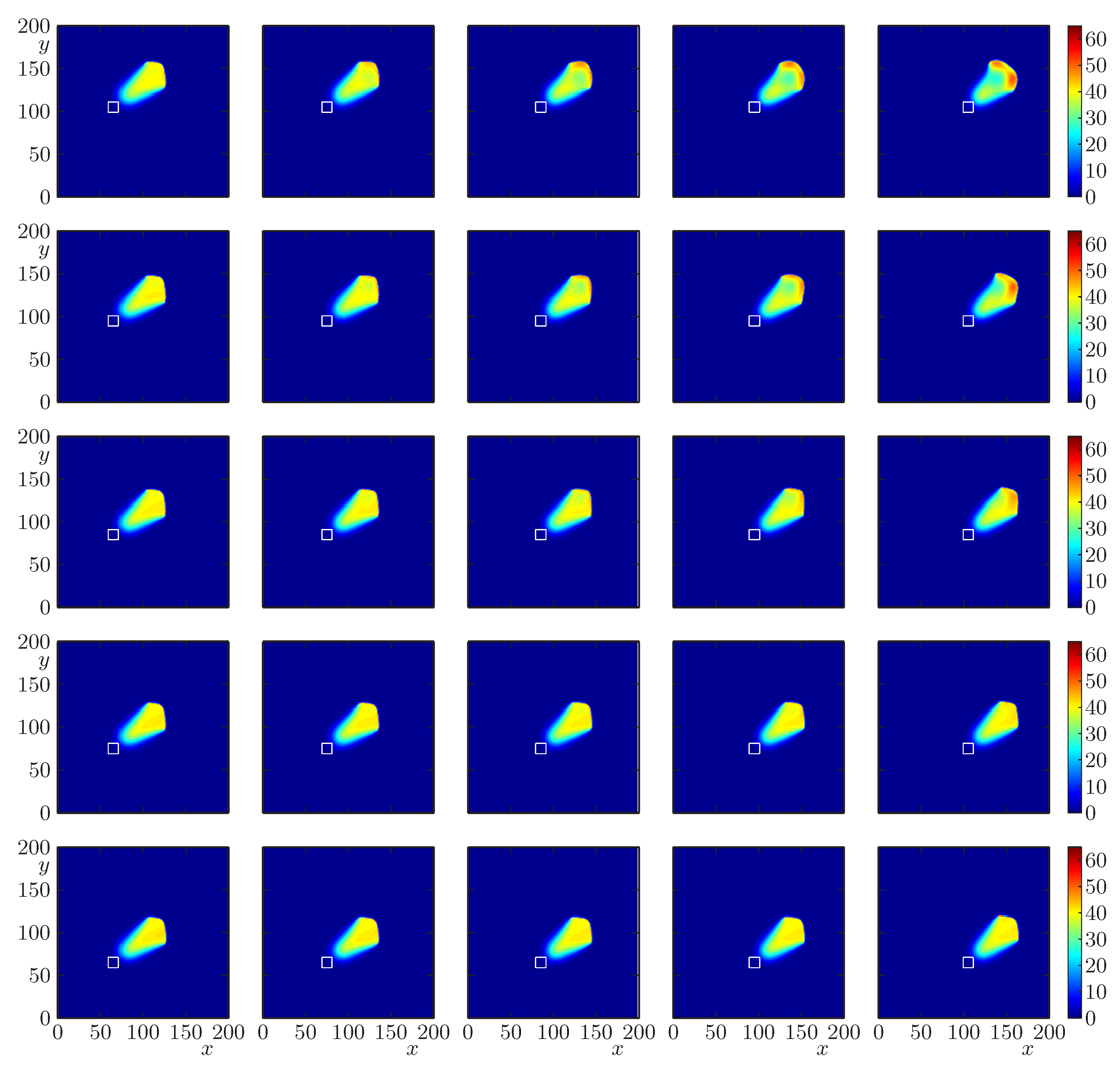
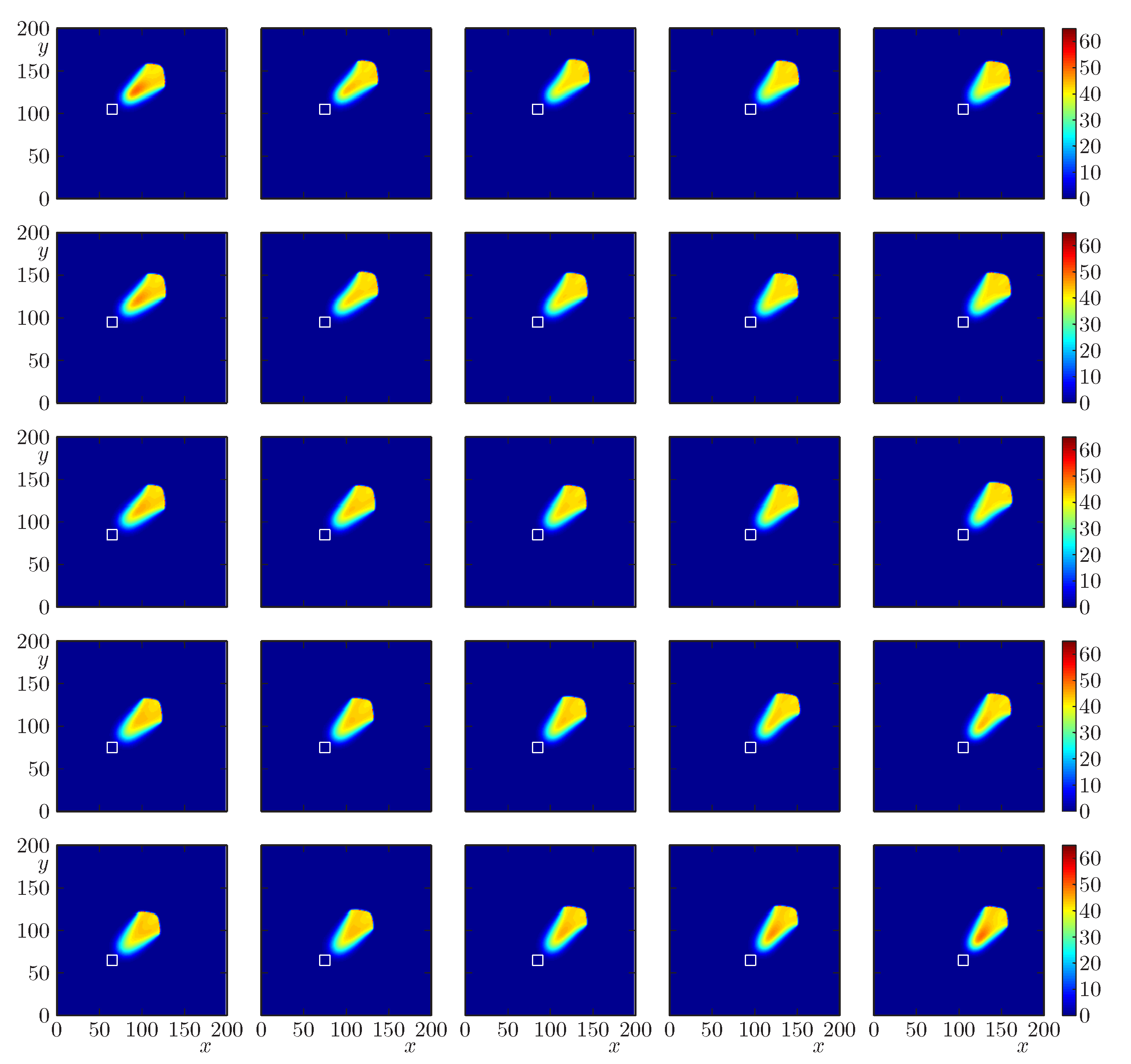
4.3. Scenarios 2.0 to 2.4: Effect of the Variability of Topography
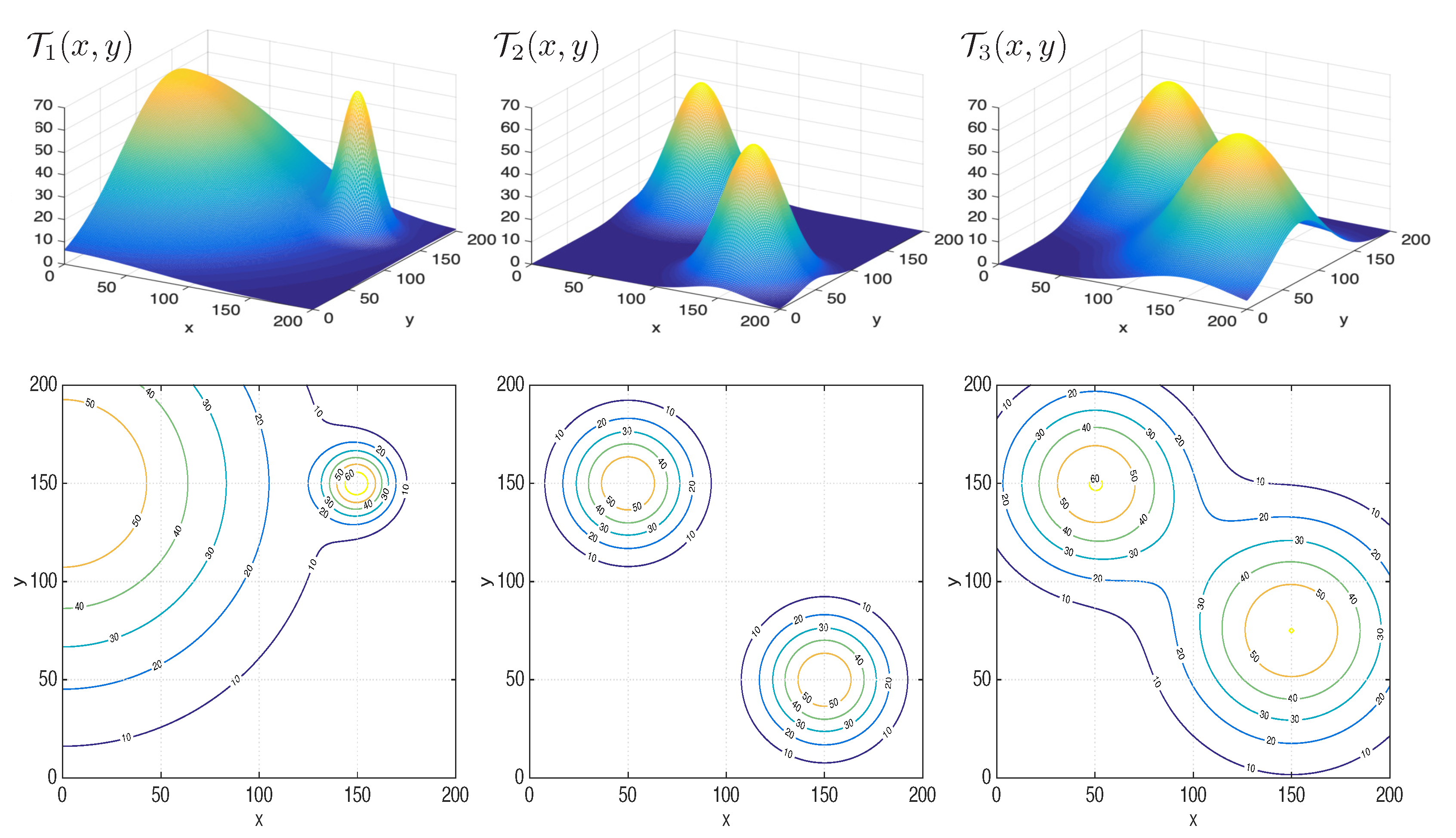
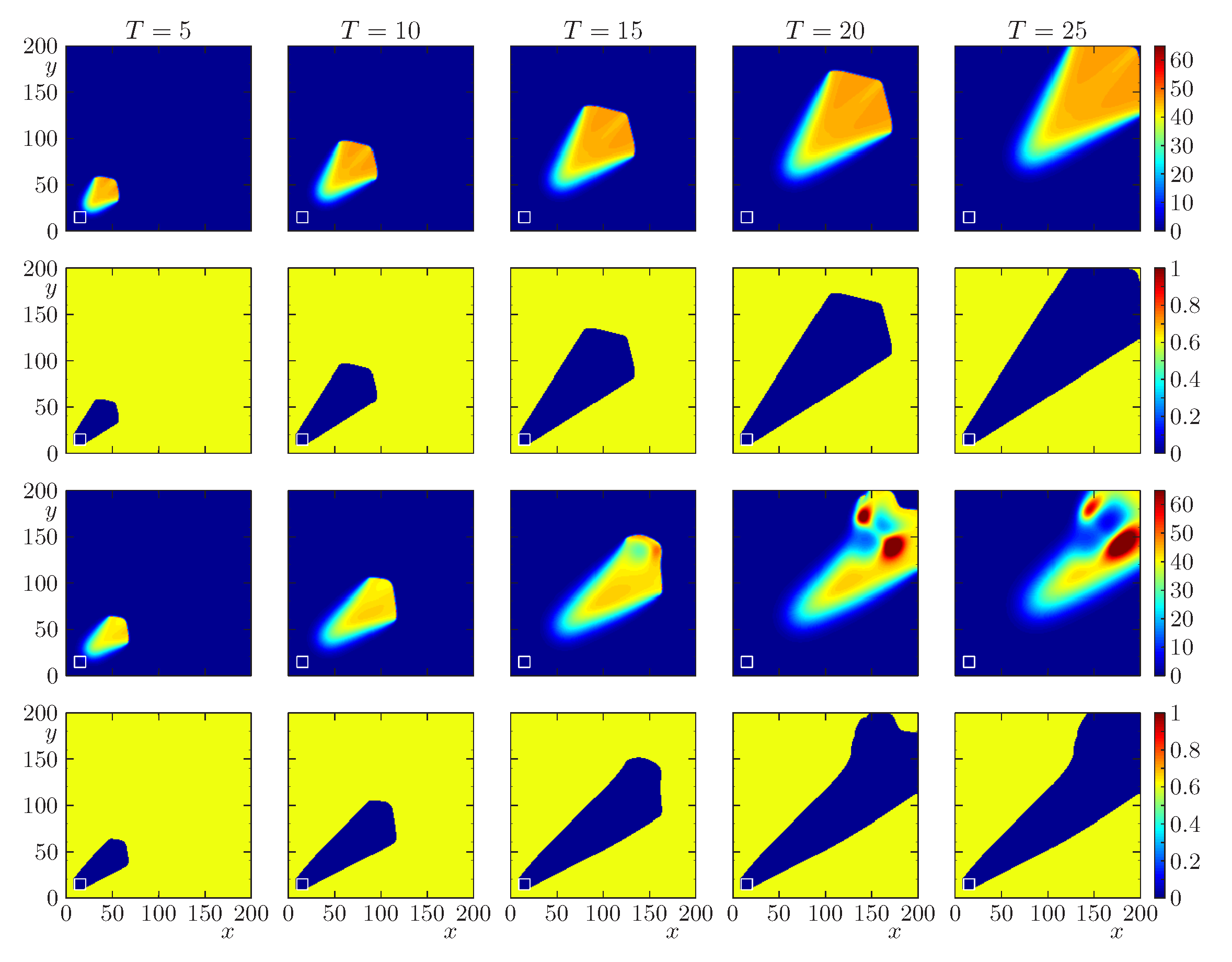
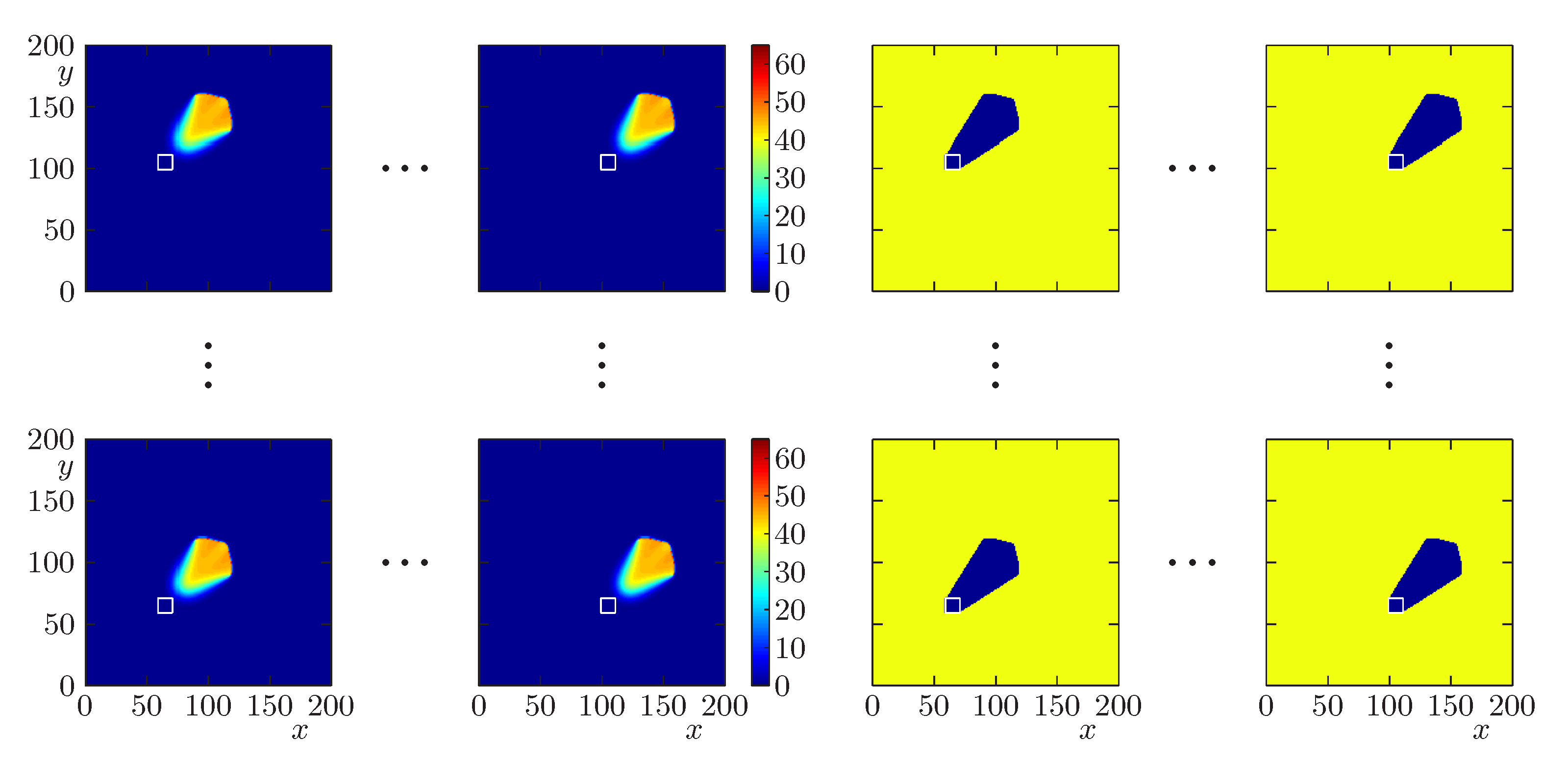
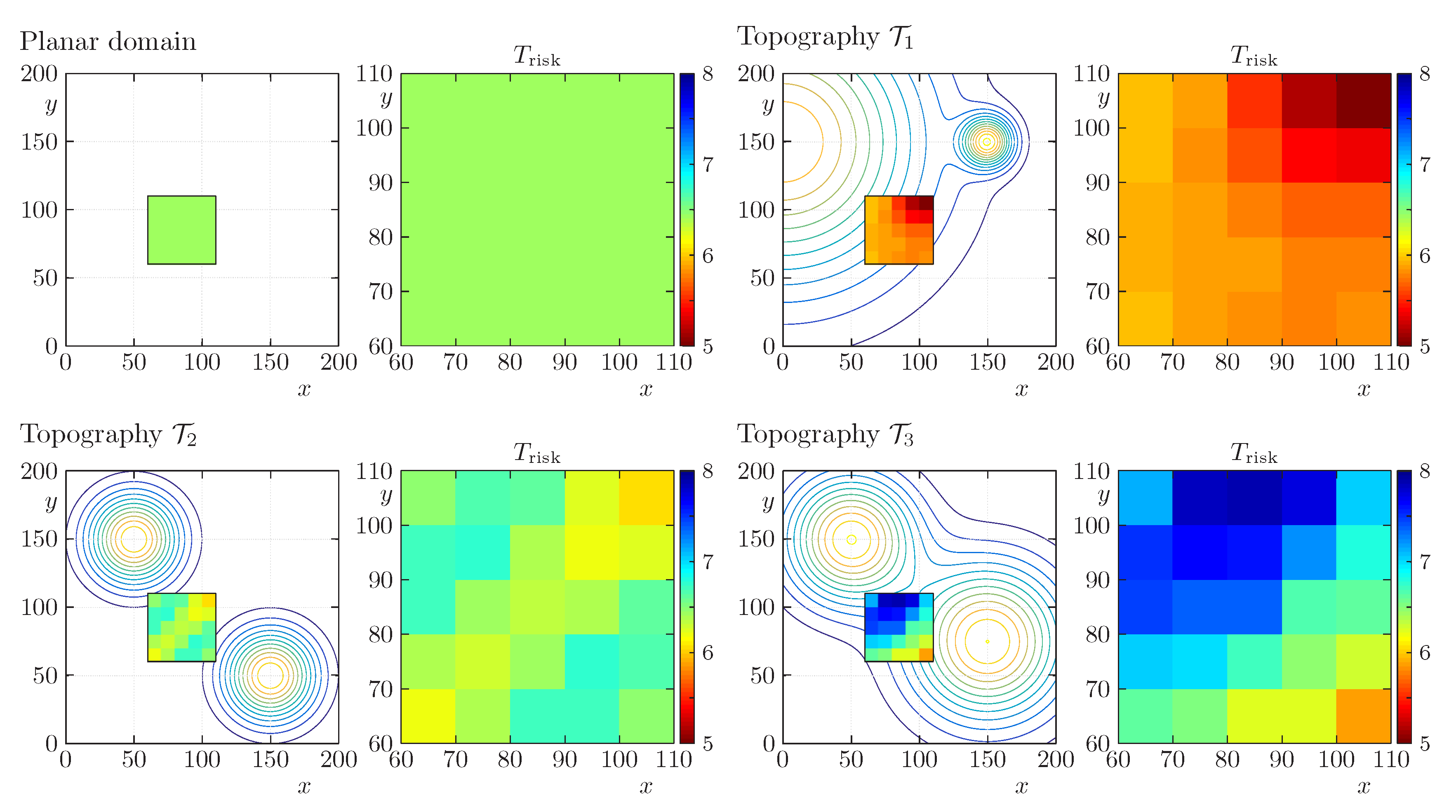
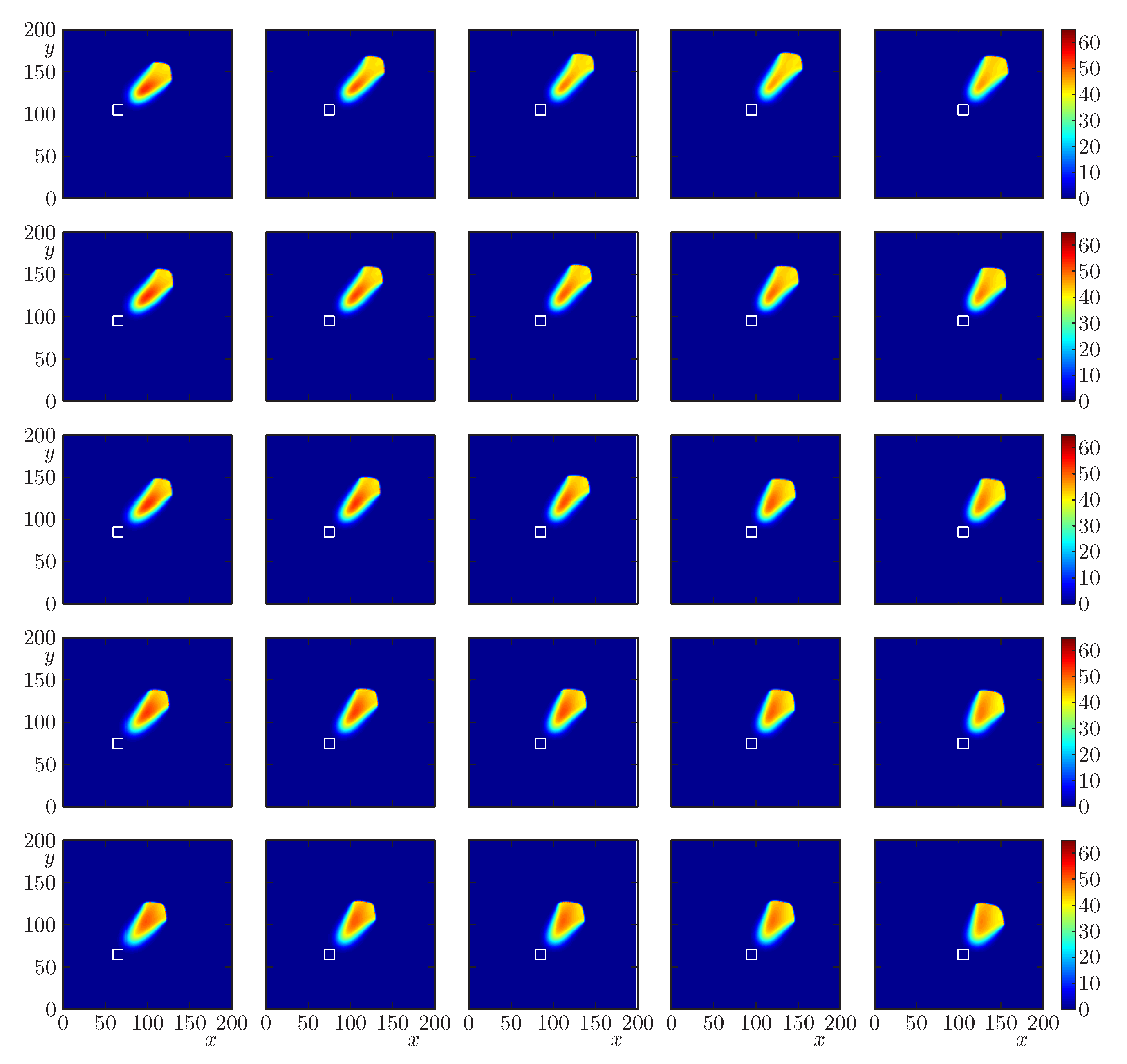
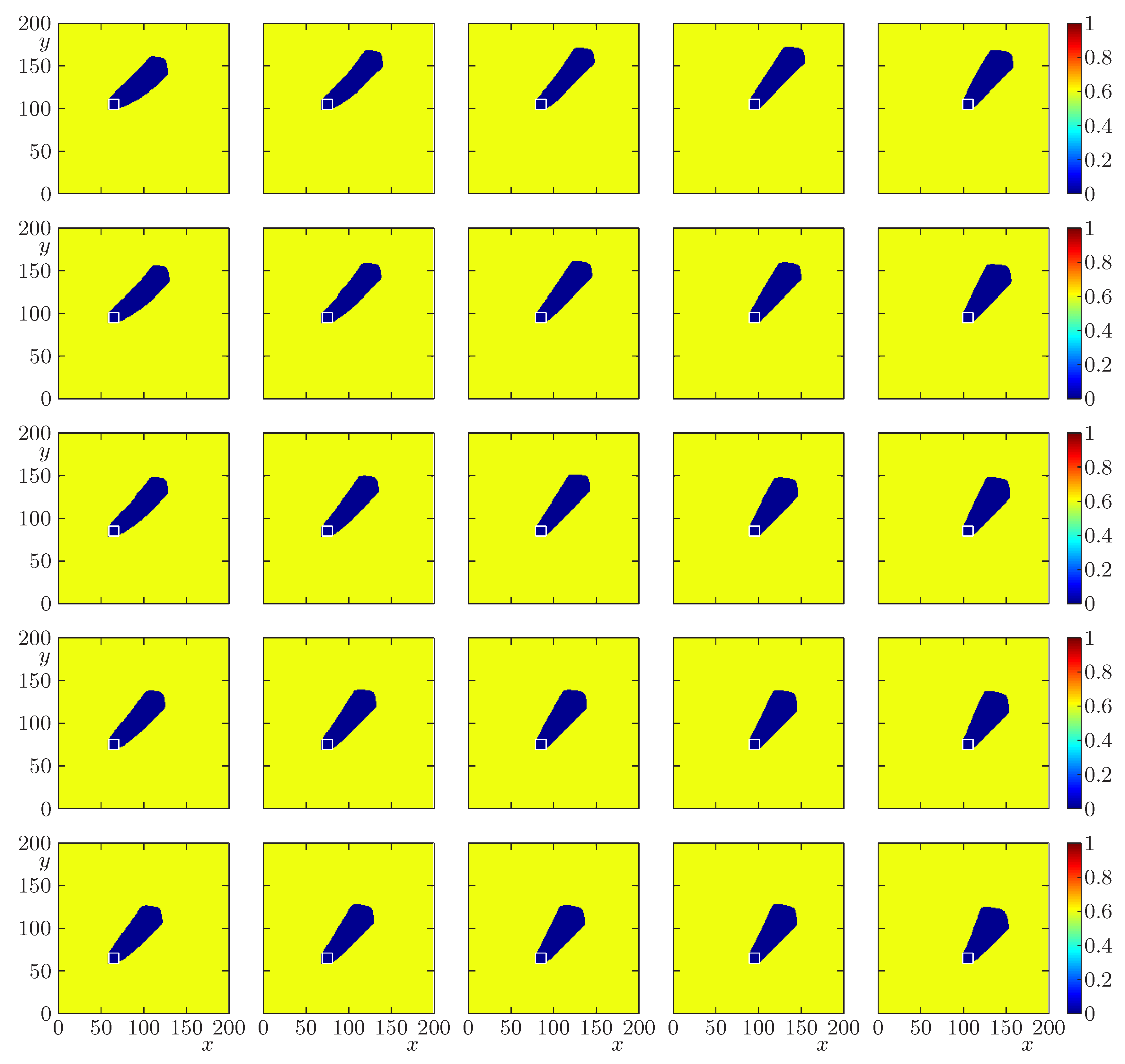
4.4. Scenarios 3.1 to 3.4: Risk Maps
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| List of symbols: | |
| Latin symbols: | |
| A | pre-exponential factor [s−1] |
| C | specific heat [kJ/(kg K)] |
| phase change function [-] | |
| discretization of convective term [-] | |
| discretization of diffusive term [-] | |
| reaction energy [ kcal/mol] | |
| numerical flux in the l-coordinate [-] | |
| reactive term for u [-] | |
| reactive term for v [-] | |
| index vector [-] | |
| k | conductivity coefficient [W/(mK)] |
| approximate value [-] | |
| diffusion coefficient function [-] | |
| L | length of domain x or y coordinate [-] |
| length scale [m] | |
| M | number points x or y coordinate [-] |
| reaction heat [-] | |
| r | Arrhenius expression [-] |
| R | Universal gas constant [cal/(K mol)] |
| topography term [-] | |
| t | time variable [-] |
| time discretization [-] | |
| time scale [s] | |
| u | average temperature [-] |
| phase change temperature [-] | |
| maximum temperature [-] | |
| U | absolute temperature [K] |
| ambient temperature [K] | |
| vector of components | |
| approximate value [-] | |
| v | mass fraction of solid fuel [-] |
| , | vector of components [-] |
| approximate value [-] | |
| w | vector field [-] |
| wind speed [-] | |
| spatial variables [-] | |
| nodes in the Cartesian grid [-] | |
| Greek symbols: | |
| natural convection coefficient [-] | |
| length of optical path for radiation [-] | |
| , | space and time discretizations [-] |
| inverse of the activation energy [-] | |
| inverse of conductivity coefficient [-] | |
| density of the fuel [kg/m3] | |
| Stefan-Boltzmann constant | |
| solution operator of (12) [-] | |
| solution operator defined in (11) [-] | |
| domain [-] | |
| Abbreviations: | |
| CFL | Courant–Friedrichs–Lewy |
| CPU | central processing unit |
| DIRK | diagonally implicit Runge–Kutta |
| ERK | explicit Runge–Kutta |
| H-LDIRK3(2,2,2) | acronym of particular IMEX-RK scheme |
| IMEX | implicit–explicit |
| IMEX-RK | implicit–explicit Runge–Kutta |
| LI-IMEX | linearly implicit–explicit |
| NI-IMEX | nonlinearly implicit–explicit |
| ODE | ordinary differential equation |
| PDE | partial differential equation |
| RK | Runge–Kutta |
| S-LIMEX | Strang-type splitting scheme |
| SSP | strong stability-preserving |
| WENO | weighted essentially non-oscillatory |
References
- Bürger, R.; Gavilán, E.; Inzunza, D.; Mulet, P.; Villada, L.M. Implicit–explicit methods for a convection-diffusion-reaction model of the propagation of forest fires. Mathematics 2020, 8, 1034. [Google Scholar] [CrossRef]
- Asensio, M.I.; Ferragut, L. On a wildland fire model with radiation. Int. J. Numer. Methods Eng. 2002, 54, 137–157. [Google Scholar] [CrossRef]
- Pastor, E.; Zárate, L.; Planas, E.; Arnaldos, J. Mathematical models and calculation systems for the study of wildland fire behaviour. Prog. Energy Combust. Sci. 2003, 29, 139–153. [Google Scholar] [CrossRef]
- Eberle, S.; Freeden, W.; Matthes, U. Forest fire spreading. In Handbook of Geomathematics, 2nd ed.; Freeden, W., Nashed, M.Z., Sonar, T., Eds.; Springer: Berlin, Germany, 2015; pp. 1349–1385. [Google Scholar]
- Ferragut, L.; Asensio, M.I.; Monedero, S. Modelling radiation and moisture content in fire spread. Commun. Numer. Methods Eng. 2007, 23, 819–833. [Google Scholar] [CrossRef]
- Ferragut, L.; Asensio, M.I.; Monedero, S. A numerical method for solving convection-reaction-diffusion multivalued equations in fire spread modelling. Adv. Eng. Softw. 2007, 38, 366–371. [Google Scholar] [CrossRef]
- Asensio, M.I.; Ferragut, L.; Simon, J. A convection model for fire spread simulation. Appl. Math. Lett. 2005, 18, 673–677. [Google Scholar] [CrossRef]
- Prieto, D.; Asensio, M.I.; Ferragut, L.; Cascón, J.M.; Morillo, A. A GIS-based fire spread simulator integrating a simplified physical wildland fire model and a wind field model. Int. J. Geogr. Inf. Sci. 2017, 31, 2142–2163. [Google Scholar] [CrossRef]
- Ferragut, L.; Asensio, M.I.; Cascón, J.M.; Prieto, D. A simplified wildland fire model applied to a real case. In Advances in Differential Equations and Applications; Casas, F., Martínez, V., Eds.; SEMA Springer Series 4; Springer International Publishing: Cham, Switzerland, 2014; pp. 155–167. [Google Scholar]
- San Martín, D.; Torres, C.E. Ngen-Kütral: Toward an open source framework for Chilean wildfire spreading. In Proceedings of the 37th International Conference of the Chilean Computer Science Society (SCCC), Santiago, Chile, 5–9 November 2018; pp. 1–8. [Google Scholar]
- San Martín, D.; Torres, C.E. Exploring a spectral numerical algorithm for solving a wildfire mathematical model. In Proceedings of the 38th International Conference of the Chilean Computer Science Society (SCCC), Concepción, Chile, 4–9 November 2019; pp. 1–7. [Google Scholar]
- Barovik, D.; Taranchuk, V. Mathematical modelling of running crown forest fires. Math. Model. Anal. 2010, 15, 161–174. [Google Scholar] [CrossRef][Green Version]
- Taranchuk, V.; Barovik, D. Numerical modeling of surface forest fire spread in nonuniform woodland. In Computer Algebra Systems in Teaching and Research Vol. VIII; Prokopenya, A.N., Gil-Świderska, A., Siłuszyk, M., Eds.; Siedlce University of Natural Sciences and Humanities, Institute of Mathematics and Physics: Siedlce, Poland, 2019; pp. 159–168. [Google Scholar]
- Bebernes, J.; Eberly, D. Mathematical Problems from Combustion Theory; Springer: New York, NY, USA, 1989. [Google Scholar]
- Glassman, I.; Yetter, R.A.; Glumac, N.G. Combustion, 5th ed.; Academic Press: Boston, MA, USA, 2015. [Google Scholar]
- Séro-Guillaume, O.; Margerit, J. Modelling forest fires. Part I: A complete set of equations derived by extended irreversible thermodynamics. Int. J. Heat Mass Transf. 2002, 45, 1705–1722. [Google Scholar] [CrossRef]
- Margerit, J.; Séro-Guillaume, O. Modelling forest fires. Part II: Reduction to two-dimensional models and simulation of propagation. Int. J. Heat Mass Transf. 2002, 45, 1723–1737. [Google Scholar] [CrossRef]
- Linn, R.R.; Canfield, J.M.; Cunningham, P.; Edminster, C.; Dupuy, J.-L.; Pimont, F. Using periodic line fires to gain a new perspective on multi-dimensional aspects of forward fire spread. Agric. For. Meteorol. 2012, 157, 60–76. [Google Scholar] [CrossRef]
- Moinuddin, K.A.M.; Sutherland, D. Modeling of tree fires and fires transitioning from the forest floor to the canopy with a physics-based model. Math. Comput. Simul. 2020, 175, 81–95. [Google Scholar] [CrossRef]
- Hundsdorfer, W.; Verwer, J.G. Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations; Springer: Berlin, Germany, 2003. [Google Scholar]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations, 2nd ed.; Wiley: Chichester, UK, 2008. [Google Scholar]
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations. I. Non-Stiff Problems; Springer Series in Computational Mathematics; Springer: Berlin, Germany, 1993; Volume 8. [Google Scholar]
- Ascher, U.; Ruuth, S.; Spiteri, J. Implicit-explicit Runge-Kutta methods for time dependent partial differential equations. Appl. Numer. Math. 1997, 25, 151–167. [Google Scholar] [CrossRef]
- Pareschi, L.; Russo, G. Implicit-Explicit Runge-Kutta schemes and applications to hyperbolic systems with relaxation. J. Sci. Comput. 2005, 25, 129–155. [Google Scholar]
- Boscarino, S.; Bürger, R.; Mulet, P.; Russo, G.; Villada, L.M. Linearly implicit IMEX Runge-Kutta methods for a class of degenerate convection-diffusion problems. SIAM J. Sci. Comput. 2015, 37, B305–B331. [Google Scholar] [CrossRef]
- Boscarino, S.; Bürger, R.; Mulet, P.; Russo, G.; Villada, L.M. On linearly implicit IMEX Runge-Kutta Methods for degenerate convection-diffusion problems modelling polydisperse sedimentation. Bull. Braz. Math. Soc. (New Ser.) 2016, 47, 171–185. [Google Scholar] [CrossRef]
- Boscarino, S.; Filbet, F.; Russo, G. High order semi-implicit schemes for time dependent partial differential equations. J. Sci. Comput. 2016, 68, 975–1001. [Google Scholar] [CrossRef]
- Boscarino, S.; LeFloch, P.G.; Russo, G. High order asymptotic-preserving methods for fully nonlinear relaxation problems. SIAM J. Sci. Comput. 2014, 36, A377–A395. [Google Scholar] [CrossRef]
- Donat, R.; Guerrero, F.; Mulet, P. Implicit-explicit methods for models for vertical equilibrium multiphase flow. Comput. Math. Appl. 2014, 68, 363–383. [Google Scholar] [CrossRef]
- Bürger, R.; Chowell, G.; Gavilán, E.; Mulet, P.; Villada, L.M. Numerical solution of a spatio-temporal gender-structured model for hantavirus infection in rodents. Math. Biosci. Eng. 2018, 15, 95–123. [Google Scholar] [CrossRef]
- Bürger, R.; Chowell, G.; Gavilán, E.; Mulet, P.; Villada, L.M. Numerical solution of a spatio-temporal predator-prey model with infected prey. Math. Biosci. Eng. 2019, 16, 438–473. [Google Scholar] [CrossRef]
- Bürger, R.; Goatin, P.; Inzunza, D.; Villada, L.M. A non-local pedestrian flow model accounting for anisotropic interactions and domain boundaries. Math. Biosci. Eng. 2020, 17, 5883–5906. [Google Scholar]
- Bürger, R.; Inzunza, D.; Mulet, P.; Villada, L.M. Implicit-explicit schemes for nonlinear nonlocal equations with a gradient flow structure in one space dimension. Numer. Methods Partial Differ. Equ. 2019, 35, 1008–1034. [Google Scholar] [CrossRef]
- Bürger, R.; Inzunza, D.; Mulet, P.; Villada, L.M. Implicit-explicit methods for a class of nonlinear nonlocal gradient flow equations modelling collective behaviour. Appl. Numer. Math. 2019, 144, 234–252. [Google Scholar] [CrossRef]
- Bürger, R.; Mulet, P.; Villada, L.M. Regularized nonlinear solvers for IMEX methods applied to diffusively corrected multi-species kinematic flow models. SIAM J. Sci. Comput. 2013, 35, B751–B777. [Google Scholar] [CrossRef]
- Abgrall, R.; Shu, C.-W. Handbook of Numerical Analysis for Hyperbolic Problems. Basic and Fundamental Issues; North-Holland: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Shu, C.-W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In Advanced Numerical Approximation of Nonlinear Hyperbolic Equations; Quarteroni, A., Ed.; Lecture Notes in Mathematics; Springer: Berlin, Germany, 1998; Volume 1697, pp. 325–432. [Google Scholar]
- Shu, C.-W. High order weighted essentially nonoscillatory schemes for convection dominated problems. SIAM Rev. 2009, 51, 82–126. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Hesthaven, J.S. Numerical Methods for Conservation Laws; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2018. [Google Scholar]
- Marin, M.; Vlase, S.; Paun, M. Considerations on double porosity structure for micropolar bodies. AIP Adv. 2015, 5, 037113. [Google Scholar] [CrossRef]
- Holden, H.; Karlsen, K.H.; Lie, K.-A.; Risebro, N.H. Splitting Methods for Partial Differential Equations with Rough Solutions; European Mathematical Society: Zurich, Switzerland, 2010. [Google Scholar]
- Strang, G. On the construction and comparison of difference schemes. SIAM J. Numer. Anal. 1968, 5, 506–517. [Google Scholar] [CrossRef]
- Bennett, M.; Fitzgerald, S.A.; Parker, B.; Main, M.L.; Perleberg, A.; Schnepf, C.; Mahoney, R.L. Reduce the Risk of Fire on Your Forest Property; Oregon State University: Corvallis, OR, USA, 2010. [Google Scholar]




| 40 | 2.2 | 3.7 | 3.2 | 4.5 | 4.9 | 6.4 |
| 80 | 1.2 | 1.6 | 2.0 | 2.3 | 3.3 | 3.7 |
| 160 | 0.7 | 1.0 | 1.2 | 1.5 | 2.0 | 2.4 |
| 320 | 0.4 | 5.7 | 0.6 | 8.9 | 1.1 | 1.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bürger, R.; Gavilán, E.; Inzunza, D.; Mulet, P.; Villada, L.M. Exploring a Convection–Diffusion–Reaction Model of the Propagation of Forest Fires: Computation of Risk Maps for Heterogeneous Environments. Mathematics 2020, 8, 1674. https://doi.org/10.3390/math8101674
Bürger R, Gavilán E, Inzunza D, Mulet P, Villada LM. Exploring a Convection–Diffusion–Reaction Model of the Propagation of Forest Fires: Computation of Risk Maps for Heterogeneous Environments. Mathematics. 2020; 8(10):1674. https://doi.org/10.3390/math8101674
Chicago/Turabian StyleBürger, Raimund, Elvis Gavilán, Daniel Inzunza, Pep Mulet, and Luis Miguel Villada. 2020. "Exploring a Convection–Diffusion–Reaction Model of the Propagation of Forest Fires: Computation of Risk Maps for Heterogeneous Environments" Mathematics 8, no. 10: 1674. https://doi.org/10.3390/math8101674
APA StyleBürger, R., Gavilán, E., Inzunza, D., Mulet, P., & Villada, L. M. (2020). Exploring a Convection–Diffusion–Reaction Model of the Propagation of Forest Fires: Computation of Risk Maps for Heterogeneous Environments. Mathematics, 8(10), 1674. https://doi.org/10.3390/math8101674






