Modelling Population Dynamics of Social Protests in Time and Space: The Reaction-Diffusion Approach
Abstract
1. Introduction
2. Mathematical Models in the Non-Spatial Case
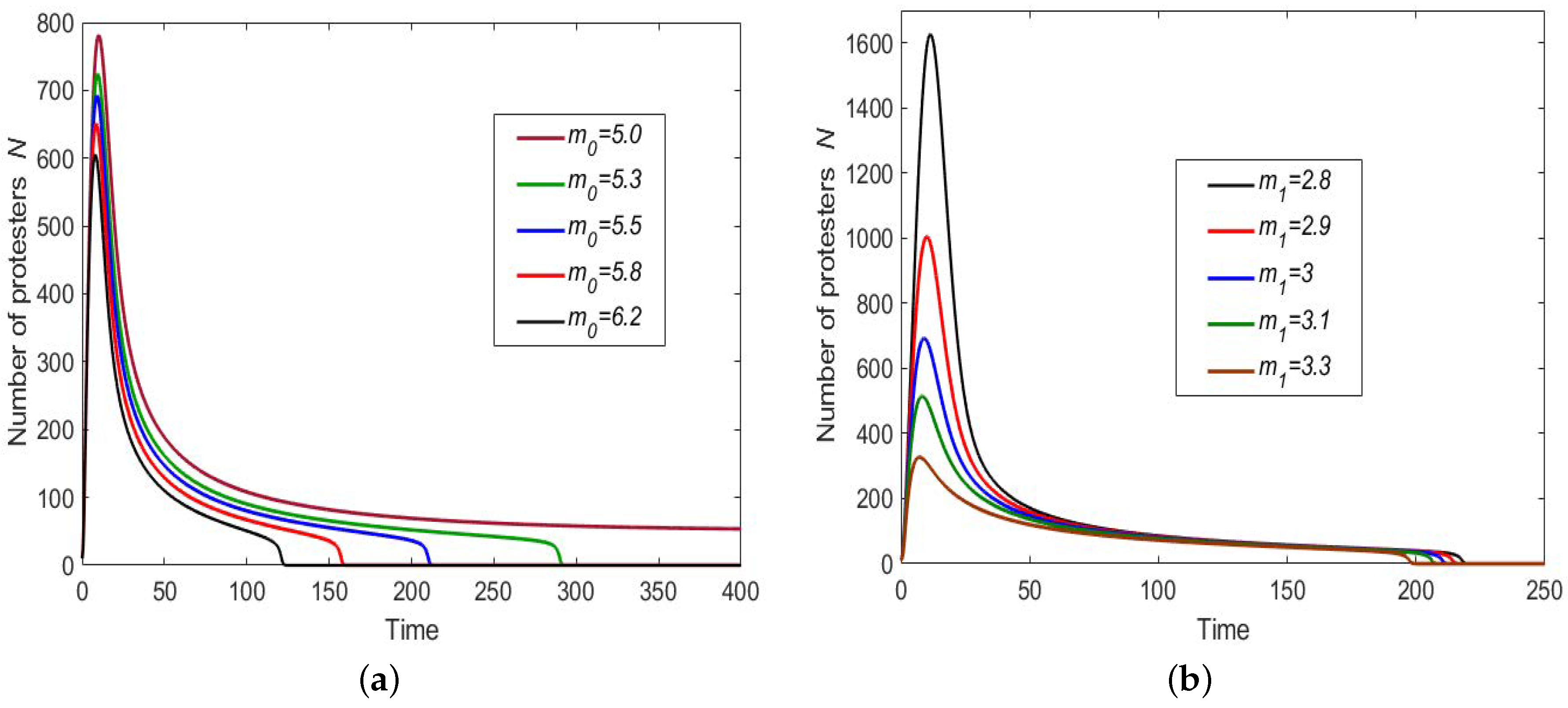
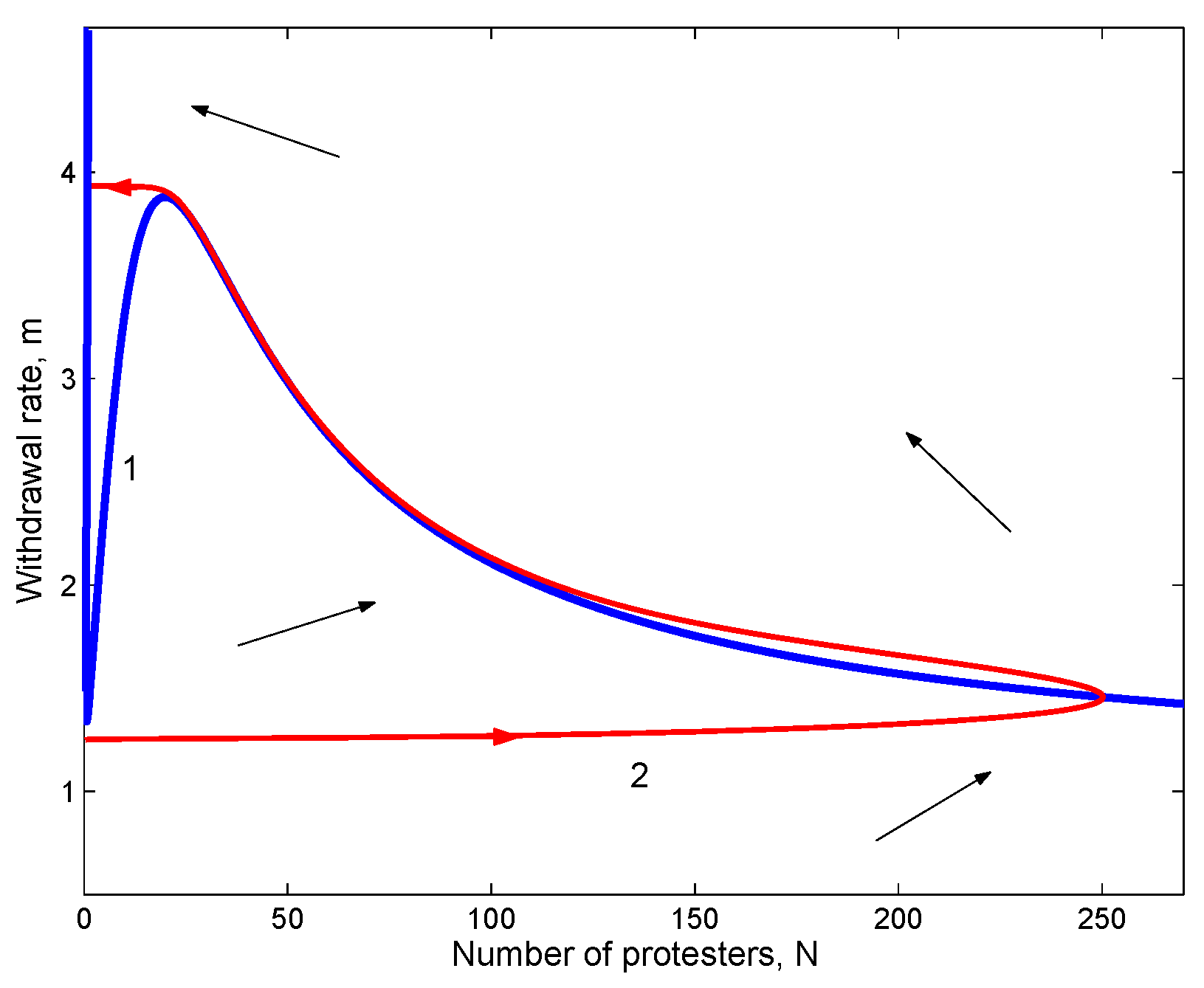
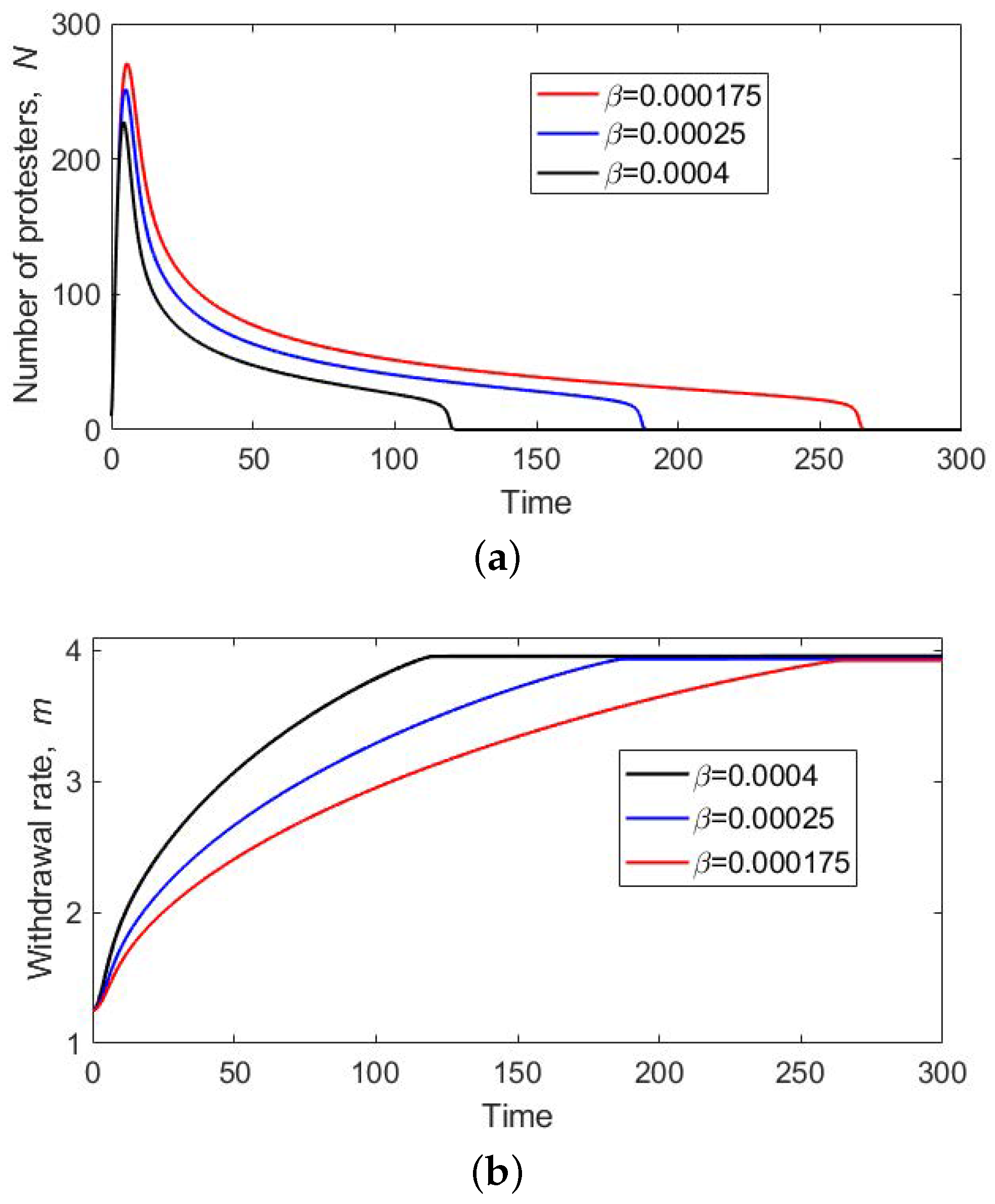
2.1. Single Species Model
- The rate of change in the number of people attending the event is a result of the interplay between two processes, recruitment (people joining) and withdrawal (people quitting);
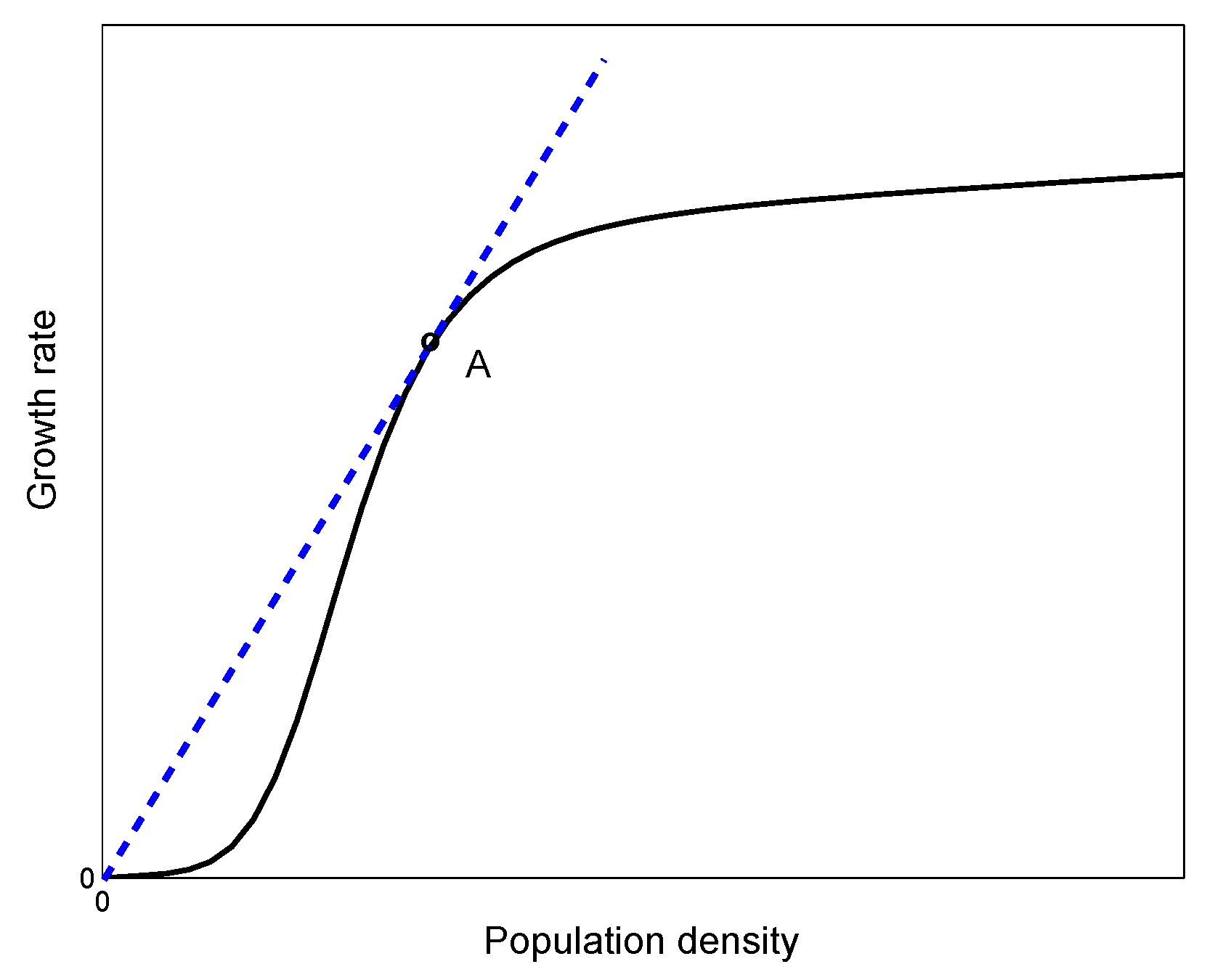
- Following earlier studies [18], we consider recruitment to be a collective phenomenon so that the recruitment rate is a nonlinear function of the number of people currently involved in the event;
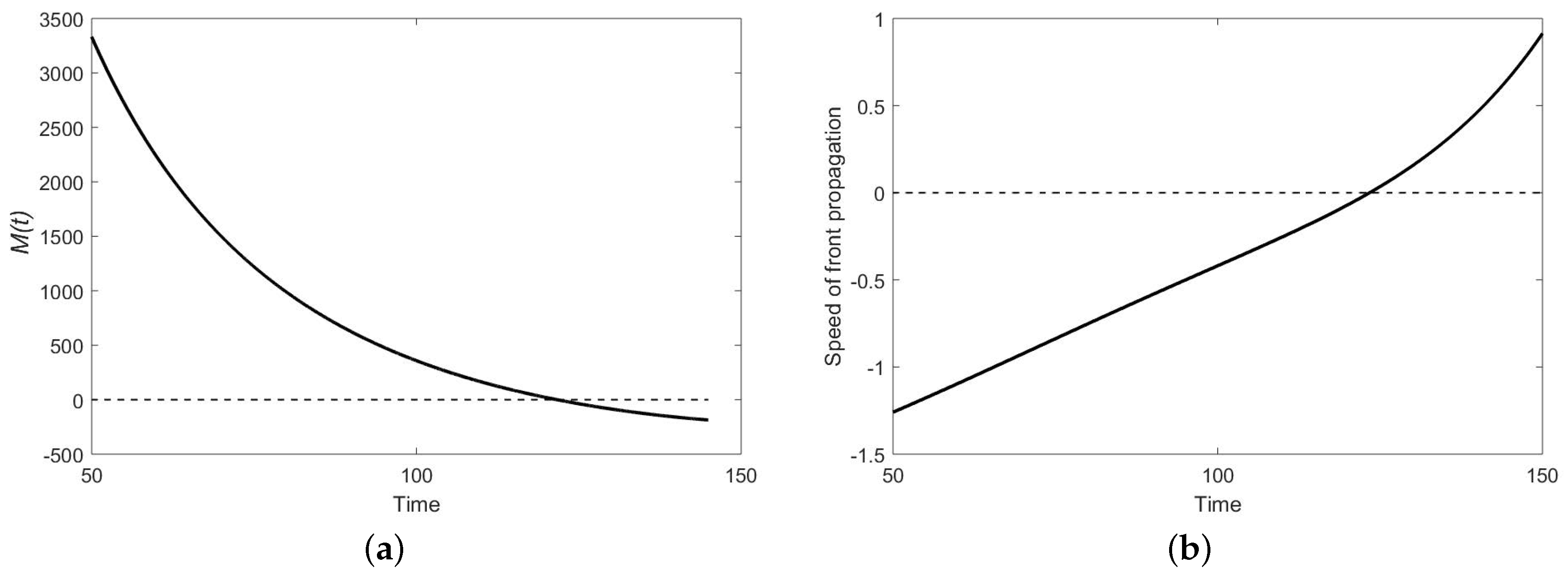
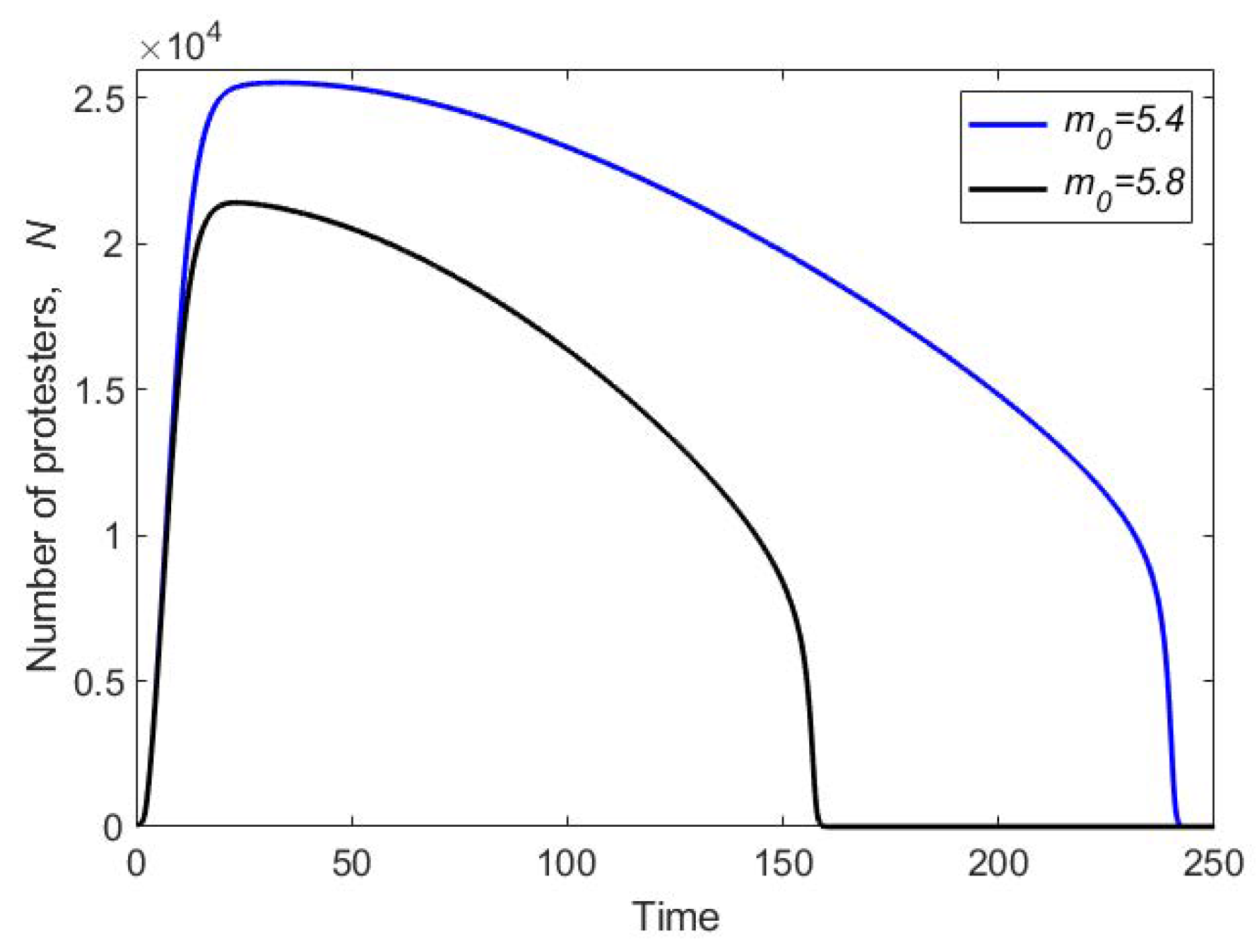
- Decision of withdrawal is made individually, so that the withdrawal rate is a linear function of the number of people participating in the event, where the per capita withdrawal rate (say m) depends on time.
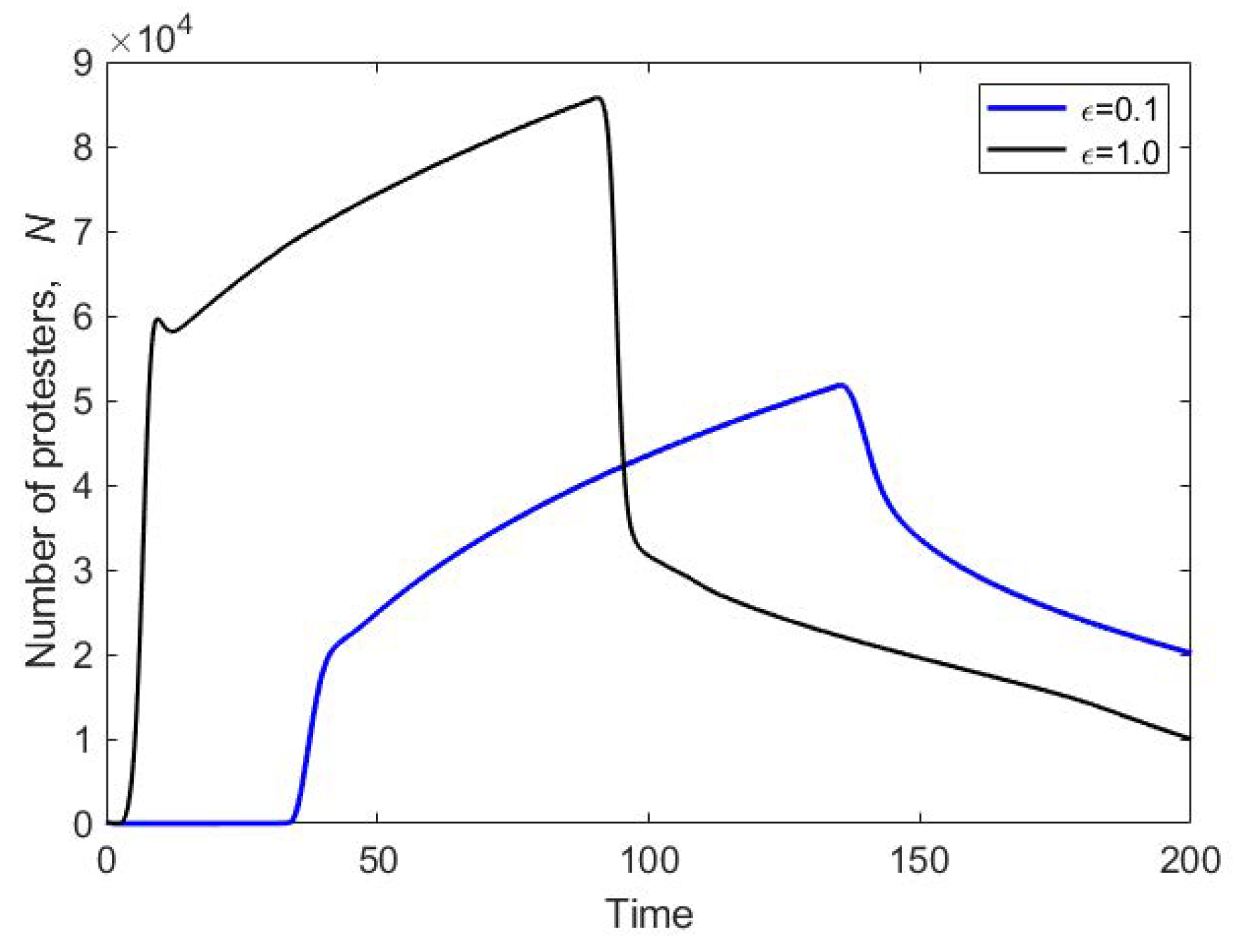
2.2. Two Component Model
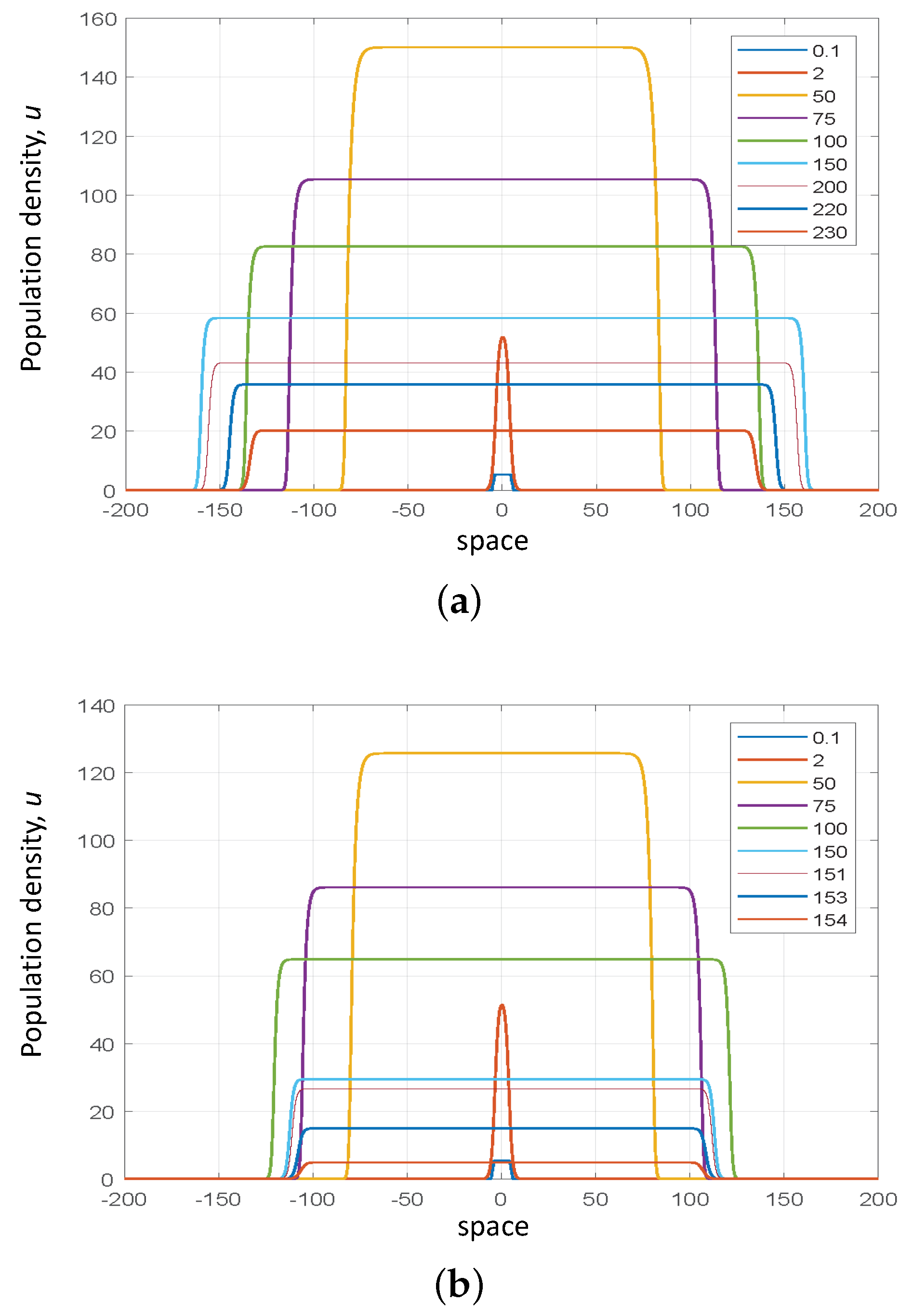
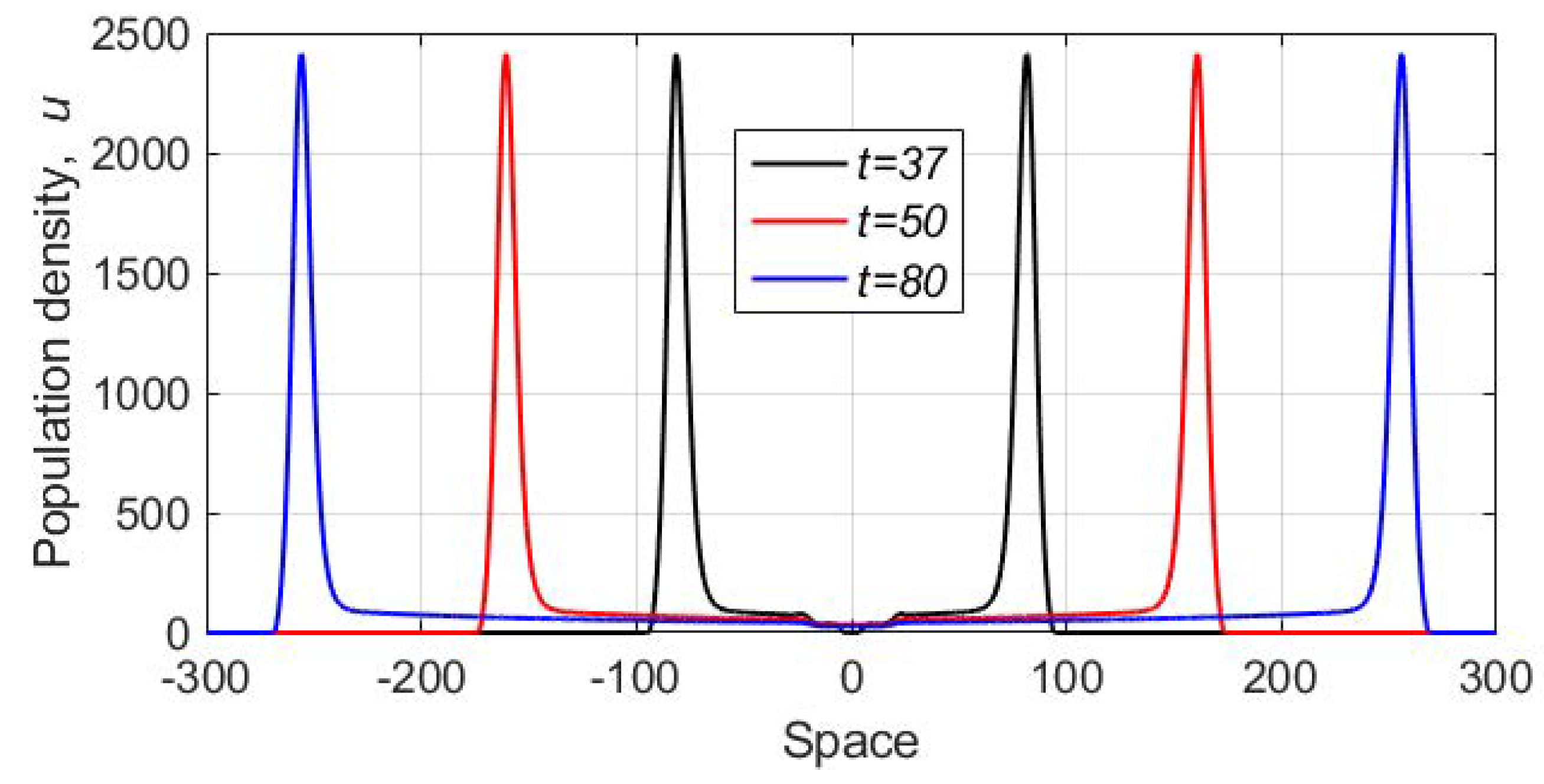
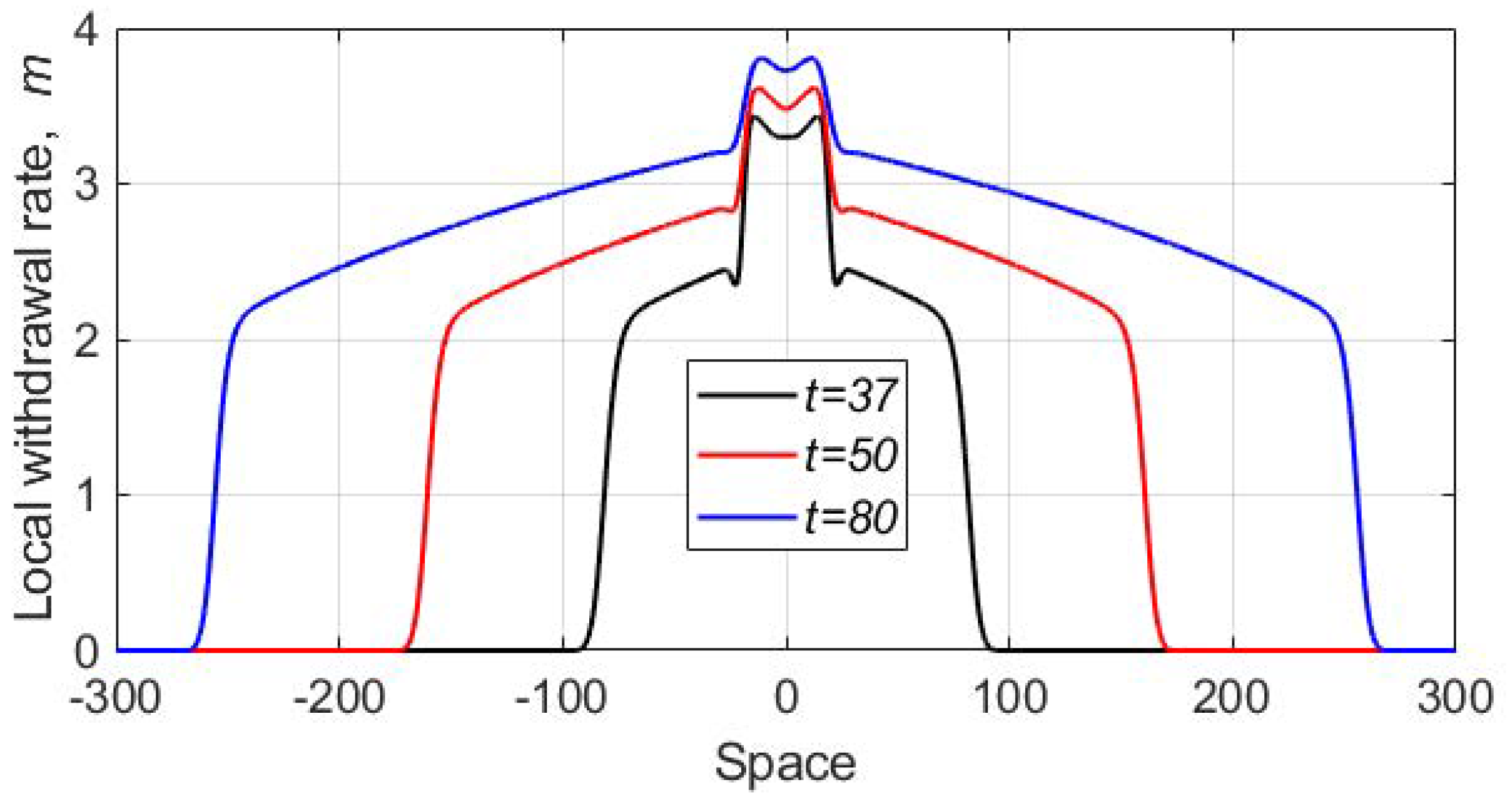
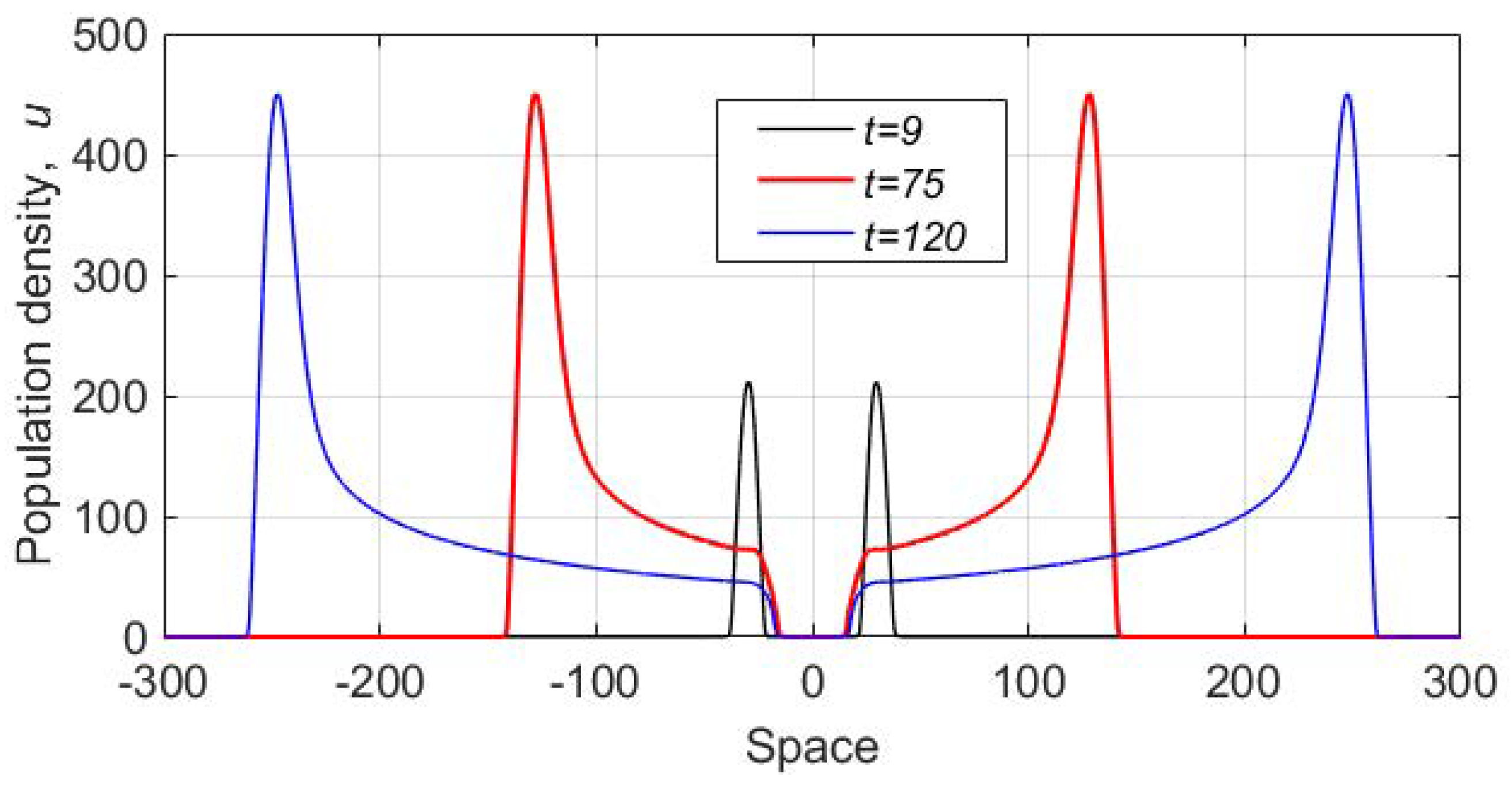
3. Spatially Explicit Model
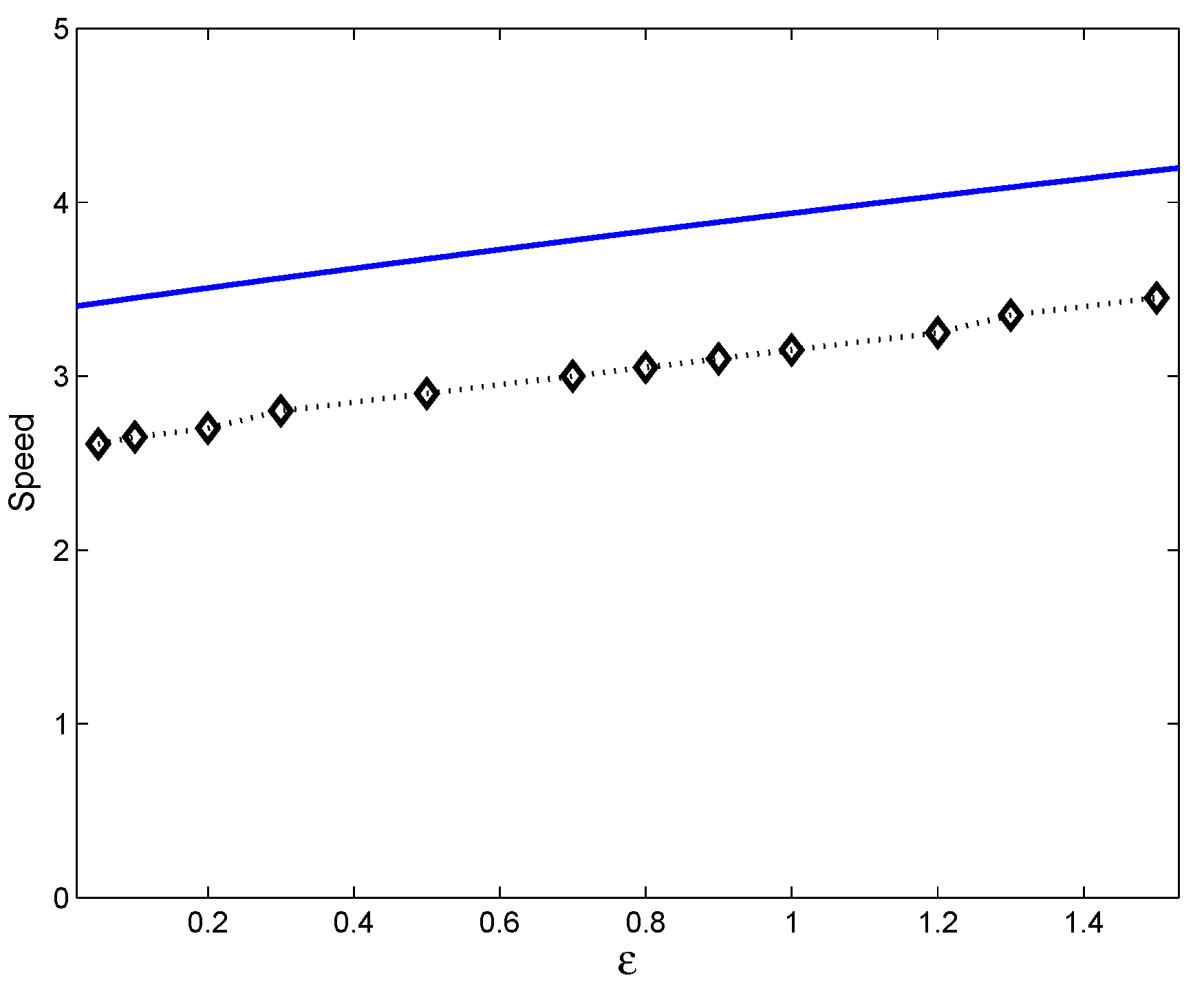
3.1. Single Species Model
3.2. Two Component Model
4. Discussion and Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Andreev, A.; Borodkin, L.; Levandovskii, M. Using methods of non-linear dynamics in historical social research: Application of chaos theory in the analysis of the worker’s movement in pre-revolutionary Russia. Hist. Soc. Res./Historische Sozialforschung 1997, 22, 64–83. [Google Scholar]
- Epstein, J.M. Nonlinear Dynamics, Mathematical Biology, and Social Science; Addison-Wesley: Reading, MA, USA, 1997. [Google Scholar]
- Epstein, J.M. Modeling civil violence: An agent-based computational approach. Proc. Natl. Acad. Sci. USA 2002, 99 (Suppl. 3), 7243–7250. [Google Scholar] [CrossRef] [PubMed]
- Turchin, P. Historical Dynamics: Why States Rise and Fall; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Eguiluz, V.M.; Zimmermann, M.G.; Cela-Conde, C.J.; San Miguel, M. Cooperation and emergence of role differentiation in the dynamics of social networks. arXiv 2006, arXiv:physics/0602053v1. [Google Scholar] [CrossRef]
- Brantingham, P.J.; Tita, G.E.; Short, M.B.; Reid, S.E. The ecology of gang territorial boundaries. Criminology 2012, 50, 851–885. [Google Scholar] [CrossRef]
- Fonoberova, M.; Fonoberov, V.A.; Mezic, I.; Mezic, J.; Brantingham, P.J. Nonlinear dynamics of crime and violence in urban settings. J. Artif. Soc. Soc. Simul. 2012, 15, 2. [Google Scholar] [CrossRef]
- Smith, L.M.; Bertozzi, A.L.; Brantingham, P.J.; Tita, G.E.; Valasik, M. Adaptation of an ecological territorial model to street gang spatial patterns in Los Angeles. Discret. Contin. Dyn. Syst. 2012, 32, 3223–3244. [Google Scholar] [CrossRef]
- Davies, T.P.; Fry, H.M.; Wilson, A.G.; Bishop, S.R. A mathematical model of the London riots and their policing. Sci. Rep. 2013, 3, 1303. [Google Scholar] [CrossRef]
- Turalska MWest, B.J.; Grigolini, P. Role of committed minorities in times of crisis. Sci. Rep. 2013, 3, 1371. [Google Scholar] [CrossRef]
- Khosaeva, Z.H. The mathematics model of protests. Comp. Res. Model. 2015, 7, 1331–1341. (In Russian) [Google Scholar] [CrossRef]
- Berestycki, H.; Nadal, J.-P.; Rodíguez, N. A model of riots dynamics: Shocks, diffusion and thresholds. Netw. Heterog. Media 2015, 103, 443–475. [Google Scholar] [CrossRef]
- Bonnasse-Gahot, L.; Berestycki, H.; Marie-Aude Depuiset, M.A. Epidemiological modelling of the 2005 French riots: A spreading wave and the role of contagion. Sci. Rep. 2018, 8, 107. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Rodriguez, N. A numerical perspective on traveling wave solutions in a system for rioting activity. Appl. Math. Comput. 2020, 364, 124646. [Google Scholar] [CrossRef]
- Gavrilets, S. Collective action problem in heterogeneous groups. Philos. Trans. R. Soc. Lond. B 2015, 370, 20150016. [Google Scholar] [CrossRef] [PubMed]
- Lang, J.C.; De Sterck, H. The Arab Spring: A simple compartmental model for the dynamics of a revolution. Math. Soc. Sci. 2014, 69, 12–21. [Google Scholar] [CrossRef]
- Morozov, A.; Petrovskii, S.V.; Gavrilets, S. Dynamics of Social Protests: Case study of the Yellow Vest Movement. SocArXiv 2019. [Google Scholar] [CrossRef]
- Granovetter, M. Threshold models of collective behavior. Am. J. Sociol. 1978, 83, 1420–1443. [Google Scholar] [CrossRef]
- Haynes, M.J. Patterns of conflict in the 1905 revolution. In The Russian Revolution of 1905: Change through Struggle; Glatter, P., Ed.; Porcupine Press: London, UK, 2005; pp. 215–233. [Google Scholar]
- Perrie, M. The Russian peasant movement of 1905–1907: Its social composition and revolutionary significance. Past Present 1972, 57, 123–155. [Google Scholar] [CrossRef]
- Gelbwestenbewegung. Wikipedia. Available online: https://de.wikipedia.org/wiki/Gelbwestenbewegung (accessed on 1 October 2019). (In German).
- Malchow, H.; Petrovskii, S.V.; Venturino, E. Spatiotemporal Patterns in Ecology and Epidemiology: Theory, Models, Simulations; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Gnedenko, B.V.; Kolmogorov, A.N. Limit Distributions for Sums of Independent Random Variables; Addison-Wesley Mathematics Series; Addison-Wesley: Cambridge, MA, USA, 1954. [Google Scholar]
- Altbach, P.G.; Klemencic, M. Student activism remains a potent force worldwide. Int. High. Educ. 2014, 76, 2–3. [Google Scholar] [CrossRef]
- Mohamed, E.; Gerber, H.R.; Aboulkacem, S. (Eds.) Education and the Arab Spring; Sense Publishers: Rotterdam, The Netherlands; Boston, MA, USA; Taipei, Taiwan, 2016. [Google Scholar]
- Biggs, M. Size matters: Quantifying protest by counting participants. Sociol. Methods Res. 2018, 47, 351–383. [Google Scholar] [CrossRef]
- Raafat, R.M.; Chater, N.; Frith, C. Herding in humans. Trends Cognit. Sci. 2009, 13, 420–428. [Google Scholar] [CrossRef]
- Courchamp, F.; Berek, L.; Gascoigne, J. Allee Effects in Ecology and Conservation; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Schussman, A.; Soule, S.A. Process and protest: Accounting for individual protest participation. Soc. Forces 2005, 84, 1083–1108. [Google Scholar] [CrossRef]
- Hastings, A.; Abbott, K.C.; Cuddington, K.; Francis, T.; Gellner, G.; Lai, Y.C.; Morozov, A.; Petrovskii, S.; Scranton, K.; Zeeman, M.L. Transient phenomena in ecology. Science 2018, 361, eaat6412. [Google Scholar] [CrossRef] [PubMed]
- Morozov, A.; Abbott, K.; Cuddington, K.; Francis, T.; Gellner, G.; Hastings, A.; Lai, Y.C.; Petrovskii, S.; Scranton, K.; Zeeman, M.L. Long transients in ecology: Theory and applications. Phys. Life Rev. 2019, in press. [Google Scholar] [CrossRef]
- Braha, D. Global civil unrest: Contagion, self-organization, and prediction. PLoS ONE 2012, 7, e48596. [Google Scholar] [CrossRef]
- Brockmann, D.; Hufnagel, L.; Theo Geisel, T. The scaling laws of human travel. Nature 2006, 439, 462–465. [Google Scholar] [CrossRef]
- Kendall, D.G. Discussion of “Measles periodicity and community size” by M.S. Bartlett. J. R. Stat. Soc. Ser. A 1957, 120, 64–67. [Google Scholar]
- Mendez, V.; Fedotov, S.; Horsthemke, W. Reaction-Transport Systems: Mesoscopic Foundations, Fronts, and Spatial Instabilities; Springer: Berlin, Germany, 2010. [Google Scholar]
- Mendez, V.; Campos, D.; Bartumeus, F. Stochastic Foundations in Movement Ecology: Anomalous Diffusion, Front Propagation and Random Searches; Springer: Berlin, Germany, 2014. [Google Scholar]
- Lewis, M.A.; Petrovskii, S.V.; Potts, J. The Mathematics behind Biological Invasions; Interdisciplinary Applied Mathematics; Springer: Berlin, Germany, 2016; Volume 44. [Google Scholar]
- Murray, J.D. Mathematical Biology; Springer: Berlin, Germany, 1989. [Google Scholar]
- Volpert, A.; Volpert Vit Volpert, V.L. Traveling Wave Solutions of Parabolic Systems; AMS: Providence, RI, USA, 1994. [Google Scholar]
- Fife, P.C. Mathematical Aspects of Reacting and Diffusing Systems; Lecture Notes in Biomathematics; Springer: Berlin, Germany, 1979; Volume 28. [Google Scholar]
- Zeldovich, Y.B.; Barenblatt, G.I.; Librovich, V.B.; Makhviladze, G.M. The Mathematical Theory of Combustion and Explosions; Consultants Bureau: New York, NY, USA, 1985. [Google Scholar]
- Kolmogorov, A.N.; Petrovskii, I.G.; Piskunov, N.S. A study of the diffusion equation with increase in the quantity of matter, and its application to a biological problem. Bull. Moscow Univ. Math. Ser. A 1937, 1, 1–25. [Google Scholar]
- Kolmogorov, A.N.; Petrovskii, I.G.; Piskunov, N.S. A study of the diffusion equation with increase in the amount of substance, and its application to a biological problem. In Selected Works of A. N. Kolmogorov; Tikhomirov, V.M., Ed.; Kluwer Academic: Dordrecht, The Netherlands, 1991; pp. 242–270. [Google Scholar]
- Protter, M.H.; Weinberger, H.F. Maximum Principles in Differential Equations; Springer: New York, NY, USA, 1984. [Google Scholar]
- Hastings, A.; Higgins, K. Persistence of transients in spatially structured ecological models. Science 1994, 263, 1133–1136. [Google Scholar] [CrossRef]
- Lai, Y.C.; Tél, T. Transient Chaos—Complex Dynamics on Finite-Time Scales; Springer: New York, NY, USA, 2011. [Google Scholar]
- Map of White Supremacy Mob Violence. Available online: http://www.monroeworktoday.org/explore/ (accessed on 1 October 2019).
- Homer-Dixona, T.; Maynardb, J.L.; Mildenbergerc, M.; Milkoreita, M.; Mocka, S.J.; Quilleyd, S.; Schröder, T.; Thagarde, P. A complex systems approach to the study of ideology: Cognitive-affective structures and the dynamics of belief systems. J. Soc. Political Psychol. 2013, 1, 337–363. [Google Scholar]
- Mistry, D.; Zhang, Q.; Perra, N.; Baronchelli, A. Committed activists and the reshaping of the status-quo social consensus. Phys. Rev. E 2015, 92, 042805. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrovskii, S.; Alharbi, W.; Alhomairi, A.; Morozov, A. Modelling Population Dynamics of Social Protests in Time and Space: The Reaction-Diffusion Approach. Mathematics 2020, 8, 78. https://doi.org/10.3390/math8010078
Petrovskii S, Alharbi W, Alhomairi A, Morozov A. Modelling Population Dynamics of Social Protests in Time and Space: The Reaction-Diffusion Approach. Mathematics. 2020; 8(1):78. https://doi.org/10.3390/math8010078
Chicago/Turabian StylePetrovskii, Sergei, Weam Alharbi, Abdulqader Alhomairi, and Andrew Morozov. 2020. "Modelling Population Dynamics of Social Protests in Time and Space: The Reaction-Diffusion Approach" Mathematics 8, no. 1: 78. https://doi.org/10.3390/math8010078
APA StylePetrovskii, S., Alharbi, W., Alhomairi, A., & Morozov, A. (2020). Modelling Population Dynamics of Social Protests in Time and Space: The Reaction-Diffusion Approach. Mathematics, 8(1), 78. https://doi.org/10.3390/math8010078




