1. Introduction
During the past two decades, coherent multidimensional spectroscopy (CMDS) has emerged as a powerful tool that can overcome the limitations of traditional one-dimensional techniques [
1,
2,
3,
4,
5]. High-resolution coherent multidimensional spectroscopy (HRCMDS) is a form of CMDS that is designed to overcome congestion problems commonly found in the high-resolution spectra of gas-phase molecules [
6]. Above cryogenic temperatures, gas molecules can yield spectra that contain a wealth of information (e.g., thousands or millions of peaks), but spectral congestion often precludes the ability to resolve and assign these peaks. Assigning peaks by quantum number is needed in order to calculate molecular constants that provide details on the structure and behavior of molecules. Historically, strategies for assigning resolved peaks in 1D spectroscopy have typically involved making initial guesses, trial and error, and pattern recognition. For example, the Loomis–Wood rotational-branch-picking pattern-recognition scheme was developed in 1928 [
7] and involves plotting data from one-dimensional spectra onto a two-dimensional display, to help identify peaks that belong to the same rotational branch [
8]. High-resolution coherent two-dimensional spectroscopy (HRC2DS) is a powerful new technique that improves spectral resolution while automatically organizing peaks into easily recognizable 2D patterns, where they appear sorted sequentially by quantum number [
9]. This new capability suggests that a new method can be developed to assign peaks that does not rely upon things like initial guesses or trial and error.
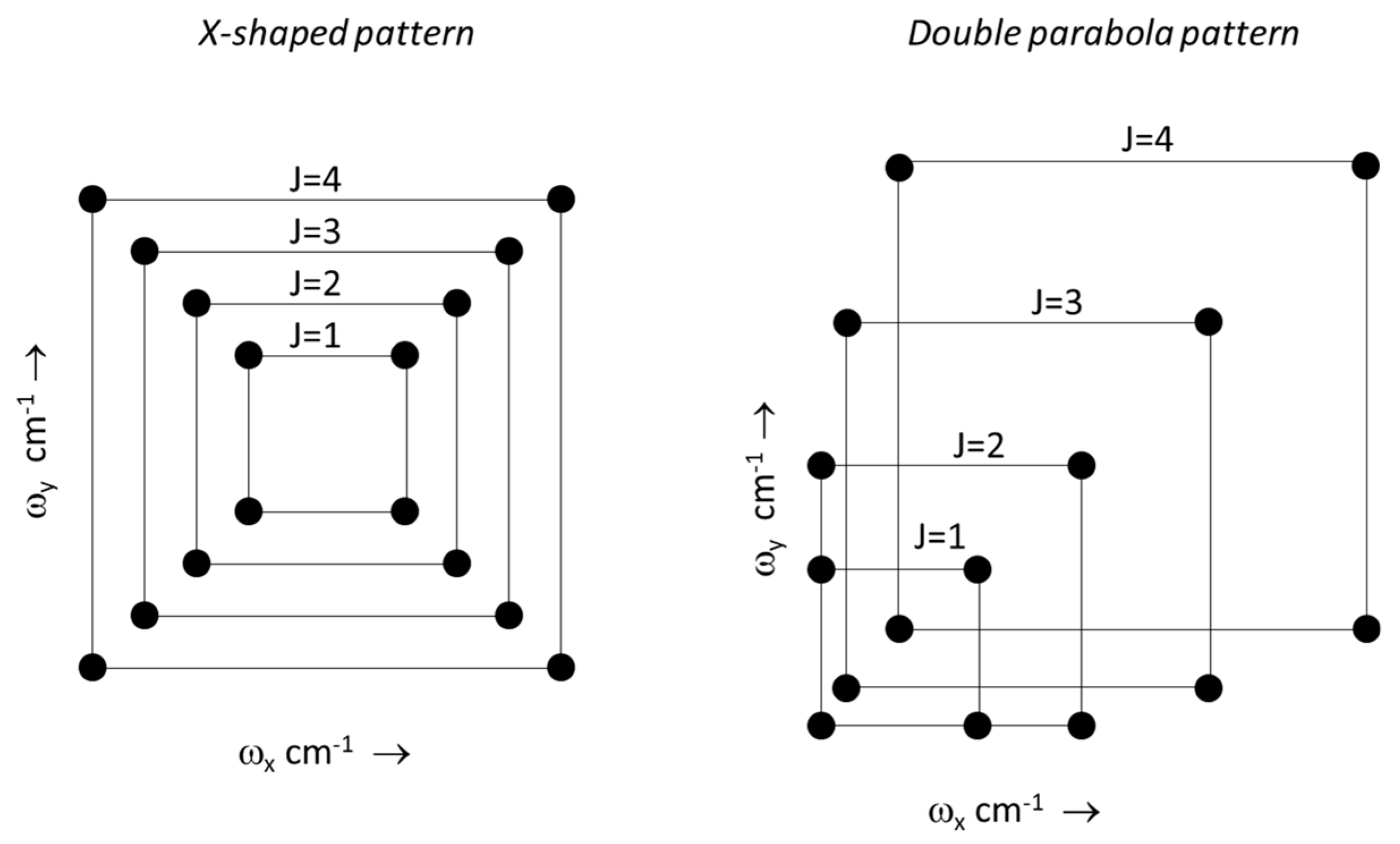
Figure 1 shows two kinds of patterns that are commonly observed in HRC2DS spectra. The basic unit for both patterns is a rectangle, formed by four rotational peaks in 2D space [
10]. Each of these peaks forms the corner of a rectangle, and all four peaks have identical vibrational quantum numbers and initial rotational quantum numbers. The peaks within each rectangle differ by whether they involve a P or an R process for both the
x and
y axes, and the size of the rectangle increases with increasing initial rotational quantum number, J. Throughout this paper, J is used (instead of the customary J”) to represent the initial rotational quantum number.
A three-dimensional form of HRCMDS has also been developed to provide even higher spectral resolution than HRC2DS [
11]. The improved resolution provided by high-resolution coherent 3D spectroscopy (HRC3DS) can be useful when dealing with more complex molecular systems [
12]. HRC3DS also provides selectivity by species and/or quantum number, and can therefore be useful for mixtures [
13]. Unlike the 2D basic rotational, unit which consists of four peaks in the shape of a rectangle, the 3D basic rotational unit consists of six peaks that form two triangles that reside in parallel planes in 3D space (see
Figure 2). Both the 2D basic rotational pattern and the 3D basic rotational pattern make assigning peaks convenient; for both techniques, all the peaks in that basic unit have the same vibrational quantum numbers (v) and the same initial rotational quantum number (J), and the size of the basic unit grows sequentially with the increasing J value.
The main advantages of HRC2DS over conventional 1D spectroscopy are the dramatic improvement in spectral resolution and the automated peak organization and sorting capabilities. These capabilities make it relatively easy to identify peaks with the same vibrational and rotational quantum numbers. Furthermore, since the basic rotational units increase in size with J and are sequentially juxtaposed, the technique makes it easy to find series of basic rotational units that are sequentially ordered by J. As a result, if one unit has its peaks assigned by rotational and vibrational quantum numbers, then all the others can easily be assigned. For example, in HRC2DS, if the J value is determined for one rectangle, then the J values are easy to determine for all other rectangles that belong to the same pattern. Furthermore, all of the rectangles in that pattern will have the same vibrational quantum numbers. If multiple patterns are observed, then the assigned rectangles for one can be used to assign J values for the other pattern, since their peaks may have the same x-axis or y-axis wavelengths. For example, nearly identical patterns that differ by one vibrational quantum number can often be seen adjacent to each other. Therefore, the successful assignment of just one rectangle could facilitate the assignment of all peaks in the entire 2D spectrum.
In principle, one could assign all rectangles in an HRC2DS spectrum by looking for the smallest rectangle, which should be located at the center of the pattern, and assigning its peaks a J value of 1. In practice, however, the smaller rectangles can be difficult to resolve, especially if the rotational constants are small (which occurs for larger and heavier molecules). For HRC3DS, the smallest pair of triangles with a J value of 1 may also be difficult to locate in 3D space. Therefore, an alternative method is needed to determine or confirm the value of J assigned to each peak and basic rotational pattern, so that molecular constants can subsequently be determined. The purpose of this paper is to describe such a method and to provide a proof that its solution is unique.
2. Materials and Methods
The method of combination differences [
14] has long been used for analyzing one-dimensional rotationally resolved spectra. The rotationally resolved energy levels of a diatomic molecule can be described by the following equation:
for both the upper- and lower-state levels. For the common selection rule of
±1, the energy difference between peaks that have the same J value can be described by the following:
where the J’s are rotational quantum numbers for the initial ground state, and the Dunham coefficients, Y
0,1 and Y
0,2, are for the upper level of the corresponding resonances.
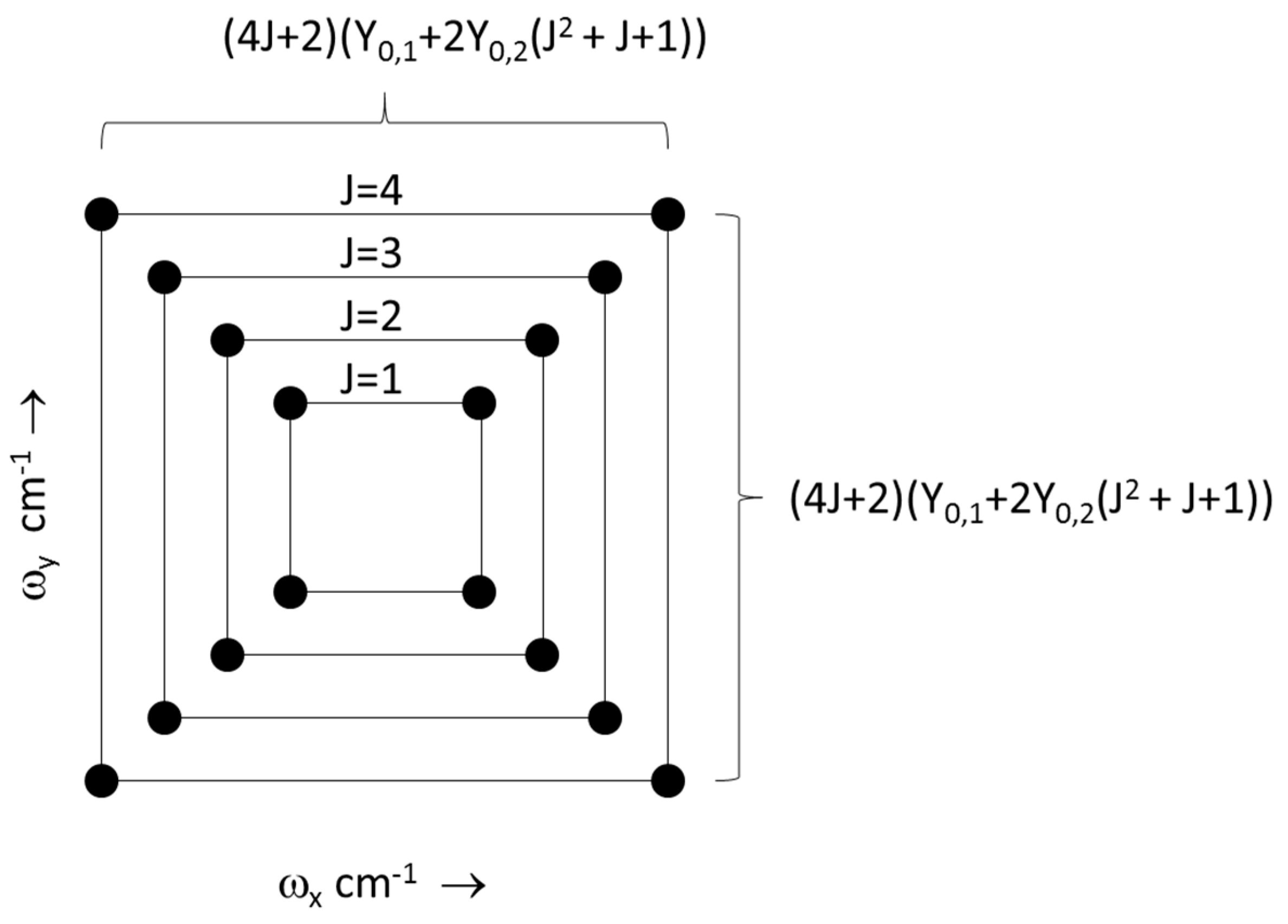
In HRCMDS, combination differences such as these correspond to the widths and heights of rectangles and triangles in the observed 2D and 3D spectra (see
Figure 3) [
6,
13]. If a series of adjacent rectangles or triangles is observed, then their initial rotational quantum numbers (J) should increase sequentially with the size of the rectangle or triangle. The challenge is to determine the values of both the variable J and the parameters Y
0,1, Y
0,2, … from the observed sequence of combined differences (i.e., the widths and heights of the rectangles or triangles). For a general polynomial, each proposed integer value of J could yield a different set of parameters that would fit the data, because the function could simply be shifted. However, the energy polynomial function has some unique properties because of its special form; it is a polynomial in J(J + 1) instead of just J. We exploit this property when exploring the effects of translation in Theorem 4 below; translations of polynomials in J(J + 1) are
not polynomials in J(J + 1). The following section is a proof that using a series of sequential combined differences to solve for J and the associated parameters yields a result that is unique.
Mathematical Model
Assume that the energy function for a molecule has the form for some positive integer value of n. is therefore a function of , where the number is a positive integer. Data values are collected from the dimensions of boxes or triangles in the multidimensional spectra. As a result, However, the corresponding values for are unknown. Furthermore, we assume that sufficient data is acquired so that > 2n. The goal for a spectroscopist is to find the value and the coefficients for the energy function E(J) that would fit the observed data.
The purpose of the following is to show that the determined values for and will be uniquely determined by the observed values . For an arbitrary polynomial f(x), it is most definitely not the case that the set of equations uniquely determines f(x) and J for a given set . For if f(x) and J satisfy the constraints, then so do g(x) and A where g(x) = f(x − A + J) for any A. However, E has a special form that we exploit in the following theorems.
For polynomials, in expressions such as , the constant term always vanishes so there is no way to determine it from this observed data; hence, techniques different from the ones considered in this paper are used to determine any vibrational or electronic energies. For this paper, we will assume that such constants cancel and consider only the higher-order coefficients. Though not considered in this paper, the reader should note that they can be uniquely determined.
Theorem 1. Letdenote. Thenis linear in.
Theorem 2. Suppose E(J) and F(J) are energy functions (with zero constant terms) such thatfor all J. Then E(J) = F(J) for all J, and if E and F produce the same observables corresponding to the same quantum numbers, then E and F are the same everywhere.
Proof. The following proof is by contradiction. Suppose E(J) is the not the same polynomial as F(J). Then, there must be a highest-degree term at which they differ. Let
and
where
and s(J) represents the higher-order parts that are the same in these two functions. Consider the following expression:
which becomes
. If n = 1, this expression reduces to the following:
or
which contradicts the assumption that
. Thus, we may assume
≥ 2. Collecting similar terms and dividing by
(which is not a constant) yields the following:
where, for all terms except
and
, the numerators are degree less than n − 1. For the
and
terms, the numerator has degree equal to n − 1. Hence, letting
the lower-order terms vanish, yielding the following:
or
which yields the contradiction
□
Theorem 3. Supposeand are energy functions that describe the same data from an experiment with possibly different quantum numbers. That is, and for where . Then for all J. Therefore, and are translations of each other.
Proof. Suppose and .
Since
and
are 2nth degree polynomials, it follows
is polynomial of degree at most 2n. However, the above computation (recalling the definition of L) shows
has k zeros, namely at
for
. This result implies the following:
for all
, since k is larger than 2n. Thus, we get the following:
for all
. Theorem 2 implies the following:
□
Theorem 4. Ifis an energy function, thenis not an energy function for ≠ 0.
Proof. Suppose
for some n value with
≠ 0. Assume
is an energy function. Then, we get the following:
for some values
. We also get the following:
now we equate coefficients for the
and
terms in the two expressions for
above. Expanding the two expressions, we obtain the following:
where the former expression has
for its 2nth coefficient; the latter has
. Hence,
. Considering the
coefficient, we obtain the following:
If we substitute
, we obtain the following:
since n ≠ 0,
which implies
+ 1 = 1 or
= 0. Putting these results together completes the goal of this proof. □
Theorem 5. Given data valueswith, there exists at most one energy functionand a unique integersuch that
Proof. If two energy functions exist, by Theorem 3, they would be translations of each other. By Theorem 4, a translation of an energy function is not an energy function. □
3. Results
In order to test how well this approach can determine the correct coefficients of E and the quantum number J from the differences E(J + 1) − E(J − 1) = c
1, …, E(J + k + 1) − E(J + k − 1) = c
k, we used simulated data based upon published Dunham coefficients for the
79,81Br
2 isotopologue [
15]. The first test involved four different data sets, each with a different initial value of J, and a varying amount of simulated experimental error that was added to each calculated peak value, using a random number generator. Three separate error levels were tested: no random error (other than rounding errors), small random errors (standard deviation ~0.003 cm
−1) consistent with a tunable dye laser that has been monitored using a wavemeter, and big random errors (standard deviation ~0.03 cm
−1) consistent with a tunable dye laser that has not been used with a wavemeter. The implemented strategy was to systematically test possible J values ranging from J = 1 to J = 300, to use least squares to find the coefficients Y
0,i which worked best with each J value, and then to compute the total absolute error for each J value. The solutions that gave the smallest error for the J value were then selected as the best J and Y
0,i values. Algorithm 1 illustrates the procedure that was used.
| Algorithm 1. Strategy for Finding E(x) and the Quantum Numbers. |
| Set initial Error = 1000 and J = 0 |
| FOR x from 1 to 300 do |
| FOR i from 1 to k do |
| Solve the system using Least Squares approximation. |
| END FOR |
| If < Error, |
| set Error = |
| set J = x and store coefficients |
| END FOR |
| Output J and coefficients |
This procedure also explored the effect of varying the number of points (1 point = distance between two peaks in the HRC2D spectrum having the same J value and the same
x- or
y-axis value) included in each simulation; the number of points used was either 25, 50, 75, or 100. The results are shown in
Table A1 of
Appendix A, and the key findings are summarized here. The accuracy of the determined J value depends primarily upon the number of points and the size of the error. For the no-error and small-error cases, the value of J was always determined correctly when the number of points used was at least 50. In all but one case, the value of J was determined correctly when the number of points was reduced to 25 points. For the big-error case, the value of J could always be determined correctly when the number of points was increased to 100.
The results also show that the accuracy of the calculated Y0,i values also depended upon the number of points and the size of the error. For the no-error and small-error cases, the value of Y0,1 was always within 1% of the correct value when the number of points used was at least 50. For the big-error case, the value of Y0,1 could always be determined correctly to within 1% when the number of points was increased to 100 and within 4% when the number of points was increased to 50.
For the no-error and small-error cases, the value of Y0,2 was always within 13% of the correct value when the number of points used was at least 100. The values of Y0,2 were generally not accurate for the big-error cases, and the values of Y0,3 were generally not accurate.
The results of the first test indicated that both J and Y
0,
1 could be determined with a high degree of accuracy when the number of points was high (e.g., 100). However, the accuracies for Y
0,
2 and Y
0,
3 were much poorer and highly sensitive to the level of experimental error. One possible reason was that the size of the experimental errors was relatively large compared to the small size of bromine’s rotational constants (Y
0,
1 ≈ 0.08 and Y
0,
2 ≈ 2 × 10
−8 cm
−1). Most molecules don’t contain heavy atoms like bromine, and many are likely to have larger rotational constants. Therefore, a second test was carried out, using rotational constants that were roughly an order of magnitude larger. Once again, four different data sets were used with the same three error levels, but the values of J were changed. The results are shown in
Table 1.
The results for
Table 1 show that increasing the rotational constants by an order of magnitude caused a significant improvement for both J and the Y
0,i’s. For all values of J and all three error levels, the J values were determined correctly, the calculated Y
0,1’s were all within 0.06% of the correct value, and the Y
0,2’s were all within 18% of the correct value when 100 points were used. The Y
0,3’s were still highly susceptible to experimental errors, but were within 0.004% of the correct value for the no-error case.
4. Discussion and Conclusions
The results show that combination differences can be used to determine accurate values for J and Y0,1 for a sequence of peaks and basic rotational units recorded using HRC2DS. The accuracy is greatest when the number of points is high and when the experimental error is small relative to the rotational constants. The resulting Y0,2 values can also be close to the correct values, if the size of the error is small and the number of points is high. The Y0,3 values were not consistently accurate, but Y0,3 values often disagree in the published literature. In general, the accuracies of all quantum numbers and molecular constants improved when the molecular constants were larger, when the number of points were increased, and when the error was reduced.
Unlike a conventional 1D spectrum, an off-diagonal 2D spectrum provides the opportunity to obtain molecular constants for two different regions of a spectrum, when the range of
x-axis values is different from the range of
y-axis values. Since all four peaks in the basic unit have the same rotational quantum number (see
Figure 3), this method provides an additional mechanism for checking the assignment of the peaks; the J value calculated using the dimensions of the box along the
x axis can be compared to the J value calculated using the dimensions of the same box along the
y axis. If the analysis was carried out accurately, both of these J values should agree.
This paper explored the feasibility of determining rotational quantum numbers and molecular constants, using peak positions that appear sequentially ordered in HRCMDS spectroscopy. A mathematical proof was used to determine that the solutions should be unique due to the special form of the rotational energy function. Tests using simulated data with varying amounts of error were conducted to determine whether the technique would yield correct solutions. The tests showed that values for J and Y0,1 could be accurately obtained, and that Y0,2 could be determined if the experimental error was not too large. Y0,3 could only be determined accurately when no experimental error was added to the simulated data.