Type II Topp Leone Power Lomax Distribution with Applications
Abstract
1. Introduction
1.1. From the Lomax Distribution to the Power Lomax Distribution
1.2. On the Extensions of the PL Distribution through the Use of General Families of Distributions
1.3. Novelty and Contributions
- To improve the characteristics and flexibility of the PL distribution by using the TIITL-G family (as motivated above). In particular, increasing, decreasing, J, and reverse J shapes are observed for the probability density and hazard rate functions, illustrating this claim.
- To introduce an extended version of the PL distribution whose quantile function has a closed-form.
- To study important statistical properties of the TIITLPL distribution, including the skewness, kurtosis, and various kinds of moments and order statistics.
- To explore the inferential features of the TIITLPL distribution through the use of the maximum likelihood method, providing a comprehensive methodology for the practitioner.
1.4. Paper Organization
2. The TIITLPL Distribution
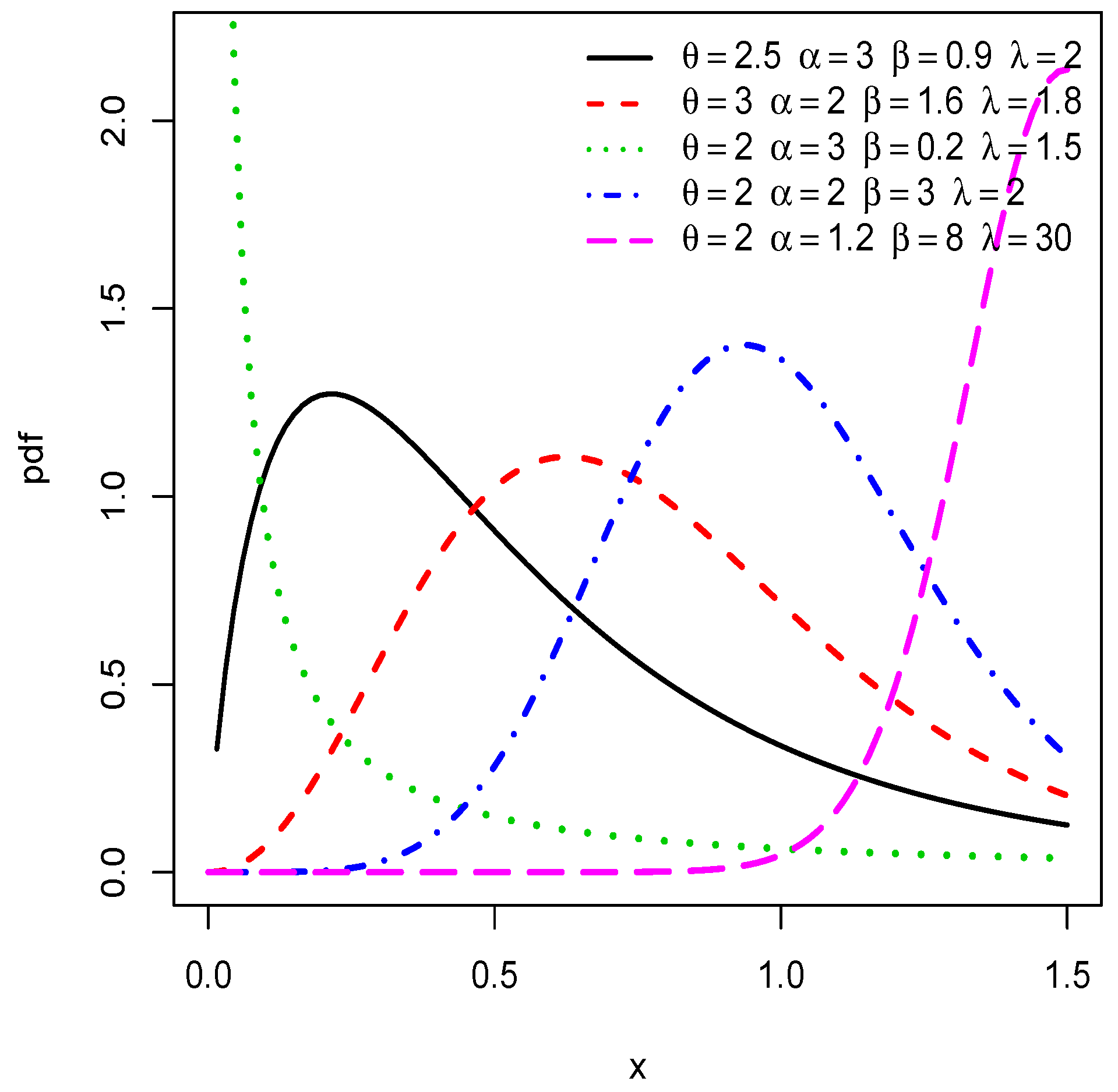
2.1. Definition
2.2. Common Reliability Functions
3. Mathematical Properties
3.1. Quantile Function and Applications
3.1.1. Definition
3.1.2. Generated Values
3.1.3. Some Related Functions
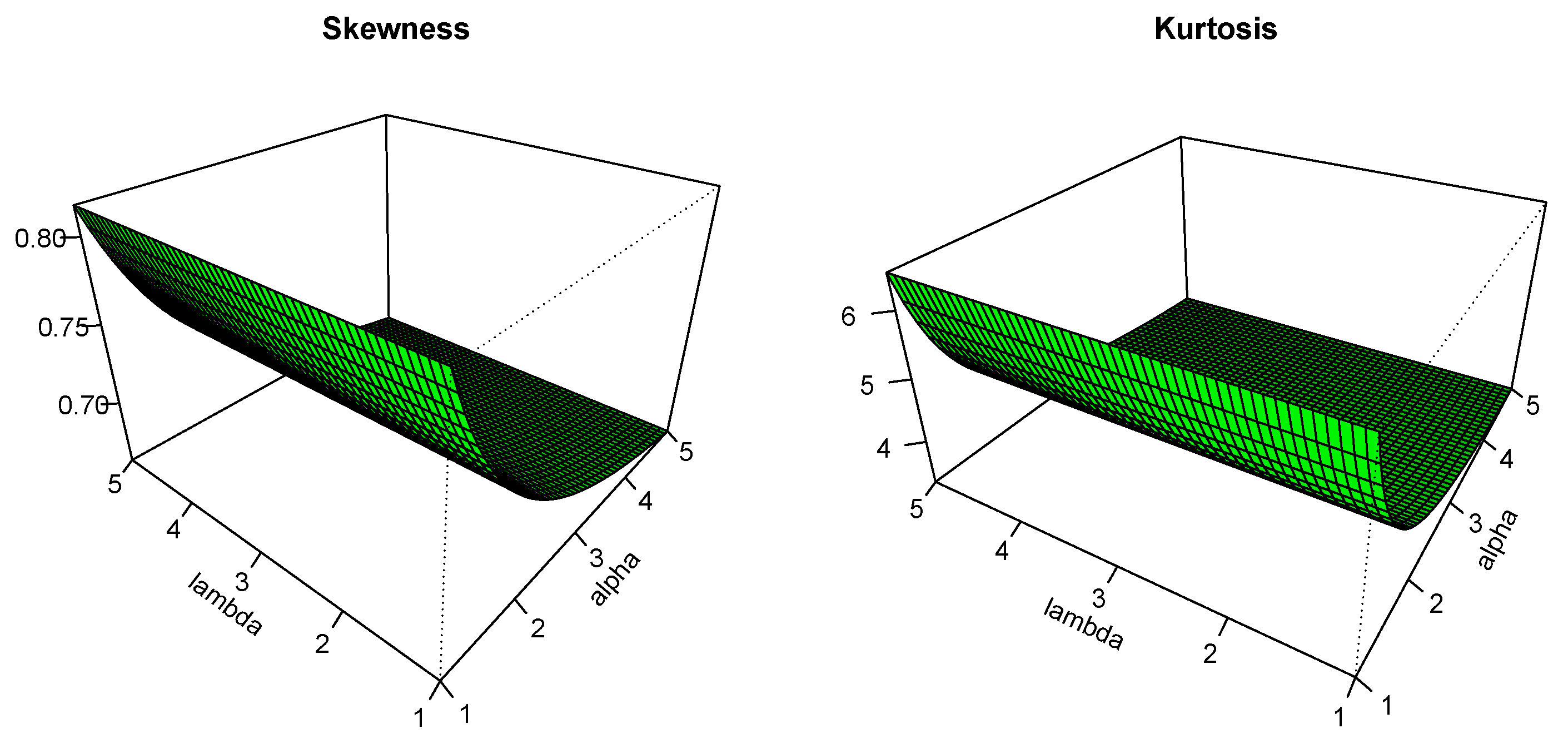
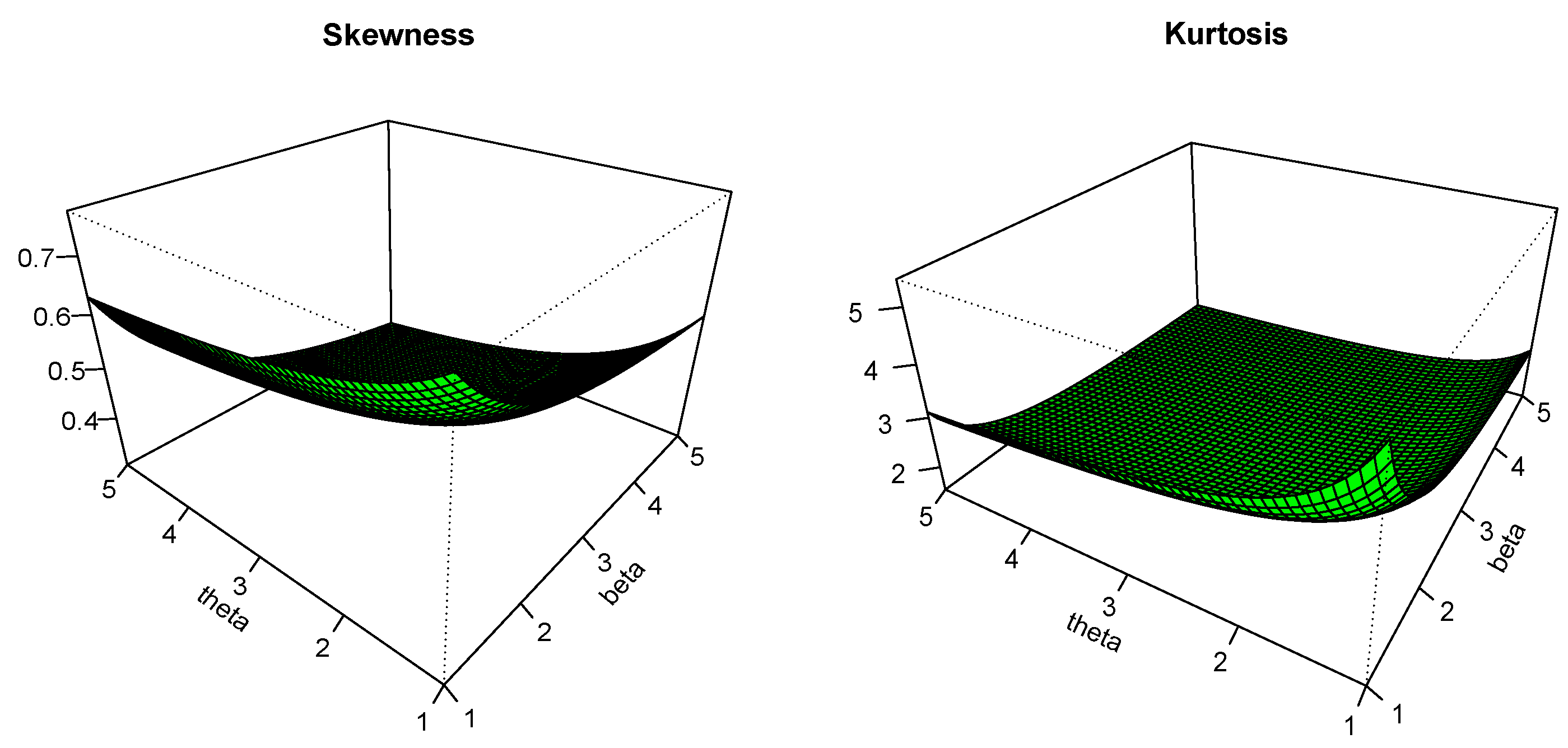
3.1.4. Skewness and Kurtosis Based on the Quantile Function
3.2. Useful Expansions
3.3. Moments
3.3.1. Ordinary moments
3.3.2. Incomplete Moments
3.4. Order Statistics
- The limiting distribution of is the Weibull distribution with the following cdf: , , i.e., there exist and such that
- The limiting distribution of is the Fréchet distribution with the following cdf: , , i.e., there exist and such that
4. Inference
4.1. Maximum Likelihood Estimation Method
4.2. Simulation
- One thousand random samples of size , 100, 200, and 500 are generated from the TIITLPL distribution by the use of the quantile function (see Section 3.1.2).
- Eight different sets of values of true parameters , , , and in order, are taken asSet 1 , Set 2 , Set 3 ,Set 4 , Set 5 , Set 6 ,Set 7 , Set 8 .
- The mean of the obtained MLEs (Estimates) and the mean squared errors (MSEs) for the selected sets of parameters are calculated.
5. Applications
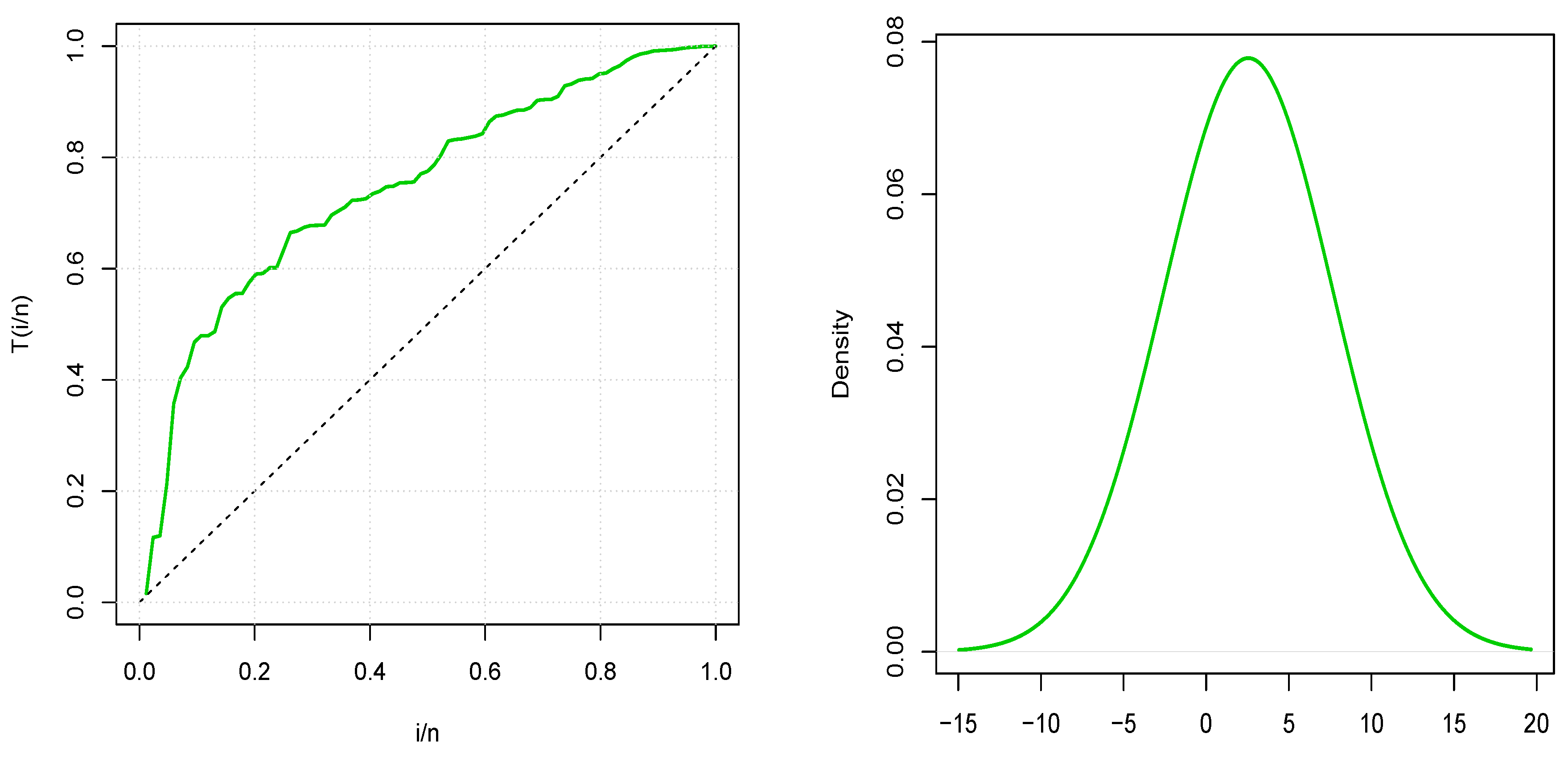
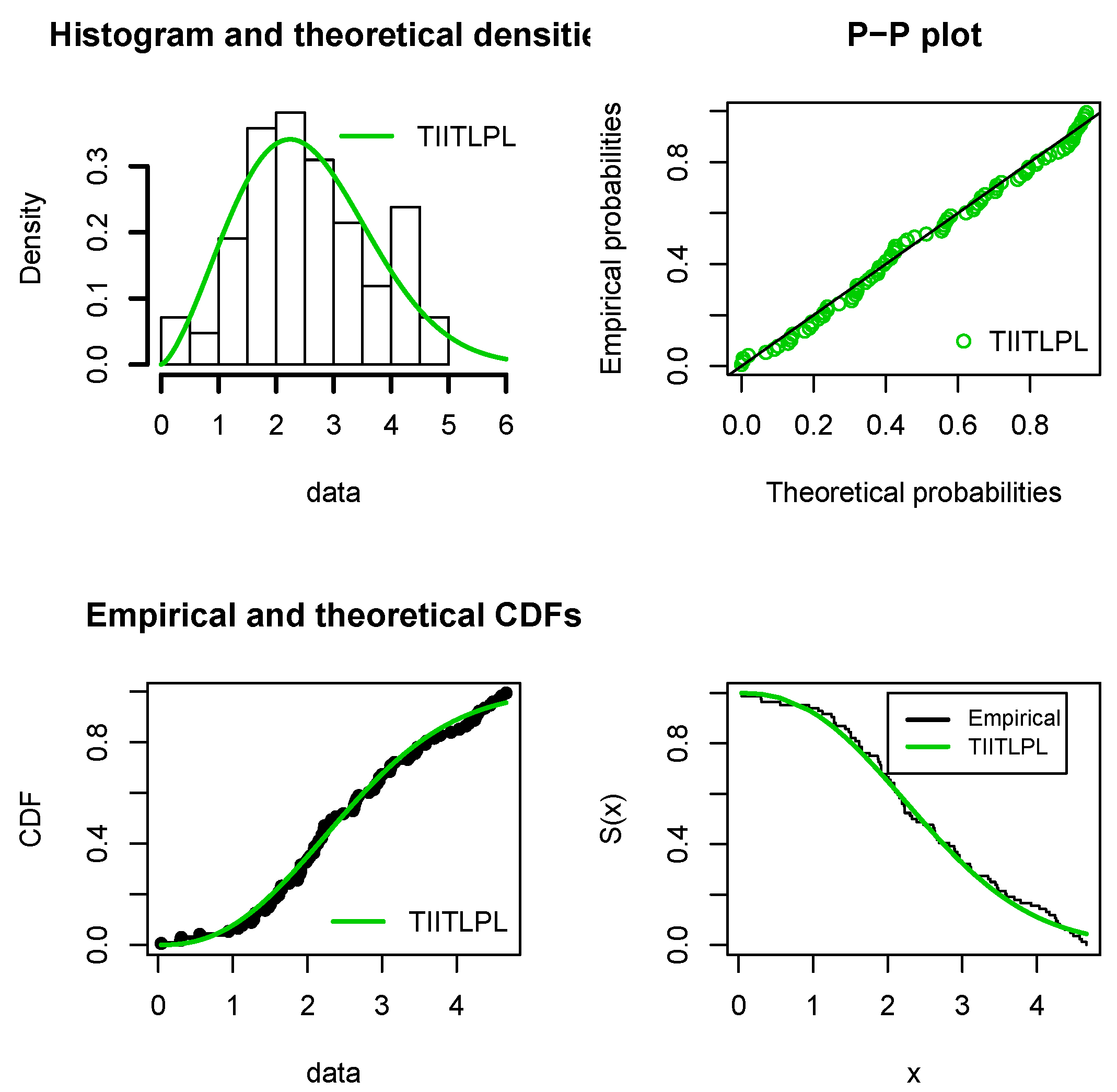
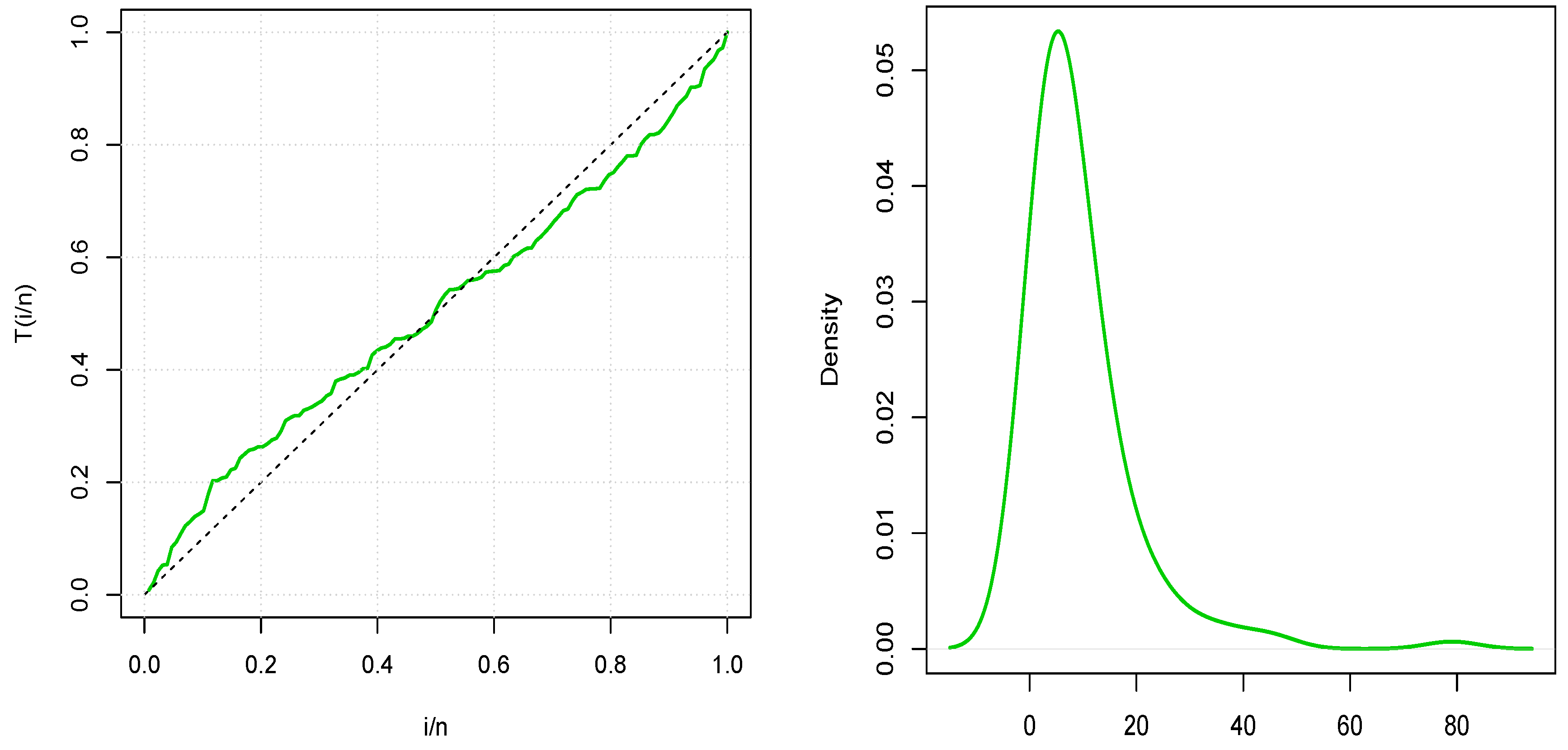
5.1. Aircraft Windshield Data
5.2. Cancer Patient Data
6. Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| cdf | cumulative distribution function |
| probability distribution function | |
| PL | Power Lomax |
| TIITL-G | type II Topp-Leone-G |
| TIITLPL | type II Topp-Leone power Lomax |
| sf | survival function |
| hrf | hazard rate function |
| MLE | maximum likelihood estimate |
| MSE | mean squared error |
| AIC | Akaike information criterion |
| CAIC | consistent Akaike information criterion |
| HQIC | Hannan-Quinn information criterion |
| Anderson-Darling | |
| Cramér-von Mises | |
| TTT | total time on test |
| GL | gamma Lomax |
| BL | beta Lomax |
| TWL | Transmuted Weibull Lomax |
| KwW | Kumaraswamy Weibull |
| McW | McDonald Weibull |
| BW | beta Weibull |
| TLL | transmuted log-logistic |
| LL | log-logistic |
| TMOFr | transmuted Marshall-Olkin Fréchet |
| SE | standard error |
| TMW | transmuted modified Weibull |
| TAW | transmuted additive Weibull |
| GIG | generalized inverse gamma |
| BEBXII | beta exponential Burr XII |
| BFr | beta Fréchet |
| KwLL | Kumaraswamy log-logistic |
| TCWG | transmuted complementary Weibull geometric |
| KwEBXII | Kumaraswamy exponentiated Burr XII |
| GTW | generalized transmuted-W |
| ETGR | exponentiated transmuted generalized Rayleigh |
| Nomenclature | |
| cdf of the Lomax distribution | |
| pdf of the Lomax distribution | |
| cdf of the power Lomax distribution | |
| pdf of the power Lomax distribution | |
| cdf of the TIITL-G family | |
| pdf of the TIITL-G family | |
| cdf of the TIITLPL distribution | |
| pdf of the TIITLPL distribution | |
| sf of the TIITLPL distribution | |
| hrf of the TIITLPL distribution | |
| reverse hazard rate function of the TIITLPL distribution | |
| cumulative hazard rate function of the TIITLPL distribution | |
| quantile function of the TIITLPL distribution | |
| M | Median of the TIITLPL distribution |
| quantile density function of the TIITLPL distribution | |
| hazard quantile function of the TIITLPL distribution | |
| S | Galton skewness of the TIITLPL distribution |
| K | Moors kurtosis of the TIITLPL distribution |
| coefficient in the considered series expansion for | |
| coefficient in the considered series expansion for | |
| sth ordinary moment of the TIITLPL distribution | |
| coefficient in the considered series expansion for | |
| sth central moment of the TIITLPL distribution | |
| sth cumulant of the TIITLPL distribution | |
| sth incomplete moment taken on t of the TIITLPL distribution | |
| mean deviation about the mean of the TIITLPL distribution | |
| mean deviation about the median of the TIITLPL distribution | |
| lower conditional moment taken on t of the TIITLPL distribution | |
| upper conditional moment taken on t of the TIITLPL distribution | |
| ith order statistic of the TIITLPL distribution | |
| pdf of the ith order statistic of the TIITLPL distribution | |
| coefficient in the considered series expansion for | |
| sth moment of the ith order statistic of the TIITLPL distribution | |
| likelihood function of the TIITLPL distribution | |
| log-likelihood function of the TIITLPL distribution | |
| , , and | MLEs of , , and , respectively |
| n | size of the considered sample or the number of data |
References
- Lomax, K.S. Business failures: Another example of the analysis of failure data. J. Am. Stat. Assoc. 1954, 49, 847–852. [Google Scholar] [CrossRef]
- Hassan, A.; Al-Ghamdi, A. Optimum step stress accelerated life testing for Lomax distribution. J. Appl. Sci. Res. 2009, 5, 2153–2164. [Google Scholar]
- Harris, C. The Pareto distribution as a queue service discipline. Oper. Res. 1968, 16, 307–313. [Google Scholar] [CrossRef]
- Atkinson, A.; Harrison, A. Distribution of Personal Wealth in Britain; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Chen, J.; Addie, R.G.; Zukerman, M.; Neame, T.D. Performance evaluation of a queue fed by a Poisson Lomax Burst Process. IEEE Commun. Lett. 2015, 19, 367–370. [Google Scholar] [CrossRef]
- Bryson, M.C. Heavy-tailed distribution: properties and tests. Technometrics 1974, 16, 61–68. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Al-Awadhi, F.A.; Alkhalfan, L.A. Marshall Olkin extended Lomax distribution and its application to censored data. Commun. Stat. Theory Methods 2007, 36, 1855–1866. [Google Scholar] [CrossRef]
- Abdul-Moniem, I.B.; Abdel-Hameed, H.F. On exponentiated Lomax distribution. Int. J. Math. Arch. 2012, 3, 2144–2150. [Google Scholar]
- Lemonte, A.J.; Cordeiro, G.M. An extended Lomax distribution. Statistics 2013, 47, 800–816. [Google Scholar] [CrossRef]
- Al-Zahrani, B.; Sagor, H. The Poisson-Lomax distribution. Rev. Colomb. Estad. 2014, 37, 225–245. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; Popovíc, B.V. The gamma Lomax distribution. J. Stat. Comput. Simul. 2015, 85, 305–319. [Google Scholar] [CrossRef]
- El-Bassiouny, A.H.; Abdo, N.F.; Shahen, H.S. Exponential Lomax distribution. Int. J. Comput. Appl. 2015, 121, 24–29. [Google Scholar]
- Ashour, S.K.; Eltehiwy, M.A. Transmuted Lomax distribution. Am. J. Appl. Math. Stat. 2013, 1, 121–127. [Google Scholar] [CrossRef]
- Kilany, N.M. Weighted Lomax distribution. SpringerPlus 2016, 5, 1862. [Google Scholar] [CrossRef] [PubMed]
- Tahir, M.H.; Cordeiro, G.M.; Mansoor, M.; Zubair, M. The Weibull-Lomax distribution: Properties and applications. Hacet. J. Math. Stat. 2015, 44, 461–480. [Google Scholar] [CrossRef]
- Oguntunde, P.E.; Khaleel, M.A.; Ahmed, M.T.; Adejumo, A.O.; Odetunmibi, O.A. A New Generalization of the Lomax Distribution with Increasing, Decreasing and Constant Failure Rate. Model. Simul. Eng. 2017, 2017, 6043169. [Google Scholar] [CrossRef]
- Alzaghal, A.; Hamed, D. New families of generalized Lomax distributions: Properties and Applications. Int. J. Stat. Probab. 2019, 8, 51–68. [Google Scholar] [CrossRef][Green Version]
- Rady, E.A.; Hassanein, W.A.; Elhaddad, T.A. The power Lomax distribution with an application to bladder cancer data. SpringerPlus 2016, 5, 1838. [Google Scholar] [CrossRef]
- Al-Marzouki, S. A new generalization of power Lomax distribution. Int. J. Math. Appl. 2018, 7, 59–68. [Google Scholar]
- Assar, S.M. On odds generalized exponential-power Lomax distribution. J. Math. Stat. 2018, 14, 167–174. [Google Scholar] [CrossRef]
- Moltok, T.T.; Dikko, H.G.; Asiribo, O.E. A transmuted Power Lomax distribution. Afr. J. Nat. Sci. 2017, 20, 67–78. [Google Scholar]
- Gupta, R.D.; Kundu, D. Exponentiated exponential family: An alternative to Gamma and Weibull distributions. Biom. J. 2001, 43, 117–130. [Google Scholar] [CrossRef]
- Tahir, M.H.; Cordeiro, G.M.; Alizadeh, M.; Mansoor, M.; Zubair, M. The odd generalized exponential family of distributions with applications. J. Stat. Distrib. Appl. 2015, 2, 1–28. [Google Scholar] [CrossRef]
- Shaw, W.T.; Buckley, I.R. The Alchemy of Probability Distributions: beyond Gram-Charlier Expansions, and a Skew-kurtotic-normal Distribution from a Rank Transmutation Map. arXiv 2009, arXiv:0901.0434. [Google Scholar]
- Elgarhy, M.; Nasir, M.A.; Jamal, F.; Ozel, G. The type II Topp-Leone generated family of distributions: Properties and applications. J. Stat. Manag. Syst. 2018, 21, 1529–1551. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; de Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2011, 81, 883–893. [Google Scholar] [CrossRef]
- Mohammed, H.F.; Yahia, N. On type II Topp-Leone inverse Rayleigh distribution. Appl. Math. Sci. 2019, 13, 607–615. [Google Scholar] [CrossRef]
- Yahia, N.; Mohammed, H.F. The type II Topp-Leone generalized inverse Rayleigh distribution. Int. J. Contemp. Math. Sci. 2019, 14, 113–122. [Google Scholar] [CrossRef]
- ZeinEldin, R.A.; Jamal, F.; Chesneau, C.; Elgarhy, M. Type II Topp-Leone inverted Kumaraswamy distribution with statistical inference and applications. Symmetry 2019, 11, 1459. [Google Scholar] [CrossRef]
- Eugene, N.; Lee, C.; Famoye, F. Beta-normal distribution and its applications. Commun. Stat. Theory Methods 2002, 31, 497–512. [Google Scholar] [CrossRef]
- Elbatal, I.; Aryal, G. On the transmuted additive Weibull distribution. Aust. J. Stat. 2013, 42, 117–132. [Google Scholar] [CrossRef]
- Mead, M. Generalized inverse gamma distribution and its application in reliability. Commun. Stat. Theory Methods 2015, 44, 1426–1435. [Google Scholar] [CrossRef]
- Afify, A.Z.; Nofal, Z.M.; Yousof, H.M.; El Gebaly, Y.M.; Butt, N.S. The transmuted Weibull Lomax distribution: Properties and application. Pak. J. Stat. Oper. Res. 2015, 11, 135–152. [Google Scholar] [CrossRef]
- Gilchrist, W. Statistical Modelling with Quantile Functions; Chapman and Hall/CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Nair, N.U.; Sankaran, P.G. Quantile-based reliability analysis. Commun. Stat. Theory Methods 2009, 38, 222–232. [Google Scholar] [CrossRef]
- Galton, F. Inquiries into Human Faculty and Its Development; Macmillan and Company: London, UK, 1883. [Google Scholar]
- Moors, J.J.A. A quantile alternative for Kurtosis. J. R. Stat. Soc. Ser. 1988, 37, 25–32. [Google Scholar] [CrossRef]
- Arnold, B.; Balakrishnan, N.; Nagaraja, H. A First Course in Order Statistics; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Leadbetter, M.; Lindgren, G.; Rootzén, H. Extremes and Related Properties of Random Sequences and Processes; Springer: New York, NY, USA, 1987. [Google Scholar]
- Murthy, D.N.P.; Xie, M.; Jiang, R. Weibull Models; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Cordeiro, G.M.; Ortega, E.M.M.; Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Frankl. Inst. 2010, 349, 1174–1197. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Hashimoto, E.M.; Ortega, E.M. The McDonald-Weibull model. Stat. J. Theor. Appl. Stat. 2014, 48, 256–278. [Google Scholar] [CrossRef]
- Lee, C.; Famoye, F.; Olumolade, O. Beta-Weibull distribution: Some properties and applications to censored data. J. Mordern Appl. Stat. Methods 2007, 6, 173–186. [Google Scholar] [CrossRef]
- Aryal, G.R. Transmuted log-logistic distribution. J. Stat. Appl. Probab. 2013, 2, 11–20. [Google Scholar] [CrossRef]
- Afify, A.Z.; Hamedani, G.G.; Ghosh, I.; Mead, E.M. The transmuted Marshall-Olkin Fréchet distribution: Properties and applications. Int. J. Probab. Stat. 2015, 4, 132–148. [Google Scholar] [CrossRef]
- Lee, E.T.; Wang, J.W. Statistical Methods for Survival Data Analysis, 3rd ed.; JohnWiley and Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Khan, M.S.; King, R. Transmuted modified Weibull distribution: A generalization of the modified Weibull probability distribution. Eur. J. Pure Appl. Math. 2013, 6, 66–88. [Google Scholar]
- Mead, M. A new generalization of Burr XII distribution. J. Stat. Adv. Theory Appl. 2014, 12, 53–73. [Google Scholar]
- Nadarajah, S.; Gupta, A.K. The beta Fréchet distribution. Far East J. Theor. Stat. 2004, 14, 15–24. [Google Scholar]
- De Santana, T.V.F.; Ortega, E.M.M.; Cordeiro, G.M.; Silva, G.O. The Kumaraswamy log-logistic distribution. J. Stat. Theory Appl. 2012, 11, 265–291. [Google Scholar]
- Afify, A.Z.; Nofal, Z.M.; Butt, N.S. Transmuted complementary Weibull geometric distribution. Pak. J. Stat. Oper. Res. 2014, 10, 435–454. [Google Scholar] [CrossRef]
- Mead, M.E.; Afify, A.Z. On five parameter Burr XII distribution: Properties and applications. S. Afr. Stat. J. 2017, 51, 67–80. [Google Scholar]
- Nofal, Z.M.; Afify, A.Z.; Yousof, H.M.; Cordeiro, G.M. The generalized transmuted-G family of distributions. Commun. Stat. Theory Methods 2017, 46, 4119–4136. [Google Scholar] [CrossRef]
- Afify, A.Z.; Nofal, Z.M.; Ebraheim, A.N. Exponentiated transmuted generalized Rayleigh: A new four parameter Rayleigh distribution. Pak. J. Stat. Oper. Res. 2015, 11, 115–134. [Google Scholar] [CrossRef]


| M | |
|---|---|
| 540.1999 | |
| 54019.99 | |
| 1800.6660 | |
| 232.4650 | |
| 141.8530 | |
| 1206.2180 | |
| 26.97185 | |
| 7.6697 | |
| 2.8015 | |
| 9.6382 | |
| 0.0358 | |
| 0.0282 | |
| 0.0077 |
| 6.5310 | 329.8982 | 21948 | 1642994 | |
| 3.0469 | 83.6055 | 4496.53 | 304584 | |
| 0.2716 | 0.8662 | 18.6814 | 905.1954 | |
| 0.03667 | 0.0061 | 0.0038 | 0.0111 | |
| 0.0210 | 0.0017 | 0.0004 | 0.0003 | |
| 1.2956 | 6.6656 | 141.9529 | 6614.0360 | |
| 0.1528 | 0.03667 | 0.0126 | 0.0061 | |
| 0.3661 | 0.1528 | 0.0712 | 0.03667 | |
| 0.6575 | 0.4426 | 0.3044 | 0.2139 | |
| 0.1467 | 0.0980 | 0.2437 | 2.3221 | |
| 3.6090 | 51.7157 | 1679.7620 | 84843.84 | |
| 1.0420 | 1.1118 | 1.2121 | 1.3482 | |
| 0.8527 | 0.7423 | 0.6583 | 0.5939 |
| Set 1 | Set 2 | Set 3 | Set 4 | |||||
|---|---|---|---|---|---|---|---|---|
| n | Estimates | MSEs | Estimates | MSEs | Estimates | MSEs | Estimates | MSEs |
| 50 | 0.471 | 0.090 | 0.602 | 0.091 | 0.587 | 0.058 | 0.554 | 0.128 |
| 0.537 | 0.238 | 0.663 | 0.223 | 2.145 | 2.429 | 1.614 | 1.138 | |
| 0.735 | 0.223 | 1.758 | 0.587 | 0.920 | 0.250 | 2.122 | 1.636 | |
| 0.771 | 0.431 | 0.662 | 0.344 | 1.790 | 1.041 | 1.650 | 1.552 | |
| 100 | 0.504 | 0.084 | 0.644 | 0.053 | 0.574 | 0.033 | 0.609 | 0.083 |
| 0.428 | 0.085 | 0.669 | 0.128 | 1.747 | 0.446 | 1.739 | 0.510 | |
| 0.660 | 0.122 | 1.633 | 0.258 | 0.865 | 0.115 | 1.665 | 0.239 | |
| 0.656 | 0.245 | 0.474 | 0.088 | 1.479 | 0.284 | 1.310 | 1.088 | |
| 200 | 0.525 | 0.081 | 0.617 | 0.046 | 0.577 | 0.017 | 0.642 | 0.058 |
| 0.546 | 0.075 | 0.585 | 0.041 | 1.623 | 0.141 | 1.719 | 0.199 | |
| 0.558 | 0.045 | 1.561 | 0.124 | 0.832 | 0.025 | 1.548 | 0.085 | |
| 0.685 | 0.233 | 0.475 | 0.071 | 1.309 | 0.149 | 1.066 | 0.293 | |
| 500 | 0.504 | 0.061 | 0.647 | 0.035 | 0.592 | 0.013 | 0.660 | 0.051 |
| 0.477 | 0.051 | 0.612 | 0.027 | 1.620 | 0.058 | 1.729 | 0.137 | |
| 0.539 | 0.013 | 1.449 | 0.035 | 0.815 | 5.258 * | 1.515 | 0.023 | |
| 0.636 | 0.169 | 0.419 | 0.018 | 1.226 | 0.106 | 0.942 | 0.141 |
| Set 5 | Set 6 | Set 7 | Set 8 | |||||
|---|---|---|---|---|---|---|---|---|
| n | Estimates | MSEs | Estimates | MSEs | Estimates | MSEs | Estimates | MSEs |
| 50 | 0.651 | 0.147 | 0.773 | 0.210 | 0.699 | 0.206 | 1.268 | 0.48 |
| 0.613 | 0.303 | 0.486 | 0.228 | 1.464 | 4.786 | 1.143 | 3.391 | |
| 2.442 | 1.194 | 2.549 | 1.534 | 1.588 | 0.918 | 1.603 | 0.247 | |
| 0.746 | 0.758 | 1.058 | 1.221 | 1.752 | 2.663 | 1.432 | 1.103 | |
| 100 | 0.667 | 0.133 | 0.806 | 0.147 | 0.767 | 0.161 | 1.199 | 0.248 |
| 0.621 | 0.156 | 0.437 | 0.074 | 1.326 | 0.386 | 0.774 | 0.895 | |
| 2.296 | 0.714 | 2.310 | 0.440 | 1.247 | 0.115 | 1.592 | 0.123 | |
| 0.652 | 0.484 | 0.845 | 0.612 | 1.286 | 0.630 | 1.148 | 0.600 | |
| 200 | 0.735 | 0.109 | 0.828 | 0.109 | 0.750 | 0.102 | 1.197 | 0.168 |
| 0.647 | 0.078 | 0.456 | 0.039 | 1.247 | 0.177 | 0.703 | 0.093 | |
| 2.064 | 0.121 | 2.099 | 0.169 | 1.253 | 0.061 | 1.468 | 0.033 | |
| 0.478 | 0.222 | 0.819 | 0.594 | 1.115 | 0.582 | 1.098 | 0.222 | |
| 500 | 0.725 | 0.07 | 0.898 | 0.036 | 0.768 | 0.090 | 1.167 | 0.140 |
| 0.680 | 0.056 | 0.483 | 0.017 | 1.269 | 0.139 | 0.639 | 0.043 | |
| 1.880 | 0.073 | 2.043 | 0.048 | 1.195 | 0.013 | 1.484 | 0.016 | |
| 0.406 | 0.043 | 0.612 | 0.121 | 1.004 | 0.314 | 1.054 | 0.221 |
| n | Mean | Median | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|
| 84 | 2.56 | 2.35 | 1.12 | 0.10 | −0.71 |
| Distributions | MLEs and SEs | ||||
|---|---|---|---|---|---|
| TIITLPL(, , , ) | 213.2225 (8.0985) | 3.6880 (0.7192) | 1.2282 (0.1149) | 186.8420 (7.6076) | - |
| BL(, , , ) | 3.6036 (0.6187) | 32.6387 (13.7145) | 4.8307 (9.2382) | 119.0374 (42.9269) | - |
| KwW(, , , ) | 34.6604 (17.5270) | 81.8464 (52.0142) | 14.4338 (27.0952) | 0.2040 (0.0423) | - |
| McW(, , , , ) | 17.6864 (6.2220) | 33.6392 (19.9941) | 1.9406 (1.0111) | 0.3062 (0.0454) | 16.7211 (9.6221) |
| BW(, , , ) | 34.1808 (14.8389) | 11.4968 (6.7300) | 1.3609 (1.0020) | 0.2982 (0.0603) | - |
| TMOFr(, , , ) | 200.7472 (87.2751) | 1.9524 (0.1252) | 0.1022 (0.0173) | −0.8692 (0.1012) | - |
| (, , ) | 2.0589 (0.2759) | 3.1025 (0.3408) | −0.4839 (0.3853) | - | - |
| (, ) | 2.3911 (0.1369) | 3.2235 (0.2971) | - | - | - |
| Distributions | AIC | CAIC | HQIC | A | W |
|---|---|---|---|---|---|
| 269.0398 | 269.5461 | 272.9485 | 0.6245 | 0.0621 | |
| 285.4354 | 285.9355 | 289.3650 | 1.4080 | 0.1684 | |
| 281.4345 | 281.9411 | 291.1585 | 1.5062 | 0.1851 | |
| 283.8993 | 284.6692 | 296.0532 | 1.5917 | 0.1992 | |
| BW | 305.0283 | 305.5343 | 314.7519 | 3.2277 | 0.4655 |
| 309.4725 | 309.9785 | 319.1953 | 2.4042 | 0.3209 | |
| 284.7719 | 285.0719 | 287.7034 | 1.4922 | 0.1842 | |
| 283.1625 | 283.3106 | 285.1168 | 1.5203 | 0.1866 |
| n | Mean | Median | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|
| 128 | 9.37 | 6.39 | 10.51 | 3.25 | 15.20 |
| Distribution | MLEs and SEs | ||||
|---|---|---|---|---|---|
| (, , , ) | 3.7264 (0.1187) | 1.8637 (0.2335) | 0.8039 (0.1253) | 13.3937 (1.2256) | - |
| (, , , ) | 4.6580 (13.1634) | 0.2984 (0.1675) | 7.8661 (4.4933) | 113.0181 (23.364) | - |
| (, , , ) | 106.0695 (124.8000) | 1.7124 (0.0992) | 0.2173 (0.6104) | 0.0090 (0.0070) | - |
| (, , , , ) | 2.7805 (44.5102) | 67.636 (104.728) | 0.3380 (0.3857) | 3.0833 (49.3534) | 0.8398 (1.7235) |
| (, , , , ) | 22.1869 (21.9561) | 20.2778 (17.2968) | 0.2243 (0.1446) | 1.7804 (1.0763) | 1.3067 (1.0794) |
| (, , , , ) | 2.3272 (0.3698) | 0.0002 (0.0002) | 17.9315 (7.3857) | 0.5430 (0.0420) | 0.0010 (0.0003) |
| (, , , ) | 12.5268 (24.4699) | 33.342 (36.348) | 27.7533 (71.5078) | 0.1690 (0.1040) | - |
| (, , , ) | 7.3765 (5.3893) | 0.0473 (0.0042) | 0.1182 (0.2600) | 0.0491 (0.0362) | - |
| (, , , ) | 0.0002 (0.0114) | 0.1208 (0.0240) | 0.8955 (0.6260) | 0.4075 (0.4070) | - |
| (, , , , ) | 0.00003 (0.0061) | 1.0065 (0.0353) | 0.1139 (0.0322) | 0.9722 (0.125) | −0.1630 (0.2803) |
| (, , , , ) | 2.7965 (1.117) | 0.0128 (7.214) | 0.2991 (0.1512) | 0.6542 (0.1216) | 0.0020 (1.7691) |
| Distributions | AIC | CAIC | HQIC | A | W |
|---|---|---|---|---|---|
| 828.1981 | 828.5239 | 832.8331 | 0.2043 | 0.0340 | |
| 829.5312 | 829.8570 | 834.1672 | 0.3173 | 0.0494 | |
| 829.9953 | 830.3201 | 834.6335 | 0.3064 | 0.0435 | |
| 831.6514 | 832.1432 | 837.4453 | 0.3244 | 0.0485 | |
| 841.2684 | 841.7644 | 855.5283 | 0.9515 | 0.1345 | |
| 839.8243 | 840.3163 | 854.0853 | 2.6188 | 0.4100 | |
| 842.9651 | 843.2924 | 854.3735 | 1.1218 | 0.1689 | |
| 866.3500 | 866.6755 | 877.7588 | 2.3617 | 0.3980 | |
| 836.4555 | 836.7759 | 847.8586 | 0.1259 | 0.7609 | |
| 838.47833 | 838.9777 | 852.7390 | 0.1130 | 0.7030 | |
| 831.3475 | 831.8395 | 837.1411 | 0.3058 | 0.0469 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Marzouki, S.; Jamal, F.; Chesneau, C.; Elgarhy, M. Type II Topp Leone Power Lomax Distribution with Applications. Mathematics 2020, 8, 4. https://doi.org/10.3390/math8010004
Al-Marzouki S, Jamal F, Chesneau C, Elgarhy M. Type II Topp Leone Power Lomax Distribution with Applications. Mathematics. 2020; 8(1):4. https://doi.org/10.3390/math8010004
Chicago/Turabian StyleAl-Marzouki, Sanaa, Farrukh Jamal, Christophe Chesneau, and Mohammed Elgarhy. 2020. "Type II Topp Leone Power Lomax Distribution with Applications" Mathematics 8, no. 1: 4. https://doi.org/10.3390/math8010004
APA StyleAl-Marzouki, S., Jamal, F., Chesneau, C., & Elgarhy, M. (2020). Type II Topp Leone Power Lomax Distribution with Applications. Mathematics, 8(1), 4. https://doi.org/10.3390/math8010004








