Links between Contractibility and Fixed Point Property for Khalimsky Topological Spaces

Abstract

Given a Khalimsky (for short, K-) topological space X, the present paper examines if there are some relationships between the contractibility of X and the existence of the fixed point property of X. Based on a K-homotopy for K-topological spaces, we firstly prove that a K-homeomorphism preserves a K-homotopy between two K-continuous maps. Thus, we obtain that a K-homeomorphism preserves K-contractibility. Besides, the present paper proves that every simple closed K-curve in the n-dimensional K-topological space, $S{C}_K^{n,l},n\ge 2,l\ge 4$, is not K-contractible. This feature plays an important role in fixed point theory for K-topological spaces. In addition, given a K-topological space X, after developing the notion of K-contractibility relative to each singleton $\left\{x\right\}(\subset X)$, we firstly compare it with the concept of K-contractibility of X. Finally, we prove that the K-contractibility does not imply the K-contractibility relative to each singleton $\left\{x_0\right\}(\subset X)$. Furthermore, we deal with certain conjectures involving the (almost) fixed point property in the categories KTC and KAC, where KTC (see Section 3) (resp. KAC (see Section 5)) denotes the category of K-topological (resp. KA-) spaces, KA-) spaces are subgraphs of the connectedness graphs of the K-topology on ${\mathbb{Z}}^n$.

1. Introduction

First of all, we recall that in a category an object X has the fixed point property (FPP, for short) if every self-morphism f of X has a point $x\in X$ such that $f\left(x\right)=x$. Since every singleton obviously has the FPP, when studying the FPP of topological spaces, each topological space X (resp. digital image $(X,k)$) is assumed to be connected (resp.k-connected) and $\left|X\right|\ge 2$. Thus, each set X involving the FPP considered in this paper is assumed to follow this requirement. As stated in [1], associated with the Borsuk and the Lefschetz fixed point theorems [2,3,4], there was the following conjecture [3]: Let X be a contractible and locally contractible space.

$$\mathrm{Then}\mathrm{it}\mathrm{has}\mathrm{the}FPP\mathrm{for}\mathrm{compact}\mathrm{mappings}.$$

(1)

Indeed, as mentioned in [1], Borsuk proved in [2] that this conjecture is true in finite dimensional metric spaces. As referred in (1), the contractibility of a metric space X plays an important role in studying the FPP of a metric space X. Thus, many works [2,5,6,7,8,9,10] associated with contractibility are well developed. Meanwhile, it is obvious that a K-topological space is not metrizable [1] because it is not even a regular space. Hence it cannot be metrizable, according to Nagata-Smirnov theorem [11]. Hereafter, since we often use the term “Khalimsky”, we will use instead of it ‘$K$-’ for short if there is no danger of confusion. Indeed, a paper [1] studied the conjecture (1) from the viewpoint of the category of K-topological spaces by using a certain new approach. At the moment, a paper [1] developed a new homotopy for K-topological spaces, the so-called K-homotopy, which can be used in fixed point theory for K-topological spaces.

Then, a paper [1] proposed a K-topological version of the conjecture (1) and some related works. At this moment, we need to remind that there are some differences between metric-based fixed point theory and K-topological-based fixed point theory. Furthermore, unlike the difference between contractibility and local contractibility in metric-based topological spaces, a paper [1] proved that their K-topological versions have their own features. Namely, based on a K-homotopy for K-topological spaces, it turns out that in K-topology whereas every K-topological space is locally contractible, it need not be K-contractible. To be specific, it turns out that [1] in K-topology, the K-contractibility implies the local K-contractibility, the converse does not hold. Let us now recall the K-topological version of (1) stated in [1], as follows: Let X be a K-topological space with K-contractibility.

$$\mathrm{Then}\mathrm{it}\mathrm{has}\mathrm{the}FPP\mathrm{for}K-\mathrm{continuous}\left(\mathrm{compact}\right)\mathrm{mappings}.$$

(2)

Then, the paper [1] asserted that a simple closed K-curve with four elements in the K-plane, $S{C}_K^{2,4}$, is K-contractible relative to a certain singleton $\left\{x\right\}\subset S{C}_K^{2,4}$. Indeed, after intensively studying the K-contractibility of a K-topological space, in this paper we now prove that $S{C}_K^{n,4}$ is not K-contractible and further, it is not K-contractible relative to a certain singleton $\left\{x\right\}\subset S{C}_K^{2,4}$ (Theorem 3 and Remark 4). This means that we now correct the assertion. Namely, $S{C}_K^{2,4}$ cannot be a space against the conjecture (2) (see Theorem 3 and Remark 6). In this paper we will often use the notation: For $a,b\in \mathbb{Z}$, ${[a,b]}_{\mathbb{Z}}:=\{x\in \mathbb{Z}|a\le x\le b\}$ with K-topology or only a set depending on the situation [12].

The rest of the paper is organized as follows: Section 2 provides basic terminology which can be used in this paper. Section 3 explores some properties involving K-homotopies and K-homeomorphisms. Section 4 firstly proves that $S{C}_K^{n,l},n\ge 2,l\ge 4$ is not K-contractible. Besides, we study some properties of “contractibility relative to a certain subset” compared with the typical contractibility in K-homotopy theory. Finally, we conclude that the conjecture (2) still remains open. Section 5 investigates some properties of the so-called A-homotopy and A-contractibility. Besides, in the category KAC, after proposing a new version inherited from the conjecture (2) which is suitable for studying the FPP or the AFPP for spaces in KAC, we prove that this new conjecture is negative with respect to the FPP or the almost fixed point property (AFPP, for brevity) [13]. Section 6 concludes the paper with summary and a further work.

2. Preliminaries

Let $\mathbb{Z}$, $\mathbb{N}$ and ${\mathbb{Z}}^n$ represent the sets of integers, natural numbers and points in the Euclidean n-dimensional space with integer coordinates, respectively. Let us now briefly recall some notions related to K-topology. The Khalimsky line topology on $\mathbb{Z}$, as an Alexandroff space [14], is induced by the set $\{{[2n-1,2n+1]}_{\mathbb{Z}}:n\in \mathbb{Z}\}$ as a subbase [14]. Furthermore, the product topology on ${\mathbb{Z}}^n$ induced by $(\mathbb{Z},\kappa )$ is called the Khalimsky product topology on ${\mathbb{Z}}^n$ (or Khalimsky n-dimensional space) which is denoted by $({\mathbb{Z}}^n,{\kappa }^n)$. A point $x=(x_1,x_2,\cdots ,x_n)\in {\mathbb{Z}}^n$ is pure open if all coordinates are odd; and it is pure closed if each of the coordinates is even [15]. The other points in ${\mathbb{Z}}^n$ are called mixed [15]. For a point $p:=(p_1,p_2)$ in $({\mathbb{Z}}^2,{\kappa }^2)$, its smallest open neighborhood $S{O}_K\left(p\right)$ is obtained, as follows [15]. For $m,n\in \mathbb{Z}$,

$$S{O}_K\left(p\right):=\left\{\begin{array}{l}\left\{p\right\}\mathrm{if}p=(2m+1,2n+1),\\ \{(p_1-1,p_2),p,(p_1+1,p_2)\}\mathrm{if}p=(2m,2n+1),\\ \{(p_1,p_2-1),p,(p_1,p_2+1)\}\mathrm{if}p=(2m+1,2n),\\ {[2m-1,2m+1]}_{\mathbb{Z}}\times {[2n-1,2n+1]}_{\mathbb{Z}}\mathrm{if}p=(2m,2n).\end{array}\right.$$

(3)

In this paper each space $X(\subset {\mathbb{Z}}^n)$ related to K-topology is considered to be a subspace $(X,{\kappa }_X^n)$ induced by $({\mathbb{Z}}^n,{\kappa }^n)$ [15,16].

Let us now recall the structure of $({\mathbb{Z}}^n,{\kappa }^n)$. In each of the spaces of Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, a black jumbo dot means a pure open point and further, the symbols ∎ and ● mean a pure closed point and a mixed point, respectively. Many studies have examined various properties of a K-continuous map, connectedness, K-adjacency, a K-homeomorphism [15,16,17,18,19,20].

Let us recall the following terminology for studying K-topological spaces.

Definition 1.

[16] Let $X:=(X,{\kappa }_X^n)$ be a K-topological space.

(1)

Distinct points $x,y\in X$ are said to be K-adjacent if $x\in S{O}_K\left(y\right)$ or $y\in S{O}_K\left(x\right)$.

(2)

We say that a sequence ${\left(x_i\right)}_{i\in {[0,l]}_{\mathbb{Z}}},l\ge 2$ in X is a K-path from x to y if $x_0=x$, $x_l=y$ and each point $x_i$ is K-adjacent to $x_{i+1}$ and $i\in {[0,l]}_{\mathbb{Z}}$. The number l is called the length of this path.

(3)

We say that an (injective) sequence ${\left(x_i\right)}_{i\in {[0,l]}_{\mathbb{Z}}}$ in X is a simple K-path if $x_i$ and $x_j$ are K-adjacent if and only if $|i-j|=1$.

(4)

A simple closed K-curve with l elements in ${\mathbb{Z}}^n,n\ge 2,l\ge 4$, denoted by $S{C}_K^{n,l}$, is a simple K-path (or just a sequence) ${\left(x_i\right)}_{i\in {[0,l-1]}_{\mathbb{Z}}}$ in ${\mathbb{Z}}^n$ such that $x_i$ and $x_j$ are K-adjacent if and only if $|i-j|=\pm 1\left(modl\right)$.

For instance, we can see $S{C}_K^{3,4}$ in Figure 4.

3. K-Homotopies and K-Homeomorphisms

In this section we examine if a K-homeomorphism preserves a K-homotopy between two K-continuous maps. Let us now recall the notion of K-continuity of a map from $f:X\to Y$, where $X:=(X,{\kappa }_X^{n_0})$ and $Y:=(Y,{\kappa }_Y^{n_1})$, as follows:

$$f\left(S{O}_K\left(x\right)\right)\subset S{O}_K\left(f\left(x\right)\right),$$

(4)

because each point x in a K-topological space X always has $S{O}_K\left(x\right)\subset X$, where $S{O}_K\left(x\right)$ (resp. $S{O}_K\left(f\left(x\right)\right)$) is the smallest open set of x (resp. $f\left(x\right)$) in X(resp.Y).

Using spaces $X:=(X,{\kappa }_X^n)$ and K-continuous maps, we have a topological category, denoted by KTC, consisting of the following two data [16]:

(1)

For any set $X\subset {\mathbb{Z}}^n$, the set of spaces $(X,{\kappa }_X^n)$ as objects of KTC denoted by $\mathit{Ob}\left(\mathit{KTC}\right)$;

(2)

for all pairs of elements in $\mathit{Ob}\left(\mathit{KTC}\right)$, the set of all K-continuous maps between them as morphisms.

To study K-topological spaces, we need to recall a K-homeomorphism as follows:

Definition 2.

[15,16] For two spaces $X:=(X,{\kappa }_X^{n_0})$ and $Y:=(Y,{\kappa }_Y^{n_1})$, a map $h:X\to Y$ is called a K-homeomorphism if h is a K-continuous bijection, and $h^{-1}:Y\to X$ is K-continuous.

Owing to (4), the Alexandroff topological structure of a K-topological space and the bijection of a K-homeomorphism, we obtain the following:

Proposition 1.

A K-homeomorphism $h:X\to Y$ implies that for any point $x\in X$,

$$h\left(S{O}_K\left(x\right)\right)=S{O}_K\left(h\left(x\right)\right).$$

(5)

In view of (5), we can represent a K-homeomorphism as follows: A map $h:X\to Y$ is a K-homeomorphism if and only if h is a bijection satisfying the property $h\left(S{O}_K\left(x\right)\right)=S{O}_K\left(h\left(x\right)\right)$ for any point $x\in X$.

Example 1.

Consider the two K-topological spaces $(X,{\kappa }_X^2)$ and $(Y,{\kappa }_Y^2)$ in Figure 1. Although they have the same shape with the same cardinality, they are not K-homeomorphic. To be precise, for the points $p_1:=(0,0,0),p_2:=(2,0,0)\in X$, we obtain

$$|S{O}_K\left(p_1\right)|=9and|S{O}_K\left(p_2\right)|=11,$$

where $|·|$ mean the cardinality of the given set. However, the space $(Y,{\kappa }_Y^2)$ does not contain any points whose cardinalities are 9 or 11. Thus, we complete the proof contrary to (5).

Let us recall the notion of K-homotopy for K-topological spaces. Consider $(X,{\kappa }_X^n)$ and $({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})$, where ${[a,b]}_{\mathbb{Z}}\in \{{[0,m]}_{\mathbb{Z}},{[1,m+1]}_{\mathbb{Z}}\}$.

Definition 3.

[1] In KTC, for two spaces $X:=(X,{\kappa }_X^{n_0})$ and $Y:=(Y,{\kappa }_Y^{n_1})$, let $f,g:X\to Y$ be K-continuous functions. Suppose there exist a K-interval $({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})$, and a function $F:X\times ({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})\to Y$ such that

$(*1)$ for all $x\in X$, $F(x,a)=f\left(x\right)$ and $F(x,b)=g\left(x\right)$;

$(*2)$ for all $x\in X$, the induced function $F_x:({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})\to Y$ defined by $F_x\left(t\right)=F(x,t)$ for all $t\in ({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})$ is K-continuous;

$(*3)$ for all $t\in {[a,b]}_{\mathbb{Z}}$, the induced function $F_t:X\to Y$ defined by $F_t\left(x\right)=F(x,t)$ for all $x\in X$ is K-continuous.

Then we say that F is a K-homotopy between f and g, and f and g are K-homotopic in Y. In addition, we use the notation $f{\simeq }_{K}g$.

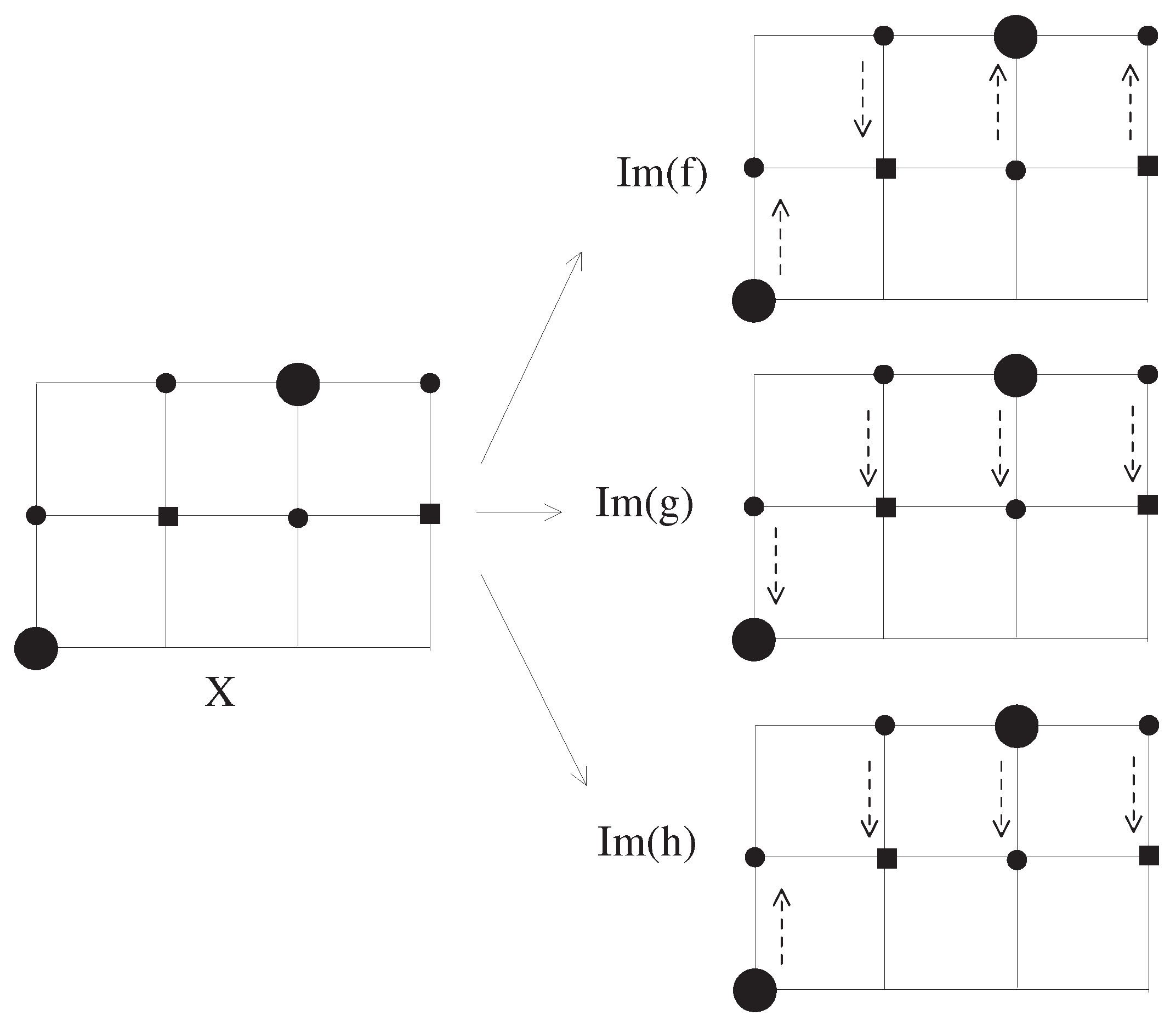
Example 2.

Consider certain three K-continuous self-maps f, g, and h of X shown in Figure 2 with their $Im\left(f\right)$, $Im\left(g\right)$, and $Im\left(h\right)$ in Figure 2. Then we observe $1_X{\simeq }_{K}f$, $1_X{\simeq }_{K}g$, and $f{\simeq }_{K}h$ (the improvement of Figure 3c of [1]).

Remark 1.

In view of the properties $(*2)$ and $(*3)$ of Definition 3, for the homotopy $F:X\times {[a,b]}_{\mathbb{Z}}\to Y$, the set $X\times ({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})$ need not be a subspace of the product space $({\mathbb{Z}}^{n_0+1},{\kappa }^{n_0+1})$. Namely, we may consider it as just a Cartesian product of two K-topological spaces X and $({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})$.

Let us now examine if a K-homeomorphism preserves a K-homotopy between two K-continuous maps.

Theorem 1.

A K-homeomorphism preserves a K-homotopy.

Proof. 

Suppose a K-homotopy between two K-continuous maps f and g. Namely, given two spaces $X:=(X,{\kappa }_X^{n_0})$, $Y:=(Y,{\kappa }_Y^{n_1})$, and the two K-continuous functions $f,g:X\to Y$, we consider a K-homotopy $F:X\times ({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})\to Y$ supporting $f{\simeq }_{K}g$. Besides, further assume two K-homeomorphisms $h_1:X\to X^{\prime }$ and $h_2:Y\to Y^{\prime }$, where $X^{\prime }:=(X^{\prime },{\kappa }_{X^{\prime }}^{n_0})$ and $Y^{\prime }:=(Y^{\prime },{\kappa }_{Y^{\prime }}^{n_1})$. Indeed, the dimensions $n_0$ and $n_1$ of $X^{\prime }$ and $Y^{\prime }$ need not be equal to those of X and Y, respectively. Then, it is obvious that the two composites

$$h_2\circ f\circ h_1^{-1}\mathrm{and}{h}_2\circ g\circ h_1^{-1}$$

are also K-continuous maps from $X^{\prime }$ to $Y^{\prime }$. To be specific, based on the given K-homotopy and the two K-homeomorphisms $h_1$ and $h_2$, let us now define the new map

$$H:=h_2\circ F\circ h_1^{-1}:X^{\prime }\times {[a,b]}_{\mathbb{Z}}\to Y^{\prime }.$$

Then, we obtain the following:

$(★1)$ for all $x^{\prime }\in X^{\prime }$, $H(x^{\prime },a)=h_2\circ f\circ h_1^{-1}\left(x^{\prime }\right)$ and $F(x^{\prime },b)=h_2\circ g\circ h_1^{-1}\left(x^{\prime }\right)$;

$(★2)$ for all $x^{\prime }\in X^{\prime }$, the induced function $H_{x^{\prime }}:({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})\to Y^{\prime }$ defined by $H_{x^{\prime }}\left(t\right)=H(x^{\prime },t)$ for all $t\in ({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})$ is K-continuous;

$(★3)$ for all $t\in {[a,b]}_{\mathbb{Z}}$, the induced function $H_t:X^{\prime }\to Y^{\prime }$ defined by $H_t\left(x^{\prime }\right)=H(x^{\prime },t)$ for all $x^{\prime }\in X^{\prime }$ is K-continuous.

Thus, we conclude that H is a K-homotopy between $h_2\circ f\circ h_1^{-1}$ and $h_2\circ g\circ h_1^{-1}$, i.e., $h_2\circ f\circ h_1^{-1}{\simeq }_K{h}_2\circ g\circ h_1^{-1}$.  □

Indeed, Theorem 1 will be strongly used in Section 4.

4. The Non-K-contractibility of $S{C}_K^{n,4}$ and the Non-FPP of $S{C}_K^{n,l}$

In this section, given a K-topological space X, after developing the notion of K-contractibility relative to each singleton $\left\{x_0\right\}(\subset X)$, we compare it with the concept of K-contractibility of X. Finally, we prove that the K-contractibility does not imply the K-contractibility relative to each singleton $\left\{x_0\right\}(\subset X)$. Besides, every $S{C}_K^{n,l},n\ge 2,l\ge 4$, is proved not to be K-contractible. Indeed, this feature is quite different from that of the $(3^n-1)$-contractibility of a simple closed $(3^n-1)$-curve with four elements in ${\mathbb{Z}}^n$ (see [21] for more details). Based on this fact, we correct the assertion relating to the K-contractibility of $S{C}_K^{2,4}$ in [1]. Then, we deal with the issue proposed in (2). To do this work, we need to recall the notion of a K-homotopy involving with both contractibility and local contractibility for K-topological spaces.

Definition 4.

[1] In KTC, we say that a K-topological space X is K-contractible if the identity map $1_X$ is K-homotopic in X to a constant map with a singleton consisting of a certain point $x\in X$. We use the notation $1_X{\simeq }_K{C}_{\left\{x\right\}}$.

Motivated by many kinds of homotopy equivalences for digital images [16,18,22,23], the K-topological version of them were established in [1]. To classify K-topological spaces in terms of a certain homotopy equivalence in KTC, we use the following:

Definition 5.

[1] In KTC, for two spaces $X:=(X,{\kappa }_X^{n_0})$ and $Y:=(Y,{\kappa }_Y^{n_1})$, if there are K-continuous maps $h:X\to Y$ and $l:Y\to X$ such that $l\circ h$ is K-homotopic to $1_X$ and $h\circ l$ is K-homotopic to $1_Y$, then the map $h:X\to Y$ is called a K-homotopy equivalence. We use the notation $X{\simeq }_{K·h·e}Y$.

Owing to Theorem 1, we obtain the following:

Remark 2.

A K-homeomorphism preserves a K-homotopy equivalence and the K-contractibility.

Definition 6.

Consider a subspace $(B,{\kappa }_B^{n_0})$ and $B\subset X$. Then we call $(X,B)$ a K-topological pair. Then, with the K-homotopy in Definition 3, we further consider the following:

$(*4)$ For all $t\in {[a,b]}_{\mathbb{Z}}$, assume that $F_t\left(x\right)=f\left(x\right)=g\left(x\right)$ for all $x\in B$.

Then we call F an K-homotopy relative to B between f and g, and we say that f and g are K-homotopic relative to B in Y, $f{\simeq }_{K·\mathit{rel}.B}g$ in symbol.

Definition 7.

We say that $(X,{\kappa }_X^n)$ is K-contractible relative to a certain singleton $\left\{x\right\}(\subset X)$ if $X{\simeq }_{K·h·e}\left\{x\right\}$ relative to a certain singleton $\left\{x\right\}(\subset X)$. Then we use the notation $1_X{\simeq }_{K·\mathit{rel}.\left\{x\right\}}{C}_{\left\{x\right\}}$.

Using a method similar to the proof of Theorem 1, we obtain the following:

Remark 3.

A K-homeomorphism preserves the K-contractibility of X relative to a certain singleton $\left\{x\right\}(\subset X)$.

Let us compare the K-contractibility of a K-topological space X with the K-contractibility relative to each singleton $\left\{x\right\}(\subset X)$. Namely, although the K-contractibility relative to each singleton $\left\{x\right\}(\subset X)$ implies the K-contractibility of X, the converse does not hold, as follows:

Theorem 2.

The K-contractibility of X does not imply the K-contractibility relative to each singleton $\left\{x\right\}(\subset X)$.

Proof. 

To prove the assertion, we consider the space $X:=(X,{\kappa }_X^3)$ in Figure 3.

(Step 1) It is obvious that the given space X is K-contractible relative to the singleton $\left\{p\right\}$, i.e., $X{\simeq }_{K·\mathit{rel}.\left\{p\right\}}{C}_{\left\{p\right\}}$, where

$$p\in \left\{\begin{array}{l}(0,0,0),(0,1,0),(1,-1,0),(1,0,0),\\ (1,1,0),(2,-1,0),(2,0,0),(2,1,0)\end{array}\right\}\subset X.$$

(Step 2) We prove that the given space X is not K-contractible relative to the singleton $\left\{q\right\}\subset X$, where

$$q\in \left\{\right(0,0,1),(0,1,1),(1,-1,1),(1,1,1),(2,-1,1),(2,0,1),(2,1,1\left)\right\}.$$

(6)

Namely, we may consider the point q to be a point in the second level of the set X of Figure 3.

Without loss of generality, we may take any point q in (6) and prove that X is not K-contractible relative to the singleton $\left\{q\right\}$. For convenience, let us consider $q:=(1,1,1)$. Then we prove X is not K-contractible relative to the singleton $\left\{q\right\}$. Using the ‘reductio ad absurdum’, suppose that there is a K-homotopy, $F:X\times ({[a,b]}_{\mathbb{Z}},{\kappa }_{{[a,b]}_{\mathbb{Z}}})\to X$, satisfying $1_X{\simeq }_{K·\mathit{rel}.\left\{q\right\}}{C}_{\left\{q\right\}}$. Let us now consider the point $x:=(2,0,0)$. Then we obtain

$$S{O}_K\left(x\right)=X\backslash \{(0,0,0),(0,1,0),(0,0,1),(0,1,1)\}.$$

According to the K-homotopy satisfying $1_X{\simeq }_{K·\mathit{rel}.\left\{q\right\}}{C}_{\left\{q\right\}}$, based on (6), we may assume the mappings of the point x by F in the following way:

$$x\to p(\ne x)\in S{O}_K\left(q\right)$$

(7)

or

$$x\to p(\ne x)\in S{O}_K\left((0,0,0)\right).$$

(8)

In case we follow the mapping (7), we observe that the mapping does not support the property $(*2)$ of Definition 3. In case we take the mapping (8), we find that the mapping does not support the property $(*2)$ of Definition 3 either. The other cases are similarly proved by using the above method. Thus, we conclude that for the point q of (6), there is no K-homotopy supporting $1_X{\simeq }_{K·\mathit{rel}.\left\{q\right\}}{C}_{\left\{q\right\}}$.  □

Based on the properties of contractibility, regarding the conjecture (1), we need to deal with the notion of local K-contractibility. As referred in (1), the notions of contractibility and locally contractibility play important role in many areas of mathematics [2,5,6,24]. In typical homotopy theory, we say that a contractible space is precisely one with the same homotopy type of a singleton [24]. In typical mathematics, it is well known that contractible spaces are not necessarily locally contractible nor vice versa [11] (see [1] for more details). To deal with the conjecture (2), we need to recall the K-topological version of the local contractibility, as follows:

Definition 8.

[1] In KTC, a K-topological space $(X,{\kappa }_X^n)$ is said to be locally K-contractible if it has a basis of open subsets each of which is a K-contractible space under the subspace K-topology.

Proposition 2.

[1] Every space in KTC is locally contractible.

A paper [1] proved the following:

Lemma 1.

[1] Any K-path in $({\mathbb{Z}}^n,{\kappa }^n)$ is K-contractible.

Proposition 3.

[1] In KTC, the FPP is a K-topological invariant.

For $S{C}_K^{n,4},n\ge 2$, we prove the following which can be essentially used in Section 4.

Theorem 3.

$S{C}_K^{n,4}$ is not K-contractible, $n\ge 2$.

Proof. 

Suppose $S{C}_K^{n,4}$ is K-contractible. By Remark 2, since a K-homeomorphism preserves the K-contractibility and $S{C}_K^{n,4}$ is K-homeomorphic to $S{C}_K^{3,4}$ in Figure 4, we may suppose the K-contractibility of $S{C}_K^{3,4}$. Then we must prove that there is a K-homotopy making $S{C}_K^{3,4}$K-contractible, i.e., $1_{S{C}_K^{3,4}}{\simeq }_K{C}_{\left\{x\right\}}$ for a certain point $x\in S{C}_K^{3,4}$. For convenience, put $S{C}_K^{3,4}:=\{c_0,c_1,c_2,c_3\}$ (see Figure 4). Take any singleton as a subset of $S{C}_K^{3,4}$ for the examination of the K-contractibility of $S{C}_K^{3,4}$. Without loss of generality, we may take a singleton $\left\{c_0\right\}$ or $\left\{c_1\right\}$ because the former is pure closed point and the latter is pure open point. Then we prove that $1_{S{C}_K^{3,4}}$ cannot be K-homotopic to the constant maps $C_{\left\{c_0\right\}}$ and $C_{\left\{c_1\right\}}$. First suppose $1_{S{C}_K^{3,4}}$ is K-homotopic to $C_{\left\{c_0\right\}}$. Then, for some $b\in \mathbb{Z}$, consider a certain K-homotopy

$$F:S{C}_K^{3,4}\times {[0,b]}_{\mathbb{Z}}\to S{C}_K^{3,4}$$

(9)

satisfying $1_{S{C}_K^{3,4}}{\simeq }_K{C}_{\left\{c_0\right\}}$. Then the point $c_2$ must be mapped by the homotopy F onto the point $c_0$, $c_1$ or $c_3$.

(Case 1): In case $c_2$ is assumed to be mapped onto the point $c_0$, the mapping does not satisfy the property $(*2)$ of Definition 2 because of the non-K-continuity of the mapping from the point $c_2$ to $c_0$, contrary to the given property $(*2)$ of the K-homotopy (9).

(Case 2): As another case, let us now assume that the point $c_2$ is mapped by the homotopy F onto the point $c_1$. Since

$$S{O}_K\left(c_2\right)=\{c_1,c_2,c_3\}\mathrm{and}S{O}_K\left(c_1\right)=\left\{c_1\right\},$$

owing to the property of the K-homotopy, F must map $S{O}_K\left(c_2\right)$ onto $S{O}_K\left(c_1\right)$ (see the property $(*3)$ of Definition 2). Then the homotopy F does not satisfy the property $(*2)$ of Definition 2 because of the non-K-continuity of the mapping from the point $c_3$ to $c_1$, contrary to the given K-homotopy (9). Finally, let us now assume that the point $c_2$ is mapped by the homotopy F onto the point $c_3$. Then, using a method similar to the just above case, this case is also proved to be negative. Thus, we conclude that there is no K-homotopy supporting $1_{S{C}_K^{3,4}}{\simeq }_K{C}_{\left\{c_0\right\}}$.

Next, using a method similar to the proof of the above assertion that $1_{S{C}_K^{3,4}}$ is not K-homotopic to the constant map $C_{\left\{c_1\right\}}$, we prove that there is no K-homotopy supporting $1_{S{C}_K^{3,4}}{\simeq }_K{C}_{\left\{c_1\right\}}$ or $1_{S{C}_K^{3,4}}{\simeq }_K{C}_{\left\{c_3\right\}}$. In view of the above all cases, we have a contradiction to the hypothesis of the K-contractibility of $S{C}_K^{n,4}$. Finally, we complete that $S{C}_K^{n,4}$ is not K-contractible. □

In view of the proof of Theorem 3, we observe the following:

Remark 4.

$S{C}_K^{n,4}$ is not K-contractible relative to a certain singleton $\left\{x\right\}\subset S{C}_K^{n,4}$, $n\ge 2$.

By Theorem 3 and Remark 4, we obtain the following (correction of the assertion of the K-contractibility of $S{C}_K^{2,4}$ of Lemma 4.3 of [1]).

Remark 5.

Every $S{C}_K^{n,l}$ is neither K-contractible nor K-contractible relative to a certain singleton $\left\{x\right\}\subset S{C}_K^{n,l}$, $n\ge 2,l\ge 4$.

This feature is quite different from the k-contractibility of simple closed k-curve with four elements in ${\mathbb{Z}}^n,n\ge 2$, in typical digital topology using digital k-graphs in ${\mathbb{Z}}^n,n\ge 2,k=3^n-1$ (see [21,23,25]).

Let us now move onto the conjecture posed in (2). We say that a K-topological space $(X,{\kappa }_X^n)$ has the FPP if every K-continuous self-map f of X has a point $x\in X$ such that $f\left(x\right)=x$.

Let us now study some properties of K-topological spaces from the viewpoint of fixed point theory.

In KTC, we say that a K-topological invariant is a property of a K-topological space which is invariant under K-homeomorphisms.

Theorem 4.

[1,26] Let X be a simple K-path in the n-dimensional K-topological space. Then it has the FPP.

Theorem 5.

[26,27] Let $(X,{\kappa }_X^2)$ be a convex and compact K-plane as a subspace of $({\mathbb{Z}}^2,{\kappa }^2)$, where $X:={[a,b]}_{\mathbb{Z}}\times {[c,d]}_{\mathbb{Z}}$. Then it has the FPP.

Corollary 1.

$S{C}_K^{n,l}$ does not have the FPP, $n\ge 2,l\ge 4$.

For $S{C}_K^{n,l}:={\left(x_i\right)}_{i\in {[0,l-1]}_{\mathbb{Z}}}$, consider the self-map f of $S{C}_K^{n,l}$ given by $f\left(x_i\right)=x_{i+2\left(modl\right)}$. Then it is clear that f is a K-continuous map without any fixed point [1].

Regarding the conjecture (2), owing to Lemma 1, Theorems 3–5, Remark 5 and Corollary 1, we have observed that the conjecture (2) seems to be positive. However, we now obtain the following:

Remark 6.

In KTC, the conjecture (2) still remains open.

Let us now consider another category, the so-called KDTC, which means the $KD$-topological category in [17,28]. To do this work, let us just recall two concepts for objects and morphisms for this category. For any set $X\subset {\mathbb{Z}}^n$, let $X_{n,k}$ be a space $(X,{\kappa }_X^n)$ with digital k-connectivity [17]. For two spaces $X:=X_{n_1,k_1}$ and $Y:=Y_{n_2,k_2}$, a map $f:X\to Y$ is called $KD$-$(k_1,k_2)$-continuous at a point $x\in X$ [17] if f is K-continuous at the point x and further, digitally $(k_1,k_2)$-continuous at a point x. In case f is $KD$-$(k_1,k_2)$-continuous at every point $x\in X$, we say that f is a $KD$-$(k_1,k_2)$-continuous map. In other words, a map with the $KD$-$(k_1,k_2)$-continuity is equivalent to the map satifying both K-continuity and the typical digital $(k_1,k_2)$-continuity in [21]. The category KDTC consists of the following two data.

(1)

The set of spaces $X_{n,k}$ with digital k-connectivity as objects of KDTC denoted by $\mathit{Ob}\left(\mathit{KDTC}\right)$;

(2)

for all pairs of elements in $\mathit{Ob}\left(\mathit{KDTC}\right)$, the set of all $KD$-continuous maps between them as morphisms.

A paper [28] established the notion of $KD$-$(k_1,k_2)$-homotopy in the category KDTC (see Definition 6 of [28]) by replacing $Obj\left(KTC\right)$ (resp. $Mor\left(KTC\right)$) with $Obj\left(KDTC\right)$ (resp. $Mor\left(KDTC\right)$). Based on this replacement, it also formulated the notion of $KD$-k-contractibility considered as the KDTC-version of Definitions 3 and 6 using $(*1)$–$(*4)$ in the present paper. Namely, for $X:=X_{n,k}\in Obj\left(KDTC\right)$, X is called $KD$-kcontractible relative to a certain singleton $\left\{x\right\}(\subset X)$ (or $KD$-kcontractible for short) if $1_X$ is $KD$-k-homotopic to a constant map $C_{\left\{x\right\}}$ relative to a certain singleton $\left\{x\right\}(\subset X)$. Then we use the notation $1_X{\simeq }_{KD·k·\mathit{rel}.\left\{x\right\}}{C}_{\left\{x\right\}}$. Then, the paper asserted that the spaces $Y,Z\in Obj\left(KDTC\right)$ are $KD$-8contractible (see Example 4.1 of [28]). However, we need to correct it as follows:

Example 3.

(correction of Example 4.1 of [28]) Each of $Y,Z\in Obj\left(KDTC\right)$ in Figure 5 is not $KD$-8-contractible. To be specific, by Theorem 3 and Remark 4, we observe the non-$KD$-8-contractibility of Y. Similarly, we see the non-$KD$-8-contractibility of Z.

5. Homotopies in the Category KAC and a Certain Conjecture Involving the FPP in KAC

Unlike the conjecture (2) studied in Section 4, let us now consider the conjecture in the more generalized category, the so-called category KAC which is a topological graph version of KTC. Namely, after establishing KAC-versions of the K-contractibility and the local K-contractibility, we may pose a more generalized version of (2) (see (11) and (13)). This approach can facilitate the study of the FPP and the almost fixed point property (AFPP, for short) of some digital spaces. Indeed, the K-homotopy in KTC in Section 4 is focused on studying the $FPP$ for K-topological spaces. Let us now generalize the conjecture (2) with respect to the FPP and the almost fixed point property (AFPP, for brevity) in KAC (see (11) and (13) for more details). To do this work, objects and morphisms in KAC are certainly assumed, as follows: Considering K-topological spaces $(X,{\kappa }_X^n)$ with K-adjacency (see Definition 9(1)), we call them $KA$-spaces which are objects of KAC (see Definition 9). Indeed, a $KA$-space is a K-topological graph with a K-adjacency inherited from a K-topological space $(X,{\kappa }_X^n)$ (see Definition 9). Besides, regarding morphisms in KAC, we will use the so-called A-maps (see Definition 10).

Definition 9.

[29] (1) A $KA$-space is a set X with K-adjacency derived from a K-topological space $(X,{\kappa }_X^n)$. Namely, a $KA$-space X is a K-topological graph inherited from the K-topological space $(X,{\kappa }_X^n)$ with the adjacency between two distinct points introduced in Definition 1(1).

(2) For a $KA$-space $X:=(X,{\kappa }_X^n)$ and a point $p\in X$, we define a K-adjacency neighborhood of p to be the set

$$A{N}_X\left(p\right):=A_X\left(p\right)\cup \left\{p\right\}$$

which is called an A-neighborhood of p, where $A_X\left(p\right)=\{x\in X|xisK-adjacenttop.\}$.

As mentioned above, since a $KA$-space X is totally derived from the K-topological space $(X,{\kappa }_X^n)$, we often denote a $KA$-space X with $X:=(X,{\kappa }_X^n)$ or X in short. Hereafter, for convenience, in a $KA$-space $X:=(X,{\kappa }_X^n)$, we will use $AN\left(p\right)$ instead of $A{N}_X\left(p\right)$ if there is no danger of ambiguity. In view of (3) and the notion of $AN\left(x\right)$, we obtain the following:

Lemma 2.

Given a $KA$-space $X:=(X,{\kappa }_X^n)$ and a point $x\in X$,

$$S{O}_K\left(x\right)\subset AN\left(x\right).$$

(10)

Proof. 

For a $KA$-space $X:=(X,{\kappa }_X^n)$, for a point $x\in X$, since

$$AN\left(x\right)=\{y\in X|x\in S{O}_K\left(y\right)\mathrm{or}y\in S{O}_K\left(x\right)\},$$

the proof is completed. □

For a $KA$-space X and a point $x\in X$, since for $x\in X$ we always have $AN\left(x\right)\subset X$, we can develop an A-map and an A-isomorphism (see Definitions 10 and 11).

Definition 10.

[29] Given two $KA$-spaces $X:=(X,{\kappa }_X^{n_0})$ and $Y:=(Y,{\kappa }_Y^{n_1})$, we say that a function $f:X\to Y$ is an A-map at $x\in X$ if

$$f\left(AN\right(x\left)\right)\subset AN\left(f\right(x\left)\right).$$

Furthermore, we say that a map $f:X\to Y$ is an A-map if the map f is an A-map at every point $x\in X$.

In view of Definition 10, we observe that an A-map $f:X\to Y$ implies a map preserving connected subsets of X into connected ones [29]. For instance, let us consider the self-map f of an $S{C}_K^{n,l}:={\left(x_i\right)}_{i\in {[0,l-1]}_{\mathbf{Z}}},n\ge 2$, such that $f\left(x_i\right)=x_{i+1\left(modl\right)}$, $l\ge 4$. Whereas f is an A-map, it is not a K-continuous map [29].

Using both $KA$-spaces and A-maps, we establish the so-called $KA$-category [29], denoted by $KAC$, consisting of the following data.

(1)

The set of $KA$-spaces as objects, denoted by $Ob\left(KAC\right)$,

(2)

for every ordered pair of objects $(X,{\kappa }_X^{n_0})$ and $(Y,{\kappa }_Y^{n_1})$, the set of all A-maps $f:(X,{\kappa }_X^{n_0})\to (Y,{\kappa }_Y^{n_1})$ as morphisms.

As observed in the above self-map f of an $S{C}_K^{n,l}$, comparing a K-continuous map and an A-map, owing to (10), we obtain the following:

Theorem 6.

(Theorem 4.5 of [29]) Given a map from $X:=(X,{\kappa }_X^{n_0})$ to $Y:=(Y,{\kappa }_Y^{n_1})$, a K-continuous map implies an A-map. But the converse does not hold.

Proof. 

Owing to (10) and Definition 10, we complete the proof. □

Based on the notion of an A-map, we obtain the following:

Definition 11.

[29] For two $KA$-spaces $X:=(X,{\kappa }_X^{n_0})$ and $Y:=(Y,{\kappa }_Y^{n_1})$, a map $h:X\to Y$ is called an A-isomorphism if h is a bijective A-map (for brevity, A-bijection) and if $h^{-1}:Y\to X$ is an A-map.

Hereafter, we denote an A-isomorphism between $KA$-spaces X and Y with $X{\approx }_{A}Y$.

In view of Definition 11, we obtain the following:

Remark 7.

An A-isomorphism $h:X\to Y$ implies that for any point $x\in X$,

$$h\left(AN\right(x\left)\right)=AN\left(h\right(x\left)\right).$$

In view of Remark 7, we can represent an A-isomorphism as follows: A map $h:X\to Y$ is an A-isomorphism if and only if h is a bijection satisfying the property $h\left(AN\right(x\left)\right)=AN\left(h\right(x\left)\right)$ for any point $x\in X$.

Definition 12.

[29] A simple closed $KA$-curve with l elements in ${\mathbb{Z}}^n,n\ge 2,l\ge 4$, denoted by $S{C}_A^{n,l}:={\left(x_i\right)}_{i\in {[0,l-1]}_{\mathbf{Z}}}$, is an (injective) sequence ${\left(x_i\right)}_{i\in {[0,l-1]}_{\mathbf{Z}}}$ such that $x_i$ and $x_j$ are K-adjacent if and only if $|i-j|=\pm 1\left(modl\right)$.

Let us now study an A-homotopy in $KAC$ [30]. For a space $X\in Ob\left(KAC\right)$, let B be a subset of X. Then $(X,B)$ is called a $KA$-space pair. Motivated by many kinds of homotopy equivalences [16,18,22,23,28,31], let us consider the notions of an A-homotopy relative to a subset $B\subset X$ [30], A-contractibility [30] and an A-homotopy equivalence [30,32,33].

Definition 13.

[30,33] Let $(X,B)$ and Y be a space pair and a space in $Ob\left(KAC\right)$, respectively. Let $f,g:X\to Y$ be A-maps. Suppose there exist $m\in \mathbf{N}$ and a function $F:X\times {[0,m]}_{\mathbf{Z}}\to Y$ such that

$(•1)$ for all $x\in X,F(x,0)=f\left(x\right)$ and $F(x,m)=g\left(x\right)$;

$(•2)$ for all $x\in X$, the induced function $F_x:{[0,m]}_{\mathbf{Z}}\to Y$ given by

$F_x\left(t\right)=F(x,t)$ for all $t\in {[0,m]}_{\mathbf{Z}}$ is an A-map;

$(•3)$ for all $t\in {[0,m]}_{\mathbf{Z}}$, the induced function $F_t:X\to Y$ given by $F_t\left(x\right)=F(x,t)$ for all $x\in X$ is an A-map.

Then we say that F is an A-homotopy between f and g.

$(•4)$ Furthermore, for all $t\in {[0,m]}_{\mathbf{Z}}$, assume that $F_t\left(x\right)=f\left(x\right)=g\left(x\right)$ for all $x\in B$.

Then we call F an A-homotopy relative to B between f and g, and we say that f and g are A-homotopic relative to B in Y, $f{\simeq }_{A·\mathit{rel}.B}g$ in symbol.

In Definition 13, if B is a certain singleton of X, then we say that F is a pointed A-homotopy at $\left\{x_0\right\}$. If, for some $x_0\in X$, $1_X$ is A-homotopic to the constant map $C_{\left\{x_0\right\}}$ relative to $\left\{x_0\right\}$, then we say that $(X,x_0)$ is pointed A-contractible (A-contractible if there is no danger of ambiguity) [28]. Let us now recall an A-homotopy equivalence and A-contractibility in $KAC$.

Definition 14.

[28] In $KAC$, for two spaces X and Y, if there are A-maps $f:X\to Y$ and $g:Y\to X$ such that $g\circ f$ is A-homotopic to $1_X$ and $f\circ g$ is A-homotopic to $1_Y$, then the map $f:X\to Y$ is called an A-homotopy equivalence. We use the notation $X{\simeq }_{A·h·e}Y$.

Definition 15.

A $KA$-space X is said to be locally A-contractible if for every $x\in X$ and every $AN\left(x\right)(\ni x)$ of X is A-contractible.

Owing to Lemma 1 and Theorem 6, it is obvious that a $KA$-space X is locally A-contractible.

Lemma 3.

Every $KA$-space is locally A-contractible.

Proof. 

For a $KA$-space X, for each point $x\in X$, $AN\left(x\right)(\ni x)$ is A-contractible in terms of just an A-homotopy with one step. □

Let us propose a certain conjecture in KAC which is the KAC-version of (2) in the KTC. Namely, let X be a $KA$-space with A-contractibility.

$$\mathrm{Then}\mathrm{it}\mathrm{has}\mathrm{the}FPP\mathrm{for}A-\mathrm{mappings}.$$

(11)

Owing to Lemma 1 and Theorem 6, we obtain the following:

Proposition 4.

(1) An A-homotopy in $KAC$ is a generalization of a K-homotopy in $KTC$.

(2) A-contractibility is a generalization of the K-contractibility relative to a certain singleton (see Definition 7).

Proof. 

Since an A-homotopy is define by using the properties $(•1)$–$(•3)$ of Definition 13, after replacing K-continuous maps in Definition 3 with A-maps, owing to Theorem 6, we prove the assertion. □

Owing to Lemma 2, Theorem 6, and Remarks 2 and 3, we obtain the following:

Proposition 5.

(1) An A-isomorphism preserves an A-homotopy between two A-maps.

(2) An A-isomorphism preserves an A-homotopy equivalence.

(3) An A-isomorphism preserves an A-contractibility of a $KA$-space.

Proof. 

(1) Using a method similar to the proof of Theorem 6, we can complete the proof. To be specific, after replacing K-continuous maps (resp. K-homeomorphism and K-homotopy) used in Theorem 6 with A-maps (resp. A-isomorphism and A-homotopy), we only follow the proof of Theorem 6, the proof is completed.

(2) Based on the fact (1), the proof is completed.

(3) Owing to the property (1), the proof is also completed. □

In KAC, we say that a $KA$-space $X:=(X,{\kappa }_X^n)$ has the FPP if every self-A-map f of X has a point $x\in X$ such that $f\left(x\right)=x$.

Lemma 4.

In KAC, the FPP is invariant up to A-isomorphism.

Proof. 

Consider a $KA$-space $X:=(X,{\kappa }_X^{n_0})$ with the FPP. With an A-isomorphism $i:X\to Y$, where $Y:=(Y,{\kappa }_Y^{n_1})$, we prove that Y has the FPP. Let f be any self-A-map of Y. Then consider the composite $f:=i\circ g\circ i^{-1}:Y\to Y$, where g is a self-A-map of X. Owing to the hypothesis, assume $x\in X$ is a fixed point for a self-A-map g of X. Due to the A-isomorphism i, there is a point $y\in Y$ such that $i\left(x\right)=y$. Let us consider the mapping

$$g\left(x\right)=i^{-1}\circ f\circ i\left(x\right)=i^{-1}\left(f\left(i\left(x\right)\right)\right)=i^{-1}\left(f\left(y\right)\right).$$

(12)

Thus, from (12) we obtain $i\left(g\right(x\left)\right)=f\left(y\right)$ and further, owing to the hypothesis of the FPP of X and the A-isomorphism i, we obtain

$$i\left(g\right(x\left)\right)=i\left(x\right)=y=f\left(y\right),$$

which implies that the point $i\left(x\right):=y$ is a fixed point of the map f, which implies that Y has the FPP. □

Using Lemma 4 and the local A-contractibility of a $KA$-space, we obtain the following:

Theorem 7.

The conjecture (11) is negative in KAC.

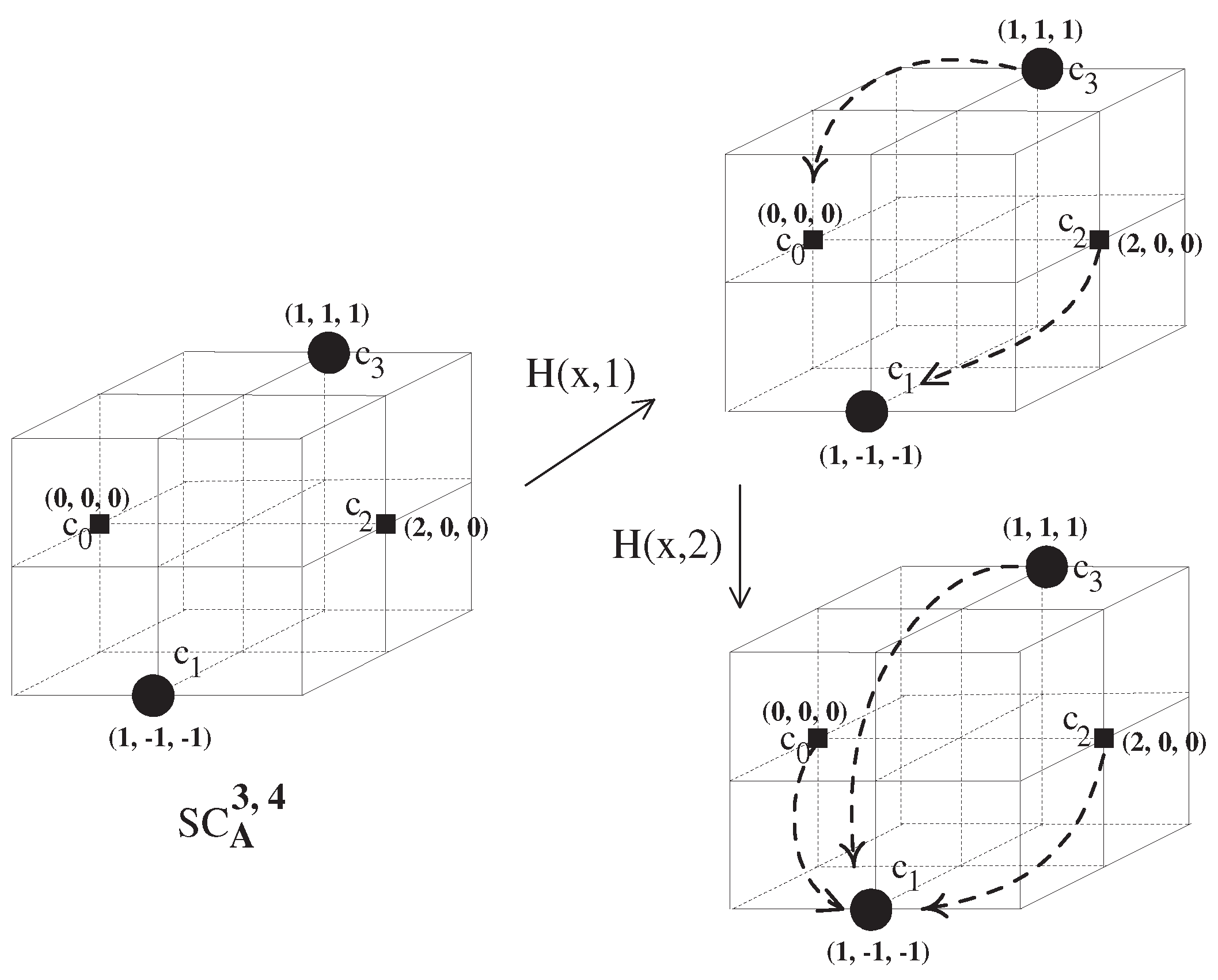
Proof. 

We prove that $S{C}_A^{n,4}:=\{c_0,c_1,c_2,c_3\}$ is A-contractible. To be specific, owing to Lemma 4, we suffice to prove that $S{C}_A^{3,4}$ is both locally A-contractible and A-contractible. It is obvious that $S{C}_A^{3,4}$ is locally A-contractible because for any point $x\in S{C}_A^{3,4}$, $AN\left(x\right)$ is obviously A-contractible, e.g., $1_{AN\left(x\right)}{\simeq }_{A·\mathit{rel}.\left\{x\right\}}{C}_{\left\{x\right\}}$. Let us now prove the A-contractibility of $S{C}_A^{3,4}$, as follows:

Consider the map (see Figure 6)

$$H:S{C}_A^{3,4}\times {[0,2]}_{\mathbb{Z}}\to S{C}_A^{3,4}$$

defined by

$$\left\{\begin{array}{l}H(x,0)=1_{S{C}_A^{3,4}},\\ H(x,1)=c_1,\mathrm{where}x\in \{c_1,c_2\}\mathrm{and}H(x,1)=c_0,\mathrm{where}x\in \{c_0,c_3\},\\ H(x,2)=c_1\mathrm{where}x\in S{C}_A^{3,4}.\end{array}\right.$$

Then the map H is an A-homotopy on $S{C}_A^{3,4}$ making

$$1_{S{C}_A^{3,4}}{\simeq }_{A·\mathit{rel}.\left\{c_1\right\}}{C}_{\left\{c_1\right\}}.$$

Finally, using Proposition 5, we observe that $S{C}_A^{n,4}$ is A-contractible.

Next, consider a self-map f of $S{C}_A^{n,4}:=\{c_0,c_1,c_2,c_3\}$ defined by $f\left(c_i\right)=c_{i+1\left(mod4\right)}$. Then the map is obviously an A-map which does not support the FPP of $S{C}_A^{n,4}$. □

Remark 8.

In Theorem 7, although we proved $1_{S{C}_A^{3,4}}{\simeq }_{A·\mathit{rel}.\left\{c_1\right\}}{C}_{\left\{c_1\right\}}$, using a same method as the proof of Theorem 7, we can obtain that for any point $x\in S{C}_A^{3,4}$, $1_{S{C}_A^{3,4}}{\simeq }_{A·\mathit{rel}.\left\{x\right\}}{C}_{\left\{x\right\}}$.

In KAC, we say that a $KA$-space $X:=(X,{\kappa }_X^n)$ has the almost (or approximate) fixed point property (AFPP, for short) if every self-A-map f of X has a point $x\in X$ such that $f\left(x\right)=x$ or $f\left(x\right)$ is K-adjacent to x. Regarding the conjecture (11) related to FPP, we now propose the following: Let X be a $KA$-space with A-contractibility.

$$\mathrm{Then}\mathrm{it}\mathrm{has}\mathrm{the}AFPP\mathrm{for}A-\mathrm{mappings}.$$

(13)

In view of Theorem 7, we obtain the following:

Corollary 2.

The conjecture (13) is negative.

Proof. 

Although $S{C}_A^{n,4}:=\{c_0,c_1,c_2,c_3\}$ is A-contractible, $n\ge 2$, for the self-A-map f of $S{C}_A^{n,4}$ defined by $f\left(c_i\right)=c_{i+2\left(mod4\right)}$, we find that this map f does not support the AFPP of $S{C}_A^{n,4}$. □

6. Concluding Remark and Further Work

We have proved that a K-homeomorphism preserves a K-homotopy, a K-homotopy equivalence and K-contractibility. Besides, we have firstly proved that $S{C}_K^{n,l}$ is not K-contractible, $n\ge 2,l\ge 4$. In addition, we proved that the K-contractibility of X does not implies the K-contractibility relative to each singleton $\left\{x_0\right\}(\subset X)$. Using these properties, we confirmed that in KTC, the conjecture (2) can be positive. Indeed, this feature is very different from that of the k-contractibility of a simple closed k-curve followed from the Rosenfeld’s approach [25]. In addition, the conjecture (2) is slightly more generalized version of the conjecture (1.3) of [1] because the K-contractibility involving (1.3) of [1] is equal to the the K-contractibility relative to a certain singleton (see Definition 7 in the present paper). Next, we proved that in KAC the conjectures (11) and (13) are negative.

As a further work, after developing new digital topological structures on ${\mathbb{Z}}^n$ or a certain space [34], we can propose a new type of homotopy on the newly-established digital topological spaces. Furthermore, we can examine if the conjecture of (2) is positive or not, and we finally use them in applied sciences such as image processing, homotopic thinning and so on.