1. Introduction
The venture capital market plays an important role in financing and nurturing innovative start-ups. Many highly successful companies, such as Google, Facebook, Amazon, and Alibaba, receive venture capital funding in their early stages of development. According to a report released by Crunchbase in January 2019, more than 56% of private technology companies complete financing through large-scale venture capital in 2018. There is a typical principal-agent relationship between the venture capitalist (VC) and the entrepreneur (EN). Signing an investment contract is an important sign for the two parties to reach a formal agency relationship.
Traditionally, financial contract models rely on the assumption that partners in two-party contracting problems have the same beliefs on the uncertainty output [
1,
2,
3,
4]. However, the lack of information in start-up enterprises may lead to the ambiguity of individual knowledge about future enterprise performance; that is, there are multiple possible distributions on firm value. The famous Ellsberg Paradox [
5] shows that people treat ambiguity and risk from different perspectives. Nowadays, it is well-accepted that economic future outcomes can be subject to ‘risk’ and ‘ambiguity/Knightian’ uncertainties. Risk refers to the situation in which the true probability distribution of the uncertain outcome is known, whereas ambiguity refers to the case in which the true probability distribution is unknown.
Since the project of a start-up company is innovative and has few performance records, it is plausible that the VC may not have a single prior belief about the project’s success probability and, therefore, face ambiguity. Recently, Kim and Wagman [
6] proposed a theoretic start-up financing model in which the VC and EN have ambiguous beliefs about the success probability. Lukas et al. [
7] demonstrated that the high uncertainty would result in a larger stake in the venture. Miao and Rivera [
8] studied two types of robust contract problems with output uncertainty; they dealt the principal’s maximization problem under the worst-case scenario and found ambiguity aversion lowers outside securities value while increases the credit yield spread. Wu et al. [
9] extended the Holmstrom and Milgrom [
1] model by incorporating model uncertainty to study robust long-term contracting and explore the connection between ambiguity sharing and relative performance evaluation. In addition, they provided a theoretical explanation of paying for luck through writing the compensation contracts on additional signals, such as industry average performance. Liu et al. [
10] investigated a principal-agent model in which the information on future firm performance is ambiguous, and the agent is both, ambiguity averse and risk-averse. Assuming the product market outcome is ambiguous, Beauchêne [
11] found that ambiguity averse companies tend to invest in more projects, while risk-averse companies invest in fewer projects.
Using a robust optimization approach, this paper studied the optimal venture capital contracting problem in which there are multiple possible probability distributions of future project revenues, and VC is ambiguity-averse. Both the risk-neutral VC and the risk-averse EN commit to the long-term relationship. The VC designs a robust contract to maximize his utility in the worst-case scenario. Our analysis contributed to the contract literature, seeking to explain the well-documented lack of relative performance evaluation in chief executive officer (CEO) compensation. Aggarwal and Samwick [
12] assumed that the industry average performance might be affected by the agent’s action and showed that strategic interactions among firms could explain the lack of relative performance-based incentives. Wu et al. [
9] found that the ambiguity reduces the use of relative performance evaluation and then increases the exposure of the common shocks in the agent’s point of view. In contrast, we found that the cash flow evolves with the joint effect of the common shock and the idiosyncratic shock. In the presence of ambiguity uncertainty, the relative performance evaluation would be less considered in order to increase the ambiguity sharing; in other words, the VC’s ambiguity on model uncertainty would lead to the lack of relative performance evaluation, which would result in an increase in compensation performance beyond his control.
An appealing feature of our model is considering the EN’s effort and the VC’s effort simultaneously, both of which play a significant role in the success of a start-up company. An EN holds an innovative project but has a lack of commercial experience and initial capital, which could be provided by a VC. Besides offering finance, the VC could also provide market operations, networking, suggestion, and experience in business management, which would improve the success probability and the revenue of the project [
13,
14,
15]. Both the EN and the VC are crucial and irreplaceable for the VC-backed new project [
16]. As a follower in the principal-agent relationship, the EN has the motive to seek private savings due to the asymmetry of his effort. This generates a moral hazard problem. As a result, the incentive contract designed by the VC is particularly important. Furthermore, this paper analyzed a special case of a double-sided moral hazard problem in which the VC’s effort is also unobservable to the EN.
This paper was related to the recent literature on venture capital contracting problem with double-sided moral hazard. Hori and Osano [
17] examined a continuous-time agency model with double moral hazard, in which both a risk-neutral EN and a risk-neutral VC provide unobservable value-adding efforts. The cumulative cash flow generated by the risk project is affected by the efforts of VC and EN. Vergara et al. [
18] studied an optimal contract design problem and analyzed how the complementarity of efforts between an EN and a VC affects the equity share that the EN is willing to allocate to the VC. Chang and Hu [
19] explored the combined impact of double-sided moral hazard and the EN’s fairness concerns on venture capital contracting. However, these pieces of literature assume that VC knows the true probability distribution of project cash flow; hence there is no ambiguity uncertainty.
The novelty of this paper focused on the effect of the efforts complementarity and the optimal pay-performance sensitivity that the VC would allocate to the EN. Following [
14,
19,
20], we assumed the VC’s investment in the project is endogenous, and the VC plays a leadership role in the game relationship. Our model took a similar angle with [
18] on considering the complementarity effect but departed from it in three ways. First, we established the model and solved the optimization problem, where the VC holds bargaining power. Second, we extended the contract analysis to a continuous-time situation, in which cash flow and the compensation awarded to the EN are dynamic. Third, we used a project revenue function proposed by [
17] to simulate the model, instead of the constant elasticity of production function in [
18].
Another paper closely related to our study is that of Wu et al. [
9], who introduced probability measure ambiguity to analyze the continuous-time contract and focus on the research of relative performance evaluation. They found ambiguity induces a tradeoff between ambiguity sharing and incentives. However, many important models in finance and economics do not consider synergy between partners in the project [
9,
21,
22,
23]. In contrast, we analyzed how complementarity of efforts affects the optimal pay-performance sensitivity level that the VC is willing to award to the EN. We simulated the model in the scenario that two efforts are complementary and found that the synergy improves the project’s output and increases the pay-performance sensitivity allocated to the EN.
The rest of this paper is structured as follows.
Section 2 characterizes the key elements of contracting and deduces the evolution process of the value function. In
Section 3, we have solved the contracting problem and provide several applications. Finally,
Section 4 concludes the paper.
2. Model Setup and Optimal Contracting
In this section, firstly, we studied the contract designing problem with the cash flow process. Second, we dealt with the belief distortion on model uncertainty by employing the discounted relative entropy. Third, we derived the Hamilton–Jacobi–Bellman (HJB) equation that characterizes the optimal contract.
2.1. General Model
We studied a continuous-time contracting problem. A risk-neutral VC (she) hires a risk-averse EN (he) to operate an innovative project. Both of their actions (efforts) are crucial to the projected revenue. The project produces cash flow
per unit of time, where
follows the process
Here, we interpreted
and
as the EN’s and the VC’s effort choice at the time
, respectively. As an agent, the EN has the motivation to hide his action (effort), we assumed the EN’s effort is unobservable and unverifiable to the VC.
is a constant nonnegative scale adjusted parameter, which describes the efficiency of the VC’s effort in the project’s output.
measures efforts complementarity, with
and
. De Bettignies [
20] pointed out that when
, both efforts are perfect substituted, but two efforts become more complementary as
increases.
is the volatility of cash flow. The last parameter
measures the elasticity (impact) of the common shock. Similar to most project management literature, we adopted the quadratic cost function for both
and
in the forms of
and
,
and
are positive constants, which measure the effects of being more or less efficient in the delivery of efforts.
denotes common shock, while
denotes idiosyncratic shock. In addition, we assumed that
is a two-dimensional independent standard Brownian motion under probability measure
.
Suppose, following [
1,
9,
24], that in addition to project performance, compensation contracts can be written on another variable that is correlated with the noise component of project performance. This variable is assumed to be uninformative about the EN’s action. An example would be the performance of other start-ups in the given industry or in the market as a whole under the assumption that the actions of an EN do not affect the performance of other firms in his industry. Similar to [
9], we introduced the industry average performance into a contract designing problem, which is not affected by efforts exerted by the EN and the VC. For a given start-up, the industry average performance refers to the average performance of other start-ups engaged in a similar business within a particular industry. Denote
as the industry’s average performance, which follows a martingale process in the following form
Both the EN and the VC discount future cash flow at the market interest rate
. Following [
1], we assume that the EN has a constant absolute risk aversion (CARA) utility function
where
is the EN’s absolute risk aversion coefficient, and
is the EN’s wage at the time
.
The VC provides a long-term compensation contract to the EN based on the past rates of project return. specifies the EN’s wage policy and the recommended effort process . In order to avoid confusion, we used that indicates EN’s actual contract policies.
For simplicity, we assumed the EN’s initial wealth as
. Then, the contract problem faced by the EN is
subject to
The first constraint represents the actual cash flows faced by the EN when he exerts actual effort . The second constraint states that, the change of the EN’s saving is the interest accrual plus the wage deposit and minus the consumption withdrawal . To save, the EN can set his consumption strictly below the wage .
The problem faced by the VC is expressed as
subject to
The value
could be interpreted as the reservation utility that the EN would achieve in the best alternative offer he has. Following Holmström and Milgrom [
1], under the CARA assumption framework, the constraint (9) is bind.
2.2. Discounted Relative Entropy
Due to the model ambiguity, we considered belief distortion on the possibility measure. The VC does not trust the probability measure
and considers alternative models under probability measure
to protect him from probability measure ambiguity. Defining two real-valued density generators
and
, satisfying Novikov-condition
for all
, we had Radon-Nikodym derivative with respect to
.
where
.
According to the Cameron-Martin-Girsanov Theorem, we knew
and, two processes
and
are defined by
where
and
are standard Brownian motions under the probability measure
.
Under probability measure
, the cash flow and the industry average performance could be rewritten as
Similar to [
25,
26], we employed the discounted relative entropy to measure the discrepancy between
and
,
To incorporate concerns on the robustness of probability measure ambiguity, in our paper, the VC’s optimization problem could be written as
The parameter could be interpreted as the ambiguity aversion coefficient. A large value of implies a high degree of probability measure ambiguity or a large degree of concern for robustness. When converges to zero, the VC’s optimization problem is reduced to be the case without probability measure ambiguity.
2.3. Contracting Problem
Definition 1. The contractoffered to the EN is incentive-compatible if the optimal solution of the EN’s problem is.
That is, the EN would choose the recommended contract , as this choice would bring him the highest revenue, that is, . Thus, . In other words, when the contract is incentive-compatible, there would be no savings.
Given contract
, the EN’s continuation value at time
is defined as
Under Equation (17), Lemma 1 summarizes the relationship between the EN’s expected time utility and his continuation value. This result is documented in [
21].
Lemma 1. (He [21]). When the EN has a CARA utility function, then. Lemma 1 indicates that the EN’s utility function can be regarded as the time discount form with respect to continuation value. This property is peculiar to the exponential utility and would be convenient to deal with the process .
By Martingale Representation Theorem [
27], there would be two measurable processes
and
which are relevant to continuation value
such that
where the second equation is obtained with the help of Lemma 1. In order to derive the specific optimal contract rather than providing the HJB equation of the VC’s value function, we assumed simple forms of
and
as
and
, respectively.
We interpreted the two real variables and as pay-performance sensitivity level and relative performance sensitivity level, which are paid to the EN. While, relative performance evaluation occurs if the optimal contract lists a negative value to the industry average performance.
According to Equations (8) and (19), it could be rewritten as
Now, we turned to deal with the EN’s incentive compatibility. It is not difficult to find that the EN’s effort
not only affects his instantaneous
but also his continuation value, thus, the EN’s optimal effort
satisfies
Taking the EN’s first-order condition of his effort decision, we have
Together with Lemma 1, the above equation implies that
Proposition 1. The contractis incentive-compatible with respect to the EN if and only if his effort satisfies. It is worth noting that, due to the complementarity between the EN and the VC, the EN’s effort depends not only on the pay-performance sensitivity level but also VC’s effort. In this section, we assume that the EN can observe and verify the VC’s effort . Thus, this is a single moral hazard problem.
By Proposition 1, the VC’s objective function (16) can be converted into
Based on Equation (3) and Lemma 1, we have .
Formally, we defined the EN’s continuation value at time
as
here
evolves as
Using Equations (25) and (26), under the measure
, the HJB equation for the VC’s problem (24) is
with
4. Conclusions
This paper explored a continuous-time model with probability measure ambiguity in which both the VC and the EN make complementary efforts into a project. We analyzed the connection between ambiguity sharing and incentives and investigated efforts of complementarity effect.
Similar to Wu et al. [
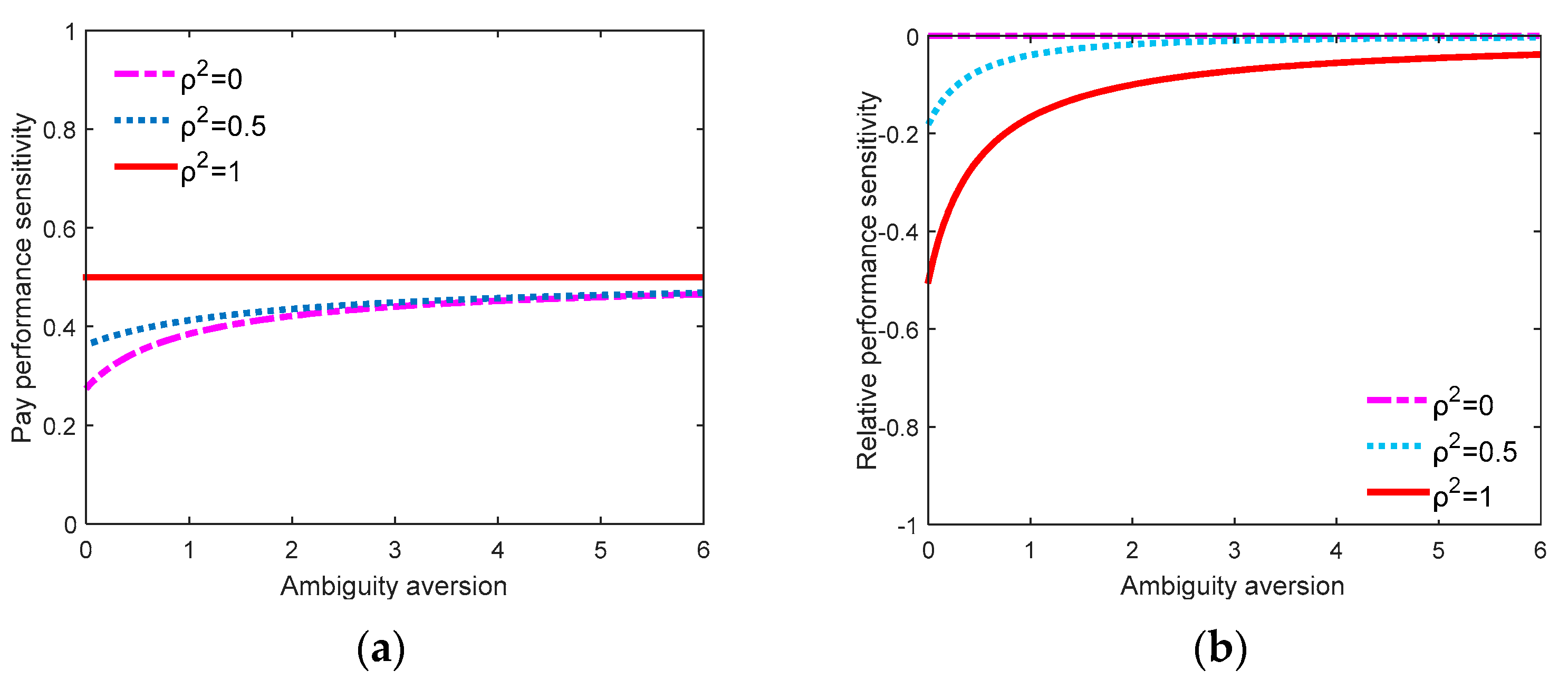
9], we assumed that the EN is ambiguity-neutral. Due to the lack of information, the VC considers alternative models to protect him from probability measure ambiguity. Our analysis showed that the probability measure ambiguity induces a trade-off between ambiguity sharing and incentives. Moreover, the probability measure ambiguity enlarges the pay-performance sensitivity level awarded to the EN.
The effort of the VC in the dynamic contract research is seldom taken into account. In this study, we considered the efforts complementarity using continuous-time principal-agent theory and analyzed the effect of efforts complementarity on the optimal pay-performance sensitivity level. We found that as efforts tend to be more complimentary, the optimal pay-performance sensitivity tends to approach those that maximize the efforts exerted by the two partners. Our model is much more complicated but is closer to reality.
There are two possible directions, deserving future research. First, in the present study, we assumed that only the VC faces ambiguity about project value. It is interesting to assume that EN also faces ambiguity about project value and investigate the effects of asymmetric ambiguity between the EN and the VC. Second, it could be seen from the existing literature that the volatility of the project cash flow importantly affects both risk-sharing and incentives in contracting [
8,
26]. Therefore, another possible work is to examine the effects of ambiguity uncertainties about the mean and volatility of the projected revenue on optimal contracting.