On the Diophantine Equation z(n) = (2 − 1/k)n Involving the Order of Appearance in the Fibonacci Sequence
Abstract
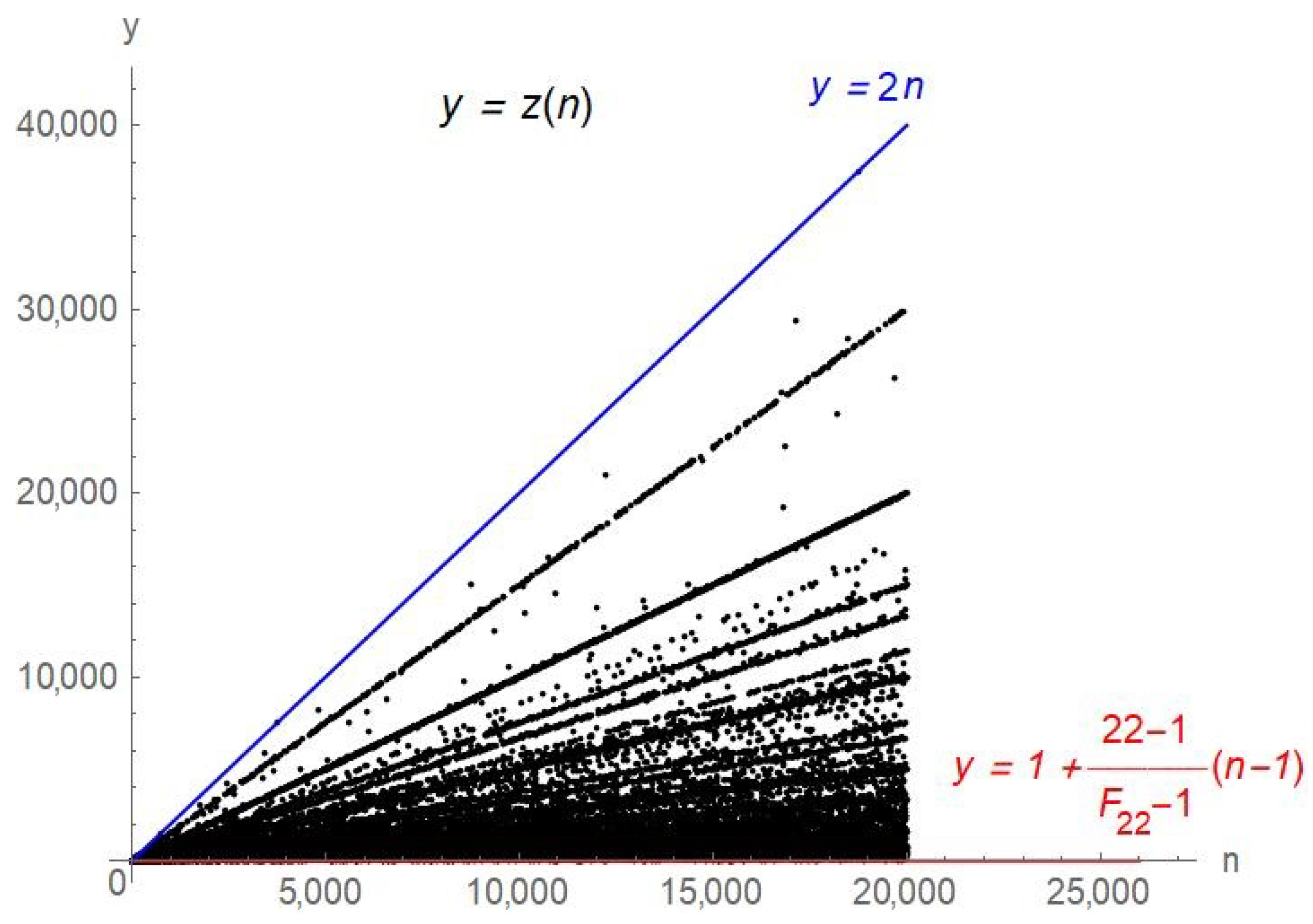
1. Introduction
2. Auxiliary Results
- (i)
- (for , (for and (for .
- (ii)
- If is a prime, thenwhere, as usual, denotes the Legendre symbol of a with respect to a prime .
- (i)
- If , then
- (ii)
- If , then
- (iii)
- If , then
3. The Proof of the Theorem
3.1. The Case
3.2. The Case in Which n Is Odd and
3.3. The Case in Which n Is Even and
3.3.1. The Case
3.3.2. The Case and
3.3.3. The Case and
3.3.4. The Case and
3.3.5. The Case and
3.3.6. The Case and
3.3.7. The Case
4. Conclusions
Funding
Conflicts of Interest
References
- Koshy, T. Fibonacci and Lucas Numbers with Applications; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Vorobiev, N.N. Fibonacci Numbers; Dover Publications: New York, NY, USA, 2013. [Google Scholar]
- Knott, R. Fibonacci Numbers and the Golden Section. The Mathematics Department of the University of Surrey, UK. Available online: Http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fib.html (accessed on 2 January 2020).
- The Fibonacci Association. Official Website. Available online: Https://www.mathstat.dal.ca/fibonacci/ (accessed on 2 January 2020).
- Brillhart, J.; Montgomery, P.L.; Silverman, R.D. Tables of Fibonacci and Lucas Factorizations. Math. Comput. 1988, 50, 251–260. [Google Scholar] [CrossRef]
- Dubner, H.; Keller, W. New Fibonacci and Lucas Primes. Math. Comput. 1999, 68, 417–427. [Google Scholar] [CrossRef][Green Version]
- Halton, J.H. On the divisibility properties of Fibonacci numbers. Fibonacci Q. 1966, 4, 217–240. [Google Scholar]
- Lengyel, T. The order of the Fibonacci and Lucas numbers. Fibonacci Q. 1995, 33, 234–239. [Google Scholar]
- Kreutz, A.; Lelis, J.; Marques, D.; Silva, E.; Trojovský, P. The p-adic order of the k-Fibonacci and k-Lucas numbers. p-Adic Numbers Ultrametric Anal. Appl. 2017, 9, 15–21. [Google Scholar] [CrossRef]
- Sanna, C. The p-adic valuation of Lucas sequences. Fibonacci Q. 2016, 54, 118–124. [Google Scholar]
- Marques, D.; Trojovský, P. The p-adic order of some Fibonomial Coefficients. J. Integer Seq. 2015, 18, 15.3.1. [Google Scholar]
- Trojovský, P. The p-adic order of some Fibonomial coefficients whose entries are powers of p. p-Adic Numbers Ultrametric Anal. Appl. 2017, 9, 228–235. [Google Scholar] [CrossRef]
- Phunphayap, P.; Pongsriiam, P. Explicit Formulas for the p-adic Valuations of Fibonomial Coefficients. J. Integer Seq. 2018, 21, 18.3.1. [Google Scholar]
- Pongsriiam, P. The order of appearance of factorials in the Fibonacci sequence and certain Diophantine equations. Period. Math. Hungar. 2019, 79, 141–156. [Google Scholar] [CrossRef]
- Wolfram, S. The Mathematica Book, 4th ed.; Wolfram Media/Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Cubre, P.; Rouse, J. Divisibility properties of the Fibonacci entry point. Proc. Am. Math. Soc. 2014, 142, 3771–3785. [Google Scholar] [CrossRef]
- Chung, C.L. Some Polynomial Sequence Relations. Mathematics 2019, 7, 750. [Google Scholar] [CrossRef]
- Kim, S. The density of the terms in an elliptic divisibility sequence having a fixed G.C.D. with their indices. J. Number Theory 2020, 207, 22–41. [Google Scholar] [CrossRef]
- Leonetti, P.; Sanna, C. On the greatest common divisor of n and the nth Fibonacci number. Rocky Mt. J. Math. 2018, 48, 1191–1199. [Google Scholar] [CrossRef]
- Marques, D. On integer numbers with locally smallest order of appearance in the Fibonacci sequence. Int. J. Math. Math. Sci. 2011, 2011, 407643. [Google Scholar] [CrossRef]
- Marques, D. The order of appearance of integers at most one away from Fibonacci numbers. Fibonacci Q. 2012, 50, 36–43. [Google Scholar]
- Luca, F.; Pomerance, C. On the local behavior of the order of appearance in the Fibonacci sequence. Int. J. Number Theory 2014, 10, 915–933. [Google Scholar] [CrossRef]
- Marques, D. The order of appearance the product of consecutive Lucas numbers. Fibonacci Q. 2013, 51, 38–43. [Google Scholar] [CrossRef][Green Version]
- Marques, D.; Trojovský, P. The order of appearance of the product of five consecutive Lucas numbers. Tatra Mt. Math. Publ. 2014, 59, 65–77. [Google Scholar] [CrossRef][Green Version]
- Khaochim, N.; Pongsriiam, P. The general case on the order of appearance of the product of consecutive Lucas numbers. Acta Math. Univ. Comenian. 2018, 59, 277–289. [Google Scholar]
- Marques, D. The order of appearance of product of consecutive Fibonacci numbers. Fibonacci Q. 2012, 50, 132–139. [Google Scholar]
- Khaochim, N.; Pongsriiam, P. On the order of appearance of the product of Fibonacci numbers. Contrib. Discret. Math. 2018, 13, 45–62. [Google Scholar]
- Marques, D. The order of appearance of powers of Fibonacci and Lucas numbers. Fibonacci Q. 2012, 50, 239–245. [Google Scholar]
- Pongsriiam, P. A complete formula for the order of appearance of the powers of Lucas numbers. Commun. Korean Math. Soc. 2016, 31, 447–450. [Google Scholar] [CrossRef]
- Trojovský, P. The order of appearance of the sum and difference between two Fibonacci numbers. Asian-Eur. J. Math. 2019, 12, 1950046. [Google Scholar] [CrossRef]
- Trojovský, P. On the order of appearance of the difference of two Lucas numbers. Miskolc Math. Notes 2018, 19, 641–648. [Google Scholar] [CrossRef]
- Lucas, E. Théorie des fonctions numériques simplement périodiques. Am. J. Math. 1878, 1, 289–321. [Google Scholar] [CrossRef]
- Sun, Z.H.; Sun, Z.W. Fibonacci numbers and Fermat’s last theorem. Acta Arith. 1992, 60, 371–388. [Google Scholar] [CrossRef]
- Somer, L.; Křížek, M. Fixed points and upper bounds for the rank of appearance in Lucas sequences. Fibonacci Q. 2013, 51, 291–306. [Google Scholar]
- Marques, D. Fixed points of the order of appearance in the Fibonacci sequence. Fibonacci Q. 2012, 50, 346–352. [Google Scholar]
- Lehmer, D.H. An extended theory of Lucas’ functions. Ann. Math. 1930, 31, 419–448. [Google Scholar] [CrossRef]
- Trojovský, P. On Diophantine equations related to order of appearance in Fibonacci sequence. Mathematics 2019, 7, 1073. [Google Scholar] [CrossRef]
- Sallé, H.J.A. A Maximum value for the rank of apparition of integers in recursive sequences. Fibonacci Q. 1975, 13, 159–161. [Google Scholar]
- Savin, D. About Special Elements in Quaternion Algebras Over Finite Fields. Adv. Appl. Clifford Algebr. 2017, 27, 1801–1813. [Google Scholar] [CrossRef]
- Marques, D. Sharper upper bounds for the order of appearance in the Fibonacci sequence. Fibonacci Q. 2013, 51, 233–238. [Google Scholar]
- Renault, M. Properties of the Fibonacci Sequence Under Various Moduli. Master’s Thesis, Wake Forest University, Winston-Salem, NC, USA, 1996. Available online: http://webspace.ship.edu/msrenault/fibonacci/FibThesis.pdf (accessed on 2 January 2020).
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 11 | 12 | 13 | 14 | 15 |
| 1 | 3 | 4 | 6 | 5 | 12 | 8 | 6 | 12 | 15 | 10 | 12 | 7 | 24 | 20 | 12 | 9 | 12 | 18 | 30 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trojovská, E. On the Diophantine Equation z(n) = (2 − 1/k)n Involving the Order of Appearance in the Fibonacci Sequence. Mathematics 2020, 8, 124. https://doi.org/10.3390/math8010124
Trojovská E. On the Diophantine Equation z(n) = (2 − 1/k)n Involving the Order of Appearance in the Fibonacci Sequence. Mathematics. 2020; 8(1):124. https://doi.org/10.3390/math8010124
Chicago/Turabian StyleTrojovská, Eva. 2020. "On the Diophantine Equation z(n) = (2 − 1/k)n Involving the Order of Appearance in the Fibonacci Sequence" Mathematics 8, no. 1: 124. https://doi.org/10.3390/math8010124
APA StyleTrojovská, E. (2020). On the Diophantine Equation z(n) = (2 − 1/k)n Involving the Order of Appearance in the Fibonacci Sequence. Mathematics, 8(1), 124. https://doi.org/10.3390/math8010124





