Quantitatively Inferring Three Mechanisms from the Spatiotemporal Patterns
Abstract
1. Introduction
2. Theoretical Models
2.1. Allen–Cahn Model
2.2. Cahn–Hilliard Model
2.3. Cahn–Hilliard with Population Demographics Model
3. Materials and Methods
3.1. Numerical Simulations
3.2. Spatial Correlation Functions
3.3. Structure Factors
3.4. Density Fluctuation
4. Results and Discussion
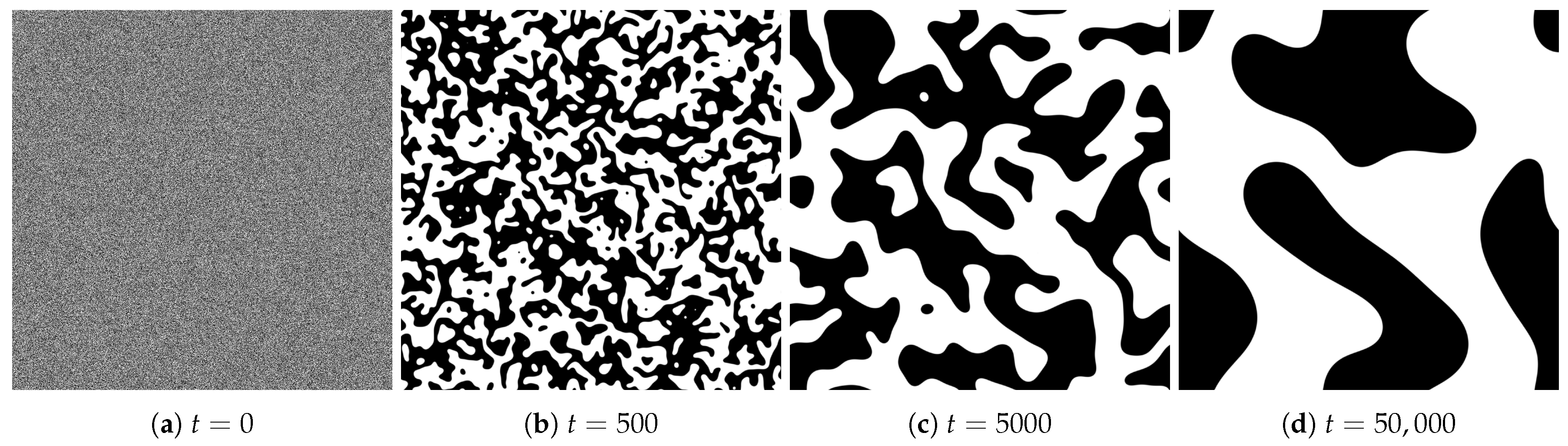
4.1. Spatial Patterns
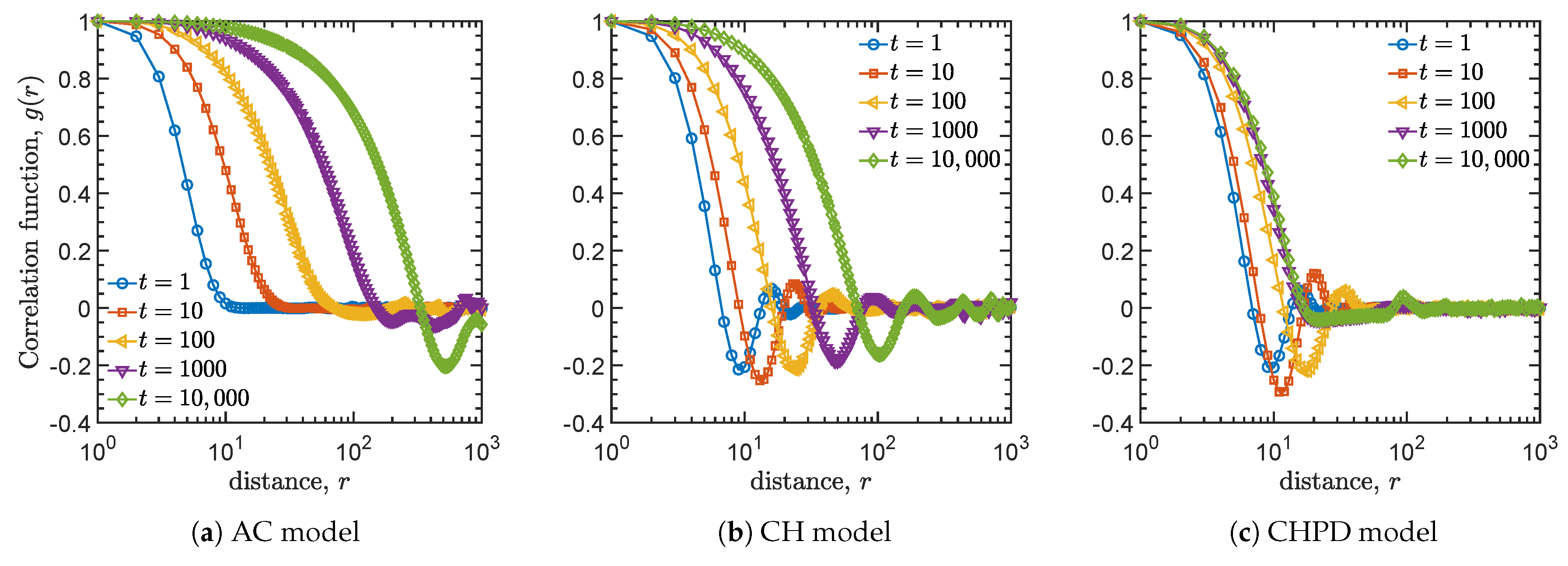
4.2. Spatial Correlation Functions
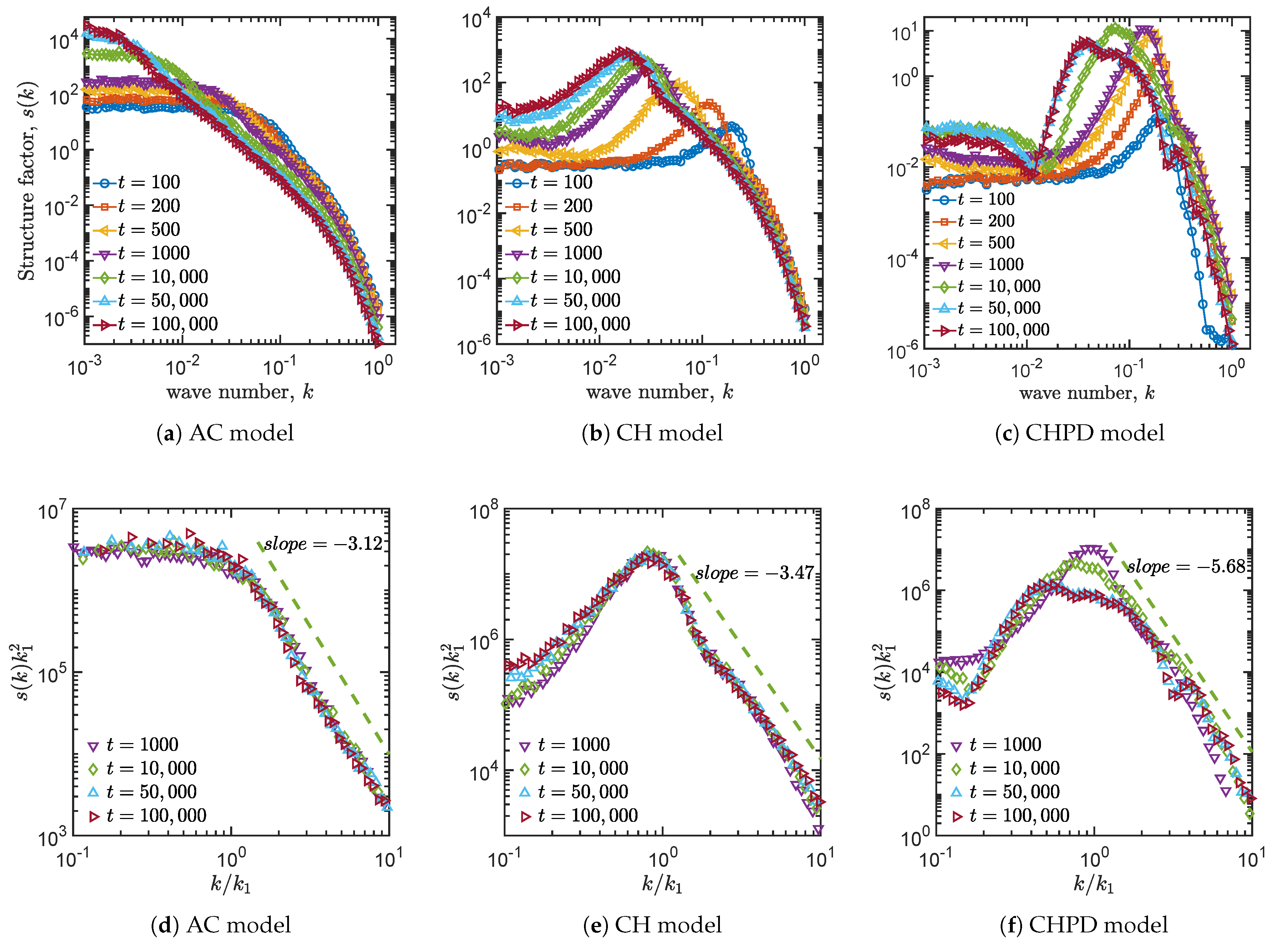
4.3. Structure Factors
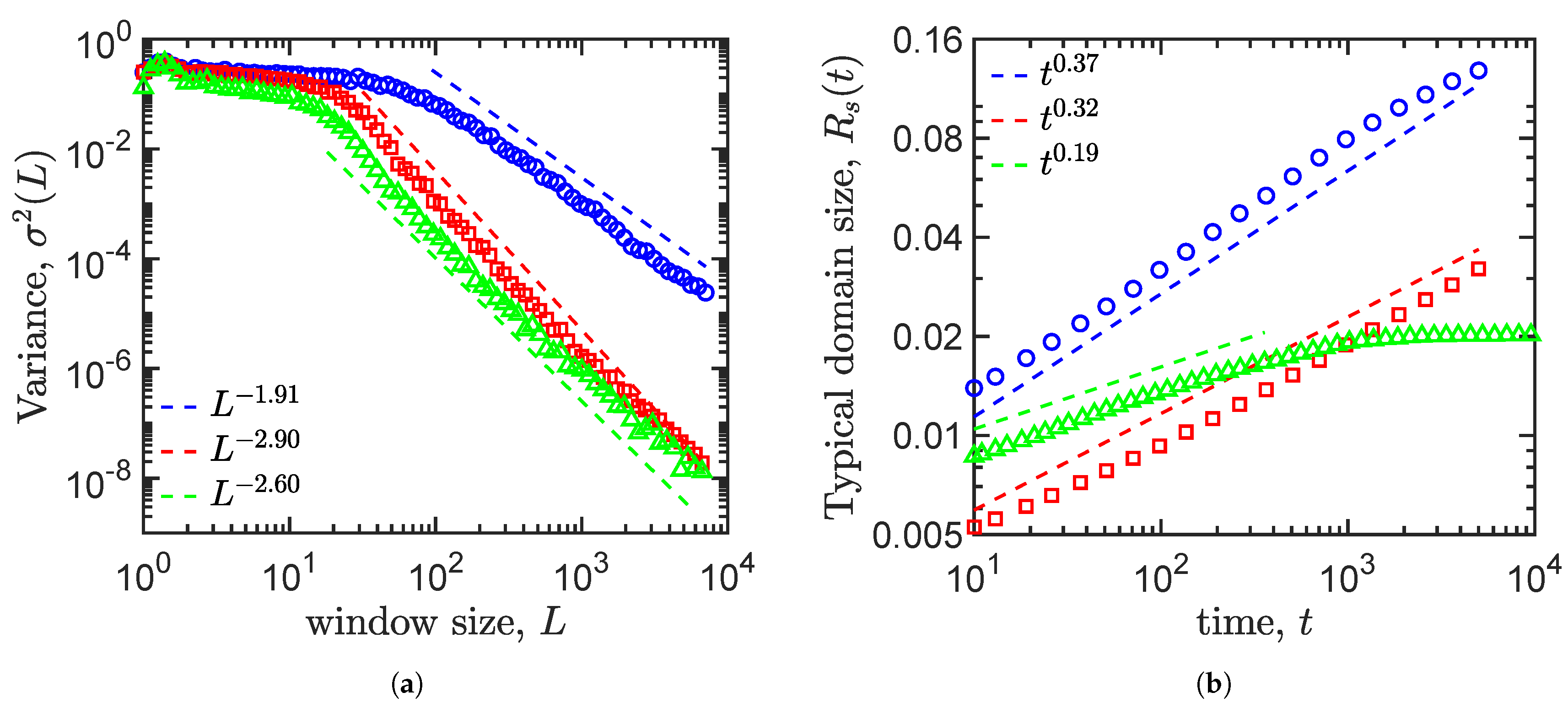
4.4. Density Fluctuation
4.5. Growth Law
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AC | Allen–Cahn |
| CH | Cahn–Hilliard |
| CHPD | Cahn–Hilliard with population demographics |
| LS | Lifshitz–Slyozov scaling |
| PDE | partial differential equation |
References
- Fisher, R.A. The wave of advance of advntageous genes. Ann. Eugen. 1937, 7, 355–369. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology; Springer: Berlin, Germany, 2002. [Google Scholar]
- Woodward, D.E.; Tyson, R.; Myerscough, M.R.; Murray, J.D.; Budrene, E.O.; Berg, H.C. Spatio-temporal patterns generated by Salmonella typhimurium. Biophys. J. 1995, 68, 2181–2189. [Google Scholar] [CrossRef]
- Meinhardt, H. The Algorithmic Beauty of Sea Shells; Springer Science & Business Media: Berlin/Heidelberg Germany, 2009. [Google Scholar]
- Klausmeier, C.A. Regular and irregular patterns in semiarid vegetation. Science 1999, 284, 1826–1828. [Google Scholar] [CrossRef]
- Ouyang, Q.; Swinney, H.L. Transition from a Uniform State to Hexagonal and Striped Turing Patterns. Nature 1991, 352, 610–612. [Google Scholar] [CrossRef]
- Kondo, S.; Miura, T. Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation. Science 2010, 329, 1616–1620. [Google Scholar] [CrossRef]
- Van de Koppel, J.; Rietkerk, M.; Dankers, N.; Herman, P.M.J. Scale-Dependent Feedback and Regular Spatial Patterns in Young Mussel Beds. Am. Nat. 2005, 165, 66–77. [Google Scholar] [CrossRef]
- Segel, L.A.; Jackson, J.L. Dissipative structure: An explanation and an ecological example. J. Theor. Biol. 1972, 37, 545–559. [Google Scholar] [CrossRef]
- Cabrera, C.V. Lateral inhibition and cell fate during neurogenesis in Drosophila: The interactions between scute, Notch and Delta. Development 1990, 110, 733–742. [Google Scholar]
- Dormann, D.; Weijer, C.J. Propagating chemoattractant waves coordinate periodic cell movement in Dictyostelium slugs. Development 2001, 128, 4535–4543. [Google Scholar]
- Rietkerk, M.; van de Koppel, J. Regular pattern formation in real ecosystems. Trends Ecol. Evol. 2008, 23, 169–175. [Google Scholar] [CrossRef]
- Liu, Q.X.; Doelman, A.; Rottschäfer, V.; de Jager, M.; Herman, P.M.; Rietkerk, M.; van de Koppel, J. Phase separation explains a new class of self-organized spatial patterns in ecological systems. Proc. Natl. Acad. Sci. USA 2013, 110, 11905–11910. [Google Scholar] [CrossRef]
- Aihara, S.; Takaki, T.; Takada, N. Multi-phase-field modeling using a conservative Allen–Cahn equation for multiphase flow. Comput. Fluids 2019, 178, 141–151. [Google Scholar] [CrossRef]
- Allen, S.M.; Cahn, J.W. Ground state structures in ordered binary alloys with second neighbor interactions. Acta Metall. 1972, 20, 423–433. [Google Scholar] [CrossRef]
- Cohen, D.S.; Murray, J.D. A Generalized Diffusion-Model for Growth and Dispersal in a Population. J. Math. Biol. 1981, 12, 237–249. [Google Scholar] [CrossRef]
- Liu, Q.X.; Rietkerk, M.; Herman, P.M.; Piersma, T.; Fryxell, J.M.; van de Koppel, J. Phase separation driven by density-dependent movement: A novel mechanism for ecological patterns. Phys. Life Rev. 2016, 19, 107–121. [Google Scholar] [CrossRef]
- McNally, L.; Bernardy, E.; Thomas, J.; Kalziqi, A.; Pentz, J.; Brown, S.P.; Hammer, B.K.; Yunker, P.J.; Ratcliff, W.C. Killing by Type VI secretion drives genetic phase separation and correlates with increased cooperation. Nat. Commun. 2017, 8, 14371. [Google Scholar] [CrossRef]
- Vicsek, T. Ecological patterns emerging as a result of the density distribution of organisms: Comment on “Phase separation driven by density-dependent movement: A novel mechanism for ecological patterns” by Quan-Xing Liu et al. Phys. Life Rev. 2016, 19, 139–141. [Google Scholar] [CrossRef]
- Cates, M.E.; Marenduzzo, D.; Pagonabarraga, I.; Tailleur, J. Arrested phase separation in reproducing bacteria creates a generic route to pattern formation. Proc. Natl. Acad. Sci. USA 2010, 107, 11715–11720. [Google Scholar] [CrossRef]
- Wittkowski, R.; Tiribocchi, A.; Stenhammar, J.; Allen, R.J.; Marenduzzo, D.; Cates, M.E. Scalar ϕ4 field theory for active-particle phase separation. Nat. Commun. 2014, 5, 4351. [Google Scholar] [CrossRef]
- Toral, R.; Chakrabarti, A.; Gunton, J.D. Droplet distribution for the two-dimensional Cahn-Hilliard model: Comparison of theory with large-scale simulations. Phys. Rev. A 1992, 45, 2147–2150. [Google Scholar] [CrossRef]
- Chen, X.; Dong, X.; Be’er, A.; Swinney, H.L.; Zhang, H.P. Scale-Invariant Correlations in Dynamic Bacterial Clusters. Phys. Rev. Lett. 2012, 108, 148101. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, L.-Q.; Shen, J.; Tikare, V. Coarsening kinetics from a variable-mobility Cahn-Hilliard equation: Application of a semi-implicit Fourier spectral method. Phys. Rev. E 1999, 60, 3564–3572. [Google Scholar] [CrossRef]
- Collet, J.F.; Goudon, T. On solutions of the Lifshitz-Slyozov model. Nonlinearity 2000, 13, 1239–1262. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Slyozov, V.V. Theory of the Ostwald ripening in multicomponent systems under non-isothermal conditions. J. Phys. Chem. Solids 1996, 57, 195–204. [Google Scholar] [CrossRef]
- Svoboda, J.; Fischer, F.D. Generalization of the Lifshitz-Slyozov-Wagner coarsening theory to non-dilute multi-component systems. Acta Mater 2014, 79, 304–314. [Google Scholar] [CrossRef]
- Kéfi, S.; Rietkerk, M.; Alados, C.L.; Pueyo, Y.; Papanastasis, V.P.; ElAich, A.; De Ruiter, P.C. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature 2007, 449, 213–215. [Google Scholar] [CrossRef]
- Torquato, S. Hyperuniform states of matter. Phys. Rep. 2018, 745, 1–95. [Google Scholar] [CrossRef]
- Allen, S.M.; Cahn, J.W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Chow, S.-N.; Conti, R.; Johnson, R.; Mallet-Paret, J.; Nussbaum, R. Dynamical systems: Lectures Given at the CIME Summer School Held in Cetraro, Italy, June 19–26, 2000; Springer: Berlin, Germany, 2003. [Google Scholar]
- Richtmyer, R.D.; Dill, E. Difference methods for initial-value problems. Phys. Today 1959, 12, 50. [Google Scholar] [CrossRef]
- Newman, M.; Barkema, G. Monte Carlo Methods in Statistical Physics; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Toral, R.; Chakrabarti, A.; Gunton, J.D. Large scale simulations of the two-dimensional Cahn-Hilliard model. Phys. A Stat. Mech. Its Appl. 1995, 213, 41–49. [Google Scholar] [CrossRef]
- Zhang, H.P.; Be’er, A.; Florin, E.L.; Swinney, H.L. Collective motion and density fluctuations in bacterial colonies. Proc. Natl. Acad. Sci. USA 2010, 107, 13626–13630. [Google Scholar] [CrossRef] [PubMed]
- Klatt, A.M.; Torquato, S. Characterization of maximally random jammed sphere packings. II. Correlation functions and density fluctuations. Phys. Rev. E 2016, 94, 022152. [Google Scholar] [CrossRef]
- Brown, G.; Rikvold, P.A.; Grant, M. Universality and scaling for the structure factor in dynamic order-disorder transitions. Phys. Rev. E 1998, 58, 5501–5507. [Google Scholar] [CrossRef]
- Lei, Q.L.; Ni, R. Hydrodynamics of random-organizing hyperuniform fluids. Proc. Natl. Acad. Sci. USA 2019, 116, 22983–22989. [Google Scholar] [CrossRef]
- Cheng, S.Z. Phase Transitions in Polymers: The Role of Metastable States; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Hammond, M.P.; Kolasa, J. Spatial variation as a tool for inferring temporal variation and diagnosing types of mechanisms in ecosystems. PLoS ONE 2014, 9, e89245. [Google Scholar] [CrossRef]
- Borgogno, F.; D’Odorico, P.; Laio, F.; Ridolfi, L. Mathematical models of vegetation pattern formation in ecohydrology. Rev. Geophys. 2009, 47. [Google Scholar] [CrossRef]
- Liu, Q.X.; Weerman, E.J.; Herman, P.M.; Olff, H.; van de Koppel, J. Alternative mechanisms alter the emergent properties of self-organization in mussel beds. Proc. R. Soc. B Biol. Sci. 2012, 279, 2744–2753. [Google Scholar] [CrossRef]
- Ball, P. Patterns in Nature: Why the Natural World Looks the Way it Does; University of Chicago Press: Chicago, IL, USA, 2006. [Google Scholar]
- Mueller, E.N.; Wainwright, J.; Parsons, A.J.; Turnbull, L. Patterns of Land Degradation in Drylands; Springer: Berlin, Germany, 2014. [Google Scholar]
- Thompson, S.E.; Daniels, K.E. A Porous Convection Model for Grass Patterns. Am. Nat. 2010, 175, 10–15. [Google Scholar] [CrossRef]
- Petrovskii, S. Pattern, process, scale, and model’s sensitivity Comment on “Phase separation driven by density-dependent movement: Anovel mechanism for ecological patterns”. Phys. Life Rev. 2016, 19, 131–134. [Google Scholar] [CrossRef]
- Ellis, J.; Petrovskaya, N.; Petrovskii, S. Effect of density-dependent individual movement on emerging spatial population distribution: Brownian motion vs Levy flights. J. Theor. Biol. 2019, 464, 159–178. [Google Scholar] [CrossRef]
- Tyutyunov, Y.; Senina, I.; Arditi, R. Clustering due to acceleration in the response to population gradient: A simple self-organization model. Am. Nat. 2004, 164, 722–735. [Google Scholar] [CrossRef]
- Bais, H.P.; Vepachedu, R.; Gilroy, S.; Callaway, R.M.; Vivanco, J.M. Allelopathy and exotic plant invasion: From molecules and genes to species interactions. Science 2003, 301, 1377–1380. [Google Scholar] [CrossRef]
- Jackson, J.B.C.; Buss, L.E.O. Alleopathy and spatial competition among coral reef invertebrates. Proc. Natl. Acad. Sci. USA 1975, 72, 5160–5163. [Google Scholar] [CrossRef]
- Theraulaz, G.; Bonabeau, E.; Nicolis, S.C.; Solé, R.V.; Fourcassié, V.; Blanco, S.; Fournier, R.; Joly, J.L.; Fernández, P.; Grimal, A.; et al. Spatial patterns in ant colonies. Proc. Natl. Acad. Sci. USA 2002, 99, 9645–9649. [Google Scholar] [CrossRef]
- Liu, C.; Fu, X.; Liu, L.; Ren, X.; Chau, C.K.; Li, S.; Xiang, L.; Zeng, H.; Chen, G.; Tang, L.H.; et al. Sequential establishment of stripe patterns in an expanding cell population. Science 2011, 334, 238–241. [Google Scholar] [CrossRef]
- Fu, X.; Tang, L.H.; Liu, C.; Huang, J.D.; Hwa, T.; Lenz, P. Stripe formation in bacterial systems with density-suppressed motility. Phys. Rev. Lett. 2012, 108, 198102. [Google Scholar] [CrossRef]
- Folmer, E.O.; Olff, H.; Piersma, T. The spatial distribution of flocking foragers: Disentangling the effects of food availability, interference and conspecific attraction by means of spatial autoregressive modeling. Oikos 2012, 121, 551–561. [Google Scholar] [CrossRef]
- Haydon, D.T.; Morales, J.M.; Yott, A.; Jenkins, D.A.; Rosatte, R.; Fryxell, J.M. Socially informed random walks: Incorporating group dynamics into models of population spread and growth. Proc. R. Soc. B Biol. Sci. 2008, 275, 1101–1109. [Google Scholar] [CrossRef]
- Yamanaka, H.; Kondo, S. In vitro analysis suggests that difference in cell movement during direct interaction can generate various pigment patterns in vivo. Proc. Natl. Acad. Sci. USA 2014, 111, 1867–1872. [Google Scholar] [CrossRef]
- Fisher, H.S.; Giomi, L.; Hoekstra, H.E.; Mahadevan, L. The dynamics of sperm cooperation in a competitive environment. Proc. R. Soc. B Biol. Sci. 2014, 281, 20140296. [Google Scholar] [CrossRef] [PubMed]
- Kessler, M.A.; Werner, B.T. Werner. Self-organization of sorted patterned ground. Science 2003, 299, 380–383. [Google Scholar] [CrossRef] [PubMed]


| Model Types | Structure Factors | Density Fluctuation | Growth Law | Saturation |
|---|---|---|---|---|
| Allen–Cahn | −3.12 | −1.91 | 0.37 | No |
| Cahn–Hillard | −3.47 | −2.90 | 0.32 | No |
| Cahn–Hillard and logistic term | −5.68 | −2.60 | 0.19 | Yes |
| Validity of the indicators | Yes | Yes | Yes | Yes |
| Model | Ecosystem | Ecological Processes | Refs. |
|---|---|---|---|
| AC | Bacteria (Vibrio cholerae) | Phase separation caused by competition | [18] |
| Plant (Centaurea maculosa) | Allelopathy and exotic plant invasion | [50] | |
| Coral reef | Allelopathy and spatial competition | [51] | |
| CH | Mussels | Density-dependent movement behavior | [8,13] |
| Ants | Density-dependent movement behavior | [52] | |
| Bacteria (Escherichia coli) | Density-dependent chemo-taxis behavior | [53,54] | |
| Birds | Resource-dependent movement behavior | [55] | |
| Elk (Cervus canadensis) | Socially inform | [56] | |
| Zebrafish | Run-and-chase behavior movement | [57] | |
| Sperm | Integrated geometry with minima drag | [58] | |
| CHPD | Bacteria (Escherichia coli, Bacillus subtilis) | Density-dependent motility and birth-death | [19,20] |
| Stones and soil | Freeze–thaw cycles | [59] | |
| Insect | General theory | [16] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Hu, W.-S.; Liu, Q.-X. Quantitatively Inferring Three Mechanisms from the Spatiotemporal Patterns. Mathematics 2020, 8, 112. https://doi.org/10.3390/math8010112
Zhang K, Hu W-S, Liu Q-X. Quantitatively Inferring Three Mechanisms from the Spatiotemporal Patterns. Mathematics. 2020; 8(1):112. https://doi.org/10.3390/math8010112
Chicago/Turabian StyleZhang, Kang, Wen-Si Hu, and Quan-Xing Liu. 2020. "Quantitatively Inferring Three Mechanisms from the Spatiotemporal Patterns" Mathematics 8, no. 1: 112. https://doi.org/10.3390/math8010112
APA StyleZhang, K., Hu, W.-S., & Liu, Q.-X. (2020). Quantitatively Inferring Three Mechanisms from the Spatiotemporal Patterns. Mathematics, 8(1), 112. https://doi.org/10.3390/math8010112





