Result Achieved
In
Table 3,
Table 4,
Table 5 and
Table 6, a comparison of both algorithms after
is shown. All the obtained results are gathered according to CEC’06 [
30] algorithms’ evaluation criteria for problems g01 to g24. The criteria include collecting statistics of the best (minimum), worst (maximum), median, mean and standard deviation of the function error values
, where
is the best objective function value obtained by the algorithm after
and
is the know objective function value at the optimal solution. The numbers in parenthesis after the objective function value show the number of violated constraints, whereas
c determines the number of violated constraints at the median solution with violation greater than
.
shows mean violation at median solution,
is the feasibility rate which is defined as the number of feasible runs over total runs, and
is success rate given by the number of successful runs over total runs. A run is called a feasible run, if the algorithm attains in
at least one feasible solution. Likewise, a run is successful, if the algorithm gets a feasible solution for which the function error value is smaller than 0.0001 in
.
Table 3 compares the experimental results achieved by JADE-ECHT and SaDE-ECHT for problems g01–g06. This table shows that SaDE-ECHT achieved better statistics in terms of best, median, mean and standard deviation values than JADE-ECHT on problems g01 and g03, whereas JADE-ECHT surpasses SaDE-ECHT on problems g02 and g05 except the best value of g02. It can also be observed from the same table that both algorithms show comparable performance on problems g04 and g06. The table also shows that both algorithms have achieved
FR on all six problems, as can be confirmed from the
in parenthesis after the objective function values, and columns for
c and
. The SR of SaDE-ECHT on problems g01–g03 is higher than JADE-ECHT. JADE-ECHT’s SR is better than SaDE-ECHT on problem g05, while both algorithms obtained the same SR of
on problems g04 and g06.
Table 4 presents the experimental statistics achieved by JADE-ECHT and SaDE-ECHT for problems g07–g12. The results of this table show that both algorithms obtained comparable statistics for problems g08, g11 and g12. This table also shows superior performance of SaDE-ECHT in terms median, mean and standard deviation values than JADE-ECHT on the problems g07, g09 and g10 except the best values on problems g07 and g10, where JADE-ECHT got better best values. The table also confirms that both algorithms have achieved
FR on all six problems, as can be seen from the
in parenthesis after the objective function values, and columns for
c and
. The SR of JADE-ECHT on problems g07 and g10 is higher than SaDE-ECHT. SaDE-ECHT’s SR is better than JADE-ECHT on problem g09, while both algorithms obtained the same SR of
on problems g08, g11 and g12.
Table 5 demonstrates the experimental results achieved by JADE-ECHT and SaDE-ECHT for problems g13–g18. The results of this table show that both algorithms performed similar on problem g16. This table also shows superior performance of SaDE-ECHT in terms best, median, mean and standard deviation values than JADE-ECHT on problems g13 and g18 except the standard deviation of g13, while JADE-ECHT performed better than SaDE-ECHT on problems g14, g15 and g17 except the mean and standard deviation values of problem g14, where SaDE-ECHT got better values for the two quantities. The table also confirms that both algorithms have achieved
FR on all six problems, as can be seen from the
in parenthesis after the objective function values, and columns for
c and
. The SR of JADE-ECHT on problems g14, g15, and g17 is higher than SaDE-ECHT. SaDE-ECHT’s SR is better than JADE-ECHT on problems g13 and g18, while both algorithms obtained the same SR of
on problem g16.
Table 6 presents the experimental results achieved by JADE-ECHT and SaDE-ECHT for problems g19–g24. The results of this table show that both algorithms performed similar on problem g24. This table also shows superior performance of JADE-ECHT in terms best, median, mean and standard deviation values than SaDE-ECHT on problems g19, g20 g21 and g23, except the best value of problem g20 and standard deviation value of problem g23, while SaDE-ECHT performed better than JADE-ECHT on problem g22. The table also confirms that both algorithms have achieved
FR on problems g19 and g24, as can be seen from the
in parenthesis after the objective function values, and columns for
c and
. Both algorithms are unsuccessful in solving problems g20 and g20. The FR of JADE-ECHT on problem g21 is lower than SaDE-ECHT, while the situation is vice versa in case of SR. The FR and SR of JADE-ECHT on problem g23 is higher than SaDE-ECHT.
Figure 3 compares the convergence graphs of JADE-ECHT and SaDE-ECHT for problems g01–g06. This figure shows that JADE-ECHT converges faster than SaDE-ECHT on problems g01, g05 and g06, as less number of
have been used by it. In case of problem g04, the convergence of SaDE-ECHT is speedy than JADE-ECHT, while in case of problems g02, g03 both algorithms converge at the same rate.
Figure 4 compares the constraints’ violations vs
graphs of JADE-ECHT and SaDE-ECHT for problems g01–g06. This figure shows that both algorithms converge quickly to the feasible region and the optimal solution (s) thus has zero constraints’ violations.
Figure 5 compares the convergence graphs of JADE-ECHT and SaDE-ECHT for problems g07–g12. This figure shows that both JADE-ECHT and SaDE-ECHT converge at the same rate for all six problems except g11, where JADE-ECHT converges faster than SaDE-ECHT.
Figure 6 compares the constraints’ violations vs
graphs of JADE-ECHT and SaDE-ECHT for problems g07–g12. This figure too shows that both algorithms converge quickly to the feasible region and optimal solution(s) thus has zero constraints’ violations.
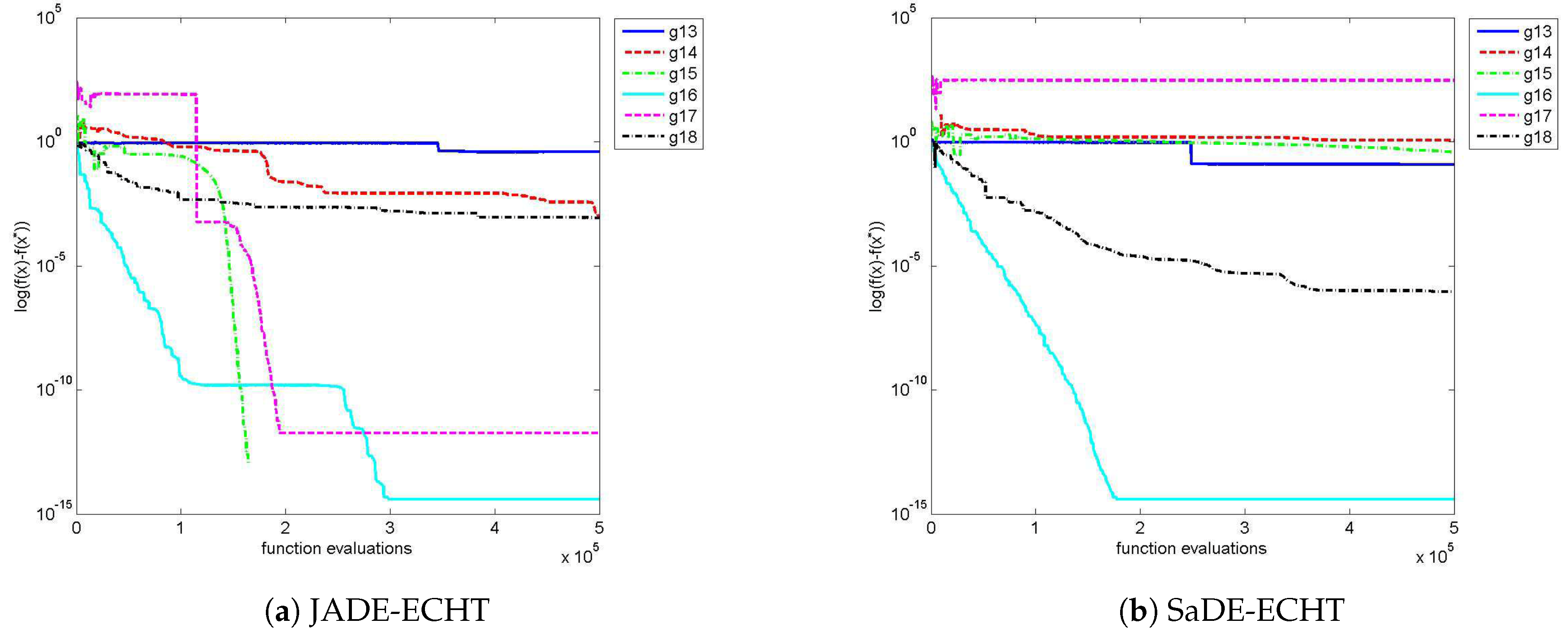
Figure 7 compares the convergence graphs of JADE-ECHT and SaDE-ECHT for problems g13–g18. This figure shows that both JADE-ECHT and SaDE-ECHT converge at the same rate for all six problems except g15, where JADE-ECHT converges faster than SaDE-ECHT.
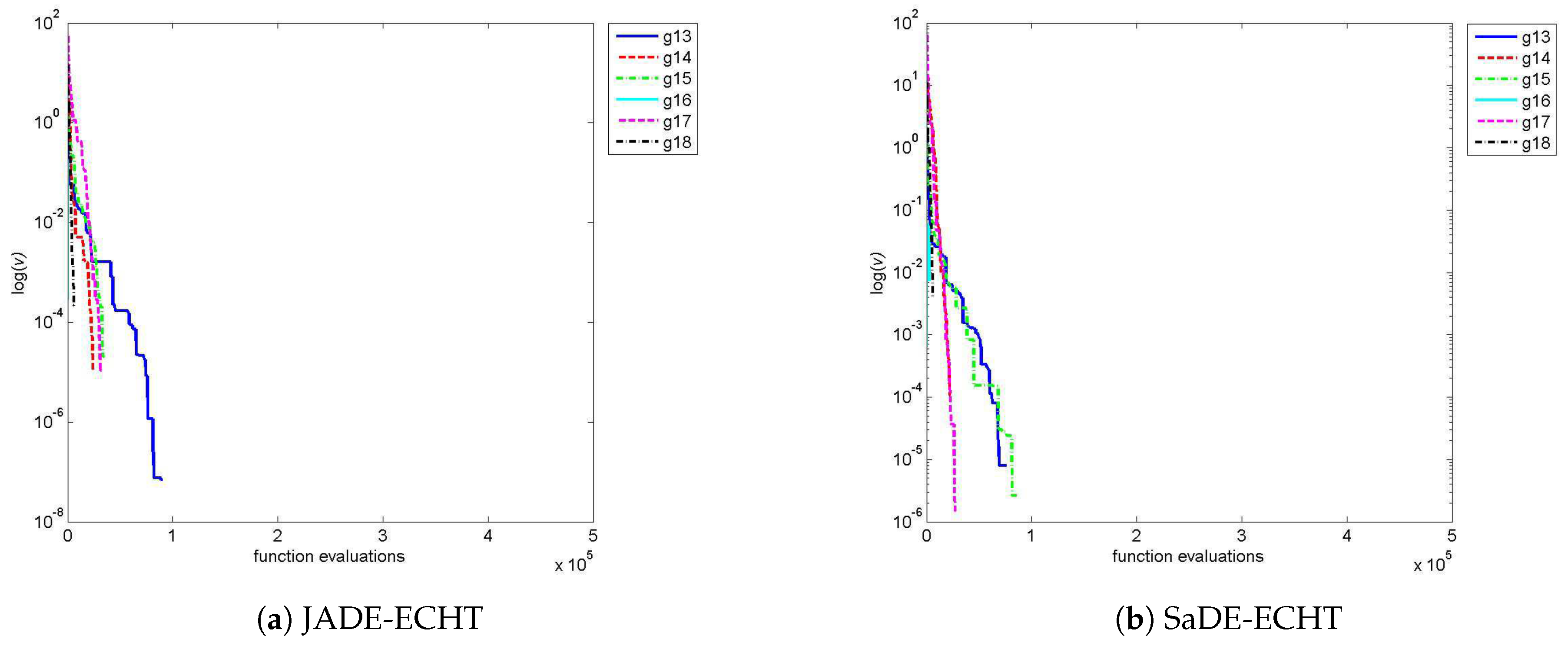
Figure 8 compares the constraints’ violations vs
graphs of JADE-ECHT and SaDE-ECHT for problems g13–g18. This figure shows that both algorithms explore the infeasible region for about 1000 iterations and then converge to the feasible region. As a result, optimal solution(s) thus obtained has zero constraints’ violations.
Figure 9 compares the convergence graphs of JADE-ECHT and SaDE-ECHT for problems g19–g24. This figure shows that both JADE-ECHT and SaDE-ECHT converge almost at the same rate for all six problems and utilize the maximum function evaluations.
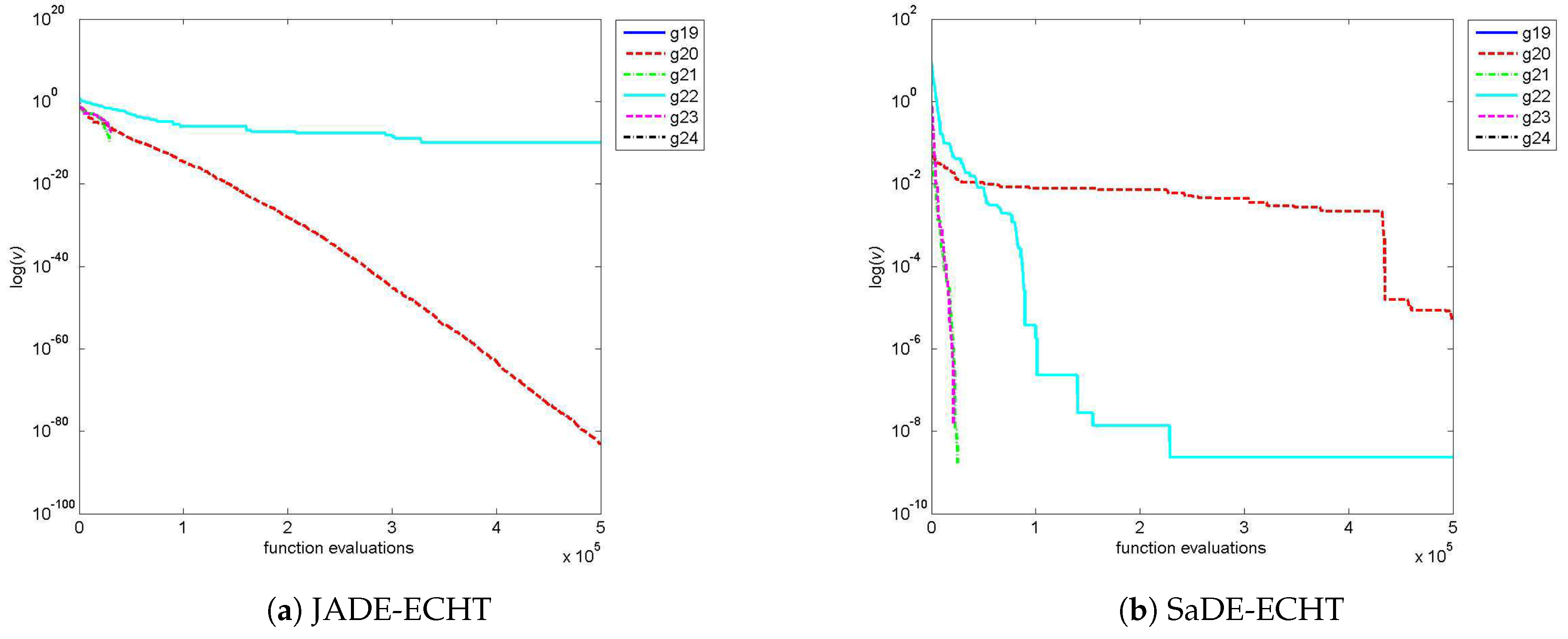
Figure 10 compares the constraints’ violations vs
graphs of JADE-ECHT and SaDE-ECHT for problems g19–g24. This figure clearly shows that both algorithms failed to obtain any feasible solution in case of problems g20 and g22, although maximum function evaluations have been used.
Overall, it can be concluded from the tabulated results and figures that both algorithms have achieved feasible solution (s) and near optimal solution (s) on 22 problems out of 24 except problems g20 and g22. The tables show that the FR of JADE-ECHT on 20 problems out of 24 is and that of SaDE-ECHT on 22 problems out of 24 is . The SR of JADE-ECHT on most of the problems is better than SaDE-ECHT. On two problems g20 and g22, the FR and SR of both algorithms are 0%. The dimension of these two problems is higher than other 22 problems. Also, these two problems had a large number of equality constraints. It can be noted from our experiments and some other literature review that equality constraints were hard to handle.
Table 7 compares the FR and SR of JADE-ECHT and SaDE-ECHT with other competing algorithms of CEC’2006. It can be seen from the said table that both JADE-ECHT and SaDE-ECHT achieved better FR, and can be placed at positions second and fourth, respectively. However, they failed to achieve better SR than the competing algorithms. A reason of failure could be the use of four different CHTs, where the resources (
) are distributed based on the success of each individual CHT, while the competing algorithms used just one CHT. The same can also be observed from
Table 8 and
Table 9, where the median and standard deviation values obtained after
of JADE-ECHT and SaDE-ECHT are compared with other competing algorithms (the values of the two quantities for the competing algorithms are taken from each source paper). Another reason of low SR could be observed from the figures showing constraints’ violations vs
graphs. It can be noticed from these graphs that both algorithms converge quickly to the feasible region. As a result, they less explore the infeasible region and consequently suffer from stagnation and premature convergence.