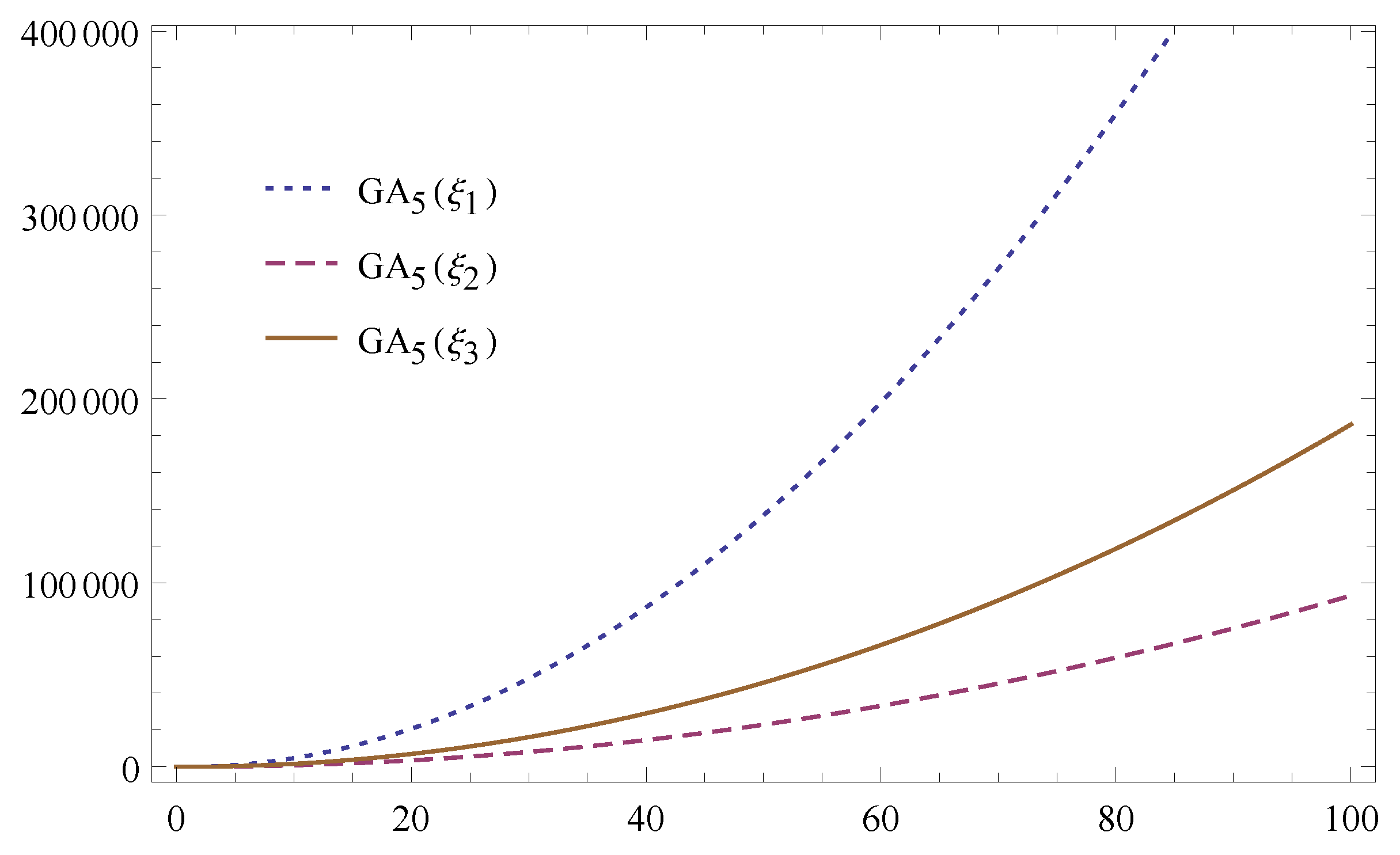On the Degree-Based Topological Indices of Some Derived Networks

Abstract

There are numeric numbers that define chemical descriptors that represent the entire structure of a graph, which contain a basic chemical structure. Of these, the main factors of topological indices are such that they are related to different physical chemical properties of primary chemical compounds. The biological activity of chemical compounds can be constructed by the help of topological indices. In theoretical chemistry, numerous chemical indices have been invented, such as the Zagreb index, the Randić index, the Wiener index, and many more. Hex-derived networks have an assortment of valuable applications in drug store, hardware, and systems administration. In this analysis, we compute the Forgotten index and Balaban index, and reclassified the Zagreb indices, $AB{C}_4$ index, and $G{A}_5$ index for the third type of hex-derived networks theoretically.

1. Introduction

Topological indices are very useful tools for chemists which are provided by Graph Theory. In a molecular graph, vertices denotes the atoms and edges are represented as chemical bonds in the terms of graph theory. To predict bioactivity of the chemical compounds, the topological indices such as ABC index, Wiener index, Randi$\acute{c}$ index, Szeged index and Zagreb indices are very useful.

A graph $\xi$ is a tuple, which consists of the n-connected vertex set $|V(\xi )|$ and the edge set |$E(\xi )$|. $\tau (m)$ denotes the degree of a vertex ‘m’ in a graph $\xi$. A graph can be represented by the polynomials, numeric numbers, a sequence of numbers, or a matrix. Throughout this article, all graphs examined are simple, finite, and connected.

As a chemical descriptor, the topological index has an integer attached to the graph which features the graph, and there is no change under graph automorphism. Previously, interest in the computing chemistry domain has grown in terms of topological descriptors and is mainly associated with the use of unusual quantities, the relationship between the structure property, and the relationship of the structure quantity. The topological indices that are based on distance, degree, and polynomials are some of the main classes of these indices. In a number of these segments, degree-based displayers are widely important and chemical graphs play an integral part in theory and theoretical chemistry.

In this article, we consider some important topological indices and some important derived graphs. We examine their chemical behavior by the help of topological indices. These topological indices are of use to chemists.

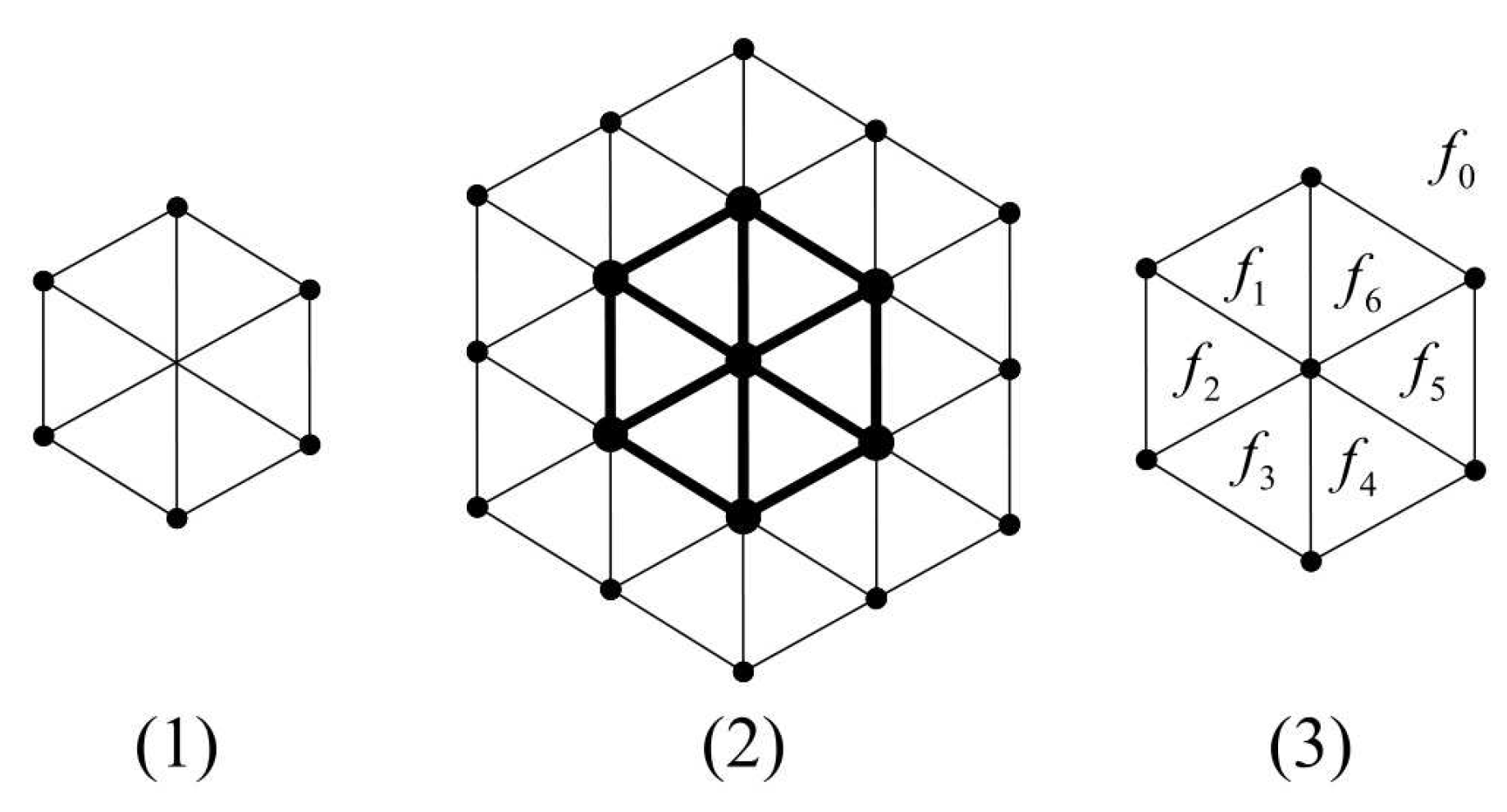
Chen et al. [1] gleaned a hexagonal mesh which consists of triangles. Triangle graphs are called oxide graphs in terms of chemistry. We can construct a hexagonal mesh by joining these triangles, as shown in Figure 1. There does not exist any hexagonal mesh whose dimension equals 1. By the joining of six triangles, we make a hexagonal mesh of dimension 2, $HX(2)$ (see Figure 1 (1)). By putting the triangles around the all sides of $HX(2)$, we obtain hexagonal mesh of dimension 3, $HX(3)$ (see Figure 1 (2)). Furthermore, we assemble the nth hexagonal mesh by putting n triangles around the boundary of each hexagon.

Drawing Algorithm of Third Type of Hex-Derived Networks $HD{N}_3$

Step-1: For $HD{N}_3$, we should draw a hexagonal mesh of dimension m.

Step-2: Draw a $K_3$ graph in each subgraph of $K_3$ and join all the vertices to the outer vertices of each $K{}_3$. The new graph is called an $HDN3$ (see Figure 2) network.

Step-3: By $HD{N}_3$ network, we can simply design $THD{N}_3$ (see Figure 3) and $RHD{N}_3$ (see Figure 4).

In this paper, ‘$\xi$’ is taken as a simple connected graph and the degree of any vertex $\acute{m}\in V(\xi )$ is stands for $\tau (\acute{m})$.

The oldest, most desired and supremely studied degree-based topological index was introduced by Milan Randić and is known as Randić index [2] denoted by $R_{-\frac{1}{2}}(\xi )$ and described as

$$R_{-\frac{1}{2}}(\xi )=\sum _{\acute{m}\acute{n}\in \mathrm{E}(\xi )}\frac{1}{\sqrt{\tau (\acute{m})\tau (\acute{n})}}.$$

(1)

The Forgotten index, also called F-index, was discovered by Furtula and Ivan Gutman [3] and described as

$$F(\xi )=\sum _{\acute{m}\acute{n}\in \mathrm{E}(\xi )}({(\tau (\acute{m}))}^2+{(\tau (\acute{n}))}^2).$$

(2)

In 1982, Balaban [4,5] found another important index known as Balaban index. For a graph $\xi$ of ‘n’ vertices and ‘m’ edges, and is described as

$$J(\xi )=\left(\frac{m}{m-n+2}\right)\sum _{\acute{m}\acute{n}\in \mathrm{E}(\xi )}\frac{1}{\sqrt{\tau (\acute{m})\times \tau (\acute{n})}}.$$

(3)

The reclassified the Zagreb indices which are proposed by Ranjini et al. [6], is of three types. For a graph $\xi$, it is described as

$$ReZ{G}_1(\xi )=\sum _{\acute{m}\acute{n}\in \mathrm{E}(\xi )}\left(\frac{\tau (\acute{m})\times \tau (\acute{n})}{\tau (\acute{m})+\tau (\acute{n})}\right),$$

(4)

$$ReZ{G}_2(\xi )=\sum _{\acute{m}\acute{n}\in \mathrm{E}(\xi )}\left(\frac{\tau (\acute{m})+\tau (\acute{n})}{\tau (\acute{m})\times \tau (\acute{n})}\right),$$

(5)

$$ReZ{G}_3(\xi )=\sum _{\acute{m}\acute{n}\in \mathrm{E}(\xi )}(\tau (\acute{m})\times \tau (\acute{n}))(\tau (\acute{m})+\tau (\acute{n})).$$

(6)

The atom-bond connectivity (ABC) index is a useful predictive index in the study of the heat of formation in alkanes [7] and is introduced by Estrada et al. [8].

Ghorbani et al. [9] introduced the $AB{C}_4$ index and is described as

$$AB{C}_4(\xi )=\sum _{\acute{m}\acute{n}\in \mathrm{E}(\xi )}\sqrt{\frac{S_{\acute{m}}+S_{\acute{n}}-2}{S_{\acute{m}}{S}_{\acute{n}}}}.$$

(7)

Graovac et al. [10] introduced the $G{A}_5$ index and is described as

$$G{A}_5(\xi )=\sum _{\acute{m}\acute{n}\in \mathrm{E}(\xi )}\frac{2\sqrt{S_{\acute{m}}{S}_{\acute{n}}}}{(S_{\acute{m}}+S_{\acute{n}})}.$$

(8)

2. Main Results

Simonraj et al. [11] created the new network which is named as third type of hex-derived networks. Chang-Cheng Wei et al. [12] found some topological indices of certain new derived networks. In this paper, we compute the exact results for all the above descriptors. For these results on different degree-based topological descriptors for a variety of graphs, we recommend [13,14,15,16,17,18,19,20]. For the basic notations and definitions, see [21,22].

2.1. Results for $HD{N}_3(m)$

In this part, the Forgotten index, Balaban index, reclassified the Zagreb indices, $AB{C}_4$ index, and $G{A}_5$ index are under consideration for the third type of hex-derived network.

Theorem 1.

Consider the third type of hex-derived network $HD{N}_3(m)$; its Forgotten index is equal to

$$F(HD{N}_3(m))=6(5339-8132n+3108n^2).$$

Proof. 

Let ${\xi }_1$ be the hex-derived network of Type 3, $HD{N}_3(m)$ shown in Figure 2, where $m\ge 4$. The hex derived network ${\xi }_1$ has $21m^2-39m+19$ vertices and the edge set of ${\xi }_1$ is divided into nine partitions based on the degrees of end vertices as shown in

Table 1. Edge partition of third type of hex-derived network $HD{N}_3(m)$, based on degrees of end vertices of each edge.

$({\mathit{\tau }}_{\acute{\mathit{m}}},{\mathit{\tau }}_{\acute{\mathit{n}}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_1)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$	$({\mathit{\tau }}_{\acute{\mathit{m}}},{\mathit{\tau }}_{\acute{\mathit{n}}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_1)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$
$(4,4)$	$18m^2-36m+18$	$(7,18)$	6
$(4,7)$	24	$(10,10)$	$6m-18$
$(4,10)$	$36m-72$	$(10,18)$	$12m-24$
$(4,18)$	$36m^2-108m+84$	$(18,18)$	$9m^2-33m+30$
$(7,10)$	12	-	-

.

Forgotten index can be calculated by using Table 1. Thus, from $(2)$, it follows,

$$\begin{array}{ccc}\hfill F({\xi }_1)& =& 32|E_1({\xi }_1)|+65|E_2({\xi }_1)|+116|E_3({\xi }_1)|+340|E_4({\xi }_1)|+149|E_5({\xi }_1)|+373|E_6({\xi }_1)|+\hfill \\ & & 200|E_7({\xi }_1)|+424|E_8({\xi }_1)|+648|E_9({\xi }_1)|.\hfill \end{array}$$

After some calculations, we have the final result

$$⟹F({\xi }_1)=6(5339-8132n+3108n^2).$$

 □

In the subsequent theorem, we compute the Balaban index of the third type of hex-derived network, ${\xi }_1$.

Theorem 2.

For the third type of hex-derived network ${\xi }_1$, the Balaban index is equal to

$$\begin{array}{ccc}\hfill J({\xi }_1)& =& \left(\frac{1}{70(43-84m+42m^2)}\right)((20-41m+21m^2)(1595.47+7(-307-270\sqrt{2}+12\sqrt{5}+\hfill \\ & & 54\sqrt{10})m)+210(5+3\sqrt{2})m^2)\hfill \end{array}$$

Proof. 

Let ${\xi }_1$ be the third type of hex-derived network $HD{N}_3(m)$. The Balaban index can be calculated by using (3) and with the help of Table 1, we have.

$$\begin{array}{ccc}\hfill J({\xi }_1)& =& \left(\frac{63n^2-123n+60}{43-84n+42n^2}\right)(\frac{1}{4}|E_1({\xi }_1)|+\frac{1}{2\sqrt{7}}|E_2({\xi }_1)|+\frac{1}{2\sqrt{10}}|E_3({\xi }_1)|+\frac{1}{6\sqrt{2}}|E_4({\xi }_1)|+\hfill \\ & & \frac{1}{\sqrt{70}}|E_5({\xi }_1)|+\frac{1}{3\sqrt{14}}|E_6({\xi }_1)|+\frac{1}{10}|E_7({\xi }_1)|+\frac{1}{6\sqrt{5}}|E_8({\xi }_1)|+\frac{1}{18}|E_9({\xi }_1)|).\hfill \end{array}$$

After some calculations, we have the result

$$\begin{array}{ccc}\hfill ⟹J({\xi }_1)& =& \left(\frac{1}{70(43-84m+42m^2)}\right)((20-41m+21m^2)(1595.47+7(-307-270\sqrt{2}+12\sqrt{5}+\hfill \\ & & 54\sqrt{10})m)+210(5+3\sqrt{2})m^2).\hfill \end{array}$$

 □

Now, we compute $ReZ{G}_1$, $ReZ{G}_2$ and $ReZ{G}_3$ indices of the third type of hex-derived network ${\xi }_1$.

Theorem 3.

Let ${\xi }_1$ be the third type of hex-derived network, then

• $ReZ{G}_1({\xi }_1)$ = $19-39m+21m^2$,
• $ReZ{G}_2({\xi }_1)$ = $\frac{115452}{425}-\frac{5637m}{11}+\frac{2583m^2}{11}$,
• $ReZ{G}_3({\xi }_1)$ = $12(27381-38996m+13692m^2)$.

Proof. 

Reclassified Zagreb index can be calculated by using Table 1, the ReZ$G_1({\xi }_1)$ by using Equation (4) as follows.

$$\begin{array}{ccc}\hfill ReZ{G}_1({\xi }_1)& =& 2|E_1({\xi }_1)|+\frac{28}{11}|E_2({\xi }_1)|+\frac{20}{7}|E_3({\xi }_1)|+\frac{36}{11}|E_4({\xi }_1)|+\frac{70}{17}|E_5({\xi }_1)|+\frac{126}{25}|E_6({\xi }_1)|+\hfill \\ & & 5|E_7({\xi }_1)|+\frac{45}{7}|E_8({\xi }_1)|+9|E_9({\xi }_1)|.\hfill \end{array}$$

After some calculations, we have

$$⟹ReZ{G}_1({\xi }_1)=19-39m+21m^2.$$

The ReZG${}_2({\xi }_1)$ can be calculated by using $(5)$ as follows.

$$\begin{array}{ccc}\hfill ReZ{G}_2({\xi }_1)& =& \frac{1}{2}|E_1({\xi }_1)|+\frac{11}{28}|E_2({\xi }_1)|+\frac{7}{20}|E_3({\xi }_1)|+\frac{11}{36}|E_4({\xi }_1)|+\frac{17}{70}|E_5({\xi }_1)|+\hfill \\ & & \frac{25}{126}|E_6({\xi }_1)|+\frac{1}{5}|E_7({\xi }_1)|+\frac{7}{45}|E_8({\xi }_1)|+\frac{1}{9}|E_9({\xi }_1)|.\hfill \end{array}$$

After some calculations, we have

$$⟹ReZ{G}_2({\xi }_1)=\frac{115452}{425}-\frac{5637m}{11}+\frac{2583m^2}{11}.$$

The ReZG${}_3({\xi }_1)$ index can be calculated from (6) as follows.

$$\begin{array}{ccc}\hfill ReZ{G}_3({\xi }_1)& =& \sum _{\acute{m}\acute{n}\in \mathrm{E}({\xi }_1)}(\tau (\acute{m})\times \tau (\acute{n}))(\tau (\acute{m})+\tau (\acute{n})=\sum _{\acute{m}\acute{n}\in E_j({\xi }_1)}\sum _{j=1}^9(\tau (\acute{m})\times \tau (\acute{n}))(\tau (\acute{m})+\tau (\acute{n}))\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ReZ{G}_3({\xi }_1)& =& 128|E_1({\xi }_1)|+308|E_2({\xi }_1)|+560|E_3({\xi }_1)|+1584|E_4({\xi }_1)|+1190|E_5({\xi }_1)|+\hfill \\ & & 3150|E_6({\xi }_1)|+2000|E_7({\xi }_1)|+5040|E_8({\xi }_1)|+11664|E_9({\xi }_1)|.\hfill \end{array}$$

After some calculations, we have

$$\begin{array}{ccc}\hfill ⟹ReZ{G}_3({\xi }_1)& =& 12(27381-38996m+13692m^2).\hfill \end{array}$$

 □

Now, we find $AB{C}_4$ and $G{A}_5$ indices of third type of hex-derived network ${\xi }_1$.

Theorem 4.

Let ${\xi }_1$ be the third type of hex-derived network, then

• $AB{C}_4({\xi }_1)$ = $51.706+\frac{3}{20}\sqrt{\frac{79}{2}}(-5+m)+3\sqrt{\frac{53}{70}}(-4+m)+\frac{3}{5}\sqrt{\frac{109}{14}}(-4+m)+\sqrt{\frac{114}{5}}(-4+m)+\frac{3}{35}\sqrt{\frac{139}{2}}(-4+m)+3\sqrt{\frac{14}{65}}(-3+m)+12\sqrt{\frac{26}{55}}(-3+m)+2\sqrt{\frac{174}{35}}(-3+m)+\sqrt{\frac{62}{7}}(-3+m)+\sqrt{\frac{78}{11}}(-2+m)+\frac{9}{11}\sqrt{\frac{43}{2}}{(-2+m)}^2+\frac{1}{3}\sqrt{\frac{35}{2}}(-5+2m)+\frac{1}{26}\sqrt{\frac{155}{2}}(24-17m+3m^2)+3\sqrt{\frac{6}{13}}(19-15m+3m^2)$;
• $G{A}_5({\xi }_1)$ = $315.338+\frac{288}{29}\sqrt{5}(-4+m)+\frac{48}{11}\sqrt{7}(-4+m)+\frac{16}{9}\sqrt{35}(-4+m)+\frac{9}{2}\sqrt{7}(-3+m)+\frac{36}{11}\sqrt{35}(-3+m)+\frac{48}{23}\sqrt{385}(-3+m)+\frac{12}{37}\sqrt{1365}(-3+m)+\frac{18}{5}\sqrt{11}(-2+m)-99m+27m^2+\frac{12}{25}\sqrt{429}(19-15m+3m^2)$.

Proof. 

The $AB{C}_4({\xi }_1)$ index can be calculated by using $(7)$ and by

Table 2. Edge partition of the third type of hex-derived network $HD{N}_3(m)$ based on sum of degrees of end vertices of each edge.

$({\mathit{\tau }}_{\acute{\mathit{m}}},{\mathit{\tau }}_{\acute{\mathit{n}}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_1)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$	$({\mathit{\tau }}_{\acute{\mathit{m}}},{\mathit{\tau }}_{\acute{\mathit{n}}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_1)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$
$(25,33)$	12	$(44,44)$	$18m^2-72m+72$
$(25,36)$	12	$(44,129)$	36
$(25,54)$	12	$(44,140)$	$48m-144$
$(25,77)$	12	$(44,156)$	$36m^2-180m+228$
$(28,36)$	$12m-36$	$(54,77)$	12
$(28,77)$	12	$(54,129)$	6
$(28,80)$	$12m-48$	$(77,80)$	12
$(33,36)$	12	$(77,129)$	12
$(33,54)$	12	$(77,140)$	12
$(33,129)$	12	$(80,80)$	$6m-30$
$(36,36)$	$12m-30$	$(80,140)$	$12m-48$
$(36,44)$	$12m-24$	$(129,140)$	12
$(36,77)$	48	$(129,156)$	6
$(36,80)$	$24m-96$	$(140,140)$	$6m-24$
$(36,129)$	24	$(140,156)$	$12m-36$
$(36,140)$	$24m-72$	$(156,156)$	$9m^2-51m+72$

, as follows.

$$\begin{array}{ccc}\hfill AB{C}_4({\xi }_1)& =& \frac{2}{5}\sqrt{\frac{14}{33}}|E_{10}({\xi }_1)|+\frac{\sqrt{59}}{30}|E_{11}({\xi }_1)|+\frac{1}{15}\sqrt{\frac{77}{6}}|E_{12}({\xi }_1)|+\frac{36}{11}\frac{2}{\sqrt{77}}|E_{13}({\xi }_1)|+\hfill \\ & & \frac{1}{6}\sqrt{\frac{31}{14}}|E_{14}({\xi }_1)|+\frac{1}{14}\sqrt{\frac{103}{11}}|E_{15}({\xi }_1)|+\frac{1}{4}\sqrt{\frac{53}{70}}|E_{16}({\xi }_1)|+\frac{1}{6}\sqrt{\frac{67}{33}}|E_{17}({\xi }_1)|+\hfill \\ & & \frac{1}{9}\sqrt{\frac{85}{22}}|E_{18}({\xi }_1)|+\frac{4}{3}\sqrt{\frac{10}{473}}|E_{19}({\xi }_1)|+\frac{1}{18}\sqrt{\frac{32}{2}}|E_{20}({\xi }_1)|+\frac{1}{2}\sqrt{\frac{13}{66}}|E_{21}({\xi }_1)|+\hfill \\ & & \frac{1}{2}\sqrt{\frac{37}{231}}|E_{22}({\xi }_1)|+\frac{1}{4}\sqrt{\frac{19}{30}}|E_{23}({\xi }_1)|+\frac{1}{6}\sqrt{\frac{163}{129}}|E_{24}({\xi }_1)|+\frac{1}{2}\sqrt{\frac{29}{210}}|E_{25}({\xi }_1)|+\hfill \\ & & \frac{1}{22}\sqrt{\frac{43}{2}}|E_{26}({\xi }_1)|+\frac{1}{2}\sqrt{\frac{57}{473}}|E_{27}({\xi }_1)|+\frac{1}{2}\sqrt{\frac{13}{110}}|E_{28}({\xi }_1)|+\frac{1}{2}\sqrt{\frac{3}{26}}|E_{29}({\xi }_1)|+\hfill \\ & & \frac{1}{3}\sqrt{\frac{43}{154}}|E_{30}({\xi }_1)|+\frac{1}{9}\sqrt{\frac{181}{86}}|E_{31}({\xi }_1)|+\frac{1}{4}\sqrt{\frac{31}{77}}|E_{32}({\xi }_1)|+2\sqrt{\frac{17}{3311}}|E_{33}({\xi }_1)|+\hfill \\ & & \frac{1}{14}\sqrt{\frac{43}{11}}|E_{34}({\xi }_1)|+\frac{1}{40}\sqrt{\frac{79}{2}}|E_{35}({\xi }_1)+\frac{1}{20}\sqrt{\frac{109}{14}}|E_{36}({\xi }_1)|+\frac{1}{2}\sqrt{\frac{99}{1505}}|E_{37}({\xi }_1)+\hfill \\ & & \frac{1}{6}\sqrt{\frac{283}{559}}|E_{38}({\xi }_1)|+\frac{1}{70}\sqrt{\frac{139}{2}}|E_{3}9({\xi }_1)|+\frac{1}{2}\sqrt{\frac{7}{130}}|E_{40}({\xi }_1)|+\frac{1}{78}\sqrt{\frac{155}{2}}|E_{41}({\xi }_1)|.\hfill \end{array}$$

After some calculations, we have

$$\begin{array}{ccc}\hfill ⟹AB{C}_4({\xi }_1)& =& 51.706+\frac{3}{20}\sqrt{\frac{79}{2}}(-5+m)+3\sqrt{\frac{53}{70}}(-4+m)+\frac{3}{5}\sqrt{\frac{109}{14}}(-4+m)+\hfill \\ & & \sqrt{\frac{114}{5}}(-4+m)+\frac{3}{35}\sqrt{\frac{139}{2}}(-4+m)+3\sqrt{\frac{14}{65}}(-3+m)+12\sqrt{\frac{26}{55}}(-3+m)+\hfill \\ & & 2\sqrt{\frac{174}{35}}(-3+m)+\sqrt{\frac{62}{7}}(-3+m)+\sqrt{\frac{78}{11}}(-2+m)+\frac{9}{11}\sqrt{\frac{43}{2}}{(-2+m)}^2+\hfill \\ & & \frac{1}{3}\sqrt{\frac{35}{2}}(-5+2m)+\frac{1}{26}\sqrt{\frac{155}{2}}(24-17m+3m^2)+3\sqrt{\frac{6}{13}}(19-15m+3m^2).\hfill \end{array}$$

The $G{A}_5({\xi }_1)$ index can be determined from (8) as follows.

$$\begin{array}{ccc}\hfill G{A}_5({\xi }_1)& =& \frac{5}{29}\sqrt{33}|E_{10}({\xi }_1)|+\frac{60}{11}|E_{11}({\xi }_1)|+\frac{30}{79}\sqrt{6}|E_{12}({\xi }_1)|+\frac{5}{51}\sqrt{77}|E_{13}({\xi }_1)|+\hfill \\ & & \frac{3}{8}\sqrt{7}|E_{14}({\xi }_1)|+\frac{4}{15}\sqrt{11}|E_{15}({\xi }_1)|+\frac{4}{27}\sqrt{35}|E_{16}({\xi }_1)|+\frac{4}{23}\sqrt{33}|E_{17}({\xi }_1)|+\hfill \\ & & \frac{6}{29}\sqrt{22}|E_{18}({\xi }_1)|+\frac{1}{31}\sqrt{957}|E_{19}({\xi }_1)|+|E_{20}({\xi }_1)|+\frac{3}{10}\sqrt{11}|E_{21}({\xi }_1)|+\hfill \\ & & \frac{12}{113}\sqrt{77}|E_{22}({\xi }_1)|+\frac{12}{29}\sqrt{5}|E_{23}({\xi }_1)|+\frac{4}{55}\sqrt{129}|E_{24}({\xi }_1)|+\frac{3}{22}\sqrt{35}|E_{25}({\xi }_1)|+\hfill \\ & & |E_{26}({\xi }_1)|+\frac{4}{173}\sqrt{1419}|E_{27}({\xi }_1)|+\frac{1}{23}\sqrt{385}|E_{28}({\xi }_1)|+\frac{1}{25}\sqrt{429}|E_{29}({\xi }_1)|+\hfill \\ & & \frac{6}{131}\sqrt{462}|E_{30}({\xi }_1)|+\frac{6}{61}\sqrt{86}|E_{31}({\xi }_1)|+\frac{8}{157}\sqrt{385}|E_{32}({\xi }_1)|+\frac{1}{103}\sqrt{9933}|E_{33}({\xi }_1)|+\hfill \\ & & \frac{4}{31}\sqrt{55}|E_{34}({\xi }_1)|+|E_{35}({\xi }_1)+\frac{4}{11}\sqrt{7}|E_{36}({\xi }_1)|+\frac{4}{269}\sqrt{4515}|E_{37}({\xi }_1)|+\hfill \\ & & \frac{4}{95}\sqrt{559}|E_{38}({\xi }_1)|+|E_{39}({\xi }_1)|+\frac{1}{37}\sqrt{1365}|E_{40}({\xi }_1)|+|E_{41}({\xi }_1)|.\hfill \end{array}$$

After some calculations, we have

$$\begin{array}{ccc}\hfill ⟹G{A}_5({\xi }_1)& =& 315.338+\frac{288}{29}\sqrt{5}(-4+m)+\frac{48}{11}\sqrt{7}(-4+m)+\frac{16}{9}\sqrt{35}(-4+m)+\frac{9}{2}\hfill \\ & & \sqrt{7}(-3+m)+\frac{36}{11}\sqrt{35}(-3+m)+\frac{48}{23}\sqrt{385}(-3+m)+\frac{12}{37}\sqrt{1365}(-3+m)+\hfill \\ & & \frac{18}{5}\sqrt{11}(-2+m)-99m+27m^2+\frac{12}{25}\sqrt{429}(19-15m+3m^2).\hfill \end{array}$$

 □

2.2. Results for Third Type of Triangular Hex-Derived Network $THD{N}_3(m)$

Now, we discuss the third type of rectangular hex-derived network and compute exact results for Forgotten index and Balaban index, and reclassified the Zagreb indices, $AB{C}_4$ index, and $G{A}_5$ index for $THD{N}_3(m)$.

Theorem 5.

Consider the third type of triangular hex-derived network of $THD{N}_3(n)$; its Forgotten index is equal to

$$F(THD{N}_3(m))=12(990-997m+259m^2).$$

Proof. 

Let ${\xi }_2$ be the third type of triangular hex-derived network, $THD{N}_3(m)$ shown in Figure 3, where $m\ge 4$. The third type of triangular hex-derived network ${\xi }_2$ has $\frac{7m^2-11m+6}{2}$ vertices and the edge set of ${\xi }_2$ is divided into six partitions based on the degree of end vertices as shown in

Table 3. Edge partition of the third type of triangular hex-derived network $THD{N}_3(m)$ based on degrees of end vertices of each edge.

$({\mathit{\tau }}_{\mathit{x}},{\mathit{\tau }}_{\mathit{y}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_1)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$	$({\mathit{\tau }}_{\mathit{u}},{\mathit{\tau }}_{\mathit{v}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_1)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$
$(4,4)$	$3m^2-6m+9$	$(10,10)$	$3m-6$
$(4,10)$	$18m-30$	$(10,18)$	$6m-18$
$(4,18)$	$6m^2-30m+36$	$(18,18)$	$\frac{3m^2-21m+36}{2}$

.

By using edge partition from Table 3, we get. Thus, from $(2)$ it follows that

$$\begin{array}{ccc}\hfill F({\xi }_2)& =& 32|E_1({\xi }_2)|+116|E_2({\xi }_2)|+340|E_3({\xi }_2)|+200|E_4({\xi }_2)|+424|E_5({\xi }_2)|+648|E_6({\xi }_2)|.\hfill \end{array}$$

By doing some calculations, we get

$$⟹F({\xi }_2)=12(990-997m+259m^2).$$

 □

In the following theorem, we compute the Balaban index of the third type of triangular hex-derived network, ${\xi }_2$.

Theorem 6.

For the third type of triangular hex-derived network ${\xi }_2$, the Balaban index is equal to

$$\begin{array}{ccc}\hfill J({\xi }_2)& =& \left(\frac{1}{40(8-14m+7m^2)}\right)(6-13m+7m^2)(159+1802\sqrt{2}-36\sqrt{5}-90\sqrt{10}+(-107-150\sqrt{2}+\hfill \\ & & 12\sqrt{5}+54\sqrt{10})m+10(5+3\sqrt{2})m^2).\hfill \end{array}$$

Proof. 

Let ${\xi }_2$ be the third type of triangular hex-derived network $THD{N}_3(m)$. By using edge partition from Table 3, the result follows. The Balaban index can be calculated by using (3) as follows.

$$\begin{array}{ccc}\hfill J({\xi }_2)& =& \frac{3}{2}\left(\frac{6-13m+7m^2}{8-14m+7m^2}\right)(\frac{1}{4}|E_1({\xi }_2)|+\frac{1}{2\sqrt{10}}|E_2({\xi }_2)|+\frac{1}{6\sqrt{2}}|E_3({\xi }_2)|+\frac{1}{10}|E_4({\xi }_2)|+\hfill \\ & & \frac{1}{6\sqrt{5}}|E_5({\xi }_2)|+\frac{1}{18}|E_6({\xi }_2)|).\hfill \end{array}$$

After some calculation, we have

$$\begin{array}{ccc}\hfill ⟹J({\xi }_2)& =& \left(\frac{1}{40(8-14m+7m^2)}\right)(6-13m+7m^2)(159+1802\sqrt{2}-36\sqrt{5}-90\sqrt{10}+(-107-\hfill \\ & & 150\sqrt{2}+12\sqrt{5}+54\sqrt{10})m+10(5+3\sqrt{2})m^2).\hfill \end{array}$$

 □

Now, we compute $ReZ{G}_1$, $ReZ{G}_2$ and $ReZ{G}_3$ indices of third type of triangular hex-derived network ${\xi }_2$.

Theorem 7.

Let ${\xi }_2$ be the third type of triangular hex-derived network, then

• $ReZ{G}_1({\xi }_2)$ = $\frac{3}{154}(3408-5117m+2009m^2)$,
• $ReZ{G}_2({\xi }_2)$ = $\frac{1}{2}(6-11m+7m^2)$,
• $ReZ{G}_3({\xi }_2)$ = $24(6192-5185m+1141m^2)$.

Proof. 

By using edge partition given in Table 3, the ReZG${}_1({\xi }_2)$ can be calculated by using $(4)$ as follows.

$$\begin{array}{ccc}\hfill ReZ{G}_1({\xi }_2)& =& 2|E_1({\xi }_2)|+\frac{20}{7}|E_2({\xi }_2)|+\frac{36}{11}|E_3({\xi }_2)|+5|E_4({\xi }_2)|+\frac{45}{7}|E_5({\xi }_2)|+9|E_6({\xi }_2)|.\hfill \end{array}$$

After some calculation, we have

$$⟹ReZ{G}_1({\xi }_2)=\frac{3}{154}(3408-5117m+2009m^2).$$

The ReZG${}_2({\xi }_2)$ can be calculated by using $(5)$ as follows.

$$\begin{array}{ccc}\hfill ReZ{G}_2({\xi }_2)& =& \frac{1}{2}|E_1({\xi }_2)|+\frac{7}{20}|E_2({\xi }_2)|+\frac{11}{36}|E_3({\xi }_2)|+\frac{1}{5}|E_4({\xi }_2)|+\frac{7}{45}|E_5({\xi }_2)|+\frac{1}{9}|E_6({\xi }_2)|.\hfill \end{array}$$

After some calculation, we have

$$⟹ReZ{G}_2({\xi }_2)=\frac{1}{2}(6-11m+7m^2).$$

The ReZG${}_3({\xi }_2)$ index can be calculated from (6) as follows.

$$\begin{array}{ccc}\hfill ReZ{G}_3({\xi }_2)& =& 128|E_1({\xi }_2)|+560|E_2({\xi }_2)|+1584|E_3({\xi }_2)|+2000|E_4({\xi }_2)|+5040|E_5({\xi }_2)|+\hfill \\ & & 11664|E_6({\xi }_2)|.\hfill \end{array}$$

After some calculation, we have

$$\begin{array}{ccc}\hfill ⟹ReZ{G}_3({\xi }_2)& =& 24(6192-5185m+1141m^2).\hfill \end{array}$$

 □

Now, we compute $AB{C}_4$ and $G{A}_5$ indices of third type of triangular hex-derived network ${\xi }_2$.

Theorem 8.

Let ${\xi }_2$ be the third type of triangular hex-derived network, then

• $AB{C}_4({\xi }_2)$ = $24.131+3\sqrt{\frac{7}{130}}(-6+m)+6\sqrt{\frac{26}{55}}(-5+m)+\sqrt{\frac{174}{35}}(-5+m)+\frac{3}{10}\sqrt{\frac{109}{14}}(-5+m)+\frac{3}{40}\sqrt{\frac{79}{2}}(-5+m)+\frac{3}{70}\sqrt{\frac{139}{2}}(-5+m)+\frac{3}{2}\sqrt{\frac{53}{70}}(-4+m)+\sqrt{\frac{39}{22}}(-4+m)+\sqrt{\frac{57}{10}}(-4+m)+\frac{3}{22}\sqrt{\frac{43}{2}}{(-4+m)}^2+\frac{1}{3}\sqrt{\frac{35}{2}}(-3+m)+2\sqrt{\frac{7}{11}}(-2+m)+\frac{1}{52}\sqrt{\frac{155}{2}}(42-13m+m^2)+3\sqrt{\frac{3}{26}}(30-11m+m^2)$;
• $G{A}_5({\xi }_2)$ = $110.66+\frac{6}{37}\sqrt{1365}(-6+m)+\frac{24}{11}\sqrt{7}(-5+m)+\frac{18}{11}\sqrt{35}(-5+m)+\frac{24}{23}\sqrt{385}(-5+m)+\frac{144}{29}\sqrt{5}(-4+m)+\frac{9}{5}\sqrt{11}(-4+m)+\frac{8}{9}\sqrt{35}(-4+m)+\frac{36}{29}\sqrt{22}(-2+m)-12m+3m^2+\frac{3}{2}(42-13m+m^2)+\frac{6}{25}\sqrt{429}(30-11m+m^2)$.

Proof. 

By using the edge partition given in

Table 4. Edge partition of the third type of triangular hex-derived network $THD{N}_3(m)$ based on the sum of degrees of end vertices of each edge.

$({\mathit{\tau }}_{\mathit{x}},{\mathit{\tau }}_{\mathit{y}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_2)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$	$({\mathit{\tau }}_{\mathit{u}},{\mathit{\tau }}_{\mathit{v}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_2)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$
$(22,22)$	3	$(44,124)$	12
$(22,28)$	12	$(44,140)$	$24m-120$
$(22,36)$	6	$(44,156)$	$6m^2-66m+180$
$(22,66)$	$6m-12$	$(66,66)$	3
$(28,66)$	24	$(66,80)$	6
$(28,80)$	$6m-24$	$(66,124)$	6
$(36,36)$	$6m-18$	$(80,80)$	$3m-15$
$(36,44)$	$6m-24$	$(80,124)$	6
$(36,66)$	12	$(80,140)$	$6m-30$
$(36,80)$	$12m-48$	$(124,140)$	6
$(36,124)$	24	$(140,140)$	$3m-15$
$(36,140)$	$12m-60$	$(140,156)$	$6m-36$
$(44,44)$	$3m^2-24m+48$	$(156,156)$	$\frac{3m^2-39m+126}{2}$

, the $AB{C}_4({\xi }_2)$ index can be calculated by using $(7)$ as follows.

$$\begin{array}{ccc}\hfill AB{C}_4({\xi }_2)& =& \frac{1}{11}\sqrt{\frac{21}{2}}|E_7({\xi }_2)|+\sqrt{\frac{6}{77}}|E_8({\xi }_2)|+\frac{1}{3}\sqrt{\frac{7}{11}}|E_9({\xi }_2)|+\frac{1}{11}\sqrt{\frac{43}{6}}|E_{10}({\xi }_2)|+\hfill \\ & & \sqrt{\frac{23}{462}}|E_{11}({\xi }_2)|+\frac{1}{4}\sqrt{\frac{53}{70}}|E_{12}({\xi }_2)|+\frac{1}{18}\sqrt{\frac{32}{2}}|E_{13}({\xi }_2)|+\frac{1}{2}\sqrt{\frac{13}{66}}|E_{14}({\xi }_2)|+\hfill \\ & & \frac{5}{3}\frac{1}{\sqrt{6}}|E_{15}({\xi }_2)|+\frac{1}{4}\sqrt{\frac{19}{30}}|E_{16}({\xi }_2)|+\frac{1}{6}\sqrt{\frac{79}{62}}|E_{17}({\xi }_2)|+\frac{1}{2}\sqrt{\frac{29}{210}}|E_{18}({\xi }_2)|+\hfill \\ & & \frac{1}{22}\sqrt{\frac{43}{2}}|E_{19}({\xi }_2)|+\frac{1}{2}\sqrt{\frac{83}{682}}|E_{20}({\xi }_2)|+\frac{1}{2}\sqrt{\frac{13}{110}}|E_{21}({\xi }_2)|+\frac{1}{2}\sqrt{\frac{3}{26}}|E_{22}({\xi }_2)|+\hfill \\ & & \frac{1}{33}\sqrt{\frac{65}{2}}|E_{23}({\xi }_2)|+\sqrt{\frac{3}{110}}|E_{24}({\xi }_2)|+\sqrt{\frac{47}{2046}}|E_{25}({\xi }_2)|+\frac{1}{40}\sqrt{\frac{79}{2}}|E_{26}({\xi }_2)|+\hfill \\ & & \frac{1}{4}\sqrt{\frac{101}{310}}|E_{27}({\xi }_2)|+\frac{1}{20}\sqrt{\frac{109}{14}}|E_{28}({\xi }_2)|+\frac{1}{2}\sqrt{\frac{131}{2170}}|E_{29}({\xi }_2)|+\frac{1}{70}\sqrt{\frac{139}{2}}|E_{30}({\xi }_2)|+\hfill \\ & & \frac{1}{2}\sqrt{\frac{7}{130}}|E_{31}({\xi }_2)|+\frac{1}{78}\sqrt{\frac{155}{2}}|E_{32}({\xi }_2)|.\hfill \end{array}$$

After some calculation, we have

$$\begin{array}{ccc}\hfill ⟹AB{C}_4({\xi }_2)& =& 24.131+3\sqrt{\frac{7}{130}}(-6+m)+6\sqrt{\frac{26}{55}}(-5+m)+\sqrt{\frac{174}{35}}(-5+m)+\hfill \\ & & \frac{3}{10}\sqrt{\frac{109}{14}}(-5+m)+\frac{3}{40}\sqrt{\frac{79}{2}}(-5+m)+\frac{3}{70}\sqrt{\frac{139}{2}}(-5+m)+\frac{3}{2}\sqrt{\frac{53}{70}}(-4+m)+\hfill \\ & & \sqrt{\frac{39}{22}}(-4+m)+\sqrt{\frac{57}{10}}(-4+m)+\frac{3}{22}\sqrt{\frac{43}{2}}{(-4+m)}^2+\frac{1}{3}\sqrt{\frac{35}{2}}(-3+m)+\hfill \\ & & 2\sqrt{\frac{7}{11}}(-2+m)+\frac{1}{52}\sqrt{\frac{155}{2}}(42-13m+m^2)+3\sqrt{\frac{3}{26}}(30-11m+m^2).\hfill \end{array}$$

The $G{A}_5({\xi }_2)$ index can be calculated from (8) as follows.

$$\begin{array}{ccc}\hfill G{A}_5({\xi }_2)& =& 1|E_7({\xi }_2)|+\frac{2}{25}\sqrt{154}|E_8({\xi }_2)|+\frac{6}{29}\sqrt{22}|E_9({\xi }_2)|+\frac{1}{2}\sqrt{3}|E_{10}({\xi }_2)|+\hfill \\ & & \frac{2}{47}\sqrt{462}|E_{11}({\xi }_2)|+\frac{4}{27}\sqrt{35}|E_{12}({\xi }_2)|+1|E_{13}({\xi }_2)|+\frac{3}{10}\sqrt{11}|E_{14}({\xi }_2)|+\hfill \\ & & \frac{2}{17}\sqrt{66}|E_{15}({\xi }_2)|+\frac{12}{29}\sqrt{5}|E_{16}({\xi }_2)|+\frac{3}{20}\sqrt{31}|E_{17}({\xi }_2)|+\frac{3}{22}\sqrt{35}|E_{18}({\xi }_2)|+\hfill \\ & & 1|E_{19}({\xi }_2)|+\frac{1}{21}\sqrt{341}|E_{20}({\xi }_2)|+\frac{1}{23}\sqrt{385}|E_{21}({\xi }_2)|+\frac{1}{25}\sqrt{429}|E_{22}({\xi }_2)|+\hfill \\ & & 1|E_{23}({\xi }_2)|+\frac{4}{73}\sqrt{330}|E_{24}({\xi }_2)|+\frac{2}{95}\sqrt{2046}|E_{25}({\xi }_2)|+1|E_{26}({\xi }_2)|+\hfill \\ & & \frac{4}{51}\sqrt{155}|E_{27}({\xi }_2)|+\frac{4}{11}\sqrt{7}|E_{28}({\xi }_2)|+\frac{1}{33}\sqrt{1085}|E_{29}({\xi }_2)|+1|E_{30}({\xi }_2)|+\hfill \\ & & \frac{1}{37}\sqrt{1365}|E_{31}({\xi }_2)|+1|E_{32}({\xi }_2)|.\hfill \end{array}$$

After some calculation, we have

$$\begin{array}{ccc}\hfill ⟹G{A}_5({\xi }_2)& =& 110.66+\frac{6}{37}\sqrt{1365}(-6+m)+\frac{24}{11}\sqrt{7}(-5+m)+\frac{18}{11}\sqrt{35}(-5+m)+\frac{24}{23}\sqrt{385}(-5+\hfill \\ & & m)+\frac{144}{29}\sqrt{5}(-4+m)+\frac{9}{5}\sqrt{11}(-4+m)+\frac{8}{9}\sqrt{35}(-4+m)+\frac{36}{29}\sqrt{22}(-2+m)-12m+\hfill \\ & & 3m^2+\frac{3}{2}(42-13m+m^2)+\frac{6}{25}\sqrt{429}(30-11m+m^2).\hfill \end{array}$$

 □

2.3. Results for Third Type of Rectangular Hex-Derived Network, $RHD{N}_3(m,n)$

In this section, we calculate certain degree-based topological indices of the third type of rectangular hex-derived network, $RHD{N}_3(m,n)$ of dimension $m=n$. We compute Forgotten index and Balaban index, and reclassified the Zagreb indices, forth version of $ABC$ index, and fifth version of $GA$ index in the coming theorems of $RHD{N}_3(m,n)$.

Theorem 9.

Consider the third type of rectangular hex-derived network $RHD{N}_3(m)$, its Forgotten index is equal to

$$F(RHD{N}_3(m))=19726-20096m+6216m^2.$$

Proof. 

Let ${\xi }_3$ be the third type of rectangular hex-derived network, $RHD{N}_3(m)$ shown in Figure 4, where $m=s\ge 4$. The third type of rectangular hex-derived network ${\xi }_3$ has $7m^2-12m+6$ vertices and the edge set of ${\xi }_3$ is divided into nine partitions based on the degree of end vertices as shown in

Table 5. Edge partition of the third type of rectangular hex-derived network, $RHD{N}_3(m)$ based on degrees of end vertices of each edge.

$({\mathit{\tau }}_{\acute{\mathit{m}}},{\mathit{\tau }}_{\acute{\mathit{n}}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_1)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$	$({\mathit{\tau }}_{\acute{\mathit{m}}},{\mathit{\tau }}_{\acute{\mathit{n}}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_1)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$
$(4,4)$	$6m^2-12m+10$	$(7,18)$	2
$(4,7)$	8	$(10,10)$	$4m-10$
$(4,10)$	$24m-44$	$(10,18)$	$8m-20$
$(4,18)$	$12m^2-48m+48$	$(18,18)$	$3m^2-16m+21$
$(7,10)$	4	-	-

.

Thus, from $(2)$, it follows that.

$$F(G)=\sum _{\acute{m}\acute{n}\in \mathrm{E}(\xi )}({(\tau (\acute{m}))}^2+{(\tau (\acute{n}))}^2)$$

Let ${\xi }_3$ be the third type of rectangular hex-derived network, $THD{N}_3(m)$. By using edge partition from Table 5, the result follows.

$$F({\xi }_3)=\sum _{\acute{m}\acute{n}\in \mathrm{E}({\xi }_3)}({(\tau (\acute{m}))}^2+{(\tau (\acute{n}))}^2)=\sum _{\acute{m}\acute{n}\in {\mathrm{E}}_{\mathrm{j}}({\xi }_3)}\sum _{j=1}^9({(\tau (\acute{m}))}^2+{(\tau (\acute{n}))}^2)$$

$$\begin{array}{ccc}\hfill F({\xi }_3)& =& 32|E_1({\xi }_3)|+65|E_2({\xi }_3)|+116|E_3({\xi }_3)|+340|E_4({\xi }_3)|+149|E_5({\xi }_3)|+373|E_6({\xi }_3)|+\hfill \\ & & 200|E_7({\xi }_3)|+424|E_8({\xi }_3)|+648|E_9({\xi }_3)|.\hfill \end{array}$$

After some calculation, we have

$$⟹F({\xi }_3)=19726-20096m+6216m^2.$$

 □

In the following theorem, we compute the Balaban index of the third type of rectangular hex-derived network, ${\xi }_3$.

Theorem 10.

For the third type of rectangular hex-derived network ${\xi }_3$, the Balaban index is equal to

$$\begin{array}{ccc}\hfill J({\xi }_3)& =& \left(\frac{1}{315(15-28m+14m^2)}\right)7(-157-180\sqrt{2}+12\sqrt{5}+54\sqrt{10})m+105(5+3\sqrt{2})m^2)(19-\hfill \\ & & 40m+21m^2)(3(280+420\sqrt{2}-70\sqrt{5}+60\sqrt{7}-231\sqrt{10}+5\sqrt{14}+6\sqrt{70})).\hfill \end{array}$$

Proof. 

Let ${\xi }_3$ be the rectangular hex-derived network $RHD{N}_3(m)$. By using edge partition from Table 5, the result follows. The Balaban index can be calculated by using (3) as follows.

$$\begin{array}{ccc}\hfill J({\xi }_3)& =& \left(\frac{m}{m-n+2}\right)\sum _{\acute{m}\acute{n}\in \mathrm{E}({\xi }_3)}\frac{1}{\sqrt{\tau (\acute{m})\times \tau (\acute{n})}}=\left(\frac{m}{m-n+2}\right)\sum _{\acute{m}\acute{n}\in {\mathrm{E}}_{\mathrm{j}}({\xi }_3)}\sum _{j=1}^9\frac{1}{\sqrt{\tau (\acute{m})\times \tau (\acute{n})}}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill J({\xi }_3)& =& \left(\frac{19-40m+21m^2}{15-28m+14m^2}\right)(\frac{1}{4}|E_1({\xi }_3)|+\frac{1}{2\sqrt{7}}|E_2({\xi }_3)|+\frac{1}{2\sqrt{10}}|E_3({\xi }_3)|+\frac{1}{6\sqrt{2}}|E_4({\xi }_3)|+\hfill \\ & & \frac{1}{\sqrt{70}}|E_5({\xi }_3)|+\frac{1}{3\sqrt{14}}|E_6({\xi }_3)|+\frac{1}{10}|E_7({\xi }_3)|+\frac{1}{6\sqrt{5}}|E_8({\xi }_3)|+\frac{1}{18}|E_9({\xi }_3)|).\hfill \end{array}$$

After some calculation, we have

$$\begin{array}{ccc}\hfill ⟹J({\xi }_3)& =& \left(\frac{1}{315(15-28m+14m^2)}\right)7(-157-180\sqrt{2}+12\sqrt{5}+54\sqrt{10})m+105(5+3\sqrt{2})m^2)\hfill \\ & & (19-40m+21m^2)(3(280+420\sqrt{2}-70\sqrt{5}+60\sqrt{7}-231\sqrt{10}+5\sqrt{14}+6\sqrt{70})).\hfill \end{array}$$

 □

Now, we compute $ReZ{G}_1$, $ReZ{G}_2$ and $ReZ{G}_3$ indices of the third type of rectangular hex-derived network ${\xi }_3$.

Theorem 11.

Let ${\xi }_3$ be the third type of rectangular hex-derived network, then

• $ReZ{G}_1({\xi }_3)$ = $\frac{10102843}{32725}-\frac{2036m}{11}+\frac{861m^2}{11}$,
• $ReZ{G}_2({\xi }_3)$ = $56-12m+7m^2$,
• $ReZ{G}_3({\xi }_3)$ = $4(50785-50608m+13692m^2)$.

Proof. 

By using the edge partition given in Table 5, the ReZG${}_1({\xi }_3)$ can be calculated by using $(4)$ as follows.

$$\begin{array}{ccc}\hfill ReZ{G}_1(\xi )& =& \sum _{\acute{m}\acute{n}\in \mathrm{E}({\xi }_3)}\left(\frac{\tau (\acute{m})\times \tau (\acute{n})}{\tau (\acute{m})+\tau (\acute{n})}\right)=\sum _{j=1}^9\sum _{\acute{m}\acute{n}\in E_j({\xi }_3)}\left(\frac{\tau (\acute{m})\times \tau (\acute{n})}{\tau (\acute{m})+\tau (\acute{n})}\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ReZ{G}_1({\xi }_3)& =& 2|E_1({\xi }_3)|+\frac{28}{11}|E_2({\xi }_3)|+\frac{20}{7}|E_3({\xi }_3)|+\frac{36}{11}|E_4({\xi }_3)|+\frac{70}{17}|E_5({\xi }_3)|+\frac{126}{25}|E_6({\xi }_3)|+\hfill \\ & & 5|E_7({\xi }_3)|+\frac{45}{7}|E_8({\xi }_3)|+9|E_9({\xi }_3)|.\hfill \end{array}$$

After some calculation, we have

$$⟹ReZ{G}_1({\xi }_3)=\frac{10102843}{32725}-\frac{2036m}{11}+\frac{861m^2}{11}.$$

The ReZG${}_2({\xi }_3)$ can be calculated by using $(5)$ as follows.

$$ReZ{G}_2({\xi }_3)=\sum _{\acute{m}\acute{n}\in \mathrm{E}({\xi }_3)}\left(\frac{\tau (\acute{m})+\tau (\acute{n})}{\tau (\acute{m})\times \tau (\acute{n})}\right)=\sum _{\acute{m}\acute{n}\in E_j({\xi }_3)}\sum _{j=1}^9\left(\frac{\tau (\acute{m})+\tau (\acute{n})}{\tau (\acute{m})\times \tau (\acute{n})}\right)$$

$$\begin{array}{ccc}\hfill ReZ{G}_2({\xi }_3)& =& \frac{1}{2}|E_1({\xi }_3)|+\frac{11}{28}|E_2({\xi }_3)|+\frac{7}{20}|E_3({\xi }_3)|+\frac{11}{36}|E_4({\xi }_3)|+\frac{17}{70}|E_5({\xi }_3)|+\frac{25}{126}|E_6({\xi }_3)|+\hfill \\ & & \frac{1}{5}|E_7({\xi }_3)|+\frac{7}{45}|E_8({\xi }_3)|+\frac{1}{9}|E_9({\xi }_3)|.\hfill \end{array}$$

After some calculation, we have

$$⟹ReZ{G}_2({\xi }_3)=56-12m+7m^2.$$

The ReZG${}_3({\xi }_3)$ index can be calculated from (6) as follows.

$$\begin{array}{ccc}\hfill ReZ{G}_3({\xi }_3)& =& \sum _{\acute{m}\acute{n}\in \mathrm{E}({\xi }_3)}(\tau (\acute{m})\times \tau (\acute{n}))(\tau (\acute{m})+\tau (\acute{n})=\sum _{\acute{m}\acute{n}\in E_j({\xi }_3)}\sum _{j=1}^9(\tau (\acute{m})\times \tau (\acute{n}))(\tau (\acute{m})+\tau (\acute{n}))\hfill \end{array}$$

$$\begin{array}{ccc}\hfill ReZ{G}_3({\xi }_3)& =& 128|E_1({\xi }_3)|+308|E_2({\xi }_3)|+560|E_3({\xi }_3)|+1584|E_4({\xi }_3)|+1190|E_5({\xi }_3)|+\hfill \\ & & 3150|E_6({\xi }_3)|+2000|E_7({\xi }_3)|+5040|E_8({\xi }_3)|+11664|E_9({\xi }_3)|.\hfill \end{array}$$

After some calculation, we have

$$\begin{array}{ccc}\hfill ⟹ReZ{G}_3({\xi }_3)& =& 4(50785-50608m+13692m^2).\hfill \end{array}$$

 □

Now, we compute $AB{C}_4$ and $G{A}_5$ indices of the third type of rectangular hex-derived network ${\xi }_3$.

Theorem 12.

Let ${\xi }_3$ be the third type of rectangular hex-derived network, then

• $AB{C}_4({\xi }_3)$ = $22.459+8\sqrt{\frac{26}{55}}(-4+m)+4\sqrt{\frac{58}{105}}(-4+m)+\frac{4}{7}\sqrt{\frac{67}{15}}(-4+m)+3\sqrt{\frac{6}{13}}{(-4+m)}^2+2\sqrt{\frac{26}{33}}(-3+m)+\frac{3}{11}\sqrt{\frac{43}{2}}{(-3+m)}^2+\sqrt{\frac{14}{65}}(-9+2m)+\frac{1}{35}\sqrt{\frac{139}{2}}(-9+2m)+\frac{1}{3}\sqrt{\frac{62}{7}}(-5+2m)+\frac{4}{63}\sqrt{31}(-5+2m)+\frac{4}{9}\sqrt{\frac{97}{7}}(-3+2m)+\frac{2}{21}\sqrt{89}(-3+2m)+\frac{1}{9}\sqrt{\frac{35}{2}}(-11+4m)+\frac{1}{78}\sqrt{\frac{155}{2}}(65-28m+3m^2)$;
• $G{A}_5({\xi }_3)$ = $173.339+\frac{96}{29}\sqrt{5}(-4+m)+\frac{24}{11}\sqrt{35}(-4+m)+\frac{32}{23}\sqrt{385}(-4+m)+\frac{12}{25}\sqrt{429}{(-4+m)}^2+\frac{12}{5}\sqrt{11}(-3+m)-48m+9m^2+\frac{4}{37}\sqrt{1365}(-9+2m)+\frac{3}{2}\sqrt{7}(-5+2m)+\frac{48}{13}(-3+2m)+\frac{32}{11}\sqrt{7}(-3+2m)$.

Proof. 

By using the edge partition given in

Table 6. Edge partition of the third type of rectangular hex-derived network $RHD{N}_3(m)$ based on the sum of degrees of end vertices of each edge.

$({\mathit{\tau }}_{\mathit{x}},{\mathit{\tau }}_{\mathit{y}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_3)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$	$({\mathit{\tau }}_{\mathit{u}},{\mathit{\tau }}_{\mathit{v}})$ Where $\acute{\mathit{m}}\acute{\mathit{n}}\in \mathit{E}({\mathit{\xi }}_3)$	$\mathbf{Number}\mathbf{of}\mathbf{Edges}$
$(22,22)$	2	$(44,44)$	$6m^2-36m+54$
$(22,28)$	8	$(44,124)$	8
$(22,63)$	4	$(44,129)$	12
$(25,33)$	4	$(44,140)$	$32m-128$
$(25,36)$	4	$(44,156)$	$12m^2-96m+192$
$(25,54)$	4	$(54,63)$	4
$(25,63)$	4	$(54,129)$	2
$(28,36)$	$8m-20$	$(63,63)$	$4m-10$
$(28,63)$	$8m-12$	$(63,124)$	8
$(33,36)$	4	$(63,129)$	4
$(33,54)$	4	$(63,140)$	$8m-32$
$(33,129)$	4	$(124,140)$	4
$(36,36)$	$8m-22$	$(129,140)$	4
$(36,44)$	$8m-24$	$(129,156)$	2
$(36,63)$	$16m-40$	$(140,140)$	$4m-18$
$(36,124)$	16	$(140,156)$	$8m-36$
$(36,129)$	8	$(156,156)$	$3m^2-28m+65$
$(36,140)$	$16m-64$	-	-

, the $AB{C}_4({\xi }_3)$ can be calculated by using $(7)$ as follows.

$$AB{C}_4({\xi }_3)=\sum _{\acute{m}\acute{n}\in \mathrm{E}({\xi }_3)}\sqrt{\frac{S_{\acute{m}}+S_{\acute{n}}-2}{S_{\acute{m}}{S}_{\acute{n}}}}=\sum _{\acute{m}\acute{n}\in E_j({\xi }_3)}\sum _{j=10}^{44}\sqrt{\frac{S_{\acute{m}}+S_{\acute{n}}-2}{S_{\acute{m}}{S}_{\acute{n}}}}$$

$$\begin{array}{ccc}\hfill AB{C}_4({\xi }_3)& =& \frac{1}{11}\sqrt{\frac{21}{2}}|E_{10}({\xi }_3)|+\sqrt{\frac{6}{77}}|E_{11}({\xi }_3)|+\frac{1}{3}\sqrt{\frac{83}{154}}|E_{12}({\xi }_3)|+\frac{1}{5}\sqrt{\frac{46}{33}}|E_{13}({\xi }_3)|+\hfill \\ & & \frac{1}{30}\sqrt{59}|E_{14}({\xi }_3)|+\frac{1}{15}\sqrt{\frac{77}{6}}|E_{15}({\xi }_3)|+\frac{1}{15}\sqrt{\frac{86}{7}}|E_{16}({\xi }_3)|+\frac{1}{6}\sqrt{\frac{31}{14}}|E_{17}({\xi }_3)|+\hfill \\ & & \frac{1}{42}\sqrt{89}|E_{18}({\xi }_3)|+\frac{1}{6}\sqrt{\frac{67}{33}}|E_{19}({\xi }_3)|+\frac{1}{9}\sqrt{\frac{85}{22}}|E_{20}({\xi }_3)|+\frac{4}{3}\sqrt{\frac{10}{473}}|E_{21}({\xi }_3)|+\hfill \\ & & \frac{1}{18}\sqrt{\frac{35}{2}}|E_{22}({\xi }_3)|+\frac{1}{2}\sqrt{\frac{13}{66}}|E_{23}({\xi }_3)|+\frac{1}{18}\sqrt{\frac{97}{7}}|E_{24}({\xi }_3)|+\frac{1}{6}\sqrt{\frac{79}{62}}|E_{25}({\xi }_3)|+\hfill \\ & & \frac{1}{6}\sqrt{\frac{163}{129}}|E_{26}({\xi }_3)|+\frac{1}{2}\sqrt{\frac{29}{210}}|E_{27}({\xi }_3)|+\frac{1}{22}\sqrt{\frac{43}{2}}|E_{28}({\xi }_3)|+\frac{1}{2}\sqrt{\frac{83}{682}}|E_{29}({\xi }_3)|+\hfill \\ & & \frac{1}{2}\sqrt{\frac{57}{473}}|E_{30}({\xi }_3)|+\frac{1}{2}\sqrt{\frac{13}{110}}|E_{31}({\xi }_3)|+\frac{1}{2}\sqrt{\frac{3}{26}}|E_{32}({\xi }_3)+\frac{1}{9}\sqrt{\frac{115}{42}}|E_{33}({\xi }_3)+\hfill \\ & & \frac{1}{9}\sqrt{\frac{181}{86}}|E_{34}({\xi }_3)|+\frac{1}{63}\sqrt{31}|E_{35}({\xi }_3)|+\frac{1}{6}\sqrt{\frac{185}{217}}|E_{36}({\xi }_3)|+\frac{1}{3}\sqrt{\frac{190}{903}}|E_{37}({\xi }_3)|+\hfill \\ & & \frac{1}{14}\sqrt{\frac{67}{15}}|E_{38}({\xi }_3)|+\frac{1}{2}\sqrt{\frac{131}{2170}}|E_{39}({\xi }_3)|+\frac{1}{2}\sqrt{\frac{89}{1505}}|E_{40}({\xi }_3)+\frac{1}{70}\sqrt{\frac{283}{559}}|E_{41}({\xi }_3)+\hfill \\ & & \frac{1}{70}\sqrt{\frac{139}{2}}|E_{42}({\xi }_3)|+\frac{1}{2}\sqrt{\frac{7}{130}}|E_{43}({\xi }_3)|+\frac{1}{78}\sqrt{\frac{155}{2}}|E_{44}({\xi }_3)|.\hfill \end{array}$$

After some calculation, we have

$$\begin{array}{ccc}\hfill ⟹AB{C}_4({\xi }_3)& =& 22.459+8\sqrt{\frac{26}{55}}(-4+m)+4\sqrt{\frac{58}{105}}(-4+m)+\frac{4}{7}\sqrt{\frac{67}{15}}(-4+m)+3\sqrt{\frac{6}{13}}\hfill \\ & & {(-4+m)}^2+2\sqrt{\frac{26}{33}}(-3+m)+\frac{3}{11}\sqrt{\frac{43}{2}}{(-3+m)}^2+\sqrt{\frac{14}{65}}(-9+2m)+\frac{1}{35}\sqrt{\frac{139}{2}}\hfill \\ & & (-9+2m)+\frac{1}{3}\sqrt{\frac{62}{7}}(-5+2m)+\frac{4}{63}\sqrt{31}(-5+2m)+\frac{4}{9}\sqrt{\frac{97}{7}}(-3+2m)+\frac{2}{21}\sqrt{89}\hfill \\ & & (-3+2m)+\frac{1}{9}\sqrt{\frac{35}{2}}(-11+4m)+\frac{1}{78}\sqrt{\frac{155}{2}}(65-28m+3m^2).\hfill \end{array}$$

The $G{A}_5({\xi }_3)$ index can be calculated from (8) as follows.

$$\begin{array}{c}\hfill G{A}_5({\xi }_3)=\sum _{\acute{m}\acute{n}\in \mathrm{E}({\xi }_3)}\frac{2\sqrt{S_{\acute{m}}{S}_{\acute{n}}}}{(S_{\acute{m}}+S_{\acute{n}})}=\sum _{\acute{m}\acute{n}\in E_j({\xi }_3)}\sum _{j=10}^{44}\frac{2\sqrt{S_{\acute{m}}{S}_{\acute{n}}}}{(S_{\acute{m}}+S_{\acute{n}})}\end{array}$$

$$\begin{array}{ccc}\hfill G{A}_5({\xi }_3)& =& 1|E_{10}({\xi }_3)|+\frac{2}{25}\sqrt{154}|E_{11}({\xi }_3)|+\frac{6}{85}\sqrt{154}|E_{12}({\xi }_3)|+\frac{5}{29}\sqrt{33}|E_{13}({\xi }_3)|+\hfill \\ & & \frac{60}{61}|E_{14}({\xi }_3)|+\frac{30}{79}\sqrt{6}|E_{15}({\xi }_3)|+\frac{15}{44}\sqrt{7}|E_{16}({\xi }_3)|+\frac{3}{8}\sqrt{7}|E_{17}({\xi }_3)|+\frac{12}{13}|E_{18}({\xi }_3)|+\hfill \\ & & \frac{4}{23}\sqrt{33}|E_{19}({\xi }_3)|+\frac{6}{29}\sqrt{22}|E_{20}({\xi }_3)|+\frac{1}{27}\sqrt{473}|E_{21}({\xi }_3)|+1|E_{22}({\xi }_3)|+\hfill \\ & & \frac{3}{10}\sqrt{11}|E_{23}({\xi }_3)|+\frac{4}{11}\sqrt{7}|E_{24}({\xi }_3)|+\frac{3}{20}\sqrt{31}|E_{25}({\xi }_3)|+\frac{4}{55}\sqrt{129}|E_{26}({\xi }_3)|+\hfill \\ & & \frac{3}{22}\sqrt{35}|E_{27}({\xi }_3)|+|E_{28}({\xi }_3)|+\frac{1}{21}\sqrt{341}|E_{29}({\xi }_3)|+\frac{4}{173}\sqrt{1419}|E_{30}({\xi }_3)|+\hfill \\ & & \frac{1}{23}\sqrt{385}|E_{31}({\xi }_3)|+\frac{1}{25}\sqrt{429}|E_{32}({\xi }_3)|+\frac{2}{13}\sqrt{42}|E_{33}({\xi }_3)|+\frac{6}{61}\sqrt{86}|E_{34}({\xi }_3)|+\hfill \\ & & 1|E_{35}({\xi }_3)|+\frac{12}{187}\sqrt{217}|E_{36}({\xi }_3)|+\frac{1}{32}\sqrt{903}|E_{37}({\xi }_3)|+\frac{12}{29}\sqrt{5}|E_{38}({\xi }_3)|+\hfill \\ & & \frac{1}{33}\sqrt{1085}|E_{39}({\xi }_3)|+\frac{4}{269}\sqrt{4515}|E_{40}({\xi }_3)|+\frac{4}{95}\sqrt{559}|E_{41}({\xi }_3)|+1|E_{42}({\xi }_3)|+\hfill \\ & & \frac{1}{37}\sqrt{1365}|E_{43}({\xi }_3)|+1|E_{44}({\xi }_3)|.\hfill \end{array}$$

After some calculations, we have

$$\begin{array}{ccc}\hfill ⟹G{A}_5({\xi }_3)& =& 173.339+\frac{96}{29}\sqrt{5}(-4+m)+\frac{24}{11}\sqrt{35}(-4+m)+\frac{32}{23}\sqrt{385}(-4+m)+\frac{12}{25}\sqrt{429}\hfill \\ & & {(-4+m)}^2+\frac{12}{5}\sqrt{11}(-3+m)-48m+9m^2+\frac{4}{37}\sqrt{1365}(-9+2m)+\frac{3}{2}\sqrt{7}(-5+2m)+\hfill \\ & & \frac{48}{13}(-3+2m)+\frac{32}{11}\sqrt{7}(-3+2m).\hfill \end{array}$$

 □

The graphical representations of topological indices of these networks are depicted in Figure 5 and Figure 6 for certain values of m. By varying the different values of m, the graphs are increasing. These graphs show the correctness of the results.

3. Conclusions

The study of topological descriptors are very useful to acquire the basic topologies of networks. In this paper, we find the exact results for Forgotten index, Balaban index, reclassified the Zagreb indices, ABC${}_4$ index and GA${}_5$ index of the Hex-derived networks of type 3. Due to their fascinating and challenging features, hex-derived networks have studied literature in relation to different graph-ideological parameters. However, their developmental circulatory features have been read for the foremost in this paper.

We are also very keen in designing some new networks and then study their topological indices which will be quite helpful to understand their primary priorities.