Dynamic Analysis of a Pest Management Smith Model with Impulsive State Feedback Control and Continuous Delay
Abstract
:1. Introduction
2. Dynamic Analysis of Impulsive State Feedback Control Model
2.1. Qualitative Analysis of Pest Management Model without Impulsive
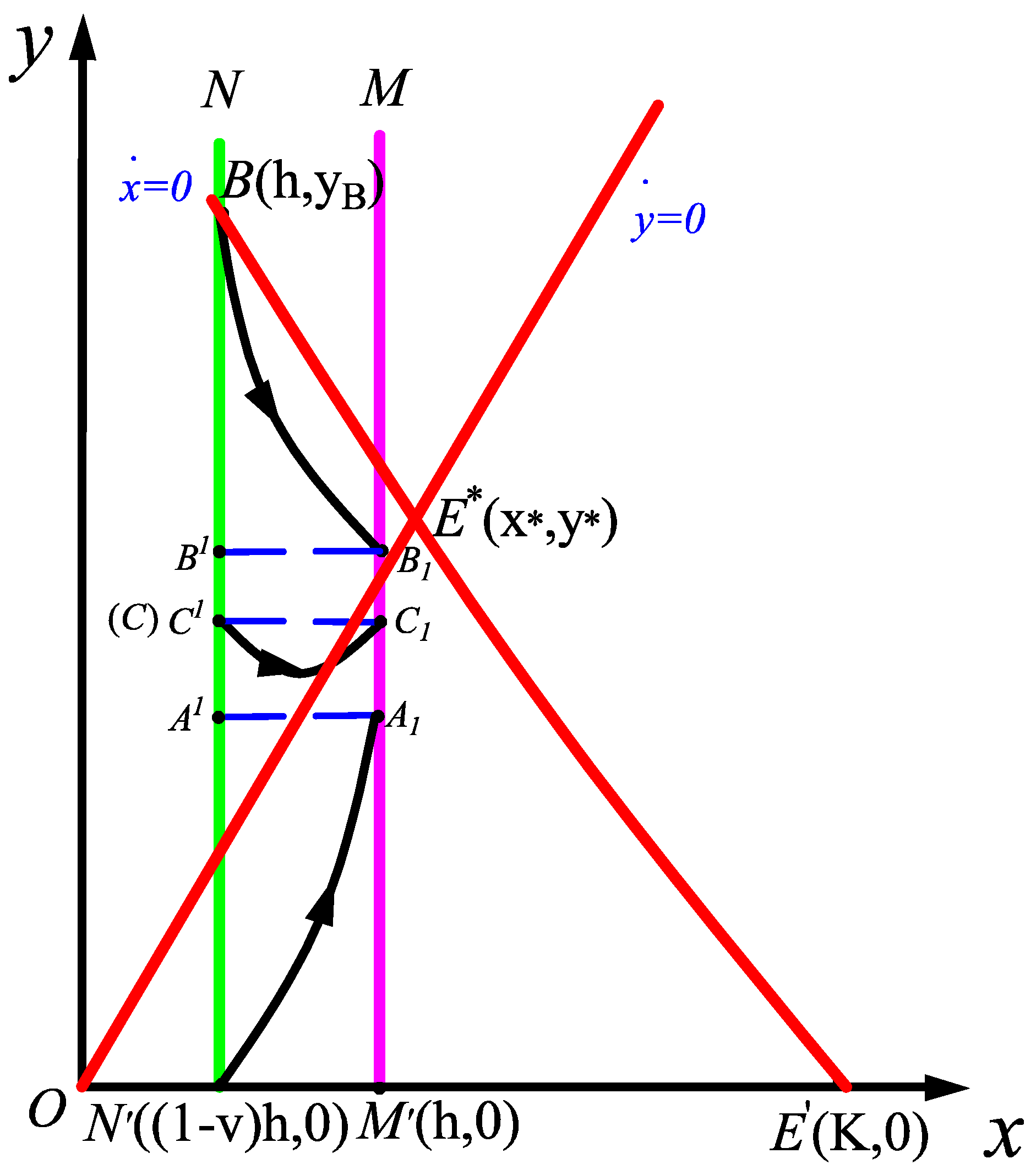
2.2. Existence and Uniqueness of the Order-One Periodic Orbit of Impulsive State Feedback Control Model
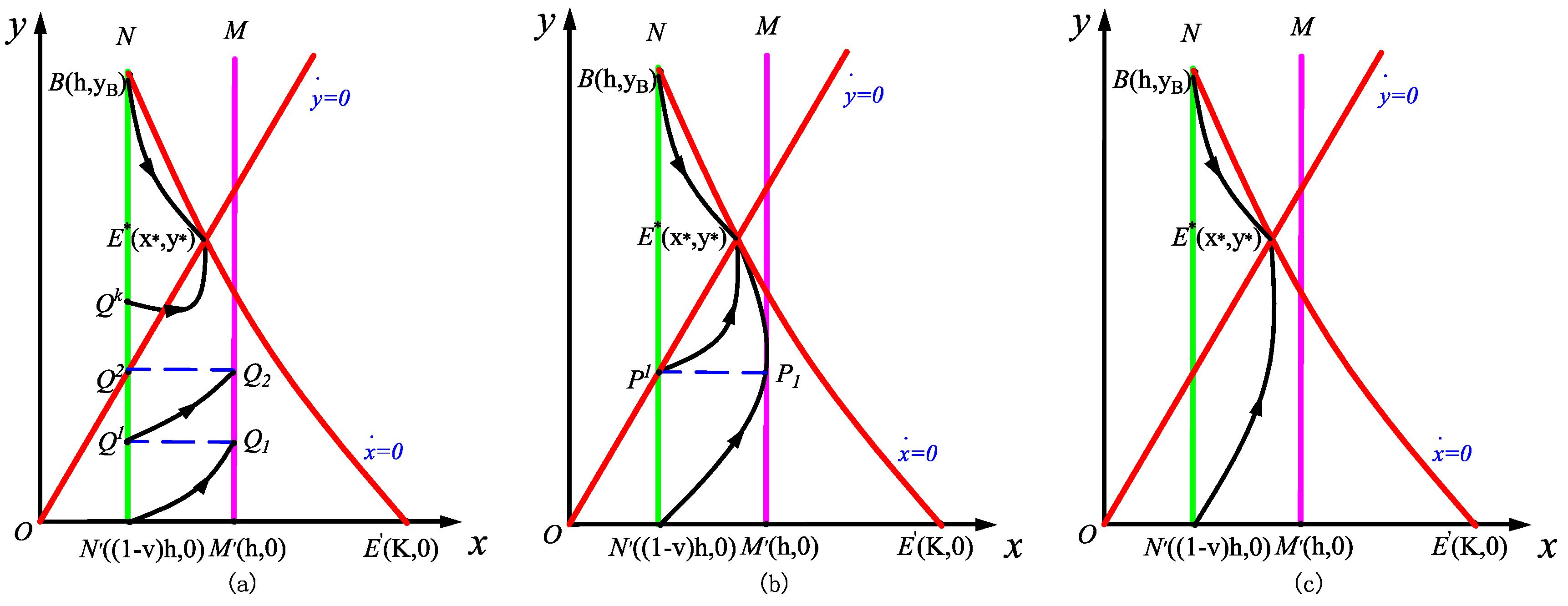
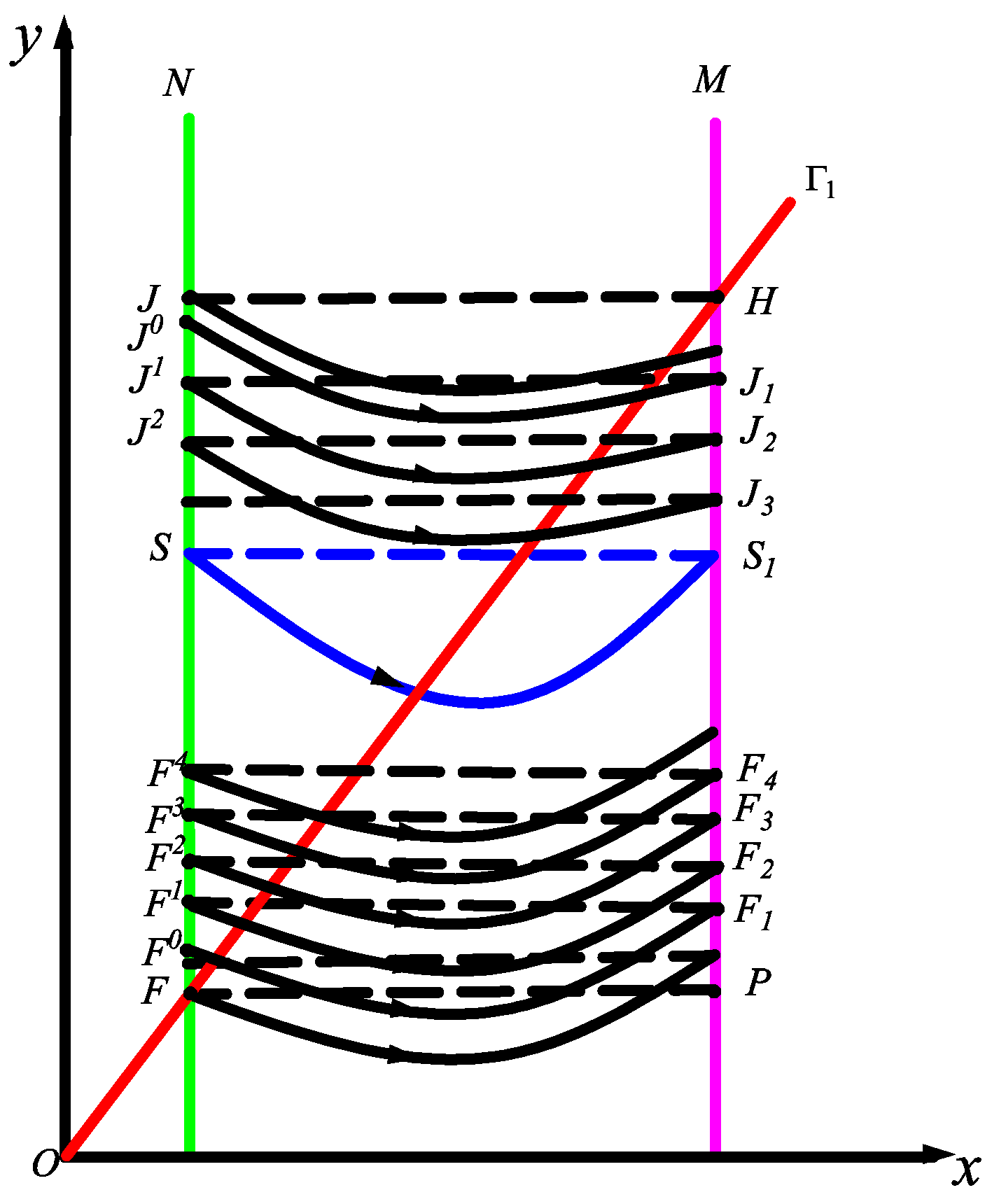
2.3. Stability of the Order-One Periodic Orbit of Impulsive State Feedback Control Model
3. Numerical Simulations and Conclusions
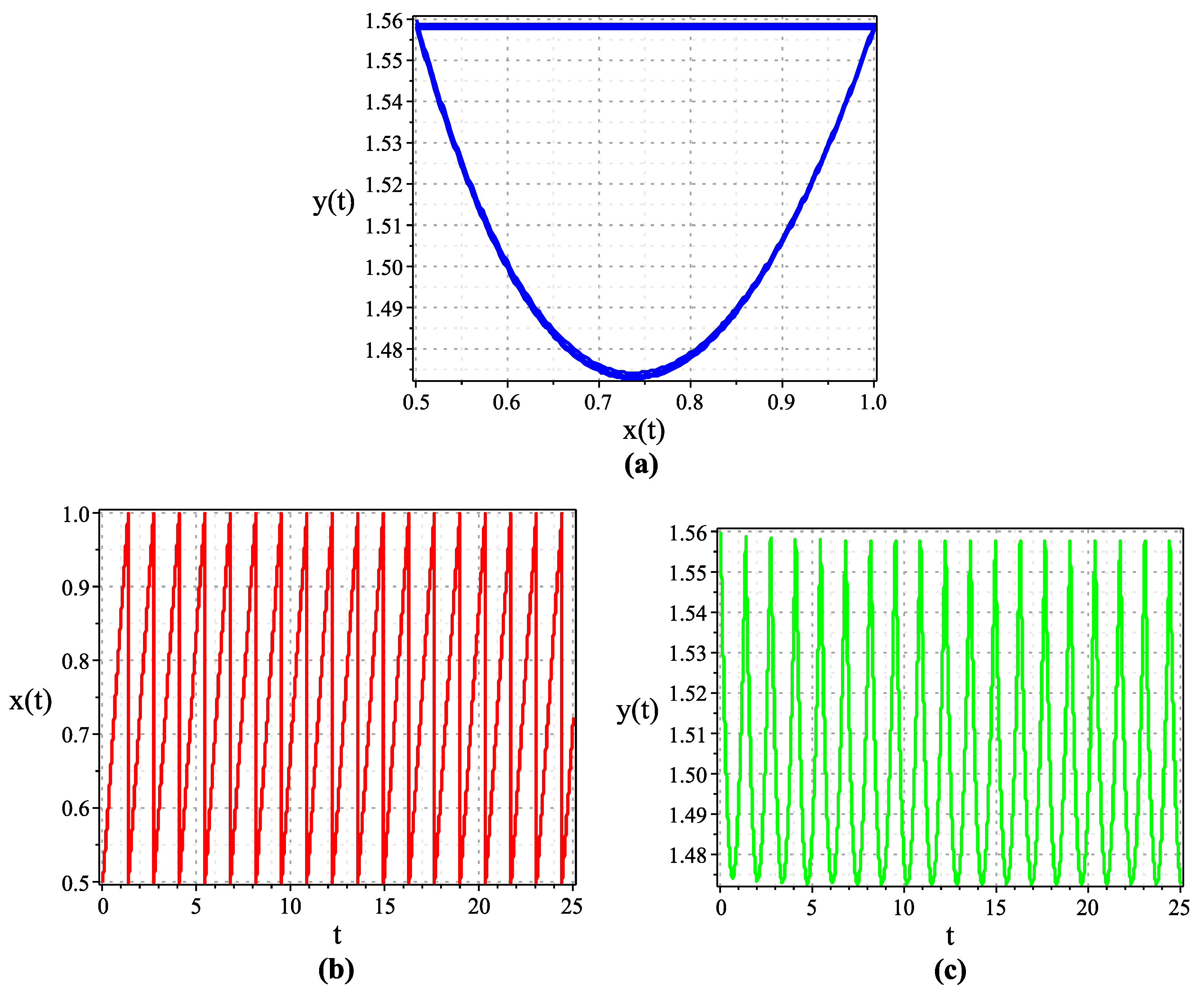
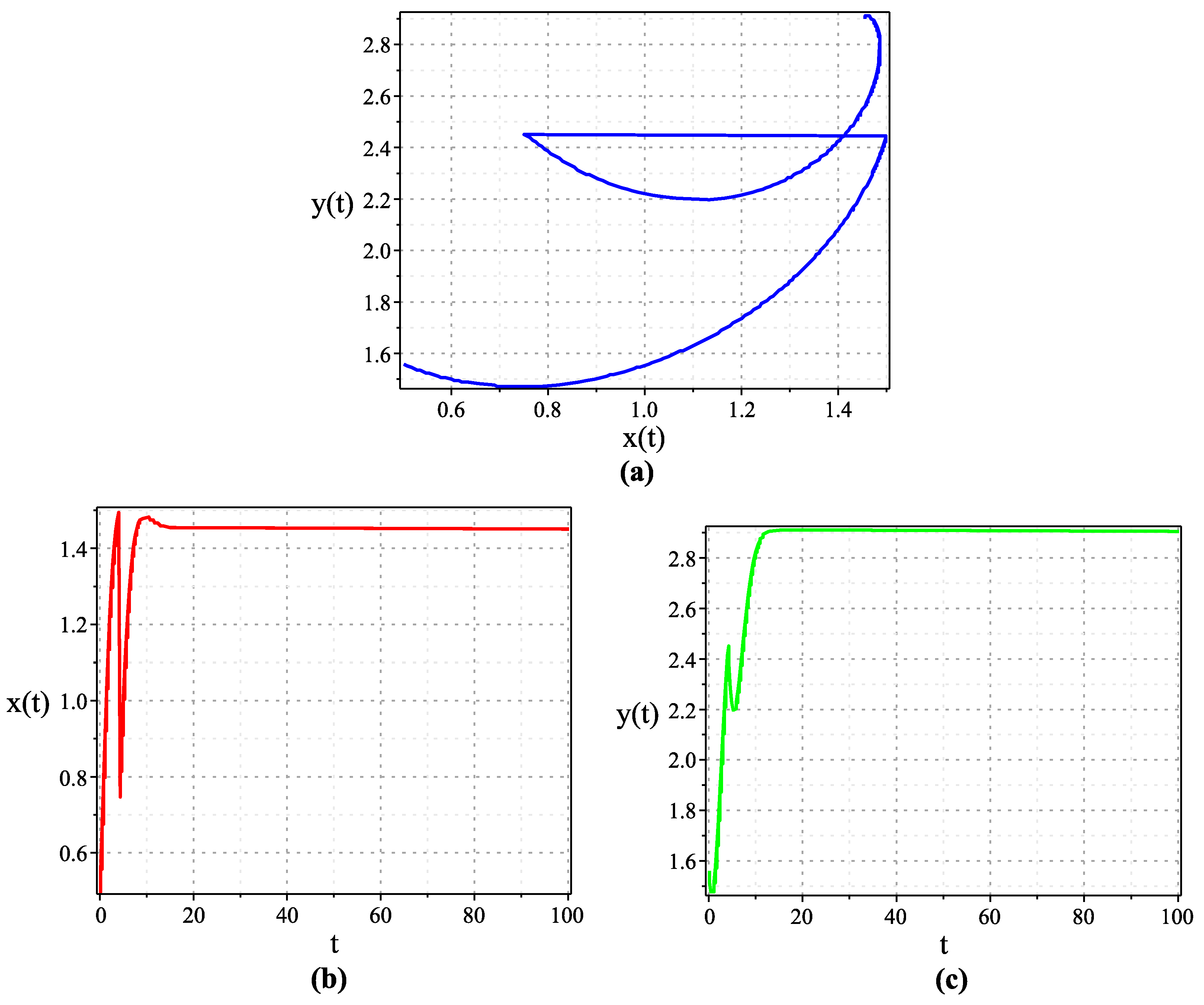
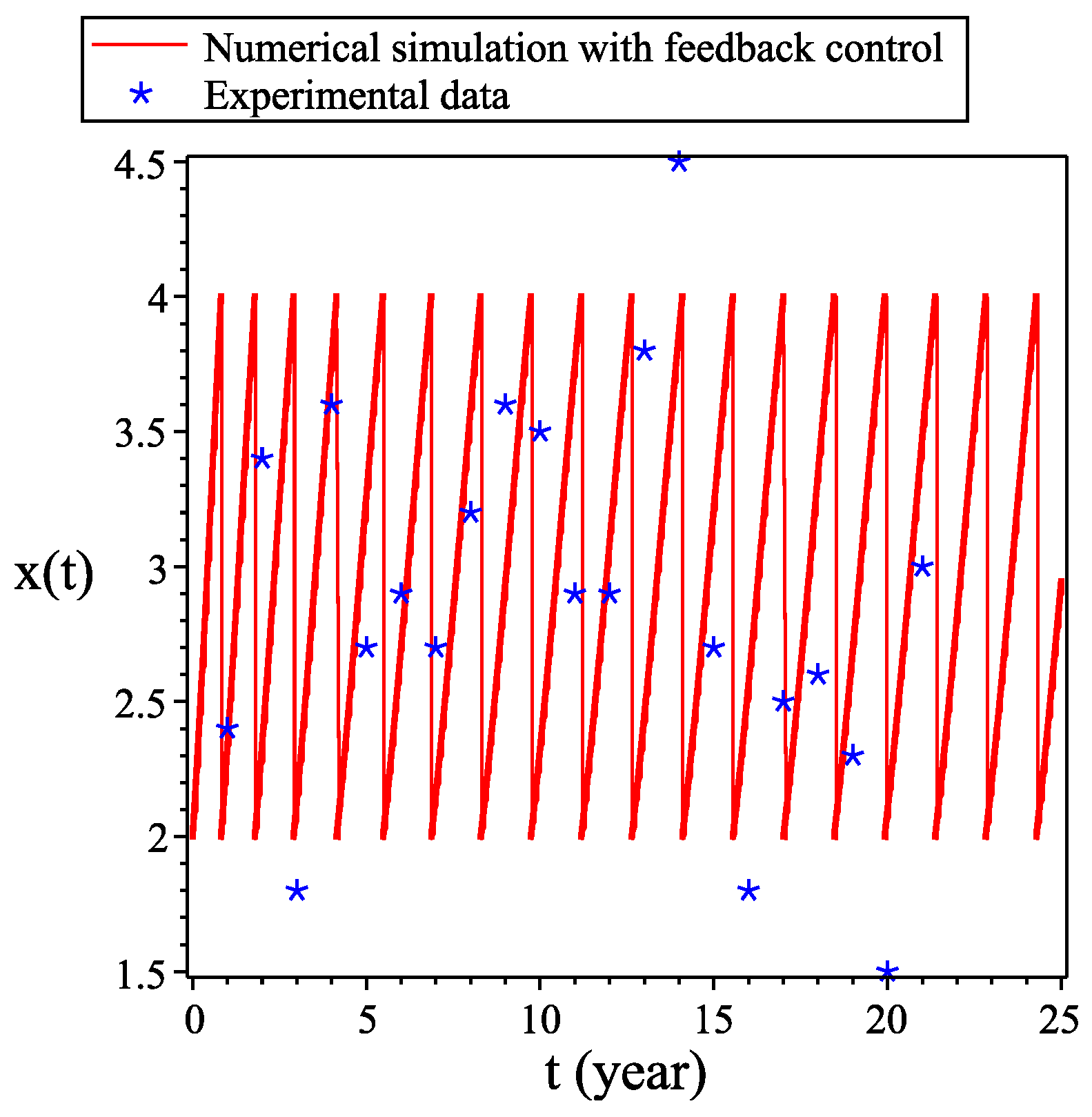
3.1. Numerical Simulations
3.2. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, T.Q.; Meng, X.Z.; Liu, R.; Zhang, T.H. Periodic solution of a pest management Gompertz model with impulsive state feedback control. Nonlinear Dyn. 2014, 78, 921–938. [Google Scholar] [CrossRef]
- Li, Y.N.; Li, Y.; Liu, Y.; Cheng, H.D. Stability Analysis and Control Optimization of a Prey-Predator Model with Linear Feedback Control. Discret. Dyn. Nat. Soc. 2018, 2018, 12. [Google Scholar] [CrossRef]
- Logan, J.A.; Régnière, J.; Powell, J.A. Assessing the impacts of global warming on forest pest dynamics. Front. Ecol. Environ. 2003, 1, 130–137. [Google Scholar] [CrossRef]
- Chen, L.S. Pest control and geometric theory of semi-continuous dynamical system. J. Beihua Univ. 2011, 12, 1–12. [Google Scholar]
- Fu, L.; Chen, Y.D.; Yang, H.W. A new predator-prey model with a profitless delay of digestion and impulsive perturbation on the prey. Appl. Math. Comput. 2011, 217, 9198–9208. [Google Scholar]
- Liu, Q.; Huang, L.Z.; Chen, L.S. A pest management model with state feedback control. Adv. Differ. Equ. 2016, 2016, 292. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.N.; Cheng, H.D.; Wang, J.M.; Wang, Y.H. Dynamic analysis of unilateral diffusion Gompertz model with impulsive control strategy. Adv. Differ. Equ. 2018, 2018, 32. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.M.; Cheng, H.D.; Li, Y.; Zhang, X.N. The geometrical analysis of a predator-prey model with multi-state dependent impulsive. J. Appl. Anal. Comput. 2018, 8, 427–442. [Google Scholar]
- Wang, J.M.; Cheng, H.D.; Liu, H.X.; Wang, Y.H. Periodic solution and control optimization of a prey-predator model with two types of harvesting. Adv. Differ. Equ. 2018, 2018, 41. [Google Scholar] [CrossRef]
- Zhao, W.C.; Li, J.; Zhang, T.Q.; Meng, X.Z.; Zhang, T.H. Persistence and ergodicity of plant disease model with markov conversion and impulsive toxicant input. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 70–84. [Google Scholar] [CrossRef]
- Liu, F. Continuity and approximate differentiability of multisublinear fractional maximal functions. Math. Inequal. Appl. 2018, 21, 25–40. [Google Scholar] [CrossRef]
- Zhang, M.; Song, G.H.; Chen, L.S. A state feedback impulse model for computer worm control. Nonlinear Dyn. 2016, 85, 1561–1569. [Google Scholar] [CrossRef]
- Pang, G.P.; Chen, L.S. Periodic solution of the system with impulsive state feedback control. Nonlinear Dyn. 2014, 78, 743–753. [Google Scholar] [CrossRef]
- Zeng, G.Z.; Chen, L.S.; Chen, J.F. Persistence and periodic orbits for two-species nonautonomous diffusion lotka-volterra models. Math. Comput. Model. 1994, 20, 69–80. [Google Scholar] [CrossRef]
- Tang, S.Y.; Chen, L.S. Global attractivity in a food-limited population model with impulsive effects. J. Math. Anal. Appl. 2004, 292, 211–221. [Google Scholar] [CrossRef]
- Meng, X.Z.; Chen, L.S. A stage-structured SI eco-epidemiological model with time delay and impulsive controlling. J. Syst. Sci. Complex. 2008, 21, 427–440. [Google Scholar] [CrossRef]
- Shi, Z.Z.; Wang, J.M.; Li, Q.J.; Cheng, H.D. Control optimization and homoclinic bifurcation of a prey-predator model with ratio-dependent. Adv. Differ. Equ. 2019, 2, 1–14. [Google Scholar] [CrossRef]
- Guo, H.J.; Chen, L.S.; Song, X.Y. Dynamical properties of a kind of SIR model with constant vaccination rate and impulsive state feedback control. Int. J. Biomath. 2017, 10, 21. [Google Scholar] [CrossRef]
- Zhou, A.R.; Pairote, S.; Jiao, J.J. Dynamics of an SIR epidemic model with stage structure and pulse vaccination. Adv. Differ. Equ. 2016, 2016, 140. [Google Scholar] [CrossRef]
- Gu, J.Y.; Zhang, Y.; Dong, H.H. Dynamic behaviors of interaction solutions of (3+1)-dimensional Shallow Water wave equation. Comput. Math. Appl. 2018, 76, 1408–1419. [Google Scholar] [CrossRef]
- Liu, T.S.; Dong, H.H. The Prolongation Structure of the Modified Nonlinear Schrödinger Equation and Its Initial-Boundary Value Problem on the Half Line via the Riemann-Hilbert Approach. Mathematics 2019, 7, 170. [Google Scholar] [CrossRef]
- Chang, Z.B.; Meng, X.Z.; Lu, X. Analysis of a novel stochastic SIRS epidemic model with two different saturated incidence rates. Phys. A Stat. Mech. Appl. 2017, 472, 103–116. [Google Scholar] [CrossRef]
- Meng, X.Z.; Wang, L.; Zhang, T.H. Global dynamics analysis of a nonlinear impulsive stochastic chemostat system in a polluted environment. J. Appl. Anal. Comput. 2016, 6, 865–875. [Google Scholar]
- Zhang, T.H.; Zhang, T.Q.; Meng, X.Z. Stability analysis of a chemostat model with maintenance energy. Appl. Math. Lett. 2017, 68, 1–7. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, X.Y.; Li, Y. Adaptive finite time control of nonlinear systems under time-varying actuator failures. IEEE Trans. Syst. Man Cybern. Syst. 2018. [Google Scholar] [CrossRef]
- Zhang, T.Q.; Ma, W.B.; Meng, X.Z. Global dynamics of a delayed chemostat model with harvest by impulsive flocculant input. Adv. Differ. Equ. 2017, 2017, 115. [Google Scholar] [CrossRef]
- Meng, X.Z.; Li, Z.Q.; Nieto, J.J. Dynamic analysis of michaelis-menten chemosta-type competition models with time delay and pulse in a polluted environment. J. Math. Chem. 2010, 47, 123–144. [Google Scholar] [CrossRef]
- Ballinger, G.; Liu, X. Permanence of population growth models with impulsive effects. Math. Comput. Model. 1997, 26, 59–72. [Google Scholar] [CrossRef]
- Zhang, H.; Jiao, J.J.; Chen, L.S. A Pest management through continuous and impulsive control strategies. Biosystems 2007, 90, 350–361. [Google Scholar] [CrossRef]
- Li, Y.N.; Cheng, H.D.; Wang, Y.H. A Lycaon pictus impulsive state feedback control model with Allee effect and continuous time delayi equations: The wronskian technique. Adv. Differ. Equ. 2018, 2018, 367. [Google Scholar] [CrossRef]
- Zhang, L.J.; Wang, Y.; Khalique, C.M.; Bai, Y.Z. Peakon and cuspon solutions of a generalized Camassa-Holm-Novikov equation. J. Appl. Anal. Comput. 2018, 8, 1938–1958. [Google Scholar]
- Jiao, J.J.; Yang, X.S.; Cai, S.H.; Chen, L.S. Dynamical analysis of a delayed predator-prey model with impulsive diffusion between two patches. Math. Comput. Simul. 2009, 80, 522–532. [Google Scholar] [CrossRef]
- Wang, J.M.; Cheng, H.D.; Meng, X.Z.; Aruna, P.B. Geometrical analysis and control optimization of a predator-prey model with multi state-dependent impulse. Adv. Differ. Equ. 2017, 2017, 252. [Google Scholar] [CrossRef] [Green Version]
- Jiang, G.R.; Lu, Q.S. Impulsive state feedback control of a predator-prey model. J. Comput. Appl. Math. 2007, 200, 193–207. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, T.H.; Sun, K.B. Dynamics analysis of a pest management prey-predator model by means of interval state monitoring and control. Nonlinear Anal. Hybrid Syst. 2017, 23, 122–141. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, T.H.; Meng, X.Z.; Zhang, T.Q. Turing-hopf bifurcations in a predator-prey model with herd behavior, quadratic mortality and prey-taxis. Phys. A Stat. Mech. Appl. 2018, 496, 446–460. [Google Scholar] [CrossRef]
- Liu, F.; Xue, Q.Y.; Yabuta, K. Rough maximal singular integral and maximal operators supported by subvarieties on Triebel-Lizorkin spaces. Nonlinear Anal. 2018, 171, 41–72. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Sun, Y.M.; Lin, C. Finite time control of switched stochastic nonlinear systems. Fuzzy Sets Syst. 2019, 365, 140–152. [Google Scholar] [CrossRef]
- Jiang, Z.C.; Wang, L. Global hopf bifurcation for a predator-prey system with three delays. Int. J. Bifur. Chaos 2017, 27, 1750108. [Google Scholar] [CrossRef]
- Terry, A.J. Biocontrol in an impulsive predator-prey model. Math. Biosci. 2014, 256, 102–115. [Google Scholar] [CrossRef]
- Ghosh, B.; Grognard, F.; Mailleret, L. Natural enemies deployment in patchy environments for augmentative biological control. Appl. Math. Comput. 2015, 266, 982–999. [Google Scholar] [CrossRef]
- Liu, G.D.; Wang, X.H.; Meng, X.Z. Extinction and persistence in mean of a novel delay impulsive stochastic infected predator-prey system with jumps. Complexity 2017, 2017, 115. [Google Scholar] [CrossRef]
- Wang, L.M.; Chen, L.S.; Nieto, J.J. The dynamics of an epidemic model for pest control with impulsive effect. Nonlinear Anal. Real World Appl. 2010, 11, 1374–1386. [Google Scholar] [CrossRef]
- Chi, M.N.; Zhao, W.C. Dynamical analysis of multi-nutrient and single microorganism chemostat model in a polluted environment. Adv. Differ. Equ. 2018, 2018, 120. [Google Scholar] [CrossRef]
- Song, Y.; Miao, A.Q.; Zhang, T.Q. Extinction and persistence of a stochastic SIRS epidemic model with saturated incidence rate and transfer from infectious to susceptible. Adv. Differ. Equ. 2018, 2018, 293. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Chen, L.S.; Georgescu, P. Impulsive control strategies for pest management. J. Biol. Syst. 2007, 15, 235–260. [Google Scholar] [CrossRef]
- Lv, W.S.; Wang, F. Adaptive tracking control for a class of uncertain nonlinear systems with infinite number of actuator failures using neural networks. Adv. Differ. Equ. 2017, 2017, 374. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.C.; Chen, L.S.; Zhang, Q.L. The geometrical analysis of a predator-prey model with two state impulses. Math. Biosci. 2012, 238, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.B.; Zhang, T.H.; Tian, Y. Dynamics analysis and control optimization of a pest management predator-prey model with an integrated control strategy. Appl. Math. Comput. 2017, 292, 253–271. [Google Scholar] [CrossRef]
- Chen, S.D.; Xu, W.J.; Chen, L.S.; Huang, Z.H. A white-headed langurs impulsive state feedback control model with sparse effect and continuous delay. Commun. Nonlinear Sci. Numer. Simul. 2017, 50, 88–102. [Google Scholar] [CrossRef]
- Wei, F.Y.; Wang, K. Economic Harvesting Model with Variabe Price and Cost for Population with Smith Growth and Cui Lawson Growth. J. Biomath. 2004, 19, 328–336. [Google Scholar]
- Smith, F.K. Population dynamics in daphnia magna and a new model for population growth. Ecology 1963, 44, 651–663. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Li, Y.; Cheng, H. Dynamic Analysis of a Pest Management Smith Model with Impulsive State Feedback Control and Continuous Delay. Mathematics 2019, 7, 591. https://doi.org/10.3390/math7070591
Shi Z, Li Y, Cheng H. Dynamic Analysis of a Pest Management Smith Model with Impulsive State Feedback Control and Continuous Delay. Mathematics. 2019; 7(7):591. https://doi.org/10.3390/math7070591
Chicago/Turabian StyleShi, Zhenzhen, Yaning Li, and Huidong Cheng. 2019. "Dynamic Analysis of a Pest Management Smith Model with Impulsive State Feedback Control and Continuous Delay" Mathematics 7, no. 7: 591. https://doi.org/10.3390/math7070591
APA StyleShi, Z., Li, Y., & Cheng, H. (2019). Dynamic Analysis of a Pest Management Smith Model with Impulsive State Feedback Control and Continuous Delay. Mathematics, 7(7), 591. https://doi.org/10.3390/math7070591



