Global Stability of a Markovian Jumping Chaotic Financial System with Partially Unknown Transition Rates under Impulsive Control Involved in the Positive Interest Rate
Abstract
:1. Introduction and Preparation
- ★
- Deriving the globally exponential stability criterion for the null solution of the impulsive system (6);
- ★
- Deducing the globally exponential stability criterion for the null solution of the impulsive system (10).
2. Globally Exponential Stability of with the Positive Interest Rate for the Reaction-Diffusion Model
3. Impulse Control on the Financial System without Time-Delays
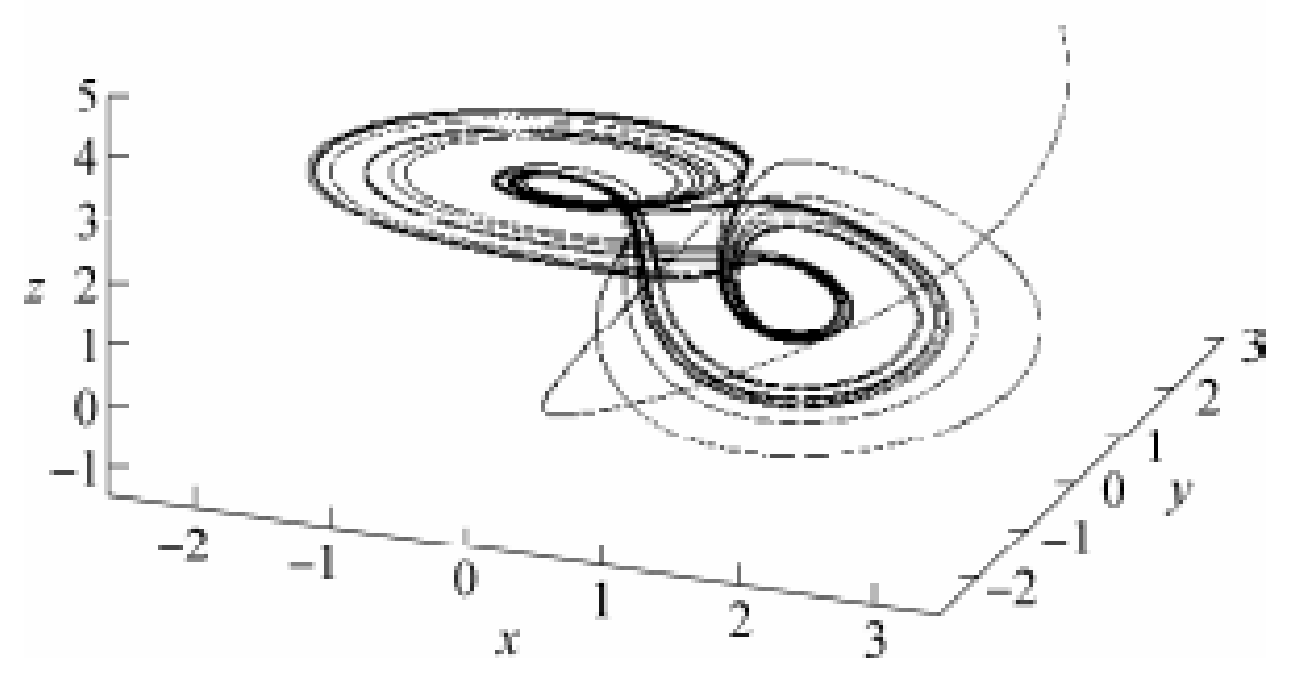
4. Numerical Example
5. Conclusions and Further Considerations
Funding
Conflicts of Interest
References
- Cheng, S. Complicated Science and Management. Article Collection of Beijing Xiangshan Conference; Science Press: Beijing, China, 1998; pp. 1–9. (In Chinese) [Google Scholar]
- Huang, D.; Li, H. Theory and Method of Nonlinear Economics; Sichuan University Press: Chengdu, China, 1993. [Google Scholar]
- Ma, J.; Chen, Y. Study for the bifurcation topological structure and the global complicated character of a kind of nonlinear finance system (I). Appl. Math. Mech. 2001, 11, 1240–1251. [Google Scholar] [CrossRef]
- Ma, J.; Chen, Y. Study for the bifurcation topological structure and the global complicated character of a kind of nonlinear finance system (II). Appl. Math. Mech. 2001, 12, 1375–1382. [Google Scholar] [CrossRef]
- Chen, W. Dynamics and control of a financial system with time-delayed feedbacks. Chaos Solitons Fractals 2008, 37, 1198–1207. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, J. H∞ control of a chaotic finance system in the presence of external disturbance and input time-delay. Appl. Math. Comput. 2014, 233, 320–327. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Z.; Li, S. Synchronization of a chaotic finance system. Appl. Math. Comput. 2011, 217, 6031–6039. [Google Scholar] [CrossRef]
- Chen, Y. Chaos control for a class of nonlinear finance systems model. Math. Pract. Theory 2019, 49, 18–26. (In Chinese) [Google Scholar]
- Wang, Y. Impulsive Control of a Chaotic Financial System. In Proceedings of the 4th International Conference on Machinery, Materials and Computer (MACMC 2017), Xi’an, China, 27–29 November 2017; Volume 150, pp. 548–552. [Google Scholar]
- Li, X.; Yang, X.; Huang, T. Persistence of delayed cooperative models: Impulsive control method. Appl. Math. Comput. 2019, 342, 130–146. [Google Scholar] [CrossRef]
- Zhang, R. Bifurcation Analysis for a Kind of Nonlinear Finance System with Delayed Feedback and Its Application to Control of Chaos. J. Appl. Math. 2012. [Google Scholar] [CrossRef]
- Yi, A.; Zi, A.; Rao, R.; Zhao, F.; Huang, H. Impulse Control of Financial System with Probabilistic Delay Feedback. Appl. Math. Mech. 2019. (In Chinese) [Google Scholar] [CrossRef]
- Luo, M.; Liu, X.; Zhong, S. Synchronization of stochastic complex networks with discrete-time and distributed coupling delayed via hybrid nonlinear and impulsive control. Chaos Solitons Fractals 2018, 114, 381–393. [Google Scholar] [CrossRef]
- Rao, R.; Zhong, S.; Wang, X. Stochastic stability criteria with LMI conditions for Markovian jumping impulsive BAM neural networks with mode-dependent time-varying delays and nonlinear reaction-diffusion. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 258–273. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Zheng, W.; Wang, Q. Instability and Unboundedness Analysis for Impulsive Differential Systems with Applications to Lurie Control Systems. Int. J. Control Autom. Syst. 2018, 16, 1521–1531. [Google Scholar] [CrossRef]
- Yang, H.; Wang, X.; Zhong, S. Synchronization of nonlinear complex dynamical systems via delayed impulsive distributed control. Appl. Math. Comput. 2018, 320, 75–85. [Google Scholar] [CrossRef]
- Wang, X.; She, K.; Zhong, S. Pinning cluster synchronization of delayed complex dynamical networks with nonidentical nodes and impulsive effects. Nonlinear Dyn. 2017, 8, 2771–2782. [Google Scholar] [CrossRef]
- Li, X.; Shen, J.; Rakkiyappan, R. Persistent impulsive effects on stability of functional differential equations with finite or infinite delay. Appl. Math. Comput. 2018, 329, 14–22. [Google Scholar] [CrossRef]
- Li, X.; Li, P.; Wang, Q. Input/output-to-state stability of impulsive switched systems. Syst. Control Lett. 2018, 116, 1–7. [Google Scholar] [CrossRef]
- Li, X.; Shen, J.; Akca, H. Comparison principle for impulsive functional differential equations with infinite delays and applications. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 309–321. [Google Scholar] [CrossRef]
- Song, Q.; Cao, J. Dynamics of bidirectional associative memory networks with distributed delays and reaction-diffusion terms. Nonlinear Anal. Real World Appl. 2007, 8, 345–361. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, X.; Yang, X. Exponential stability for stochastic reaction-diffusion BAM neural networks with time-varying and distributed delays. Appl. Math. Comput. 2011, 217, 6078–6091. [Google Scholar] [CrossRef]
- Zeng, D.; Pu, Z.; Zhang, R.; Zhong, S.; Liu, Y.; Wu, G. Stochastic reliable synchronization for coupled Markovian reaction-diffusion neural networks with actuator failures and generalized switching policies. Appl. Math. Comput. 2019, 357, 88–106. [Google Scholar] [CrossRef]
- Song, Q.; Cao, J.; Zhao, Z. Periodic solutions and its exponential stability of reaction-diffusion recurrent neural networks with continuously distributed delays. Nonlinear Anal. Real World Appl. 2006, 7, 65–80. [Google Scholar] [CrossRef]
- Rao, R.; Zhong, S.; Pu, Z. Fixed point and p-stability of T-S fuzzy impulsive reaction-diffusion dynamic neural networks with distributed delay via Laplacian semigroup. Neurocomputing 2019, 335, 170–184. [Google Scholar] [CrossRef]
- Hodara, P.; Papageorgiou, I. Poincare-Type Inequalities for Compact Degenerate Pure Jump Markov Processes. Mathematics 2019, 7, 518. [Google Scholar] [CrossRef]
- Zhang, R.; Zeng, D.; Park, J.; Zhong, S. A New Approach to Stochastic Stability of Markovian Neural Networks With Generalized Transition Rates. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 499–510. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Rakkiyappan, R.; Sakthivel, N. Non-Fragile Synchronization Control For Markovian Jumping Complex Dynamical Networks With Probabilistic Time-Varying Coupling Delays. Asian J. Control 2015, 17, 1678–1695. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, X.; Zeng, D.; Zhong, S.M.; Shi, K.B. A novel approach to stability and stabilization of fuzzy sampled-data Markovian chaotic systems. Fuzzy Sets Syst. 2018, 344, 108–128. [Google Scholar] [CrossRef]
- Ding, Y.; Zhong, S.; Long, S. Asymptotic stability in probability of singular stochastic systems with Markovian switchings. Int. J. Robust Nonlinear Control 2017, 27, 4312–4322. [Google Scholar] [CrossRef]
- Li, X.; Rakkiyappan, R. Delay-dependent global asymptotic stability criteria for stochastic genetic regulatory networks with Markovian jumping parameters. Appl. Math. Model. 2012, 36, 1718–1730. [Google Scholar] [CrossRef]
- Rao, R. Delay-Dependent exponential stability for nonlinear reaction-diffusion uncertain Cohen-Grossberg neural networks with partially known transition rates via Hardy-Poincare inequality. Chin. Ann. Math. Ser. B 2014, 35, 575–598. [Google Scholar] [CrossRef]
- Rao, R.; Zhong, S.; Pu, Z. On the role of diffusion factors in stability analysis for p-Laplace dynamical equations involved to BAM Cohen-Grossberg neural network. Neurocomputing 2017, 223, 54–62. [Google Scholar] [CrossRef]
- Pu, Z.; Rao, R. Delay-dependent LMI-based robust stability criterion for discrete and distributed time-delays Markovian jumping reaction-diffusion CGNNs under Neumann boundary value. Neurocomputing 2016, 171, 1367–1374. [Google Scholar] [CrossRef]
- Temam, R. Infinite Dimensional Dynamical Systems in Mechanics and Physics; Springer: NewYork, NY, USA; Berlin, Germany, 1998. [Google Scholar]
- Rao, R.; Hang, J.; Zhong, S. Global Exponential Stability of Reaction-Diffusion BAM Neural Networks. J. Jilin Univ. (Sci. Ed.) 2012, 50, 1086–1090. (In Chinese) [Google Scholar]

| System (1) | System (10) | Positive or Negative | |
|---|---|---|---|
| 0.0050 | 0.0050 | ||
| −3.8500 | −3.8500 | ||
| system state | chaos | global stability | |
| interest rate of | 8.93% | 8.93% |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, R. Global Stability of a Markovian Jumping Chaotic Financial System with Partially Unknown Transition Rates under Impulsive Control Involved in the Positive Interest Rate. Mathematics 2019, 7, 579. https://doi.org/10.3390/math7070579
Rao R. Global Stability of a Markovian Jumping Chaotic Financial System with Partially Unknown Transition Rates under Impulsive Control Involved in the Positive Interest Rate. Mathematics. 2019; 7(7):579. https://doi.org/10.3390/math7070579
Chicago/Turabian StyleRao, Ruofeng. 2019. "Global Stability of a Markovian Jumping Chaotic Financial System with Partially Unknown Transition Rates under Impulsive Control Involved in the Positive Interest Rate" Mathematics 7, no. 7: 579. https://doi.org/10.3390/math7070579




