Some Properties and Generating Functions of Generalized Harmonic Numbers
Abstract
:1. Introduction
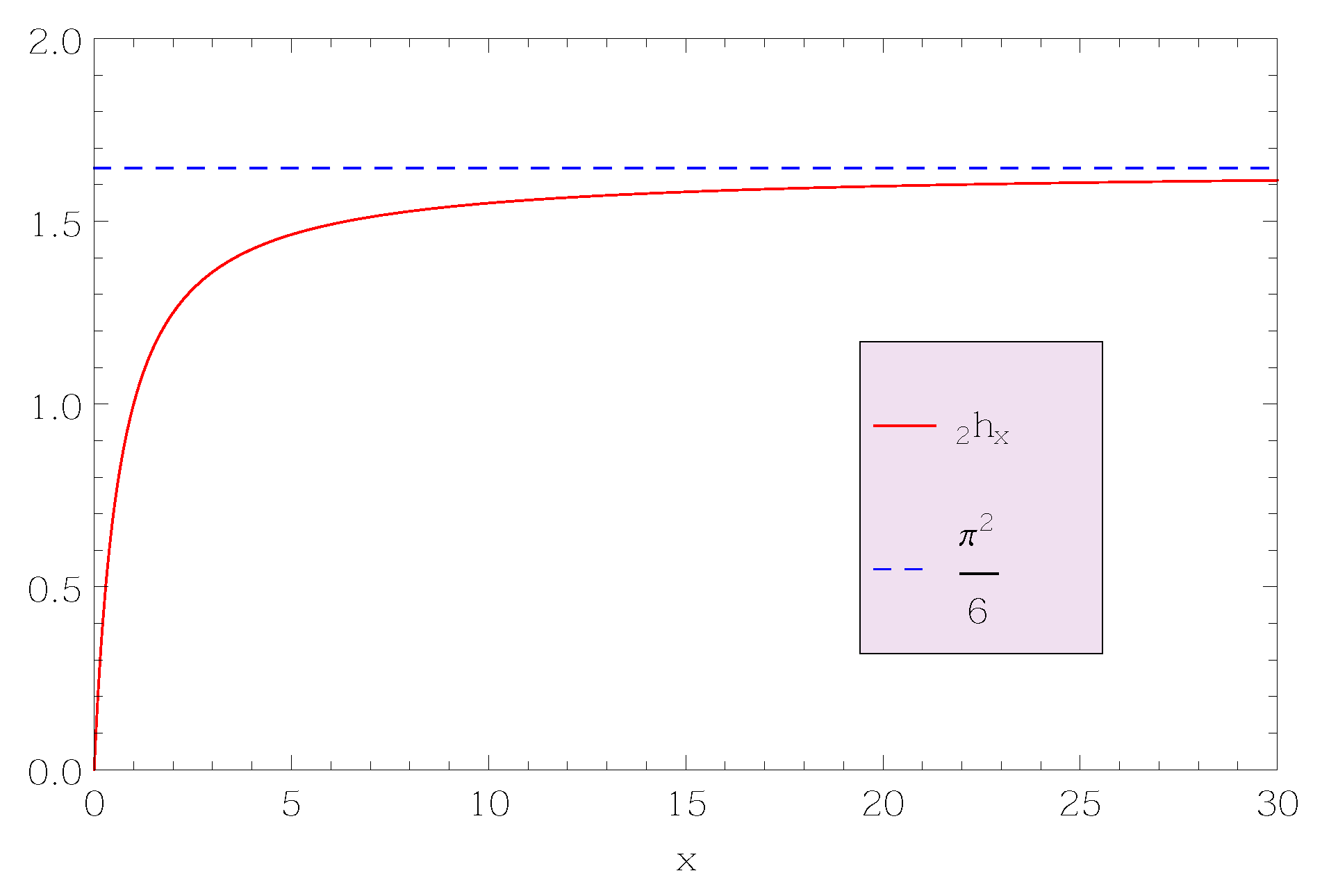
2. Harmonic Numbers and Integral Transforms
3. Final Comments
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roman, S. The Umbral Calculus; Academic Press: New York, NY, USA, 1984; pp. 93–100. [Google Scholar]
- Dattoli, G.; Cesarano, C.; Lorenzutta, S. Bernoulli numbers and polynomials from a more general point of view. Rendiconti Matematica 2002, 22, 193–202. [Google Scholar]
- Dattoli, G.; Migliorati, M. Operational Methods, Harmonic Numbers and Riemann Function; Internal Report Enea Frascati (Rome) RT/2008/29/FIM; Edizioni Scientifiche—ENEA Centro Ricerche Frascati: Rome, Italy, 2008. [Google Scholar]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1994. [Google Scholar]
- Dattoli, G.; Srivastava, H.M. A Note on Harmonic Numbers, Umbral Calculus and Generating Functions. Appl. Math. Lett. 2008, 21, 686–693. [Google Scholar] [CrossRef]
- Dattoli, G.; Zhukovsky, K. Umbral Methods, Combinatorial Identities and Harmonic Numbers. Appl. Math. 2011, 1, 46–49. [Google Scholar]
- Dattoli, G.; Germano, B.; Licciardi, S.; Martinelli, M.R. Umbral Methods and Harmonic Numbers. Axioms 2018, 7, 62. [Google Scholar]
- Coffey, M.W. Expressions for harmonic humber exponential generating functions. In Contemporary Mathematics, Gems in Experimental Mathematics; Amdeberhan, T., Simos, E.T., Moll, V.H., Eds.; American Mathematical Society: Washington, DC, USA, 2009; Volume 517, pp. 113–126. [Google Scholar]
- Cvijović, D. The Dattoli-Srivastava Conjectures Concerning Generating Functions Involving the Harmonic Numbers. Appl. Math. Comput. 2010, 215, 4040–4043. [Google Scholar] [CrossRef]
- Licciardi, S. Umbral Calculus, a Different Mathematical Language. arXiv 2018, arXiv:1803.03108. [Google Scholar]
- Choi, J. Finite summation formulas involving binomial coefficients, harmonic numbers and generalized harmonic numbers. J. Inequal. Appl. 2013, 49, 11. [Google Scholar] [CrossRef]
- Sofo, A.; Srivastava, H.M. A family of shifted harmonic sums. Ramanujan J. 2015, 37, 89–108. [Google Scholar] [CrossRef]
- Sofo, A.; Srivastava, H.M. dentities for the harmonic numbers and binomial coefficients. Ramanujan J. 2011, 25, 93–113. [Google Scholar] [CrossRef]
- Choi, J.; Srivastava, H.M. Some summation formulas involving harmonic numbers and generalized harmonic numbers. Math. Comput. Model. 2011, 54, 2220–2234. [Google Scholar] [CrossRef]
- Mezo, I. Exponential Generating Function of Hyper-Harmonic Numbers Indexed by Arithmetic Progressions. Cent. Eur. J. Math. 2013, 11, 931–939. [Google Scholar]
- Dattoli, G.; Ricci, P.E.; Marinelli, L. Generalized Truncated Exponential Polynomials and Applications, in: Rendiconti dell’Istituto di Matematica dell’Università di Trieste. Int. J. Math. 2002, 34, 9–18. [Google Scholar]
- Dattoli, G.; Migliorati, M.; Srivastava, H.M. Sheffer polynomials, monomiality principle, algebraic methods and the theory of classical polynomials. Math. Comput. Model. 2007, 45, 1033–1041. [Google Scholar] [CrossRef]
- Dattoli, G.; Sabia, E. Generalized Transforms and Special functions. arXiv 2010, arXiv:1010.1679. [Google Scholar]
- Gosper, R.W. Harmonic summation and exponential gfs. math-fun@cs.arizona.edu posting, 2 August 1996. In Harmonic Number. MathWorld—A Wolfram Web Resource; Sondow, J., Weisstein, E.W., Eds.; 1996; Available online: http://mathworld.wolfram.com/HarmonicNumber.html (accessed on 1 May 2019).
- Schmidt, M.D. Zeta Series Generating Function Transformations Related to Polylogarithm Functions and the k-Order Harmonic Numbers. Online J. Anal. Comb. 2017, 12, 2. [Google Scholar]
- Dattoli, G.; Germano, B.; Martinelli, M.R.; Ricci, P.E. Touchard like polynomials and generalized Stirling numbers. Appl. Math. Comput. 2012, 218, 6661–6665. [Google Scholar] [CrossRef] [Green Version]
- Lang, W. On Generalizations of the Stirling Number Triangles. J. Integer. Seq. 2000, 3, 3. [Google Scholar]
- Srivastava, H.M.; Manocha, H.L. A Treatise on Generating Functions; Halsted Press (Ellis Horwood Limited, Chichester): Chichester, UK; John Wiley and Sons: New York, NY, USA, 1984. [Google Scholar]
- Comtet, L. Advanced combinatorics: The Art of Finite and Infinite Expansions; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Johnson, W.P. The Curious History of Faá di Bruno’s Formula. Am. Math. Mon. 2002, 109, 217–234. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dattoli, G.; Licciardi, S.; Sabia, E.; Srivastava, H.M. Some Properties and Generating Functions of Generalized Harmonic Numbers. Mathematics 2019, 7, 577. https://doi.org/10.3390/math7070577
Dattoli G, Licciardi S, Sabia E, Srivastava HM. Some Properties and Generating Functions of Generalized Harmonic Numbers. Mathematics. 2019; 7(7):577. https://doi.org/10.3390/math7070577
Chicago/Turabian StyleDattoli, Giuseppe, Silvia Licciardi, Elio Sabia, and Hari M. Srivastava. 2019. "Some Properties and Generating Functions of Generalized Harmonic Numbers" Mathematics 7, no. 7: 577. https://doi.org/10.3390/math7070577
APA StyleDattoli, G., Licciardi, S., Sabia, E., & Srivastava, H. M. (2019). Some Properties and Generating Functions of Generalized Harmonic Numbers. Mathematics, 7(7), 577. https://doi.org/10.3390/math7070577






