Long-Time Asymptotics of a Three-Component Coupled mKdV System

Abstract

We present an application of the nonlinear steepest descent method to a three-component coupled mKdV system associated with a $4\times 4$ matrix spectral problem. An integrable coupled mKdV hierarchy with three potentials is first generated. Based on the corresponding oscillatory Riemann-Hilbert problem, the leading asympototics of the three-component mKdV system is then evaluated by using the nonlinear steepest descent method.

1. Introduction

Asymptotic analysis has become an important area in soliton theory and its basic approaches are used to determine limiting behaviors of Cauchy problems of integrable systems. Significant work on long-time asympototics of integrable systems was carried out by Manakov [1] and Ablowitz and Newell [2]. Zakharov and Manakov [3] wrote down precise expressions, depending explicitly on initial data, for the leading asymptotics for the nonlinear Schrödinger equation in the physically interesting region $x=\mathrm{O}(t)$. A complete description was presented for the leading asymptotics of the Cauchy problem of the Korteweg-de Vries (KdV) equation by Ablowitz and Segur [4]. The method of Zakharov and Manakov starts an ansatz for the asymptotic form of the solution and utilizes some techniques which are removed from the classical framework of Riemann-Hilbert (RH) problems. Segur and Ablowitz [5] began with the similarity solution form to derive the leading two terms in each of the asymptotic expansions for the amplitude and phase for the nonlinear Schrödinger equation, based on conservation laws. However, all those results were presented, without applying the method of stationary phase.

Its [6] used the stationary phase idea to conjugate the RH problem associated with the nonlinear Schrödinger equation, up to small errors which decay as $t\to \infty$, by an appropriate parametrix to a model RH problem solvable by the technique from the theory of isomonodromic deformations. Deift and Zhou [7] determined the long-time asymptotics of the mKdV equation, by manipulating an associated oscillatory RH problem systematically and rigorously, in the spirit of the stationary phase method. Their technique, further developed in [8,9] and also in [10], opens a nonlinear steepest descent method to explore asymptotics of integrable systems through analyzing oscillatory RH problems associated with matrix spectral problems. A crucial ingredient of the Deift-Zhou approach is the asymptotic analysis of singular integrals on contours by deformations. Applications have been made for a few of integrable equations, including the KdV equation, the nonlinear Schrödinger equation, the sine-Gordon equation, the derivative nonlinear Schrödinger equation, the Camassa-Holm equation and the Kundu-Eckhaus equation (see, e.g., [11,12,13,14,15,16,17,18]). McLaughlin and Miller [19] generalized the steepest descent method to the case when the jump matrix fails to be analytic and their method is now called a nonlinear $\overline{\partial }$ steepest descent method. One important factor in the nonlinear steepest descent method is the order of involved spectral matrices in RH problems or equivalently the inverse scattering theory. However, only $2\times 2$ spectral matrices and their RH problems have been systematically considered (see, e.g., [20]), which lead to algebro-geometric solutions to integrable systems expressed by hyperelliptic functions [21]. There are very few $3\times 3$ spectral matrices, whose long-time asymptotics or RH problems are considered (see, e.g., [22,23]) and whose associated inverse scattering transforms are solved (see, e.g., [24,25]). Associated trigonal curves exhibit much more diverse asymptotic behaviors and algebro-geometric solutions than hyperelliptic curves [26,27]. There has been no application of the nonlinear steepest descent method to the 4th-order or higher-order matrix spectral problems so far.

In this paper, we would like to present an application to a $4\times 4$ matrix spectral problem

$$-i{\varphi }_x=U\varphi ,U=\left[\begin{array}{cccc}-k& p_1& p_2& p_3\\ -p_1^{*}& k& 0& 0\\ -p_2^{*}& 0& k& 0\\ -p_3^{*}& 0& 0& k\end{array}\right],$$

(1)

where i denotes the unit imaginary number, k is the spectral parameter and the superscript ∗ denotes the complex conjugate. This spectral problem generates a three-component coupled mKdV system

$$p_{j,t}=-p_{j,xxx}+3(|p_1{|}^2+|p_2{|}^2+|p_3{|}^2)p_{j,x}+3(p_1^{*}{p}_{1,x}+p_2^{*}{p}_{2,x}+p_3^{*}{p}_{3,x})p_j,1\le j\le 3,$$

(2)

where

$$|p_i{|}^2=p_i{p}_i^{*},1\le j\le 3.$$

We will compute the leading asymptotics of this mKdV system by analyzing an associated oscillatory RH problem. Symmetry constraints and RH problems have been made for an unreduced combined mKdV system in [28,29]. It is worth noting that this mKdV system (2) has a slightly different matrix spectral problem from the one for the multiple wave interaction equations [30].

Let $|M|$ denote an equivalent matrix norm for a matrix M (may not be square):

$$|M|={[\mathrm{tr}(M^{†}M)]}^{\frac{1}{2}},$$

(3)

where $M^{†}$ stands for the Hermitian transpose of M, and

$${\mathcal{S}}^3=\{(f_1,f_2,f_3)|f_i\in \mathcal{S},1\le i\le 3\},$$

where $\mathcal{S}$ denotes the Schwartz space. The primary result of the paper can be stated as follows.

Theorem 1.

Let $p(x,t)=(p_1(x,t),p_2(x,t),p_3(x,t))$ solves the Cauchy problem of the three-component coupled mKdV system (2) with initial data in ${\mathcal{S}}^3$. Suppose that $\gamma (k)=({\gamma }_1(k),{\gamma }_2(k),{\gamma }_3(k))$ is the reflection coefficient vector in ${\mathcal{S}}^3$ associated with the initial data and it satisfies

$${\gamma }^{*}(-k^{*})=\gamma (k),\underset{k\in \mathbb{R}}{sup}|\gamma (k)|<1.$$

Then, in the physically interesting region $x=\mathrm{O}(t)$, the leading asymptotics of the solution for $x<0$ is given by

$$\begin{array}{c}p(x,t)=(p_1(x,t),p_2(x,t),p_3(x,t))\hfill \\ =-i\sqrt{\frac{{\mathrm{e}}^{\pi \nu }\nu }{6t{k}_{0}sinh\pi \nu }}(|{\gamma }_1(k_0)|cos{\phi }_1,|{\gamma }_2(k_0)|cos{\phi }_2,|{\gamma }_3(k_0)|cos{\phi }_3)+\mathrm{O}(\frac{lnt}{t}),\hfill \end{array}$$

(4)

where

$$\left\{\begin{array}{c}{\displaystyle k_0=\sqrt{\frac{-x}{12t}},\nu =-\frac{1}{2\pi }ln(1-|\gamma (k_0{|}^2),}\hfill \\ {\displaystyle {\phi }_j={\phi }_0+arg{\gamma }_j(k_0),1\le j\le 3,}\hfill \\ {\displaystyle {\phi }_0=-\nu ln192t{k}_0^3-2i\chi (k_0)+16t{k}_0^3+\frac{\pi }{4}+arg\Gamma (i\nu ),}\hfill \\ {\displaystyle \chi (k_0)=\frac{1}{2\pi i}{\int }_{-k_0}^{k_0}ln\left(\frac{1-{|\gamma (\xi )|}^2}{1-|\gamma (k_0){|}^2}\right)\frac{d\xi }{\xi -k_0},}\hfill \end{array}\right.$$

(5)

$\Gamma (·)$ being the Gamma function.

The rest of the paper is organized as follows. In Section 2, within the zero-curvature formulation, we derive an integrable coupled hierarchy with three potentials and furnish its bi-Hamiltonian structure, based on the $4\times 4$ matrix spectral problem (1) suited for the RH theory. In Section 3, taking the three-component coupled mKdV system (2) as an example, we present an associated oscillatory RH problem. In Section 4, we explore long-time asymptotics for the three-component coupled mKdV system through manipulating the oscillatory RH problem by the nonlinear steepest descent method. In the last section, we give a summary of our conclusions, together with some discussions.

2. An Integrable Three-Component Coupled mKdV Hierarchy

2.1. Zero Curvature Formulation

Let us first recall the zero curvature formulation to construct integrable hierarchies [31]. Let u be a vector potential, k be a spectral parameter, and $I_n$ stand for the n-th order identity matrix. Choose a square spectral matrix $U=U(u,k)$ from a given matrix loop algebra. Suppose that

$$W=W(u,k)={\displaystyle \sum _{m=0}^{\infty }}{W}_m{k}^{-m}={\displaystyle \sum _{m=0}^{\infty }}{W}_m(u)k^{-m}$$

(6)

presents a solution to the corresponding stationary zero curvature equation

$$W_x=i[U,W].$$

(7)

By using the solution W, we define an infinite sequence of Lax matrices

$$V^{[r]}=V^{[r]}(u,k)={(k^{r}W)}_{+}+{\Delta }_r,r\ge 0,$$

(8)

where the subscript + denotes the operation of taking a polynomial part in k, and ${\Delta }_r$, $r\ge 0$, are appropriate modification terms, and then construct an integrable hierarchy

$$u_t=K_r(u)=K_r(x,t,u,u_x,\cdots ),r\ge 0,$$

(9)

from an infinite sequence of zero curvature equations

$$U_t-V_x^{[r]}+i[U,V^{[r]}]=0,r\ge 0.$$

(10)

The two matrices U and $V^{[r]}$ here are called a Lax pair [32] of the r-th integrable system in the soliton hierarchy (9). The zero curvature equations in (10) present the compatibility requirements of the spatial and temporal matrix spectral problems

$$\left\{\begin{array}{c}-i{\varphi }_x=U\varphi =U(u,k)\varphi ,\hfill \\ -i{\varphi }_t=V^{[r]}\varphi =V^{[r]}(u,k)\varphi ,r\ge 0,\hfill \end{array}\right.$$

(11)

with $\varphi$ being the matrix eigenfunction.

To show the Liouville integrability of the soliton hierarchy (9), we usually furnish a bi-Hamiltonian structure [33]:

$$u_t=K_r=J_1\frac{\delta {\tilde{H}}_{r+1}}{\delta u}=J_2\frac{\delta {\tilde{H}}_r}{\delta u},r\ge 1,$$

(12)

where $J_1$ and $J_2$ constitute a Hamiltonian pair and $\frac{\delta }{\delta u}$ is the variational derivative. The Hamiltonian structures are normally achieved through the trace identity [31]:

$$\frac{\delta }{\delta u}\int \mathrm{tr}(W\frac{\partial U}{\partial k})dx=k^{-{\gamma }^{\prime }}\frac{\partial }{\partial k}\left[k^{{\gamma }^{\prime }}\mathrm{tr}(W\frac{\partial U}{\partial u})\right],{\gamma }^{\prime }=-\frac{k}{2}\frac{d}{dk}ln|\mathrm{tr}(W^2)|,$$

(13)

or more generally, the variational identity [34]:

$$\frac{\delta }{\delta u}\int \langle W,\frac{\partial U}{\partial k}\rangle dx=k^{-{\gamma }^{\prime }}\frac{\partial }{\partial k}\left[k^{{\gamma }^{\prime }}\langle W,\frac{\partial U}{\partial u}\rangle \right],{\gamma }^{\prime }=-\frac{k}{2}\frac{d}{dk}ln|\langle W,W\rangle |,$$

(14)

with $\langle ·,·\rangle$ being a symmetric and ad-invariant non-degenerate bilinear form on the underlying matrix loop algebra [35]. The bi-Hamiltonian structure often guarantees the existence of infinitely many commuting Lie symmetries ${\{K_n\}}_{n=0}^{\infty }$ and conserved quantities ${\{{\tilde{H}}_n\}}_{n=0}^{\infty }$:

$$[K_{n_1},K_{n_2}]=K_{n_1}^{\prime }[K_{n_2}]-K_{n_2}^{\prime }[K_{n_1}]=0,$$

(15)

and

$${\{{\tilde{\mathcal{H}}}_{n_1},{\tilde{\mathcal{H}}}_{n_2}\}}_N=\int {\left(\frac{\delta {\tilde{\mathcal{H}}}_{n_1}}{\delta u}\right)}^{T}N\frac{\delta {\tilde{\mathcal{H}}}_{n_2}}{\delta u}dx=0,$$

(16)

where $n_1,n_2\ge 0$, $N=J_1$ or $J_2$, and $K^{\prime }$ denotes the Gateaux derivative of K with respect to the potential u:

$$K^{\prime }(u)[S]=\frac{\partial }{\partial \epsilon }{|}_{\epsilon =0}K(u+\epsilon S,u_x+\epsilon S_x,\cdots ).$$

Such Abelian algebras of symmetries and conserved quantities can be generated directly from Lax pairs (see, e.g., [36,37]). We also know that for a system of evolution equations,

$$\tilde{H}=\int Hdx$$

is a conserved functional if and only if $\frac{\delta \tilde{H}}{\delta u}$ is an adjoint symmetry [38], and thus, Hamiltonian structures connect conserved functionals with adjoint symmetries and further symmetries. Pairs of adjoint symmetries and symmetries actually correspond to conservation laws [39].

When the underlying matrix loop algebra in the zero curvature formulation is simple, semisimple and non-semisimple, the associated zero curvature equations generate classical integrable hierarchies [40,41], a collection of different integrable hierarchies, and hierarchies of integrable couplings [42], respectively. Integrable couplings require extra care in presenting lumps and solitons.

2.2. Three-Component mKdV Hierarchy

Let us consider a $4\times 4$ matrix spectral problem

$$-i{\varphi }_x=U\varphi =U(u,k)\varphi ,U={(U_{jl})}_{4\times 4}=\left[\begin{array}{cccc}-k& p_1& p_2& p_3\\ -p_1^{*}& k& 0& 0\\ -p_2^{*}& 0& k& 0\\ -p_3^{*}& 0& 0& k\end{array}\right],$$

(17)

where k is a spectral parameter and $u=p^T={(p_1,p_2,p_3)}^T$ is a three-component potential. A special case of $p_3=0$ transforms (17) into the Manakov type spectral problem [43]. Since the leading matrix $\mathrm{diag}(-1,1,1,1)$ has a multiple eigenvalue, the spectral problem (17) is degenerate, which is different from the case of multiple wave interaction equations [30].

To derive an associated integrable coupled mKdV hierarchy, we first solve the stationary zero curvature Equation (7) corresponding to (17). We assume that a solution W is determined by

$$W=\left[\begin{array}{cc}a& b\\ -b^{†}& d\end{array}\right],$$

(18)

where a is a real scalar, b is a three-dimensional row, and d is a $3\times 3$ Hermitian matrix. It is direct to observe that the stationary zero curvature Equation (7) becomes

$$\left\{\begin{array}{c}{a}_x=i(b{p}^{†}-p{b}^{†}),\hfill \\ b_x=i(-2kb+pd-ap),\hfill \\ d_x=i(b^{†}p-p^{†}b).\hfill \end{array}\right.$$

(19)

We search for a formal series solution as follows:

$$W=\left[\begin{array}{cc}a& b\\ -b^{†}& d\end{array}\right]={\displaystyle \sum _{m=0}^{\infty }}{W}_m{k}^{-m},W_m=W_m(u)=\left[\begin{array}{cc}{a}^{[m]}& b^{[m]}\\ -b^{[m]†}& d^{[m]}\end{array}\right],m\ge 0,$$

(20)

with $b^{[m]}$ and $d^{[m]}$ being assumed to be

$$b^{[m]}=(b_1^{[m]},b_2^{[m]},b_3^{[m]}),d^{[m]}={(d_{jl}^{[m]})}_{3\times 3},m\ge 0.$$

(21)

Obviously, the system (19) is equivalent to the following recursion relations:

$$\begin{array}{c}{b}^{[0]}=0,a_x^{[0]}=0,d_x^{[0]}=0,\end{array}$$

(22a)

$$\begin{array}{c}{\displaystyle b^{[m+1]}=\frac{1}{2}(i{b}_x^{[m]}+p{d}^{[m]}-a^{[m]}p),m\ge 0,}\end{array}$$

(22b)

$$\begin{array}{c}{a}_x^{[m]}=i(b^{[m]}{p}^{†}-p{b}^{[m]†}),d_x^{[m]}=i(b^{[m]†}p-p^{†}{b}^{[m]}),m\ge 1.\end{array}$$

(22c)

The three-component mKdV system (2) can correspond to the specific initial values:

$$a^{[0]}=-6,d^{[0]}=2I_3.$$

(23)

Besides those initial values, we set all constants of integration in (22c) to be zero, that is, demand

$$W_m{|}_{u=0}=0,m\ge 1.$$

(24)

This way, with $a^{[0]}$ and $d^{[0]}$ given by (23), all matrices $W_m,m\ge 1$, will be uniquely determined. For instance, by a direct computation, (22) generates

$$\begin{array}{c}{b}_j^{[1]}=4p_j,a^{[1]}=0,d_{jl}^{[1]}=0;\end{array}$$

(25a)

$$\begin{array}{c}{b}_j^{[2]}=2i{p}_{j,x},a^{[2]}=-2{\displaystyle \sum _{l=1}^3}{|p_l|}^2,d_{jl}^{[2]}=2p_l{p}_j^{*};\end{array}$$

(25b)

$$\begin{array}{c}{b}_j^{[3]}=-p_{j,xx}+2({\displaystyle \sum _{l=1}^3}|p_l{|}^2)p_j,\end{array}$$

(25c)

$$\begin{array}{c}{a}^{[3]}=i{\displaystyle \sum _{l=1}^3}(p_l{p}_{l,x}^{*}-p_{l,x}{p}_l^{*}),d_{jl}^{[3]}=i(p_{l,x}{p}_j^{*}-p_l{p}_{j,x}^{*});\end{array}$$

(25d)

$$\begin{array}{c}{b}_j^{[4]}=-\frac{1}{2}i[p_{j,xxx}-3({\displaystyle \sum _{l=1}^3}|p_l{|}^2)p_{j,x}-3({\displaystyle \sum _{l=1}^3}{p}_{l,x}{p}_l^{*})p_j],\end{array}$$

(25e)

$$\begin{array}{c}{a}^{[4]}=-\frac{1}{2}[3({\displaystyle \sum _{l=1}^3}|p_l{|}^2{)}^2-{\displaystyle \sum _{l=1}^3}(p_l{p}_{l,xx}^{*}-p_{l,x}{p}_{l,x}^{*}+p_{l,xx}{p}_l^{*})],\end{array}$$

(25f)

$$\begin{array}{c}{d}_{jl}^{[4]}=\frac{1}{2}[3p_l({\displaystyle \sum _{l=1}^3}|p_l{|}^2)p_j^{*}-p_{l,xx}{p}_j^{*}+p_{l,x}{p}_{j,x}^{*}-p_l{p}_{j,xx}^{*}];\end{array}$$

(25g)

where $1\le j,l\le 3$. Based on (22b) and (22c), we can obtain a recursion relation for $b^{[m]}$ and $c^{[m]}=-b^{[m]†}$:

$$\left[\begin{array}{c}{c}^{[m+1]}\\ b^{[m+1]T}\end{array}\right]=\Psi \left[\begin{array}{c}{c}^{[m]}\\ b^{[m]T}\end{array}\right],m\ge 1,$$

(26)

where $\Psi$ is a $6\times 6$ matrix operator

$$\Psi =-\frac{i}{2}\left[\begin{array}{cc}(\partial +{\displaystyle \sum _{l=1}^3}{q}_l{\partial }^{-1}{p}_l)I_3+q{\partial }^{-1}p& -q{\partial }^{-1}{q}^T-{(q{\partial }^{-1}{q}^T)}^T\\ p^T{\partial }^{-1}p+{(p^T{\partial }^{-1}p)}^T& -(\partial +{\displaystyle \sum _{l=1}^3}{p}_l{\partial }^{-1}{q}_l)I_3-p^T{\partial }^{-1}{q}^T\end{array}\right],$$

(27)

with $q=-p^{†}$. Obviously, this tells

$$b^{[m+1]T}=\frac{i}{2}\left\{[p^T{\partial }^{-1}p+{(p^T{\partial }^{-1}p)}^T]b^{[m]†}+[(\partial -{\displaystyle \sum _{l=1}^3}{p}_l{\partial }^{-1}{p}_l^{*})I_3-p^T{\partial }^{-1}{p}^{*}]b^{[m]T}\right\},m\ge 1.$$

(28)

To generate an integrable coupled mKdV hierarchy with three components, we introduce, for all integers $r\ge 0$, the following Lax matrices

$$V^{[r]}=V^{[r]}(u,\lambda )={(V_{jl}^{[r]})}_{4\times 4}={({\lambda }^{r}W)}_{+}={\displaystyle \sum _{s=0}^r}{W}_s{\lambda }^{r-s},r\ge 0,$$

(29)

where the modification terms are chosen as zero. The compatibility requirements of (11), i.e., the zero curvature equations (10), lead to the integrable coupled mKdV hierarchy with three components:

$$u_t=p_t^T=K_r=-2i{b}^{[r+1]T},r\ge 0.$$

(30)

The first two nonlinear systems in the above integrable coupled mKdV hierarchy (30) are the three-component coupled nonlinear Schrödinger system

$$p_{j,t}=2i{p}_{j,xx}-4i(|p_1{|}^2+|p_2{|}^2+|p_3{|}^2)p_j,1\le j\le 3,$$

(31)

and the three-component coupled mKdV system (2). Under a reduction $p_3=0$, the three-component coupled system (31) is reduced to the Manakov system [43], for which a decomposition into finite-dimensional integrable Hamiltonian systems was made in [44], whileas the three-component coupled system (2) contains various examples of mKdV equations, for which there are diverse kinds of integrable decompositions through symmetry constraints (see, e.g., [45,46]).

The three-component coupled mKdV hierarchy (30) with an extended six-component potential $u={(p,q^T)}^T={(p,-p^{*})}^T$ possesses a Hamiltonian structure [29,38], which can be computed through applying the trace identity [31], or more generally, the variational identity [34]. A direct computation tells

$$-i\mathrm{tr}(W\frac{\partial U}{\partial k})=-a+\mathrm{tr}(d)={\displaystyle \sum _{m=0}^{\infty }}(-a^{[m]}+d_{11}^{[m]}+\mathrm{tr}{d}_{22}^{[m]})k^{-m},$$

and

$$-i\mathrm{tr}(W\frac{\partial U}{\partial u})=\left[\begin{array}{c}c\\ b^T\end{array}\right]=\sum _{m\ge 0}{G}_{m-1}{k}^{-m},$$

where $W=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$ and $c=-b^{†}$. Plugging these into the corresponding trace identity and considering the case of $m=2$ tell ${\gamma }^{\prime }=0$, and thus

$$\frac{\delta {\tilde{H}}_m}{\delta u}=i{G}_{m-1},{\tilde{H}}_m=-\frac{i}{m}\int (-a^{[m+1]}+d_{11}^{[m+1]}+\mathrm{tr}{d}_{22}^{[m+1]})dx,G_{m-1}=\left[\begin{array}{c}{c}^{[m]}\\ b^{[m]T}\end{array}\right],m\ge 1,$$

(32)

where $c^{[m]}=-b^{[m]†}$. A bi-Hamiltonian structure for the extended six-component coupled mKdV systems, consisting of (30) and its conjugate compartment, then follows:

$$u_t=K_r=J_1{G}_r=J_1\frac{\delta {\tilde{H}}_{r+1}}{\delta u}=J_2\frac{\delta {\tilde{H}}_r}{\delta u},r\ge 1,$$

(33)

where the Hamiltonian pair $(J_1,J_2=J_1\Psi )$ is defined by

$$\begin{array}{c}{J}_1=\left[\begin{array}{cc}0& -2I_3\\ 2I_3& 0\end{array}\right],\end{array}$$

(34a)

$$\begin{array}{c}{J}_2=i\left[\begin{array}{cc}{p}^T{\partial }^{-1}p+{(p^T{\partial }^{-1}p)}^T& {\displaystyle -(\partial +{\displaystyle \sum _{k=1}^3}{p}_k{\partial }^{-1}{q}_k)I_3-p^T{\partial }^{-1}{q}^T}\\ {\displaystyle -(\partial +{\displaystyle \sum _{k=1}^3}{p}_k{\partial }^{-1}{q}_k)I_3-q{\partial }^{-1}p}& q{\partial }^{-1}{q}^T+{(q{\partial }^{-1}{q}^T)}^T\end{array}\right],\end{array}$$

(34b)

where $q=-p^{†}$ again. Adjoint symmetry constraints (or equivalently symmetry constraints) decompose a four-component nonlinear Schrödinger system with $p_3=q_3=0$ into two commuting finite-dimensional Liouville integrable Hamiltonian systems in [38]. In the next section, we will concentrate on the three-component coupled mKdV system (2).

3. An Associated Oscillatory Riemann-Hilbert Problem

For a matrix $M=M(k;x,t)$, we define

$${\parallel M\parallel }_p={\parallel |M|\parallel }_p,$$

(35)

where $|M|$ is the matrix norm of M given by (3) and ${\parallel f\parallel }_p$ is the ${\mathcal{L}}^p$-norm of a function f of k. We assume that as $t\to \infty$,

$$A(t)\lesssim B(t)\mathrm{means}\exists C,T>0\mathrm{such}\mathrm{that}|A(t)|\le CB(t),\mathrm{when}t\ge T.$$

(36)

If the constant C depends on a few parameters ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n$, then we write $A(t){\lesssim }_{{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n}B(t)$, but on some situations where the dependence of C on some parameters is not important, we will often suppress those parameters for brevity.

For an oriented contour, we denote the left-hand side by + and the right-hand side by −, as one travels on the contour in the direction of the arrow. A Riemann-Hilbert (RH) problem $(\Gamma ,J)$ on an oriented contour $\Gamma \subset \mathbb{C}$ (open or closed) with a jump matrix J defined on $\Gamma$ reads

$$\left\{\begin{array}{c}{M}_{+}(k)=M_{-}(k)J(k),k\in \Gamma ,\hfill \\ M(k)\to J_0,\mathrm{as}k\to \infty ,\hfill \end{array}\right.$$

(37)

where $J_0$ is a given matrix determining a boundary condition at infinity, and $M_{\pm }$ are analytic in the ± side regions and continuous to $\Gamma$ from the ± sides, and $M=M_{\pm }$ in the ± side regions, respectively.

3.1. An Equivalent Matrix Spectral Problem

In the previous section, we have seen that the spectral problems of the three-component coupled mKdV system (2) read

$$-i{\varphi }_x=U\varphi =U(u,k)\varphi ,-i{\varphi }_t=V^{[3]}\varphi =V^{[3]}(u,k)\varphi ,$$

(38)

with the Lax pair being of the form

$$U(u,k)=k\Lambda +P,V^{[3]}(u,k)=k^3\Omega +Q,$$

(39)

where $u=p^T={(p_1,p_2,p_3)}^T$ and

$$\Lambda =\mathrm{diag}(-1,1,1,1),\Omega =\mathrm{diag}(-6,2,2,2).$$

(40)

The other two matrices P and Q are given by

$$P=\left[\begin{array}{cc}0& p\\ -p^{†}& 0\end{array}\right],Q=\left[\begin{array}{cc}{a}^{[1]}{k}^2+a^{[2]}k+a^{[3]}& b^{[1]}{k}^2+b^{[2]}k+b^{[3]}\\ -b^{[1]†}{k}^2-b^{[2]†}k-b^{[3]†}& d^{[1]}{k}^2+d^{[2]}k+d^{[3]}\end{array}\right]=\left[\begin{array}{cc}{Q}_{11}& Q_{12}\\ Q_{21}& Q_{22}\end{array}\right],$$

(41)

where $a^{[m]},b^{[m]},d^{[m]}$, $1\le m\le 3$, are defined in (25), and thus

$$\left\{\begin{array}{c}{Q}_{11}=-2p{p}^{†}k+i(p{p}_x^{†}-p_x{p}^{†}),Q_{12}=4p{k}^2+2i{p}_{x}k-p_{xx}+2p{p}^{†}p,\hfill \\ Q_{21}=-4p^{†}{k}^2+2i{p}_x^{†}k+p_{xx}^{†}-2p^{†}p{p}^{†},Q_{22}=2p^{†}pk+i(p^{†}{p}_x-p_x^{†}p).\hfill \end{array}\right.$$

(42)

As normal, for the spectral problems in (38), upon making the variable transformation

$$\varphi =\psi E_g,E_g={\mathrm{e}}^{ik\Lambda x+i{k}^3\Omega t},$$

(43)

we can impose the canonical normalization condition:

$${\psi }_{\pm }\to I_4,\mathrm{when}x,t\to \pm \infty .$$

(44)

The equivalent pair of matrix spectral problems reads

$${\psi }_x=ik[\Lambda ,\psi ]+\check{P}\psi ,$$

(45)

$${\psi }_t=i{k}^3[\Omega ,\psi ]+\check{Q}\psi ,$$

(46)

where $\check{P}=iP$ and $\check{Q}=iQ$. Noting $\mathrm{tr}(\check{P})=\mathrm{tr}(\check{Q})=0$, we have

$$det\psi =1,$$

(47)

by a generalized Liouville’s formula [47].

Applying the method of variation in parameters, and using the canonical normalization condition (44), we can transform the x-part of (38) into the following Volterra integral equations for ${\psi }_{\pm }$ [48]:

$$\begin{array}{c}{\psi }_{-}(k,x)=I_4+{\int }_{-\infty }^x{\mathrm{e}}^{ik\Lambda (x-y)}\check{P}(y){\psi }_{-}(k,y){\mathrm{e}}^{ik\Lambda (y-x)}dy,\hfill \end{array}$$

(48)

$$\begin{array}{c}{\psi }_{+}(k,x)=I_4-{\int }_x^{\infty }{\mathrm{e}}^{ik\Lambda (x-y)}\check{P}(y){\psi }_{+}(\lambda ,y){\mathrm{e}}^{ik\Lambda (y-x)}dy.\hfill \end{array}$$

(49)

Similarly, we can turn the t-part of (38) into the following Volterra integral equations:

$$\begin{array}{c}{\psi }_{-}(k,t)=I_4+{\int }_{-\infty }^t{\mathrm{e}}^{i{k}^3\Omega (t-s)}\check{Q}(s){\psi }_{-}(k,s){\mathrm{e}}^{i{k}^3\Omega (s-t)}ds,\hfill \end{array}$$

(50)

$$\begin{array}{c}{\psi }_{+}(k,t)=I_4-{\int }_t^{\infty }{\mathrm{e}}^{i{k}^3\Omega (t-s)}\check{Q}(s){\psi }_{+}(k,s){\mathrm{e}}^{i{k}^3\Omega (s-t)}ds.\hfill \end{array}$$

(51)

Observing the structures of $\Lambda$ and $\Omega$, we can know that the first column of ${\psi }_{-}$ and the last three columns of ${\psi }_{+}$ consist of analytical functions in the upper half plane ${\mathbb{C}}_{+}$, and the first column of ${\psi }_{+}$ and the last three columns of ${\psi }_{-}$ consist of analytical functions in the lower half plane ${\mathbb{C}}_{-}$ (also see [29,49]). All this will help us formulate an associated RH problem for the three-component coupled mKdV system (2).

3.2. An Oscillatory Riemann-Hilbert Problem

The scattering matrix S is determined by

$${\psi }_{-}={\psi }_{+}{\mathrm{e}}^{ikx\widehat{\Lambda }+i{k}^{3}t\widehat{\Omega }}S(k),$$

(52)

where ${\mathrm{e}}^{\alpha \widehat{M}}X={\mathrm{e}}^{\alpha M}X{\mathrm{e}}^{-\alpha M}$ for a scalar $\alpha$ and two same order square matrices M and X. We also adopt the simple expressions

$$M^{†}(k^{*})={(M(k))}^{†},M^{-1}(k^{*})={(M(k^{*}))}^{-1},$$

for a matrix M depending on $k\in \mathbb{C}$. Because

$$U^{†}(k^{*})=TU(k^{*})T^{-1},V^{[3]†}(k^{*})=T{V}^{[3]}(k^{*})T^{-1},T=\mathrm{diag}(1,-1,-1,-1),$$

(53)

we have

$${\psi }^{†}(k^{*})=T{\psi }^{-1}(k^{*})T^{-1},$$

(54)

and

$$S^{†}(k^{*})=T{S}^{-1}(k^{*})T^{-1}.$$

(55)

Notice that $detS(\lambda )=1$ due to $det{\psi }_{\pm }=1$. It then follows from $detS=1$ and (55) that

$$S_{11}^{*}(k^{*})=det[S_{22}(k)],S_{21}^{†}(k^{*})=S_{12}(k)\mathrm{adj}[S_{22}(k)],$$

where $\mathrm{adj}(M)$ is the adjoint matrix of M, and S is the block matrix

$$S={(S_{jl})}_{2\times 2},$$

with $S_{22}$ being a $3\times 3$ matrix. Thus, the scattering matrix S can be written as

$$S(k)=\left[\begin{array}{cc}det[{\underline{a}}^{†}(k^{*})]& \underline{b}(k)\\ \mathrm{adj}[{\underline{a}}^{†}(k^{*})]{\underline{b}}^{†}(k^{*})& \underline{a}(k)\end{array}\right],$$

(56)

where $\underline{a}$ is a $3\times 3$ matrix.

Introduce

$$M(k;x,t)=\left\{\begin{array}{c}(\frac{{\psi }_{-,L}(k)}{det[{\underline{a}}^{†}(k^{*})]},{\psi }_{+,R}(k)),k\in {\mathbb{C}}_{+},\hfill \\ ({\psi }_{+,L}(k),{\psi }_{-,R}(k){\underline{a}}^{-1}(k)),k\in {\mathbb{C}}_{-},\hfill \end{array}\right.$$

(57)

where ${\psi }_{\pm ,L}$ and ${\psi }_{\pm ,R}$ denote the first column and the rest columns of ${\psi }_{\pm }$. This matrix M solves an associated oscillatory RH problem

$$\left\{\begin{array}{c}{M}_{+}(k;x,t)=M_{-}(k;x,t)J(k;x,t),k\in \mathbb{R},\hfill \\ M(k;x,t)\to I_4,\mathrm{as}k\to \infty ,\hfill \end{array}\right.$$

(58)

where $M_{\pm }(k;x,t)={lim}_{\epsilon \to 0^{+}}M(k\pm i\epsilon ,x,t)$ and

$$J(k;x,t)=\left[\begin{array}{cc}1-\gamma (k){\gamma }^{†}(k^{*})& -{\mathrm{e}}^{-2it\theta (k)}\gamma (k)\\ {\mathrm{e}}^{2it\theta (k)}{\gamma }^{†}(k^{*})& I_3\end{array}\right],$$

(59)

with

$$\theta (k)=\theta (k;x,t)=\frac{kx}{t}+4k^3,\gamma (k)=\underline{b}(k){\underline{a}}^{-1}(k).$$

(60)

In the above RH problem, we assume that the matrix $a(k)$ is invertible, and so we will only analyze the solitonless case. The behavior of the oscillatory factor

$${\mathrm{e}}^{2it\theta (k)}$$

depends on the increasing and decreasing of $\theta (k)$ and the signature of $\mathrm{Re}i\theta (k)$ (see Figure 1 and Figure 2).

In what follows, we assume that $\gamma$ lies in ${\mathcal{S}}^3$ and satisfies

$${\gamma }^{*}(-k^{*})=\gamma (k),\underset{k\in \mathbb{R}}{sup}|\gamma (k)|<1.$$

(61)

The analysis on RH problems in [50] shows that the above RH problem (58) is equivalent to a Fredholm integral equation of the second kind. For such Fredholm equations, the existences and uniqueness of solutions can be guaranteed by the vanishing lemma [51]. A direct computation also shows [29] that one can compute the potential $p(x,t)$ through the solution $M(k;x,t)$ to the RH problem (58) as follows.

Theorem 2.

Assume that γ lies in ${\mathcal{S}}^3$ and satisfies the conditions in (61). Then there exists a unique solution $M(k;x,t)$ to the Riemann-Hilbert problem (58), and the solution of the three-component coupled mKdV system (2) is recovered via

$$p(x,t)=(p_1(x,t),p_2(x,t),p_3(x,t))=2\underset{k\to \infty }{lim}{(kM(k;,x,t))}_{12},$$

(62)

where we partition M into a block matrix $M={(M_{jl})}_{2\times 2}$ with $M_{22}$ being a $3\times 3$ matrix.

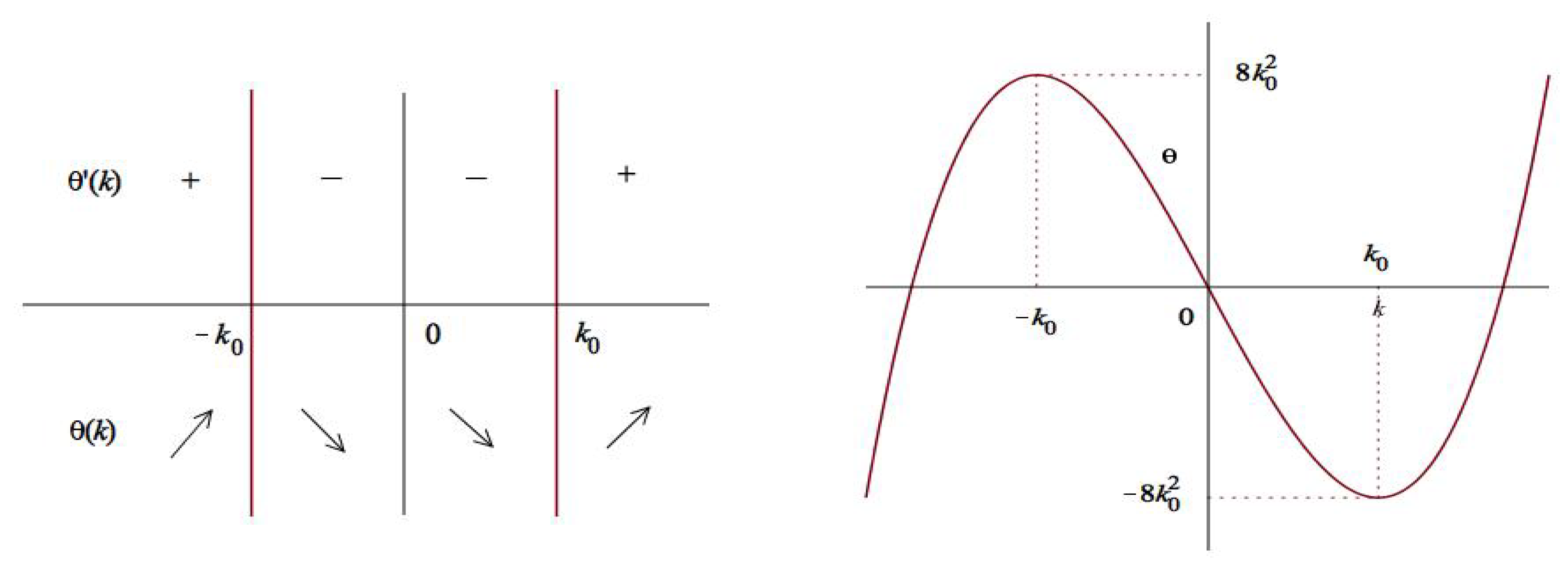
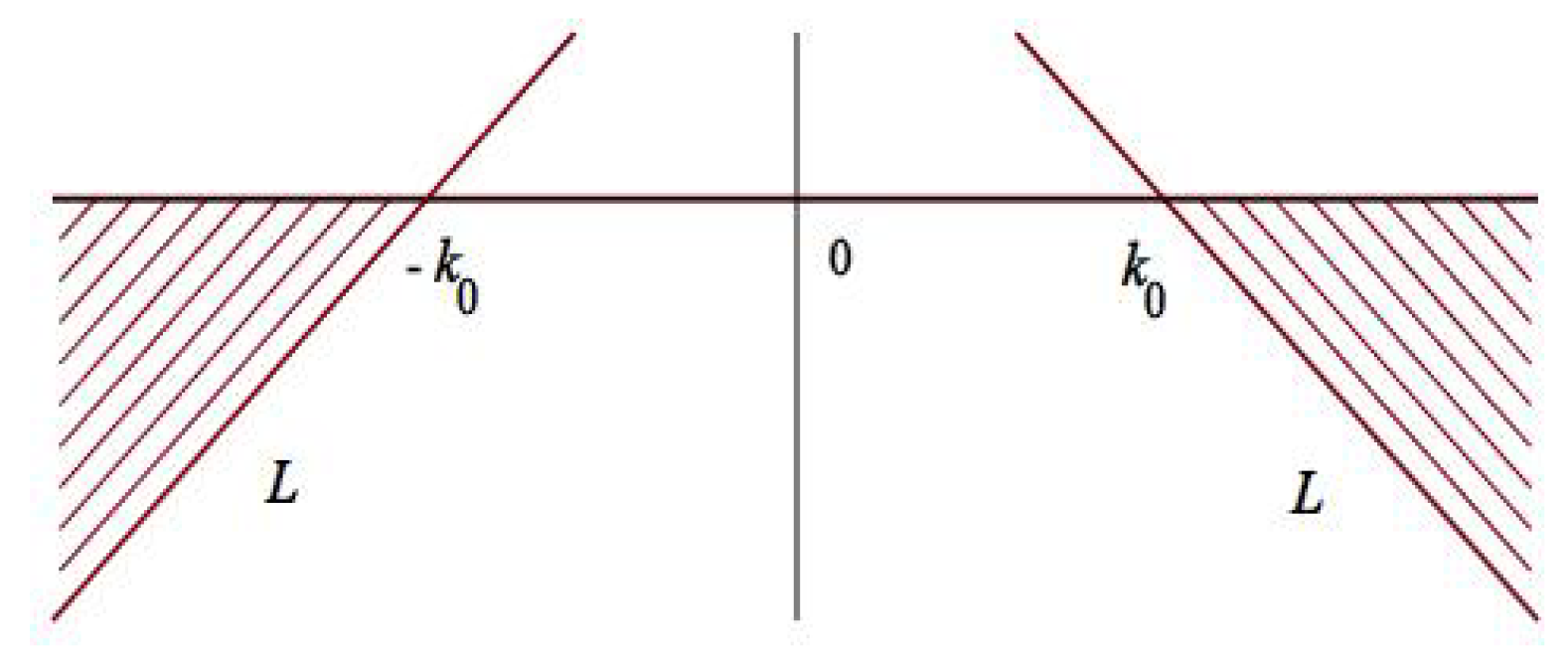
4. Long-Time Asymptotic Behavior

We will first deal with the Riemann-Hilbert (RH) problem (58) and then compute the long-time aymptotics of the three-component coupled mKdV system (2) with the leading term, by using the nonlinear steepest descent method [7]. We will be concentrated on the physically interesting region $|\frac{x}{t}|\le C$, where C is a positive constant.

4.1. Transformation of the RH Problem

Obviously, the jump matrix J has the following upper-lower and lower-upper factorizations:

$$J=\left[\begin{array}{cc}1& -{\mathrm{e}}^{-2it\theta (k)}\gamma (k)\\ 0& I_3\end{array}\right]\left[\begin{array}{cc}1& 0\\ {\mathrm{e}}^{2it\theta (k)}{\gamma }^{†}(k^{*})& I_3\end{array}\right],$$

(63)

and

$$J=\left[\begin{array}{cc}1& 0\\ \frac{{\mathrm{e}}^{2it\theta (k)}{\gamma }^{†}(k^{*})}{1-\gamma (k){\gamma }^{†}(k^{*})}& I_3\end{array}\right]\left[\begin{array}{cc}1-\gamma (k){\gamma }^{†}(k^{*})& 0\\ 0& {(I_3-{\gamma }^{†}(k^{*})\gamma (k))}^{-1}\end{array}\right]\left[\begin{array}{cc}1& \frac{-{\mathrm{e}}^{2it\theta (k)}\gamma (k)}{1-\gamma (k){\gamma }^{†}(k^{*})}\\ 0& I_3\end{array}\right].$$

(64)

We would like to introduce another RH problem to replace the upper-lower factorization with the lower-upper factorization to make the analytic and decay properties of the two factorizations consistent.

We easily see that the stationary points of $\theta$ are $\pm k_0,$ where $k_0=\sqrt{\frac{-x}{12t}}$, by computing $\frac{d\theta }{dk}{|}_{k=\pm k_0}=0$. Let $\delta (k)$ solve the RH problem

$$\left\{\begin{array}{c}{\delta }_{+}(k)=(I_3-{\gamma }^{†}(k^{*})\gamma (k)){\delta }_{-}(k),|k|<k_0,\hfill \\ ={\delta }_{-}(k),|k|>k_0,\hfill \\ \delta (k)\to I_3,\mathrm{as}k\to \infty ,\hfill \end{array}\right.$$

(65)

which implies a scalar RH problem

$$\left\{\begin{array}{c}det{\delta }_{+}(k)={(1-|\gamma (k)|}^2)det{\delta }_{-}(k),|k|<k_0,\hfill \\ =det{\delta }_{-}(k),|k|>k_0,\hfill \\ det\delta (k)\to 1,\mathrm{as}k\to \infty ,\hfill \end{array}\right.$$

(66)

noting that

$$det(I_3-{\gamma }^{†}(k^{*})\gamma (k))=1-\gamma (k)){\gamma }^{†}(k^{*})=1-{|\gamma (k)|}^2.$$

Due to (61), the jump matrix $I_3-{\gamma }^{†}(k^{*})\gamma (k)$ is positive definite. Thus, it follows from the vanishing lemma (see, e.g., [51]) that the RH problem (65) has a unique solution $\delta (k)$. In addition, the Plemelj formula [51] gives the unique solution of the above scalar RH problem (66):

$$det\delta (k)={\left(\frac{k-k_0}{k+k_0}\right)}^{i\nu }{\mathrm{e}}^{\chi (k)},$$

(67)

where

$$\nu =-\frac{1}{2\pi }ln(1-|\gamma (k_0){|}^2),\chi (k)=\frac{1}{2\pi i}{\int }_{-k_0}^{k_0}ln\left(\frac{1-{|\gamma (\xi )|}^2}{1-|\gamma (k_0){|}^2}\right)\frac{d\xi }{\xi -k}.$$

By the uniqueness, we obtain

$$\delta (k)={({\delta }^{†}(k^{*}))}^{-1}.$$

(68)

It then follows that

$$|{\delta }_{+}{(k)|}^2=\left\{\begin{array}{c}3-{|\gamma (k)|}^2,|k|<k_0,\hfill \\ 3,|k|>k_0,\hfill \end{array}\right.$$

(69)

$$|{\delta }_{-}{(k)|}^2=\left\{\begin{array}{c}3+\frac{{|\gamma (k)|}^2}{1-{|\gamma (k)|}^2},|k|<k_0,\hfill \\ 3,|k|>k_0,\hfill \end{array}\right.$$

(70)

and

$$|det{\delta }_{+}{(k)|}^2\le 1,|det{\delta }_{-}{(k)|}^2\le (1-\underset{\zeta \in \mathbb{R}}{sup}{|\gamma (\zeta )|}^2{)}^{-1}<\infty .$$

(71)

Therefore, by the maximum principle for analytic functions, we can have

$$|\delta (k)|<\infty ,|det\delta (k)|<\infty ,k\in \mathbb{C},$$

(72)

from the canonical normalization condition of the above two RH problems.

Let us now introduce

$$\Delta (k)=\left[\begin{array}{cc}det\delta (k)& 0\\ 0& {\delta }^{-1}(k)\end{array}\right],k\in \mathbb{C},$$

(73)

and a vector-valued spectral induced function

$$\rho (k)=\left\{\begin{array}{cc}-\frac{\gamma (k)}{1-\gamma (k){\gamma }^{†}(k^{*})},\hfill & |k|<k_0,\hfill \\ \gamma (k),\hfill & |k|\ge k_0.\hfill \end{array}\right.$$

(74)

Denote $M^{\Delta }$ by

$$M^{\Delta }(k;x,t)=M(k;x,t){\Delta }^{-1},$$

(75)

and reverse the orientation for $|k|>k_0$ as shown in Figure 3.

Then, we see that $M^{\Delta }$ presents the solution of the RH problem on $\mathbb{R}$ oriented as in Figure 3:

$$\left\{\begin{array}{c}{M}_{+}^{\Delta }(k;x,t)=M_{-}^{\Delta }(k;x,t)J^{\Delta }(k;x,t),k\in \mathbb{R},\hfill \\ M^{\Delta }(k;x,t)\to I_4,\mathrm{as}k\to \infty ,\hfill \end{array}\right.$$

(76)

where the jump matrix is defined by

$$\begin{array}{c}{J}^{\Delta }(k;x,t)={\Delta }_{-}(k)J(k;x,t){\Delta }_{+}^{-1}(k)\hfill \\ =\left[\begin{array}{cc}1& 0\\ -\frac{{\mathrm{e}}^{2it\theta (k)}{\delta }_{-}^{-1}(k){\rho }^{†}(k^{*})}{det{\delta }_{-}(k)}& I_3\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{e}}^{-2it\theta (k)}[det{\delta }_{+}(k)]\rho (k){\delta }_{+}(k)\\ 0& I_3\end{array}\right].\hfill \end{array}$$

(77)

We will deform this RH problem to evaluate the asymptotics of the three-component coupled mKdV system (2).

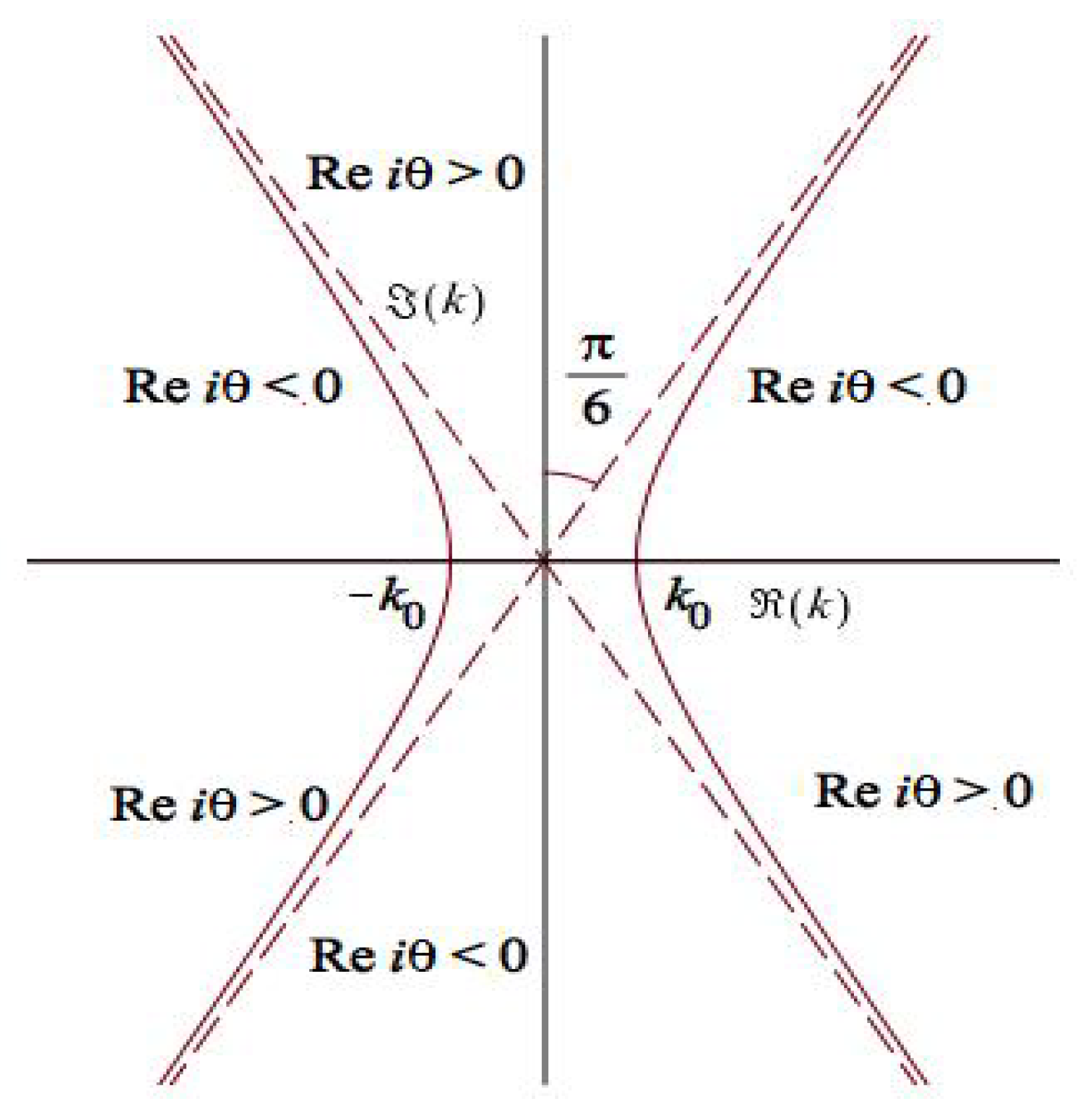
4.2. Decomposition of the Spectral Induced Function

To determine the required deformation, we first make a decomposition of the spectral induced function $\rho (k)$. By L, we denote the contour

$$L:\{k=k_0+k_0\alpha {\mathrm{e}}^{\frac{3\pi i}{4}}:-\infty <\alpha \le \sqrt{2}\}\cup \{k=-k_0+k_0\alpha {\mathrm{e}}^{\frac{\pi i}{4}}:-\infty <\alpha \le \sqrt{2}\}$$

(78)

and by $\Sigma$, denote the contour

$$\Sigma =L\cup L^{*}\cup \mathbb{R}$$

(79)

with the orientation in Figure 4.

Further let $L_{\epsilon }$ denote the following part of the contour L:

$$L_{\epsilon }:\{k=k_0+k_0\alpha {\mathrm{e}}^{\frac{3\pi i}{4}}:\epsilon <\alpha \le \sqrt{2}\}\cup \{k=-k_0+k_0\alpha {\mathrm{e}}^{\frac{\pi i}{4}}:\epsilon <\alpha \le \sqrt{2}\},$$

(80)

where $0<\epsilon <\sqrt{2}$. We will focus on the contour $\Sigma$, though any other contour of the same shape as $\Sigma$, which locates in the the region where $\mathrm{Re}i\theta (k)$ is positive, will work.

Proposition 1.

The vector-valued spectral induced function $\rho (k)$ has the following decomposition on the real axis:

$$\rho (k)=R(k)+h_1(k)+h_2(k),k\in \mathbb{R},$$

(81)

where $R(k)$ is a polynomial on $|k|<k_0$ and a rational function on $|k|\ge k_0$, $h_2(k)$ has an analytic continuation from $\mathbb{R}$ to L in the region where $\mathrm{Re}i\theta (k)>0$, and $h_1,h_2$ and R have the estimates as $t\to \infty$:

$$|{\mathrm{e}}^{-2it\theta (k)}{h}_1(k)|\lesssim \frac{1}{{(1+|k|}^2)t^l},k\in \mathbb{R},$$

(82)

$$|{\mathrm{e}}^{-2it\theta (k)}{h}_2(k)|\lesssim \frac{1}{{(1+|k|}^2)t^l},k\in L,$$

(83)

$$|{\mathrm{e}}^{-2it\theta (k)}R(k)|\lesssim {\mathrm{e}}^{-16{\epsilon }^2{k}_0^{3}t},k\in L_{\epsilon },$$

(84)

where l is an arbitrary positive integer. Taking the Hermitian conjugate

$${\rho }^{†}(k^{*})=R^{†}(k^{*})+h_1^{†}(k^{*})+h_2^{†}(k^{*})$$

(85)

yields the same estimates for ${\mathrm{e}}^{2it\theta (k)}{h}_1^{†}(k^{*}),{\mathrm{e}}^{2it\theta (k)}{h}_2^{†}(k^{*})$ and ${\mathrm{e}}^{2it\theta (k)}{R}^{†}(k^{*})$ on $\mathbb{R},L^{*}$ and $L_{\epsilon }^{*}$, respectively.

Proof. 

Throughout the proof, we use the differential notation $\overline{d}s=\frac{1}{\sqrt{2\pi }}ds$ for brevity, while dealing with the Fourier transform. We only consider the physically interesting region $x=\mathrm{O}(t)$ and so $k_0$ is bounded. Let r be a fixed positive integer.

(a) First, we consider the case of $|k|<k_0$. In this case, we have $\rho (k)=-\gamma (k){(1-\gamma (k){\gamma }^{†}(k^{*}))}^{-1}$. Splitting it into even and odd parts leads to

$$\rho (k)=H_e(k^2)+k{H}_o(k^2),$$

(86)

where $H_e$ and $H_o$ are two vector functions in ${\mathcal{S}}^3$. By Taylor’s theorem with the integral form of the remainder, we have

$$H_e(k^2)={\displaystyle \sum _{j=0}^r}{\mu }_j^e{(k^2-k_0^2)}^j+\frac{1}{r!}{\int }_{k_0^2}^{k^2}{H}_e^{(r+1)}(\xi ){(k^2-\xi )}^{r}d\xi ,$$

(87)

and

$$H_o(k^2)={\displaystyle \sum _{j=0}^r}{\mu }_j^o{(k^2-k_0^2)}^j+\frac{1}{r!}{\int }_{k_0^2}^{k^2}{H}_o^{(r+1)}(\xi ){(k^2-\xi )}^{r}d\xi .$$

(88)

Set

$$R(k)=R_r(k)={\displaystyle \sum _{j=0}^r}{\mu }_j^e{(k^2-k_0^2)}^j+k{\displaystyle \sum _{j=0}^r}{\mu }_j^o{(k^2-k_0^2)}^j.$$

(89)

Then, we have

$$\frac{d^j\rho (k)}{d{k}^j}{|}_{k=\pm k_0}=\frac{d^{j}R(k)}{d{k}^j}{|}_{k=\pm k_0},0\le j\le r,$$

(90)

and the coefficients

$${\mu }_j^e(k_0^2)=\frac{1}{j!}\frac{d^j{H}_e(w)}{d{w}^j}{|}_{w=k_0^2},{\mu }_j^o(k_0^2)=\frac{1}{j!}\frac{d^j{H}_o(w)}{d{w}^j}{|}_{w=k_0^2},0\le j\le r,$$

(91)

decay rapidly as $k_0\to \infty$.

We assume that r is of form

$$r=4q+1,q\in {\mathbb{Z}}_{+},$$

(92)

with an even number q. Express

$$\rho (k)=h(k)+R(k),|k|<k_0.$$

(93)

By the characteristic of R in (89), we have

$$\frac{d^{j}h(k)}{d{k}^j}{|}_{k=\pm k_0}=0,0\le j\le r.$$

(94)

Based on this property, we will try to split h into two parts

$$h(k)=h_1(k)+h_2(k),$$

(95)

where $h_1$ is small and $h_2$ has an analytic continuation from $\mathbb{R}$ to L in the region where $\mathrm{Re}i\theta (k)>0$. This way, we obtain the required splitting of $\rho$.

Let us introduce

$$\alpha (k)={(k^2-k_0^2)}^q.$$

(96)

We consider the Fourier transform with respect to $\theta$. Because $k\mapsto \theta (k)$ is one-to-one in $|k|<k_0$ (see Figure 1), we define

$$\left\{\begin{array}{cc}(h/\alpha )(k)=h(k(\theta ))/\alpha (k(\theta )),\hfill & -8k_0^3=\theta (k_0)<\theta <\theta (-k_0)=8k_0^3,\hfill \\ =0,\hfill & |\theta |\ge 8k_0^3.\hfill \end{array}\right.$$

(97)

Based on (94), we have

$$(h/\alpha )(\theta )=\mathrm{O}({(k^2(\theta )-k_0^2)}^{r+1-q}),|\theta |\to 8k_0^3,|\theta |<8k_0^3;$$

(98)

and as $dk/d\theta ={[12(k^2(\theta )-k_0^2)]}^{-1}$, we see that

$$h/\alpha \in H^j(-\infty <\theta <\infty ),0\le j\le \frac{3q+2}{2},$$

(99)

where the $H^j$s are Hilbert spaces. It follows from the Fourier inversion theorem that

$$(h/\alpha )(k)={\int }_{-\infty }^{\infty }{\mathrm{e}}^{is\theta (k)}(\widehat{h/\alpha })(s)\overline{d}s,|k|<k_0,$$

(100)

where $\widehat{h/\alpha }$ is the Fourier transform

$$(\widehat{h/\alpha })(s)=-{\int }_{-k_0}^{k_0}{\mathrm{e}}^{-is\theta (k)}(h/\alpha )(k)\overline{d}\theta (k),s\in \mathbb{R}.$$

(101)

By the formulae (86), (87), (88) and (93) we have

$$\begin{array}{cc}\hfill (h/\alpha )(k)=\frac{{(k^2-k_0^2)}^{3q+2}}{r!}& \left({\int }_0^1{H}_e^{(r+1)}(k_0^2+w(k^2-k_0^2)){(1-w)}^{r}dw\right.\hfill \\ & +k\left.{\int }_0^1{H}_o^{(r+1)}(k_0^2+w(k^2-k_0^2)){(1-w)}^{r}dw\right).\hfill \end{array}$$

(102)

Then, it follows that

$$\begin{array}{c}{\int }_{-k_0}^{k_0}{\left|{\left(\frac{d}{d\theta }\right)}^j\frac{h}{\alpha }(k)\right|}^2|\overline{d}\theta (k)|\hfill \\ ={\int }_{-k_0}^{k_0}{\left|{\left(\frac{1}{12(k^2-k_0^2)}\frac{d}{dk}\right)}^j\frac{h}{\alpha }(k)\right|}^2|12(k^2-k_0^2)|\overline{d}k\hfill \\ \lesssim 1,0\le j\le \frac{3q+2}{2},\hfill \end{array}$$

(103)

from which, by the Plancherel theorem, we know

$${\int }_{-\infty }^{\infty }{(1+s^2)}^j{|(\widehat{h/\alpha })(s)|}^{2}ds\lesssim 1,0\le j\le \frac{3q+2}{2}.$$

(104)

Now make a splitting for h as follows:

$$\begin{array}{cc}\hfill h(k)& =\alpha (k){\int }_t^{\infty }{\mathrm{e}}^{is\theta (k)}(\widehat{h/\alpha })(s)\overline{d}s\hfill \\ & +\alpha (k){\int }_{-\infty }^t{\mathrm{e}}^{is\theta (k)}(\widehat{h/\alpha })(s)\overline{d}s\hfill \\ & =h_1(k)+h_2(k).\hfill \end{array}$$

(105)

On one hand, based on (104) and noting $|k|<k_0$, we have

$$\begin{array}{c}|{\mathrm{e}}^{-2it\theta (k)}{h}_1(k)|\le |\alpha (k)|{\int }_t^{\infty }|(\widehat{h/\alpha })(s)|\overline{d}s\hfill \\ \le |\alpha (k)|{\left({\int }_t^{\infty }{(1+s^2)}^{-p}\overline{d}s\right)}^{\frac{1}{2}}{\left({\int }_t^{\infty }{(1+s^2)}^p|(\widehat{h/\alpha })(s)|\overline{d}s\right)}^{\frac{1}{2}}\hfill \\ \le |\alpha (k)|{\left({\int }_t^{\infty }{s}^{-2p}\overline{d}s\right)}^{\frac{1}{2}}{\left({\int }_{-\infty }^{\infty }{(1+s^2)}^p|(\widehat{h/\alpha })(s)|\overline{d}s\right)}^{\frac{1}{2}}\hfill \\ \lesssim {\left({\int }_t^{\infty }{s}^{-2p}\overline{d}s\right)}^{\frac{1}{2}}=\frac{1}{t^{p-\frac{1}{2}}},1\le p\le \frac{3q+2}{2}.\hfill \end{array}$$

(106)

On the other hand, we know that $\mathrm{Re}i\theta (k)$ is positive in the hatched region in Figure 5, and thus that $h_2(k)$ has an analytic continuation from $\mathbb{R}$ to the line segments in the upper half k-plane:

$$\begin{array}{c}k(w)=k_0+k_{0}w{\mathrm{e}}^{\frac{3\pi i}{4}},0\le w\le \sqrt{2},\hfill \end{array}$$

(107)

$$\begin{array}{c}k(w)=-k_0+k_{0}w{\mathrm{e}}^{\frac{\pi i}{4}},0\le w\le \sqrt{2}.\hfill \end{array}$$

(108)

Let k be on the line segment (107). Then, we can have that

$$\begin{array}{c}|{\mathrm{e}}^{-2it\theta (k)}{h}_2(k)|\le |k+k_0{|}^q{(k_{0}w)}^q{\mathrm{e}}^{-t\mathrm{Re}i\theta (k)}{\int }_{-\infty }^t{\mathrm{e}}^{(s-t)\mathrm{Re}i\theta (k)}|(\widehat{h/\alpha })(s)|\overline{d}s\hfill \\ \lesssim k_0^{2q}{w}^q{\mathrm{e}}^{-t\mathrm{Re}i\theta (k)}{\left({\int }_{-\infty }^t\frac{\overline{d}s}{1+s^2}\right)}^{\frac{1}{2}}{\left({\int }_{-\infty }^t(1+s^2){|(\widehat{h/\alpha })(s)|}^2\overline{d}s\right)}^{\frac{1}{2}}\hfill \\ \lesssim k_0^{2q}{w}^q{\mathrm{e}}^{-t\mathrm{Re}i\theta (k)},\hfill \end{array}$$

(109)

again based on (104). But

$$\mathrm{Re}i\theta (k)=4k_0^3{w}^2(3-\frac{w}{\sqrt{2}})\ge 8k_0^3{w}^2.$$

(110)

Therefore, we have

$$|{\mathrm{e}}^{-2it\theta (k)}{h}_2(k)|\lesssim k_0^{2q}{w}^q{\mathrm{e}}^{-8t{k}_0^3{w}^2}=k_0^{\frac{3q}{2}}{t}^{\frac{q}{2}}{w}^q{\mathrm{e}}^{-8t{k}_0^3{w}^2}{(\frac{k_0}{t})}^{\frac{q}{2}}\lesssim t^{-\frac{q}{2}}.$$

(111)

Similarly, we can show that the same estimate holds on the line segment (108).

Finally fix $0<\epsilon <\sqrt{2}$. Then on the parts of the line segments (107) and (108) with $\epsilon <w\le \sqrt{2}$ away from $\pm k_0$, we have

$$|{\mathrm{e}}^{-2it\theta (k)}R(k)|\lesssim {\mathrm{e}}^{-16t{k}_0^3{w}^2}\lesssim {\mathrm{e}}^{-16{\epsilon }^2\tau },$$

(112)

(by, e.g., (110) on the line segment (107) and $R(k)$ is a polynomial), where $\tau =t{k}_0^3$.

(b) Second, we consider the case of $|k|\ge k_0$. We only consider the sub-case $k\ge k_0$, since the other sub-case $k\le -k_0$ is completely similar. In this case, we have

$$\rho (k)=\gamma (k),|k|\ge k_0.$$

(113)

Once more, we use Taylor’s theorem to obtain

$${(k-i)}^{r+6}\rho (k)={\displaystyle \sum _{j=0}^r}{\mu }_j{(k-k_0)}^j+\frac{1}{r!}{\int }_{k_0}^k{({(·-i)}^{r+6}\rho (·))}^{(r+1)}(\xi ){(k-\xi )}^{r}d\xi .$$

(114)

Define

$$R(k)=\frac{1}{{(k-i)}^{r+6}}{\displaystyle \sum _{j=0}^r}{\mu }_j{(k-k_0)}^j,$$

(115)

and set

$$h(k)=\rho (k)-R(k).$$

(116)

As before, we know that

$$\frac{d^{j}h(k)}{d{k}^j}{|}_{k=k_0}=0,0\le j\le r,$$

(117)

and

$${\mu }_j={\mu }_j(k_0)=\frac{1}{j!}\frac{d^j}{d{k}^j}\left[{(k-i)}^{r+6}\rho (k)\right]{|}_{k=k_0},0\le j\le r,$$

(118)

decay rapidly as $k_0\to \infty$.

Similarly, introduce

$$\beta (k)=\frac{{(k-k_0)}^q}{{(k-i)}^{q+2}}.$$

(119)

Following the Fourier inversion theorem, we have

$$(h/\beta )(k)={\int }_{-\infty }^{\infty }{\mathrm{e}}^{is\theta (k)}(\widehat{h/\beta })(s)\overline{d}s,k\ge k_0,$$

(120)

where $\widehat{h/\beta }$ is the Fourier transform

$$(\widehat{h/\beta })(s)={\int }_{k_0}^{\infty }{\mathrm{e}}^{-is\theta (k)}(h/\beta )(k)\overline{d}\theta (k),s\in \mathbb{R}.$$

(121)

Based on the formulae (114), (116) and (119), we see that

$$(h/\beta )(k)=\frac{{(k-k_0)}^{3q+2}}{{(k-i)}^{3q+5}}g(k,k_0),$$

(122)

where

$$g(k,k_0)=\frac{1}{r!}{\int }_0^1{\left({(·-i)}^{r+6}\rho (·)\right)}^{(r+1)}(k_0+w(k-k_0)){(1-w)}^{r}dw,$$

(123)

from which it follows that

$$\left|\frac{d^{j}g(k,k_0)}{d{k}^j}\right|\lesssim 1,k\ge k_0,j\ge 0.$$

(124)

Noting that

$$\left|\frac{k-k_0}{k+k_0}\right|\le 1,k\ge k_0,$$

(125)

we have

$$\begin{array}{c}{\int }_{k_0}^{\infty }{\left|{\left(\frac{d}{d\theta }\right)}^j\left(\frac{h}{\beta }\right)(k)\right|}^2\overline{d}\theta (k)\hfill \\ ={\int }_{k_0}^{\infty }{\left|{\left(\frac{1}{12(k^2-k_0^2)}\frac{d}{dk}\right)}^j\left(\frac{h}{\beta }\right)(k)\right|}^2[12(k^2-k_0^2)]\overline{d}k\hfill \\ \lesssim {\int }_{k_0}^{\infty }{\left|\frac{{(k-k_0)}^{3q+2-3j}}{{(k-i)}^{3q+5}}\right|}^2(k^2-k_0^2)\overline{d}k\hfill \\ \lesssim 1,0\le j<\frac{3q+2}{3}.\hfill \end{array}$$

(126)

By the Plancherel theorem,

$${\int }_{-\infty }^{\infty }{(1+s^2)}^j|(\widehat{h/\beta }(s){|}^{2}ds<\infty ,0\le j<\frac{3q+2}{3}.$$

(127)

Again, we split

$$\begin{array}{cc}\hfill h(k)& =\beta (k){\int }_t^{\infty }{\mathrm{e}}^{is\theta (k)}(\widehat{h/\beta })(s)\overline{d}s\hfill \\ & +\beta (k){\int }_{-\infty }^t{\mathrm{e}}^{is\theta (k)}(\widehat{h/\beta })(s)\overline{d}s\hfill \\ & =h_1(k)+h_2(k).\hfill \end{array}$$

(128)

On one hand, for $k\ge k_0$, similarly as in the previous example (106), we see that

$$|{\mathrm{e}}^{-2it\theta (k)}{h}_1(k)|\lesssim \frac{1}{{|k-i|}^2{t}^{p-\frac{1}{2}}},0\le p<\frac{3q+2}{3},$$

(129)

upon noting

$$\left|\frac{k-k_0}{k-i}\right|\le 1,k\ge k_0.$$

On the other hand, $h_2(k)$ has an analytic continuation from $\mathbb{R}$ to the ray

$$k(w)=k_0+k_{0}w{\mathrm{e}}^{-\frac{\pi i}{4}},w\ge 0,$$

(130)

in two parts of the lower half k-plane, where $\mathrm{Re}i\theta (k)>0$, as shown in Figure 6.

Let k be on the ray (130). Similarly as in the previous case $|k|<k_0$, we can show that

$$|{\mathrm{e}}^{-2it\theta (k)}{h}_2(k)|\lesssim \frac{k_0^q{w}^q{\mathrm{e}}^{-t\mathrm{Re}i\theta (k)}}{{|k-i|}^{q+2}}.$$

(131)

However, we have

$$\mathrm{Re}i\theta (k)\ge 4k_0^3{w}^2(\frac{w}{\sqrt{2}}+3)\ge 2\sqrt{2}{k}_0^3{w}^3,$$

and thus, we have

$$\begin{array}{c}|{\mathrm{e}}^{-2it\theta (k)}{h}_2(k)|\lesssim \frac{k_0^q[{({(t{k}_0^3)}^{\frac{1}{3}}w)}^q{\mathrm{e}}^{-2\sqrt{2}t{k}_0^3{w}^3}]}{{|k-i|}^{q+2}{(t{k}_0^3)}^{\frac{q}{3}}}\hfill \\ \lesssim \frac{1}{{|k-i|}^{q+2}{t}^{\frac{q}{3}}}\le \frac{1}{{|k-i|}^2{t}^{\frac{q}{3}}},\hfill \end{array}$$

(132)

since $k_0$ is bounded. This completes the proof of Proposition 1.  □

We are now ready to make a deformation of the RH problem (76).

4.3. Deformation of the RH Problem

Let us first explain what a deformation of a RH problem is. Suppose that we have a RH problem $(\Gamma ,J)$ on an oriented contour $\Gamma$ (see Figure 7):

$$\left\{\begin{array}{c}{M}_{+}(k)=M_{-}(k)J(k),k\in \Gamma ,\hfill \\ M(k)\to J_0,\mathrm{as}k\to \infty ,\hfill \end{array}\right.$$

(133)

and that on a part (which could be the whole contour $\Gamma$) of $\Gamma$ from $k_1$ to $k_2$ in the direction of $\Gamma$, denoted by ${\Gamma }_{k_1{k}_2}$, we have

$$J(k)=b_{-}^{-1}(k)J_1(k)b_{+}(k),k\in {\Gamma }_{k_1{k}_2},$$

(134)

where $b_{\pm }$ have invertible and analytic continuations to the ± sides of a region D (see Figure 7) supported by $k_1$ and $k_2$, respectively. Define an extended oriented contour ${\Gamma }^{\prime }$ (see Figure 7):

$${\Gamma }^{\prime }=\Gamma \cup \partial D,\Gamma ={\Gamma }_1\cup {\Gamma }_2\cup {\Gamma }_{k_1{k}_2},\partial D=B_{+}\cup B_{-},$$

(135)

and an extended jump matrix $J^{\prime }$:

$$\left\{\begin{array}{c}{J}^{\prime }(k)=J(k),k\in \Gamma \setminus {\Gamma }_{k_1{k}_2},\hfill \\ J^{\prime }(k)=J_1(k),k\in {\Gamma }_{k_1{k}_2},\hfill \\ J^{\prime }(k)=b_{+}(k),k\in B_{+},\hfill \\ J^{\prime }(k)=b_{-}^{-1}(k),k\in B_{-}.\hfill \end{array}\right.$$

(136)

Then the RH problem (133) on $\Gamma$ is equivalent to the following RH problem on ${\Gamma }^{\prime }$:

$$\left\{\begin{array}{c}{M}_{+}^{\prime }(k)=M_{-}^{\prime }(k)J^{\prime }(k),k\in {\Gamma }^{\prime },\hfill \\ M^{\prime }(k)\to J_0,\mathrm{as}k\to \infty ,\hfill \end{array}\right.$$

(137)

and the relation between the two solutions reads

$$\left\{\begin{array}{c}{M}^{\prime }(k)=M(k),k\in \mathbb{C}\setminus D,\hfill \\ M^{\prime }(k)=M(k)b_{+}^{-1}(k),k\in D_{+},\hfill \\ M^{\prime }(k)=M(k)b_{-}^{-1}(k),k\in D_{-}.\hfill \end{array}\right.$$

(138)

It is clear that one RH problem is solvable if and only if the other RH problem is solvable, and the solution to the one problem gives the solution to the other problem automatically by (138). We call $({\Gamma }^{\prime },J^{\prime })$ a deformation of the original RH problem $(\Gamma ,J)$. If D is not bounded, then we need to require that $b_{+}(k)$ and $b_{-}(k)$ tend to the identity matrix as $k\to \infty$, in order to keep the same normalization condition.

We now deform the RH problem (76) from $\mathbb{R}$ to the augmented contour $\Sigma$. The first important step is to observe that the jump matrix $J^{\Delta }(k;,x,t)$ can be rewritten as

$$J^{\Delta }(k;x,t)={(b_{-})}^{-1}{b}_{+},b_{\pm }=I_4\pm {\omega }_{\pm },k\in \mathbb{R},$$

(139)

where

$${\omega }_{+}=\left[\begin{array}{cc}0& {\mathrm{e}}^{-2it\theta (k)}[det{\delta }_{+}(k)]\rho (k){\delta }_{+}(k)\\ 0& 0\end{array}\right],{\omega }_{-}=\left[\begin{array}{cc}0& 0\\ -\frac{{\mathrm{e}}^{2it\theta (k)}{\delta }_{-}^{-1}(k){\rho }^{†}(k^{*})}{det{\delta }_{-}(k)}& 0\end{array}\right].$$

(140)

Moreover, noting the decomposition (81), we have

$$\begin{array}{c}{\omega }_{+}={\omega }_{+}^o+{\omega }_{+}^a\hfill \\ =\left[\begin{array}{cc}0& {\mathrm{e}}^{-2it\theta (k)}[det{\delta }_{+}(k)]h_1(k){\delta }_{+}(k)\\ 0& 0\end{array}\right]+\left[\begin{array}{cc}0& {\mathrm{e}}^{-2it\theta (k)}[det{\delta }_{+}(k)][h_2(k)+R(k)]{\delta }_{+}(k)\\ 0& 0\end{array}\right],\hfill \end{array}$$

(141)

$${\omega }_{-}={\omega }_{-}^o+{\omega }_{-}^a=\left[\begin{array}{cc}0& 0\\ -\frac{{\mathrm{e}}^{2it\theta (k)}{\delta }_{-}^{-1}(k)h_1^{†}(k^{*})}{det{\delta }_{-}(k)}& 0\end{array}\right]+\left[\begin{array}{cc}0& 0\\ -\frac{{\mathrm{e}}^{2it\theta (k)}{\delta }_{-}^{-1}(k)[h_2^{†}(k^{*})+R^{†}(k^{*})]}{det{\delta }_{-}(k)}& 0\end{array}\right],$$

(142)

and thus, the decompositions for $b_{\pm }$:

$$\begin{array}{c}{b}_{+}=b_{+}^o{b}_{+}^a=(I_4+{\omega }_{+}^o)(I_4+{\omega }_{+}^a)\hfill \\ =\left[\begin{array}{cc}1& {\mathrm{e}}^{-2it\theta (k)}[det{\delta }_{+}(k)]h_1(k){\delta }_{+}(k)\\ 0& I_3\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{e}}^{-2it\theta (k)}[det{\delta }_{+}(k)][h_2(k)+R(k)]{\delta }_{+}(k)\\ 0& I_3\end{array}\right],\hfill \\ b_{-}=b_{-}^o{b}_{-}^a=(I_4-{\omega }_{-}^o)(I_4-{\omega }_{-}^a)\hfill \end{array}$$

(143)

$$\begin{array}{c}=\left[\begin{array}{cc}1& 0\\ \frac{{\mathrm{e}}^{2it\theta (k)}{\delta }_{-}^{-1}(k)h_1^{†}(k^{*})}{det{\delta }_{-}(k)}& I_3\end{array}\right]\left[\begin{array}{cc}1& 0\\ \frac{{\mathrm{e}}^{2it\theta (k)}{\delta }_{-}^{-1}(k)[h_2^{†}(k^{*})+R^{†}(k^{*})]}{det{\delta }_{-}(k)}& I_3\end{array}\right].\hfill \end{array}$$

(144)

We can also state that

$$b_{\pm }^o={\omega }_{\pm }{{|}_{\rho =h_1},b_{\pm }^a={\omega }_{\pm }|}_{\rho =h_2+R}.$$

(145)

It finally follows that the jump matrix $J^{\Delta }$ has the following factorization:

$$J^{\Delta }(k;x,t)={(b_{-}^a)}^{-1}[{(b_{-}^o)}^{-1}{b}_{+}^o]b_{+}^a,k\in \mathbb{R}.$$

(146)

It is now standard to introduce

$$M^{♯}(k;x,t)=\left\{\begin{array}{cc}{M}^{\Delta }(k;x,t),\hfill & k\in {\Omega }_1\cup {\Omega }_2,\hfill \\ M^{\Delta }(k;x,t){(b_{-}^a)}^{-1},\hfill & k\in {\Omega }_3\cup {\Omega }_4\cup {\Omega }_5,\hfill \\ M^{\Delta }(k;x,t){(b_{+}^a)}^{-1},\hfill & k\in {\Omega }_6\cup {\Omega }_7\cup {\Omega }_8,\hfill \end{array}\right.$$

(147)

and then the RH problem (76) on $\mathbb{R}$ becomes the following new RH problem on $\Sigma$:

$$\left\{\begin{array}{c}{M}_{+}^{♯}(k;x,t)=M_{-}^{♯}(k;x,t)J^{♯}(k;x,t),k\in \Sigma ,\hfill \\ M^{♯}(k;x,t)\to I_4,k\to \infty ,\hfill \end{array}\right.$$

(148)

where

$$J^{♯}={(b_{-}^{♯})}^{-1}{b}_{+}^{♯},b_{+}^{♯}=\left\{\begin{array}{cc}{b}_{+}^o,\hfill & k\in \mathbb{R},\hfill \\ b_{+}^a,\hfill & k\in L,\hfill \\ I_4,\hfill & k\in L^{*},\hfill \end{array}\right.b_{-}^{♯}=\left\{\begin{array}{cc}{b}_{-}^o,\hfill & k\in \mathbb{R},\hfill \\ I_4,\hfill & k\in L,\hfill \\ b_{-}^a,\hfill & k\in L^{*}.\hfill \end{array}\right.$$

(149)

The canonical normalization condition in (148) can be verified, indeed. For example, ${(b_{+}^a)}^{-1}$ converges to $I_4$ as $k\to \infty$ in ${\Omega }_6\cup {\Omega }_8$, because we observe that for fixed $x,t$, by the definition of $h_2$ in (128) and the boundedness of $det\delta$ and $\delta$ in (72), we have

$$\begin{array}{cc}\hfill |{\mathrm{e}}^{-2it\theta (k)}[det\delta (k)]h_2(k)\delta (k)|& \lesssim |\beta (k)|{\mathrm{e}}^{-t\mathrm{Re}i\theta (k)}{\int }_{-\infty }^t{\mathrm{e}}^{(s-t)\mathrm{Re}i\theta (k)}|(\widehat{h/\beta })(s)|\overline{d}s\hfill \\ & \le \frac{|k-k_0{|}^q}{{|k-i|}^{q+2}}{\int }_{-\infty }^t|(\widehat{h/\beta })(s)|\overline{d}s\lesssim \frac{1}{{|k-i|}^2};\hfill \end{array}$$

and by the definition of R in (115) and the boundedness of $det\delta$ and $\delta$ in (72), we have

$$|{\mathrm{e}}^{-2it\theta (k)}[det\delta (k)]R(k)\delta (k)|\lesssim \frac{|{\sum }_{j=0}^r{\mu }_j{(k-k_0)}^j|}{{|k-i|}^{r+6}}\lesssim \frac{1}{{|k-i|}^6};$$

both of which converge to 0 as $k\to \infty$ in ${\Omega }_6\cup {\Omega }_8$.

The above RH problem (148) can be solved by using the Cauchy operators as follows (see [52,53]). Let us denote by $C_{\pm }$ the two Cauchy operators

$$(C_{\pm }f)(k)={\int }_{\Sigma }\frac{f(\xi )}{\xi -k_{\pm }}\frac{d\xi }{2\pi i},k\in \Sigma ,f\in {\mathcal{L}}^2(\Sigma )$$

(150)

on $\Sigma$. As is well known, these two operators $C_{\pm }$ are bounded from ${\mathcal{L}}^2(\Sigma )$ to ${\mathcal{L}}^2(\Sigma )$, and satisfy $C_{+}-C_{-}=1$. Define

$$C_{{\omega }^{♯}}f=C_{+}(f{\omega }_{-}^{♯})+C_{-}(f{\omega }_{+}^{♯})$$

(151)

for a $4\times 4$ matrix-valued function f, where

$${\omega }_{\pm }^{♯}=\pm (b_{\pm }^{♯}-I_4),{\omega }^{♯}={\omega }_{+}^{♯}+{\omega }_{-}^{♯}.$$

(152)

Assume that ${\mu }^{♯}={\mu }^{♯}(k;x,t)\in {\mathcal{L}}^2(\Sigma )+{\mathcal{L}}^{\infty }(\Sigma )$ solves the fundamental inverse equation

$${\mu }^{♯}=I_4+C_{{\omega }^{♯}}{\mu }^{♯}.$$

(153)

Then, we can see that

$$M^{♯}(k;x,t)=I_4+{\int }_{\Sigma }\frac{{\mu }^{♯}(k;x,t){\omega }^{♯}(k;x,t)}{\xi -k}\frac{d\xi }{2\pi i},k\in \mathbb{C}\setminus \Sigma ,$$

(154)

presents the unique solution of the RH problem (148).

Theorem 3.

The solution $p(x,t)$ of the three-component coupled mKdV system (2) is expressed by

$$\begin{array}{c}p(x,t)=(p_1(x,t),p_2(x,t),p_3(x,t))\hfill \\ =2\underset{k\to \infty }{lim}{(k{M}^{♯}(k;,x,t))}_{12}\hfill \\ =i{({\int }_{\Sigma }{\mu }^{♯}(\xi ;x,t){\omega }^{♯}(\xi )\frac{d\xi }{\pi })}_{12}\hfill \\ =i{({\int }_{\Sigma }({(1-C_{{\omega }^{♯}})}^{-1}{I}_4)(\xi ){\omega }^{♯}(\xi )\frac{d\xi }{\pi })}_{12}.\hfill \end{array}$$

(155)

Proof. 

This statement can be shown by Theorem 2, (75) and (147).  □

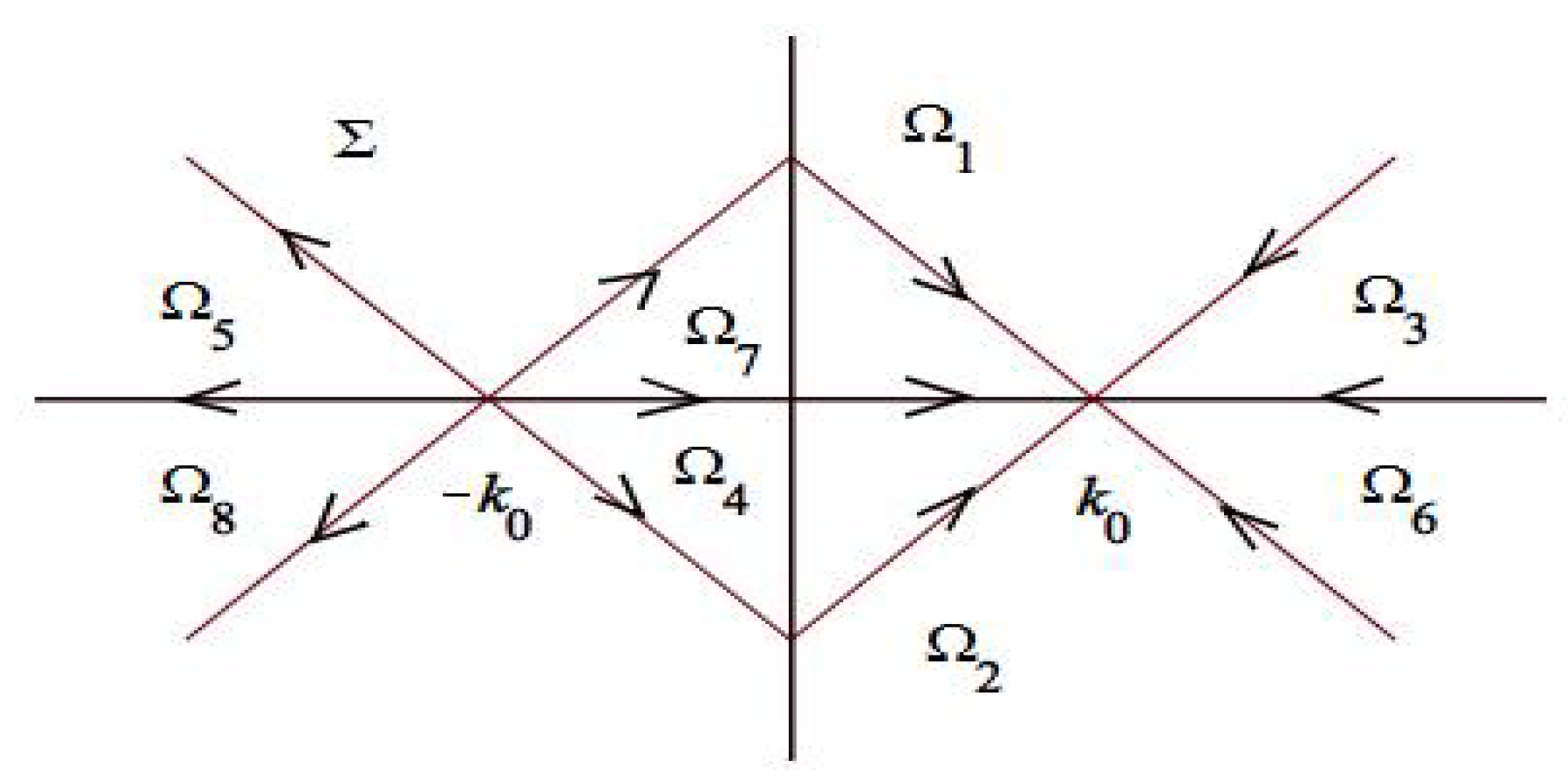
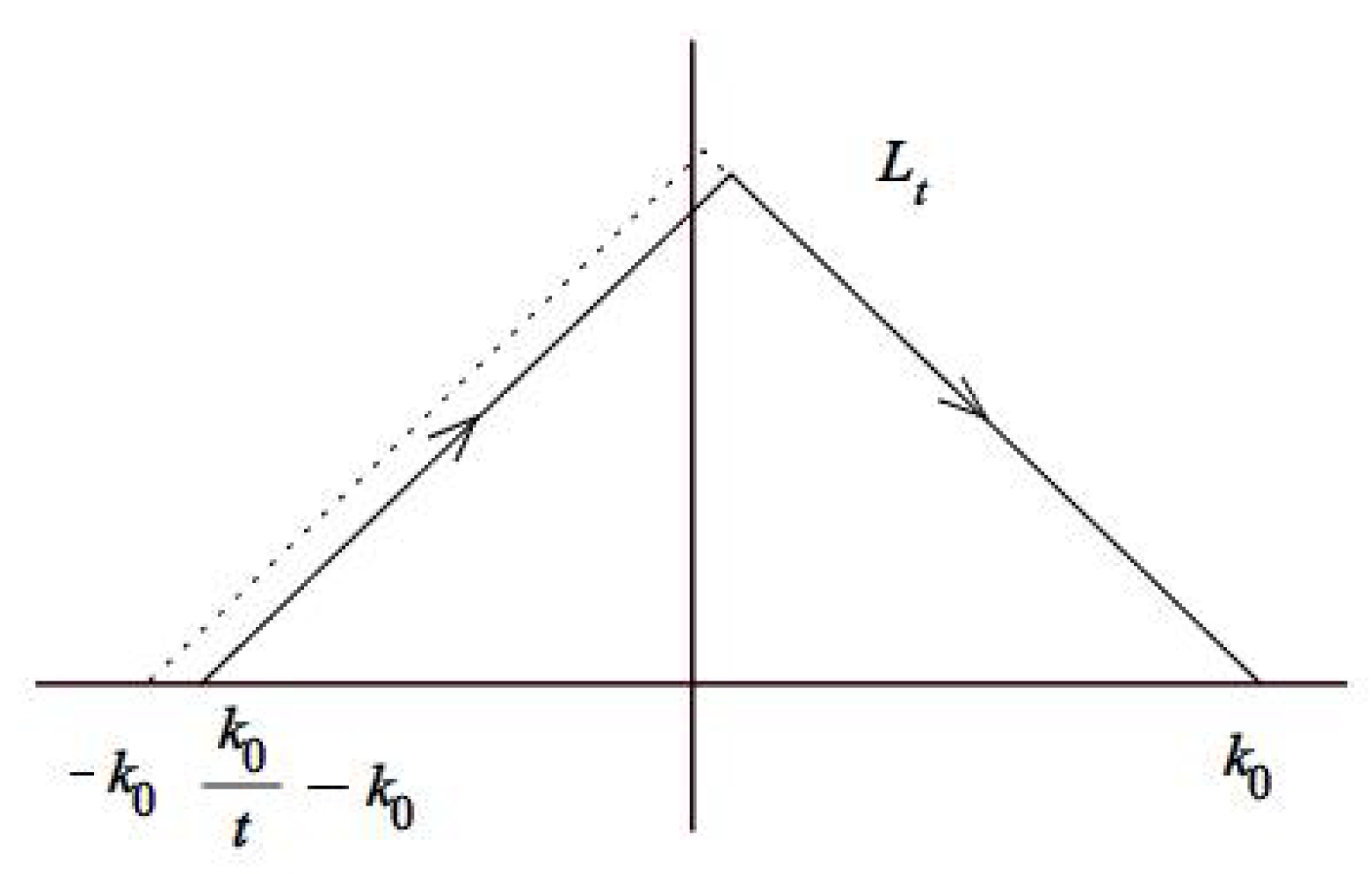
4.4. Contour Truncation

Let ${\Sigma }^{\prime }$ be the truncated contour ${\Sigma }^{\prime }=\Sigma \setminus (\mathbb{R}\cup L_{\epsilon }\cup L_{\epsilon }^{*})$ with the orientation as in Figure 8. We will reduce the RH problem (148) from $\Sigma$ to ${\Sigma }^{\prime }$, and estimate the difference between the two RH problems, one on $\Sigma$ and the other on ${\Sigma }^{\prime }$.

Let ${\omega }^e:\Sigma \to M(4,\mathbb{C})$ be a sum of three terms

$${\omega }^e={\omega }^a+{\omega }^b+{\omega }^c,$$

(156)

where ${\omega }^a={\omega }^{♯}\upharpoonright \mathbb{R}$ is supported on $\mathbb{R}$ and is composed of the contributions to ${\omega }^{♯}$ from terms of type $h_1(k)$ and $h_1^{†}(k^{*})$, ${\omega }^b={\omega }^{♯}\upharpoonright L\cup L^{*}$ is supported on $L\cup L^{*}$ and is composed of terms of type $h_2(k)$ and $h_2^{†}(k^{*})$, and ${\omega }^c={\omega }^{♯}\upharpoonright L_{\epsilon }\cup L_{\epsilon }^{*}$ is supported on $L_{\epsilon }\cup L_{\epsilon }^{*}$ and is composed of terms of type $R(k)$ and $R^{†}(k^{*})$.

Define

$${\omega }^{\prime }={\omega }^{♯}-{\omega }^e.$$

(157)

Obviously ${\omega }^{\prime }=0$ on $\Sigma \setminus {\Sigma }^{\prime }$, and hence ${\omega }^{\prime }$ is supported on ${\Sigma }^{\prime }$ from terms of type $R(k)$ and $R^{†}(k^{*})$.

Lemma 1.

For sufficiently small ε, we have

$$\parallel {\omega }^a{\parallel }_{{\mathcal{L}}^1(\mathbb{R})\cap {\mathcal{L}}^2(\mathbb{R})\cap {\mathcal{L}}^{\infty }(\mathbb{R})}\lesssim t^{-l},$$

(158)

$$\parallel {\omega }^b{\parallel }_{{\mathcal{L}}^1(L\cup L^{*})\cap {\mathcal{L}}^2(L\cup L^{*})\cap {\mathcal{L}}^{\infty }(L\cup L^{*})}\lesssim t^{-l},$$

(159)

$$\parallel {\omega }^c{\parallel }_{{\mathcal{L}}^1(L_{\epsilon }\cup L_{\epsilon }^{*})\cap {\mathcal{L}}^2(L_{\epsilon }\cup L_{\epsilon }^{*})\cap {\mathcal{L}}^{\infty }(L_{\epsilon }\cup L_{\epsilon }^{*})}\lesssim {\mathrm{e}}^{-16{\epsilon }^2\tau },$$

(160)

$$\parallel {\omega }^{\prime }{\parallel }_{{\mathcal{L}}^2(\Sigma )}{\lesssim }_{\epsilon }{\tau }^{-\frac{1}{4}},{\parallel {\omega }^{\prime }\parallel }_{{\mathcal{L}}^1(\Sigma )}{\lesssim }_{\epsilon }{\tau }^{-\frac{1}{2}},$$

(161)

where $\tau =t{k}_0^3$.

Proof. 

The estimates (158), (159) and (160) can be derived, similarly to Proposition 1. Based on the early definition of $R(k)$, we can see that

$$|R(k)|\lesssim {(1+|k|}^6{)}^{-1}$$

on the contour $\{k=k_0+k_0\alpha {\mathrm{e}}^{\frac{3\pi i}{4}}:-\infty <\alpha \le \epsilon \}$, where $\epsilon <\sqrt{2}$. On this contour, by (110), we have

$$\mathrm{Re}i\theta (k)\ge 8k_0^3{\alpha }^2,$$

and then using (72), we find that

$$|{\mathrm{e}}^{-2it\theta (k)}[det\delta (k)]R(k)\delta (k)|\lesssim {\mathrm{e}}^{-16k_0^3{\alpha }^{2}t}{(1+|k|}^6{)}^{-1}.$$

It then follows from a direct computation that the estimate (161) holds.  □

Similarly to Proposition 2.23 in [7], we can show the following estimate.

Proposition 2.

In the physically interesting region $x=\mathrm{O}(t)$, as $\tau \to \infty$, there exists the inverse of the operator $1-C_{{\omega }^{\prime }}:{\mathcal{L}}^2(\Sigma )\to {\mathcal{L}}^2(\Sigma )$, which is uniformly bounded:

$$\parallel {(1-C_{{\omega }^{\prime }})}^{-1}{\parallel }_{{\mathcal{L}}^2(\Sigma )}\lesssim 1.$$

(162)

Corollary 1.

In the physically interesting region $x=\mathrm{O}(t)$, as $\tau \to \infty$, there exists the inverse of the operator $1-C_{{\omega }^{♯}}:{\mathcal{L}}^2(\Sigma )\to {\mathcal{L}}^2(\Sigma )$, which is uniformly bounded:

$$\parallel {(1-C_{{\omega }^{♯}})}^{-1}{\parallel }_{{\mathcal{L}}^2(\Sigma )}\lesssim 1.$$

(163)

Proof. 

Noting $C_{{\omega }^{♯}}=C_{{\omega }^{\prime }}+C_{{\omega }^e}$, we have

$$\parallel C_{{\omega }^{♯}}-C_{{\omega }^{\prime }}{\parallel }_{{\mathcal{L}}^2(\Sigma )}=\parallel C_{{\omega }^e}{\parallel }_{{\mathcal{L}}^2(\Sigma )}\lesssim {\parallel {\omega }^e\parallel }_{{\mathcal{L}}^{\infty }(\Sigma )}.$$

In addition, it follows from Lemma 1 that

$$\parallel {\omega }^e{\parallel }_{{\mathcal{L}}^{\infty }(\Sigma )}\le \parallel {\omega }^a{\parallel }_{{\mathcal{L}}^{\infty }(\Sigma )}+\parallel {\omega }^b{\parallel }_{{\mathcal{L}}^{\infty }(\Sigma )}+{\parallel {\omega }^c\parallel }_{{\mathcal{L}}^{\infty }(\Sigma )}\lesssim {\tau }^{-l},$$

in the physically interesting region $x=\mathrm{O}(t)$ (where $k_0$ is bounded and thus $t=\mathrm{O}(\tau )$). Therefore, we have

$$\parallel C_{{\omega }^{♯}}-C_{{\omega }^{\prime }}{\parallel }_{{\mathcal{L}}^2(\Sigma )}\lesssim {\tau }^{-l}.$$

(164)

Now first from $1-C_{{\omega }^{♯}}=(1-C_{{\omega }^{\prime }})-(C_{{\omega }^{♯}}-C_{{\omega }^{\prime }}),$ we know, based on (164), that ${(1-C_{{\omega }^{♯}})}^{-1}$ exists.

Second, the second resolvent identity tells

$${(1-C_{{\omega }^{\prime }})}^{-1}(C_{{\omega }^{♯}}-C_{{\omega }^{\prime }}){(1-C_{{\omega }^{♯}})}^{-1}={(1-C_{{\omega }^{\prime }})}^{-1}-{(1-C_{{\omega }^{♯}})}^{-1}.$$

(165)

Again based on (164), we see from this identity that the estimate in the corollary is just a consequence of Proposition 2.  □

Theorem 4.

As $\tau \to \infty$, we have

$${\int }_{\Sigma }\left({(1-C_{{\omega }^{♯}})}^{-1}{I}_4\right)(\xi ){\omega }^{♯}(\xi )d\xi ={\int }_{\Sigma }\left({(1-C_{{\omega }^{\prime }})}^{-1}{I}_4\right)(\xi ){\omega }^{\prime }(\xi )d\xi +\mathrm{O}({\tau }^{-l}).$$

(166)

Proof. 

First, from (165), we can obtain

$$\begin{array}{cc}\hfill \left({(1-C_{{\omega }^{♯}})}^{-1}{I}_4\right){\omega }^{♯}=& \left({(1-C_{{\omega }^{\prime }})}^{-1}{I}_4\right){\omega }^{\prime }+{\omega }^e+\left({(1-C_{{\omega }^{\prime }})}^{-1}(C_{{\omega }^e}{I}_4\right){\omega }^{♯}\hfill \\ & +\left({(1-C_{{\omega }^{\prime }})}^{-1}(C_{{\omega }^{\prime }}{I}_4)\right){\omega }^e\hfill \\ & +\left({(1-C_{{\omega }^{\prime }})}^{-1}{C}_{{\omega }^e}{(1-C_{{\omega }^{♯}})}^{-1}\right)(C_{{\omega }^{♯}}{I}_4){\omega }^{♯}.\hfill \end{array}$$

(167)

Second, it follows directly from Lemma 1 that

$$\begin{array}{c}\parallel {\omega }^{\prime }{\parallel }_{{\mathcal{L}}^1(\Sigma )}\le \parallel {\omega }^a{\parallel }_{{\mathcal{L}}^1(\Sigma )}+\parallel {\omega }^b{\parallel }_{{\mathcal{L}}^1(L\cup L^{*})}+{\parallel {\omega }^c\parallel }_{{\mathcal{L}}^1(L_{\epsilon }\cup L_{\epsilon }^{*})}\lesssim {\tau }^{-l},\hfill \\ \parallel \left({(1-C_{{\omega }^{\prime }})}^{-1}(C_{{\omega }^e}{I}_4)\right){\omega }^{♯}{\parallel }_{{\mathcal{L}}^1(\Sigma )}\hfill \\ \le \parallel {(1-C_{{\omega }^{\prime }})}^{-1}{\parallel }_{{\mathcal{L}}^2(\Sigma )}\parallel C_{{\omega }^e}{I}_4{\parallel }_{{\mathcal{L}}^2(\Sigma )}{\parallel {\omega }^{♯}\parallel }_{{\mathcal{L}}^2(\Sigma )}\hfill \\ \lesssim \parallel {\omega }^e{\parallel }_{{\mathcal{L}}^2(\Sigma )}{\parallel {\omega }^{♯}\parallel }_{{\mathcal{L}}^2(\Sigma )}\hfill \\ \lesssim \parallel {\omega }^e{\parallel }_{{\mathcal{L}}^2(\Sigma )}(\parallel {\omega }^e{\parallel }_{{\mathcal{L}}^2(\Sigma )}+\parallel {\omega }^{\prime }{\parallel }_{{\mathcal{L}}^2(\Sigma )})\lesssim {\tau }^{-l-\frac{1}{4}},\hfill \\ \parallel \left({(1-C_{{\omega }^{\prime }})}^{-1}(C_{{\omega }^e}{I}_4)\right){\omega }^e{\parallel }_{{\mathcal{L}}^1(\Sigma )}\hfill \\ \le \parallel {(1-C_{{\omega }^{\prime }})}^{-1}{\parallel }_{{\mathcal{L}}^2(\Sigma )}\parallel C_{{\omega }^{\prime }}{I}_4{\parallel }_{{\mathcal{L}}^2(\Sigma )}{\parallel {\omega }^e\parallel }_{{\mathcal{L}}^2(\Sigma )}\hfill \\ \lesssim \parallel {\omega }^{\prime }{\parallel }_{{\mathcal{L}}^2(\Sigma )}{\parallel {\omega }^e\parallel }_{{\mathcal{L}}^2(\Sigma )}\lesssim {\tau }^{-l-\frac{1}{4}},\hfill \\ \parallel \left({(1-C_{{\omega }^{\prime }})}^{-1}{C}_{{\omega }^e}{(1-C_{{\omega }^{♯}})}^{-1}\right)(C_{{\omega }^{♯}}{I}_4){\omega }^{♯}{\parallel }_{{\mathcal{L}}^1(\Sigma )}\hfill \\ \le \parallel {(1-C_{{\omega }^{\prime }})}^{-1}{\parallel }_{{\mathcal{L}}^2(\Sigma )}\parallel C_{{\omega }^e}{\parallel }_{{\mathcal{L}}^2(\Sigma )}\parallel {(1-C_{{\omega }^{♯}})}^{-1}{\parallel }_{{\mathcal{L}}^2(\Sigma )}\parallel C_{{\omega }^{♯}}{I}_4{\parallel }_{{\mathcal{L}}^2(\Sigma )}{\parallel {\omega }^{♯}\parallel }_{{\mathcal{L}}^2(\Sigma )}\hfill \\ \lesssim \parallel {\omega }^e{\parallel }_{{\mathcal{L}}^{\infty }(\Sigma )}{\parallel {\omega }^{♯}\parallel }_{{\mathcal{L}}^2(\Sigma )}^2\lesssim {\tau }^{-l-\frac{1}{2}}.\hfill \end{array}$$

This proves the theorem, together with (167).  □

Note that as $k\in \Sigma \setminus {\Sigma }^{\prime },{\omega }^{\prime }(k)=0$, we can reduce $C_{{\omega }^{\prime }}$ from ${\mathcal{L}}^2(\Sigma )$ to ${\mathcal{L}}^2({\Sigma }^{\prime })$, and for simplicity’s sake, we still denote this reduced operator by $C_{{\omega }^{\prime }}$. Then

$${\int }_{\Sigma }\left({(1-C_{{\omega }^{\prime }})}^{-1}{I}_4\right)(\xi ){\omega }^{\prime }(\xi )d\xi ={\int }_{{\Sigma }^{\prime }}\left({(1-C_{{\omega }^{\prime }})}^{-1}{I}_4\right)(\xi ){\omega }^{\prime }(\xi )d\xi ,$$

and thus it follows from Theorems 3 and 4 that the following statement holds.

Theorem 5.

As $\tau \to \infty$, we have

$$p(x,t)=i{\left({\int }_{{\Sigma }^{\prime }}\left({(1-C_{{\omega }^{\prime }})}^{-1}{I}_4\right)(\xi ){\omega }^{\prime }(\xi )\frac{d\xi }{\pi }\right)}_{12}+\mathrm{O}({\tau }^{-l}).$$

(168)

Let $L^{\prime }=L\setminus L_{\epsilon }$, which yields ${\Sigma }^{\prime }=L^{\prime }\cup L^{\prime *}$, and denote ${\mu }^{\prime }={(1-C_{{\omega }^{\prime }})}^{-1}{I}_4$. Then, we see that

$$M^{\prime }(k;x,t)=I_4+{\int }_{{\Sigma }^{\prime }}\frac{{\mu }^{\prime }(k;x,t){\omega }^{\prime }(k;x,t)}{\xi -k}\frac{d\xi }{2\pi i}$$

(169)

solves the following RH problem

$$\left\{\begin{array}{c}{M}_{+}^{\prime }(k;x,t)=M_{-}^{\prime }(k;x,t)J^{\prime }(k;x,t),k\in {\Sigma }^{\prime },\hfill \\ M^{\prime }(k;x,t)\to I_4,\mathrm{as}k\to \infty ,\hfill \end{array}\right.$$

(170)

where the jump matrix is defined by

$$\begin{array}{c}{J}^{\prime }={(b_{-}^{\prime })}^{-1}{b}_{+}^{\prime },b_{\pm }^{\prime }=I_4\pm {\omega }_{\pm }^{\prime },{\omega }^{\prime }={\omega }_{+}^{\prime }+{\omega }_{-}^{\prime },\hfill \end{array}$$

(171)

$$\begin{array}{c}{\omega }_{+}^{\prime }(k)=\left[\begin{array}{cc}0& {\mathrm{e}}^{-2i\theta (k)}[det\delta (k)]R(k)\delta (k)\\ 0& 0\end{array}\right],{\omega }_{-}^{\prime }(k)=0,k\in L^{\prime },\hfill \end{array}$$

(172)

$$\begin{array}{c}{\omega }_{+}^{\prime }(k)=0,{\omega }_{-}^{\prime }(k)=\left[\begin{array}{cc}0& 0\\ -\frac{{\mathrm{e}}^{2i\theta (k)}{\delta }^{-1}(k)R^{†}(k^{*})}{det\delta (k)}& 0\end{array}\right],k\in L^{\prime *}.\hfill \end{array}$$

(173)

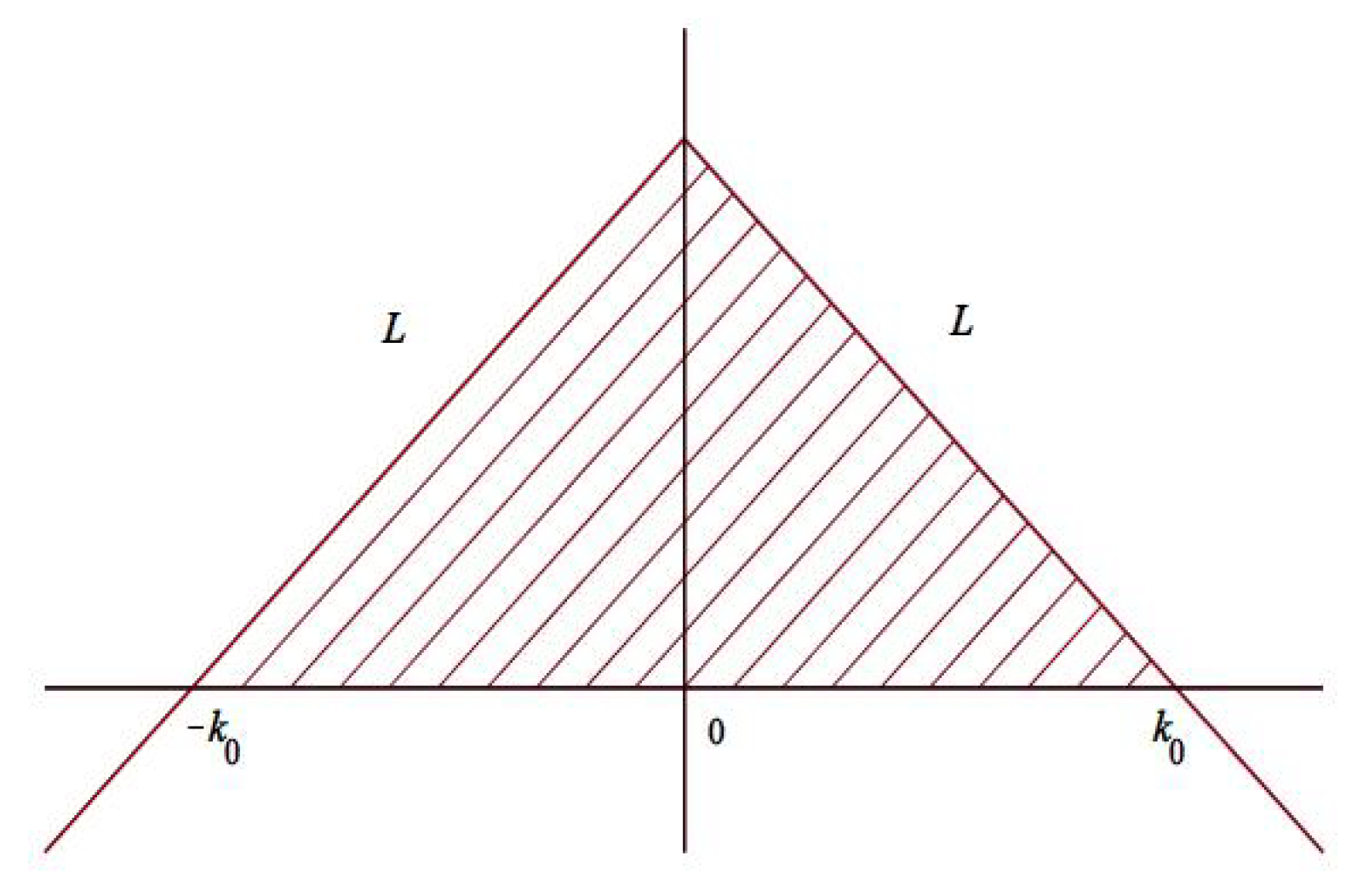
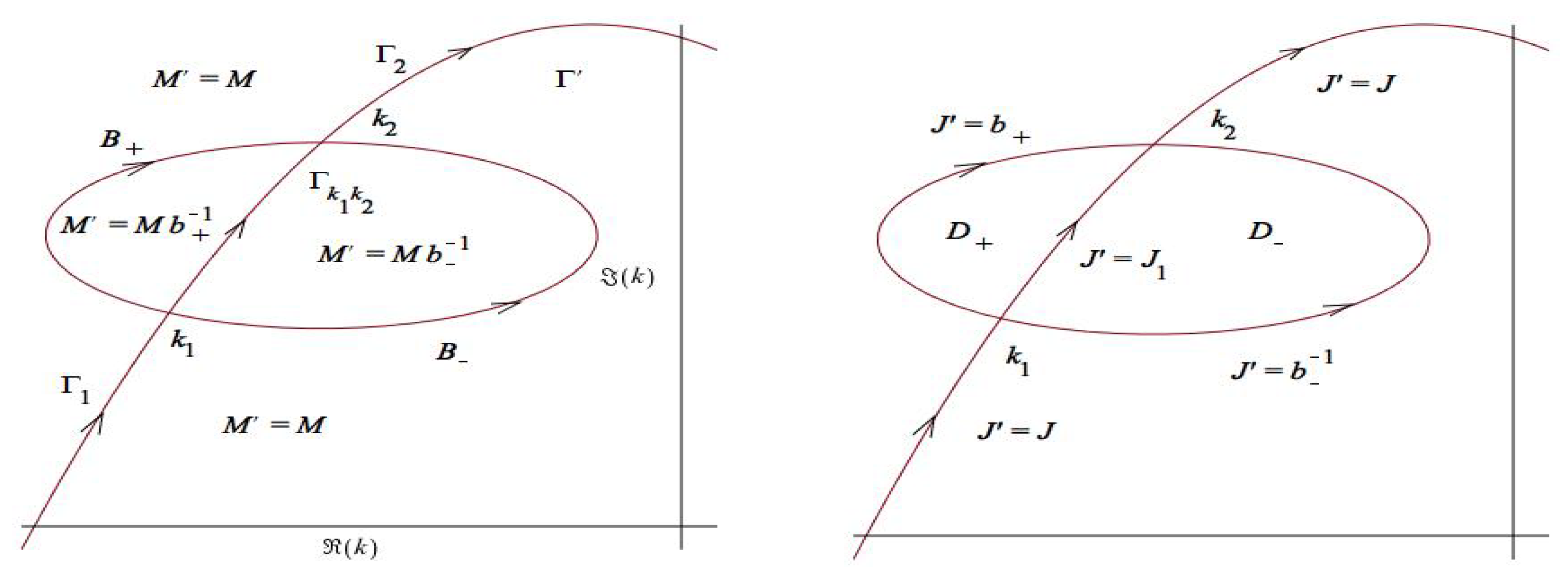
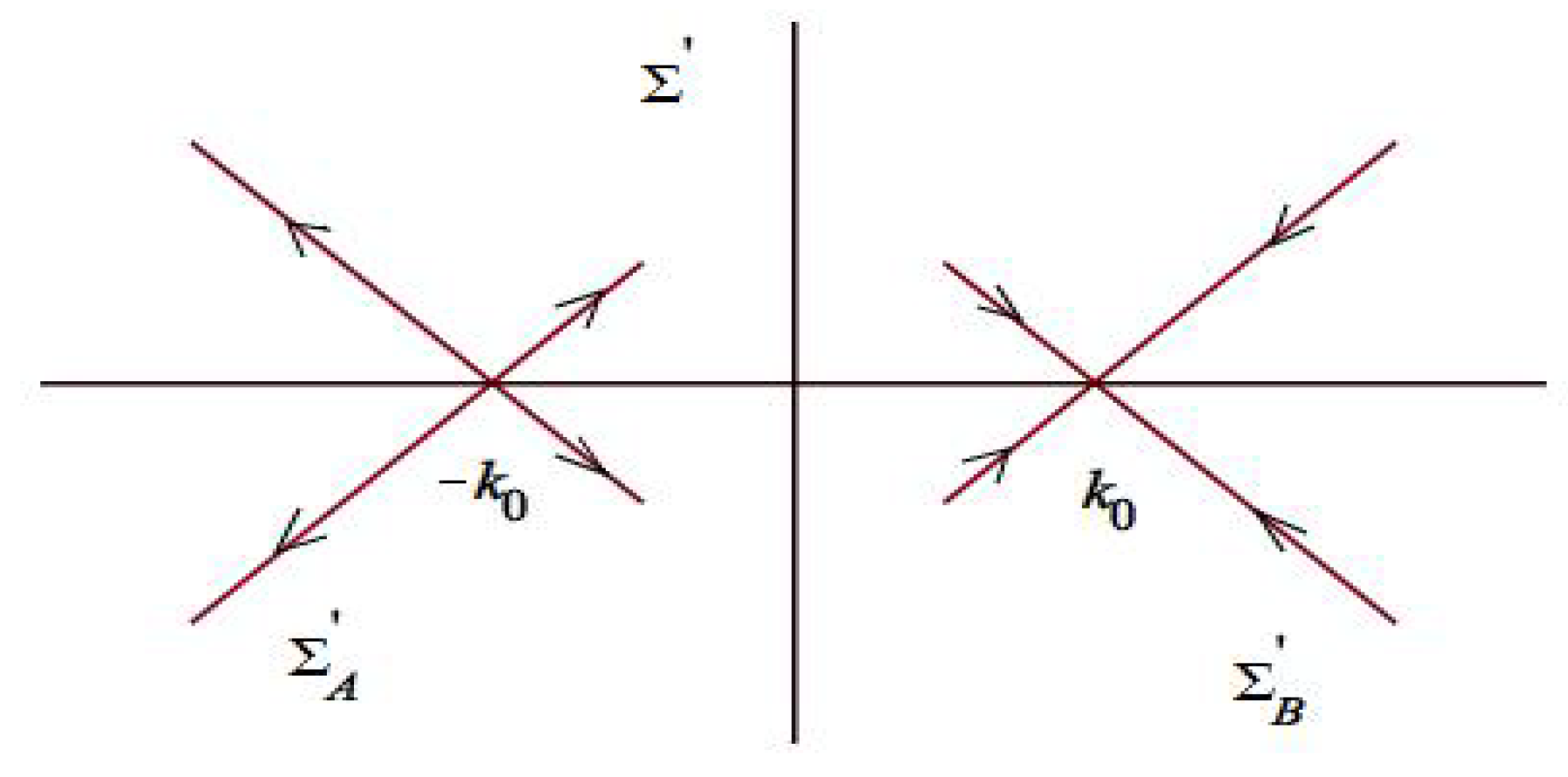
4.5. Disconnecting Contour Components

Denote the contour ${\Sigma }^{\prime }={\Sigma }_A^{\prime }\cup {\Sigma }_B^{\prime }$ (see Figure 8), and set

$${\omega }_{\pm }^{\prime }={\omega }_{A\pm }^{\prime }+{\omega }_{B\pm }^{\prime },$$

(174)

where

$${\omega }_{A\pm }^{\prime }(k)=\left\{\begin{array}{cc}{\omega }_{\pm }^{\prime },\hfill & k\in {\Sigma }_A^{\prime },\hfill \\ 0,\hfill & k\in {\Sigma }_B^{\prime },\hfill \end{array}\right.$$

(175)

$${\omega }_{B\pm }^{\prime }(k)=\left\{\begin{array}{cc}{\omega }_{\pm }^{\prime },\hfill & k\in {\Sigma }_B^{\prime },\hfill \\ 0,\hfill & k\in {\Sigma }_A^{\prime }.\hfill \end{array}\right.$$

(176)

Further define

$$\left\{\begin{array}{c}{\omega }_A^{\prime }={\omega }_{A+}^{\prime }+{\omega }_{A-}^{\prime },\hfill \\ {\omega }_B^{\prime }={\omega }_{B+}^{\prime }+{\omega }_{B-}^{\prime },\hfill \end{array}\right.$$

(177)

and thus

$${\omega }^{\prime }={\omega }_{+}^{\prime }+{\omega }_{-}^{\prime }={\omega }_A^{\prime }+{\omega }_B^{\prime }.$$

(178)

The two Cauchy operators $C_{{\omega }_A^{\prime }}$ and $C_{{\omega }_B^{\prime }}$ (see (150) for definition) are bounded operators from ${\mathcal{L}}^2({\Sigma }^{\prime })\to {\mathcal{L}}^2({\Sigma }^{\prime })$.

One can prove a similar lemma to Lemma 3.5 in [7].

Lemma 2.

We have the estimates

$$\parallel C_{{\omega }_A^{\prime }}{C}_{{\omega }_B^{\prime }}{\parallel }_{{\mathcal{L}}^2({\Sigma }^{\prime })}={\parallel C_{{\omega }_B^{\prime }}{C}_{{\omega }_A^{\prime }}\parallel }_{{\mathcal{L}}^2({\Sigma }^{\prime })}{\lesssim }_{k_0}{\tau }^{-\frac{1}{2}},$$

and

$$\parallel C_{{\omega }_A^{\prime }}{C}_{{\omega }_B^{\prime }}{\parallel }_{{\mathcal{L}}^{\infty }({\Sigma }^{\prime })\to {\mathcal{L}}^2({\Sigma }^{\prime })},{\parallel C_{{\omega }_B^{\prime }}{C}_{{\omega }_A^{\prime }}\parallel }_{{\mathcal{L}}^{\infty }({\Sigma }^{\prime })\to {\mathcal{L}}^2({\Sigma }^{\prime })}{\lesssim }_{k_0}{\tau }^{-\frac{3}{4}}.$$

Proposition 3.

As $\tau \to \infty$, we have

$$\begin{array}{cc}\hfill {\int }_{{\Sigma }^{\prime }}\left({(1-C_{{\omega }^{\prime }})}^{-1}{I}_4\right)(\xi ){\omega }^{\prime }(\xi )d\xi & ={\int }_{{\Sigma }_A^{\prime }}\left({(1-C_{{\omega }_A^{\prime }})}^{-1}{I}_4\right)(\xi ){\omega }_A^{\prime }(\xi )d\xi \hfill \\ & +{\int }_{{\Sigma }_B^{\prime }}\left({(1-C_{{\omega }_B^{\prime }})}^{-1}{I}_4\right)(\xi ){\omega }_B^{\prime }(\xi )d\xi +\mathrm{O}(\frac{1}{\tau }).\hfill \end{array}$$

(179)

Proof. 

From the identity

$$\begin{array}{c}(1-C_{{\omega }_A^{\prime }}-C_{{\omega }_B^{\prime }})[1+C_{{\omega }_A^{\prime }}{(1-C_{{\omega }_A^{\prime }})}^{-1}+C_{{\omega }_B^{\prime }}{(1-C_{{\omega }_B^{\prime }})}^{-1}]\hfill \\ =1-C_{{\omega }_B^{\prime }}{C}_{{\omega }_A^{\prime }}{(1-C_{{\omega }_A^{\prime }})}^{-1}-C_{{\omega }_A^{\prime }}{C}_{{\omega }_B^{\prime }}{(1-C_{{\omega }_B^{\prime }})}^{-1},\hfill \end{array}$$

it follows that

$$\begin{array}{c}(1-C_{{\omega }^{\prime }})\{[1+C_{{\omega }_A^{\prime }}{(1-C_{{\omega }_A^{\prime }})}^{-1}+C_{{\omega }_B^{\prime }}{(1-C_{{\omega }_B^{\prime }})}^{-1}][1+{(1-E)}^{-1}]E\}\hfill \\ =(1-C_{{\omega }^{\prime }})[1+C_{{\omega }_A^{\prime }}{(1-C_{{\omega }_A^{\prime }})}^{-1}+C_{{\omega }_B^{\prime }}{(1-C_{{\omega }_B^{\prime }})}^{-1}]+E=1,\hfill \end{array}$$

which implies that

$${(1-C_{{\omega }^{\prime }})}^{-1}=[1+C_{{\omega }_A^{\prime }}{(1-C_{{\omega }_A^{\prime }})}^{-1}+C_{{\omega }_B^{\prime }}{(1-C_{{\omega }_B^{\prime }})}^{-1}]+E.$$

In the above computation, we denote

$$E=C_{{\omega }_B^{\prime }}{C}_{{\omega }_A^{\prime }}{(1-C_{{\omega }_A^{\prime }})}^{-1}+C_{{\omega }_A^{\prime }}{C}_{{\omega }_B^{\prime }}{(1-C_{{\omega }_B^{\prime }})}^{-1}$$

for simplicity’s sake. Note that if an operator T is bounded and the inverse of $1-T$ exists, then ${(1-T)}^{-1}$ is also bounded. Further, based on the two Lemmas, Lemmas 1 and 2, and one proposition, Proposition 2, we can derive the estimate (179).  □

Now, from Theorem 5 and Proposition 3, we see that the following result holds.

Theorem 6.

As $\tau \to \infty$, we have

$$\begin{array}{cc}\hfill p(x,t)=& i{\left({\int }_{{\Sigma }_A^{\prime }}\left({(1-C_{{\omega }_A^{\prime }})}^{-1}{I}_4\right)(\xi ){\omega }_A^{\prime }(\xi )\frac{d\xi }{\pi }\right)}_{12}\hfill \\ & +i{\left({\int }_{{\Sigma }_B^{\prime }}\left({(1-C_{{\omega }_B^{\prime }})}^{-1}{I}_4\right)(\xi ){\omega }_B^{\prime }(\xi )\frac{d\xi }{\pi }\right)}_{12}\hfill \\ & +\mathrm{O}(\frac{1}{\tau }).\hfill \end{array}$$

(180)

4.6. Rescaling and Reduction of the Disconnected RH Problem

Extend the two contours ${\Sigma }_A^{\prime }$ and ${\Sigma }_B^{\prime }$ to the following two contours

$$\left\{\begin{array}{c}{\widehat{\Sigma }}_A^{\prime }=\{k=-k_0+k_0\alpha {\mathrm{e}}^{\pm \frac{\pi i}{4}}:\alpha \in \mathbb{R}\},\hfill \\ {\widehat{\Sigma }}_B^{\prime }=\{k=k_0+k_0\alpha {\mathrm{e}}^{\pm \frac{\pi i}{4}}:\alpha \in \mathbb{R}\},\hfill \end{array}\right.$$

(181)

and define ${\widehat{\omega }}_A^{\prime },{\widehat{\omega }}_B^{\prime }$ on ${\widehat{\Sigma }}_A^{\prime },{\widehat{\Sigma }}_B^{\prime }$ as

$$\left\{\begin{array}{c}{\widehat{\omega }}_A^{\prime }={\widehat{\omega }}_{A+}^{\prime }+{\widehat{\omega }}_{A-}^{\prime },\hfill \\ {\widehat{\omega }}_B^{\prime }={\widehat{\omega }}_{B+}^{\prime }+{\widehat{\omega }}_{B-}^{\prime },\hfill \end{array}\right.$$

(182)

respectively, where

$${\widehat{\omega }}_{A\pm }^{\prime }=\left\{\begin{array}{cc}{\omega }_{A\pm }^{\prime }(k),\hfill & k\in {\Sigma }_A^{\prime },\hfill \\ 0,\hfill & k\in {\widehat{\Sigma }}_A^{\prime }\setminus {\Sigma }_A^{\prime },\hfill \end{array}\right.$$

(183)

$${\widehat{\omega }}_{B\pm }^{\prime }=\left\{\begin{array}{cc}{\omega }_{B\pm }^{\prime }(k),\hfill & k\in {\Sigma }_B^{\prime },\hfill \\ 0,\hfill & k\in {\widehat{\Sigma }}_B^{\prime }\setminus {\Sigma }_B^{\prime }.\hfill \end{array}\right.$$

(184)

Let ${\Sigma }_A$ and ${\Sigma }_B$ denote the contours

$$\{k=k_0\alpha {\mathrm{e}}^{\pm \frac{\pi i}{4}}:\alpha \in \mathbb{R}\}$$

oriented outward as in ${\Sigma }_A^{\prime },{\widehat{\Sigma }}_A^{\prime }$ and inward as in ${\Sigma }_B^{\prime },{\widehat{\Sigma }}_B^{\prime }$, respectively (see Figure 9).

Motivated by the method of stationary phase, define the scaling transformations

$$N_A:{\mathcal{L}}^2({\widehat{\Sigma }}_A^{\prime })\to {\mathcal{L}}^2({\Sigma }_A),f\mapsto N_{A}f,(N_{A}f)(k)=f(\frac{k}{\sqrt{48t{k}_0}}-k_0),$$

(185)

$$N_B:{\mathcal{L}}^2({\widehat{\Sigma }}_B^{\prime })\to {\mathcal{L}}^2({\Sigma }_B),f\mapsto N_{B}f,(N_{B}f)(k)=f(\frac{k}{\sqrt{48t{k}_0}}+k_0),$$

(186)

and denote

$${\omega }_A=N_A{\widehat{\omega }}_A^{\prime },{\omega }_B=N_B{\widehat{\omega }}_B^{\prime }.$$

(187)

A direct change-of-variable argument tells that

$$C_{{\widehat{\omega }}_A^{\prime }}=N_A^{-1}{C}_{{\omega }_A}{N}_A,C_{{\widehat{\omega }}_B^{\prime }}=N_B^{-1}{C}_{{\omega }_B}{N}_B,$$

(188)

where $C_{{\omega }_A}$ (or $C_{{\omega }_B}$) is a bounded operator from ${\mathcal{L}}^2({\Sigma }_A)$ (or ${\mathcal{L}}^2({\Sigma }_B)$ into ${\mathcal{L}}^2({\Sigma }_A)$ (or ${\mathcal{L}}^2({\Sigma }_B)$). On the part

$$L_A=\{k=\alpha k_0\sqrt{48t{k}_0}{\mathrm{e}}^{-\frac{3\pi i}{4}}:-\epsilon <\alpha <\infty \}$$

(189)

of the contour ${\Sigma }_A$, we have

$${\omega }_A={\omega }_{A+}=\left[\begin{array}{cc}0& N_A{s}_1\\ 0& 0\end{array}\right],$$

(190)

and on the conjugate part $L_A^{*}$, we have

$${\omega }_A={\omega }_{A-}=\left[\begin{array}{cc}0& 0\\ N_A{s}_2& 0\end{array}\right],$$

(191)

where

$$s_1(k)={\mathrm{e}}^{-2it\theta (k)}[det\delta (k)]R(k)\delta (k),s_2(k)=\frac{{\mathrm{e}}^{2it\theta (k)}{\delta }^{-1}(k)R^{†}(k^{*})}{det\delta (k)}.$$

(192)

Lemma 3.

As $t\to \infty$, we have the estimates

$$|(N_A\tilde{\delta })(k)|\lesssim t^{-l+1},k\in L_A,$$

(193)

where $\tilde{\delta }(k)={\mathrm{e}}^{-2it\theta (k)}[R(k)\delta (k)-(det\delta (k))R(k)]$, and

$$|(N_A\widehat{\delta })(k)|\lesssim t^{-l+1},k\in L_A^{*},$$

(194)

where $\widehat{\delta }(k)={\mathrm{e}}^{2it\theta (k)}[{\delta }^{-1}(k)R^{†}(k^{*})-{(det\delta )}^{-1}(k)R^{†}(k^{*})]$.

Proof. 

We only prove the estimate (193) and the proof of the other estimate is completely similar.

From (65) and (66), we see that $\tilde{\delta }$ solves the following RH problem

$$\left\{\begin{array}{c}{\tilde{\delta }}_{+}(k)={\tilde{\delta }}_{-}{(k)(1-|\gamma (k)|}^2)+{\mathrm{e}}^{-2it\theta (k)}f(k),|k|<k_0,\hfill \\ {\tilde{\delta }}_{+}(k)={\tilde{\delta }}_{-}(k),|k|>k_0,\hfill \\ \tilde{\delta }(k)\to 0,\mathrm{as}k\to \infty ,\hfill \end{array}\right.$$

(195)

where

$$f(k)={R(k)(|\gamma (k)|}^2{I}_3-{\gamma }^{†}(k^{*})\gamma (k))\delta (k).$$

(196)

The solution of this vector RH problem is given by

$$\tilde{\delta }(k)=X(k){\int }_{-k_0}^{k_0}\frac{{\mathrm{e}}^{-2it\theta (\xi )}f(\xi )}{X_{+}(\xi )(\xi -k)}\frac{d\xi }{2\pi i},$$

(197)

with

$$X(k)={\mathrm{e}}^{\frac{1}{2\pi i}{\int }_{-k_0}^{k_0}\frac{ln(1-|\gamma (\xi ){|}^2)}{\xi -k}d\xi }.$$

Noting that

$${R|\gamma |}^2{I}_3-R{\gamma }^{†}\gamma ={(R-\rho )|\gamma |}^2{I}_3-(R-\rho ){\gamma }^{†}\gamma =(h_1+h_2){|\gamma |}^2{I}_3-(h_1+h_2){\gamma }^{†}\gamma ,$$

we can have $f(k)=\mathrm{O}({(k^2-k_0^2)}^{l+1})$ when $k\to \pm k_0$, upon noting the definition of $h=h_1+h_2$, and decompose $f(k)$ into two parts: $f(k)=f_1(k)+f_2(k)$, where $f_1(k)$ satisfies

$$|{\mathrm{e}}^{-2it\theta (k)}{f}_1(k)|\lesssim \frac{1}{{(1+|k|}^2)t^l},k\in \mathbb{R},$$

(198)

and $f_2(k)$ has an analytical continuation from $\mathbb{R}$ to $L_t$ (see Figure 10):

$$\begin{array}{cc}\hfill L_t=& \{k=k_0+k_0\alpha {\mathrm{e}}^{\frac{3\pi i}{4}}:0\le \alpha \le \sqrt{2}(1-\frac{1}{2t})\}\hfill \\ & \cup \{k=\frac{k_0}{t}-k_0+k_0\alpha {\mathrm{e}}^{\frac{\pi i}{4}}:0\le \alpha \le \sqrt{2}(1-\frac{1}{2t})\}\hfill \end{array}$$

(199)

and satisfies

$$|{\mathrm{e}}^{-2it\theta (k)}{f}_2(k)|\lesssim \frac{1}{{(1+|k|}^2)t^l},k\in L_t.$$

(200)

Let $k\in L_A$, and we decompose

$$\begin{array}{c}{\displaystyle (N_A\tilde{\delta })(k)=X(\frac{k}{\sqrt{48t{k}_0}}-k_0){\int }_{-k_0}^{\frac{k_0}{t}-k_0}\frac{{\mathrm{e}}^{-2it\theta (\xi )}f(\xi )}{X_{+}(\xi )(\xi +k_0-\frac{k}{\sqrt{48t{k}_0}})}\frac{d\xi }{2\pi i}}\hfill \\ {\displaystyle +X(\frac{k}{\sqrt{48t{k}_0}}-k_0){\int }_{\frac{k_0}{t}-k_0}^{k_0}\frac{{\mathrm{e}}^{-2it\theta (\xi )}{f}_1(\xi )}{X_{+}(\xi )(\xi +k_0-\frac{k}{\sqrt{48t{k}_0}})}\frac{d\xi }{2\pi i}}\hfill \\ {\displaystyle +X(\frac{k}{\sqrt{48t{k}_0}}-k_0){\int }_{\frac{k_0}{t}-k_0}^{k_0}\frac{{\mathrm{e}}^{-2it\theta (\xi )}{f}_2(\xi )}{X_{+}(\xi )(\xi +k_0-\frac{k}{\sqrt{48t{k}_0}})}\frac{d\xi }{2\pi i}}\hfill \\ =T_1+T_2+T_3.\hfill \end{array}$$

As $t\to \infty$, for the first and second terms, we can have

$$\begin{array}{c}{\displaystyle |T_1|\lesssim {\int }_{-k_0}^{\frac{k_0}{t}-k_0}\frac{|f(\xi )|}{|\xi +k_0-\frac{k}{\sqrt{48t{k}_0}}|}d\xi }\hfill \\ {\displaystyle \lesssim {\int }_{-k_0}^{\frac{k_0}{t}-k_0}\frac{|\xi +k_0{|}^{l+1}}{|\xi +k_0-\frac{k}{\sqrt{48t{k}_0}}|}d\xi }\hfill \\ {\displaystyle ={\int }_0^{\frac{k_0}{t}}\frac{{\eta }^{l+1}}{|\eta -\frac{k}{\sqrt{48t{k}_0}}|}d\eta }\hfill \\ {\displaystyle \lesssim t^{-l}{\int }_0^{\frac{k_0}{t}}\frac{\eta }{|\eta -\frac{k}{\sqrt{48t{k}_0}}|}d\eta }\hfill \\ {\displaystyle \left\{\begin{array}{cc}\lesssim t^{-l}{t}^{-\frac{5}{2}}\lesssim t^{-l+1},\hfill & \mathrm{if}\mathrm{k}\ne 0,\hfill \\ =t^{-l}\frac{k_0}{t}\lesssim t^{-l+1},\hfill & \mathrm{if}\mathrm{k}=0,\hfill \end{array}\right.}\hfill \\ {\displaystyle |T_2|\lesssim {\int }_{\frac{k_0}{t}-k_0}^{k_0}\frac{|{\mathrm{e}}^{-2it\theta (\xi )}{f}_1(\xi )|}{|\xi +k_0-\frac{k}{\sqrt{48t{k}_0}}|}d\xi \le t^{-l}\frac{\sqrt{2}t}{k_0}(2k_0-\frac{k_0}{t})\lesssim t^{-l+1},}\hfill \end{array}$$

which are due to $f(k)=\mathrm{O}({(k+k_0)}^{l+1})$ and

$$|\xi +k_0-\frac{k}{\sqrt{48t{k}_0}}|\ge \frac{k_0}{\sqrt{2}t},\xi \in (\frac{k_0}{t}-k_0,k_0),k\in L_A,$$

respectively. By using Cauchy’s Theorem, we can have a similar estimate $|T_3|\lesssim t^{-l+1}$ through integrating along the contour $L_t$ in ${\mathbb{C}}_{+}$ instead of the interval $(\frac{k_0}{t}-k_0,k_0)$ on $\mathbb{R}$. Now, the estimate (193) is a consequence of those three estimates. The proof is finished.  □

Express

$$J^{A^o}={(I_4-{\omega }_{A^o-})}^{-1}(I_4+{\omega }_{A^o+}),$$

(201)

where

$${\omega }_{A^o}={\omega }_{A^o+}=\left\{\begin{array}{cc}\left[\begin{array}{cc}0& {({\delta }_A)}^2{(-k)}^{-2\nu i}{\mathrm{e}}^{\frac{i{k}^2}{2}}\gamma (-k_0)\\ 0& 0\end{array}\right],\hfill & k\in {\Sigma }_A^4,\hfill \\ \left[\begin{array}{cc}0& -{({\delta }_A)}^2{(-k)}^{-2\nu i}{\mathrm{e}}^{\frac{i{k}^2}{2}}\frac{\gamma (-k_0)}{1-|\gamma (-k_0){|}^2}\\ 0& 0\end{array}\right],\hfill & k\in {\Sigma }_A^2,\hfill \end{array}\right.$$

(202)

$${\omega }_{A^o}={\omega }_{A^o-}=\left\{\begin{array}{cc}\left[\begin{array}{cc}0& 0\\ -{({\delta }_A)}^{-2}{(-k)}^{2\nu i}{\mathrm{e}}^{-\frac{i{k}^2}{2}}{\gamma }^{†}(-k_0)& 0\end{array}\right],\hfill & k\in {\Sigma }_A^3,\hfill \\ \left[\begin{array}{cc}0& 0\\ {({\delta }_A)}^{-2}{(-k)}^{2\nu i}{\mathrm{e}}^{-\frac{i{k}^2}{2}}\frac{{\gamma }^{†}(-k_0)}{1-|\gamma (-k_0){|}^2}& 0\end{array}\right],\hfill & k\in {\Sigma }_A^1,\hfill \end{array}\right.$$

(203)

with

$${\delta }_A={\mathrm{e}}^{\chi (-k_0)-8\tau i}{(192\tau )}^{\frac{\nu i}{2}}.$$

(204)

Based on (193), (194) and Lemma 3.35 in [7], we can obtain

$$\parallel {\omega }_A-{\omega }_{A^o}{\parallel }_{{\mathcal{L}}^{\infty }({\Sigma }_A)\cap {\mathcal{L}}^1({\Sigma }_A)\cap {\mathcal{L}}^2({\Sigma }_A)}{\lesssim }_{k_0}\frac{lnt}{\sqrt{t}}.$$

(205)

Therefore, we have

$$\begin{array}{c}{\displaystyle {\int }_{{\Sigma }_A^{\prime }}\left({(1-C_{{\omega }_A^{\prime }})}^{-1}{I}_4\right)(\xi ){\omega }_A^{\prime }(\xi )d\xi }\hfill \\ {\displaystyle ={\int }_{{\widehat{\Sigma }}_A^{\prime }}\left({(1-C_{{\omega }_A^{\prime }})}^{-1}{I}_4\right)(\xi ){\widehat{\omega }}_A^{\prime }(\xi )d\xi }\hfill \\ {\displaystyle ={\int }_{{\widehat{\Sigma }}_A^{\prime }}\left(N_A^{-1}{(1-C_{{\omega }_A^{\prime }})}^{-1}{N}_A{I}_4\right)(\xi ){\widehat{\omega }}_A^{\prime }(\xi )d\xi }\hfill \\ {\displaystyle ={\int }_{{\widehat{\Sigma }}_A^{\prime }}\left({(1-C_{{\omega }_A^{\prime }})}^{-1}{I}_4\right)((\xi +k_0)\sqrt{48t{k}_0})N_A{\widehat{\omega }}_A^{\prime }((\xi +k_0)\sqrt{48t{k}_0})d\xi }\hfill \\ {\displaystyle =\frac{1}{\sqrt{48t{k}_0}}{\int }_{{\Sigma }_A}\left({(1-C_{{\omega }_A})}^{-1}{I}_4\right)(\xi ){\omega }_A(\xi )d\xi }\hfill \\ {\displaystyle =\frac{1}{\sqrt{48t{k}_0}}{\int }_{{\Sigma }_A}\left({(1-C_{{\omega }_{A^o}})}^{-1}{I}_4\right)(\xi ){\omega }_{A^o}(\xi )d\xi +\mathrm{O}(\frac{lnt}{t}).}\hfill \end{array}$$

Together with a similar argument for B, we can obtain

$$\begin{array}{cc}\hfill p(x,t)& =i\frac{1}{\sqrt{48t{k}_0}}{\left({\int }_{{\Sigma }_A}\left({(1-C_{{\omega }_{A^o}})}^{-1}{I}_4\right)(\xi ){\omega }_{A^o}(\xi )\frac{d\xi }{\pi }\right)}_{12}\hfill \\ & +i\frac{1}{\sqrt{48t{k}_0}}{\left({\int }_{{\Sigma }_B}\left({(1-C_{{\omega }_{B^o}})}^{-1}{I}_4\right)(\xi ){\omega }_{B^o}(\xi )\frac{d\xi }{\pi }\right)}_{12}+\mathrm{O}(\frac{lnt}{t}).\hfill \end{array}$$

(206)

For $k\in \mathbb{C}\setminus {\Sigma }_A$, we set

$$M^{A^o}(k)=I_4+{\int }_{{\Sigma }_A}\frac{\left({(1-C_{{\omega }_{A^o}})}^{-1}{I}_4\right)(\xi ){\omega }_{A^o}(\xi )}{\xi -k}\frac{d\xi }{2\pi i},$$

(207)

which solves the following RH problem

$$\left\{\begin{array}{c}{M}_{+}^{A^o}(k;x,t)=M_{-}^{A^o}(k;x,t)J^{A^o}(k;x,t),k\in {\Sigma }_A,\hfill \\ M^{A^o}(k;x,t)\to I_4,\mathrm{as}k\to \infty .\hfill \end{array}\right.$$

(208)

Particularly, from an asymptotic expansion

$$M^{A^o}(k)=I_4+\frac{M_1^{A^o}}{k}+\mathrm{O}(k^{-2}),k\to \infty ,$$

we get

$$M_1^{A^o}=-{\int }_{{\Sigma }_A}\left({(1-C_{{\omega }_{A^o}})}^{-1}{I}_4\right)(\xi ){\omega }_{A^o}(\xi )\frac{d\xi }{2\pi i}.$$

An analogous RH problem for $B^o$ on ${\Sigma }_B$ reads

$$\left\{\begin{array}{c}{M}_{+}^{B^o}(k;x,t)=M_{-}^{B^o}(k;x,t)J^{B^o}(k;x,t),k\in {\Sigma }_B,\hfill \\ M^{B^o}(k;x,t)\to I_4,\mathrm{as}k\to \infty ,\hfill \end{array}\right.$$

(209)

and its solution is given by

$$M^{B^o}(k)=I_4+{\int }_{{\Sigma }_B}\frac{\left({(1-C_{{\omega }_{B^o}})}^{-1}{I}_4\right)(\xi ){\omega }_{B^o}(\xi )}{\xi -k}\frac{d\xi }{2\pi i}.$$

(210)

The above jump matrix is defined by

$$J^{B^o}={(I_4-{\omega }_{B^o-})}^{-1}(I_4+{\omega }_{B^o+}),$$

(211)

where

$${\omega }_{B^o}={\omega }_{B^o+}=\left\{\begin{array}{cc}\left[\begin{array}{cc}0& {({\delta }_B)}^2{k}^{2\nu i}{\mathrm{e}}^{-\frac{i{k}^2}{2}}\gamma (k_0)\\ 0& 0\end{array}\right],\hfill & k\in {\Sigma }_B^1,\hfill \\ \left[\begin{array}{cc}0& -{({\delta }_B)}^2{k}^{2\nu i}{\mathrm{e}}^{-\frac{i{k}^2}{2}}\frac{\gamma (k_0)}{1-|\gamma (k_0){|}^2}\\ 0& 0\end{array}\right],\hfill & k\in {\Sigma }_B^3,\hfill \end{array}\right.$$

(212)

$${\omega }_{B^o}={\omega }_{B^o-}=\left\{\begin{array}{cc}\left[\begin{array}{cc}0& 0\\ -{({\delta }_B)}^{-2}{k}^{-2\nu i}{\mathrm{e}}^{\frac{i{k}^2}{2}}{\gamma }^{†}(k_0)& 0\end{array}\right],\hfill & k\in {\Sigma }_B^2,\hfill \\ \left[\begin{array}{cc}0& 0\\ {({\delta }_B)}^{-2}{k}^{-2\nu i}{\mathrm{e}}^{\frac{i{k}^2}{2}}\frac{{\gamma }^{†}(k_0)}{1-|\gamma (k_0){|}^2}& 0\end{array}\right],\hfill & k\in {\Sigma }_B^4,\hfill \end{array}\right.$$

(213)

with

$${\delta }_B={\mathrm{e}}^{\chi (k_0)+8\tau i}{(192\tau )}^{-\frac{\nu i}{2}}.$$

(214)

Based on (201)–(204) and (211)–(214), we can show that

$$J^{A^o}(k)={(J^{B^o})}^{*}(-k^{*}).$$

By uniqueness,

$$M^{A^o}(k)={(M^{B^o})}^{*}(-k^{*})$$

and thus, we have

$$M_1^{A^o}=-{(M_1^{B^o})}^{*}.$$

Now from (206), we obtain

$$p(x,t)=\frac{1}{\sqrt{12t{k}_0}}{(M_1^{A^o}-{(M_1^{A^o})}^{*})}_{12}+\mathrm{O}(\frac{lnt}{t}).$$

(215)

4.7. The Model RH Problem and Its Solution

To determine ${(M^{A^o})}_{12}$ explicitly, we solve a model RH problem

$${\Phi }_{+}(k)={\Phi }_{-}(k)v(k_0),v(k_0)={(-k)}^{-i\nu \widehat{\Lambda }}{\mathrm{e}}^{\frac{1}{4}i{k}^2\widehat{\Lambda }}{({\delta }_A)}^{\widehat{\Lambda }}{J}^{A^o}.$$

(216)

The solution to this RH problem is given by

$$\Phi (k)=G(k){(-k)}^{i\nu \Lambda }{\mathrm{e}}^{-\frac{1}{4}i{k}^2\Lambda },G(k)={({\delta }_A)}^{\widehat{\Lambda }}{M}^{A^o}={({\delta }_A)}^{\Lambda }{M}^{A^o}(k){({\delta }_A)}^{-\Lambda },$$

(217)

where ${({\delta }_A)}^{\Lambda }=\mathrm{diag}({({\delta }_A)}^{-1},{\delta }_A{I}_3)$ and ${({\delta }_A)}^{-\Lambda }={({({\delta }_A)}^{\Lambda })}^{-1}$.

Since the jump matrix $v(k_0)$ does not depend on k along each ray of ${\Sigma }_A$, we have

$$\frac{d{\Phi }_{+}(k)}{dk}=\frac{d{\Phi }_{-}(k)}{dk}v(k_0).$$

(218)

Together with (216), this implies that $\frac{d\Phi (k)}{dk}{\Phi }^{-1}(k)$ has no jump discontinuity along any of the four rays. Directly from the solution, we obtain

$$\begin{array}{cc}\hfill \frac{d\Phi (k)}{dk}{\Phi }^{-1}(k)& =\frac{dG(k)}{dk}{G}^{-1}(k)-\frac{1}{2}ikG(k)\Lambda G^{-1}(k)+\frac{i\nu }{k}G(k)\Lambda G^{-1}(k)\hfill \\ & =\mathrm{O}(\frac{1}{k})-\frac{1}{2}ik\Lambda +\frac{1}{2}i{\delta }_A^{\Lambda }[\Lambda ,M_1^{A^o}]{\delta }_A^{-\Lambda }.\hfill \end{array}$$

It then follows from Liouville’s theorem that

$$\frac{d\Phi (k)}{dk}+\frac{1}{2}ik\Lambda \Phi (k)=\eta \Phi (k),$$

(219)

where

$$\eta =\frac{1}{2}i{\delta }_A^{\Lambda }[\Lambda ,M_1^{A^o}]{\delta }_A^{-\Lambda }=\left[\begin{array}{cc}0& {\eta }_{12}\\ {\eta }_{21}& 0\end{array}\right].$$

(220)

Particularly, we have

$${(M_1^{A^o})}_{12}=i{\delta }_A^2{\eta }_{12}.$$

(221)

We partition $\Phi (k)$ into the following form

$$\Phi (k)=\left[\begin{array}{cc}{\Phi }_{11}(k)& {\Phi }_{12}(k)\\ {\Phi }_{21}(k)& {\Phi }_{22}(k)\end{array}\right],$$

(222)

where ${\Phi }_{11}(k)$ is a scalar and ${\Phi }_{22}(k)$ is a $3\times 3$ matrix. From the differential Equation (219) for $\Phi$, we obtain

$$\begin{array}{c}\frac{d^2{\Phi }_{11}(k)}{d{k}^2}=\left({\eta }_{12}{\eta }_{21}+\frac{i}{2}-\frac{k^2}{4}\right){\Phi }_{11}(k),\hfill \\ {\eta }_{12}{\Phi }_{21}(k)=\frac{d{\Phi }_{11}(k)}{dk}-\frac{i}{2}k{\Phi }_{11}(k),\hfill \\ \frac{d^2{\eta }_{12}{\Phi }_{22}(k)}{d{k}^2}=\left({\eta }_{12}{\eta }_{21}-\frac{i}{2}-\frac{k^2}{4}\right){\eta }_{12}{\Phi }_{22}(k),\hfill \\ {\Phi }_{12}(k)=\frac{1}{{\eta }_{12}{\eta }_{21}}\left(\frac{d{\eta }_{12}{\Phi }_{22}(k)}{dk}+\frac{i}{2}k{\eta }_{12}{\Phi }_{22}(k)\right),\hfill \end{array}$$

where

$${\eta }_{12}{\eta }_{21}=\nu >0$$

(223)

provided that $\gamma (k_0)\ne 0$ (note that the case of $\gamma (k_0)=0$ is, of course, trivial).

As is well known, the following Weber’s equation

$$\frac{d^{2}g(\zeta )}{d{\zeta }^2}+(a+\frac{1}{2}-\frac{{\zeta }^2}{4})g(\zeta )=0$$

has a general solution

$$g(\zeta )=c_1{D}_a(\zeta )+c_2{D}_a(-\zeta ),$$

where $c_1,c_2$ are arbitrary constants and $D_a(\zeta )$ denotes the standard (entire) parabolic-cylinder function which satisfies

$$\frac{d{D}_a(\zeta )}{d\zeta }+\frac{\zeta }{2}{D}_a(\zeta )-a{D}_{a-1}(\zeta )=0,$$

(224)

$$D_a(\pm \zeta )=\frac{\Gamma (a+1){\mathrm{e}}^{\frac{i\pi a}{2}}}{\sqrt{2\pi }}{D}_{-a-1}(\pm i\zeta )+\frac{\Gamma (a+1){\mathrm{e}}^{-\frac{i\pi a}{2}}}{\sqrt{2\pi }}{D}_{-a-1}(\mp i\zeta ),$$

(225)

$\Gamma (·)$ being the Gamma function. From the textbook [54] (see pp. 347–349), we know that as $\zeta \to \infty$,

$$D_a(\zeta )=\left\{\begin{array}{cc}{\zeta }^a{\mathrm{e}}^{-\frac{{\zeta }^2}{4}}\left(1+\mathrm{O}({\zeta }^{-2})\right),\hfill & |arg\zeta |<\frac{3\pi }{4},\hfill \\ \left({\zeta }^a{\mathrm{e}}^{-\frac{{\zeta }^2}{4}}-\frac{\sqrt{2\pi }}{\Gamma (-a)}{\mathrm{e}}^{a\pi i}{\zeta }^{-a-1}{\mathrm{e}}^{\frac{{\zeta }^2}{4}}\right)\left(1+\mathrm{O}({\zeta }^{-2})\right),\hfill & \frac{\pi }{4}<arg\zeta <\frac{5\pi }{4},\hfill \\ \left({\zeta }^a{\mathrm{e}}^{-\frac{{\zeta }^2}{4}}-\frac{\sqrt{2\pi }}{\Gamma (-a)}{\mathrm{e}}^{-a\pi i}{\zeta }^{-a-1}{\mathrm{e}}^{\frac{{\zeta }^2}{4}}\right)\left(1+\mathrm{O}({\zeta }^{-2})\right),\hfill & -\frac{5\pi }{4}<arg\zeta <-\frac{\pi }{4}.\hfill \end{array}\right.$$

(226)

Denote $a=-i{\eta }_{12}{\eta }_{21}$ and then

$${\eta }_{12}{\eta }_{21}\pm \frac{i}{2}=\pm i(\pm a+\frac{1}{2}).$$

Thus we find

$$\begin{array}{c}{\Phi }_{11}(k)=d_1{D}_{-a}({\mathrm{e}}^{-\frac{\pi i}{4}}k)+d_2{D}_{-a}({\mathrm{e}}^{\frac{3\pi i}{4}}k),\hfill \\ {\eta }_{12}{\Phi }_{22}(k)=d_3{D}_a({\mathrm{e}}^{\frac{\pi i}{4}}k)+d_4{D}_a({\mathrm{e}}^{-\frac{3\pi i}{4}}k),\hfill \end{array}$$

where $d_1$ and $d_2$ are constants, and $d_3$ and $d_4$ are row vectors of constants. Note that as $argk\in (\frac{3\pi }{4},\frac{7\pi }{4})$ and $k\to \infty$,

$$\begin{array}{c}{\Phi }_{11}(k){(-k)}^{\nu i}{\mathrm{e}}^{-\frac{i{k}^2}{4}}\to 1,\hfill \\ {\Phi }_{22}(k){(-k)}^{-\nu i}{\mathrm{e}}^{\frac{i{k}^2}{4}}\to I_3.\hfill \end{array}$$

Thus, for $argk\in (\frac{3\pi }{4},\frac{5\pi }{4})$, we have

$${\Phi }_{11}(k)={\mathrm{e}}^{\frac{\pi \nu }{4}}{D}_{-a}({\mathrm{e}}^{\frac{3\pi i}{4}}k),{\eta }_{12}{\Phi }_{22}(k)={\eta }_{12}{\mathrm{e}}^{\frac{\pi \nu }{4}}{D}_a({\mathrm{e}}^{-\frac{3\pi i}{4}}k),$$

and further,

$${\eta }_{12}{\Phi }_{21}=a{\mathrm{e}}^{\frac{\pi (\nu -i)}{4}}{D}_{-a-1}({\mathrm{e}}^{\frac{3\pi i}{4}}k),{\Phi }_{12}=-{\eta }_{12}{\mathrm{e}}^{\frac{\pi (\nu +3i)}{4}}{D}_{a-1}({\mathrm{e}}^{-\frac{3\pi i}{4}}k).$$

For $argk\in (\frac{5\pi }{4},\frac{7\pi }{4})$, we have

$${\Phi }_{11}(k)={\mathrm{e}}^{\frac{\pi \nu }{4}}{D}_{-a}({\mathrm{e}}^{\frac{3\pi i}{4}}k),{\eta }_{12}{\Phi }_{22}(k)={\eta }_{12}{\mathrm{e}}^{-\frac{3\pi \nu }{4}}{D}_a({\mathrm{e}}^{\frac{\pi i}{4}}k),$$

and further,

$${\eta }_{12}{\Phi }_{21}=a{\mathrm{e}}^{\frac{\pi (\nu -i)}{4}}{D}_{-a-1}({\mathrm{e}}^{\frac{3\pi i}{4}}k),{\Phi }_{12}=-{\eta }_{12}{\mathrm{e}}^{-\frac{\pi (i+3\nu )}{4}}{D}_{a-1}({\mathrm{e}}^{\frac{\pi i}{4}}k).$$

Along the ray $argk=\frac{5\pi }{4}$, we have

$${\Phi }_{+}(k)={\Phi }_{-}(k)\left[\begin{array}{cc}1& \gamma (-k_0)\\ 0& I_3\end{array}\right],$$

from which it follows that

$${\eta }_{12}{\mathrm{e}}^{-\frac{\pi (i+3\nu )}{4}}{D}_{a-1}({\mathrm{e}}^{\frac{\pi i}{4}}k)=-{\mathrm{e}}^{\frac{\pi \nu }{4}}{D}_{-a}({\mathrm{e}}^{\frac{3\pi i}{4}}k)\gamma (-k_0)+{\eta }_{12}{\mathrm{e}}^{\frac{\pi (\nu +3i)}{4}}{D}_{a-1}({\mathrm{e}}^{-\frac{3\pi i}{4}}k).$$

(227)

In addition, based on (225), we obtain

$$D_{-a}({\mathrm{e}}^{\frac{3\pi i}{4}}k)=\frac{\Gamma (-a+1)}{\sqrt{2\pi }}{\mathrm{e}}^{\frac{\pi ai}{2}}{D}_{a-1}({\mathrm{e}}^{\frac{\pi i}{4}}k)+\frac{\Gamma (-a+1)}{\sqrt{2\pi }}{\mathrm{e}}^{-\frac{\pi ai}{2}}{D}_{a-1}({\mathrm{e}}^{-\frac{3\pi i}{4}}k).$$

(228)

Upon plugging (228) into (227), separating the coefficients of the two independent special functions presents

$${\eta }_{12}=-\frac{\Gamma (-a+1)}{\sqrt{2\pi }}{\mathrm{e}}^{\frac{\pi \nu }{2}+\frac{\pi i}{4}}\gamma (-k_0)=-\frac{\nu \Gamma (-i\nu )}{\sqrt{2\pi }}{\mathrm{e}}^{\frac{\pi \nu }{2}-\frac{\pi i}{4}}\gamma (-k_0).$$

(229)

Finally, we conclude that (4) is a consequence of (215), (221) and (229).

5. Concluding Remarks

The paper is dedicated to determination of long-time asymptotics of the three-component coupled mKdV system, based on an associated Riemann-Hilbert (RH) problem. The crucial step is to deform the associated RH problem to the one which is solvable explicitly, and estimate small errors between solutions to different deformed RH problems. This is an example of applications of the nonlinear steepest descent method to asymptotics in the case of $4\times 4$ matrix spectral problems.

The nonlinear steepest descent method is powerful in exploring long-time asymptotics for integrable systems and even nonlocal integrable systems (see also, e.g., [55]). Moreover, it has been generalized to determine asymptotics of initial-boundary value problems of integrable systems on the half-line (see, e.g., [56,57,58]), and asymptotics of integrable systems whose RH problems possess rational phases (see, e.g., [16]) or non-analytic jumps (see, e.g., [19]).

There are various other approaches in the field of integrable systems, which include the Hirota direct method [59], the generalized bilinear technique [60], the Wronskian technique [61,62] and the Darboux transformation [63]. Connections between different approaches would be interesting. About coupled mKdV equations, there are many other studies such as integrable couplings [64], super hierarchies [65] and fractional analogous equations [66,67], and an important topic for further study is long-time asymptotics of those generalized integrable counterparts via the nonlinear steepest descent method. It is hoped that our result could be helpful in computing limiting behaviors of solutions incorporating features of other exact solutions, such as lumps [68,69], from the perspective of steepest descent based on RH problems.