An Adaptive Multi-Swarm Competition Particle Swarm Optimizer for Large-Scale Optimization

Abstract

As a powerful tool in optimization, particle swarm optimizers have been widely applied to many different optimization areas and drawn much attention. However, for large-scale optimization problems, the algorithms exhibit poor ability to pursue satisfactory results due to the lack of ability in diversity maintenance. In this paper, an adaptive multi-swarm particle swarm optimizer is proposed, which adaptively divides a swarm into several sub-swarms and a competition mechanism is employed to select exemplars. In this way, on the one hand, the diversity of exemplars increases, which helps the swarm preserve the exploitation ability. On the other hand, the number of sub-swarms adaptively changes from a large value to a small value, which helps the algorithm make a suitable balance between exploitation and exploration. By employing several peer algorithms, we conducted comparisons to validate the proposed algorithm on a large-scale optimization benchmark suite of CEC 2013. The experiments results demonstrate the proposed algorithm is effective and competitive to address large-scale optimization problems.

1. Introduction

Particle swarm optimization (PSO), as an active tool in dealing with optimization problems, have been widely applied to various kinds of optimization problems [1,2], such as industry, transportation, economics and so forth. Especially, in current years, with the rising development of the industrial network, many optimization problems with complex properties of nonlinearity, multi-modularity, large-scale and so on are proposed. To well address these problems, PSO exhibits powerful abilities to meet the requirement of practical demands and thus gains much attention in deep research and further applications [3,4]. However, according to the current research, there exists a notorious problem in PSO: the algorithm lacks the ability in diversity maintenance and therefore the solutions trend to local optima, especially for complex optimization problems. In the algorithm design, a large weight on diversity maintenance will break down the convergence process, while a small weight on diversity maintenance will cause a poor ability to get rid of local optima. Therefore, as a crucial aspect in the design of PSO, population diversity maintenance has been a hot issue and drawn much attention globally.

To improve PSO’s ability in population diversity maintenance, many works are conducted, which can be generally categorized into the following aspects: (1) mutation strategy [5,6,7,8]; (2) distance-based indicator [9,10,11]; (3) adaptive control strategy [12,13,14]; (4) multi-swarm strategy [15,16,17,18,19,20,21]; and (5) hybridization technology [22,23,24]. However, in the five categories, there exists many parameters and laws in the design of PSO. Improper parameters or laws will negatively affect an algorithm’s performance. To provide an easy tool for readers in the design of PSO, Spolaor [25] and Nobile [26] proposed reboot strategies based PSO and fuzzy self-tuning PSO, respectively, to provide a simple way to tube PSO parameters. However, for large-scale optimization, it is also a challenge for PSO implementation. To address this issue, in this paper, we propose a novel algorithm named adaptive multi-swarm competition PSO (AMCPSO), which randomly divides the whole swarm into several sub-swarms. In each sub-swarm, a competitive mechanism is adopted to select a winner particle who attracts the poor particles in the same sub-swarm. The number of winners, namely exemplars, is equal to the number of sub-swarms. In multi-swarm strategy, each exemplar is selected from each sub-swarm. In this way, the diversity of exemplars increases, which is helpful for algorithms to eliminate the effects of local optima.

The contributions of this paper are listed as follows. First, in this proposed algorithm, the exemplars are all selected from the current swarm, rather than personal historical best positions. In this way, no historical information is needed in the design of the algorithm. Second, we consider different optimization stages and propose a law to adaptively adjust the size of sub-swarms. For an optimization process, in the beginning, exploration ability is crucial for algorithms to explore searching space. To enhance algorithm’s ability in exploration, we set a large number of sub-swarms, which means a large number of exemplars will be obtained. On the other hand, in the late stage, algorithms should pay more attention to exploitation for enhancing the accuracy of optimization results. Hence, a small number of exemplars is preferred. Third, to increase the ability of diversity maintenance, we do not employ the global best solution, but the mean value of each sub-swarm, which is inspired by Arabas and Biedrzycki [27]. According to Arabas and Biedrzycki [27], the quality of mean value has a higher probability to be better than that of a global best solution. In addition, because the mean value is calculated by the whole swarm, it has a high probability to be updated, unlike the global best solution, which is consistent for several generations.

The rest of this paper is organized as follows. Section 2 introduces related work on diversity maintenance for PSO and some comments and discussions on the works are presented. In Section 3, we design an adaptive multi-swarm competition PSO. The algorithm structure and pseudo-codes are presented in the section. We employed several state-of-the-art algorithms to compare the proposed algorithm on large-scale optimization problems and analyzed the performance, which is presented in Section 4. Finally, we end this paper with conclusions and present our future work in Section 5.

2. Related Work

In standard PSO, each particle has two attributes: velocity and position. The update mechanism for the two attributes is given in Equation (1).

$$\begin{array}{ccc}\hfill v_i(t+1)& =& \omega v_i(t)+r_1\ast c_1(pbes{t}_i-p_i(t))+r_2\ast c_2(gbest-p_i(t))\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill p_i(t+1)& =& p_i(t)+v_i(t)\hfill \end{array}$$

(2)

where $v_i$ and $p_i$ are the velocity and position of ith particle, t is the index of generation, $pbes{t}_i$ is the best position that particle i found thus far, and $gbest$ is the global best position. $r_1$ and $r_2$$\in {[0,1]}^D$ are two random values and $c_1$ and $c_2$ are the acceleration coefficients. On the right side of the velocity update equation, there are three components. The first one is called inertia term, which retains the particle’s own property, e.g. its current velocity. The weight of the property is controlled by $\omega$ named inertia weight. The second component and the third component are called cognitive component and social component, respectively. The two components guide the ith particle to move towards better positions. Since $gbest$ guides the whole swarm, if it is in local optimal position, the standard PSO has a poor ability to get rid of it. Moreover, the algorithm gets premature convergence.

To improve PSO’s ability in diversity maintenance, many works are conducted. As mentioned in Section 1, there are generally five ways. The first is about the mutation operator. In most canonical swarm intelligence, there is no mutation operator. To pursue a better performance, several kinds of mutation, such as Gaussian mutation, wavelet mutation, etc., are implemented to SI [6,7] so that the population diversity can be regained to some extent. In [5], Sun et al. defined a lower distance-based limit. Once the diversity is below the limit, a mutation happens on the current global best individual. Wang proposed a Gauss mutation PSO in [8] to help the algorithm retain population diversity. Nevertheless, mutation rate and mutation degree are difficult to predefine. A small mutation rate/degree plays a weak role to increase population diversity, while a large rate/degree is harmful to the algorithm’s convergence, as mentioned in [28].

The second way is based on the distance-based indicator. The diversity maintenance is considered as a compensation term. During the optimization process, the distances among particles are continuously monitored. By predefining a limit, if the diversity situation is worse than the threshold, some strategies are activated to increase the distance. In [9], the authors used criticality to depict the diversity status of a swarm. During the optimization process, if the criticality value is larger than a predefined threshold, a relocating strategy is activated to disperse the particles. In this way, particles will not be too close. Inspired from the electrostatics, Blackwell and Bentley endowed particles with a new attribute, called charging status [10]. For two charged particles, an electrostatic reaction is launched to modulate their velocities. The same authors presented a similar idea in a follow up work [11]. The big challenge in this kind of method is the difficulty to predefine a suitable threshold as for the requirement of diversity is different for different problems or different optimization phases.

The third method to increase swarm diversity is based on an adaptive way. According to the authors of [12,13], the parameters in the velocity and position update mechanism play different roles during the whole optimization process. At the beginning phase, exploration helps the swarm explore the searching space, while exploitation occupies a priority position in the later phase of an optimization process. According to the update mechanism in standard PSO, the values of $\omega$, $c_1$ and $c_2$ are influential to the weights of exploitation and exploration. Hence, time-varying weights are employed in [12,13]. In [12], the value of $\omega$ decreases from 0.9 to 0.4, which changes the focus from exploration to exploitation. In [13,14], some mathematical functions are empirically established to dynamically and adaptively adjust parameters during the optimization process. However, the performances of these proposed algorithms are very sensitive to the adaptive rules which depend much on authors’ experiences. Therefore, it is not easy to apply these methods in real applications.

Hybridization is also an effective way to help integrate the advantages of different meta-heuristics. To improve PSO’s ability in diversity maintenance, some works are conducted to prevent particles from searching discovered areas, which is similar to the idea of tabu searching. The prevention methods including deflecting, stretching, repulsion and so forth [22]. A cooperative strategy is employed to improve PSO in [23]. In the proposed algorithm, the essence of the algorithm divides the problem into several subproblems. By solving the sub-problems, final solutions can be integrated by the sub-solutions. Similar ideas are also investigated in [24].

As a feasible and effective way, the multi-swarm strategy is well applied to PSO. Generally, there are two kinds of design in multi-swarm strategy. The first one is the niching strategy. By defining a niche radius, the particles in one niche are considered as similar individuals and only the particles in the different niche will be selected for information recombination [16]. In the standard niching strategy, the algorithm’s performance is sensitive to the niche radius [17]. To overcome this problem, Li proposed a parameter-free method in [15]. The author constructed a localized ring topology instead of the niche radius. In addition, in [21], the authors proposed a multi-swarm particle swarm optimizer for large-scale optimization problems. However, the size of each sub-swarm is fixed, which means that the strategy does not consider the swarm size to dynamically manage exploitation and exploration. The second method is to assign different tasks to different sub-swarms. In [18], the authors proposed to regulate population diversity according to predefined value named decreasing rate of the number of sub-swarms. In [20], the authors defined a frequency to switch exploitation and exploration for different sub-swarms. In this way, the algorithm can give considerations to convergence speed and diversity maintenance. In [19], the authors divided the swarm into pairs. By comparing the fitness in pairs, the loser will learn from the winner, which increases the diversity of exemplars. However, the learning efficiency decreases since the learn may happen between two good particles or two bad particles.

However, in the above methods, there is still no research focusing on large-scale optimization problems. To address large-scale optimization problems, there are generally two ways, which are cooperation co-evolution and balancing of exploration and exploitation. For the first kind of methods, a cooperative co-evolution (CC) framework is proposed, which divides a whole dimension into several segments. For the segments, conventional evolutionary algorithms are employed to address them to access sub-solutions. By integrating the sub-solutions, the final solution will be obtained. The framework now has been well applied to various kinds of evolutionary algorithms. Cooperative coevolution differential evolution (DECC), proposed by Omidvar et al., is a series of DE algorithm for large-scale optimization problems. DECC-DG2 first groups the variables considering the interrelationship between them and then optimizes the sub-components using DECC [29]. CBCC3 was proposed by Omidvar for large-scale optimization based on Contribution-Based Cooperative Co-evolution (CBCC). It includes an exploration phase that is controlled by a random method and an exploitation phase controlled by a contribution information based mechanism where the contribution information of a given component is computed based on the last non-zero difference in the objective value of two consecutive iterations [30]. In [31], the authors applied the CC-framework to PSO and obtained satisfactory performance. However, the CC framework will cost huge computational resources in the sub-space division. In the second way to address large-scale optimization problems, researchers propose novel operators of exploitation and exploration. In addition, the balance between the two abilities is also crucial to the final performance. Cheng and Jin proposed SL-PSO (social learning PSO) i [32]. In the algorithm, the authors proposed novel ideas in dealing with the selection of poor particles. However, the algorithm’s performance is sensitive to parameter setting.

To summarize, in the current research, the algorithms either lack parameter tuning during the optimization process or aggravate a huge burden to computational resources. To address the problems, in Section 3, we propose an adaptive multi-swarm competition PSO.

3. Adaptive Multi-Swarm Competition PSO

As mentioned in Section 1, the global best position always attracts all particles until it is updated. When the global best position gets trapped into local optima, it is very difficult for the whole swarm to get rid of it. Hence, the optimization progress stagnates or a premature convergence occurs. To overcome this problem, in this paper, we employ an adaptive multi-swarm strategy and propose a novel swarm optimization algorithm termed adaptive multi-swarm competition PSO (AMCPSO). From the beginning to the end of the optimization process, we uniformly and randomly divide the whole swarm into several sub-swarms. In each sub-swarm, the particles compare with each other. The losers will learn from the winner in the same sub-swarm, while the winners do nothing in the generation. The number of the winners is equal to the number of sub-swarms and the number is adaptive to the optimization process. At the beginning stages, a large number of sub-swarms will help algorithm increase the diversity of exemplars and explore the searching space. With the optimization process, the number of sub-swarms decreases in the algorithm’s exploitation. On the one hand, for each generation, there are several exemplars, i.e., winners, for losers’ updating. Even some exemplars are in local optimal positions, they will not affect the whole swarm. On the other hand, since we divide the swarm randomly, both winners and losers may be different, which means the exemplars are not consistent for many generations. In this way, the ability of diversity maintenance for the whole swarm is improved. Compared with the standard PSO, we abandon the historical information, e.g., the personal historical best position, etc., which is easier for users in implementations. Inspired by Arabas and Biedrzycki [27], the quality of mean value has a higher probability to be better than that of a global best solution. Therefore, we employ the mean position of the whole swarm to attract all particles. On the one hand, the global information can be achieved in particles update. On the other hand, the mean position generally changes for every generation, which has a large probability to avoid local optima. For the proposed algorithm, the velocity and position update mechanisms are given in Equation (3).

$$\begin{array}{ccc}\hfill v_{l\_i}(t+1)& =& \omega v_{l\_i}(t)+r_1\ast c_1(p_w(t)-p_{l\_i}(t))+r_2\ast c_2(p_{mean}-p_{l\_i}(t))\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill p_{l\_i}(t+1)& =& p_{l\_i}(t)+v_{l\_i}(t)\hfill \end{array}$$

(4)

where t records the index of generation, i is the index of losers in each sub-swarm, and v and p are velocity and position, respectively, for each particle. The subscript l means the loser particles, while the subscript w means the winner particle in the same sub-swarm. $p_{mean}$ is employed as global information to depict the mean position of the whole swarm. $\omega$, called the inertia coefficient, is used to control the weight of particle’s own velocity property. $c_1$ and $c_2$ are cognitive coefficient and social coefficient, respectively. $r_1$ and $r_2$$\in [0,1]$ are parameters to control the weights of the cognitive component and social component, respectively. In the proposed algorithm, a number of sub-swarms is involved, which also defines the number of exemplars in advance. To help algorithm change the focus from exploration to exploitation, in this paper, we employ an adaptive strategy for the division strategy, which means that the number of sub-swarms are not consistent, but a varying number from a large number of sub-swarms to a small number. The number of the sub-swarms is set according to experimental experience and presented as follows.

$$m=round\left(g{s}_{ini}-0.9g{s}_{ini}\ast \left(1-exp\left(-\frac{FEs}{Max\_Gen\ast Dr}\right)\right)\right);$$

(5)

where $round(\Omega )$ is the symbol to round a real value $\Omega$, $g{s}_{ini}$ is the initial number of sub-swarms, $Max\_Gen$ is maximum generation limit, and $Dr$ is used to control the decreasing rate. A small value of $Dr$ causes a sharp decreasing for the number of sub-swarms, while a large value of $Dr$ provides a gentle slope for number decreasing. In Equation (5), the population size of each sub-swarm increases from 5‰ to 5%. For Equation (5), it provides an adaptive way to set the number of sub-swarms, namely m. Meanwhile, the number of exemplars is also adaptive. Considering that, for some generations, the whole population size cannot exact divide m, we randomly select particles with size of the residual and do nothing for them in the generation, which means at most 5% particles are not involved in the update. However, in the algorithm’s implementation, we use maximum fitness evaluations as termination condition to guarantee adequate runs for the algorithm. The pseudo-codes of AMCPSO are given in Algorithm 1.

Algorithm 1: Pseudo-codes of adaptive multi-swarm particle swarm optimization.

Input:  Number of particles $ps$, parameters $omega$, $c_1$, $c_2$, Maximum number of fitness evaluations $Max\_FEs$    Output:  The current global best particle

1  Randomly generate a swarm P and evaluate their fitness f.; 2  $Loop$: Calculate the mean position according to the whole swarm’s positions; 3  Calculate m (the size of each sub-swarm) by Equation (5); 4  Randomly select $ps-mod(ps,m)$ particles for update; 5  In each sub-swarm, compare the particles according to their fitness, and select the local best particle by Equation (3); 6  Up date $FEs$; 7  If $FEs\ge Max\_FEs$, output the current global best particle; Otherwise, goto $Loop$;

For the proposed algorithm, the analysis on the time complexity is presented as follows. According to Algorithm 1, the time complexity for the sub-swarm division is $O(m)$, while the calculation of the mean value in each sub-swarm is also $O(m)$. Since the two operations do not aggravate the burden of computational cost, the main computational cost in the proposed algorithm is the update of each particle, which is $O(mn)$. It is an inevitable cost in most swarm-based evolutionary optimizers. Therefore, the whole time cost of the proposed algorithm is $O(mn)$, where m is the swarm size and n is the search dimensionality.

4. Experiments and Discussions

Experimental Settings

As explained above, large-scale optimization problems demand an algorithm much ability in balancing of diversity maintenance and convergence. To validate the performance of the proposed algorithm, we employed a benchmark suite in CEC 2013 on large-scale optimization problems [33]. In the performance comparisons, four popular algorithms were adopted: CBCC3 [30], DECC-dg [24], DECC-dg2 [29] and SL-PSO [34]. The four algorithms are proposed to address large-scale optimization problems in the corresponding papers. DECC-dg and DECC-dg2 are two improved DECC algorithms with differential evolution strategy [24,29]. SL-PSO was proposed by Cheng [34] to address large-scale optimization problems and achieve competitive performance. For the comparison, we ran each algorithm 25 times to pursue an average performance. The termination condition for each run was set by the maximum number of fitness evaluations (FEs) predefined as $3\times {10}^6$. The parameters of the peer algorithms were set as the same as in their reported paper. For the proposed algorithm AMCPSO, we set the parameter as follows. For the $g{s}_{ini}$, we set the value as 20, which means the number of sub-swarms increases from 2 to 20. $c_1$ and $c_2$ were set as 1 and 0.001. The performances of the five algorithms are presented in Table 1.

Table 1. The experimental results of 1000-dimensional IEEE CEC’ 2013 benchmark functions with fitness evaluations of $3\times {10}^6$.

Function	Quality	SLPSO	CBCC-3	DECC-dg	DECC2	AMCPSO
	Mean	3.70$\times {10}^{-14}$	8.65$\times {10}^5$	2.79$\times {10}^6$	8.65$\times {10}^5$	4.55$\times {10}^{-2}$
$F_1$	Std	1.44$\times {10}^{-15}$	2.27$\times {10}^4$	6.70$\times {10}^5$	2.27$\times {10}^4$	4.92$\times {10}^{-3}$
	Mean	6.70$\times {10}^3$	1.41$\times {10}^4$	1.41$\times {10}^4$	1.41$\times {10}^4$	2.51$\times {10}^3$
$F_2$	Std	4.98$\times {10}^1$	3.02$\times {10}^2$	3.03$\times {10}^2$	3.02$\times {10}^2$	2.61$\times {10}^2$
	Mean	2.16$\times {10}^1$	2.06$\times {10}^1$	2.07$\times {10}^1$	2.06$\times {10}^1$	2.15$\times {10}^1$
$F_3$	Std	1.14$\times {10}^{-3}$	1.69$\times {10}^{-3}$	2.19$\times {10}^{-3}$	1.69$\times {10}^{-3}$	2.16$\times {10}^{-3}$
	Mean	1.20$\times {10}^{10}$	3.39$\times {10}^7$	6.72$\times {10}^{10}$	2.51$\times {10}^8$	1.12$\times {10}^{10}$
$F_4$	Std	5.54$\times {10}^8$	3.48$\times {10}^6$	5.76$\times {10}^9$	1.89$\times {10}^7$	1.49$\times {10}^9$
	Mean	7.58$\times {10}^5$	2.14$\times {10}^6$	3.13$\times {10}^6$	2.74$\times {10}^6$	4.54$\times {10}^5$
$F_5$	Std	2.14$\times {10}^4$	8.31$\times {10}^4$	1.23$\times {10}^5$	5.66$\times {10}^4$	3.14$\times {10}^4$
	Mean	1.06$\times {10}^6$	1.05$\times {10}^6$	1.06$\times {10}^6$	1.06$\times {10}^6$	1.06$\times {10}^6$
$F_6$	Std	1.64$\times {10}^2$	6.61$\times {10}^2$	3.70$\times {10}^2$	4.50$\times {10}^2$	2.19$\times {10}^2$
	Mean	1.73$\times {10}^7$	2.95$\times {10}^7$	3.45$\times {10}^8$	8.93$\times {10}^7$	4.40$\times {10}^6$
$F_7$	Std	1.49$\times {10}^6$	5.44$\times {10}^6$	7.60$\times {10}^7$	7.16$\times {10}^6$	6.71$\times {10}^5$
	Mean	2.89$\times {10}^{14}$	6.74$\times {10}^{10}$	1.73$\times {10}^{15}$	1.01$\times {10}^{14}$	9.76$\times {10}^{13}$
$F_8$	Std	1.75$\times {10}^{13}$	2.08$\times {10}^9$	2.78$\times {10}^{14}$	1.31$\times {10}^{13}$	1.69$\times {10}^{13}$
	Mean	4.44$\times {10}^7$	1.70$\times {10}^8$	2.79$\times {10}^8$	3.08$\times {10}^8$	2.63$\times {10}^7$
$F_9$	Std	1.47$\times {10}^6$	6.20$\times {10}^6$	1.32$\times {10}^7$	1.39$\times {10}^7$	2.58$\times {10}^6$
	Mean	9.43$\times {10}^7$	9.28$\times {10}^7$	9.43$\times {10}^7$	9.44$\times {10}^7$	9.11$\times {10}^7$
$F_{10}$	Std	3.99$\times {10}^4$	1.40$\times {10}^5$	6.45$\times {10}^4$	5.82$\times {10}^4$	6.41$\times {10}^4$
	Mean	9.98$\times {10}^9$	7.70$\times {10}^8$	1.26$\times {10}^{11}$	9.93$\times {10}^9$	4.08$\times {10}^8$
$F_{11}$	Std	1.82$\times {10}^9$	6.80$\times {10}^7$	2.44$\times {10}^{10}$	3.26$\times {10}^8$	2.83$\times {10}^7$
	Mean	1.13$\times {10}^3$	5.81$\times {10}^7$	5.89$\times {10}^7$	5.81$\times {10}^7$	1.60$\times {10}^3$
$F_{12}$	Std	2.12$\times {10}^1$	1.53$\times {10}^7$	2.75$\times {10}^6$	1.53$\times {10}^6$	1.72$\times {10}^2$
	Mean	2.05$\times {10}^9$	6.03$\times {10}^8$	1.06$\times {10}^{10}$	6.03$\times {10}^8$	3.88$\times {10}^8$
$F_{13}$	Std	2.13$\times {10}^8$	2.69$\times {10}^7$	7.94$\times {10}^8$	2.69$\times {10}^7$	4.21$\times {10}^7$
	Mean	1.60$\times {10}^{10}$	1.11$\times {10}^9$	3.69$\times {10}^{10}$	1.11$\times {10}^9$	9.36$\times {10}^8$
$F_{14}$	Std	1.62$\times {10}^9$	2.10$\times {10}^8$	6.58$\times {10}^9$	2.10$\times {10}^8$	8.14$\times {10}^7$
	Mean	6.68$\times {10}^7$	7.11$\times {10}^6$	6.32$\times {10}^6$	7.11$\times {10}^6$	6.27$\times {10}^7$
$F_{15}$	Std	1.01$\times {10}^6$	2.70$\times {10}^5$	2.69$\times {10}^5$	2.70$\times {10}^5$	7.04$\times {10}^6$

In Table 1, “Mean” is the mean performance of 25 runs for each algorithm, while “Std” is the standard deviation of the algorithms’ performance. The best performance of “Mean” for each algorithm is marked by bold font. For the 15 benchmark functions, AMCPSO won eight times. For the five other benchmark functions, AMCPSO also had very competitive performance. Therefore, according to the comparison results, the proposed algorithm AMCPSO exhibits powerful ability in addressing large-scale optimization problems, which also demonstrates that the proposed strategy is feasible and effective to help PSO enhance the ability in balancing diversity maintenance and convergence. The convergence figures are presented in Figure 1.

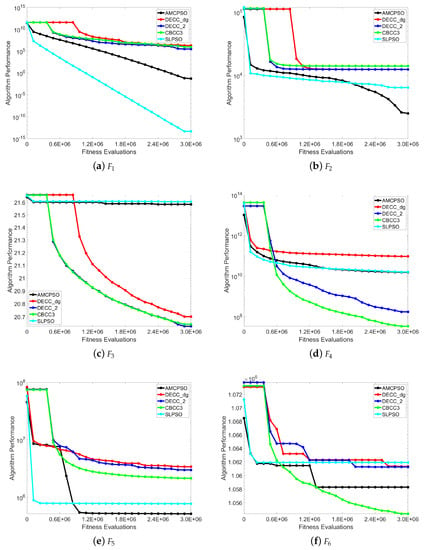
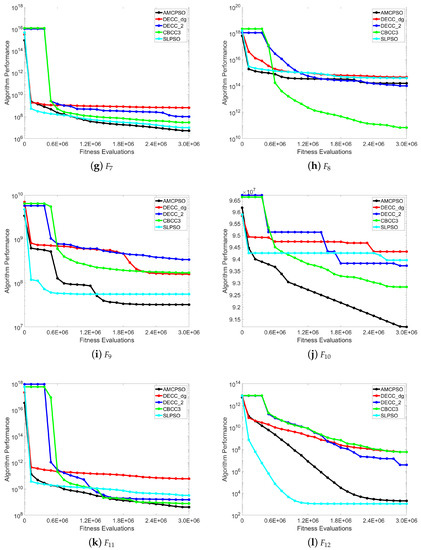
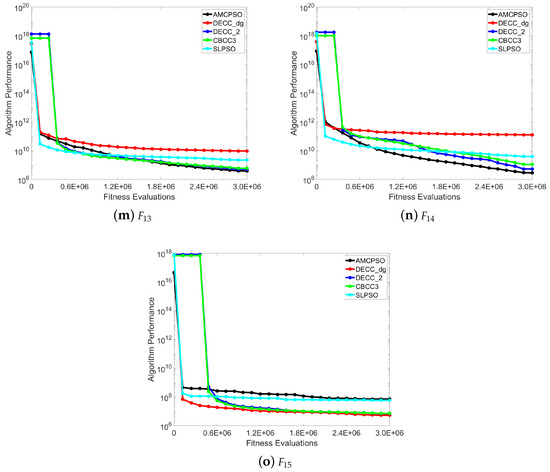
Figure 1. Convergence profiles of different algorithms obtained on the CEC’2013 test suite with 1000 dimensions.

According to the figures, for many benchmark functions, the final optimization performances of AMCPSO was better than the performances of the other algorithms, which demonstrates the proposed algorithm is competitive to address large-scale optimization problems. For some benchmarks, such as $F_1$, $F_{12}$, and $F_{15}$, even though AMCPSO was not the best, its performance kept getting better with the increase of FES, as shown in Figure 1a,m,p, which demonstrates the algorithm has a competitive performance in optimization.

As shown in Equation (3), $c_1$ and $c_2$ are employed to balance the abilities of exploration and exploitation. In this study, we fixed the value of $c_1$ as 1 and conducted experiments on tuning the value of $c_2$ to investigate the sensitivity. For the value of $c_2$, we tested 0.001, 0.002, 0.005, 0.008 and 0.01, respectively, and present the results in Table 2. In the table, for the first line, the value of $c_2$ decreased from 0.01 to 0.001. For other parameter settings, we still employed the same values as in Table 1. According to the results, there were not significant differences in the algorithm’s performance, which demonstrates that the value of $c_2$ is not too sensitive to the algorithm’s performance.

Table 2. The sensitivity of $c_2$ to AMCPSO’s performance.

Function	Quality	0.01	0.008	0.005	0.002	0.001
$F_1$	Mean	5.39$\times {10}^{-2}$	4.83$\times {10}^{-2}$	3.90$\times {10}^{-2}$	3.31$\times {10}^{-2}$	4.55$\times {10}^{-2}$
	Std	6.55$\times {10}^{-3}$	3.35$\times {10}^{-3}$	4.49$\times {10}^{-3}$	3.13$\times {10}^{-3}$	6.78$\times {10}^{-3}$
$F_2$	Mean	1.74$\times {10}^3$	1.51$\times {10}^3$	2.18$\times {10}^3$	2.10$\times {10}^3$	2.51$\times {10}^3$
	Std	5.67$\times {10}^2$	7.43$\times {10}^2$	3.92$\times {10}^2$	6.51$\times {10}^2$	4.37$\times {10}^2$
$F_3$	Mean	2.14$\times {10}^1$	2.15$\times {10}^1$	2.15$\times {10}^1$	2.15$\times {10}^1$	2.15$\times {10}^1$
	Std	1.57$\times {10}^{-3}$	4.31$\times {10}^{-3}$	3.92$\times {10}^{-3}$	6.71$\times {10}^{-3}$	3.92$\times {10}^{-3}$
$F_4$	Mean	1.41$\times {10}^{10}$	1.30$\times {10}^{10}$	1.41$\times {10}^{10}$	1.63$\times {10}^{10}$	1.12$\times {10}^{10}$
	Std	6.05$\times {10}^9$	3.18$\times {10}^9$	2.77$\times {10}^9$	4.17$\times {10}^9$	4.37$\times {10}^9$
$F_5$	Mean	4.61$\times {10}^5$	4.62$\times {10}^5$	4.53$\times {10}^5$	4.44$\times {10}^5$	4.54$\times {10}^5$
	Std	2.94$\times {10}^4$	4.83$\times {10}^4$	3.17$\times {10}^4$	2.05$\times {10}^4$	6.78$\times {10}^4$
$F_6$	Mean	1.06$\times {10}^6$	1.06$\times {10}^6$	1.06$\times {10}^6$	1.06$\times {10}^6$	1.06$\times {10}^6$
	Std	4.38$\times {10}^2$	3.81$\times {10}^2$	2.55$\times {10}^2$	1.38$\times {10}^2$	5.97$\times {10}^2$
$F_7$	Mean	4.98$\times {10}^6$	3.26$\times {10}^6$	4.45$\times {10}^6$	5.46$\times {10}^6$	4.40$\times {10}^6$
	Std	6.79$\times {10}^5$	4.45$\times {10}^5$	4.63$\times {10}^5$	5.47$\times {10}^5$	6.18$\times {10}^5$
$F_8$	Mean	1.31$\times {10}^{14}$	1.47$\times {10}^{14}$	2.01$\times {10}^{14}$	1.39$\times {10}^{14}$	9.76$\times {10}^{13}$
	Std	2.76$\times {10}^{13}$	4.97$\times {10}^{13}$	5.51$\times {10}^{13}$	1.62$\times {10}^{13}$	1.17$\times {10}^{13}$
$F_9$	Mean	3.71$\times {10}^7$	3.68$\times {10}^7$	3.61$\times {10}^7$	4.21$\times {10}^7$	2.63$\times {10}^7$
	Std	3.24$\times {10}^6$	2.14$\times {10}^6$	1.31$\times {10}^6$	6.97$\times {10}^6$	5.41$\times {10}^6$
$F_{10}$	Mean	9.22$\times {10}^7$	9.23$\times {10}^7$	9.17$\times {10}^7$	9.14$\times {10}^7$	9.11$\times {10}^7$
	Std	8.18$\times {10}^4$	6.59$\times {10}^4$	4.37$\times {10}^4$	2.37$\times {10}^4$	5.22$\times {10}^4$
$F_{11}$	Mean	4.41$\times {10}^8$	4.33$\times {10}^8$	2.08$\times {10}^9$	7.66$\times {10}^8$	4.08$\times {10}^8$
	Std	5.24$\times {10}^7$	5.91$\times {10}^7$	4.39$\times {10}^7$	2.28$\times {10}^7$	2.11$\times {10}^7$
$F_{12}$	Mean	1.56$\times {10}^3$	2.07$\times {10}^3$	1.67$\times {10}^3$	1.81$\times {10}^3$	1.60$\times {10}^3$
	Std	2.27$\times {10}^2$	4.51$\times {10}^2$	3.41$\times {10}^2$	3.97$\times {10}^2$	5.22$\times {10}^2$
$F_{13}$	Mean	4.85$\times {10}^8$	5.27$\times {10}^8$	3.49$\times {10}^8$	4.98$\times {10}^8$	3.88$\times {10}^8$
	Std	3.17$\times {10}^7$	2.25$\times {10}^7$	2.94$\times {10}^7$	8.57$\times {10}^7$	5.19$\times {10}^7$
$F_{14}$	Mean	7.76$\times {10}^8$	1.43$\times {10}^9$	2.25$\times {10}^9$	7.21$\times {10}^8$	9.36$\times {10}^8$
	Std	2.58$\times {10}^7$	6.97$\times {10}^7$	4.55$\times {10}^7$	3.93$\times {10}^7$	2.88$\times {10}^7$
$F_{15}$	Mean	5.19$\times {10}^7$	5.98$\times {10}^7$	6.16$\times {10}^7$	6.05$\times {10}^7$	6.27$\times {10}^7$
	Std	2.81$\times {10}^6$	3.08$\times {10}^6$	7.01$\times {10}^6$	4.78$\times {10}^6$	8.53$\times {10}^6$

5. Conclusions and Future Work

In this paper, to enhance PSO’s ability in dealing with large-scale optimization problems, we propose a novel PSO named adaptive multi-swarm competition PSO (AMCPSO), which adaptively divides a swarm into several sub-swarms. In each sub-swarm, a local winner is selected, while the local losers will learn from the local winner. In this way, for the whole swarm, not only one position is selected to attract all others and therefore the diversity of exemplars increases. On the other hand, with the process of optimization, the number of sub-swarms decreases, which helps the algorithm adaptively change the swarm’s focus from exploration to exploitation. At the beginning of optimization process, many sub-swarms are adopted, which makes the algorithm focus on exploration, while the number of sub-swarms decreases with the optimization process to help the algorithm enhance the ability in exploitation. By employing benchmark functions in CEC 2013, the performance of the proposed algorithm AMCPSO was validated and the comparison results demonstrate AMCPSO has a competitive ability in dealing with large-scale optimization problems.

In our future work, on the one hand, the proposed algorithm’s structure will be investigated on several different kinds of algorithms [26,35,36,37] to improve their performances in addressing large-scale optimization problems. On the other hand, we will apply the proposed algorithm to real applications, such as optimization problems in an industrial network, traffic network, location problems and so forth [38,39].