The Generalized Viscosity Implicit Midpoint Rule for Nonexpansive Mappings in Banach Space

Abstract

This paper constructs the generalized viscosity implicit midpoint rule for nonexpansive mappings in Banach space. It obtains strong convergence conclusions for the proposed algorithm and promotes the related results in this field. Moreover, this paper gives some applications. Finally, the paper gives six numerical examples to support the main results.

1. Introduction

Let $E$ be a Banach Space and $E^{*}$ the dual space. $J$ denotes the normalized duality mapping from $E$ to $2^{E^{*}}$ and is defined by

$$J(x)=\{f\in E^{*}:<x,f>={\Vert x\Vert }^2={\Vert f\Vert }^2\},x\in E.$$

It is well known that if $E$ is a Hilbert space, then $J$ is the identity mapping; if $E$ is a smooth Banach space, then $J$ is single-valued and denoted by $j$. More information on the normalized duality mapping can be found, for example, in [1,2].

Let $C$ be a nonempty set of $E$. Mapping of $f:C\to C$ is contractive if $\Vert f(x)-f(y)\Vert \le \alpha \Vert x-y\Vert$, $\forall x,y\in C$, and $\alpha \in [0,1)$. Mapping of $T:C\to C$ is nonexpansive if $\Vert T(x)-T(y)\Vert \le \Vert x-y\Vert$ and $\forall x,y\in C$. Let $F(T)$ denote the fixed point set of $T$. More information on nonexpansive mappings and their fixed points can be found, for example, in [3].

The implicit midpoint rule can effectively solve ordinary differential equations (see [4,5,6,7,8,9] and the references therein). Meanwhile, many authors have used viscosity iterative algorithms for finding common fixed points for nonlinear operators and solutions of variational inequality problems (see [10,11,12,13,14,15,16,17] and the references therein).

In 2004, Xu [10] proposed the explicit viscosity method for nonexpansive mappings in Hilbert space or uniformly smooth Banach space:

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T{x}_n,n\ge 0.$$

$\left\{x_n\right\}$ was generated by the above iterative algorithm and strongly converged to $q\in F(T)$, where $q$ was the solution of variational inequality $⟨(I-f)q,x-q⟩\ge 0$ and $x\in F(T)$.

In 2015, Xu et al. [18] constructed the viscosity implicit midpoint rule for nonexpansive mapping in Hilbert space:

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T\left(\frac{x_n+x_{n+1}}{2}\right),n\ge 0.$$

$\left\{x_n\right\}$ was generated by the above. Under many conditions of $\left\{{\alpha }_n\right\}$, $\left\{x_n\right\}$ strongly converged to $q\in F(T)$, where $q$ was the solution of variational inequality $⟨(I-f)q,x-q⟩\ge 0$ and $x\in F(T)$.

In 2015, Ke et al. [19] improved the results of Xu et al. [18] from the viscosity implicit midpoint rule to generalized viscosity implicit rules for nonexpansive mappings in Hilbert spaces:

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T\left(s_n{x}_n+(1-s_n)x_{n+1}\right),n\ge 0$$

(1)

and

$$x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_{n}T\left(s_n{x}_n+(1-s_n)x_{n+1}\right),n\ge 0.$$

(2)

Under some conditions of $\left\{{\alpha }_n\right\}$, they proved that $\left\{x_n\right\}$ generated by (1) and (2) all strongly converged to $q\in F(T)$, where $q$ was the solution of variational inequality $⟨(I-f)q,x-q⟩\ge 0$ and $x\in F(T)$.

In 2017, Luo et al. [20] generalized the conclusions of Xu et al. [18] from Hilbert space to uniformly smooth Banach space:

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T\left(\frac{x_n+x_{n+1}}{2}\right),n\ge 0.$$

$\left\{x_n\right\}$ was generated by the above. Under many conditions, $\left\{x_n\right\}$ strongly converged to $q\in F(T)$, where $q$ was the solution of variational inequality $⟨(I-f)q,j(x-q)⟩\ge 0$ and $x\in F(T)$.

Motivated and inspired by Xu et al. [18], Ke et al. [19], and Luo et al. [20], this paper proposes the generalized viscosity implicit rules for nonexpansive mappings in Banach space and proves strong convergence results. Next, this paper applies the results to a general system of variational inequality problems in Banach space and fixed-point problems of strict pseudocontractive mappings. Finally, this paper gives numerical examples to support the main results.

2. Preliminaries

Let $E$ be a Banach space. A mapping ${\rho }_E:[0,\infty )\to [0,\infty )$ is defined by

$${\rho }_E(t)=\sup \left\{\frac{\Vert x+y\Vert +\Vert x-y\Vert }{2}-1:x\in S(E),\Vert y\Vert \le t\right\},$$

where $S(E)$ is the modulus of smoothness of $E$. $E$ is uniformly smooth if $\underset{t\to 0}{\lim }\frac{{\rho }_E(t)}{t}=0$. For example, $L^p(p>1)$ is uniformly smooth Banach space. $E$ is q-uniformly smooth if $c>0$ such that ${\rho }_E(t)\le c{t}^q$.

We needed the following lemmas to prove our main results.

Lemma 1.

([10,21]) Assume $\left\{a_n\right\}$ is a sequence of non-negative real numbers such that

$$a_{n+1}\le (1-{\alpha }_n)a_n+{\delta }_n,n\ge 0,$$

where $\left\{{\alpha }_n\right\}$ is a sequence in $(0,1)$ and $\left\{{\delta }_n\right\}$ is a sequence in $R$ such that

$$(\mathrm{i}){\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty ;(\mathrm{ii})\underset{n\to \infty }{\lim \sup }\frac{{\delta }_n}{{\alpha }_n}\le 0\mathrm{or}{\displaystyle \sum _{n=1}^{\infty }\left|{\delta }_n\right|}<\infty$$

Then, $\underset{n\to \infty }{\lim }{a}_n=0$.

Lemma 2.

([10,22]) Let $E$ be a uniformly smooth Banach space, $C$ be a closed convex subset of $E$, $T:C\to C$ be a nonexpansive mapping with $F(T)\ne \varnothing$, and $f:C\to C$ be a contractive mapping. Then the sequence $\left\{x_t\right\}$ defined by $x_t=tf(x_t)+(1-t)T{x}_t$ converges strongly to a point in $F(T)$. If we define a mapping $Q:{\mathsf{\Pi }}_C\to F(T)$ by $Q(f):=\underset{t\to 0}{\lim }{x}_t$, where ${\mathsf{\Pi }}_C$ is the set of contractive mapping from $C$ to itself, then $Q(f)$ solves the following variational inequality:

$$⟨(I-f)Q(f),j(Q(f)-p)⟩\le 0,\forall f\in {\mathsf{\Pi }}_C,p\in F(T).$$

Lemma 3.

([12]) Let $C$ be a nonempty, closed convex subset of a real Banach space $E$, which has a uniformly $G\widehat{a}teaux$ differentiable norm, and $T:C\to C$ be a nonexpansive mapping with $F(T)\ne \varnothing$. Assume that $\left\{z_t\right\}$ strongly converges to a fixed point $z$ of $T$ as $t\to 0$, where $\left\{z_t\right\}$ is defined by $z_t=tf(z_t)+(1-t)T{z}_t$. Suppose $\left\{x_n\right\}\subset C$ is bounded and $\underset{n\to \infty }{\lim }\Vert x_n-T{x}_n\Vert =0$. Then $\underset{n\to \infty }{\lim \sup }⟨f(z)-z,j(x_{n+1}-z)⟩\le 0$.

3. Main Results

Theorem 1.

Let $E$ be a uniformly smooth Banach space, $C$ be a closed convex subset of $E$, $f:C\to C$ be a contractive mapping with $\alpha \in [0,1)$, and $T:C\to C$ be a nonexpansive mapping with $F(T)\ne \varnothing$. $\left\{x_n\right\}$ is generated by the generalized viscosity implicit midpoint rule

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T\left(s_n{x}_n+(1-s_n)x_{n+1}\right),n\ge 0,$$

(3)

where $\left\{{\alpha }_n\right\},\left\{s_n\right\}\subset (0,1)$ and satisfies the conditions:

(i) 

$\underset{n\to \infty }{\lim }{\alpha }_n=0$;

(ii) 

${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$;

(iii) 

$\underset{n\to \infty }{\lim }\frac{{\alpha }_{n+1}}{{\alpha }_n}=1$or ${\displaystyle \sum _{n=1}^{\infty }\left|{\alpha }_{n+1}-{\alpha }_n\right|}<\infty$;

(iv) 

$0<\epsilon \le s_n\le s_{n+1}<1$, $\forall n\ge 0$.

Then $\left\{x_n\right\}$ converges strongly to $q\in F(T)$, which is also the unique solution of the variational inequality $⟨(I-f)q,j(x-q)⟩\ge 0$, and $x\in F(T)$.

Proof. 

The proof is split into five steps.

Step 1: Show that $\left\{x_n\right\}$ is bounded.

Take $p\in F(T)$, then we have

$$\begin{array}{cc}\hfill \Vert x_{n+1}-p\Vert & \le {\alpha }_n\Vert f(x_n)-p\Vert +(1-{\alpha }_n)\Vert T(s_n{x}_n+(1-s_n)x_{n+1})-p\Vert \hfill \\ & \le \alpha {\alpha }_n\Vert x_n-p\Vert +{\alpha }_n\Vert f(p)-p\Vert +(1-{\alpha }_n)s_n\Vert x_n-p\Vert \hfill \\ & +(1-{\alpha }_n)(1-s_n)\Vert x_{n+1}-p\Vert \hfill \\ & =[(1-{\alpha }_n)s_n+\alpha {\alpha }_n]\Vert x_n-p\Vert +(1-{\alpha }_n)(1-s_n)\Vert x_{n+1}-p\Vert \hfill \\ & +{\alpha }_n\Vert f(p)-p\Vert .\hfill \end{array}$$

It follows that

$$\begin{array}{cc}\hfill \Vert x_{n+1}-p\Vert & \le \frac{(1-{\alpha }_n)s_n+\alpha {\alpha }_n}{1-(1-{\alpha }_n)(1-s_n)}\Vert x_n-p\Vert +\frac{{\alpha }_n}{1-(1-{\alpha }_n)(1-s_n)}\Vert f(p)-p\Vert \hfill \\ & =\left[1-\frac{(1-\alpha ){\alpha }_n}{1-(1-{\alpha }_n)(1-s_n)}\right]\Vert x_n-p\Vert +\frac{(1-\alpha ){\alpha }_n}{1-(1-{\alpha }_n)(1-s_n)}\frac{\Vert f(p)-p\Vert }{(1-\alpha )}.\hfill \end{array}$$

Then we get $\Vert x_{n+1}-p\Vert \le \max \left\{\Vert x_n-p\Vert ,\frac{\Vert f(p)-p\Vert }{(1-\alpha )}\right\}$. By induction, we get

$$\Vert x_n-p\Vert \le \max \left\{\Vert x_0-p\Vert ,\frac{\Vert f(p)-p\Vert }{(1-\alpha )}\right\},\forall n\ge 0.$$

So, $\left\{x_n\right\}$ is bounded. Then $\{f(x_n)\}$ and $\{T(s_n{x}_n+(1-s_n)x_{n+1})\}$ are also bounded.

Step 2: Show that $\underset{n\to \infty }{\lim }\Vert x_{n+1}-x_n\Vert =0$.

By (3), we have

$$\begin{array}{cc}\hfill \Vert x_{n+1}-x_n\Vert & =\Vert {\alpha }_{n}f(x_n)+(1-{\alpha }_n)T(s_n{x}_n+(1-s_n)x_{n+1})-{\alpha }_{n-1}f(x_{n-1})\hfill \\ & -(1-{\alpha }_{n-1})T(s_{n-1}{x}_{n-1}+(1-s_{n-1})x_n)\Vert \hfill \\ & \le {\alpha }_n\Vert f(x_n)-f(x_{n-1})\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|\cdot \Vert f(x_{n-1})-T(s_{n-1}{x}_{n-1}+(1-s_{n-1})x_n)\Vert \hfill \\ & +(1-{\alpha }_n)\Vert T(s_n{x}_n+(1-s_n)x_{n+1})-T(s_{n-1}{x}_{n-1}+(1-s_{n-1})x_n)\Vert \hfill \\ & \le \alpha {\alpha }_n\Vert x_n-x_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|M+(1-{\alpha }_n)\Vert \left[s_n{x}_n+(1-s_n)x_{n+1}\right]\hfill \\ & -\left[s_{n-1}{x}_{n-1}+(1-s_{n-1})x_n\right]\Vert \hfill \\ & \le \alpha {\alpha }_n\Vert x_n-x_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|M+(1-{\alpha }_n)(1-s_n)\Vert x_{n+1}-x_n\Vert \hfill \\ & +(1-{\alpha }_n)s_{n-1}\Vert x_n-x_{n-1}\Vert \hfill \\ & =(1-{\alpha }_n)(1-s_n)\Vert x_{n+1}-x_n\Vert +\left[\alpha {\alpha }_n+(1-{\alpha }_n)s_{n-1}\right]\Vert x_n-x_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|M,\hfill \end{array}$$

where $M\ge \underset{n\ge 0}{\sup }$$\Vert f(x_n)-T(s_n{x}_n+(1-s_n)x_{n+1})\Vert$.

It follows that

$$\begin{array}{cc}\hfill \Vert x_{n+1}-x_n\Vert & \le \frac{\alpha {\alpha }_n+(1-{\alpha }_n)s_{n-1}}{1-(1-{\alpha }_n)(1-s_n)}\Vert x_n-x_{n-1}\Vert +\frac{M}{1-(1-{\alpha }_n)(1-s_n)}\left|{\alpha }_n-{\alpha }_{n-1}\right|\hfill \\ & =\left[1-\frac{(1-\alpha ){\alpha }_n+(1-{\alpha }_n)(s_n-s_{n-1})}{1-(1-{\alpha }_n)(1-s_n)}\right]\Vert x_n-x_{n-1}\Vert +\frac{M}{1-(1-{\alpha }_n)(1-s_n)}\left|{\alpha }_n-{\alpha }_{n-1}\right|.\hfill \end{array}$$

From $0<\epsilon \le s_n\le s_{n+1}<1$, we have $0<\epsilon \le s_n\le 1-(1-{\alpha }_n)(1-s_n)<1$ and $\frac{(1-\alpha ){\alpha }_n+(1-{\alpha }_n)(s_n-s_{n-1})}{1-(1-{\alpha }_n)(1-s_n)}\ge (1-\alpha ){\alpha }_n$. Then we get

$$\Vert x_{n+1}-x_n\Vert \le \left[1-(1-\alpha ){\alpha }_n\right]\Vert x_n-x_{n-1}\Vert +\frac{M}{\epsilon }\left|{\alpha }_n-{\alpha }_{n-1}\right|.$$

From ${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$, ${\displaystyle \sum _{n=1}^{\infty }\left|{\alpha }_{n+1}-{\alpha }_n\right|}<\infty$, and Lemma 1, we get $\underset{n\to \infty }{\lim }\Vert x_{n+1}-x_n\Vert =0$.

Step 3: Show that $\underset{n\to \infty }{\lim }\Vert x_n-T{x}_n\Vert =0$.

$$\begin{array}{cc}\hfill \Vert x_n-T{x}_n\Vert & \le \Vert x_n-x_{n+1}\Vert +\Vert x_{n+1}-T(s_n{x}_n+(1-s_n)x_{n+1})\Vert +\Vert T(s_n{x}_n+(1-s_n)x_{n+1})-T{x}_n\Vert \hfill \\ & \le \Vert x_n-x_{n+1}\Vert +{\alpha }_n\Vert f(x_n)-T(s_n{x}_n+(1-s_n)x_{n+1})\Vert +(1-s_n)\Vert x_n-x_{n+1}\Vert \hfill \\ & \le (2-s_n)\Vert x_n-x_{n+1}\Vert +{\alpha }_{n}M\hfill \\ & \le 2\Vert x_n-x_{n+1}\Vert +{\alpha }_{n}M.\hfill \end{array}$$

From $\underset{n\to \infty }{\lim }{\alpha }_n=0$ and Step 2, we get $\underset{n\to \infty }{\lim }\Vert x_n-T{x}_n\Vert =0$.

Step 4: Show that $\underset{n\to \infty }{\lim \sup }⟨f(q)-q,j(x_{n+1}-q)⟩\le 0$.

Let $\left\{x_t\right\}$ be defined by $x_t=tf(x_t)+(1-t)T{x}_t$. Then, from Lemma 2, $\left\{x_t\right\}$ converges strongly to $q\in F(T)$, which is also the unique solution of the variational inequality $⟨(I-f)q,j(x-q)⟩\ge 0$, $x\in F(T)$. From Steps 1–3 and Lemma 3, we get $\underset{n\to \infty }{\lim \sup }⟨f(q)-q,j(x_{n+1}-q)⟩\le 0$.

Step 5: Show that $\underset{n\to \infty }{\lim }{x}_n=q$.

$$\begin{array}{cc}\hfill {\Vert x_{n+1}-q\Vert }^2& ={\Vert {\alpha }_n\left(f(x_n)-q\right)+(1-{\alpha }_n)\left(T(s_n{x}_n+(1-s_n)x_{n+1})-q\right)\Vert }^2\hfill \\ & =(1-{\alpha }_n)⟨T(s_n{x}_n+(1-s_n)x_{n+1})-q,j(x_{n+1}-q)⟩+{\alpha }_n⟨f(x_n)-q,j(x_{n+1}-q)⟩\hfill \\ & \le (1-{\alpha }_n)\Vert s_n(x_n-q)+(1-s_n)(x_{n+1}-q)\Vert \cdot \Vert x_{n+1}-q\Vert +\alpha {\alpha }_n\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert \hfill \\ & +{\alpha }_n⟨f(q)-q,j(x_{n+1}-q)⟩\hfill \\ & \le (1-{\alpha }_n)s_n\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert +(1-{\alpha }_n)(1-s_n){\Vert x_{n+1}-q\Vert }^2+\alpha {\alpha }_n\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert \hfill \\ & +{\alpha }_n⟨f(q)-q,j(x_{n+1}-q)⟩\hfill \\ & =\left[(1-{\alpha }_n)s_n+\alpha {\alpha }_n\right]\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert +(1-{\alpha }_n)(1-s_n){\Vert x_{n+1}-q\Vert }^2\hfill \\ & +{\alpha }_n⟨f(q)-q,j(x_{n+1}-q)⟩\hfill \\ & \le \frac{(1-{\alpha }_n)s_n+\alpha {\alpha }_n}{2}\left({\Vert x_n-q\Vert }^2+{\Vert x_{n+1}-q\Vert }^2\right)+(1-{\alpha }_n)(1-s_n){\Vert x_{n+1}-q\Vert }^2\hfill \\ & +{\alpha }_n⟨f(q)-q,j(x_{n+1}-q)⟩.\hfill \end{array}$$

It follows that

$$\begin{array}{cc}\hfill {\Vert x_{n+1}-q\Vert }^2& \le \frac{(1-{\alpha }_n)s_n+\alpha {\alpha }_n}{2-\left[(1-{\alpha }_n)s_n+\alpha {\alpha }_n\right]-2(1-{\alpha }_n)(1-s_n)}{\Vert x_n-q\Vert }^2\hfill \\ & +\frac{2{\alpha }_n}{2-\left[(1-{\alpha }_n)s_n+\alpha {\alpha }_n\right]-2(1-{\alpha }_n)(1-s_n)}⟨f(q)-q,j(x_{n+1}-q)⟩\hfill \\ & =\left[1-\frac{2(1-\alpha ){\alpha }_n}{2-\left[(1-{\alpha }_n)s_n+\alpha {\alpha }_n\right]-2(1-{\alpha }_n)(1-s_n)}\right]{\Vert x_n-q\Vert }^2\hfill \\ & +\frac{2{\alpha }_n(1-\alpha )}{2-\left[(1-{\alpha }_n)s_n+\alpha {\alpha }_n\right]-2(1-{\alpha }_n)(1-s_n)}\frac{⟨f(q)-q,j(x_{n+1}-q)⟩}{1-\alpha }.\hfill \end{array}$$

Because

$$\frac{2{\alpha }_n(1-\alpha )}{2-\left[(1-{\alpha }_n)s_n+\alpha {\alpha }_n\right]-2(1-{\alpha }_n)(1-s_n)}=\frac{2{\alpha }_n(1-\alpha )}{{\alpha }_n(2-\alpha )+(1-{\alpha }_n)s_n}>\frac{2-2\alpha }{3-\alpha }{\alpha }_n,$$

so, from ${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$, Step 4, and Lemma 1, we get $\underset{n\to \infty }{\lim }{x}_n=q$. This completes the proof. □

It is well known that Hilbert space is uniformly smooth Banach space. So, we can get the main results of [19].

Corollary 1.

([19]) Let $C$ be a nonempty, closed convex subset of the real Hilbert space $H$. Let $T:C\to C$ be a nonexpansive mapping with $F(T)\ne \varnothing$ and $f:C\to C$ be a contraction with coefficient $\theta \in [0,1)$. Pick any $x_0\in C$ and let $\left\{x_n\right\}$ be a sequence generated by

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T\left(s_n{x}_n+(1-s_n)x_{n+1}\right),$$

where $\left\{{\alpha }_n\right\},\left\{s_n\right\}\subset (0,1)$ that satisfies the following conditions:

(1) 

$\underset{n\to \infty }{\lim }{\alpha }_n=0$;

(2) 

${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$;

(3) 

${\displaystyle \sum _{n=1}^{\infty }\left|{\alpha }_{n+1}-{\alpha }_n\right|}<\infty$;

(4) 

$0<\epsilon \le s_n\le s_{n+1}<1$, $\forall n\ge 0$.

Then $\left\{x_n\right\}$ converges strongly to a fixed point $x^{*}$ of the nonexpansive mapping $T$, which is also the unique solution of the variational inequality $⟨(I-f)x,y-x⟩\ge 0$, $\forall y\in F(T)$.

If we let $s_n=\frac{1}{2}$, we can get the main results of [20].

Corollary 2.

([20]) Let $C$ be a closed convex subset of a uniformly smooth Banach space $E$. Let $T:C\to C$ be a nonexpansive mapping with $F(T)\ne \varnothing$, and $f:C\to C$ a contraction with coefficient $\alpha \in [0,1)$. Let $\left\{x_n\right\}$ be a sequence generated by the following viscosity implicit midpoint rule:

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T\left(\frac{x_n+x_{n+1}}{2}\right),n\ge 0,$$

where $\left\{{\alpha }_n\right\}$ is a sequence in $(0,1)$ such that:

(i) 

$\underset{n\to \infty }{\lim }{\alpha }_n=0$;

(ii) 

${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$;

(iii) 

either ${\displaystyle \sum _{n=1}^{\infty }\left|{\alpha }_{n+1}-{\alpha }_n\right|}<\infty$ or $\underset{n\to \infty }{\lim }\frac{{\alpha }_{n+1}}{{\alpha }_n}=1$.

Then $\left\{x_n\right\}$ converges strongly to a fixed point of $T$, which also solves the following variational inequality: $⟨(I-f)q,j(x-q)⟩\ge 0$, $x\in F(T)$.

Theorem 2.

Let $E$ be a uniformly smooth Banach space, $C$ be a closed convex subset of $E$, $f:C\to C$ be a contractive mapping with $\alpha \in [0,1)$ and $T:C\to C$ be a nonexpansive mapping with $F(T)\ne \varnothing$. $\left\{x_n\right\}$ is generated by the generalized viscosity implicit midpoint rule

$$x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_{n}T\left(s_n{x}_n+(1-s_n)x_{n+1}\right)+e_n,n\ge 0,$$

(4)

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\},\left\{s_n\right\}\subset (0,1),\left\{e_n\right\}\subset E$ and satisfies the conditions:

(i) 

${\alpha }_n+{\beta }_n+{\gamma }_n=1,\underset{n\to \infty }{\lim }{\gamma }_n=1$;

(ii) 

${\displaystyle \sum _{n=0}^{\infty }{\beta }_n}=\infty$;

(iii) 

${\displaystyle \sum _{n=1}^{\infty }\left|{\alpha }_{n+1}-{\alpha }_n\right|}<\infty$and ${\displaystyle \sum _{n=1}^{\infty }\left|{\beta }_{n+1}-{\beta }_n\right|}<\infty$;

(iv) 

$0<\epsilon \le s_n\le s_{n+1}<1$, $\forall n\ge 0$;

(v) 

${\displaystyle \sum _{n=0}^{\infty }\Vert e_n\Vert }<\infty$and $\Vert e_n\Vert =o({\beta }_n)$.

Then $\left\{x_n\right\}$ converges strongly to $q\in F(T)$, which is also the unique solution of the variational inequality $⟨(I-f)q,j(x-q)⟩\ge 0$, and $x\in F(T)$.

Proof. 

The proof is split into five steps.

Step 1: Show that $\left\{x_n\right\}$ is bounded.

Take $p\in F(T)$, then we have

$$\begin{array}{cc}\hfill \Vert x_{n+1}-p\Vert & =\Vert {\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_{n}T\left(s_n{x}_n+(1-s_n)x_{n+1}\right)+e_n-p\Vert \hfill \\ & \le {\alpha }_n\Vert x_n-p\Vert +\alpha {\beta }_n\Vert x_n-p\Vert +{\beta }_n\Vert f(p)-p\Vert +{\gamma }_n{s}_n\Vert x_n-p\Vert \hfill \\ & +{\gamma }_n(1-s_n)\Vert x_{n+1}-p\Vert +\Vert e_n\Vert \hfill \\ & =({\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n)\Vert x_n-p\Vert +{\gamma }_n(1-s_n)\Vert x_{n+1}-p\Vert +{\beta }_n\Vert f(p)-p\Vert +\Vert e_n\Vert .\hfill \end{array}$$

It follows that

$$\left[1-{\gamma }_n(1-s_n)\right]\Vert x_{n+1}-p\Vert \le ({\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n)\Vert x_n-p\Vert +{\beta }_n\Vert f(p)-p\Vert +\Vert e_n\Vert .$$

From ${\alpha }_n+{\beta }_n+{\gamma }_n=1$, we have

$$\begin{array}{cc}\hfill \Vert x_{n+1}-p\Vert & \le \frac{{\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n}{1-{\gamma }_n(1-s_n)}\Vert x_n-p\Vert +\frac{{\beta }_n}{1-{\gamma }_n(1-s_n)}\Vert f(p)-p\Vert +\frac{\Vert e_n\Vert }{1-{\gamma }_n(1-s_n)}\hfill \\ & \le \left[1-\frac{1-{\alpha }_n-{\gamma }_n-\alpha {\beta }_n}{1-{\gamma }_n(1-s_n)}\right]\Vert x_n-p\Vert +\frac{{\beta }_n}{1-{\gamma }_n(1-s_n)}\Vert f(p)-p\Vert +\frac{\Vert e_n\Vert }{\epsilon }\hfill \\ & =\left[1-\frac{{\beta }_n(1-\alpha )}{1-{\gamma }_n(1-s_n)}\right]\Vert x_n-p\Vert +\frac{{\beta }_n(1-\alpha )}{1-{\gamma }_n(1-s_n)}\frac{\Vert f(p)-p\Vert }{(1-\alpha )}+\frac{\Vert e_n\Vert }{\epsilon }\hfill \\ & \le \max \left\{\Vert x_0-p\Vert ,\frac{\Vert f(p)-p\Vert }{(1-\alpha )}+\frac{\Vert e_n\Vert }{\epsilon }\right\}.\hfill \end{array}$$

So, $\left\{x_n\right\}$ is bounded. Then $\{f(x_n)\}$ and $\{T(s_n{x}_n+(1-s_n)x_{n+1})\}$ are also bounded.

Step 2: Show that $\underset{n\to \infty }{\lim }\Vert x_{n+1}-x_n\Vert =0$.

By (4), we have

$$\begin{array}{cc}\hfill \Vert x_{n+1}-x_n\Vert & =\Vert {\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_{n}T\left(s_n{x}_n+(1-s_n)x_{n+1}\right)+e_n-[{\alpha }_{n-1}{x}_{n-1}+{\beta }_{n-1}f(x_{n-1})\hfill \\ & +{\gamma }_{n-1}T\left(s_{n-1}{x}_{n-1}+(1-s_{n-1})x_n\right)+e_{n-1}]\Vert \hfill \\ & =\Vert {\alpha }_n(x_n-x_{n-1})+({\alpha }_n-{\alpha }_{n-1})x_{n-1}+{\beta }_n\left[f(x_n)-f(x_{n-1})\right]+({\beta }_n-{\beta }_{n-1})f(x_{n-1})\hfill \\ & +{\gamma }_n\left[T(s_n{x}_n+(1-s_n)x_{n+1})-T(s_{n-1}{x}_{n-1}+(1-s_{n-1})x_n)\right]\hfill \\ & -\left[({\alpha }_n-{\alpha }_{n-1})+({\beta }_n-{\beta }_{n-1})\right]T(s_{n-1}{x}_{n-1}+(1-s_{n-1})x_n)+e_n-e_{n-1}\Vert \hfill \\ & \le {\alpha }_n\Vert x_n-x_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|\cdot \Vert x_{n-1}-T(s_{n-1}{x}_{n-1}+(1-s_{n-1})x_n)\Vert \hfill \\ & +{\beta }_n\Vert f(x_n)-f(x_{n-1})\Vert +\left|{\beta }_n-{\beta }_{n-1}\right|\cdot \Vert f(x_{n-1})-T(s_{n-1}{x}_{n-1}+(1-s_{n-1})x_n)\Vert \hfill \\ & +{\gamma }_n\Vert T(s_n{x}_n+(1-s_n)x_{n+1})-T(s_{n-1}{x}_{n-1}+(1-s_{n-1})x_n)\Vert +\Vert e_n-e_{n-1}\Vert \hfill \\ & \le {\alpha }_n\Vert x_n-x_{n-1}\Vert +\left|{\alpha }_n-{\alpha }_{n-1}\right|M_1+\alpha {\beta }_n\Vert x_n-x_{n-1}\Vert +\left|{\beta }_n-{\beta }_{n-1}\right|M_1\hfill \\ & +{\gamma }_n\Vert (1-s_n)(x_{n+1}-x_n)+s_{n-1}(x_n-x_{n-1})\Vert +\Vert e_n-e_{n-1}\Vert \hfill \\ & \le {\gamma }_n(1-s_n)\Vert x_{n+1}-x_n\Vert +({\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_{n-1})\Vert x_n-x_{n-1}\Vert \hfill \\ & +(\left|{\alpha }_n-{\alpha }_{n-1}\right|+\left|{\beta }_n-{\beta }_{n-1}\right|)M_1+2\Vert e_n\Vert ,\hfill \end{array}$$

where $M_1\ge \max \left\{\underset{n\ge 0}{\sup }\Vert x_n-T(s_n{x}_n+(1-s_n)x_{n+1})\Vert ,\underset{n\ge 0}{\sup }\Vert f(x_n)-T(s_n{x}_n+(1-s_n)x_{n+1})\Vert \right\}$.

It follows that

$$\begin{array}{cc}\hfill \Vert x_{n+1}-x_n\Vert & \le \frac{{\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_{n-1}}{1-{\gamma }_n(1-s_n)}\Vert x_n-x_{n-1}\Vert +\frac{M_1}{1-{\gamma }_n(1-s_n)}\left(\left|{\alpha }_n-{\alpha }_{n-1}\right|+\left|{\beta }_n-{\beta }_{n-1}\right|\right)+2\Vert e_n\Vert \hfill \\ & =\left[1-\frac{(1-\alpha ){\beta }_n+{\gamma }_n(s_n-s_{n-1})}{1-{\gamma }_n(1-s_n)}\right]\Vert x_n-x_{n-1}\Vert +\frac{M_1}{1-{\gamma }_n(1-s_n)}\left(\left|{\alpha }_n-{\alpha }_{n-1}\right|+\left|{\beta }_n-{\beta }_{n-1}\right|\right)+2\Vert e_n\Vert \hfill \end{array}$$

From $0<\epsilon \le s_n\le s_{n+1}<1$, we have $0<\epsilon \le s_n\le 1-(1-{\alpha }_n)(1-s_n)<1$ and $\frac{(1-\alpha ){\beta }_n+{\gamma }_n(s_n-s_{n-1})}{1-{\gamma }_n(1-s_n)}\ge (1-\alpha ){\beta }_n$. Then we get

$$\Vert x_{n+1}-x_n\Vert \le \left[1-(1-\alpha ){\beta }_n\right]\Vert x_n-x_{n-1}\Vert +\frac{M_1}{\epsilon }\left(\left|{\alpha }_n-{\alpha }_{n-1}\right|+\left|{\beta }_n-{\beta }_{n-1}\right|\right)+2\Vert e_n\Vert .$$

From ${\displaystyle \sum _{n=0}^{\infty }{\beta }_n}=\infty$, ${\displaystyle \sum _{n=1}^{\infty }\left|{\alpha }_{n+1}-{\alpha }_n\right|}<\infty$, ${\displaystyle \sum _{n=1}^{\infty }\left|{\beta }_{n+1}-{\beta }_n\right|}<\infty$, ${\displaystyle \sum _{n=1}^{\infty }\Vert e_n\Vert }<\infty$, and Lemma 1 we get $\underset{n\to \infty }{\lim }\Vert x_{n+1}-x_n\Vert =0$.

Step 3: Show that $\underset{n\to \infty }{\lim }\Vert x_n-T{x}_n\Vert =0$.

$$\begin{array}{cc}\hfill \Vert x_n-T{x}_n\Vert & \le \Vert x_n-x_{n+1}\Vert +\Vert x_{n+1}-T(s_n{x}_n+(1-s_n)x_{n+1})\Vert +\Vert T(s_n{x}_n+(1-s_n)x_{n+1})-T{x}_n\Vert \hfill \\ & \le \Vert x_n-x_{n+1}\Vert +{\alpha }_n\Vert x_n-T(s_n{x}_n+(1-s_n)x_{n+1})\Vert +(1-s_n)\Vert x_n-x_{n+1}\Vert \hfill \\ & +{\beta }_n\Vert f(x_n)-T(s_n{x}_n+(1-s_n)x_{n+1})\Vert +\Vert e_n\Vert \hfill \\ & \le (2-s_n)\Vert x_n-x_{n+1}\Vert +({\alpha }_n+{\beta }_n)M_1+\Vert e_n\Vert \hfill \\ & \le 2\Vert x_n-x_{n+1}\Vert +(1-{\gamma }_n)M_1+\Vert e_n\Vert .\hfill \end{array}$$

From $\underset{n\to \infty }{\lim }{\gamma }_n=1$, ${\displaystyle \sum _{n=1}^{\infty }\Vert e_n\Vert }<\infty$ and Step 2, we get $\underset{n\to \infty }{\lim }\Vert x_n-T{x}_n\Vert =0$.

Step 4: Show that $\underset{n\to \infty }{\lim \sup }⟨f(q)-q,j(x_{n+1}-q)⟩\le 0$.

Let $\left\{x_t\right\}$ be defined by $x_t=tf(x_t)+(1-t)T{x}_t$. Then, from Lemma 2, $\left\{x_t\right\}$ converges strongly to $q\in F(T)$, which is also the unique solution of the variational inequality $⟨(I-f)q,j(x-q)⟩\ge 0$ and $x\in F(T)$. From Steps 1–3 and Lemma 3, we get $\underset{n\to \infty }{\lim \sup }⟨f(q)-q,j(x_{n+1}-q)⟩\le 0$.

We have

$$\begin{array}{cc}\hfill {\Vert x_t-x_n\Vert }^2& =(1-t)⟨S{x}_t-S{x}_n+S{x}_n-x_n,J(x_t-x_n)⟩+t⟨f{x}_t-x_t+x_t-x_n,J(x_t-x_n)⟩\hfill \\ & \le (1-t){\Vert x_t-x_n\Vert }^2+(1-t)\Vert S{x}_n-x_n\Vert \cdot \Vert x_t-x_n\Vert \hfill \\ & +t{\Vert x_t-x_n\Vert }^2+t⟨f{x}_t-x_t,J(x_t-x_n)⟩\hfill \\ & ={\Vert x_t-x_n\Vert }^2+(1-t)\Vert S{x}_n-x_n\Vert \cdot \Vert x_t-x_n\Vert +t{\Vert x_t-x_n\Vert }^2+t⟨f{x}_t-x_t,J(x_t-x_n)⟩.\hfill \end{array}$$

It follows that $⟨f{x}_t-x_t,J(x_t-x_n)⟩\le \frac{1-t}{t}\Vert S{x}_n-x_n\Vert \cdot \Vert x_t-x_n\Vert$. From Step 3, we get $\underset{n\to \infty }{\lim \sup }⟨f(q)-q,j(x_{n+1}-q)⟩\le 0$.

Step 5: Show that $\underset{n\to \infty }{\lim }{x}_n=q$.

$$\begin{array}{cc}\hfill {\Vert x_{n+1}-q\Vert }^2& ={\Vert {\alpha }_n\left(x_n-q\right)+{\beta }_n(f(x_n)-q)+{\gamma }_n\left(T(s_n{x}_n+(1-s_n)x_{n+1})-q\right)+e_n\Vert }^2\hfill \\ & ={\alpha }_n⟨x_n-q,j(x_{n+1}-q)⟩+{\beta }_n⟨f(x_n)-q,j(x_{n+1}-q)⟩\hfill \\ & +{\gamma }_n⟨T(s_n{x}_n+(1-s_n)x_{n+1})-q,j(x_{n+1}-q)⟩+⟨e_n,j(x_{n+1}-q)⟩\hfill \\ & \le {\alpha }_n\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert +\alpha {\beta }_n\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert +{\beta }_n⟨f(q)-q,j(x_{n+1}-q)⟩\hfill \\ & +{\gamma }_n\Vert s_n(x_n-q)+(1-s_n)(x_{n+1}-q)\Vert \cdot \Vert x_{n+1}-q\Vert +\Vert e_n\Vert \cdot \Vert x_{n+1}-q\Vert \hfill \\ & \le ({\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n)\Vert x_n-q\Vert \cdot \Vert x_{n+1}-q\Vert +(1-s_n){\gamma }_n{\Vert x_{n+1}-q\Vert }^2\hfill \\ & +{\beta }_n⟨f(q)-q,j(x_{n+1}-q)⟩+\Vert e_n\Vert \cdot \Vert x_{n+1}-q\Vert \hfill \\ & \le \frac{{\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n}{2}{\Vert x_n-q\Vert }^2+\left[\frac{{\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n}{2}+(1-s_n){\gamma }_n\right]{\Vert x_{n+1}-q\Vert }^2\hfill \\ & +{\beta }_n⟨f(q)-q,j(x_{n+1}-q)⟩+\Vert e_n\Vert \cdot \Vert x_{n+1}-q\Vert .\hfill \end{array}$$

It follows that

$$\begin{array}{cc}\hfill {\Vert x_{n+1}-q\Vert }^2& \le \frac{{\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n}{2-({\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n)-2{\gamma }_n(1-s_n)}{\Vert x_n-q\Vert }^2\hfill \\ & +\frac{2{\beta }_n}{2-({\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n)-2{\gamma }_n(1-s_n)}⟨f(q)-q,j(x_{n+1}-q)⟩+\frac{2M_2\Vert e_n\Vert }{2-({\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n)-2{\gamma }_n(1-s_n)}\hfill \\ & =\left[1-\frac{2(1-\alpha ){\beta }_n}{2-({\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n)-2{\gamma }_n(1-s_n)}\right]{\Vert x_n-q\Vert }^2\hfill \\ & +\frac{2(1-\alpha ){\beta }_n}{2-({\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n)-2{\gamma }_n(1-s_n)}\frac{⟨f(q)-q,j(x_{n+1}-q)⟩}{1-\alpha }+\frac{2M_2\Vert e_n\Vert }{2-({\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n)-2{\gamma }_n(1-s_n)}\hfill \end{array}$$

where $M_2\ge \max \left\{\underset{n\ge 0}{\sup }\Vert x_{n+1}-q\Vert \right\}$

Because

$$\begin{array}{cc}\hfill \frac{2{\beta }_n(1-\alpha )}{2-({\alpha }_n+\alpha {\beta }_n+{\gamma }_n{s}_n)-2{\gamma }_n(1-s_n)}& =\frac{2{\beta }_n(1-\alpha )}{2-{\alpha }_n-\alpha {\beta }_n-2{\gamma }_n+{\gamma }_n{s}_n}\hfill \\ & =\frac{2{\beta }_n(1-\alpha )}{1+1-{\alpha }_n-\alpha {\beta }_n-{\gamma }_n-{\gamma }_n+{\gamma }_n{s}_n}\hfill \\ & =\frac{2{\beta }_n(1-\alpha )}{1+(1-\alpha ){\beta }_n-(1-s_n){\gamma }_n}>\frac{2-2\alpha }{2-\alpha }{\beta }_n,\hfill \end{array}$$

so from ${\displaystyle \sum _{n=0}^{\infty }{\beta }_n}=\infty$, $\Vert e_n\Vert =o({\beta }_n)$, Step 4, and Lemma 1, we get $\underset{n\to \infty }{\lim }{x}_n=q$. This completes the proof. □

If ${\alpha }_n=0$, we can get Theorem 1. So, Theorem 2 is a generalization of Theorem 1. And, the computational efficiency of Theorem 2 is better than Theorem 1.

It is well known that Hilbert space is uniformly smooth Banach space. So, we can get the main results of [19].

Corollary 3.

([19]) Let $C$ be a nonempty, closed convex subset of the real Hilbert space $H$. Let $T:C\to C$ be a nonexpansive mapping with $F(T)\ne \varnothing$ and $f:C\to C$ be a contraction with coefficient $\theta \in [0,1)$. Pick any $x_0\in C$ and let $\left\{x_n\right\}$ be a sequence generated by

$$x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_{n}T\left(s_n{x}_n+(1-s_n)x_{n+1}\right),$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\},\left\{s_n\right\}\subset (0,1)$ that satisfies the following conditions:

(1) 

${\alpha }_n+{\beta }_n+{\gamma }_n=1,\underset{n\to \infty }{\lim }{\gamma }_n=1$;

(2) 

${\displaystyle \sum _{n=0}^{\infty }{\beta }_n}=\infty$;

(3) 

${\displaystyle \sum _{n=1}^{\infty }\left|{\alpha }_{n+1}-{\alpha }_n\right|}<\infty$and ${\displaystyle \sum _{n=1}^{\infty }\left|{\beta }_{n+1}-{\beta }_n\right|}<\infty$;

(4) 

$0<\epsilon \le s_n\le s_{n+1}<1$, $\forall n\ge 0$.

Then $\left\{x_n\right\}$ converges strongly to a fixed point $x^{*}$ of the nonexpansive mapping $T$, which is also the unique solution of the variational inequality $⟨(I-f)x,y-x⟩\ge 0$ and $\forall y\in F(T)$.

If we let $s_n=\frac{1}{2}$ and ${\alpha }_n=0$, we can also get the main results of [20]. The results of Theorem 2 generalize the relevant results of [23].

Corollary 4.

([23]) Let $E$ be a uniformly smooth Banach space and $C$ a nonempty closed convex subset of $E$. Let $T:C\to C$ be a nonexpansive mapping with $F(T)\ne \varnothing$ and $f:C\to C$ a generalized contraction mapping. Pick any $x_0\in C$. Let $\left\{x_n\right\}$ be a sequence generated by

$$x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_{n}T\left(s_n{x}_n+(1-s_n)x_{n+1}\right),$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$, and $\left\{{\gamma }_n\right\}$ are three sequences in $[0,1]$ satisfying the following conditions:

(i) 

${\alpha }_n+{\beta }_n+{\gamma }_n=1$;

(ii) 

${\displaystyle \sum _{n=0}^{\infty }{\beta }_n}=\infty ,\underset{n\to \infty }{\lim }{\beta }_n=0$;

(iii) 

$\underset{n\to \infty }{\lim }\left|{\alpha }_{n+1}-{\alpha }_n\right|=0$and $0<\underset{n\to \infty }{\lim \inf }{\alpha }_n\le \underset{n\to \infty }{\lim \sup }{\alpha }_n<1$;

(iv) 

$0<\epsilon \le s_n\le s_{n+1}<1$for all $n\ge 0$.

Then $\left\{x_n\right\}$ converges strongly to a fixed point $x^{*}$ of the nonexpansive mapping $T$, which is also the solution of the variational inequality $⟨(I-f)x^{*},j(y-x^{*})⟩\ge 0$ for all $y\in F(T)$.

4. Applications

(1) A fixed point problem for strict pseudocontractive mapping.

If there exists $\lambda \in (0,1)$ such that

$$⟨Tx-Ty,j(x-y)⟩\le {\Vert x-y\Vert }^2-\lambda {\Vert (I-T)x-(I-T)y\Vert }^2,\forall x,y\in C,$$

then $T:C\to C$ is called $\lambda$-strict pseudocontractive mapping.

Zhou [24] obtained the relationship between nonexpansive mapping and $\lambda$-strict pseudocontractive mapping.

Lemma 4.

([24]) Let $C$ be a nonempty, closed convex subset of a real 2-uniformly smooth Banach space $E$ and $T:C\to C$ be a $\lambda$-strict pseudocontractive mapping. For $\alpha \in (0,1)$, we define $T_{\alpha }x:=(1-\alpha )x+\alpha Tx$. Then, $\alpha \in (0,\frac{\lambda }{K^2}]$, where $K$ is the 2-uniformly smooth constant. Then, $T_{\alpha }:C\to C$ is nonexpansive such that $F(T_{\alpha })=F(T)$.

So $T_{\alpha }:C\to C$ is nonexpansive, and then we can get the following results.

Theorem 3.

Let $E$ be a 2-uniformly smooth Banach space, $C$ be a closed convex subset of $E$, $f:C\to C$ be a contractive mapping with $k\in [0,1)$, $T:C\to C$ be a $\lambda$-strict pseudocontractive mapping, and $T_{\alpha }:C\to C$ be defined by $T_{\alpha }x:=(1-\alpha )x+\alpha Tx$ with $\alpha \in (0,\frac{\lambda }{K^2}]$. $\left\{x_n\right\}$ is generated by the generalized viscosity implicit midpoint rule

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T_{\alpha }\left(s_n{x}_n+(1-s_n)x_{n+1}\right),n\ge 0,$$

(5)

where $\left\{{\alpha }_n\right\},\left\{s_n\right\}\subset (0,1)$ and satisfies the conditions:

(i) 

$\underset{n\to \infty }{\lim }{\alpha }_n=0$;

(ii) 

${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$;

(iii) 

$\underset{n\to \infty }{\lim }\frac{{\alpha }_{n+1}}{{\alpha }_n}=1$or ${\displaystyle \sum _{n=1}^{\infty }\left|{\alpha }_{n+1}-{\alpha }_n\right|}<\infty$;

(iv) 

$0<\epsilon \le s_n\le s_{n+1}<1$, $\forall n\ge 0$.

Then $\left\{x_n\right\}$ converges strongly to $q\in F(T)$, which is also the unique solution of the variational inequality $⟨(I-f)q,j(x-q)⟩\ge 0$, and $x\in F(T)$.

Theorem 4.

Let $E$ be a 2-uniformly smooth Banach space, $C$ be a closed convex subset of $E$, $f:C\to C$ be a contractive mapping with $k\in [0,1)$, $T:C\to C$ be a $\lambda$-strict pseudocontractive mapping, and $T_{\alpha }:C\to C$ be defined by $T_{\alpha }x:=(1-\alpha )x+\alpha Tx$ with $\alpha \in (0,\frac{\lambda }{K^2}]$. $\left\{x_n\right\}$ is generated by the generalized viscosity implicit midpoint rule

$$x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_n{T}_{\alpha }\left(s_n{x}_n+(1-s_n)x_{n+1}\right)+e_n,n\ge 0,$$

(6)

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\},\left\{s_n\right\}\subset (0,1),\left\{e_n\right\}\subset E$ and satisfies the conditions:

(i) 

${\alpha }_n+{\beta }_n+{\gamma }_n=1,\underset{n\to \infty }{\lim }{\gamma }_n=1$;

(ii) 

${\displaystyle \sum _{n=0}^{\infty }{\beta }_n}=\infty$;

(iii) 

${\displaystyle \sum _{n=1}^{\infty }\left|{\alpha }_{n+1}-{\alpha }_n\right|}<\infty$and ${\displaystyle \sum _{n=1}^{\infty }\left|{\beta }_{n+1}-{\beta }_n\right|}<\infty$;

(iv) 

$0<\epsilon \le s_n\le s_{n+1}<1$, $\forall n\ge 0$;

(v) 

${\displaystyle \sum _{n=0}^{\infty }\Vert e_n\Vert }<\infty$and $\Vert e_n\Vert =o({\beta }_n)$.

Then $\left\{x_n\right\}$ converges strongly to $q\in F(T)$, which is also the unique solution of the variational inequality $⟨(I-f)q,j(x-q)⟩\ge 0$, and $x\in F(T)$.

(2) A general system of a variational inequality problem in Banach space.

The problem of finding $(x^{*},y^{*})\in C\times C$ such that

$$\{\begin{array}{l}⟨\lambda A{y}^{*}+x^{*}-y^{*},j(x-x^{*})⟩\ge 0,\forall x\in C,\\ ⟨\mu B{x}^{*}+y^{*}-x^{*},j(x-y^{*})⟩\ge 0,\forall x\in C,\end{array}$$

is called the general system of variational inequalities in Banach space, where $\lambda ,\mu >0$ and $A,B$ are two nonlinear mappings.

If there exists $j(x-y)\in J(x-y)$ satisfying $⟨Ax-Ay,j(x-y)⟩\ge 0,\forall x,y\in C$, then $A:C\to E$ is called accretive. If there exists $j(x-y)\in J(x-y)$ and $\alpha >0$ satisfying $⟨Ax-Ay,j(x-y)⟩\ge \alpha {\Vert Ax-Ay\Vert }^2,\forall x,y\in C$, then $A:C\to E$ is called $\alpha$-inverse-strongly accretive.

Lemma 5.

([25]) Let $C$ be a nonempty, closed convex subset of a real 2-uniformly smooth Banach space $E$. Let $Q_C$ be the sunny, nonexpansive retraction from $E$ onto $C$. Let $A,B:C\to E$ be $\alpha$-inverse-strongly accretive and $\beta$-inverse-strongly accretive, respectively. Let $G:C\to C$ be a mapping defined by $G(x)=Q_C\left[Q_C(x-\mu Bx)-\lambda A{Q}_C(x-\mu Bx)\right]$, $\forall x\in C$. If $0<\lambda \le \frac{\alpha }{K^2}$ and $0<\mu \le \frac{\alpha }{K^2}$, then $G:C\to C$ is nonexpansive.

Thus, $G:C\to C$ is nonexpansive, and we can get the following results. More information on nonexpansive retracts and retractions can be found in [26,27].

Theorem 5.

Let $E$ be a 2-uniformly smooth Banach space, $C$ be a closed convex subset of $E$, $A,B:C\to E$ be, respectively, $\alpha$-inverse-strongly accretive and $\beta$-inverse-strongly accretive, $f:C\to C$ be a contractive mapping with $k\in [0,1)$, and $G:C\to C$ be defined by Lemma 5. $\left\{x_n\right\}$ is generated by the generalized viscosity implicit midpoint rule

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)G\left(s_n{x}_n+(1-s_n)x_{n+1}\right),n\ge 0,$$

(7)

where $\left\{{\alpha }_n\right\},\left\{s_n\right\}\subset (0,1)$ and satisfies the conditions:

(i) 

$\underset{n\to \infty }{\lim }{\alpha }_n=0$;

(ii) 

${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n}=\infty$;

(iii) 

$\underset{n\to \infty }{\lim }\frac{{\alpha }_{n+1}}{{\alpha }_n}=1$or ${\displaystyle \sum _{n=1}^{\infty }\left|{\alpha }_{n+1}-{\alpha }_n\right|}<\infty$;

(iv) 

$0<\epsilon \le s_n\le s_{n+1}<1$, $\forall n\ge 0$.

Then $\left\{x_n\right\}$ converges strongly to $q\in F(G)$, which is also the unique solution of the variational inequality $⟨(I-f)q,j(x-q)⟩\ge 0$, and $x\in F(G)$.

Theorem 6.

Let $E$ be a 2-uniformly smooth Banach space, $C$ be a closed convex subset of $E$, $A,B:C\to E$ be, respectively, $\alpha$-inverse-strongly accretive and $\beta$-inverse-strongly accretive, $f:C\to C$ be a contractive mapping with $k\in [0,1)$, and $G:C\to C$ be defined by Lemma 5. $\left\{x_n\right\}$ is generated by the generalized viscosity implicit midpoint rule

$$x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_{n}G\left(s_n{x}_n+(1-s_n)x_{n+1}\right)+e_n,n\ge 0,$$

(8)

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\},\left\{s_n\right\}\subset (0,1),\left\{e_n\right\}\subset E$ and satisfies the conditions:

(i) 

${\alpha }_n+{\beta }_n+{\gamma }_n=1,\underset{n\to \infty }{\lim }{\gamma }_n=1$;

(ii) 

${\displaystyle \sum _{n=0}^{\infty }{\beta }_n}=\infty$;

(iii) 

${\displaystyle \sum _{n=1}^{\infty }\left|{\alpha }_{n+1}-{\alpha }_n\right|}<\infty$and ${\displaystyle \sum _{n=1}^{\infty }\left|{\beta }_{n+1}-{\beta }_n\right|}<\infty$;

(iv) 

$0<\epsilon \le s_n\le s_{n+1}<1$, $\forall n\ge 0$;

(v) 

${\displaystyle \sum _{n=0}^{\infty }\Vert e_n\Vert }<\infty$and $\Vert e_n\Vert =o({\beta }_n)$.

Then $\left\{x_n\right\}$ converges strongly to $q\in F(G)$, which is also the unique solution of the variational inequality $⟨(I-f)q,j(x-q)⟩\ge 0$, and $x\in F(G)$.

5. Numerical Examples

We give six numerical examples to support the main results.

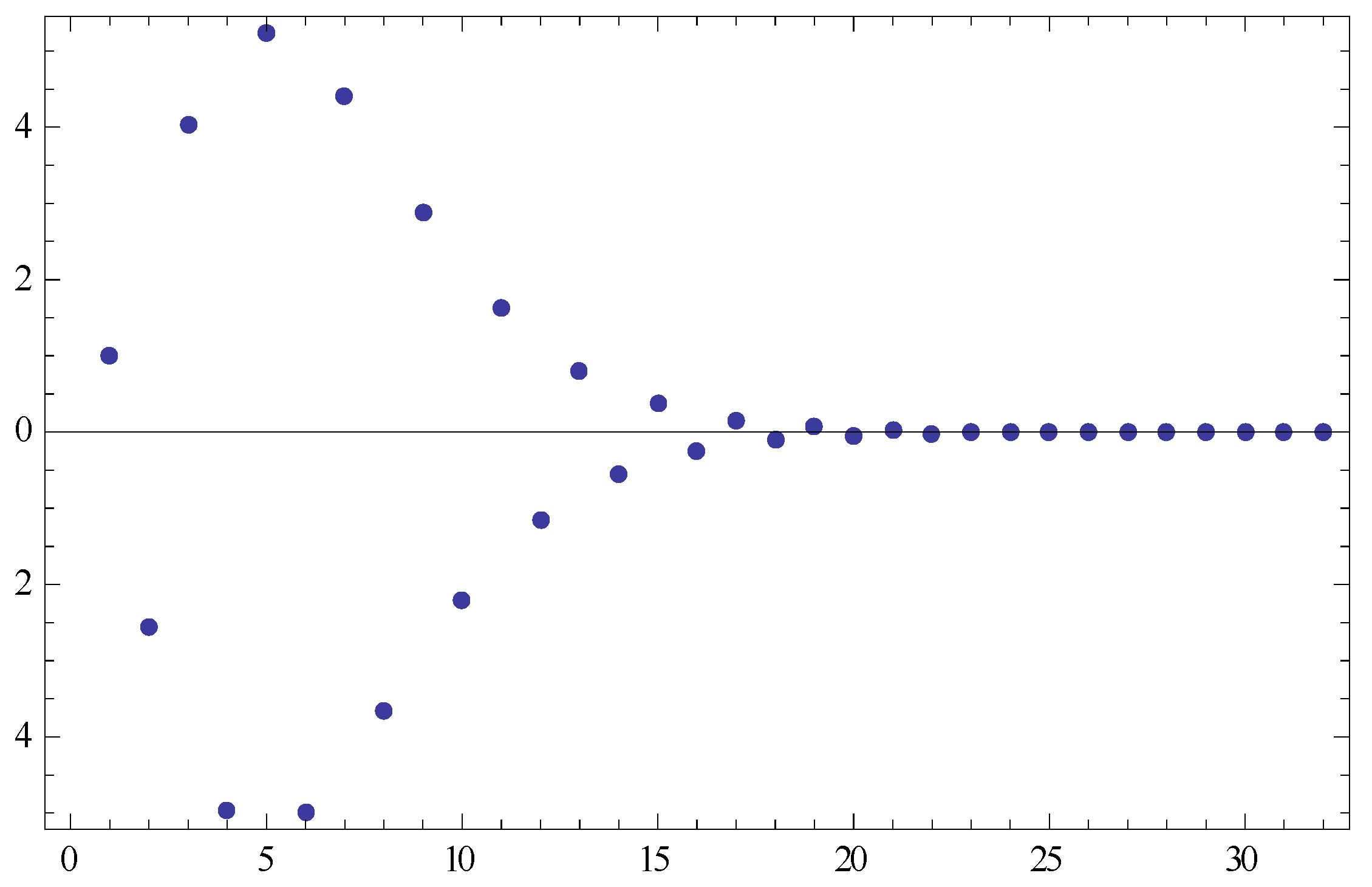
Example 1.

Let $R$ be the real line with Euclidean norm, $f:R\to R$ be defined by $f(x)=\frac{x}{4}$, $T:R\to R$ be defined by $T(x)=\frac{x}{2}$, ${\alpha }_n=\frac{1}{n}$, and $s_n=1-\frac{1}{n}$. So, $F(T)=\left\{0\right\}$. $\left\{x_n\right\}$ is generated by (3). From Theorem 1, $\left\{x_n\right\}$ converges strongly to 0.

Next, we simplify the form of (3) and get

$$x_{n+1}=\frac{2-4n+2n^2+n^3}{6n^2-2n^3}{x}_n.$$

(9)

Next, we take $x_0=1$ into (9). Finally, we get the following numerical results in Figure 1.

Figure 1. Numerical results.

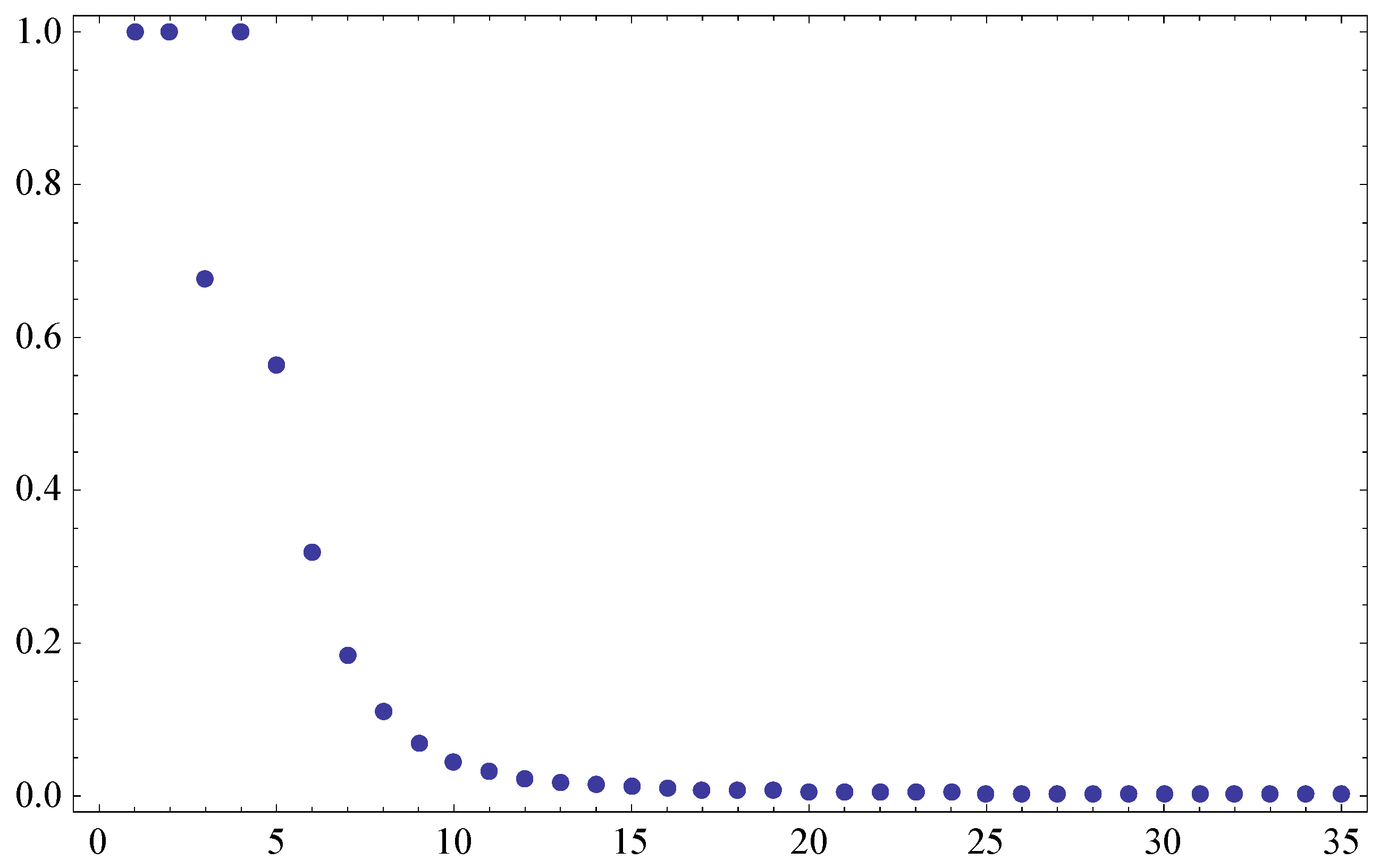
Example 2.

Let $R$ be the real line with Euclidean norm, $f:R\to R$ be defined by $f(x)=\frac{x}{4}$, $T:R\to R$ be defined by $T(x)=\frac{x}{2}$, ${\alpha }_n=\frac{1}{n}$, ${\beta }_n=\frac{1}{n}$, ${\gamma }_n=1-\frac{2}{n}$, $e_n=\frac{1}{n^2}$, and $s_n=1-\frac{1}{n}$. So, $F(T)=\left\{0\right\}$. $\left\{x_n\right\}$ is generated by (4). From Theorem 2, $\left\{x_n\right\}$ converges strongly to 0.

Next, we simplify the form of (4) and get

$$x_{n+1}=\frac{4-n+2n^2}{4-2n+4n^2}{x}_n+\frac{2}{2-n+2n^2}.$$

(10)

Next, we take $x_0=1$ into (10). Finally, we get the following numerical results in Figure 2.

Figure 2. Numerical results.

Example 3.

Let $⟨\cdot ,\cdot ⟩:R^3\times R^3\to R$ be the inner product and defined by

$$⟨x,y⟩=x_1{y}_1+x_2{y}_2+x_2{y}_3.$$

Let $\Vert \cdot \Vert :R^3\to R$ be the usual norm and defined by $\Vert x\Vert =\sqrt{x_1^2+x_2^2+x_3^2}$ for any $x=(x_1,x_2,x_3)$. For any $x\in R^3$, let $f:R^3\to R^3$ be defined by $f(x)=\frac{x}{6}$ and $T:R^3\to R^3$ be defined by $T(x)=\frac{x}{4}$. So, $F(T)=\left\{0\right\}$. Let ${\alpha }_n=\frac{1}{n}$ and $s_n=1-\frac{1}{n}$, then they satisfy the conditions of Theorem 1.$\left\{x_n\right\}$ is generated by (3). From Theorem 1, $\left\{x_n\right\}$ converges strongly to 0.

Next, we simplify the form of (3) and get

$$x_{n+1}=\frac{3-4n+3n^2}{3-3n+12n^2}{x}_n.$$

(11)

Next, we take $x_1=(1,2,3)$ into (11). Finally, we get the following numerical results in Figure 3.

Figure 3. Numerical results.

Example 4.

Let $⟨\cdot ,\cdot ⟩:R^3\times R^3\to R$ be the inner product and defined by

$$⟨x,y⟩=x_1{y}_1+x_2{y}_2+x_2{y}_3.$$

Let $\Vert \cdot \Vert :R^3\to R$ be the usual norm and defined by $\Vert x\Vert =\sqrt{x_1^2+x_2^2+x_3^2}$ for any $x=(x_1,x_2,x_3)$. For any $x\in R^3$, let $f:R^3\to R^3$ be defined by $f(x)=\frac{x}{6}$ and $T:R^3\to R^3$ be defined by $T(x)=\frac{x}{4}$. So, $F(T)=\left\{0\right\}$. Let ${\alpha }_n=\frac{1}{n},{\beta }_n=\frac{1}{n},{\gamma }_n=1-\frac{2}{n},e_n=\frac{1}{n^2}$, and $s_n=1-\frac{1}{n}$, then they satisfy the conditions of Theorem 2. $\left\{x_n\right\}$ is generated by (4). From Theorem 2, $\left\{x_n\right\}$ converges strongly to 0.

Next, we simplify the form of (4) and get

$$x_{n+1}=\frac{6+5n+3n^2}{6-3n+12n^2}{x}_n+\frac{4}{2-n+4n^2}.$$

(12)

Next, we take $x_1=(1,2,3)$ into (12). Finally, we get the following numerical results in Figure 4.

Figure 4. Numerical results.

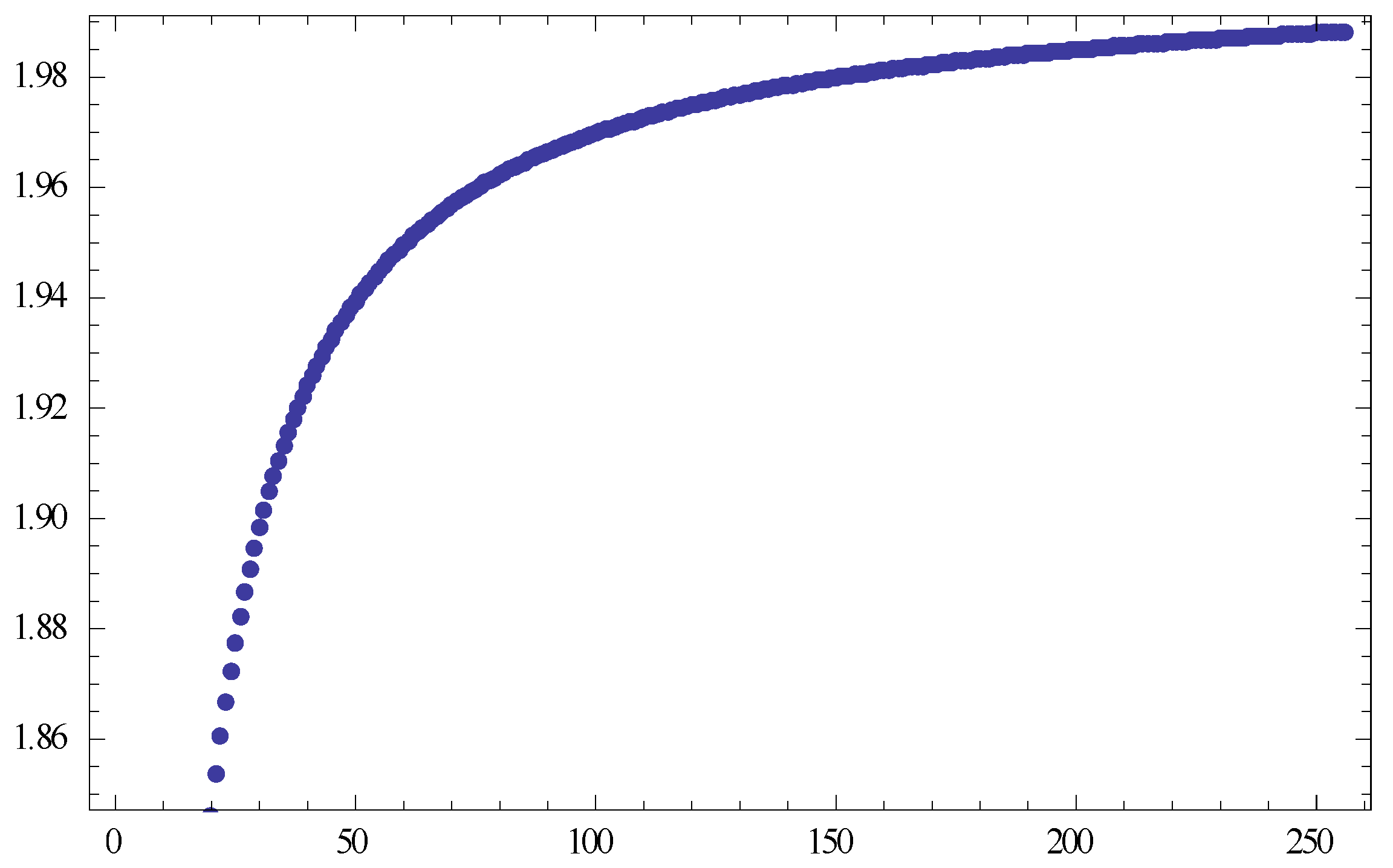
Example 5.

Let $R$ be the real line with Euclidean norm, $f:R\to R$ be defined by $f(x)=\frac{x}{4}$, $T:R\to R$ be defined by $T(x)=\frac{x}{2}+1$, ${\alpha }_n=\frac{1}{n}$, and $s_n=1-\frac{1}{n}$. So, $F(T)=\left\{2\right\}$. $\left\{x_n\right\}$ is generated by (3). From Theorem 1, $\left\{x_n\right\}$ converges strongly to 2.

Next, we simplify the form of (3) and get

$$x_{n+1}=\frac{2-3n+2n^2}{2-2n+4n^2}{x}_n+\frac{2n^2-2n}{1-n+2n^2}.$$

(13)

Next, we take $x_0=1$ into (13). Finally, we get the following numerical results in Figure 5.

Figure 5. Numerical results.

Example 6.

Let $R$ be the real line with Euclidean norm, $f:R\to R$ be defined by $f(x)=\frac{x}{4}$, $T:R\to R$ be defined by $T(x)=\frac{x}{2}+1$, ${\alpha }_n=\frac{1}{n}$, ${\beta }_n=\frac{1}{n}$, ${\gamma }_n=1-\frac{2}{n}$, $e_n=\frac{1}{n^2}$, and $s_n=1-\frac{1}{n}$. So, $F(T)=\left\{2\right\}$. $\left\{x_n\right\}$ is generated by (4). From Theorem 2, $\left\{x_n\right\}$ converges strongly to 2.

Next, we simplify the form of (4) and get

$$x_{n+1}=\frac{4-n+2n^2}{4-2n+4n^2}{x}_n+\frac{2{(n-1)}^2}{2-n+2n^2}.$$

(14)

Next, we take $x_0=1$ into (14). Finally, we get the following numerical results in Figure 6.

Figure 6. Numerical results.

6. Conclusions

This paper proposes the generalized viscosity implicit rules for nonexpansive mappings in Banach space and concretely constructs two iterative algorithms:

$$\begin{array}{cc}\hfill x_{n+1}& ={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T\left(s_n{x}_n+(1-s_n)x_{n+1}\right),\hfill \\ \hfill x_{n+1}& ={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_{n}T\left(s_n{x}_n+(1-s_n)x_{n+1}\right)+e_n.\hfill \end{array}$$

This paper obtains strong convergence results. Results promote the work of Ke et al. [19], Luo et al. [20], and Yan et al. [23] from Hilbert spaces to a general Banach spaces and their iterative algorithms and relevant conclusions. In the end, this paper gives six numerical examples to support the main results.