1. Introduction
In 1965, L. A. Zadeh [
1] introduced the idea of fuzzy sets which has been successfully applied to solve the various real life decision problems, which are often uncertain. Fuzzy set is a generalization of crisp set, where the elements of the set have varying degrees of membership. Since the crisp set consists of two truth values ( 0 (‘false’) and 1 (‘true’)) which is unable to work with uncertain real life problem. Fuzzy set permits its member to have the value of membership degree between 0 and 1 for better outcome, instead of considering only 0 or 1. The membership degree of a member is not same as probability, rather it indicates the belongingness degree of the element to the fuzzy set, which is a single value within the interval
. However, those single values of membership degree cannot handle the uncertainties due to lack of knowledge of the problem. Atanassov [
2] has proposed the intuitionistic fuzzy set to manage this kind of uncertain situation using an additional membership degree, defined as hesitation margin. Intuitionistic fuzzy set is as an extension of Zadeh’s fuzzy set. The fuzzy set can consider only the membership degree of a member in a given set and sum of the membership degree and non membership is always equal to 1, while intuitionistic fuzzy set can consider independent membership degree and non membership degree, the only requirement is that sum of membership degree and non membership degree is not greater than 1. It is more flexible and efficient compared to classical fuzzy set to work with uncertainty due to the presence of hesitation margin. The intuitionistic fuzzy set is used significantly in those real life scenarios, where human perception and knowledge are required, which are generally imprecise and not fully reliable. Over the last few decades, the intuitionistic fuzzy set has been obtaining lots of attention from researchers and scientists. Intuitionistic fuzzy set is used in successfully in different field including image processing [
3], decision making [
4], social network [
5], logic programming [
6], market prediction [
7], machine learning [
8], medical diagnosis recognition [
9], robotic systems [
10], etc. The concept of neutrality degree cannot be considered in intuitionistic fuzzy set theory. However, neutrality degree needs to consider in many real life scenarios, such as democratic election station. Human beings generally give opinions having more answers of the type: yes, no, abstain and refusal. For example, in a democratic voting system, 1000 people participated in the election. The election commission issues 1000 ballot paper and one person can take only one ballot for giving his/her vote and
is only one candidate. The results of the election are generally divided into four groups came with the number of ballot papers namely “vote for the candidate (500)”, “abstain in vote (200)”, “vote against candidate (200)” and “refusal of voting (100)”. The “abstain in vote” describes that ballot paper is white which contradicts both “vote for the candidate” and “vote against candidate” but it considers the vote. However, “refusal of voting” means bypassing the vote. This type of real life scenarios cannot be handled by intuitionistic fuzzy set. If we use intuitionistic fuzzy sets to describe the above voting system, the information of voting for non-candidates may be ignored. To solve this problem, Cuong and Kreinovich [
11] proposed the concept of picture fuzzy set which is a modified version of fuzzy set and Intuitionistic fuzzy set. Picture fuzzy set (PFS) allows the idea degree of positive membership, degree of neutral membership and degree of negative membership of an element. Numerous papers [
12,
13,
14,
15,
16,
17,
18,
19,
20,
21] have been published on the picture fuzzy set. Cuong [
22] described several properties of PFS and also studied a ranking method based on distance measurement between two PFSs. Phong et al. [
23] have proposed several compositions of picture fuzzy relations. Then, Cuong and Hai [
24] have extended some fuzzy logic operators such as conjunctions, complements, disjunctions and implications for PFSs. They proposed fuzzy inference processes for picture fuzzy systems. Peng and Dai [
19] have proposed an algorithmic approach for PFS and used it in a decision making problem. Garg [
20] have introduced some aggregation operations of PFS and their applications in multi-criteria decision making.
The basic idea of fuzzy graph was proposed by Rosenfeld [
25], 10 years after Zadeh’s significant paper on fuzzy sets. Fuzzy graphs have numerous applications in modern engineering, science and medicine especially in the areas of telecommunication, information theory, logistics, neural networks, transportation, expert systems, manufacturing, cluster analysis, social network, medical diagnosis, control theory etc. Fuzzy graph is used as an essential tool to model those problems and it gives more efficient, flexibility and compatibility to model any real world problem when compared to the classic graph. The concept of a complement fuzzy graph was introduced by Mordeson and Nair [
26] and further described by Sunitha and Kumar [
27]. Shannon and Atanassov [
28] have proposed the definition of intuitionistic fuzzy relation and intuitionistic fuzzy graphs and described several proprieties in [
28]. Parvathi et al. [
29,
30,
31] described different operations on intuitionistic fuzzy graphs. Rashmanlou et al. [
32] introduced several operations such as direct product, lexicographic product and strong product on intuitionistic fuzzy graphs. They have also described the join, union, composition, and Cartesian production between two intuitionistic fuzzy graphs. For more details on intuitionistic fuzzy graphs, please refer to [
33,
34,
35,
36].
Fuzzy graph has used to model many decision making problem in uncertain environment. A number of generalizations of fuzzy graphs have been introduced to deal the uncertainty of the complex real life problems. As uncertainties are well expressed using picture fuzzy set, picture fuzzy graph would be prominent research direction for modeling the uncertain optimization problems. This motivated us to introduce the idea picture fuzzy graph its related operations. In this study, we propose the definition of picture fuzzy graph based on picture fuzzy relation. We also introduce several types of picture fuzzy graph such as regular picture fuzzy graph, strong picture fuzzy graph, complete picture fuzzy graph, connected picture fuzzy graph and complement picture fuzzy graph. The idea of isomorphism of picture fuzzy graph is introduced in this paper. We describe the weak and co weak isomorphic picture fuzzy graph. We describe the degree, size and order of a picture fuzzy graph. Busy and free nodes of picture fuzzy graph are also defined in this paper. Six operations on picture fuzzy graphs, viz. Cartesian product, composition, join, direct product, lexicographic and strong product are introduced in this paper. Finally, we describe the utility of picture fuzzy graph and its application in social network.
2. Preliminaries
Definition 1. A fuzzy set A, on the universe of discourse of X can also be described a set of ordered pairs as: In classical set theory, has only the two membership values 0 (‘false’) and 1 (‘true’). Instead of considering only those two truth values, fuzzy set can assign the value of within the interval between 0 (‘false’) and 1 (‘true’) for better outcome.
Definition 2. Let A be a intuitionistic fuzzy set. A in X is defined bywhere and follows with the condition . The is used to represent the degree of membership and represents the degree of non-membership of the element x in the set A. For each intuitionistic fuzzy set A in X, the intuitionistic fuzzy index is described as . Definition 3. Let A be a picture fuzzy set. A in X is defined bywhere , and follow the condition . The , denote respectively the positive membership degree, neutral membership degree and negative membership degree of the element x in the set A. For each picture fuzzy set A in X, the refusal membership degree is described as . Definition 4. A picture fuzzy relation R is a picture fuzzy subset of described by Here, , and must satisfy the condition for every .
Definition 5. Let A and B be two picture fuzzy sets. The union, intersection and complement are described as follows.
- 1.
- 2.
- 3.
Definition 6. Let A and B be two picture fuzzy sets on two universes and . The Cartesian product of A and B is described as follows. Definition 7. Let V be a finite nonempty set of vertices. A fuzzy graph G is described by an order pair of functions σ and μ, G = . σ represents a fuzzy subset of V and μ represents a symmetric fuzzy relation on σ, i.e., σ: and μ: V such that Definition 8. A fuzzy graph G = is called complete fuzzy graph if Definition 9. A fuzzy graph G = is called strong fuzzy graph if Definition 10. The complement of a fuzzy graph G = is a fuzzy graph and it is represented as , where and Definition 11. Let V be a finite nonempty set of vertices. An intuitionistic fuzzy graph is described by an order pair , where A is an intuitionistic fuzzy set on V and B is an intuitionistic fuzzy set on . A and B satisfy , and . Here, and are used to denote the degree of membership and non membership of the node x and and are used to denote the degree of membership and non membership of the arcs .
Definition 12. Let and be two classical (crisp) graph. The Cartesian product of two graph and is an another graph , where and .
Definition 13. Let and be two classical (crisp) graph. The direct product of two graph and is an another graph , where and .
Definition 14. Let and be two classical (crisp) graph. The lexicographic product of two graph and is an another graph , where and .
Definition 15. Let and be two classical (crisp) graph. The strong product of two graph and is an another graph , where and .
Definition 16. Let and be two classical (crisp) graph. The union of two graphs and is an another graph , where and .
Definition 17. Let and be two classical (crisp) graph. The joining of two graphs and is an another graph , where and , where represents the set of all arcs joining the nodes and .
3. Picture Fuzzy Graph
In this section, we define the picture fuzzy graph and introduce different types of regular picture fuzzy graphs, strong picture fuzzy graphs, complete picture fuzzy graphs, and complement picture fuzzy graph.
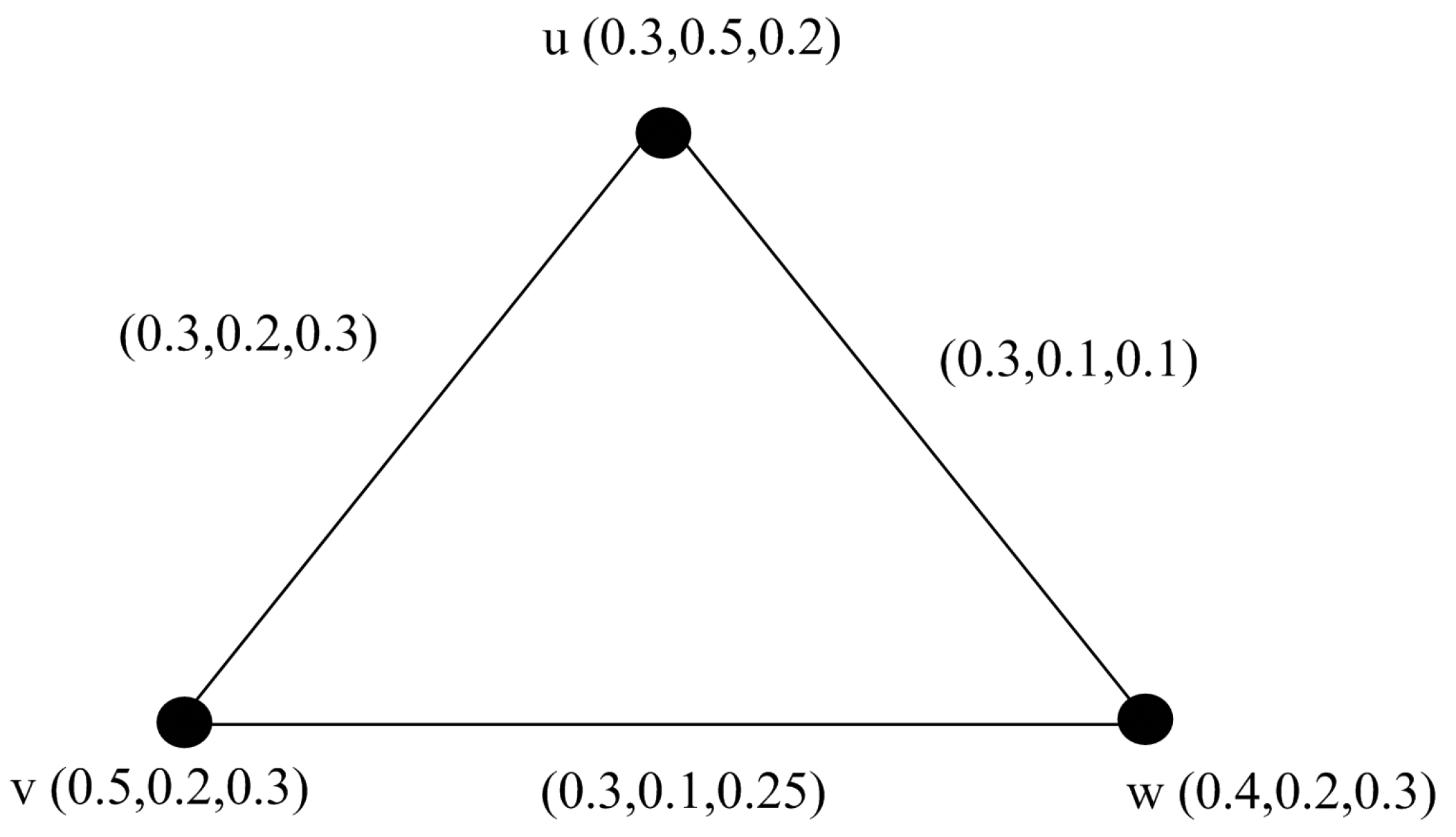
Definition 18. Let be a graph. A pair is called a picture fuzzy graph on where is a picture fuzzy set on V and is a picture fuzzy set on such that for each arc . An example of picture fuzzy graph is shown in
Figure 1.
Definition 19. A picture fuzzy graph is said to be regular picture fuzzy graph if Figure 1 is also an example of regular picture fuzzy graph.
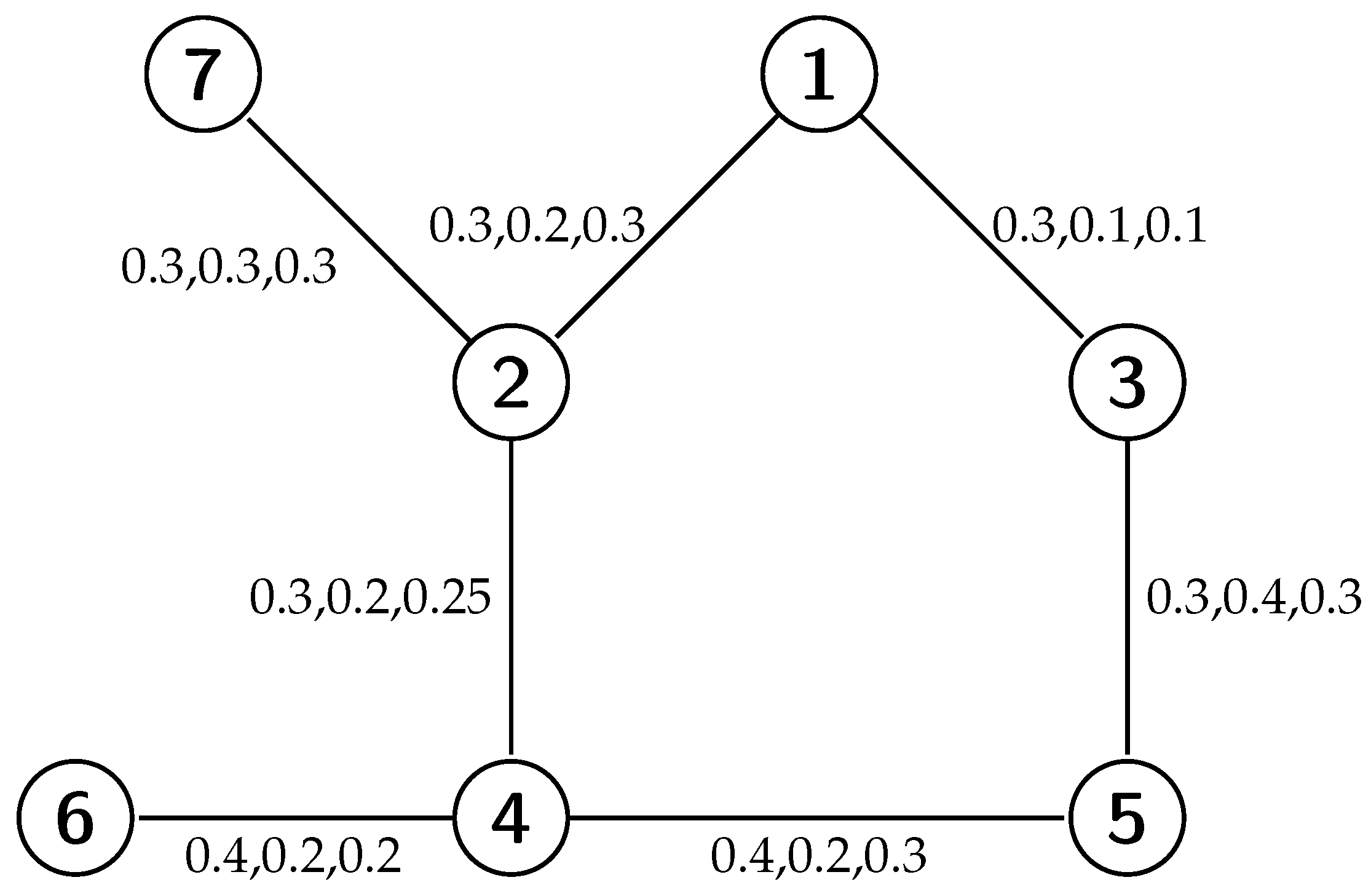
Definition 20. A picture fuzzy graph is defined as strong picture fuzzy graph if An example of a strong picture fuzzy graph is shown in
Figure 2.
Definition 21. A picture fuzzy graph is defined as complete picture fuzzy graph if An example of a complete picture fuzzy graph is shown in
Figure 3. Note that every complete picture fuzzy graph is a strong picture fuzzy graph but not conversely.
Definition 22. A path p in a picture fuzzy graph is a sequence of different vertices such that Here, k represents the length of path.
Definition 23. Let be a picture fuzzy graph. If two nodes u and v are connected by a path of length k in G such as p: then , and are described as follows.
Let be the strength of connectedness between the two nodes u and v of a picture fuzzy graph G. Then , and are defined as follows.
=
where inf is used to find the minimum and sup is used to find maximum membership value. Consider a connected picture fuzzy graph as shown in the Figure 3 and the paths are - P1:
with membership value (0.4,0.3,0.2),
- P2:
with membership value (0.3,0.3,0.2),
- P3:
with membership value (0.4,0.3,0.3),
- P4:
with membership value (0.3,0.3,0.3),
- P5:
with membership value (0.3,0.3,0.3).
By routine computation, we have
,
,
=
The strength of connectedness between the two nodes x and u of a picture fuzzy graph G (Figure 3) is (0.4,0.3,0.2). Definition 24. Let be a picture fuzzy graph. Then, G is said to be connected picture fuzzy graph if for every vertices , or or .
Figure 3 is an example of connected picture fuzzy graph.
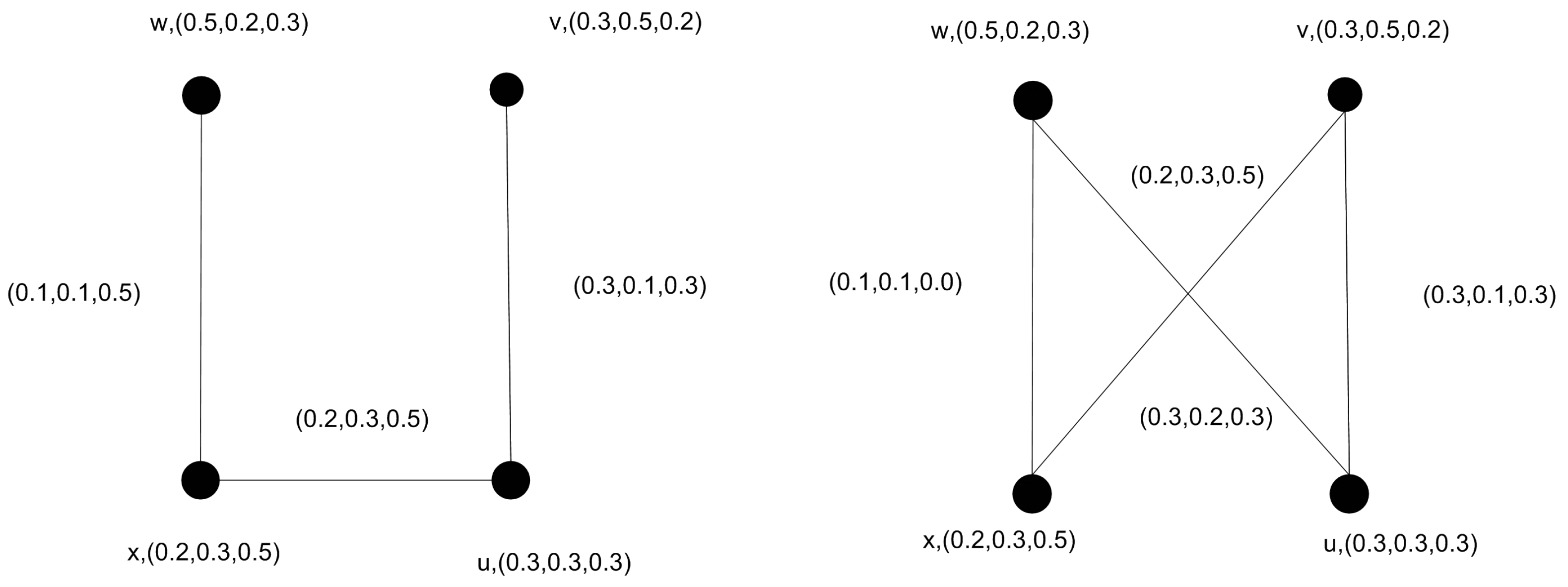
Definition 25. The complement of a picture fuzzy graph is a picture fuzzy graph if and only if follows the (15). An example of complement picture fuzzy graph is shown in Figure 4. Similarly, we can prove that = and = . Hence, .
Definition 26. Let and be two picture fuzzy graphs.
A homomorphism h from picture fuzzy graph to is a mapping function which always satisfy followings:
- (i)
- (a)
,
- (b)
.
A isomorphism h from a picture fuzzy graph to is a bijective mapping function which always satisfy followings:
- (i)
- (c)
,
- (d)
.
A weak isomorphism h from picture fuzzy graph to is a bijective mapping function which always satisfy followings:
- (i)
- (e)
h is homomorphism.
- (f)
. Thus, a weak isomorphism maintains the costs of the vertices but not necessarily the costs of the edges.
A co weak isomorphism h from picture fuzzy graph to is a bijective mapping function which always satisfy followings:
- (i)
- (g)
h is homomorphism.
- (h)
.
Definition 27. A picture fuzzy graph G is said to be
- 1.
Self complementary picture fuzzy graph if and only if .
- 2.
Self weak complement picture fuzzy graph if G is weak isomorphic to .
5. Operations on Picture Fuzzy Graph
In this section, we introduce six operations on picture fuzzy graph, viz., Cartesian product, composition, join, direct product, lexicographic and strong product.
Definition 33. Let and are two picture fuzzy graph of and respectively. The Cartesian product of picture fuzzy graph and is defined by , where and are two picture fuzzy sets on V = , and respectively which satisfies the followings:
- (i)
,
- (a)
,
- (b)
- (c)
,
- (ii)
and ,
- (a)
,
- (b)
,
- (c)
.
- (iii)
and ,
- (a)
,
- (b)
,
- (c)
.
Definition 34. The composition of two picture fuzzy graph and defined as a pair , where and are two picture fuzzy sets on V = , and respectively, which satisfies the followings:
- (i)
,
- (a)
,
- (b)
,
- (c)
.
- (ii)
and ,
- (a)
,
- (b)
,
- (c)
.
- (iii)
and ,
- (a)
,
- (b)
,
- (c)
.
- (iv)
, and ,
- (a)
,
- (b)
,
- (c)
.
Definition 35. The union of two picture fuzzy graph and is defined as , where is a picture fuzzy set on and is an another picture fuzzy set on , which satisfies the following:
- (i)
- (a)
if and ,
- (b)
if and ,
- (c)
if ,
- (ii)
- (a)
if and ,
- (b)
if and ,
- (c)
if ,
- (iii)
- (a)
if and ,
- (b)
if and ,
- (c)
if ,
- (iv)
- (a)
if and ,
- (b)
if and ,
- (c)
if ,
- (v)
- (a)
if and ,
- (b)
if and ,
- (c)
if ,
- (vi)
- (a)
if and ,
- (b)
if and ,
- (c)
if .
Definition 36. The join of two picture fuzzy graph and is defined as , where is a picture fuzzy set on and is an another picture fuzzy set on (( represents all edges joining the vertex of and ), which satisfies the following:
- (i)
- (a)
if and
- (b)
if and
- (c)
if
- (ii)
- (a)
if and
- (b)
if and
- (c)
if
- (iii)
- (a)
if and
- (b)
if and
- (c)
if
- (iv)
- (a)
if and
- (b)
if and
- (c)
if
- (v)
- (a)
if and
- (b)
if and
- (c)
if
- (vi)
- (a)
if and
- (b)
if and
- (c)
if
- (vii)
- (a)
if
- (b)
if
- (c)
if
Definition 37. The direct product of two picture fuzzy graph and is defined as a pair , where is a picture fuzzy set on and is an another picture fuzzy set on , which satisfies the followings:
- (i)
- (a)
- (b)
- (c)
- (ii)
- (a)
- (b)
- (c)
.
Definition 38. The lexicographic product of two picture fuzzy graph and is defined as a pair , where is a picture fuzzy set on and is an another picture fuzzy set on which satisfies the followings:
- (i)
- (a)
- (ii)
- (a)
- (b)
- (c)
- (iii)
- (a)
- (b)
- (c)
Definition 39. The strong product of two picture fuzzy graph and is defined as a pair , where is a picture fuzzy set on and is an another picture fuzzy set on which satisfies the followings:
- (i)
- (a)
- (b)
- (c)
- (ii)
- (a)
- (b)
- (c)
- (iii)
- (a)
- (b)
- (c)
- (iv)
- (a)
- (b)
- (c)
6. Application of Picture Fuzzy Graph in Social Network
The popularity of social networks like Facebook, Twitter, WhatsApp, ResearchGate, Instagram, and LinkedIn is increasing day by day. They are well known platforms for connecting hung number of people in everywhere in the world. We generally exchange various types of information and issues in social network. It helps us in online marketing (e-commerce and e-business), efficient social and political campaigns, future events, connecting to clients. Social networks are also used as important tools for public awareness by sending information quickly to a wide audience about any natural disaster and terrorist/criminal attack.
A social network is a collection of nodes and links. The nodes are used to represent individual, groups, country, organizations, places, enterprises, etc., and links are used to describe the relationships between nodes. We generally use classical graph to represent the social network where actors are represented by vertices and the relations/flows between vertices are represented as edges. Several manuscripts have been published on the social networks. However, social network cannot be modeled properly by classical graph. Since, in a classical graph, all vertices have equal importance. Due to this reason, all social units (individual or organization) in present social networks are considered of equal importance. But in real life, all social units do not have same the importance. Similarly, all edges (relationships) have equal strength in classical graph. In all existing social networks, it is considered that the strength of relationship between two social units are equal, but in real life it may not be true. Samanta and Pal [
37] have introduced an idea to model the social network using a type 1 fuzzy graph. Many researchers [
38,
39,
40] believed that these uncertainties phenomena can be modeled by a fuzzy graph. But type 1 fuzzy graph are unable to capture more complex relational states between nodes. Since the membership degree of node and edges are determined by human perception. This motivate us to introduce a new social network model using picture fuzzy graph. We define this social network as a picture fuzzy social network.
In a picture fuzzy social network, an account of a person or organization, i.e., a social unit is represented by node and if there is a relationship or flow between two social units then they are connected by one arc. In reality, each node, i.e., a social unit (person or individual) has some good, neutral and bad activities. We represent the good, neutral and bad activities using the good, neutral and bad membership values of the node and similarity the good, neutral and bad membership degree of the edge can be used to describe the strength of relationship between two nodes. For example, three persons have good knowledge of some activities such as educational activity and teaching methodology. However, they have no knowledge in some activities such administration and finance and they also have very bad knowledge in some activities such as health condition and food habit. We can easily represent this three types of node and edge membership degree using picture fuzzy set which consists each element has three membership values. This type of social network is a real life example of a picture fuzzy graph. Centrality is one of the most key ideas in social networking which finds the node effect on the social network. The centrality of a node is more central from other node. Central person is more close than other person and he can send or access more information. Freeman [
41] introduced three different type of measures: degree, closeness, and betweenness of any node centrality. The degree of centrality finds the linkage of a social unit between the others social units. It basically determines the involvement of the social unit (person) in the social network. We can find this degree value any picture node as defined (28). The betweenness determines the number of paths of communication between any two social units though a unit and closeness of any node is as the inverse sum of shortest path length [
42,
43] to all other social nodes from a specified node. Let
represents the shortest path length from node
i to
j. The diameter of a social network is defined as the longest distance between two nodes in the network. It is described as follows.
In this study, we use picture fuzzy set to represent the arc length of a social network. The problem of finding shortest path between two social units is a fundamental and important criteria to find the closeness, betweenness and diameter of a social network. This picture social network model is more flexible and efficient than classical social network model.
The online social network can be represented by a directed or undirected weighted picture fuzzy graph. Let
be an undirected picture fuzzy graph. We can define an undirected picture fuzzy social network as a picture fuzzy relational structure
, where
represents a non-empty set of picture vertices or actors or nodes, and
represents an undirected picture fuzzy relation on
V. A small example of undirected picture fuzzy social network is shown in
Figure 5. For undirected picture fuzzy social network where arcs are simply an absent or present undirected picture fuzzy relation with no other information attached.
Let be a directed picture fuzzy graph. We can describe a directed picture fuzzy social network as a picture fuzzy relational structure , where denotes a non-empty set of picture fuzzy nodes, and denotes an undirected picture fuzzy relation on V.
The directed picture fuzzy relation is considered in directed picture fuzzy social network. Directed picture fuzzy graph is more efficient to model the social network, because where arcs are considered with directed picture fuzzy relation would contain more information. The values of
and
are equal in undirected picture fuzzy social network. However,
and
are not equal in directed picture fuzzy social network. A small example of a directed picture fuzzy social network is shown in
Figure 6. Let
be a directed picture fuzzy social network and the picture fuzzy sets are used to describe the arc lengths of
. The sum of the lengths of the arcs that are adjacent to a social node
is called the picture fuzzy in degree centrality of the node
. The picture in degree centrality of node
,
, is described as follows.
The sum of the lengths of the arcs that that are adjacent from social node
is called the picture out degree centrality of
. The picture out degree centrality of node
,
, is described as follows.
Here, the symbol ∑ is an addition operation of picture fuzzy set and
is a picture fuzzy set associated with the arc
. The sum of picture in degree centrality and picture out of degree centrality of node
is called picture degree centrality (PDC) of
.
⊕ is an addition operation of picture fuzzy set.
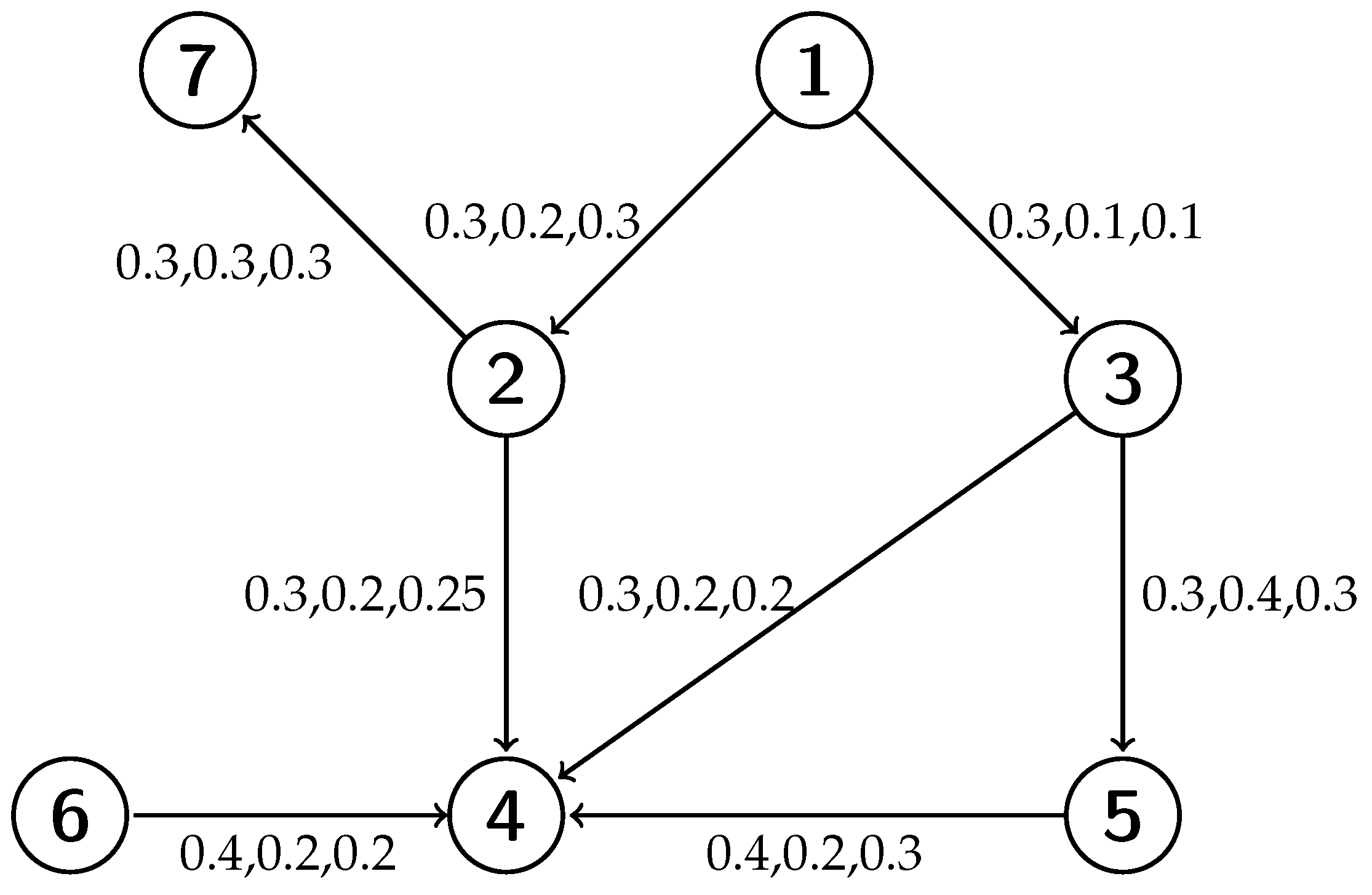
Let
be a directed picture fuzzy social network of the a research Team, where
represents a collection of seven researchers,
represents directed picture fuzzy relation between the seven researchers. This social network is shown in
Figure 6. We determine the picture fuzzy in degree, picture fuzzy in degree and picture fuzzy degree centrality of the research term using (
23)–(
25). This three degree values are shown in
Table 1. We use the raking method [
44,
45] of picture fuzzy set to compare the different degree values. Based on the ranking of picture fuzzy set, research (node) 4 has got highest score value of picture fuzzy in degree centrality. It means that researcher 4 has higher acceptance and good interpersonal relationship in network. The research 2 has got the highest score value of picture fuzzy out degree centrality. It describes that node 2 can nominate many other researchers.
In this study, we have provided one simple numerical examples of picture fuzzy graph to represent one small social network. The small sized examples are very much helpful to understand the advantage of our proposed model. Social networks are based on millions of users and big data paradigm. Therefore, as future work, we need to model a large scale practical social network using the picture fuzzy graph and to compute the closeness, betweenness and diameter of the social network. Furthermore, we wish to introduce some heuristic algorithms to find those measurements of any large scale practical social network. Despite the need for future study, the proposed model discussed in this study is an important initial contributions to picture fuzzy graph and social network analysis under uncertain environment.
7. Conclusions
Fuzzy graph is an important tool for modeling many uncertain real world decision making problems in different field, e.g., operations research, computer science, optimization problems, number theory, algebra, geometry, etc. To deal with the complex real life problems, a number of generalizations of fuzzy graph have been studied. The picture fuzzy set is a direct extension of fuzzy set and intuitonistic fuzzy set. The main objective of this paper is to introduce the idea of picture fuzzy graph and its different operation. In this paper, first we propose the definition of a picture fuzzy graph based on the picture fuzzy relation. We also describe some different types of picture fuzzy graphs such as regular picture fuzzy graph, strong picture fuzzy graph, complete picture fuzzy graph, and complement picture fuzzy graph. We describe some different types of isomorphic picture fuzzy graph. Six different operations on picture fuzzy graph, viz. Cartesian product, composition, join, direct product, lexicographic and strong product are described in this paper. The picture fuzzy graph can increase flexibility, efficiency, precision and comparability to model the complex real life scenarios system compared to the classical fuzzy graph models. We have also described a model to represent the social network using picture fuzzy graph and we also introduce some centrality measure called picture fuzzy in degree centrality, picture fuzzy out degree centrality and picture fuzzy out degree centrality which are applicable to the picture fuzzy social network. The idea of picture fuzzy graph can be applied in several areas of database system, computer network, social network, transportation network and image processing.