Solving the Systems of Equations of Lane-Emden Type by Differential Transform Method Coupled with Adomian Polynomials
Abstract
1. Introduction
2. Dtm and Adomian Polynomial
2.1. Dtm
2.2. Adomian Polynomial
3. Differential Transform of Nonlinearities
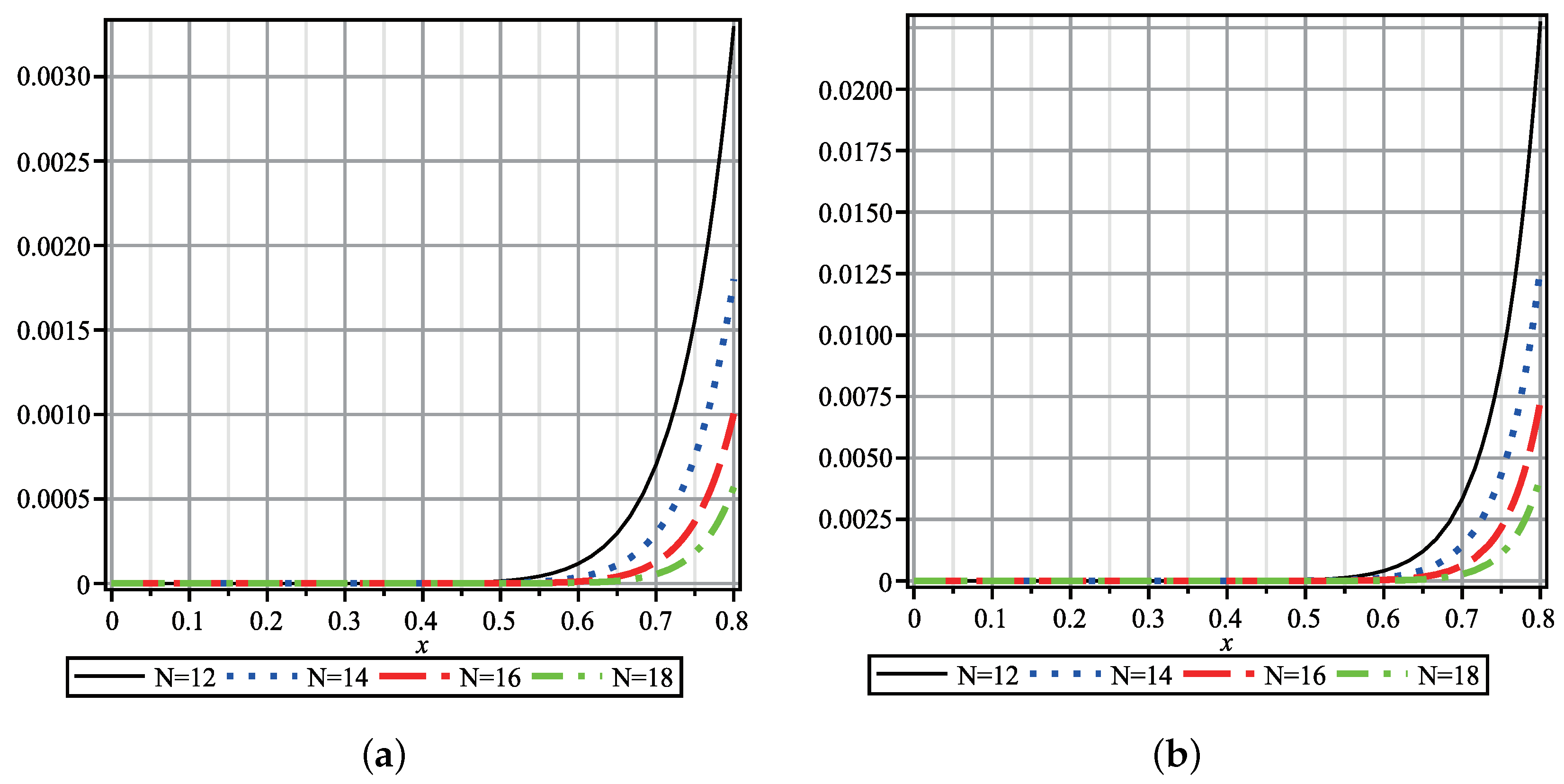
4. Applications
- The exact solution: .
- The approximate solutions:
- The maximal absolute errors of : .
- The maximal absolute errors of : .
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pukhov, G.E. Differential Transforms of Functions and Equations; Naukova Dumka: Kiev, Russian, 1980. [Google Scholar]
- Pukhov, G.E. Differential transforms and circuit theory. Int. J. Circ. Theor. Appl. 1982, 10, 265–276. [Google Scholar] [CrossRef]
- Pukhov, G.E. Differential Transformations and Mathematical Modeling of Physical Processes; Naukova Dumka: Kiev, Russian, 1986. [Google Scholar]
- Zhou, J.K. Differential Transformation and Its Applications for Electrical Circuits; Huazhong University Press: Wuhan, China, 1986. [Google Scholar]
- Bervillier, C. Status of the differential transform method. Appl. Math. Comput. 2012, 218, 10158–10170. [Google Scholar]
- Momani, S.; Ertürk, V.S. Solutions of non-linear oscillators by the modified differential transform method. Comput. Math. Appl. 2008, 55, 833–842. [Google Scholar] [CrossRef]
- Momani, S.; Noor, M.A. Numerical comparison of methods for solving a special fourth-order boundary value problem. Appl. Math. Comput. 2007, 191, 218–224. [Google Scholar] [CrossRef]
- Chang, S.H.; Chang, I.L. A new algorithm for calculating one-dimensional differential transform of nonlinear functions. Appl. Math. Comput. 2008, 195, 799–808. [Google Scholar] [CrossRef]
- Ertürk, V.S.; Momani, S. Comparing numerical methods for solving fourth-order boundary value problems. Appl. Math. Comput. 2007, 188, 1963–1968. [Google Scholar] [CrossRef]
- Arikoglu, A.; Ozkol, I. Solution of difference equations by using differential transform method. Appl. Math. Comput. 2006, 174, 1216–1228. [Google Scholar] [CrossRef]
- Arikoglu, A.; Ozkol, I. Solution of differential-difference equations by using differential transform method. Appl. Math. Comput. 2006, 181, 153–162. [Google Scholar] [CrossRef]
- Odibat, Z.M. Differential transform method for solving Volterra integral equation with separable kernels. Math. Comput. Model. 2008, 48, 1144–1149. [Google Scholar] [CrossRef]
- Arikoglu, A.; Ozkol, I. Solutions of integral and integro-differential equation system by using differential transform method. Comput. Math. Appl. 2008, 56, 2411–2417. [Google Scholar] [CrossRef][Green Version]
- Arikoglu, A.; Ozkol, I. Solution of boundary value problems for integro-differential equations by using differential transform method. Appl. Math. Comput. 2005, 168, 1145–1158. [Google Scholar] [CrossRef]
- Xie, L.-J.; Zhou, C.-L.; Xu, S. A new algorithm based on differential transform method for solving multi-point boundary value problems. Int. J. Comput. Math. 2016, 93, 981–994. [Google Scholar] [CrossRef]
- Al-sawalha, M.M.; Noorani, M.S.M. On solving the Lorenz system by differential transformation method. Chin. Phys. Lett. 2008, 25, 1217–1219. [Google Scholar] [CrossRef]
- Al-sawalha, M.M.; Noorani, M.S.M. A numeric-analytic method for approximating the chaotic Chen system. Chaos Soliton. Fract. 2009, 42, 1784–1791. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Bertelle, C.; Aziz-Alaoui, M.A.; Duchamp, G.H.E. A multi-step differential transform method and application to non-chaotic or chaotic systems. Comput. Math. Appl. 2010, 59, 1462–1472. [Google Scholar] [CrossRef]
- Thongmoon, M.; Pusjuso, S. The numerical solutions of differential transform method and the Laplace method for a system of differential equations. Nonlinear Anal. Hybrid Syst. 2010, 4, 425–431. [Google Scholar] [CrossRef]
- Gökdoğan, A.; Merdan, M.; Yildirim, A. A multistage differential transformation method for approximate solution of Hantavirus infection model. Commun. Nonlinear Sci. 2012, 17, 1–8. [Google Scholar] [CrossRef]
- Gökdoğan, A.; Merdan, M.; Yildirim, A. The modified algorithm for the differential transform method to solution of Genesio systems. Commun. Nonlinear Sci. 2012, 17, 45–51. [Google Scholar] [CrossRef]
- Chang, S.H.; Chang, I.L. A new algorithm for calculating two-dimensional differential transform of nonlinear functions. Appl. Math. Comput. 2009, 215, 2486–2494. [Google Scholar] [CrossRef]
- Fatoorehchi, H.; Abolghasemi, H. Improving the differential transform method: A novel technique to obtain the differential transforms of nonlinearities by the Adomian polynomials. Appl. Math. Model. 2013, 37, 6008–6017. [Google Scholar] [CrossRef]
- Elsaid, A. Fractional differential transform method combined with the Adomian polynomials. Appl. Math. Comput. 2012, 218, 6899–6911. [Google Scholar] [CrossRef]
- Duan, J.-S. Convenient analytic recurrence algorithms for the Adomian polynomials. Appl. Math. Comput. 2011, 217, 6337–6348. [Google Scholar] [CrossRef]
- Muatjetjeja, B.; Khalique, C.M. First integrals for a generalized coupled Lane-Emden system. Nonlinear Anal. Real World Appl. 2011, 12, 1202–1212. [Google Scholar] [CrossRef]
- Serrin, J.; Zou, H. Non-existence of positive solutions of Lane-Emden systems. Differ. Integral Equ. 1996, 9, 635–653. [Google Scholar]
- Qi, Y. The existence of ground states to a weakly coupled elliptic system. Nonlinear Anal. Theor. 2002, 48, 905–925. [Google Scholar] [CrossRef]
- Dalmasso, R. Existence and uniqueness of positive radial solutions for the Lane-Emden system. Nonlinear Anal. Theor. 2004, 57, 341–348. [Google Scholar] [CrossRef]
- Bozhkov, Y.; Martins, A.C.G. Lie point symmetries of the Lane-Emden systems. J. Math. Anal. Appl. 2004, 294, 334–344. [Google Scholar] [CrossRef][Green Version]
- Dalmasso, R. Existence and uniqueness of solutions for a semilinear elliptic system. Int. J. Math. Math. Sci. 2005, 10, 1507–1523. [Google Scholar] [CrossRef]
- Khalique, C.M.; Mahomed, F.M.; Muatjetjeja, B. Lagrangian formulation of a generalized Lane-Emden equation and double reduction. J. Nonlinear Math. Phys. 2008, 15, 152–161. [Google Scholar] [CrossRef]
- Bozhkov, Y.; Freire, I.L. On the Lane-Emden system in dimension one. Appl. Math. Comput. 2012, 218, 10762–10766. [Google Scholar] [CrossRef]
- Hosseini, S.Gh.; Abbasbandy, S. Solution of Lane-Emden type equations by combination of the spectral method and Adomian decomposition method. Math. Probl. Eng. 2015, 2015, 534754. [Google Scholar] [CrossRef]
- Azarnavid, B.; Parvaneh, F.; Abbasbandy, S. Picard-reproducing kernel Hilbert space method for solving generalized singular nonlinear Lane-Emden type equations. Math. Model. Anal. 2015, 20, 754–767. [Google Scholar] [CrossRef]
- Xie, L.-J.; Zhou, C.-L.; Xu, S. An effective numerical method to solve a class of nonlinear singular boundary value problems using improved differential transform method. SpringerPlus 2016, 5, 1066. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The variational iteration method for solving systems of equations of Emden-Fowler type. Int. J. Comput. Math. 2011, 88, 3406–3415. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Rach, R.; Duan, J.-S. A study on the systems of the Volterra integral forms of the Lane-Emden equations by the Adomian decomposition method. Math. Methods Appl. Sci. 2014, 37, 10–19. [Google Scholar] [CrossRef]
- Adomian, G. A review of the decomposition method and some recent results for nonlinear equations. Math. Comput. Model. 1990, 13, 17–43. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Adomian, G.; Rach, R. Generalization of Adomian polynomials to functions of several variables. Comput. Math. Appl. 1992, 24, 11–24. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; El-Sayed, S.M. A new modification of the Adomian decomposition method for linear and nonlinear operators. Appl. Math. Comput. 2001, 122, 393–405. [Google Scholar] [CrossRef]
- Abbaoui, K.; Cherruault, Y.; Seng, V. Practical formulae for the calculus of multivariable Adomian polynomials. Math. Comput. Model. 1995, 22, 89–93. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A new algorithm for calculating Adomian polynomials for nonlinear operators. Appl. Math. Comput. 2000, 111, 33–51. [Google Scholar] [CrossRef]
- Rach, R. A new definition of the Adomian polynomials. Kybernetes 2008, 37, 910–955. [Google Scholar] [CrossRef]
- Duan, J.-S. Recurrence triangle for Adomian polynomials. Appl. Math. Comput. 2010, 216, 1235–1241. [Google Scholar] [CrossRef]
- Duan, J.-S. An efficient algorithm for the multivariate Adomian polynomials. Appl. Math. Comput. 2010, 217, 2456–2467. [Google Scholar]
- Adomian, G.; Rach, R. Nonlinear transformation of series-Part II. Comput. Math. Appl. 1992, 23, 79–83. [Google Scholar] [CrossRef]
| Original Function | Transformed Function |
|---|---|
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | |||||||||
| 9 |
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| − | 0 | 0 | − | 0 | 0 | 0 | ||||
| 0 | − | 0 | − | 0 | − | 0 | 0 |
| N | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|---|
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | −6 | 7 | −8 | 9 | −10 | |||||
| −3 | −5 | −6 | −7 | −8 | −9 | −10 | −11 | −12 | −13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.-j.; Zhou, C.-l.; Xu, S. Solving the Systems of Equations of Lane-Emden Type by Differential Transform Method Coupled with Adomian Polynomials. Mathematics 2019, 7, 377. https://doi.org/10.3390/math7040377
Xie L-j, Zhou C-l, Xu S. Solving the Systems of Equations of Lane-Emden Type by Differential Transform Method Coupled with Adomian Polynomials. Mathematics. 2019; 7(4):377. https://doi.org/10.3390/math7040377
Chicago/Turabian StyleXie, Lie-jun, Cai-lian Zhou, and Song Xu. 2019. "Solving the Systems of Equations of Lane-Emden Type by Differential Transform Method Coupled with Adomian Polynomials" Mathematics 7, no. 4: 377. https://doi.org/10.3390/math7040377
APA StyleXie, L.-j., Zhou, C.-l., & Xu, S. (2019). Solving the Systems of Equations of Lane-Emden Type by Differential Transform Method Coupled with Adomian Polynomials. Mathematics, 7(4), 377. https://doi.org/10.3390/math7040377





