Numerical Approximation for Nonlinear Noisy Leaky Integrate-and-Fire Neuronal Model

Abstract

We consider a noisy leaky integrate-and-fire (NLIF) neuron model. The resulting nonlinear time-dependent partial differential equation (PDE) is a Fokker-Planck Equation (FPE) which describes the evolution of the probability density. The finite element method (FEM) has been proposed to solve the governing PDE. In the realistic neural network, the irregular space is always determined. Thus, FEM can be used to tackle those situations whereas other numerical schemes are restricted to the problems with only a finite regular space. The stability of the proposed scheme is also discussed. A comparison with the existing Weighted Essentially Non-Oscillatory (WENO) finite difference approximation is also provided. The numerical results reveal that FEM may be a better scheme for the solution of such types of model problems. The numerical scheme also reduces computational time in comparison with time required by other schemes.

1. Introduction

The large-scale neural network models in computational neuroscience have become familiar. The classical description of these (excitatory-inhibitory) neural network models is based on the deterministic/stochastic system. One of the most common models is known as the noisy leaky integrate-and-fire (NLIF) neuron model in which the behavior of the whole population of neurons is encoded in a stochastic differential equation (SDE) for the time evolution of membrane potential of a single neuron representative of the network. The dynamics of a single neuron is given by ([1,2,3,4,5,6])

$$\begin{array}{c}\hfill {\tau }_m{\displaystyle \frac{dV}{dt}}=-V\left(t\right)+I\left(t\right),\end{array}$$

(1)

where $V\left(t\right)$ represents the membrane potential of a single neuron and ${\tau }_m$ is the time relaxation of the membrane potential in the absence of any communication. The communication of a single neuron with the network is modeled by the synaptic input current, $I\left(t\right).$ The form of $I\left(t\right)$ is a stochastic process, given by ([7])

$$I\left(t\right)=J_E{\displaystyle \sum _{n=1}^{N_E}}{\displaystyle \sum _m}\delta (t-t_{E_m}^n)-J_I{\displaystyle \sum _{n=1}^{N_I}}{\displaystyle \sum _m}\delta (t-t_{I_m}^n).$$

Here, each spike is treated as a delta function, and if a spike occurs at time $t=t_0,$ it is denoted by $\delta (t-t_0).$ The terms $t_{E_m}^n$ and $t_{I_m}^n$ in above equation represent the time of mth-spike receiving from nth-presynaptic neuron for excitatory and inhibitory neurons, respectively. Moreover, the terms $N_E$ and $N_I$ are the total number of presynaptic neurons, where $J_E$ and $J_I$ are the strength of the synapses for excitatory and inhibitory neurons, respectively. Since the above form of synaptic input current is the discrete Poisson process, it becomes very difficult for further investigation. In addition, the researchers have used the diffusion approximation in which the synaptic input current $I\left(t\right)$ is approximated by a continuous in time Ornstein-Uhlenbeck-type stochastic process as given by

$$I\left(t\right)dt\approx {\mu }_{c}dt+{\sigma }_c{d}_{B_t}.$$

Initially, it is assumed that every neuron generates spikes according to a stationary Poisson process with constant probability of generating a spike per unit time $r,$ and it is also assumed that all these processes are independent between neurons, because of these assumptions, the mean value of the current, indicated by ${\mu }_c$, is given by $br=(N_E{J}_E-N_I{J}_I)r$ and its variance, ${\sigma }_c^2=(N_E{J}_E^2+N_I{J}_I^2)r.$ Here, we have to depict the likelihood of firing per unit time of the Poissonian spike train r and it is thus recognized as the firing rate, which should be computed as $r=I_{ext}+N\left(t\right),$ where $N\left(t\right)$ is the mean firing rate of the network. On the other side, $B_t$ is the standard Brownian motion in above equation.

The next important factor in the modeling is that the neurons generate a spike only when its membrane potential $V\left(t\right)$ arrives at a certain voltage, known as threshold $V_F,$ and instantly reset toward a resetting potential $V_R<V_F$ and sends a signal over the network.

Comprising the continuous form of $I\left(t\right)$ in SDE model (1), we obtain

$${\tau }_{m}dV=(-V+{\mu }_c)dt+{\sigma }_{c}d{B}_t,V\le V_F,t\ge 0,$$

where ${\tau }_m=1.$ We suppose that the voltage of a neuron arrives at threshold level at time $t_o^{-}$, i.e., $V\left(t_o^{-}\right)=V_F$ and after that the voltage arrives suddenly at resting potential, i.e., $V\left(t_o^{+}\right)=V_R,V_R<V_F.$ Furthermore, one can write the associated FPE with source term by using Ito’s rule [8], for the evolution of probability density function $p(v,t)\ge 0$ of finding neurons at a voltage $v\in (-\infty ,V_F],$ with time ($t\ge 0$)

$$\begin{array}{ccc}\hfill \frac{\partial }{\partial t}p(v,t)+\frac{\partial }{\partial v}\left[h(v,N)p(v,t)\right]-a\left(N\left(t\right)\right)\frac{{\partial }^2}{\partial v^2}p(v,t)& =& N\left(t\right)\delta (v-V_R),\hfill \end{array}$$

(2)

where $h(v,N)=-v+{\mu }_c,$ $a\left(N\left(t\right)\right)=\frac{{\sigma }_c^2}{2},$ and $N\left(t\right)$ is the mean firing rate of the network which is computed as the flux of neuron at the firing voltage. The source term of the Equation (2) comes from the fact that when the neurons generate spikes and send the signals over the network, their voltage immediately reset to the reset potential $V_R.$ At the relaxation time, no neuron have the firing voltage, for this reason, the initial and boundary conditions are given by

$$p(v,0)=p^0\left(v\right)\ge 0,p(V_F,t)=0,p(-\infty ,t)=0.$$

(3)

We can easily verify the conservation of the total number of neurons in above equation. For this purpose, we need to describe the mean firing rate for the network. Since the mean firing rate is the flux of neurons at $V_F$, the value of $N\left(t\right)$ is given by $N\left(t\right)=-a\left(N\left(t\right)\right)\frac{\partial p(V_F,t)}{\partial v}.$ Integrating (3) across the voltage domain and using the above boundary conditions, we obtain the required condition.

Equation (2) represents the evolution of probability density function and therefore

$$\begin{array}{c}\hfill {\displaystyle \underset{-\infty }{\overset{V_F}{\int }}}p(v,t)dv={\displaystyle \underset{-\infty }{\overset{V_F}{\int }}}{p}^0\left(v\right)dv=1.\end{array}$$

(4)

If we translate the new voltage variable by considering $v=v+b{I}_{ext}$ then we have $h(v,N)=-v+{\mu }_c=-v+br=-v-b{I}_{ext}+br=-v-b{I}_{ext}+b(I_{ext}+N\left(t\right))=-v+bN,$ and diffusion coefficient is of the form $a\left(N\right)=a_0+a_{1}N,a_0>0,a_1\ge 0.$

In [8], the authors provide theoretical and numerical analysis using finite difference approximation. For the references of mathematical aspects of nonlinear NLIF models, we refer [9,10,11,12,13]. We are concern about finding the value of the unknown $p(v,t)$ using alternative approach. The problem (2)–(4) cannot be solved analytically, because of its complexity arising from nonlinearity and having a source term [14,15,16]. Therefore, numerical methods are generally used, for example, finite difference method (FDM) is used to find the approximate solution of the governing equation [8]. However, FDM has some disadvantages, for instance, the singularity in the delta source term, as in the above mentioned equation, makes the solution divergent. In order to use the FDM appropriately, the governing equation must be modified, due to the fact that the procedure becomes complicated.

Hence, in the present work, we propose a formulation based on finite element approximation to find the solution of governing equation. FEM is one of the powerful numerical methods for the solutions of problems that describe the real-life situations. Moreover, the characteristics of FEM tackle the singularity problem in an effective manner [17,18,19,20,21,22,23,24,25,26,27]. The applicability of FEM regarding this model problem is demonstrated in the final section.

Description of the present paper is as follows: We consider the NLIF model described by Equations (2) and (3). In Section 2, we develop the numerical approximation based on the finite element approach. The analysis for the stability is provided in Section 3. We report some numerical examples from [8] and discuss the solution behavior graphically in Section 4. In the last section, we conclude the work done in this research article.

Preliminaries

Here, we state some basic definitions and auxiliary results, which will be used throughout the manuscript. As we are studying a nonlinear version of the FPE, we start with the notion of weak solution.

Definition 1.

We say that a pair of non-negative functions$(p,N)$with$p\in L^{\infty }({\mathbb{R}}^{+};L_{+}^1(-\infty ,V_F)),N\in L_{loc,+}^1\left({\mathbb{R}}^{+}\right)$is a weak solution of (2) and (3) if for any test function$\varphi (v,t)\in C^{\infty }((-\infty ,V_F)\times (0,T))$such that${\displaystyle \frac{{\partial }^2\varphi }{\partial v^2}},v{\displaystyle \frac{\partial \varphi }{\partial v}}\in L^{\infty }((-\infty ,V_F)\times (0,T))$, we have

$$\begin{array}{l}{\displaystyle \underset{0}{\overset{T}{\int }}}{\displaystyle \underset{-\infty }{\overset{V_F}{\int }}}p(v,t)\left[-{\displaystyle \frac{\partial \varphi }{\partial t}}-{\displaystyle \frac{\partial \varphi }{\partial v}}h(v,N)-a{\displaystyle \frac{{\partial }^2\varphi }{\partial v^2}}\right]dvdt\\ ={\displaystyle \underset{0}{\overset{T}{\int }}}N\left(t\right)\left[\varphi (V_R,t)-\varphi (V_F,t)\right]dt\\ +{\displaystyle \underset{-\infty }{\overset{V_F}{\int }}}{p}^0\left(v\right)\varphi (0,v)dv-{\displaystyle \underset{-\infty }{\overset{V_F}{\int }}}p(v,T)\varphi (T,v)dv.\end{array}$$

Here, the space $L^p\left(\mathsf{\Omega }\right),1\le p<\infty$, refers to the space of functions such that $f^p$ is integrable in $\mathsf{\Omega }$, while $L^{\infty }$ corresponds to the space of bounded functions in $\mathsf{\Omega }$. The set of infinitely differentiable functions in $\mathsf{\Omega }$ is denoted by $C^{\infty }\left(\mathsf{\Omega }\right)$ used as test functions in the notion of weak solution. The blow-up of solution and a priori estimates are given in [8]. We here just state the results.

Theorem 1.

(Blow-up) Assume that the drift and diffusion coefficients satisfy

$$h(v,N)+v\ge bN\mathrm{and}a\left(N\right)\ge a_m>0,$$

(5)

for all$-\infty <v\le V_F$and all$N\ge 0$, and let us consider the average-excitatory network where$b>0$. Choose$\mu >max\left(\frac{V_F}{a_m},\frac{b}{1}\right)$. If the initial data is concentrated enough around$v=V_F$, in the sense that

$${\displaystyle \underset{-\infty }{\overset{V_F}{\int }}}{e}^{\mu v}{p}^0\left(v\right)dv$$

is close enough to$e^{\mu V_F}$, then there are no global-in-time weak solutions to (2)–(4).

Lemma 1 (A priori estimates).

Assume$h(v,N)=-v+bN,a\left(N\right)=a_0+a_{1}N$on the drift and diffusion coefficients and that$(p,N)$is a global-in-time solution of (2)–(4) in the sense of Definition 1 fast decaying at$-\infty$, then the following a priori estimates hold for all$T>0$:

• If$b\ge V_F-V_R$, then

  $${\displaystyle \underset{-\infty }{\overset{V_F}{\int }}}(V_F-v)p(v,t)dv\le max\left(V_F,{\displaystyle \underset{-\infty }{\overset{V_F}{\int }}}(V_F-v)p^0\left(v\right)dv\right),$$

  $$(b-V_F+V_R){\displaystyle \underset{0}{\overset{T}{\int }}}N\left(t\right)dt\le V_{F}T+{\displaystyle \underset{-\infty }{\overset{V_F}{\int }}}(V_F-v)p^0\left(v\right)dv.$$
• If$b<V_F-V_R,$then

  $${\displaystyle \underset{-\infty }{\overset{V_F}{\int }}}(V_F-v)p(v,t)dv\ge min\left(V_F,{\displaystyle \underset{-\infty }{\overset{V_F}{\int }}}(V_F-v)p^0\left(v\right)dv\right).$$

  Moreover, if in addition a is constant, then

  $${\displaystyle \underset{0}{\overset{T}{\int }}}N\left(t\right)dt\le (1+T)C(V_F,V_R,a,p^0).$$

In a latest work [8], it was demonstrated that the problem (2)–(4) can produce a finite time blow-up solution for excitatory networks $b>0$ when the initial data is concentrated near sufficient to the threshold voltage. This result was obtained by giving no information about the behavior at the blow-up time. In a recent work [12], we state the theorem gives a characterization of this blow-up time when it occurs for $b>0.$

Theorem 2.

Let$p^0\left(v\right)$be a non-negative$C^1((-\infty ,V_F)\bigcap L^1(-\infty ,V_F)$function such that$p^0\left(V_F\right)=0$and

$${\displaystyle \frac{\partial p^0}{\partial v}}=0.$$

There exist a classical solution of (2)–(4) in the time interval$[0,T^{*})$ with $T^{*}>0.$ The maximal existence time $T^{*}>0$ can be characterized as

$$T^{*}=sup\{t>0:N\left(t\right)<\infty \}.$$

Moreover, when$b\le 0$we have that$T^{*}=\infty ,$while for$b>0$there exist classical solutions which blow up at a finite time$T^{*}$and consequently have diverging mean firing rate as$t\uparrow T^{*}.$

We now state the main result on steady states from [8].

Theorem 3.

Let$h(v,N)=bN-v$,$a\left(N\right)=a_0+a_{1}N$with$a_0,a_1>0$.

• Under either the conditions$b>0$and$2a_{0}b+2a_1{V}_R<{(V_F-V_R)}^2{V}_R$, or the condition$b<V_F-V_R$, then there exists at least one steady state solution to (2)–(4).
• If both$2a_{0}b+2a_1{V}_R<{(V_F-V_R)}^2{V}_R$and$b>V_F-V_R$hold, then there are at least two steady states to solution to (2)–(4).
• There is no steady state to (2)–(4) under the high connectivity condition’

  $$b>max(2(V_F-V_R),2V_{F}I\left(0\right)).$$

  (6)

2. Finite Element Approximation

We construct the numerical approximation of the problem given in (2) and (3) in two ways: First we use FEM for space discretization that provides a system of ordinary differential equations, which is then solved by Euler’s backward difference for time. Spatial discretization involves the construction of a weak formulation of problem over a given domain $\mathsf{\Omega }=[v_0,v_n]$ with specified boundary conditions at $v=v_0$ and $v=v_n.$ Weak formulation of the problem (2) and (3) is obtained by multiplying the equation with some test function $w\left(v\right)$ and integrating over $\mathsf{\Omega }$,

$$\begin{array}{c}\hfill {\int }_{\mathsf{\Omega }}w\left(v\right)\left\{\frac{\partial p}{\partial t}+\frac{\partial }{\partial v}\left(h(v,N)p\right)+a\left(N\left(t\right)\right){\displaystyle \frac{{\partial }^{2}p}{\partial v^2}}\right\}dv=N\left(t\right){\int }_{\mathsf{\Omega }}w\left(v\right)\delta (v-V_R)dv.\end{array}$$

(7)

In the present study, the mean firing rate $N\left(t\right)$ is approximated by using backward FDM. Performing the integration by parts in above equation, we get the following equation:

$$\begin{array}{c}\hfill {\int }_{\mathsf{\Omega }}\left\{w\frac{\partial p}{\partial t}-\left(h(v,N)p\frac{\partial w}{\partial v}\right)+a\left(N\left(t\right)\right){\displaystyle \frac{\partial p}{\partial v}}{\displaystyle \frac{\partial w}{\partial v}}\right\}dv=N\left(t\right){\int }_{\mathsf{\Omega }}w\left(v\right)\delta (v-V_R)dv.\end{array}$$

(8)

This resulting integral (8) is called weak formulation because it allows approximate function with less continuity (or differentiability) than the strong form given in Equation (2). Once we obtained the weak formulation, next step is to discretize the weak form for the easy representation and to capture the local effects more precisely. Weak form discretization consists of dividing the entire domain into set of elements, then developing the finite element model by seeking the approximation of a solution over a typical element. This discretization is tackled by taking n non-overlapping elements say $D_i=[v_i,v_{i+1}]$ for $i=1,2,\dots ,n$ with step size h given by:

$$\begin{array}{c}\hfill {\int }_{v_i}^{v_{i+1}}\left\{w\frac{\partial p}{\partial t}-\left(h(v,N)p\frac{\partial w}{\partial v}\right)+a\left(N\left(t\right)\right){\displaystyle \frac{\partial p}{\partial v}}{\displaystyle \frac{\partial w}{\partial v}}\right\}dv=N\left(t\right){\int }_{v_i}^{v_{i+1}}w\left(v\right)\delta (v-V_R)dv.\end{array}$$

(9)

The unknown function $p(v,t)$ must be approximated in a manner so that continuity or differentiability demands by weak formulation can be met. Since the weak formulation contains the first order derivative of $p,$ any function with non-zero first derivative would be a candidate for approximation. Thus, semi discretization consists of finding

$$\begin{array}{c}\hfill p_i={\displaystyle \sum _{j=i}^{i+1}}{\widehat{p}}_j\left(t\right){\psi }_j\left(v\right),\end{array}$$

(10)

where ${\widehat{p}}_j$ are the nodal values and ${\psi }_j$ are the basis functions given by

$$\begin{array}{ccc}{\psi }_i\left(v\right)& =& {\displaystyle \frac{v_{i+1}-v}{h}},\\ {\psi }_{i+1}\left(v\right)& =& {\displaystyle \frac{v-v_i}{h}}.\end{array}$$

(11)

There are many choices of weight function $w\left(v\right)$ to be used. Particular choice for the weight function $w\left(v\right)$ in Galerkin approach is the same as the choice of basis function ${\psi }_j\left(v\right).$ Thus, substituting weight function $w={\psi }_l\left(x\right),l=i,i+1$ and approximation for the solution defined by Equation (10) in weak formulation obtained in Equation (9) leads to the following equation:

$$\begin{array}{r}{\displaystyle {\int }_{v_i}^{v_{i+1}}}[{\psi }_l\left({\displaystyle \sum _{j=i}^{i+1}}{\displaystyle \frac{d{\widehat{p}}_j}{dt}}{\psi }_j\right)-h(v,N){\displaystyle \frac{d{\psi }_l}{dv}}\left({\displaystyle \sum _{j=i}^{i+1}}{\widehat{p}}_j{\psi }_j\right)+a\left(N\left(t\right)\right){\displaystyle \frac{d{\psi }_l}{dv}}\left({\displaystyle \sum _{j=i}^{i+1}}{\widehat{p}}_j{\displaystyle \frac{{\psi }_j}{dv}}\right)]dv\\ =N\left(t\right){\displaystyle {\int }_{v_i}^{v_{i+1}}}\delta (v-V_R){\psi }_{l}dv.\end{array}$$

On simplification of the above, we get as follows

$$\begin{array}{r}{\displaystyle \sum _{j=i}^{i+1}}[\left({\displaystyle {\int }_{v_i}^{v_{i+1}}}{\psi }_l{\psi }_{j}dv\right){\displaystyle \frac{d{\widehat{p}}_j}{dt}}-\left({\displaystyle {\int }_{v_i}^{v_{i+1}}}h(v,N){\psi }_j{\displaystyle \frac{d{\psi }_l}{dv}}dv\right){\widehat{p}}_j+a\left(N\left(t\right)\right)\left({\displaystyle {\int }_{v_i}^{v_{i+1}}}{\displaystyle \frac{d{\psi }_l}{dv}}{\displaystyle \frac{d{\psi }_j}{dv}}dv\right){\widehat{p}}_j]\\ =N\left(t\right){\displaystyle {\int }_{v_i}^{v_{i+1}}}\delta (v-V_R){\psi }_{l}dv.\end{array}$$

(12)

Solving Equation (12), we get the system of ordinary differential equations for $\widehat{p}={({\widehat{p}}_0,{\widehat{p}}_1)}^T,$ which can be expressed in matrix notation given by

$$\begin{array}{c}\hfill A{\widehat{p}}_t\left(t^k\right)+\left(B-C+D\right)\widehat{p}\left(t^k\right)=f,\end{array}$$

(13)

where

$$\begin{array}{c}\begin{array}{l}A={\displaystyle {\int }_{v_i}^{v_{i+1}}}{\psi }_l{\psi }_{j}dv=\frac{h}{6}\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right],\\ B={\displaystyle {\int }_{v_i}^{v_{i+1}}}v{\psi }_l^{\prime }{\psi }_{j}dv={\displaystyle \frac{1}{6h^2}}\left[\begin{array}{cc}-a_1& -a_2\\ a_1& a_2\end{array}\right],\mathrm{where}\left\{\begin{array}{c}{a}_1=3v_i{h}^2+h^3\hfill \\ a_2=3v_i{h}^2+2h^3\hfill \end{array}\right.\\ C=bN\left(t^{k-1}\right){\displaystyle {\int }_{v_i}^{v_{i+1}}}{\psi }_l^{\prime }{\psi }_{j}dv=bN\left(t^{k-1}\right)\left[\begin{array}{cc}-1/2& -1/2\\ 1/2& 1/2\end{array}\right],\\ D={\displaystyle \frac{a\left(N\left(t^{k-1}\right)\right)}{h}}{\displaystyle {\int }_{v_i}^{v_{i+1}}}{\psi }_l^{\prime }{\psi }_j^{\prime }dv={\displaystyle \frac{a\left(N\left(t^{k-1}\right)\right)}{h}}\left[\begin{array}{cc}1& -1\\ -1& 1\end{array}\right],\\ f=N\left(t^{k-1}\right){\displaystyle {\int }_{v_i}^{v_{i+1}}}\delta (v-V_R){\psi }_{l}dv=N\left(t^{k-1}\right)\left[\begin{array}{c}{\delta }_{\left(i\right)V_R}\\ {\delta }_{(i+1)V_R}\end{array}\right].\end{array}\end{array}$$

By assembling the contribution from all elements, we get the following system for the global nodal vector $p={[p_0,p_1,\dots ,p_n]}^T$ on the entire domain

$$\begin{array}{c}\hfill A{p}_t\left(t^k\right)+\left(B-C+D\right)p\left(t^k\right)=f,\end{array}$$

(14)

where f is the column vector with all entries are zero except at reset potential $V_R.$ Ordinary differential Equation (14) requires implicit and stable time-stepping method to avoid extremely small time-step. Firstly we discretize the time domain $[0,T]$ into m subintervals with time step $\Delta t.$ We use the Euler’s backward difference in time and get the following system from Equation (14):

$$\begin{array}{c}\hfill M{p}^k={\displaystyle \frac{A}{\Delta t}}{p}^{k-1}+f,\mathrm{where}M={\displaystyle \frac{A}{\Delta t}}+B-C+D,\end{array}$$

(15)

this algebraic system (15) can be solved for $p_j.$

3. Stability Analysis of the Scheme

Fourier method is a very flexible tool for analyzing stability developed by von Neumann. In this method, initial data is demonstrated in terms of finite Fourier series and we examine the growth of individual Fourier component. After assembling the reduced system (13) and using $b_1=bN\left(t^{k-1}\right)$ and $b_2=a\left(N\left(t^{k-1}\right)\right)$, we get the finite element difference-differential equation at the $i-$th node given by

$$\begin{array}{ccc}\hfill {\alpha }_1{p}_{i-1}^k+{\alpha }_2{p}_i^k+{\alpha }_3{p}_{i+1}^k& =& {\beta }_1{p}_{i-1}^{k-1}+{\beta }_2{p}_i^{k-1}+{\beta }_3{p}_{i+1}^{k-1},\hfill \end{array}$$

(16)

where

$$\begin{array}{r}{\alpha }_1={\displaystyle \frac{h}{3}}+{\displaystyle \frac{\Delta t}{6h^2}}(a_1-3b_1{h}^2-6b_{2}h),\\ {\alpha }_2={\displaystyle \frac{4h}{6}}+{\displaystyle \frac{\Delta t}{6h^2}}((a_2-a1)+12b_{2}h),\\ {\alpha }_3={\displaystyle \frac{h}{6}}+{\displaystyle \frac{\Delta t}{6h^2}}(-a_2+3b_1{h}^2-6b_{2}h),\\ {\beta }_1=h/6,{\beta }_2=2h/3,{\beta }_3=h/6.\end{array}$$

Let us denote the error as $e_j^{k-1}$ at the $(k-1)$th stage for nodal value j to satisfy Equation (16)

$$\begin{array}{c}\hfill {\alpha }_1{e}_{j-1}^k+{\alpha }_2{e}_j^k+{\alpha }_3{e}_{j+1}^k={\beta }_1{e}_{j-1}^{k-1}+{\beta }_2{e}_j^{k-1}+{\beta }_3{e}_{j+1}^{k-1}.\end{array}$$

(17)

At each time level, error can be expanded as $e_j^k=A{\xi }^k{e}^{i{\beta }_{j}h}.$ Thus, substituting the error in Equation (17), we get as follows:

$$\begin{array}{c}{\alpha }_1\left(A{\xi }^k{e}^{i{\beta }_{j-1}h}\right)+{\alpha }_2\left(A{\xi }^k{e}^{i{\beta }_{j}h}\right)+{\alpha }_3\left(A{\xi }^k{e}^{i{\beta }_{j+1}h}\right)={\beta }_1\left(A{\xi }^{k-1}{e}^{i{\beta }_{j-1}h}\right)+\\ {\beta }_2\left(A{\xi }^{k-1}{e}^{i{\beta }_{j}h}\right)+{\beta }_3\left(A{\xi }^{k-1}{e}^{i{\beta }_{j+1}h}\right).\end{array}$$

(18)

Simplification of the above equation, we get the following

$$\begin{array}{c}\xi ({\alpha }_1+{\alpha }_{2}exp\left(i\beta h\right)+{\alpha }_{3}exp\left(i2\beta h\right))={\beta }_1+{\beta }_{2}exp\left(i\beta h\right)+{\beta }_{3}exp\left(i2\beta h\right)\end{array}$$

(19)

$$\xi ={\displaystyle \frac{{\beta }_1+{\beta }_{2}exp\left(i\beta h\right)+{\beta }_{3}exp\left(i2\beta h\right)}{{\alpha }_1+{\alpha }_{2}exp\left(i\beta h\right)+{\alpha }_{3}exp\left(i2\beta h\right)}}.$$

Performing some algebraic manipulation, we get

$$\xi ={\displaystyle \frac{P}{P+Q}},$$

where $P={\displaystyle \frac{h}{3}}cos\left(\beta h\right)+\frac{2h}{3}$, and $Q={\displaystyle \frac{\Delta t}{h}}\left(2b_2\right)(1-cos\left(\beta h\right))-{\displaystyle \frac{\Delta t}{3}}(1+2cos\left(\beta h\right)$.

Whenever $Q\ge 0,$ we get $\left|\xi \right|\le 1,$ hence, the scheme is conditionally stable.

4. Numerical Experiments

In this section, we present some numerical examples to demonstrate the behavior of the solutions of the nonlinear NLIF model. The performance of the developed scheme is tested by comparing our results with the existing scheme in the literature. Consider the system (2) and (3) with initial data as follows

$$p(v,0)=\frac{1}{{\sigma }_0\sqrt{2\pi }}{e}^{\frac{-{(v-v_0)}^2}{2{\sigma }_0^2}},$$

(20)

where change in mean $v_0$ and variance ${\sigma }_0^2$ describe different scenario of a solution. We notice that the behavior of the solution depends upon the value of excitatory ($b>0$) and inhibitory $(b<0)$ average network. First we take constant diffusion coefficient $a\left(N\right)=a_0$ and find the effect on solution with change in value of $b.$

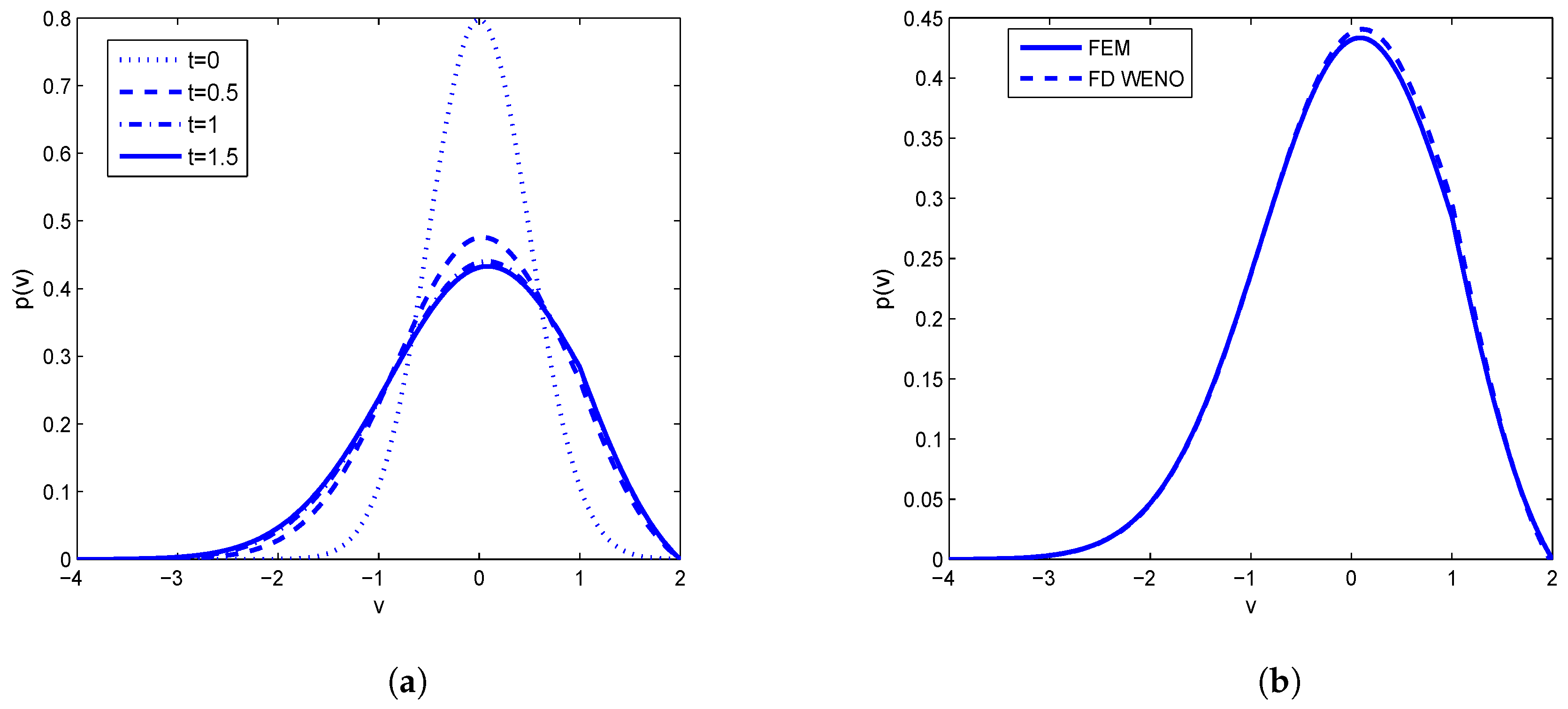
In Figure 1a, we find that after some time the solution $p(v,t)$ goes to steady state by taking excitatory case i.e., $b=0.5>0$ small enough.

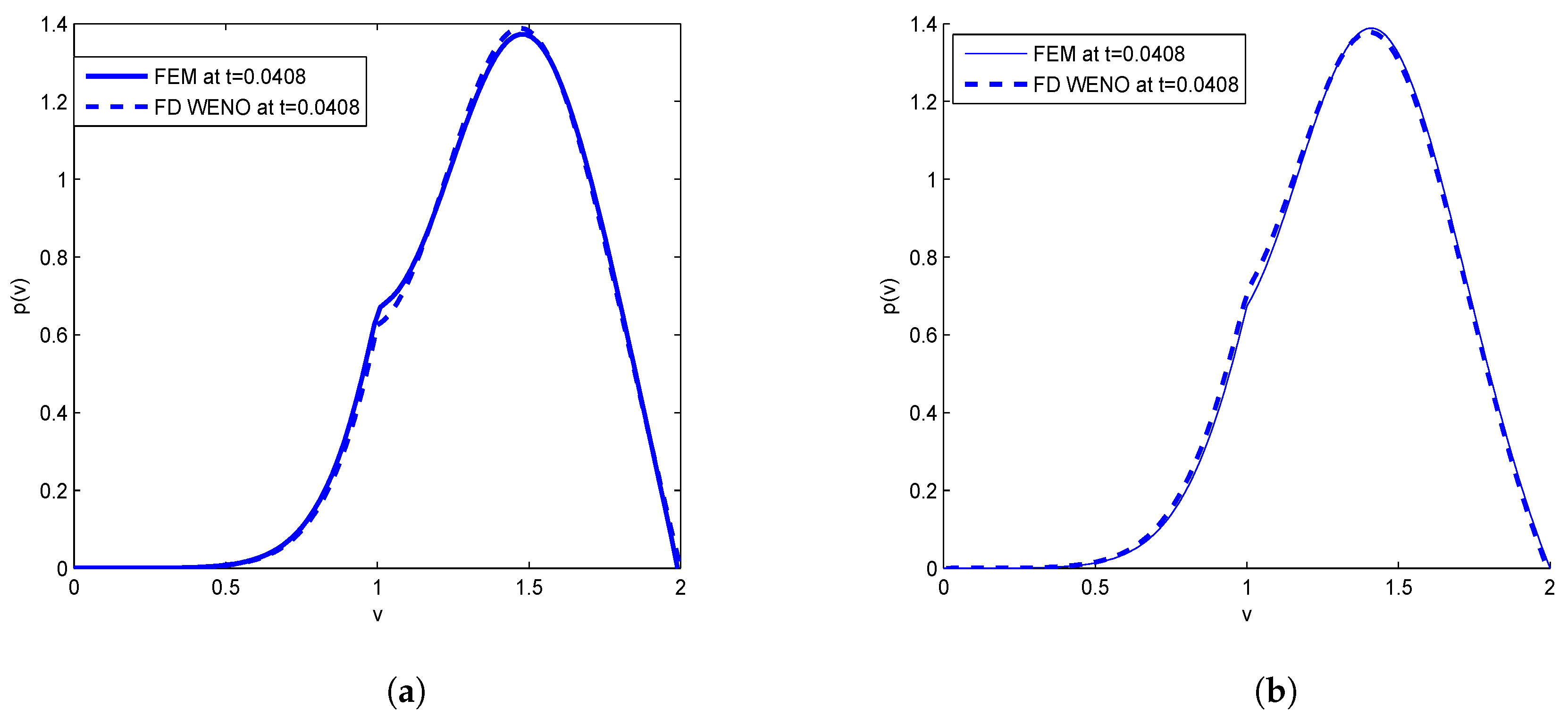
The approximate solution $p(v,t)$ for $v\in [-4,2]$ at different time levels $t>0$ is plotted in Figure 1 with a reset potential $V_R=1.$ From Figure 1a, we see that height of impulse decreases as time increases and after some time it reaches a steady state. In Figure 1b, we perform numerical approximation based upon FEM and compare the results obtained in [8] at a final time $t=1.5.$

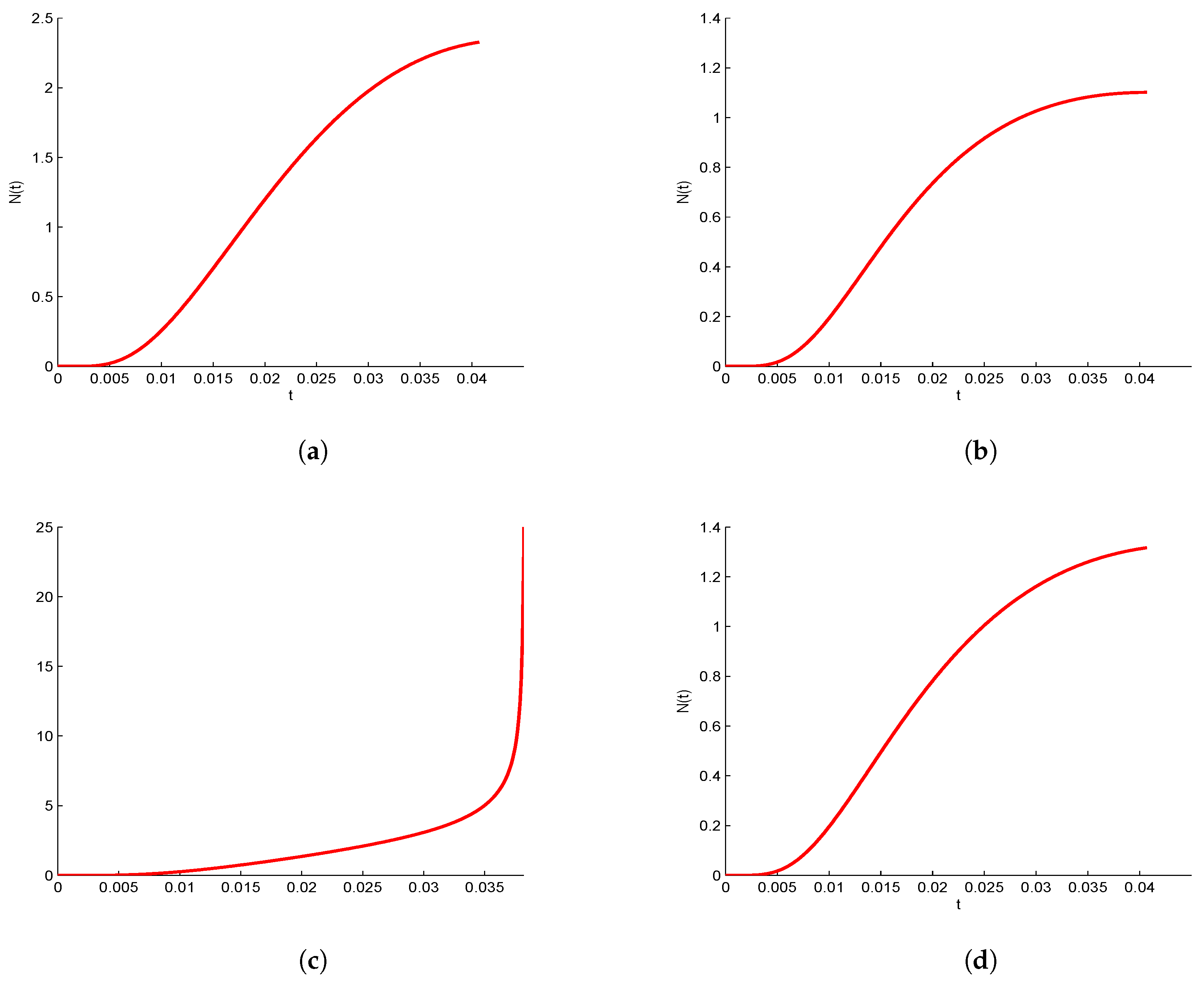
The evolution of firing rate $N\left(t\right)$ with the time $t>0$, is plotted in Figure 2. We find that firing rate has different range with change in $b>0$ excitatory case as well as the inhibitory case $b<0.$ In Figure 2a, we consider the case when the initial data is centered at $v_0=0$ with $b=0.5.$ We observe that the solution reaches a steady state. We also take the cases when the initial data is centered at $v_0=-1$ and different values of $b=3,1.5,-1.5,$ to find different phenomena based on these values in Figure 2.

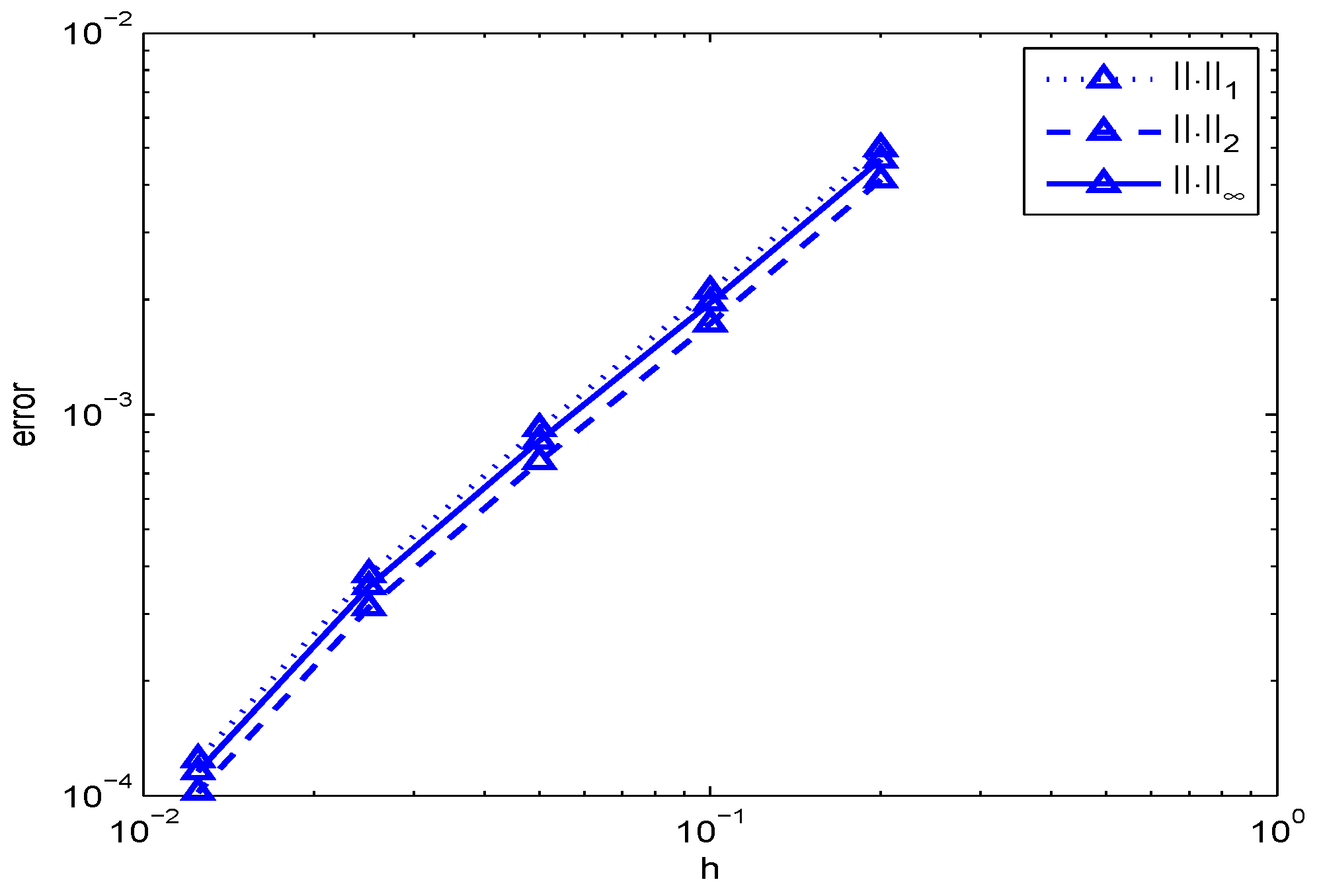
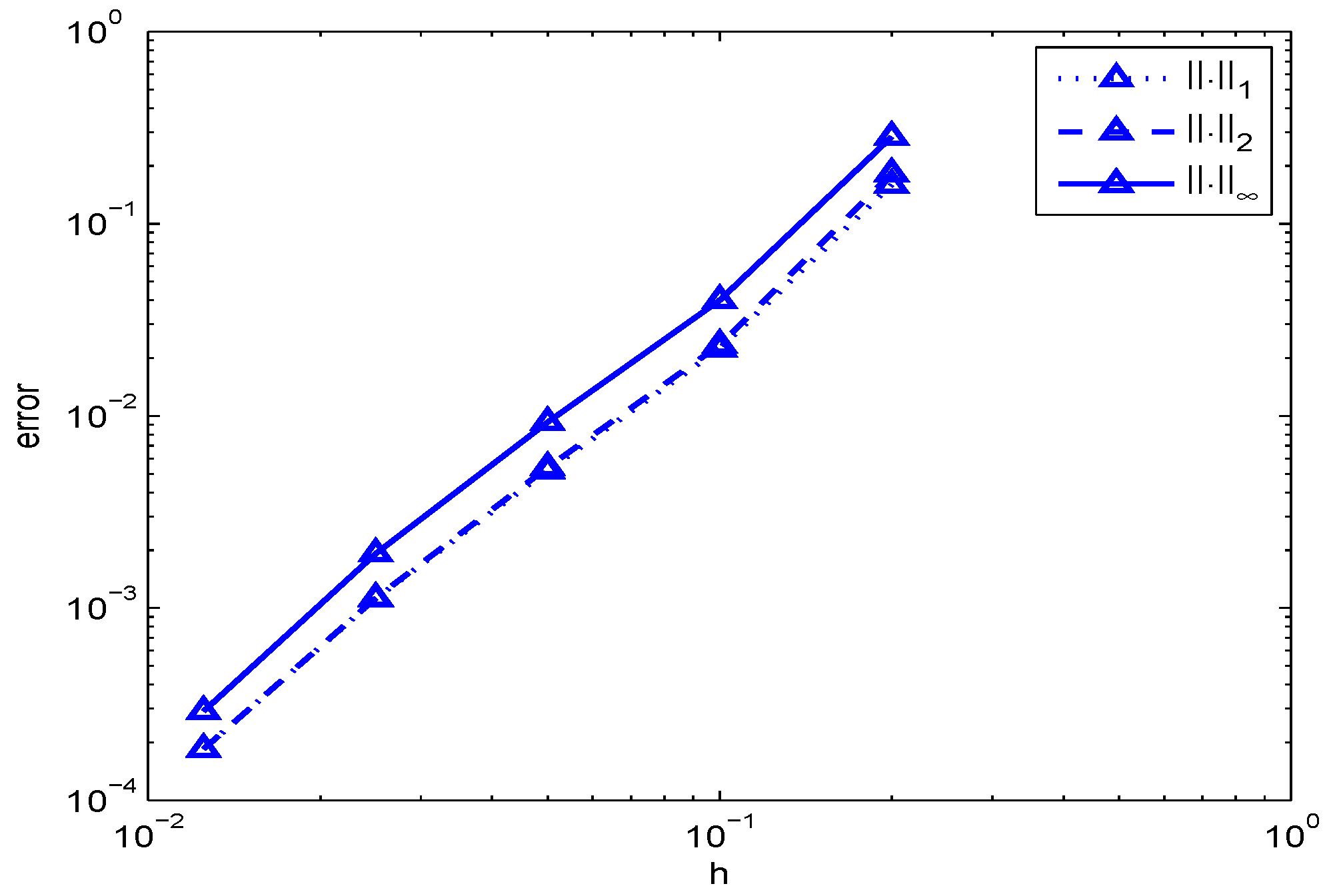
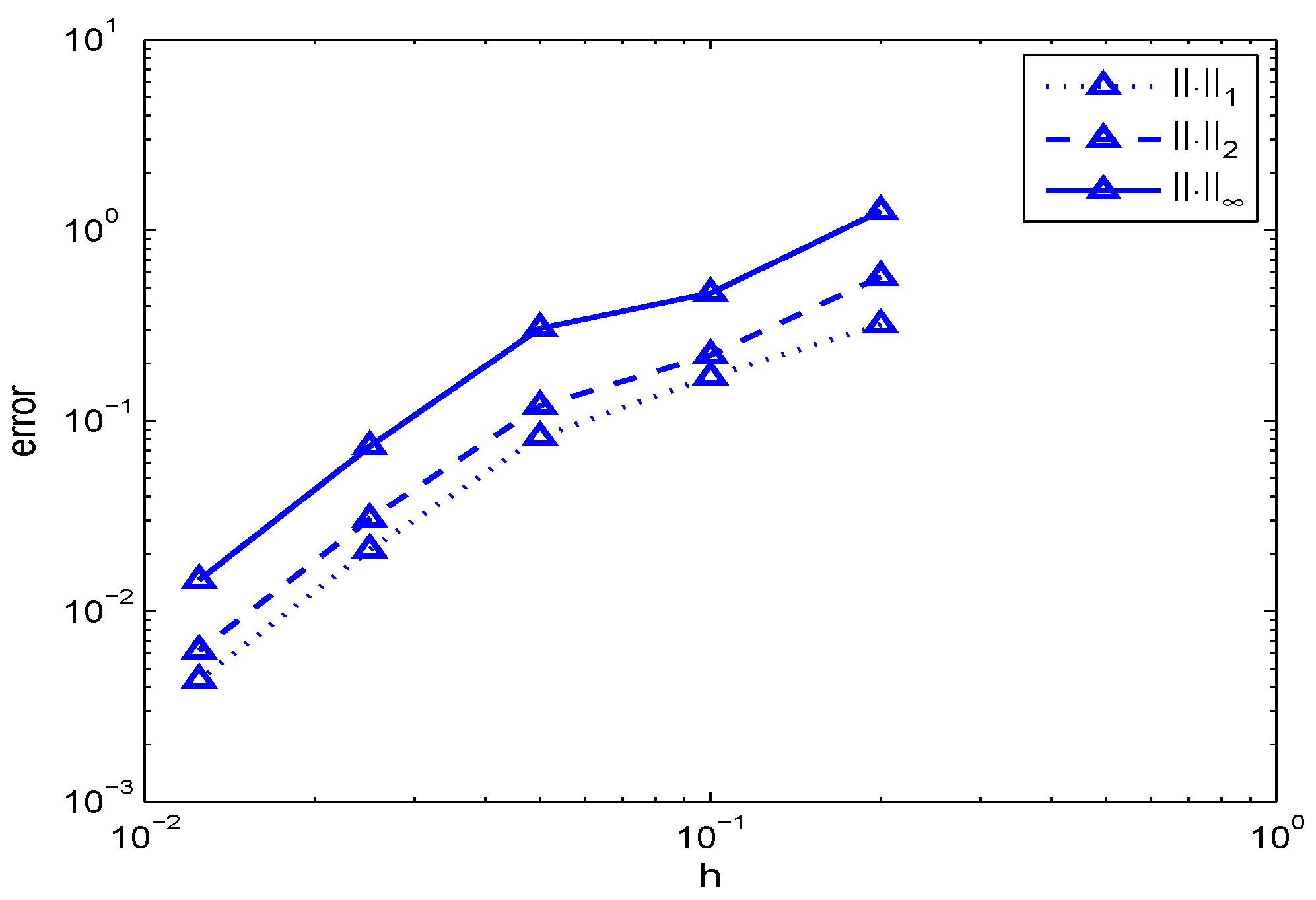
The errors for the approximate solution simulated in Figure 1, Figure 3 and Figure 4 are plotted in Figure 5, Figure 6 and Figure 7 respectively. Numerical values of these errors and CPU time (MATLAB and Statistics Toolbox Release 2013a, The MathWorks, Inc., Natick, MA, United States) of the two methods are shown in

Table 1. Error table using FEM for the approximate solution $p(v,t)$ graphically represented in Figure 1, at a final time $t=1.5$ with the finest grid being $N^{*}=320.$

N	${\parallel \mathit{·}\parallel }_1$	${\parallel \mathit{·}\parallel }_2$	${\parallel \mathit{·}\parallel }_{\mathit{\infty }}$	CPU Time (s)
20	0.010161	0.005158	0.004335	0.067127
40	0.003960	0.001973	0.001516	0.371851
80	0.001542	0.000773	0.000542	3.080583
160	0.000489	0.000247	0.000171	33.034109

and

Table 2. Error table using finite difference-WENO scheme for the approximate solution $p(v,t)$ graphically represented in Figure 1, at a final time $t=1.5$ with the finest grid being $N^{*}=320.$

N	${\parallel \mathit{·}\parallel }_1$	${\parallel \mathit{·}\parallel }_2$	${\parallel \mathit{·}\parallel }_{\mathit{\infty }}$	CPU Time (s)
20	0.289460	0.325151	0.283239	1.037672
40	0.135309	0.151787	0.039987	6.045227
80	0.047782	0.051424	0.009268	46.438833
160	0.013548	0.012541	0.001921	361.179426

.

Errors of the numerical solution $p(v,t)$ are calculated in different norms ${\parallel ·\parallel }_1{,\parallel ·\parallel }_2,{\parallel ·\parallel }_{\infty },$ norms which are defined as follows

$$\begin{array}{ccc}{\parallel ·\parallel }_1& =& \Delta v{\displaystyle \sum _i}|{\left(p_{\Delta v}\right)}_i-{\left(p^{*}\right)}_i|,\\ {\parallel ·\parallel }_2& =& \sqrt{\Delta v{\displaystyle \sum _i}{|{\left(p_{\Delta v}\right)}_i-{\left(p^{*}\right)}_i|}^2,}\\ {\parallel ·\parallel }_{\infty }& =& max|{\left(p_{\Delta v}\right)}_i-{\left(p^{*}\right)}_i|,\end{array}$$

where $p^{*}$ is the numerical solution at finest grid $N^{*}.$ For the numerical experiments, we find the errors with the finest grid being $N^{*}=320.$ Our test outcomes show that the error defined above is sure a monotone decreasing function as N increases i.e., $N=20,40,80,160.$

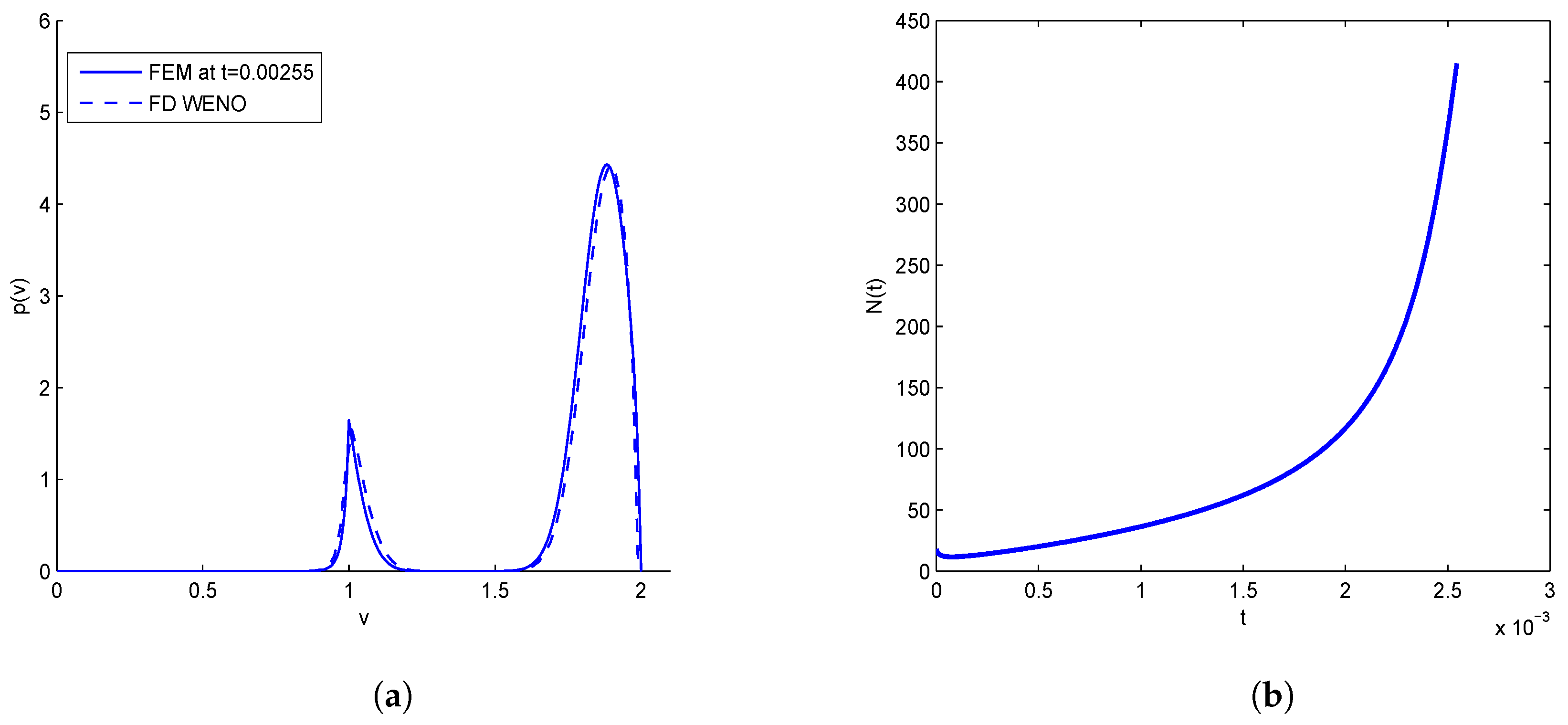
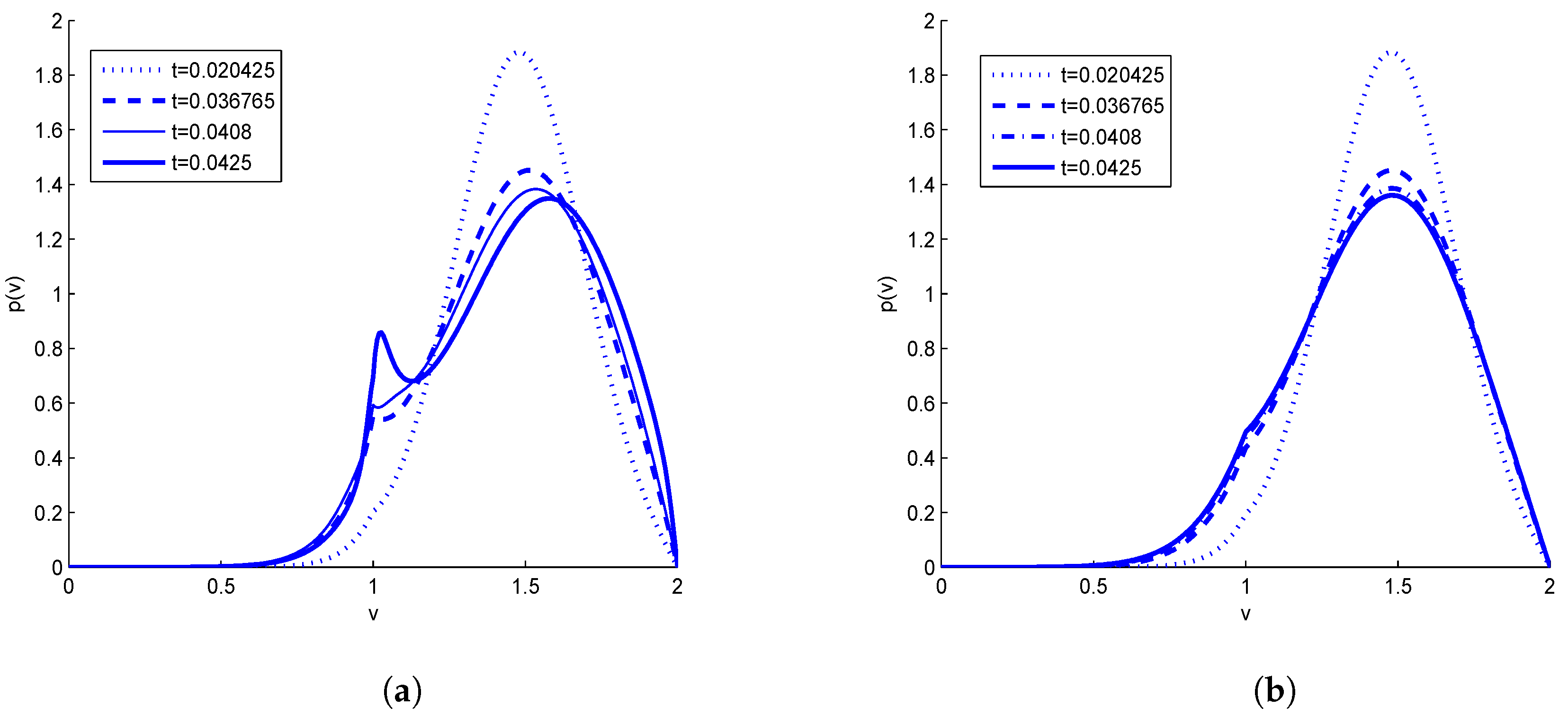
In Figure 3a, we performed numerical approximation based upon FEM and compared the results obtained in [8] at a time $t=0.0408.$ The evolution of firing rate $N\left(t\right)$ with the time $t>0$, is plotted in Figure 3b, which describes the blow-up situation when the initial data is concentrated around $v_0=1.5$ with $b=1.5>0.$

Table 3. Error table using FEM for the approximate solution $p(v,t)$ graphically represented in Figure 3, at a final time $t=0.0408$ with the finest grid being $N^{*}=320.$

N	${\parallel \mathit{·}\parallel }_1$	${\parallel \mathit{·}\parallel }_2$	${\parallel \mathit{·}\parallel }_{\mathit{\infty }}$	CPU Time (s)
20	0.159578	0.182739	0.283239	0.039572
40	0.022391	0.023427	0.039987	0.109250
80	0.005192	0.005395	0.009268	0.751499
160	0.001122	0.001127	0.001921	8.015343

and

Table 4. Error table using WENO-FDM for the approximate solution $p(v,t)$ graphically represented in Figure 3, at a final time $t=0.0408$ with the finest grid being $N^{*}=320.$

N	${\parallel \mathit{·}\parallel }_1$	${\parallel \mathit{·}\parallel }_2$	${\parallel \mathit{·}\parallel }_{\mathit{\infty }}$	CPU Time (s)
20	0.289460	0.325151	0.538803	0.431218
40	0.135309	0.151787	0.262857	1.588952
80	0.047782	0.051424	0.089970	10.601858
160	0.013548	0.012541	0.018749	83.066463

gives the different error values at the final time $t=0.0408$ for the same data that is graphically represented in Figure 6.

From Figure 4a, it is clear that when initial data is concentrated enough near the threshold point $V_F,$ solution blows up at a finite time $t=0.0025,$ which is earlier than the phenomena described in Figure 3b. This happens because initial data is concentrated enough near the threshold point i.e., $v_0=1.83,$ with $b=0.5>0$ small enough. For different error values and CPU time for the data graphically represented in Figure 4, see

Table 5. Error table using FEM for the approximate solution $p(v,t)$ graphically represented in Figure 4, at a final time $t=0.00255$ with the finest grid being $N^{*}=320.$

N	${\parallel \mathit{·}\parallel }_1$	${\parallel \mathit{·}\parallel }_2$	${\parallel \mathit{·}\parallel }_{\mathit{\infty }}$	CPU Time (s)
20	0.319312	0.568807	1.260046	0.024043
40	0.170528	0.221119	0.466656	0.031783
80	0.082213	0.119544	0.305763	0.079694
160	0.021068	0.030539	0.073327	0.536440

and

Table 6. Error table using WENO-FDM for the approximate solution $p(v,t)$ graphically represented in Figure 4, at a final time $t=0.00255$ with the finest grid being $N^{*}=320.$

N	${\parallel \mathit{·}\parallel }_1$	${\parallel \mathit{·}\parallel }_2$	${\parallel \mathit{·}\parallel }_{\mathit{\infty }}$	CPU Time (s)
20	0.372501	0.536629	1.056888	0.295874
40	0.173326	0.253474	0.501970	0.375890
80	0.073974	0.109328	0.221484	0.967150
160	0.024875	0.036970	0.075089	5.550542

.

In Figure 8, we treat the cases for $a\left(N\right)=a_0+a_{1}N\left(t\right),a_0,a_1>0$ type activity dependence noise. Figure 8a shows that by taking $b=0.5$ and $a\left(N\right(t\left)\right)=0.5+N\left(t\right)/8$ solution goes to steady state. This further indicates that solution goes to a steady state earlier than the solution behavior provided in Figure 8b by taking $a\left(N\right(t\left)\right)=0.4+N\left(t\right)/100$. Figure 8c shows blow-up situation of a solution by taking $b>1$ and $a\left(N\right(t\left)\right)=0.5+N\left(t\right)/8$. From Figure 8d, we find that by reducing the noise factor $a\left(N\right(t\left)\right)=0.4+N\left(t\right)/100$, solution goes to steady state.

The behavior of the solution by taking noise factor $a\left(N\right(t\left)\right)=1+N\left(t\right)/100$ for both the cases of excitatory and inhibitory are represented in Figure 9. From Figure 10a, we find that solution blows up in a finite time and right figure indicate the situation of steady state by reducing the noise factor.

5. Conclusions

In this article, we proposed a finite element method to find the approximate solution of the nonlinear NLIF model. The performance of the proposed method is validated by comparing with an existence scheme in the literature. The approximate solutions determined by Galerkin finite element method have same accuracy as achieved by high-order finite difference scheme (WENO-FDM). The proposed scheme takes less computational time as compared to WENO-FDM. The reason behind that the existing scheme contains many computational factors such as smoothness indicator functions and non-negativity weights etc. Moreover, we also included the role of both excitatory and inhibitory impulses in the model equation. The stability analysis of the proposed scheme is discussed which shows that the scheme is conditionally stable. The behavior of the solution is plotted by taking some test examples. The results reveal that the continuous Galerkin FEM is better than the WENO-FDM for simulating dynamics of large-scale neuronal networks in the brain.