1. Introduction
First, we prove that Klement Dand Mesiar’s lattices [
1] do not fit the general definition of neutrosophic set, and we construct the appropriate nonstandard neutrosophic lattices of the first type (as neutrosophically ordered set) [
2], and of the second type (as neutrosophic algebraic structure, endowed with two binary neutrosophic laws,
and
) [
2].
We also present the novelties that neutrosophy, neutrosophic logic, set, and probability and statistics, with respect to the previous classical and multi-valued logics and sets, and with the classical and imprecise probability and statistics, respectively.
Second, we prove that Zhang-Zhang’s YinYang bipolar fuzzy set [
3,
4] is not equivalent with but a subclass of the Single-Valued bipolar neutrosophic set.
Third, we show that Montero, Bustince, Franco, Rodríguez, Gómez, Pagola, Fernández, and Barrenechea’s paired structure of the knowledge representation model [
5] is a particular case of Refined Neutrosophy (a branch of philosophy that generalized dialectics) and of the Refined Neutrosophic Set [
6]. We disprove again the claim that the bipolar fuzzy set (renamed as YinYang bipolar fuzzy set) is the same of neutrosophic set as asserted by Montero et al [
5].
About the three types of neutralities presented by Montero et al., we show, by examples and formally, that there may be any finite number or an infinite number of types of neutralities , or that indeterminacy (), as neutrosophic component, can be refined (split) into number of sub-indeterminacies (not only 3 as Montero et al. said) as needed to each application to solve.
Also, we show, besides numerous neutrosophic applications, many innovatory contributions to science were brought on by the neutrosophic theories, such as: generalization of Yin Yang Chinese philosophy and dialectics to neutrosophy [
7], a new branch of philosophy that is based on the dynamics of opposites and their neutralities, the sum of the neutrosophic components
T,
I,
F up to 3, the degrees of dependence/independence between the neutrosophic components [
8,
9]; the distinction between absolute truth and relative truth in the neutrosophic logic [
10], the introduction of nonstandard neutrosophic logic, set, and probability after we have extended the nonstandard analysis [
11,
12], the refinement of neutrosophic components into subcomponents [
6]; the ability to express incomplete information, complete information, paraconsistent (conflicting) information [
13,
14]; and the extension of the middle principle to the multiple-included middle principle [
15], introduction of neutrosophic crisp set and topology [
16], and so on.
2. Answers to Erich Peter Klement and Radko Mesiar
2.1. Oversimplification of the Neutrosophic Set
At [
1], page 10 (Section 3.3) in their paper, related to neutrosophic sets, they wrote:
“As a straightforward generalization of the product lattice , for each n ∈ N, the n-dimensional unit cube , i.e., the n-dimensional product of the lattice (, ≤comp), can be defined by means of (1) and (2).
The so-called “neutrosophic” sets introduced by F. Smarandache [93] (see also [94–97], which are based on the bounded latticesand, where the ordersandon the unit cube I3 are defined by the Equations below.
The authors have defined Equations
(1) and
(2) as follows:
The authors did not specify what type of lattices they employ: of the first type (lattice, as a partially ordered set), or the second type (lattice, as an algebraic structure). Since their lattices are endowed with some inequality (referring to the neutrosophic case), we assume it is as the first type.
The authors have used the notations:
,
,
.
The order relationship
on
can be defined as:
The three lattices they constructed are denoted by , , , respectively.
Contain only the very particular case of standard single-valued neutrosophic set, i.e., when the neutrosophic components (truth-membership), (indeterminacy-membership), and (false-membership) of the generic element , of a neutrosophic set are single-valued (crisp) numbers from the unit interval .
The authors have
oversimplified the neutrosophic set. Neutrosophic is much more complex. Their lattices do not characterize the
initial definition of the neutrosophic set ([
10], 1998): a set whose elements have the degrees of appurtenance
T,
I,
F, where
T,
I,
F are standard or nonstandard subsets of the nonstandard unit interval:
, where
overpasses the classical real unit interval
to the left and to the right.
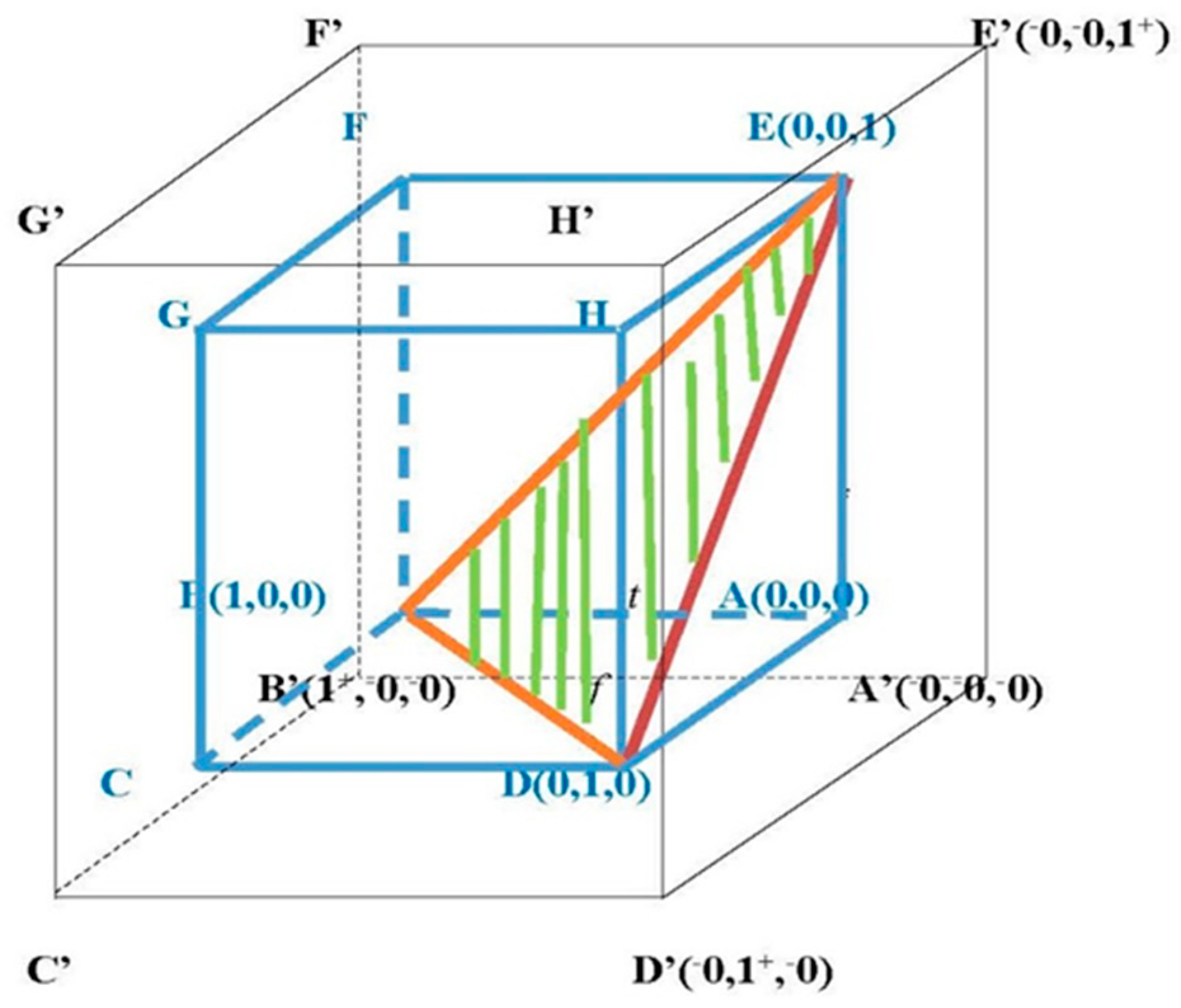
2.2. Neutrosophic Cube vs. Unit Cube
Clearly, their
that is our neutrosophic cube (
Figure 1), where
is the left nonstandard monad of number 0, and
is the right nonstandard monad of number 1.
The unit cube
used by the authors does not equal the above neutrosophic cube. The neutrosophic cube
A’B’C’D’E’F’G’H’ was introduced by Dezert [
17] in 2002.
2.3. The Most General Neutrosophic Lattices
The authors’ lattices are far from catching the most general definition of the neutrosophic set.
Let
be a universe of discourse, and
be a set. Then an element
, where
are standard or nonstandard subsets of nonstandard interval:
[, where
, with
, whose values
and
depend on each application, and
where
,
are monads or binads [
12].
It follows that the nonstandard neutrosophic mobinad real offsets lattices and of the first type and, respectively, of the second type are the most general (non-refined) neutrosophic lattices.
While the most general refined neutrosophic lattices of the first type is:
, where
is the n-tuple nonstandard neutrosophic inequality dealing with nonstandard subsets, defined as:
2.4. Distinction between Absolute Truth and Relative Truth
The authors’ lattices are incapable of making distinctions between absolute truth (when ) and relative truth (when ) in the sense of Leibniz, which is the essence of nonstandard neutrosophic logic.
2.5. Neutrosophic Standard Subset Lattices
Their three lattices are not even able to deal with
standard subsets [including intervals [
8], and hesitant (discrete finite) subsets]
,
,
, since they have defined the 3D-inequalities with respect to single-valued (crisp) numbers:
,
,
and
,
,
.
In order to deal with standard subsets, they should use inf/sup, i.e.,
and ,
and ,
and and
[I have displayed the most used 3D-inequality by the neutrosophic community.]
2.6. Nonstandard and Standard Refined Neutrosophic Lattices
The
Nonstandard Refined Neutrosophic Set [
2,
6,
12], defined on
, strictly includes their n-dimensional unit cube (
), and we use a nonstandard neutrosophic inequality, not the classical inequalities, to deal with inequalities of monads and binads, such as
and
.
Not even the Standard Refined Single-Valued Neutrosophic Set [
6] (2013) may be characterized with
,
, and
nor with
, since the
n-D neutrosophic inequality is different from
n-D
, and from
n-D extensions of
or
respectively, as follows:
Let be refined into , , …, ;
be refined into , , …, ;
and be refined into , , …, ;
with are integers, and , produced the following n-D neutrosophic inequality.
Let , and .
2.7. Neutrosophic Standard Overset/Underset/Offset Lattice
Their three lattices
,
and
are no match for neutrosophic overset (when the neutrosophic components
), nor for neutrosophic underset (when the neutrosophic components
), and, in general, no match for the neutrosophic offset (when the neutrosophic components
take values outside the unit interval
as needed in real life applications [
13,
14,
18,
19,
20] (2006–2018):
with
.)
Therefore, a lattice may similarly be built on the non-unitary neutrosophic cube .
2.8. Sum of Neutrosophic Components up to 3
The authors do not mention the novelty of neutrosophic theories regarding the sum of single-valued neutrosophic components extended up to 3, and, similarly, the corresponding inequality when T, I, F are subsets of : , for neutrosophic set, neutrosophic logic, and neutrosophic probability never done before in the previous classic logic and multiple-valued logics and set theories, nor in the classical or imprecise probabilities.
This makes a big difference, since, for a single-valued neutrosophic set all unit cubes are fulfilled with points, each point into the unit cube may represent the neutrosophic coordinates of an element , which was not the case for previous logics, sets, and probabilities.
This is not the case for the Picture Fuzzy Set (Cuong [
21], 2013) whose domain is
of the unit cube (a cube corner):
For Intuitionistic Fuzzy Set (Atanassov [
22], 1986), the following is true.
where
= membership degree,
= hesitant degree, and
= nonmembership degree, whose domain is the main cubic diagonal triangle that connects the vertices:
,
, and
, i.e., triangle BDE (its sides and its interior) in
Figure 1.
2.9. Etymology of Neutrosophy and Neutrosophic
The authors [
1] write ironically twice, in between quotations, “neutrosophic” because they did not read the etymology [
10] of the word published into my first book (1998), etymology, which also appears into Denis Howe’s 1999
The Free Online Dictionary of Computing [
23], and, afterwards, repeated by many researchers from the neutrosophic community in their published papers:
Neutrosophy [
23]:
<philosophy> (From Latin “neuter”—neutral, Greek “sophia”—skill/wisdom). A branch of philosophy, introduced by Florentin Smarandache in 1980, which studies the origin, nature, and scope of neutralities, as well as their interactions with different ideational spectra. Neutrosophy considers a proposition, theory, event, concept, or entity, “A”in relation to its opposite, “Anti-A” and that which is not A, “Non-A”, and that which is neither “A” nor “Anti-A”, denoted by “Neut-A”. Neutrosophy is the basis of neutrosophic logic, neutrosophic probability, neutrosophic set, and neutrosophic statistics. While neutrosophic means what is derived/resulted from neutrosophy.
Unlike the “intuitionistic|” and “picture fuzzy” notions, the notion of neutrosophic was carefully and meaningfully chosen, coming from neutral (or indeterminate, denoted by <neutA>) between two opposites, and , which made the main distinction between neutrosophic logic/set/probability, and the previous fuzzy, intuitionistic fuzzy logics and sets, i.e.,
- -
For neutrosophic logic neither true nor false, but neutral (or indeterminate) in between them;
- -
Similarly for neutrosophic set: neither membership nor non-membership, but in between (neutral, or indeterminate);
- -
And analogously for neutrosophic probability: chance that an event occurs, chance that the event does not occur, and indeterminate (neutral) chance of the event of occurring or not occuring.
Their irony is malicious and ungrounded.
2.10. Neutrosophy as Extension of Dialectics
Let be a concept, notion, idea, or theory.
Then is the opposite of , while is the neutral (or indeterminate) part between them.
While in philosophy, Dialectics is the dynamics of opposites ( and ), Neutrosophy is an extension of dialectics. In other words, neutrosophy is the dynamics of opposites and their neutrals (, , ), because the neutrals play an important role in our world, interfering in one side or the other of the opposites.
Refined Neutrosophy is an extension of Neutrosophy, and it is the dynamics of the refined-items <A1>, <A2>, …, <An>, their refined-opposites <antiA1>, <antiA2>, …, <antiAn>, and their refined-neutrals <neutA1>, <neutA2>, …, <neutAn>.
As an extension of Refined Neutrosophy one has the Plithogeny [
24,
25,
26,
27].
2.11. Refined Neutrosophic Set and Lattice
At page 11, Klement and Mesiar ([
1], 2018) assert that: Considering, for
lattices which are isomorphic to
, further generalizations of “neutrosophic” sets can be introduced.
The authors are uninformed so that a generalization was done in 2013 when we have published a paper [
6] that introduced, for the first time, the refined neutrosophic set/logic/probability, where
T,
I,
F were refined into
neutrosophic subcomponents:
, , …, ; , , …, ; , , …, ,
With are integers and .
But in our lattice , the neutrosophic inequality is adjusted to the categories of sub-truths, sub-indeterminacies, and sub-falsehood, respectively.
Therefore, is different from the n-D inequalities , and from and (extending from authors inequalities and , respectively).
2.12. Nonstandard Refined Neutrosophic Set and Lattice
Even more, Nonstandard Refined Neutrosophic Set/Logic/Probability (which include infinitesimals, monads, and closed monads, binads and closed binads) has no connection and no isomorphism whatsoever with any of the authors’ lattices or extensions of their lattices for 2D and 3D to nD.
2.13. Nonstandard Neutrosophic Mobinad Real Lattice
We have built ([
2], 2018) a more complex Nonstandard Neutrosophic Mobinad Real Lattice, on the nonstandard mobinad unit interval
defined as:
which is both
nonstandard neutrosophic lattice of the first type (as partially ordered set, under neutrosophic inequality
) and lattice of the second type (as algebraic structure, endowed with two binary nonstandard neutrosophic laws:
and
).
Now, is a nonstandard unit cube, with much higher density than and which comprise not only real numbers but also infinitesimals and monads and binads neutrosophically included in .
2.14. New Ideas Brought by the Neutrosophic Theories and Never Done Before
- —
The sum of the neutrosophic components is up to 3 (previously the sum was up to 1);
- —
Degree of independence and dependence between the neutrosophic components T, I, F, making their sum vary between 0 and 3.
For example, when T, I, and F are totally dependent with each other, then . Therefore, we obtain the particular cases of intuitionistic fuzzy set (when ) and picture set when .
- —
Nonstandard analysis used in order to distinguish between absolute and relative (truth, membership, chance).
- —
Refinement of the components into sub-components:
with the newly introduced Refined Neutrosophic Logic/Set/Probability.
- —
Ability to express incomplete information () and paraconsistent (conflicting) and subjective information ().
- —
Law of Included Middle explicitly/independently expressed as (indeterminacy, neutral).
- —
Law of Included Middle expanded to the Law of Included Multiple-Middles within the refined neutrosophic set as well as logic and probability.
- —
A large array of applications [
28,
29,
30] in a variety of fields, after two decades from their foundation ([
10], 1998), such as: Artificial Intelligence, Information Systems, Computer Science, Cybernetics, Theory Methods, Mathematical Algebraic Structures, Applied Mathematics, Automation, Control Systems, Communication, Big Data, Engineering, Electrical, Electronic, Philosophy, Social Science, Psychology, Biology, Biomedical, Engineering, Medical Informatics, Operational Research, Management Science, Imaging Science, Photographic Technology, Instruments, Instrumentation, Physics, Optics, Economics, Mechanics, Neurosciences, Radiology Nuclear, Medicine, Medical Imaging, Interdisciplinary Applications, Multidisciplinary Sciences, and more [
30].
Klement’s and Mesiar’s claim that the neutrosophic set (I do not talk herein about intuitionistic fuzzy set, picture fuzzy set, and Pythagorean fuzzy set that they criticized) is not a new result is far from the truth.
3. Neutrosophy vs. Yin Yang Philosophy
Ying Han, Zhengu Lu, Zhenguang Du, Gi Luo, and Sheng Chen [
3] have defined the “YinYang bipolar fuzzy set” (2018).
However, the “YinYang bipolar” is already a pleonasm, because, in Taoist Chinese philosophy, from the 6th century BC, Yin and Yang was already a bipolarity, between negative (Yin)/positive (Yang), or feminine (Yin)/masculine (Yang).
Dialectics was derived, much later in time, from Yin Yang.
Neutrosophy, as the dynamicity and harmony between opposites (Yin <A> and Yang (antiA>) together with their neutralities (things which are neither Yin nor Yang, or things which are blends of both: <neutA>) is an extension of Yin Yang Chinese philosophy. Neutrosophy came naturally since, into the dynamicity, conflict, cooperation, and even ignorance between opposites, the neutrals are attracted and play an important role.
3.1. YinYang Bipolar Fuzzy Set Is the Bipolar Fuzzy Set
The authors sincerely recognize that: “In the existing papers, YinYang bipolar fuzzy set also was called bipolar fuzzy set [5] and bipolar-valued fuzzy set [13,16].”
These papers are cited as References [
31,
32,
33].
We prove that the YinYang bipolar fuzzy set is not equivalent with the neutrosophic set, but a particular case of the bipolar neutrosophic set.
The authors [
3] say that: “Denote
IP = [0, 1] and
IN = [−1, 0], and
, then
is called the YinYang bipolar fuzzy number. (YinYang bipolar fuzzy set)
X = {
x1, ···,
xn} represents the finite discourse. YinYang bipolar fuzzy set in
X is defined by the mapping below.
where the functions
and
define the satisfaction degree of the element
x ∈
X to the property, and the implicit counter-property to the YinYang bipolar fuzzy set
in
X, respectively (see [
3], page 2).
With simpler notations, the above set L is equivalent to:
L = {(a, b), with a ∈ [0, 1], b ∈ [−1, 0]}, and the authors denote (a, b) as the YinYang bipolar fuzzy number.
Further on, again with simpler notations, the so-called YinYang bipolar fuzzy set in
X = {x1, …, xn} is equivalent to:
X = {
x1(
a1,
b1), …,
xn(
an,
bn)}, where all
a1, …,
an ∈ [0, 1], and all
b1, …,
bn ∈ [−1, 0]}. Clearly, this is the bipolar fuzzy set and there is no need to call it the “YinYang bipolar fuzzy set.” The authors added that: “Montero et al. pointed out that the neutrosophic set is equivalent to the YinYang bipolar fuzzy set in syntax.” However, the bipolar fuzzy set is not equivalent to the neutrosophic set at all. The bipolar fuzzy set is actually a particular case of the bipolar neutrosophic set, defined as (keeping the previous notations):
where
all a1, …,an, c1, …, cn, e1, …,en ∈ [0, 1], and all b1, …, bn, d1, …, dn, f1, …, fn ∈ [−1, 0]};
for a generic xj((aj, bj),(cj, dj), (ej, fj)) ∈ X, 1 ≤ j ≤ n,
ai = positive membership degree of xi, and bi = negative membership degree of xi;
ci = positive indeterminate-membership degree of xi, and di = negative indeterminate membership degree of xi;
ei = positive non-membership degree of xi, and fi = negative non-membership degree of xi.
Using notations adequate to the neutrosophic environment, one found the following.
Let be a universe of discourse, and be a set. is a single-valued bipolar fuzzy set (that authors call YinYang bipolar fuzzy set) if, for any element, , , and , where is the positive membership of , and is the negative membership of . (BFS).
The authors write that: “Montero et al. pointed that the neutrosophic set [22] is equivalent to the YinYang bipolar fuzzy set in syntax [17]”.
Montero et al.’s paper is cited below as Reference [
5].
If somebody says something, it does not mean it is true. They have to verify. Actually, it is untrue, since the neutrosophic set is totally different from the so-called YinYang bipolar fuzzy set.
Let be a universe of discourse, and be a set, if for any element.
are standard or nonstandard real subsets of the nonstandard real subsets of the nonstandard real unit interval . (NS).
Clearly, the definitions (BFS) and (NS) are totally different. In the so-called YinYang bipolar fuzzy set, there is no indeterminacy , no nonstandard analysis involved, and the neutrosophic components may be subsets as well.
3.2. Single-Valued Bipolar Fuzzy Set as a Particular Case of the Single-Valued Bipolar Neutrosophic Set
The Single-Valued bipolar fuzzy set (alias YinYang bipolar fuzzy set) is a particular case of the Single-Valued bipolar neutrosophic set, employed by the neutrosophic community, and defined as follows:
Let
be a universe of discourse, and
be a set.
is a single-valued bipolar neutrosophic set, if for any element:
3.3. Dependent Indeterminacy vs. Independent Indeterminacy
The authors say: “Attanassov’s intuitionistic fuzzy set [4] perfectly reflects indeterminacy but not bipolarity.”
We disagree, since Atanassov’s intuitionistic fuzzy set [
22] perfectly reflects
hesitancy between membership and non-membership not
indeterminacy, since
hesitancy is dependent on membership and non-membership:
, where
H = hesitancy,
T = membership, and
F = non-membership.
It is the single-valued neutrosophic set that “perfectly reflects indeterminacy” since indeterminacy () in the neutrosophic set is independent from membership () and from nonmembership ().
On the other hand, the neutrosophic set perfectly reflects the bipolarity membership/non-membership as well, since the membership () and nonmembership () are independent of each other.
3.4. Dependent Bipolarity vs. Independent Bipolarity
The bipolarity in the single-valued fuzzy set and intuitionistic fuzzy set is dependent (restrictive) in the sense that, if the truth-membership is , then it involves the falsehood-nonmembership while the bipolarity in a single-valued neutrosophic set is independent (nonrestrictive): if the truth-membership , the falsehood-nonmebership is not influenced at all, then .
3.5. Equilibriums and Neutralities
Again: “While, in semantics, the YinYang bipolar fuzzy set suggests equilibrium, and neutrosophic set suggests a general neutrality. While the neutrosophic set has been successfully applied to a medical diagnosis [9,27], from the above analysis and the conclusion in [31], we see that the YinYang bipolar fuzzy set is clearly the suitable model to a bipolar disorder diagnosis and will be adopted in this paper.”
I’d like to add that the single-valued bipolar neutrosophic set suggests:
- —
three types of equilibrium, between: and , and , and and ;
- —
and two types of neutralities (indeterminacies) between and , and between and .
Therefore, the single-valued bipolar neutrosophic set is 3 × 2 = 6 times more complex and more flexible than the YinYang bipolar fuzzy set. Due to higher complexity, flexibility, and capability of catching more details (such as falsehood-nonmembership, and indeterminacy), the single-valued bipolar neutrosophic set is more suitable than the YinYang bipolar fuzzy set to be used in a bipolar disorder diagnosis.
3.6. Zhang-Zhang’s Bipolar Model is not Equivalent with the Neutrosophic Set
Montero et al. [
5] wrote: “
Zhang-Zhang’s bipolar model is, therefore, equivalent to the neutrosophic sets proposed by Smarandache [70]”
(p. 56).
This sentence is false and we proved previously that what Zhang & Zhang proposed in 2004 is a subclass of the single-valued bipolar neutrosophic set.
3.7. Tripolar and Multipolar Neutrosophic Sets
Not talking about the fact that, in 2016, we have extended our bipolar neutrosophic set to tripolar and even multipolar neutrosophic sets [
18], the sets have become more general than the bipolar fuzzy model.
3.8. Neutrosophic Overset/Underset/Offset
Not talking that the unit interval was extended in 2006 below 0 and above 1 into the neutrosophic overset/underset/offset: with (as explained above).
3.9. Neutrosophic Algebraic Structures
The Montero et al. [
5] continue: “
Notice that none of these two equivalent models include any formal structure, as claimed in [48]”.
First, we have proved that these two models (Zhang-Zhang’s bipolar fuzzy set, and neutrosophic logic) are not equivalent at all. Zhang-Zhang’s bipolar fuzzy set is a subclass of a particular type of neutrosophic set, called the single-valued bipolar neutrosophic set.
Second, since 2013, Kandasamy and Smarandache have developed various algebraic structures (such as neutrosophic semigroup, neutrosophic group, neutrosophic ring, neutrosophic field, neutrosophic vector space, etc.) [
28] on the set of neutrosophic numbers:
SR, where is the set of real numbers.
And extended on:
SC, where C is the set of complex numbers.
However, until 2016 [year of Montero et al.’s published paper], I did not develop a formal structure on the neutrosophic set. Montero et al. are right.
Yet, in 2018, and, consequently at the beginning of 2019, we [
2] developed, then generalized, and proved that the neutrosophic set has a structure of the lattice of the first type (as the neutrosophically partially ordered set):
, where
is the nonstandard neutrosophic mobinad (monads and binads) real unit interval, and
is the nonstandard neutrosophic inequality. Moreover,
has the structure of the bound lattice of the second type (as algebraic structure), under two binary laws
(nonstandard neutrosophic infimum) and
(nontandard neutrosophic supremum).
3.10. Neutrality (<neutA>)
Montero et al. [
5] continue: “
…the selected denominations within each model might suggest different underlying structures: while the model proposed by Zhang and Zhang suggests conflict between categories (a specific type of neutrality different from Atanassov’s indeterminacy), Smarandache suggests a general neutrality that should, perhaps jointly, cover some of the specific types of neutrality considered in our paired approach.”
In neutrosophy and neutrosophic set/logic/probability, the neutrality <neutA> means everything in between <A> and <antiA>, everything which is neither <A> nor <antiA>, or everything which is a blending of <A> and <antiA>.
Further on, in Refined Neutrosophy and Refined Neutrosophic Set/Logic/Probability [
9], the neutrality <neutA> was split (refined) in 2013 into sub-neutralities (or sub-indeterminacies), such as: <neutA
1>, <neutA
2>, …, <neutA
n> whose number could be finite or infinite depending on each application that needs to be solved.
Thus, the paired structure becomes a particular case of refined neutrosophy (see next).
4. The Pair Structure as a Particular Case of Refined Neutrosophy
Montero et al. [
5] in 2016 have defined a
paired structure: “
composed by a pair of opposite concepts and three types of neutrality as primary valuations: L = {concept, opposite, indeterminacy, ambivalence, conflict}.”
Therefore, each element
, where
is a universe of discourse, is characterized by a degree function, with respect to each attribute value from
:
where
represents the degree of
with respect to the concept;
represents the degree of with respect to the opposite (of the concept);
represents the degree of with respect to ‘indeterminacy’;
represents the degree of with respect to ‘ambivalence’;
represents the degree of with respect to ‘conflict’.
However, this paired structure is a particular case of Refined Neutrosophy.
4.1. Antonym vs. Negation
First, Dialectics is the dynamics of opposites. Denote them by and , where may be an item, a concept, attribute, idea, theory, and so on while is the opposite of .
Secondly, Neutrosophy ([
10], 1998), as a generalization of Dialectics, and a new branch of philosophy, is the dynamics of opposites and their neutralities (denoted by
). Therefore, Neutrosophy is the dynamics of
,
, and
.
means everything, which is neither nor , or which is a mixture of them, or which is indeterminate, vague, or unknown.
The antonym of is .
The
negation of
(which we denote by
) is what is not
, therefore:
We preferred to use the lower index N (neutrosophic) because we deal with items, concepts, attributes, ideas, and theories such as and, in consequence, its derivates , , , whose borders are ambiguous, vague, and not clearly delimited.
4.2. Refined Neutrosophy as an Extension of Neutrosophy
Thirdly, Refined Neutrosophy ([
6], 2013), as an extension of Neutrosophy, and a refined branch of philosophy, is the dynamics of refined opposites:
,
, …,
with
,
, …,
, and their refined neutralities:
,
, …,
, for integers p, r,
, and
. Therefore, the item
has been split into sub-items
,
, the
into sub-(anti-items)
,
, and the
into sub-(neutral-items)
,
.
4.3. Qualitative Scale as a Particular Case of Refined Neutrosophy
Montero et al.’s qualitative scale [
5] is a particular case of Refined Neutrosophy where the neutralities are split into three parts.
where:
<A> = concept,
<antiA> = opposite,
<neutA1> = indeterminacy,
<neutA2> = ambivalence,
<neutA3> = conflict.
Yin Yang, Dialectics, Neutrosophy, and Refined Neutrosophy (the last one having only as refined component), are bipolar: and are the poles.
Montero et al.’s qualitative scale is bipolar (‘concept’, and its ‘opposite’).
4.4. Multi-Subpolar Refined Neutrosophy
However, the Refined Neutrosophy, whose at least one of or is refined, is multi-subpolar.
4.5. Multidimensional Fuzzy Set as a Particular Case of the Refined Neutrosophic Set
Montero et al. [
5] defined the
Multidimensional Fuzzy Set AL as:
, where X is the universe of discourse,
L = the previous qualitative scale, and
∈
S, where
S is a valuation scale (in most cases
S = [0, 1]),
is the degree of
x with respect to
s ∈
L.
A Single-Valued Neutrosophic Set is defined as follows. Let be a universe of discourse, and a set. For each element , is the degree of truth-membership of element with respect to the set , is the degree of indeterminacy-membership of element with respect to the set , and is the degree of falsehood-nonmembership of element with respect to the set .
Let’s refine as , , sub-indeterminacies. Then we get a single-valued refined neutrosophic set.
(truth-membership);
(falsehood-non-membership);
(first sub-indeterminacy);
(second sub-indeterminacy);
(third sub-indeterminacy).
The
Single-Valued Refined Neutrosophic Set is defined as follows. Let
be a universe of discourse, and
a set. For each element:
, , are degrees of subtruth-submembership of element with respect to the set .
, , are degrees of subindeterminacy-membership of element with respect to the set .
Lastly, , , are degrees of sub-falsehood-sub-non-membership of element with respect to the set , where integers p, r, , and .
Therefore, Montero et al.’s multidimensional fuzzy set is a particular case of the refined neutrosophic set, when , , and , where .
4.6. Plithogeny and Plithogenic Set
Fourthly, in 2017 and in 2018 [
24,
25,
26,
27], the Neutrosophy was extended to Plithogeny, which is multipolar, being the dynamics and hermeneutics [methodological study and interpretation] of many opposites and/or their neutrals, together with non-opposites.
, , ;
, , ; etc.
, , etc.
In addition, the Plithogenic Set was introduced, as a generalization of Crisp, Fuzzy, Intuitionistic Fuzzy, and Neutrosophic Sets.
Unlike previous sets defined, whose elements were characterized by the attribute ‘appurtenance’ (to the set), which has only one (membership), or two (membership, nonmembership), or three (membership, nonmembership, indeterminacy) attribute values, respectively. For the Plithogenic Set, each element may be characterized by a multi-attribute, with any number of attribute values.
4.7. Refined Neutrosophic Set as a Unifying View of Opposite Concepts
Montero et al.’s statement [
5] from their paper Abstract: “
we propose a consistent and unifying view to all those basic knowledge representation models that are based on the existence of two somehow opposite fuzzy concepts.”
With respect to the “unifying” claim, their statement is not true, since, as we proved before, their paired structure together with three types on neutralities (indeterminacy, ambivalence, and conflict) is a simple, particular case of the refined neutrosophic set.
The real unifying view currently is the Refined Neutrosophic Set.
{I was notified about this paired structure article [
5] by Dr. Said Broumi, who forwarded it to me.}
4.8. Counter-Example to the Paired Structure
As a counter example to the paired structure [
5], it cannot catch a simple voting scenario.
The election for the United States President from 2016: Donald Trump vs. Hillary Clinton. USA has 50 states and since, in the country, there is an Electoral vote, not a Popular vote, it is required to know the winner of each state.
There were two opposite candidates.
The candidate that receives more votes than the other candidate in a state gets all the points of that state.
As in the neutrosophic set, there are three possibilities:
percentage of USA people voting for Mr. Trump;
percentage of USA people not voting, or voting but giving either a blank vote (not selecting any candidate) or a black vote (cutting all candidates);
percentage of USA people voting against Mr. Trump.
The opposite concepts, using Montero et al.’s knowledge representation, are T (voting for, or truth-membership) and F (voting against, or false-membership). However, , or , or that the Paired Structure can catch, mean only the Popular vote, which does not count in the United States.
Actually, it happened that in the US 2016 presidential election, or Mr. Trump lost the Popular vote, but he won the Presidency using the Electoral vote.
The paired structure is not capable of refining the opposite concepts ( and ), while the indeterminate () could be refined by the paired structure only in three parts.
Therefore, the paired structure is not a unifying view of all basic knowledge that uses opposite fuzzy concepts. However, the refined neutrosophic set/logic/probability do.
Using the refined neutrosophic set and logic, and splits (refines) , , and as:
percentage of American state people voting for Mr. Trump;
percentage of American state people not voting, or casting a blank vote or a black vote;
percentage of American state people voting against Mr. Trump, with , , and , for all .
Therefore, one has:
.
On the other hand, due to the fact that the sub-indeterminacies , , …, did not count towards the winner or looser (only for indeterminate voting statistics), it is not mandatory to refine . We could simply refine it as:
.
4.9. Finite Number and Infinite Number of Neutralities
Montero et al. [
5]: “
(…) we emphasize the key role of certain neutralities in our knowledge representation models, as pointed out by Atanassov [4], Smarandache [70], and others. However, we notice that our notion of neutrality should not be confused with the neutral value in a traditional sense (see [22–24,36,54], among others). Instead, we will stress the existence of different kinds of neutrality that emerge (in the sense of Reference [11]) from the semantic relation between two opposite concepts (and notice that we refer to a neutral category that does not entail linearity between opposites).”
In neutrosophy, and, consequently, in the neutrosophic set, logic, and probability, between the opposite items (concepts, attributes, ideas, etc.) and there may be a large number of neutralities/indeterminacies (all together denoted by even an infinite spectrum—depending on the application to solve.
We agree with different kinds of neutralities and indeterminacies (vague, ambiguous, unknown, incomplete, contradictory, linear and non-linear information, and so on), but the authors display only three neutralities.
In our everyday life and in practical applications, there are more neutralities and indeterminacies.
In another example (besides the previous one about Electoral voting), there may be any number of sub indeterminacies/sub neutralities.
The opposite concepts attributes are: white, black, while neutral concepts in between may be: yellow, orange, red, violet, green, and blue. Therefore, we have six neutralities. Example with infinitely many neutralities:
- —
The opposite concepts: white, black;
- —
The neutralities: the whole light spectrum between white and black, measured in nanometers (nn) [a nanometer is a billionth part of a meter].