Global Stability Analysis of Two-Stage Quarantine-Isolation Model with Holling Type II Incidence Function
Abstract
:1. Introduction
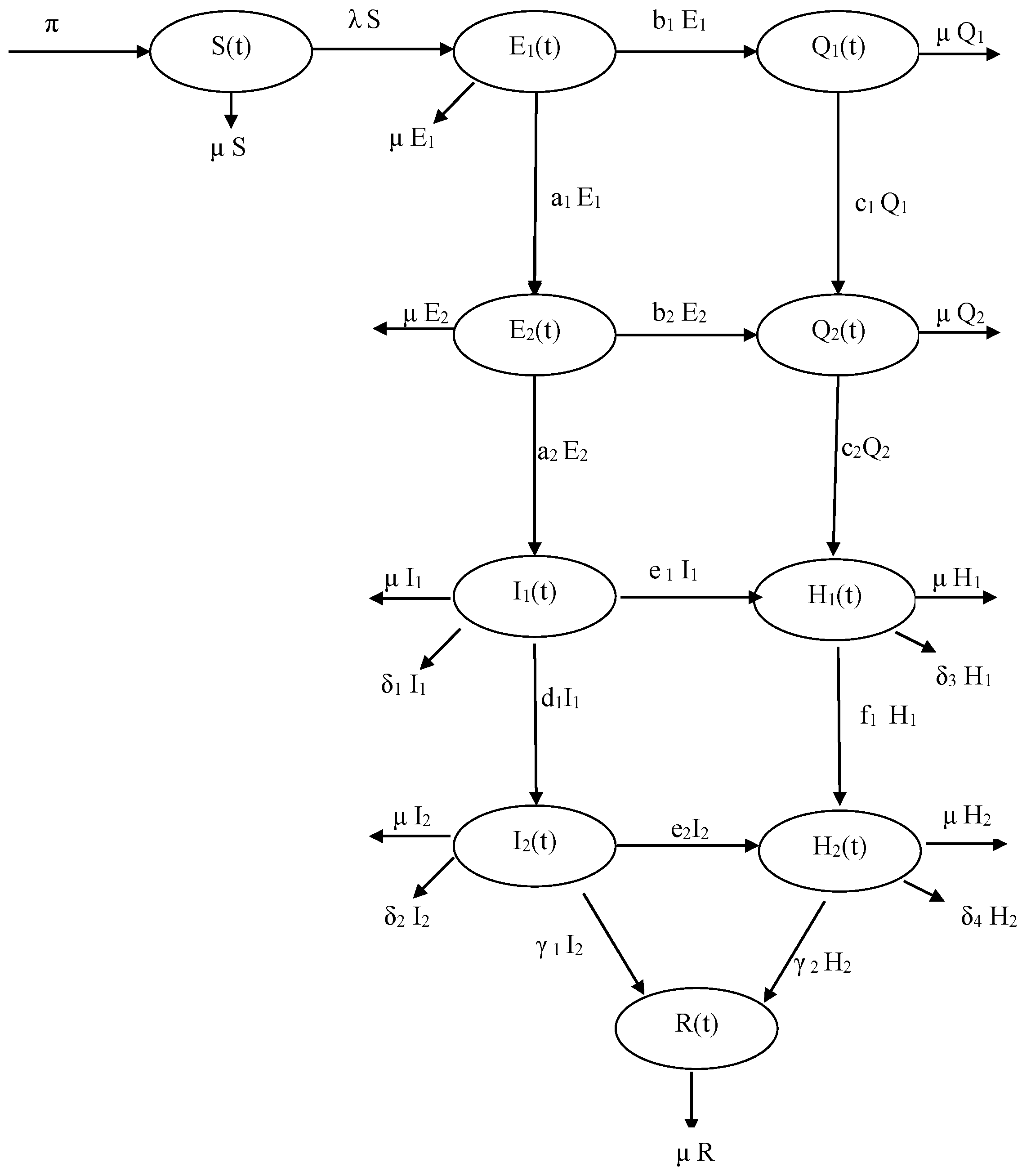
2. Model Formulation
- (a)
- Using a Holling type incidence function to model the infection rate (the standard incidence function was used in [19])
- (b)
- Considering two stages for the infectious compartments (Exposed, infected, quarantined, and isolated compartments)
2.1. Preliminaries and Basic Properties
Next-Generation Method
3. Stability of DFE
3.1. Local Stability
3.2. Global Stability of DFE
4. Existence and Stability for Endemic Equilibrium Point
4.1. Persistence of the Disease
4.2. Uniqueness of Endemic Equilibrium Point (EEP)
4.3. Global Stability for Endemic Equilibrium
5. Conclusions
- (i)
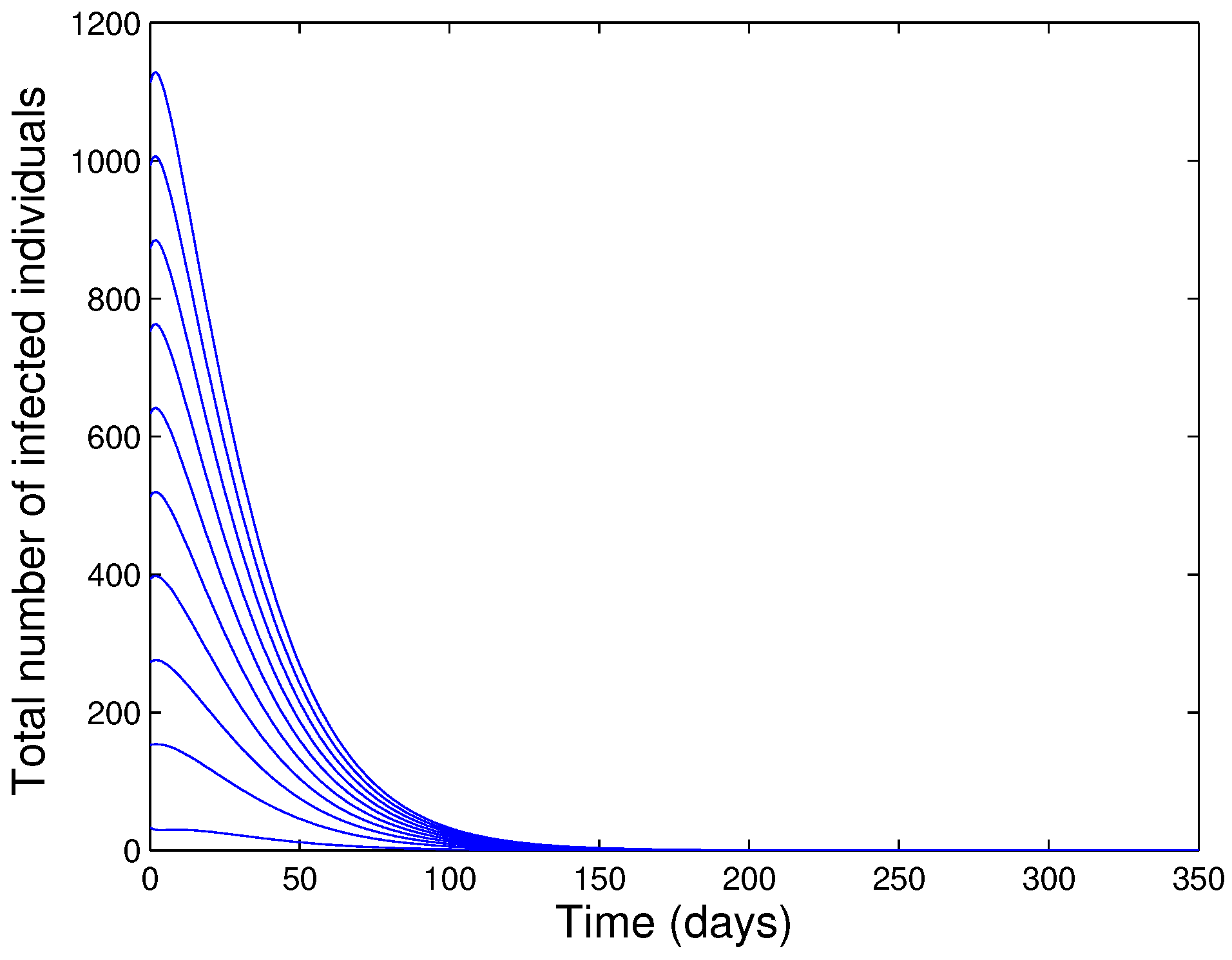
- The model (1) has a locally asymptotically stable DFE if the associated reproduction number () is less than one.
- (ii)
- The model (1) has a GAS whenever .
- (iii)
- System (1) is uniformly persistent in if and only if the reproduction number exceeds unity.
- (iv)
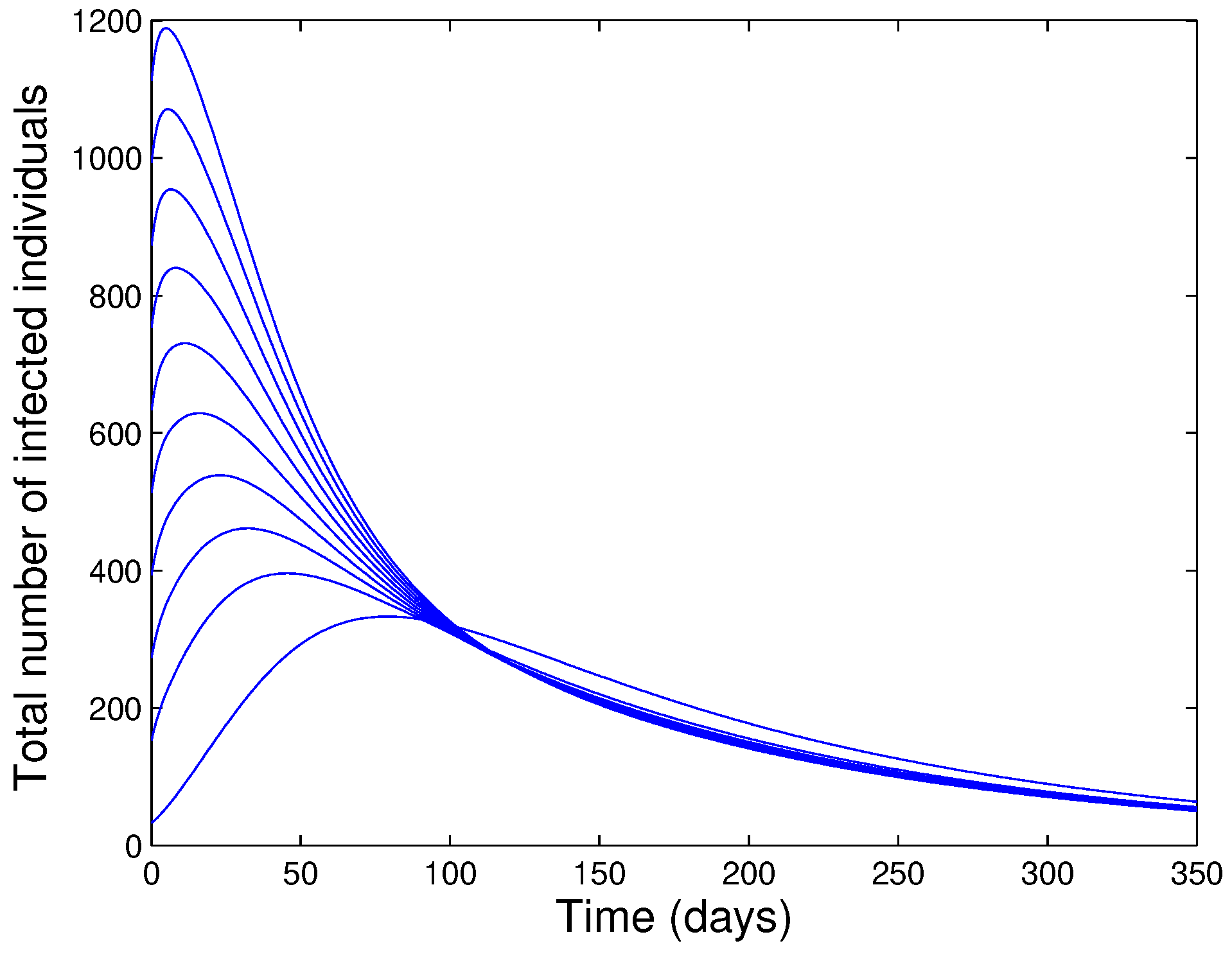
- The model has a unique endemic equilibrium whenever .
- (v)
- The unique endemic equilibrium of the model is shown to be GAS for a special case.
Funding
Acknowledgments
Conflicts of Interest
References
- Chowell, G.; Hengartner, N.W.; Castillo-Chavez, C.; Fenimore, P.W.; Hyman, J.M. The basic reproductive number of ebola and the effects of public health measures: The cases of Congo and Uganda. J. Theor. Biol. 2004, 1, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Donnelly, C.; Ghani, A.; Leung, G.; Hedley, A.; Fraser, C.; Riley, S.; Abu-Raddad, L.J.; Ho, L.M.; Thach, T.Q.; Chau, P.; et al. Epidemiological determinants of spread of casual agnet of severe acute respiratory syndrome in Hong Kong. Lancet 2003, 361, 1761–1766. [Google Scholar] [CrossRef]
- Hethcote, H.W.; Zhien, M.; Shengbing, L. Effects of quarantine in six endemic models for infectious diseases. Math. Biosci. 2002, 180, 141–160. [Google Scholar] [CrossRef]
- Lipsitch, M.; Cohen, T.; Cooper, B.; Robins, J.M.; Ma, S.; James, L.; Gopalakrishna, G.; Chew, S.K.; Tan, C.C.; Samore, M.H.; et al. Transmission dynamics and control of severe acute respiratory syndrome. Science 2003, 300, 1966–1970. [Google Scholar] [CrossRef] [PubMed]
- Lloyd-Smith, J.O.; Galvani, A.P.; Getz, W.M. Curtailing transmission of severe acute respiratory syndrome within a community and its hospital. Proc. R. Soc. Lond. B 2003, 170, 1979–1989. [Google Scholar] [CrossRef] [PubMed]
- McLeod, R.G.; Brewster, J.F.; Gumel, A.B.; Slonowsky, D.A. Sensitivity and uncertainty analyses for a SARS model with time-varying inputs and outputs. Math. Biosci. Eng. 2006, 3, 527–544. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Ruan, S. Simulating the SARS outbreak in Beijing with limited data. J. Theor. Biol. 2004, 227, 369–379. [Google Scholar] [CrossRef] [PubMed]
- Webb, G.F.; Blaser, M.J.; Zhu, H.; Ardal, S.; Wu, J. Critical role of nosocomial transmission in the Toronto SARS outbreak. Math. Biosci. Eng. 2004, 1, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Zou, Y. Optimal and sub-optimal quarantine and isolation control in SARS epidemics. Math. Comput. Model. 2008, 47, 235–245. [Google Scholar] [CrossRef]
- Day, T.; Park, A.; Madras, N.; Gumel, A.B.; Wu, J. When is quarantine a useful control strategy for emerging infectious diseases? Am. J. Epidemiol. 2006, 163, 479–485. [Google Scholar] [CrossRef] [PubMed]
- Gumel, A.B.; Ruan, S.; Day, T.; Watmough, J.; Brauer, F.; van den Driessche, P.; Gabrielson, D.; Bowman, C.; Alexander, M.E.; Ardal, S.; et al. Modelling strategies for controlling SARS outbreaks. Proc. R. Soc. Ser. B 2004, 271, 2223–2232. [Google Scholar] [CrossRef]
- Safi, M.A.; Gumel, A.B. Mathematical analysis of a disease transmission model with quarantine, isolation and an imperfect vaccine. Comput. Math. Appl. 2011, 61, 3044–3070. [Google Scholar] [CrossRef]
- Safi, M.A.; Gumel, A.B. Qualitative study of the quarantine/isolation model with multiple disease stages. Appl. Math. Comput. 2011, 218, 1941–1961. [Google Scholar] [CrossRef]
- Capasso, V.; Serio, G. A generalization of the Kermack-Mckendrick deterministic epidemic model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Liu, W.M.; Levin, S.A.; Iwasa, Y. Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J. Math. Biol. 1985, 23, 187–204. [Google Scholar] [CrossRef]
- Ruan, S.; Wang, W. Dynamical behavior of an epidemic model with a nonlinear incidence rate. J. Differ. Equ. 2003, 188, 135–163. [Google Scholar] [CrossRef]
- Eichner, M.; Schwehm, M.; Duerr, H.; Brockmann, S.O. The influenza pandemic preparedness planning tool InfluSim. BMC Infec. Dis. 2007, 7, 17. [Google Scholar] [CrossRef]
- Sharomi, O.; Podder, C.N.; Gumel, A.B.; Elbasha, E.H.; Watmough, J. Role of incidence function in vaccine-induced backward bifurcation in some HIV models. Math. Biosci. 2007, 210, 436–463. [Google Scholar] [CrossRef]
- Safi, M.A.; Gumel, A.B. Globa Asymptotic Dynamics of a Model for Quarantine and Isolation. Discret. Contin. Dyn. Syst. Ser. B 2011, 14, 209–231. [Google Scholar] [CrossRef]
- Smith, H.L.; Waltman, P. The Theory of the Chemostat; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Hethcote, H.W.; Thieme, H.R. Stability of the endemic equilibrium in epidemic models with subpopulations. Math. Biosci. 1985, 75, 205–227. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A.J. On the definition and computation of the basic reproduction ratio in models for infectious disease in heterogeneous population. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Population Biology of Infectious Diseases; Springer: Berlin/Heidelrberg, Germany; New York, NY, USA, 1982. [Google Scholar]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Hale, J.K. Ordinary Differential Equations; John Wiley and Sons: New York, NY, USA, 1969. [Google Scholar]
- Freedman, H.; Ruan, S.; Tang, M. Uniform persistence and flows near a closed positively invariant set. J. Dyn. Differ. Equ. 1994, 6, 583–600. [Google Scholar] [CrossRef]
- Thieme, H. Epidemic and demographic interaction in the spread of potentially fatal diseases in growing populations. Math. Biosci. 1992, 1, 99–130. [Google Scholar] [CrossRef]
- Li, M.; Graef, J.; Karsai, L.W.J. Global dynamics of a SEIR model with varying total population size. Math. Biosci. 1999, 160, 191–213. [Google Scholar] [CrossRef]
- Bhatia, N.P.; Szego, G.P. Dynamical Systems: Stability Theory and Applications; Springer: Berlin, Germany, 1967; Volume 35. [Google Scholar]
| Variable | Description |
|---|---|
| Population of susceptible individuals | |
| Population of exposed individuals on the first exposed stage | |
| Population of exposed individuals on the second exposed stage | |
| Population of quarantined individuals on the first quarantined stage | |
| Population of quarantined individuals on the second quarantined stage | |
| Population of infected individuals on the first infectious stage | |
| Population of infected individuals on the second infectious stage | |
| Population of Isolated individuals on the first Isolated stage | |
| Population of Isolated individuals on the second Isolated stage | |
| Population of recovered individuals | |
| Parameter | Description |
| Recruitment rate | |
| Effective contact rate | |
| Progression rate from the first exposed stage to the second one | |
| Progression rate to first infectious class from exposed individuals | |
| in the second stage | |
| Quarantine rate of exposed individuals on the first exposed stage | |
| Quarantine rate of exposed individuals on the second exposed stage | |
| Progression rate from the first quarantined stage to the second one | |
| Progression rate to first Isolated class from quarantined individuals | |
| in the second stage | |
| Progression rate from the first infectious stage to the second one | |
| Hospitalization rate of infectious individuals on the first infectious | |
| Hospitalization rate of infectious individuals on the second infectious | |
| Progression rate from the first Isolated stage to the second one | |
| Recovery rate of infectious individuals in the second stage | |
| Recovery rate of Isolated individuals in the second stage | |
| Disease-induced death rate of the first infectious stage | |
| Disease-induced death rate of the second infectious stage | |
| Disease-induced death rate of the first Isolated stage | |
| Disease-induced death rate of the second Isolated stage | |
| Natural death rate |
| Parameter(s) | Numerical Value |
|---|---|
| 0.136 | |
| 0.2 | |
| 0.1 | |
| 0.1 | |
| 0.2 | |
| 0.15 | |
| 0.11 | |
| 0.0337 | |
| 0.0386 | |
| 0.0068 | |
| 0.000034 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safi, M.A. Global Stability Analysis of Two-Stage Quarantine-Isolation Model with Holling Type II Incidence Function. Mathematics 2019, 7, 350. https://doi.org/10.3390/math7040350
Safi MA. Global Stability Analysis of Two-Stage Quarantine-Isolation Model with Holling Type II Incidence Function. Mathematics. 2019; 7(4):350. https://doi.org/10.3390/math7040350
Chicago/Turabian StyleSafi, Mohammad A. 2019. "Global Stability Analysis of Two-Stage Quarantine-Isolation Model with Holling Type II Incidence Function" Mathematics 7, no. 4: 350. https://doi.org/10.3390/math7040350
APA StyleSafi, M. A. (2019). Global Stability Analysis of Two-Stage Quarantine-Isolation Model with Holling Type II Incidence Function. Mathematics, 7(4), 350. https://doi.org/10.3390/math7040350





