Continuous Dependence of Solutions of Integer and Fractional Order Non-Instantaneous Impulsive Equations with Random Impulsive and Junction Points
Abstract
:1. Introduction
2. Main Results
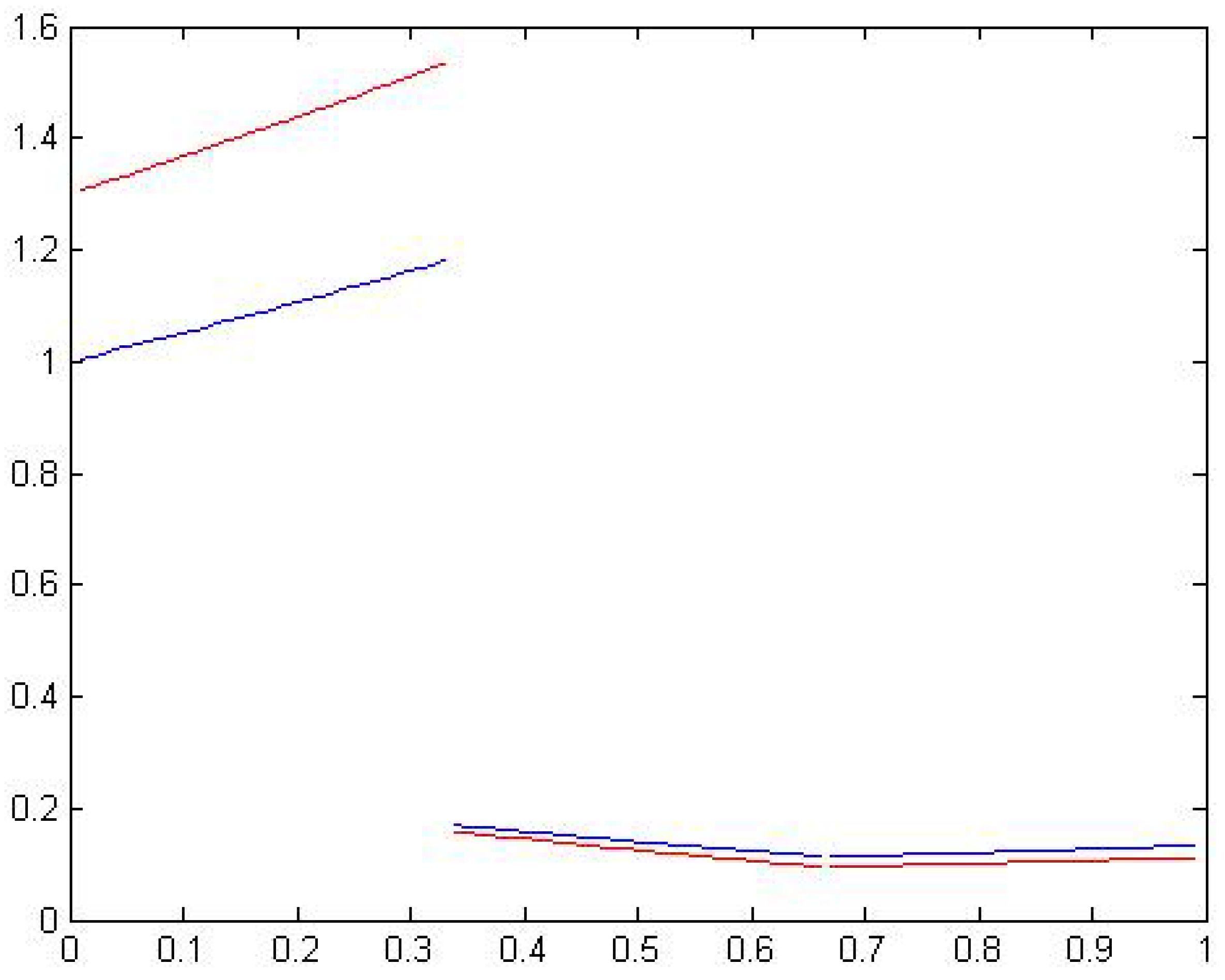
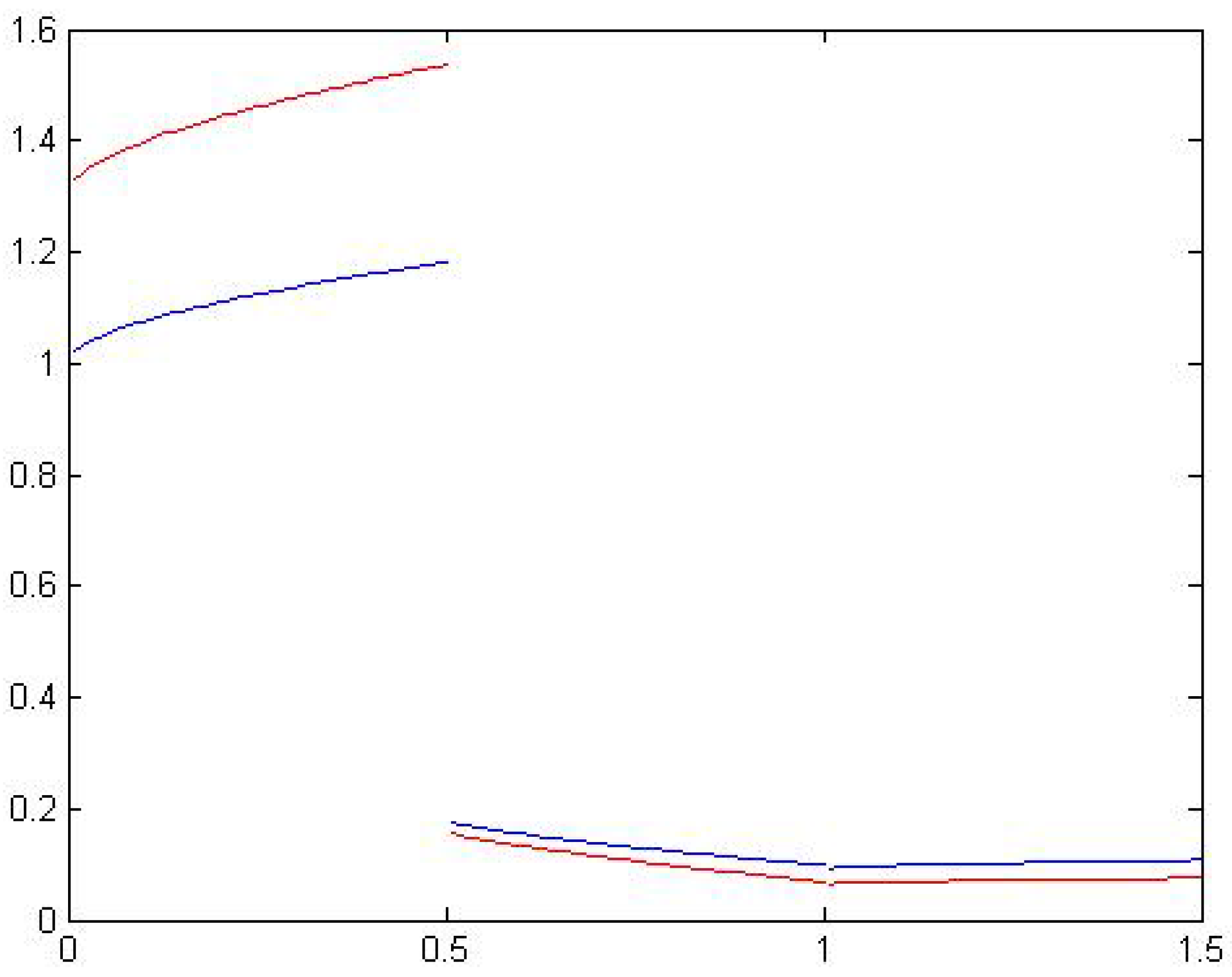
3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chalishajar, D.N.; Malar, K.; Karthikeyan, K. Approximate controllability of abstract impulsive fractional neutral evolution equations with infinite delay in Banach spaces. Electron. J. Differ. Equ. 2013, 2013, 1–21. [Google Scholar]
- Chalishajar, D.N.; Karthikeyan, K.; Anguraj, A. Existence results for impulsive perturbed partial neutral functional differential equations in Frechet spaces. Dyn. Contin. Discret. Impuls. Syst. Ser. Math. Anal. 2015, 22, 25–45. [Google Scholar]
- Hernández, E.; O’Regan, D. On a new class of abstract impulsive differential equations. Proc. Am. Math. Soc. 2013, 141, 1641–1649. [Google Scholar] [CrossRef]
- Wang, J.; Fečkan, M. A general class of impulsive evolution equations. Topol. Meth. Nonlinear Anal. 2015, 46, 915–934. [Google Scholar] [CrossRef]
- Wang, J. Stability of noninstantaneous impulsive evolution equations. Appl. Math. Lett. 2017, 73, 157–162. [Google Scholar] [CrossRef]
- Chen, P.; Li, Y.; Yang, H. Perturbation method for nonlocal impulsive evolution equations. Nonlinear Anal. Hybrid Syst. 2013, 8, 22–30. [Google Scholar] [CrossRef]
- Bai, L.; Nieto, J.J. Variational approach to differential equations with not instantaneous impulses. Appl. Math. Lett. 2017, 73, 44–48. [Google Scholar] [CrossRef]
- Pierri, M.; O’Regan, D.; Rolnik, V. Existence of solutions for semi-linear abstract differential equations with not instantaneous impulses. Appl. Math. Comput. 2013, 219, 6743–6749. [Google Scholar] [CrossRef]
- Pierri, M.; Henríquez, H.R.; Prokczyk, A. Global solutions for abstract differential equations with non-instantaneous impulses. Mediterr. J. Math. 2016, 34, 1685–1708. [Google Scholar] [CrossRef]
- Hernández, E.; Pierri, M.; O’Regan, D. On abstract differential equations with non instantaneous impulses. Topol. Methods Nonlinear Anal. 2015, 46, 1067–1085. [Google Scholar]
- Yang, D.; Wang, J. Non-instantaneous impulsive fractional-order implicit differential equations with random effects. Stoch. Anal. Appl. 2017, 35, 719–741. [Google Scholar] [CrossRef]
- Yang, D.; Wang, J.; O’Regan, D. A class of nonlinear non-instantaneous impulsive differential equations involving parameters and fractional order. Appl. Math. Comput. 2018, 321, 654–671. [Google Scholar] [CrossRef]
- Yang, D.; Wang, J.; O’Regan, D. Asymptotic properties of the solutions of nonlinear non-instantaneous impulsive differential equations. J. Frankl. Inst. 2017, 354, 6978–7011. [Google Scholar] [CrossRef]
- Yang, D.; Wang, J.; O’Regan, D. On the orbital Hausdorff dependence of differential equations with non-instantaneous impulses. C. R. Acad. Sci. Paris Ser. I 2018, 356, 150–171. [Google Scholar] [CrossRef]
- Abbas, S.; Benchohra, M. Uniqueness and Ulam stabilities results for partial fractional differential equations with not instantaneous impulses. Appl. Math. Comput. 2015, 257, 190–198. [Google Scholar] [CrossRef]
- Muslim, M.; Kumar, A.; Fečkan, M. Existence, uniqueness and stability of solutions to second order nonlinear differential equations with non-instantaneous impulses. J. King Saud Univ. 2018, 30, 204–213. [Google Scholar] [CrossRef]
- Colao, V.; Muglia, L.; Xu, H.K. An existence result for a new class of impulsive functional differential equations with delay. J. Math. Anal. Appl. 2016, 441, 668–683. [Google Scholar] [CrossRef]
- Wang, J.; Fečkan, M. Non-Instantaneous Impulsive Differential Equations Basic Theory and Computation; IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Wang, J.; Zhou, Y.; Lin, Z. On a new class of impulsive fractional differential equations. Appl. Math. Comput. 2014, 242, 649–657. [Google Scholar] [CrossRef]
- Wang, J.; Fečkan, M.; Tian, Y. Stability analysis for a general class of non-instantaneous impulsive differential equations. Mediterr. J. Math. 2017, 14, 1–21. [Google Scholar] [CrossRef]
- Wang, J.; Ibrahim, A.G.; O’Regan, D. Topological structure of the solution set for fractional non-instantaneous impulsive evolution inclusions. J. Fixed Point Theory Appl. 2018, 20, 1–25. [Google Scholar] [CrossRef]
- Wang, J.; Ibrahim, A.G.; O’Regan, D.; Zhou, Y. Controllability for noninstantaneous impulsive semilinear functional differential inclusions without compactness. Indag. Math. 2018, 29, 1362–1392. [Google Scholar] [CrossRef]
- Wang, J.; Ibrahim, A.G.; O’Regan, D. Hilfer type fractional differential switched inclusions with noninstantaneous impulsive and nonlocal conditions. Nonlinear Anal. Model. Contr. 2018, 23, 921–941. [Google Scholar] [CrossRef]
- Wang, J.; Ibrahim, A.G.; O’Regan, D. Nonempty and compactness of solution set for fractional semilinear evolution inclusions with non-instantaneous impulses. Electr. J. Differ. Equ. 2019, 2019, 1–17. [Google Scholar]
- Liu, S.; Wang, J.; Shen, D.; O’Regan, D. Iterative learning control for parabolic partial differential inclusions with noninstantaneous impulses. Appl. Math. Comput. 2019, 350, 48–59. [Google Scholar] [CrossRef]
- Luo, D.; Wang, J.; Shen, D. Learning formation control for fractional-order multi-agent systems. Math. Meth. Appl. Sci. 2018, 41, 5003–5014. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J. Numerical analysis for a class of Navier–Stokes equations with time fractional derivatives. Appl. Math. Comput. 2018, 336, 481–489. [Google Scholar]
- Zhu, B.; Liu, L.; Wu, Y. Local and global existence of mild solutions for a class of nonlinear fractional reaction-diffusion equation with delay. Appl. Math. Lett. 2016, 61, 73–79. [Google Scholar] [CrossRef]
- Ren, L.; Wang, J.; Fečkan, M. Asymptotically periodic solutions for Caputo type fractional evolution equations. Fract. Calc. Appl. Anal. 2018, 21, 1294–1312. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Shen, D.; Zhou, Y. Convergence analysis for iterative learning control of conformable fractional differential equations. Math. Meth. Appl. Sci. 2018, 41, 8315–8328. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Zhang, X.; Wu, Y. Positive solutions of a fractional semipositone differential system arising from the study of HIV infection models. Appl. Math. Comput. 2015, 258, 312–324. [Google Scholar]
- Zhang, X.; Mao, C.; Liu, L.; Wu, Y. Exact iterative solution for an abstract fractional dynamic system model for bioprocess. Qual. Theory Dyn. Syst. 2017, 16, 205–222. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Wu, B.Y. Wiwatanapataphee, Nontrivial solutions for a fractional advection dispersion equation in anomalous diffusion. Appl. Math. Lett. 2017, 66, 1–8. [Google Scholar] [CrossRef]
- Dishlieva, K. On the qualitative theory of differential equaitons with random impulsive moments. Int. J. Sci. Tech. Manag. 2015, 4, 172–180. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Bainov, D.; Simeonov, P. Integral Inequalities and Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Ye, H.; Gao, J.; Ding, Y. A generalized Gronwall inequality and its application to a fractional differential equation. J. Math. Anal. Appl. 2007, 328, 1075–1081. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, J. Continuous Dependence of Solutions of Integer and Fractional Order Non-Instantaneous Impulsive Equations with Random Impulsive and Junction Points. Mathematics 2019, 7, 331. https://doi.org/10.3390/math7040331
Chen Y, Wang J. Continuous Dependence of Solutions of Integer and Fractional Order Non-Instantaneous Impulsive Equations with Random Impulsive and Junction Points. Mathematics. 2019; 7(4):331. https://doi.org/10.3390/math7040331
Chicago/Turabian StyleChen, Yu, and JinRong Wang. 2019. "Continuous Dependence of Solutions of Integer and Fractional Order Non-Instantaneous Impulsive Equations with Random Impulsive and Junction Points" Mathematics 7, no. 4: 331. https://doi.org/10.3390/math7040331
APA StyleChen, Y., & Wang, J. (2019). Continuous Dependence of Solutions of Integer and Fractional Order Non-Instantaneous Impulsive Equations with Random Impulsive and Junction Points. Mathematics, 7(4), 331. https://doi.org/10.3390/math7040331




