Abstract
The population balance equation (PBE) is the main governing equation for modeling dynamic crystallization behavior. In the view of mathematics, PBE is a convection–reaction equation whose strong hyperbolic property may challenge numerical methods. In order to weaken the hyperbolic property of PBE, a diffusive term was added in this work. Here, the Chebyshev spectral collocation method was introduced to solve the PBE and to achieve accurate crystal size distribution (CSD). Three numerical examples are presented, namely size-independent growth, size-dependent growth in a batch process, and with nucleation, and size-dependent growth in a continuous process. Through comparing the results with the numerical results obtained via the second-order upwind method and the HR-van method, the high accuracy of Chebyshev spectral collocation method was proven. Moreover, the diffusive term is also discussed in three numerical examples. The results show that, in the case of size-independent growth (PBE is a convection equation), the diffusive term should be added, and the coefficient of the diffusive term is recommended as 2G × 10−3 to G × 10−2, where G is the crystal growth rate.
1. Introduction
Crystallization operations are widely used in chemical and pharmaceutical industries. Crystallization kinetics is the basis for the development of crystallization theory. Simultaneously, studies on crystalline kinetics also guide the design of crystallizers and the quality control of crystalline products [1]. The population balance equation (PBE) is a widely accepted equation to model the dynamic crystallization behavior [2]. Therefore, it is of great significance to accurately solve the PBE and to achieve accurate crystal size distribution (CSD).
Currently, there are a many numerical results on the study of PBE. In terms of numerical methods, they can be roughly divided into the following five categories [1,2]: (1) the method of moments [3]; (2) the method of characteristics [4,5]; (3) the method of weight residuals/orthogonal collocation [6,7]; (4) the Monte Carlo method [8,9]; (5) the finite-difference schemes/discrete population balances [10]. The review by Ramkrishna [2] is helpful in this regard. The method of moments approximates the CSD through its moments. The predictions under certain conditions are closed. However, the moment closure conditions are violated for more complex systems. The method of characteristics tries reducing the partial differential equations (PDEs) to ordinary differential equations (ODEs) using lines of characteristics. The approach is efficient with simple physics, but it is not suitable for complex physics. The method of weight residuals/orthogonal collocation approximates the distribution by the basis function; the main weakness is the dependence on the choice of basis function. The Monte Carlo method tracks the histories of individual particles. It has an incomparable degree of omnipotence. However, its computational cost is relatively expensive. The finite-difference/volume methods are approximated by finite-difference/volume schemes. They can be applied to complex cases. However, they usually require a high number of grid points in order to achieve desirable accuracy.
Recently, a large number of numerical methods with high accuracy were constructed to solve PBE, e.g., the HR-van method with a flux limiter [1,11], the Lattice Boltzmann method [12], the weighted essentially non-oscillatory (WENO) method [13], the spectral method [14,15], etc. Among these, the spectral method has the advantage of being able to accurately solve the PBE using a lower number of grid points. It was also found that the spectral collocation method is more efficient than other spectral methods [14] and finite-volume schemes [15].
Because the PBE is a convection–reaction equation in mathematics, its strong hyperbolic property may challenge the numerical methods. The numerical methods may gain unstable results, which are not applicable for physics. In order to weaken the hyperbolic property of PBE, a diffusive term is added herein. Although the diffusive term makes the numerical solution deviate from the exact solution to some extent, it guarantees the stability of the numerical results.
In this paper, Chebyshev spectral collocation is presented to solve the one-dimensional PBE. The CSD of three types of crystallization in batch crystallizers and continuous crystallizers were calculated. By comparing the analytical results and other numerical results, the validity and high accuracy of the Chebyshev spectral collocation method were verified. Furthermore, the effects of the diffusive term are also discussed using three numerical examples.
2. One-Dimensional PBE and Numerical Schemes
2.1. One-Dimensional PBE
PBE is a differential equation which describes the evolution of a population of particles. In the crystallization process, it can reflect the crystal nucleation, growth, agglomeration, and breakage [2].
One-dimensional PBE [1,2,11] can be written as follows:
where is the crystal size distribution function, is the crystal size variable, is the time, is the growth rate of crystals, and is the source term and may include the aggregation, nucleation, breakage, etc. Here, crystal size variable is typically the characteristic length, volume, or mass, but it can also represent age, composition, and other characteristics of an entity in a distribution [1]. The growth rate can be a function of size and other variables, such as the temperature and the concentration of chemical species in solution [1]. The source term is a creation/depletion rate, and it can be a function of other variables including the distribution, which occurs in nucleation processes resulting from particle–particle interactions and in agglomeration processes [1]. Since many of these processes involve integrals, PBE is considered an integro-differential equation describing the complex crystallization processes [2].
Since Equation (1) is a convection–reaction equation, its strong hyperbolic property may challenge the numerical methods. In order to weaken the hyperbolic property of Equation (1), a diffusive term “” is added to the left in Equation (1), leading to
Here, is a small positive number. Theoretically, the closer is to 0, the more accurate the result is. However, in numerical experiments, when approaches 0, the effect of the diffusive term becomes smaller, which leads to an unstable numerical solution. Therefore, in this paper, the value of was determined by numerical tests.
2.2. Chebyshev Spectral Collocation Method
The Chebyshev spectral collocation method is a kind of collocation method [16,17]. On the one hand, as a spectral method, it has high accuracy. On the other hand, as a collocation method, it transforms the derivative term into a differential matrix, which makes the equations simple and easy to solve. To date, this method was successfully applied to solve differential equations in the fields of fluid mechanics [18,19], quantum mechanics [20,21], etc.
Equation (2) can be written as follows:
where . The fourth-order Runge–Kutta method [22] is used to discretize the time, leading to
Here, is the time step, is the time on the nth step (), is the value of on and the initial distribution is written as . It is worth mentioning that the variable in Equation (4) is only a function of the spatial variable . In this way, the space can be discretized using the spectral collocation method.
In the spectral collocation method, the solution of can be written as follows [16,17]:
where is the Lagrange interpolation polynomial at the node (), which is
and is the function value at interpolation node .
In the Chebyshev spectral collocation method, Chebyshev points are chosen as the interpolation nodes. In the standard calculation domain , the Chebyshev points are (). As for the general calculation domain , the Chebyshev points can be obtained by the coordinate transformation of standard Chebyshev points, namely .
Here, we take the calculation of in Equation (4) as an example to show the implementation of the Chebyshev spectral collocation method. In fact, the right-hand term is equal to . Here, we need to show the calculation of and terms. In the Chebyshev spectral collocation method [16,17], the derivative term can be transformed into a differential matrix as follows:
Here, is a Chebyshev derivative matrix, and is a function value vector at the interpolation nodes. In the standard calculation domain , the Chebyshev derivative matrix satisfies the following properties [16,17]:
where represents the element of the th row and th column in the Chebyshev matrix, and is the constant which is determined by the following equation:
As for the general calculation domain , the Chebyshev derivative matrix can be calculated using the standard Chebyshev derivative matrix , which is
Similarly, in the Chebyshev spectral collocation method [16,17], the second-order derivative term can be written as follows:
Here, is the second-order Chebyshev derivative matrix. The relationship between the second-order Chebyshev derivative matrix and the first-order Chebyshev derivative matrix is
2.3. Other Numerical Schemes
We mainly focus our attention on the numerical schemes of spatial discretization. The numerical method for time discretization is the classic Runge–Kutta method which is shown in Equation (4). The diffusive term “” is no longer taken into account in the following two schemes. Thus, the right-hand term in Equation (4) becomes .
2.3.1. Second Upwind Scheme
In the calculation of , we use the following second-order upwind scheme [22]:
Here, represents the value of at node , represents the value of at node , and represents the distance between two adjacent nodes. During our simulation, the nodes are taken as uniformly distributed nodes, rather than Chebyshev points in the Chebyshev spectral collocation method.
2.3.2. HR-Van Scheme
In the calculation of , the following HR-van scheme is used [1]:
where , , with being the flux limiter proposed by Van. Similarly, this scheme is implemented under uniformly distributed nodes rather than Chebyshev points.
3. Numerical Experiments
In order to compare the accuracy of each numerical method, we define the following errors:
Here, is the exact solution at node .
3.1. Size-Independent Growth in a Batch Process
The first example is the crystallization in a batch process with the crystal growth rate independent of the crystal size . Here, we do not consider the aggregation, nucleation, and breakage, and we set . The crystal growth rate is set to and the initial CSD is given by with the following Gaussian distribution:
with . The other parameters in the calculation are set to . The exact solution of this example is .
Figure 1 shows the comparison of exact solution with the results of three numerical scheme sat . In order to clearly show the performances with different schemes, Figure 1b shows the predicted crystal size distributions at the local crystal size. It can be seen that second-order upwind scheme is the worst, which causes both numerical dispersion and diffusion; both the HR-van scheme and the Chebyshev spectral collocation method cause numerical diffusion, but the Chebyshev spectral collocation method causes less numerical diffusion. Table 1 shows the and errors with different numerical schemes. The error table clearly shows that the Chebyshev spectral collocation method has the smallest error. Therefore, the Chebyshev spectral collocation method has the highest accuracy among these three methods.
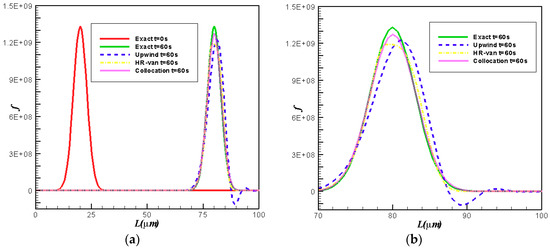
Figure 1.
Comparison for final crystal size distribution (CSD) with analytical and numerical results: (a) in the whole crystal; (b) zoomed figure.

Table 1.
and errors for different numerical schemes.
We now discuss the effects of the diffusive term. Figure 2 shows the numerical results obtained using the Chebyshev spectral collocation method with different coefficients of diffusive term. As can been seen in Figure 2a, when no diffusive term is added (), an oscillation happens near the right boundary at . Therefore, in this case, we cannot obtain stable numerical solutions. However, as shown in Figure 2b, when a diffusive term is added (), a convergent solution is obtained. The CSD function shifts to the right with the velocity of . Table 2 lists the and errors with different coefficients of the diffusive term. When , a convergent numerical solution cannot be obtained. With the increase of (), both and errors increase. This is consistent with our explanation for the diffusive term; the closer is to 0, the more accurate the result is. However, when approaches 0, the effect of the diffusive term becomes smaller which leads to an unstable numerical solution. The coefficient of the diffusive term () with is recommended as 2 × 10−3 to 10−2.
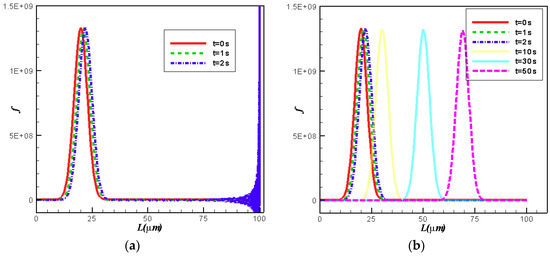
Figure 2.
Comparison for numerical results with different coefficients of the diffusive term: (a) ; (b) .

Table 2.
and errors for different coefficients of the diffusive term.
In the size-independent growth case, PBE is a convection equation () and displaysa strong hyperbolic property. The diffusive term should be added in order to obtain a stable and convergent numerical solution. Figure 3 shows the relationship between the optimal (with minimum and errors) and the growth rate G. It is clear that the optimal has a linear relationship with the growth rate G. Therefore, the coefficient of diffusive term () is recommended as 2G × 10−3 to G × 10−2, where G is the crystal growth rate.
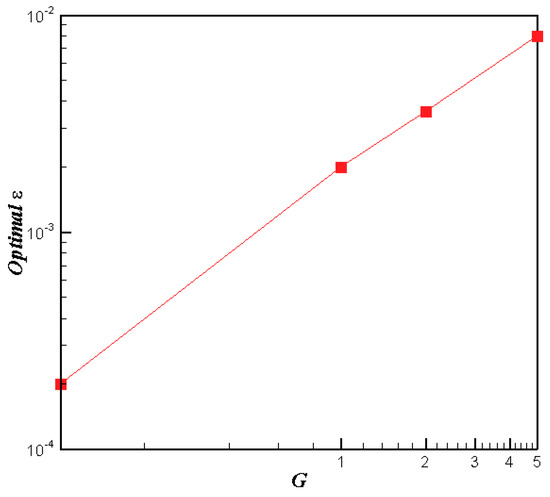
Figure 3.
Relationship between optimal and G.
3.2. Size-Dependent Growth in a Batch Process
The second example involves crystallization in a batch process with the crystal growth rate dependent on the crystal size . Similar to the first example, aggregation, nucleation, and breakage are not taken into account, which means . Crystal growth rate is supposed as the linear function of crystal size, namely , where is a constant. The initial CSD satisfies the following equation:
where are constants. The analytical solution for this case is [1] as follows:
Parameters in the simulation are taken as . The number of grids in space used for the second upwind method and HR-van method is 1000.
Figure 4 shows the comparison of analytical solutions with numerical solutions obtained by three numerical schemes at . In Figure 4a, there is no significant difference between the analytical solution and the numerical solutions. Figure 4b gives the comparison of the numerical results near the boundary . From Figure 4b, it is obvious that Chebyshev spectral collocation method performs the best and its result is almost coincident with the analytical solution; however, the second-order upwind scheme and HR-van scheme have some deviations from the analytical solution near the boundary. Table 3 gives the comparison of and errors for different numerical schemes. From Table 3, it is clear that the Chebyshev spectral collocation method has the smallest error, whereas the HR-van scheme has a smaller error and the second-order upwind scheme has the biggest error. Thus, the Chebyshev spectral collocation method also has the highest accuracy among these three schemes.
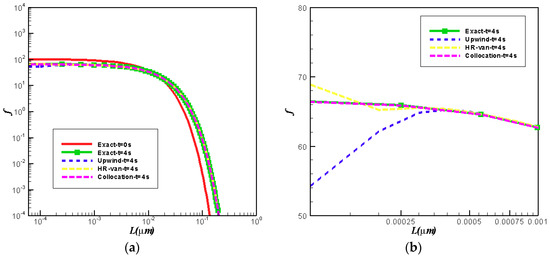
Figure 4.
Comparison for final CSD with analytical and numerical results: (a) in the whole crystal; (b) zoomed figure.

Table 3.
and errors for different numerical schemes.
Figure 5 presents the evolution of CSD obtained using the Chebyshev spectral collocation method. As we can see in Figure 5, there is no oscillation during the computation. Therefore, the diffusive term is not necessary. This is not surprising. In this size-dependent growth case, the PBE is a convection–reaction equation (). The reactive term weakens the hyperbolic property of PBE and makes it easy to solve. This is reflected in the decay term “” of the analytical solution in Equation (18).
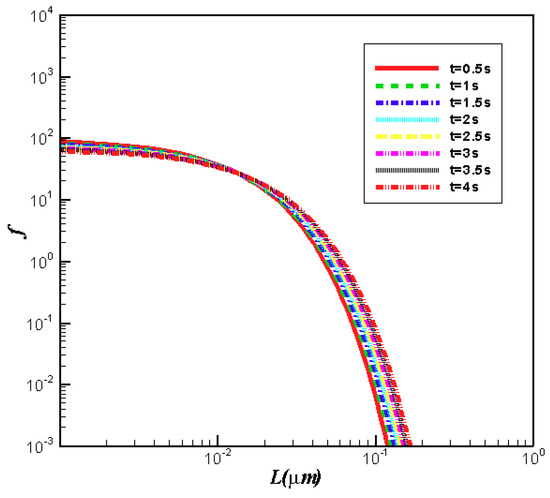
Figure 5.
Evolution of CSD obtained using the Chebyshev spectral collocation method.
3.3. Nucleation and Size-Dependent Growth in a Continuous Process
The third example is the crystallization in a continuous process with the nucleation and crystal growth rate dependent on the crystal size . Here, the source item is assumed to , where are constants, and is a Dirac function. The relationship between crystal growth rate and crystal size is , where are constants. The analytical solution for this case is [1] as follows:
In order to compare the prediction effects of each numerical method, Equation (19) is given as the initial CSD and the simulation is ended at . In our simulation, parameters are set to . The number of grids in space used for the second upwind method and HR-van method is 400.
Figure 6 shows the comparison of analytical solutions with numerical solutions of three numerical schemes. From Figure 6a,b, we can conclude that the result of the second-order upwind scheme is the worst since the predicted result has the biggest deviation from the analytical solution. Results of the HR-van method and the Chebyshev spectral collocation method are satisfactory. Figure 6b shows that the results obtained using the Chebyshev spectral collocation method are slightly better than those of the HR-van method. Table 4 shows the comparison of and errors for three different numerical schemes. From the error comparison, we know that the Chebyshev spectral collocation method is the best one, whereas the HR-van scheme is the better one and the second-order upwind scheme is the worst one. Thus, in this case, the Chebyshev spectral collocation method also shows the highest accuracy.
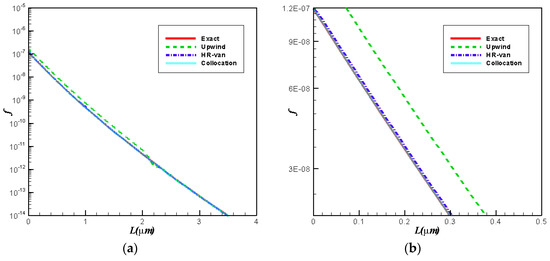
Figure 6.
Comparison for final CSD with analytical and numerical results: (a) in the whole crystal; (b) zoomed figure.

Table 4.
and errors for different numerical schemes.
Figure 7 displays the evolution of CSD obtained using the Chebyshev spectral collocation method. It can be seen that it does not result in an unstable solution in the case where no diffusive term is added. In this case, the PBE becomes . It is a convection–reaction equation. As shown in example 2, the reactive term weakens the hyperbolic property of PBE. Therefore, the diffusive term is not necessary.
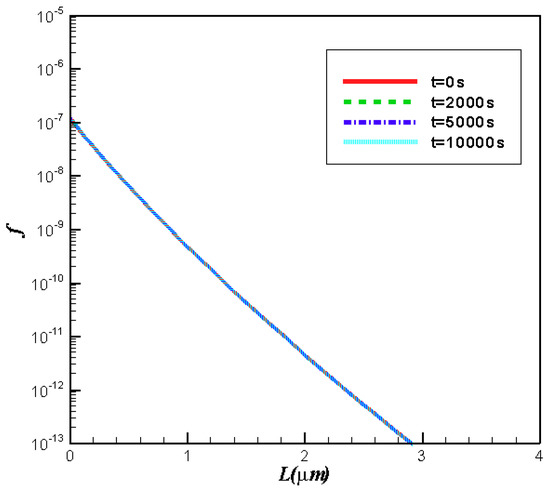
Figure 7.
Evolution of CSD obtained using the Chebyshev spectral collocation method.
4. Conclusions
In this paper, the Chebyshev spectral collocation method was introduced to solve the one-dimensional PBE. The detailed implementation and the related techniques of the Chebyshev spectral collocation method are given. Three examples are presented, namely size-independent growth, size-dependent growth in a batch process, and with nucleation, and size-dependent growth in a continuous process. The numerical results showed that the Chebyshev spectral collocation method is effective and highly accurate in solving the PBE. However, in the case of size-independent growth, when PBE is a convection equation, it displays a highly hyperbolic property. A diffusive term should be added in order to obtain a stable solution.
For the more complex crystallization processes, e.g., aggregation and breakage, PBE becomes an integro-differential equation. Other methods, e.g., the cell average method and the fixed pivot method, can be combined with the spectral collocation method to obtain accurate CSD [15]. Moreover, realistic PBE problems involve multidimensional states. The spectral collocation method can be easily implemented for two-dimensional problems, enabling its use in multivariate systems. However, the spectral collocation method as a spectral method has its limitations in solving PBE, i.e., the computational zone should be simple and the distribution of CSD should be sufficiently smooth. Therefore, under such conditions, the Chebyshev spectral collocation method is recommended to solve PBE for which a high accuracy of CSD is needed.
Acknowledgments
Financial support was provided by the Natural Sciences Foundation of China (Nos. 11402078, 51375148, U1304521).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gunawan, R.; Fusman, I.; Braatz, R.D. High resolution algorithms for multidimensional population balance equations. AICHE J. 2004, 50, 2738–2749. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances: Theory and Application to Particulate Systems in Engineering; Academic Press: New York, NY, USA, 2000. [Google Scholar]
- Li, D.Y.; Li, Z.P.; Gao, Z.M. Quadrature-based moment methods for the population balance equation: An algorithm review. Chin. J. Chem. Eng. 2019, in press. [Google Scholar] [CrossRef]
- Qamar, S.; Angelov, I.; Elsner, M.P.; Ashfaq, A.; Seidel-Morgenstern, A.; Warnecke, G. Numerical approximations of a population balance model for coupled batch preferential crystallizers. Appl. Numer. Math. 2009, 59, 739–753. [Google Scholar] [CrossRef]
- Qamar, S.; Ashfaq, A.; Angelov, I.A.; Elsner, M.P.; Warnecke, G.; Seidel-Morgenstern, A. Numercial solutions of population balance models in preferential crystallization. Chem. Eng. Sci. 2008, 63, 1342–11352. [Google Scholar] [CrossRef]
- Solsvik, J.; Jakobsen, H.A. Evaluation of weighted residual methods for the solution of a population balance model describing bubbly flows: The least-squares, Galerkin, tau, and orthogonal collocation methods. Ind. Eng. Chem. Res. 2013, 52, 15988–16013. [Google Scholar] [CrossRef]
- Sewerin, F.; Rigopoulos, S. An explicit adaptive grid approach for the numerical solution of the population balance equation. Chem. Eng. Sci. 2017, 168, 250–270. [Google Scholar] [CrossRef]
- Shah, B.H.; Ramkrishna, D.; Borwanker, J.D. Simulation of particulate systems using the concept of the interval of quiescence. AICHE J. 1977, 23, 897–904. [Google Scholar] [CrossRef]
- Gooch, J.R.P.; Hounslow, M.J. Monte Carlo simulation of size-enlargement mechanisms in crystallization. AICHE J. 1996, 42, 1864–1874. [Google Scholar] [CrossRef]
- Kumar, S.; Ramkrishna, D. On the solution of population balance equations by discretization—I. a fixed pivot technique. Chem. Eng. Sci. 1997, 52, 1311–1332. [Google Scholar] [CrossRef]
- Ma, D.L.; Tafti, D.K.; Braatz, R.D. High-resolution simulation of multidimensional crystal growth. Ind. Eng. Chem. Res. 2002, 41, 6217–6223. [Google Scholar] [CrossRef]
- Majumder, A.; Kariwala, V.; Ansumali, S.; Rajendran, A. Lattice Boltzmann method for multi-dimensional population balance models in crystallization. Chem. Eng. Sci. 2012, 70, 121–134. [Google Scholar] [CrossRef]
- Ruan, C.L.; Liang, K.F.; Chang, X.J.; Zhang, L. Weighted Essentially Nonoscillatory method for two-dimensional population balance equations in crystallization. Math. Prob. Eng. 2013, 125128, 1–11. [Google Scholar] [CrossRef]
- Mantzaris, N.V.; Daoutidis, P.; Srienc, F. Numerical simulation of multi-variable cell population balance models. II. Spectral methods. Compt& Chem. Eng. 2001, 25, 1441–1462. [Google Scholar]
- Buck, A.; Klaunick, G.; Kumar, J.; Peglow, M.; Tsotsas, E. Numerical simulation of particulate processes for control and estimation by spectral methods. AICHE J. 2012, 58, 2309–2319. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L.L. Spectral Methods: Algorithms, Analysis and Applications; Springer: Berlin, Germany, 2011. [Google Scholar]
- Zhang, X. Matlab Efficient Solution of Differential Equation: SpectralMethod; China Machine Press: Beijing, China, 2016. [Google Scholar]
- Tian, X.Y.; Li, B.W.; Wu, Y.S.; Zhang, J.K. Chebyshev collocation spectral method simulation for the 2D boundary layer flow and heat transfer in variable viscosity MHD fluid over a stretching plate. Int. J. Heat. Mass. Trans. 2015, 89, 829–837. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Li, B.W.; Zhang, J.K. Spectral collocation method for natural convection in a square porous cavity with local thermal equilibrium and non-equilibrium models. Int. J. Heat. Mass. Trans. 2016, 96, 84–96. [Google Scholar] [CrossRef]
- Fang, J.W.; Wu, B.Y.; Liu, W.J. An explicit spectral collocation method using nonpolynomial basis functions for the time-dependent Schrodinger equation. Math. Meth. App. Sci. 2019, 42, 186–203. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, X.Y.; Wang, C.; Chen, S.Z. Crank-Nicolson Fourier spectral method for the space fractional nonlinear Schrodinger equation and its parameter estimation. Int. J. Compt. Math. 2019, 96, 238–263. [Google Scholar] [CrossRef]
- Mark, H. Introduction to Numerical Methods in Differential Equaitons; Springer: Berlin, Germany, 2011. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).