On Irregularity Measures of Some Dendrimers Structures
Abstract
:1. Introduction
2. Methodology
3. Results and Discussion
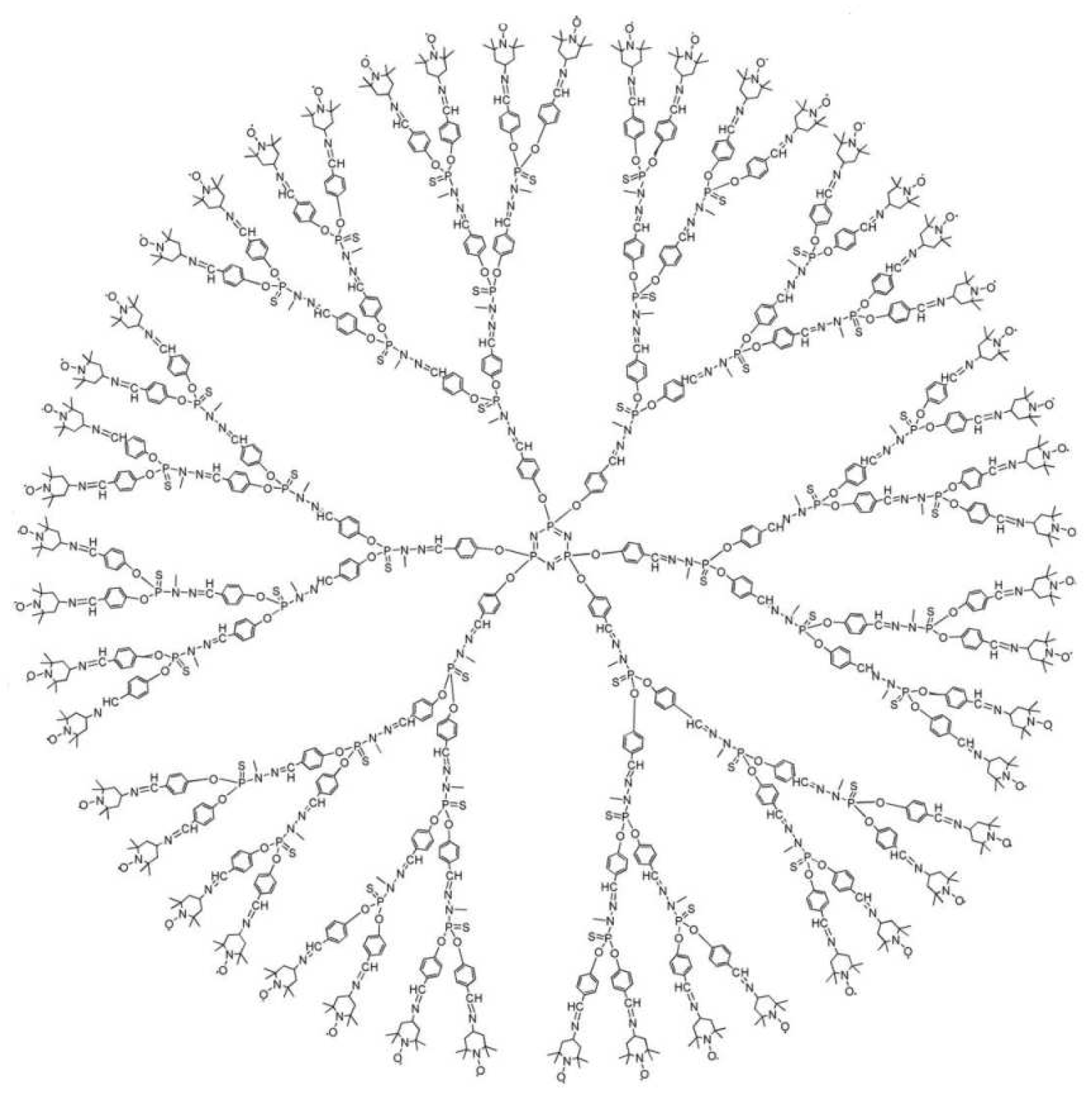
3.1. Phosphorus-Containing Dendrimers
3.2. Porphyrin-Cored Dendrimer
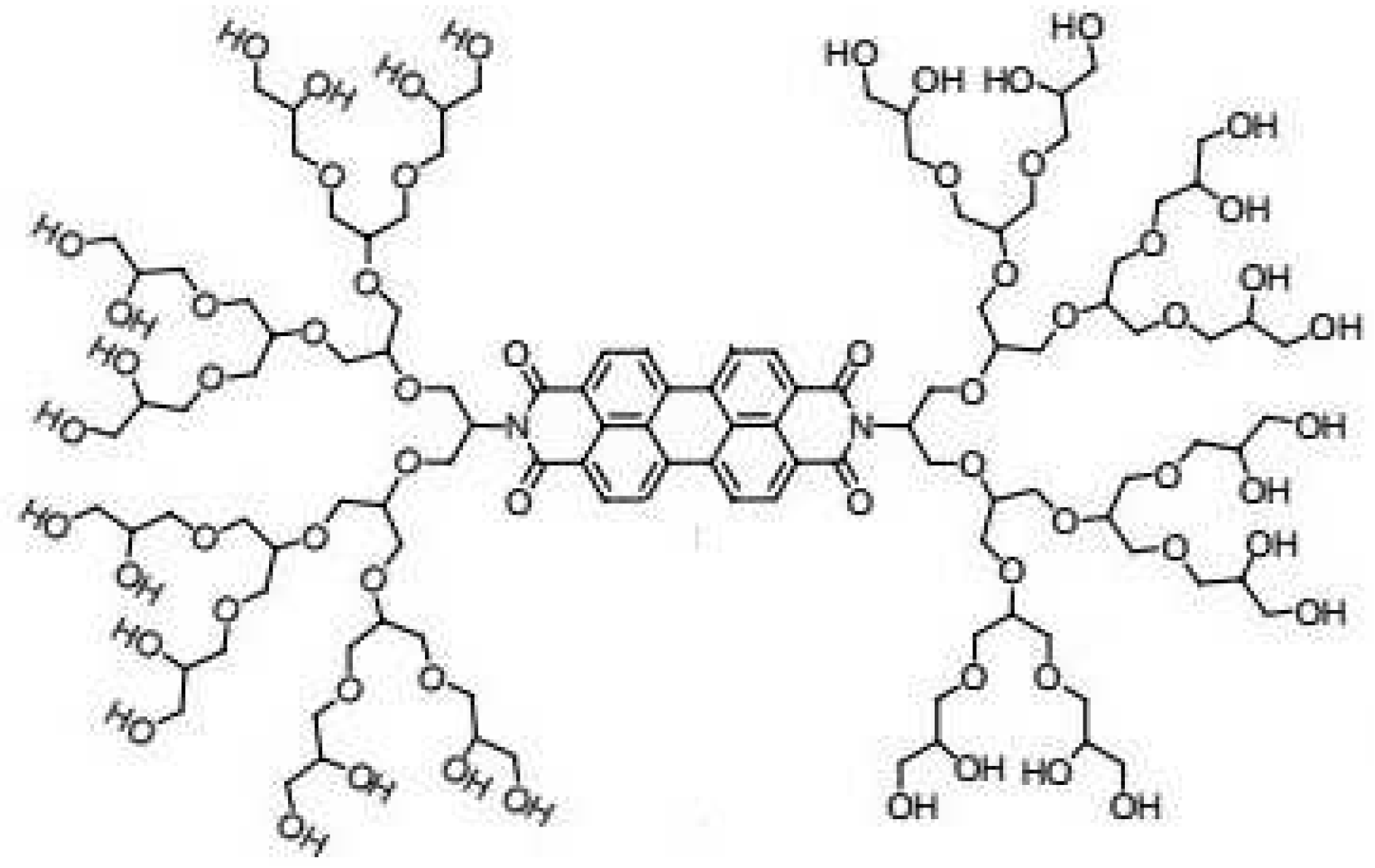
3.3. PDI-Cored Dendrimers
3.4. Triazine-Based Dendrimer
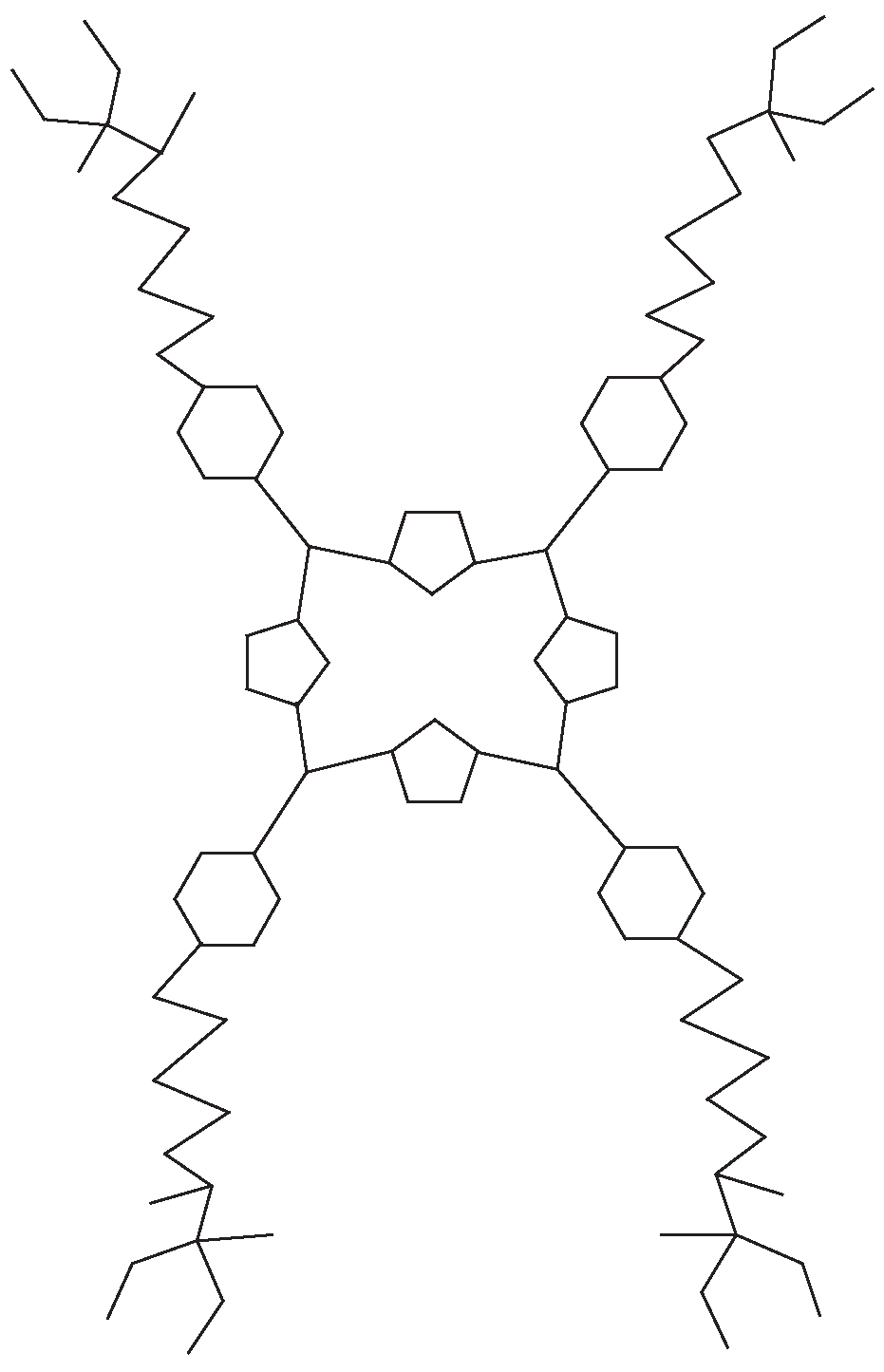
3.5. Aliphatic Polyamide Dendrimers
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Freitas, R. Nanomedicine 2. 2000. Available online: http://www. foresight.org/Nanomedicine (accessed on 18 January 2019).
- Tomalia, D.A.; Naylor, A.M.; Goddard, W.A., III. Starburst dendrimers: Molecular-level control of size, shape, surface chemistry, topology, and flexibility from atoms to macroscopic matter. Angew. Chem. Int. Ed. Engl. 1990, 29, 138–175. [Google Scholar] [CrossRef]
- Tomalia, D.A.; Christensen, J.B.; Boas, U. Dendrimers, Dendrons and Dendritic Polymers: Discovery, Applications, the Future; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Dufes, C.; Uchegbu, I.F.; Schatzlein, A.G. Dendrimers in gene delivery. Adv. Drug Deliv. Rev. 2005, 57, 2177–2202. [Google Scholar] [CrossRef] [PubMed]
- Sampathkumar, S.G.; Yarema, K.J. Dendrimers in cancer treatment and diagnosis. In Nanomaterials for Cancer Diagnosis; Wiley-VCH: Weinheim, Germany, 2007; Volume 7. [Google Scholar]
- Frechet, J.M. Functional polymers and dendrimers: Reactivity, molecular architecture, and interfacial energy. Science 1994, 263, 1710–1715. [Google Scholar] [CrossRef]
- Klajnert, B. Dendrimers in biomedical applications. Curr. Med. Chem. 2012, 19, 4895. [Google Scholar]
- Amreddy, N.; Babu, A.; Panneerselvam, J.; Srivastava, A.; Muralidharan, R.; Chen, A.; Zhao, Y.D.; Munshi, A.; Ramesh, R. Chemo-biologic combinatorial drug delivery using folate receptor-targeted dendrimer nanoparticles for lung cancer treatment. Nanomed-Nanotechnol. 2018, 14, 373–384. [Google Scholar] [CrossRef]
- Babamiri, B.; Salimi, A.; Hallaj, R. Switchable electrochemiluminescence aptasensor coupled with resonance energy transfer for selective attomolar detection of Hg2+ via CdTe@CdS/dendrimer probe and Au nanoparticle quencher. Biosens. Bioelectron. 2018, 102, 328–335. [Google Scholar] [CrossRef] [PubMed]
- Blanckenberg, A.; Kotze, G.; Swarts, A.J.; Malgas-Enus, R. Effect of nanoparticle metal composition: Mono and bimetallic gold/copper dendrimer stabilized nanoparticles as solvent-free styrene oxidation catalysts. J. Nanopart. Res. 2018, 20, 44. [Google Scholar] [CrossRef]
- Jamshidi, A.; Maleki, B.; Zonoz, F.M.; Tayebee, R. HPA-dendrimer functionalized magnetic nanoparticles (Fe3O4@D-NH2-HPA) as a novel inorganic-organic hybrid and recyclable catalyst for the one-pot synthesis of highly substituted pyran derivatives. Mater. Chem. Phys. 2018, 209, 46–59. [Google Scholar] [CrossRef]
- Kambe, T.; Imaoka, T.; Yamamoto, K. Insight into the effect of dendrimer structure on photoluminescence from assembled bismuth complexes. J. Inorg. Organomet. Polym. 2018, 28, 463–466. [Google Scholar] [CrossRef]
- Kesharwani, P.; Gothwal, A.; Iyer, A.K.; Jain, K.; Chourasia, M.K.; Gupta, U. Dendrimer nanohybrid carrier systems: An expanding horizon for targeted drug and gene delivery. Drug Discov. Today 2018, 23, 300–314. [Google Scholar] [CrossRef]
- Kurczewska, J.; Ceglowski, M.; Messyasz, B.; Schroeder, G. Dendrimer-functionalized halloysite nanotubes for effective drug delivery. Appl. Clay Sci. 2018, 153, 134–143. [Google Scholar] [CrossRef]
- Suresh, R.; Singh, C.; Rewar, P. Dendrimers as carriers and its application in therapy. Int. J. Anal. Pharm. Biomed. Sci. 2015, 4, 15–23. [Google Scholar]
- Réti, T.; Sharafdini, R.; Dregelyi-Kiss, A.; Haghbin, H. Graph irregularity indices used as molecular descriptor in QSPR studies. Match Commun. Math. Comput. Chem. 2018, 79, 509–524. [Google Scholar]
- Albertson, M.O. The irregularity of a graph. Ars Comb. 1997, 46, 219–225. [Google Scholar]
- Luo, W.; Zhou, B. On the irregularity of trees, unicyclic graphs with given matching number. Util. Math. 2010, 83, 141–147. [Google Scholar]
- Hansen, P.; Mélot, H. Variable neighborhood search for extremal graphs. 9. bounding the irregularity of a graph. Discret. Math. Theor. Comput. Sci. 2005, 69, 253–264. [Google Scholar]
- Abdo, H.; Dimitrov, D. The irregularity of graphs under graph operations. Discuss. Math. Graph Theory 2014, 34, 263–278. [Google Scholar] [CrossRef]
- Abdo, H.; Brandt, S.; Dimitrov, D. The total irregularity of a graph. Discret. Math. Theor. Comput. Sci. 2014, 16, 201–206. [Google Scholar]
- Dimitrov, D.; Skrekovski, R. Comparing the irregularity, the total irregularity of graphs. Ars Math. Contemp. 2015, 9, 45–50. [Google Scholar] [CrossRef]
- Tavakoli, M.; Rahbarnia, F.; Mirzavaziri, M.; Ashrafi, A.R.; Gutman, I. Extremely irregular graphs. Kragujev. J. Math. 2013, 37, 135–139. [Google Scholar]
- Dimitrov, D.; Réti, T. Graphs with equal irregularity indices. Acta Polytech. Hung. 2014, 11, 41–57. [Google Scholar]
- Fath-Tabar, G.H. Old, new Zagreb indices of graphs. Match Commun. Math. Comput. Chem. 2011, 65, 79–84. [Google Scholar]
- Nasiri, R.; Ellahi, H.R.; Gholami, A.; Fath-Tabar, G.H. The irregularity, total irregularity of Eulerian graphs. Iran. J. Math. Chem. 2018, 9, 101–111. [Google Scholar]
- Nasiri, R.; Fath-Tabar, G.H. The second minimum of the irregularity of graphs. Electron. Notes Discret. Math. 2014, 45, 133–140. [Google Scholar] [CrossRef]
- Chen, X.; Hou, Y.; Lin, F. Some new spectral bounds for graph irregularity. Appl. Math. Comput. 2018, 320, 331–340. [Google Scholar] [CrossRef]
- Abdo, H.; Cohen, N.; Dimitrov, D. Graphs with maximal irregularity. Filomat 2014, 28, 1315–1322. [Google Scholar] [CrossRef]
- Bell, F.K. A note on the irregularity of graphs. Linear Algebra Appl. 1992, 161, 45–54. [Google Scholar] [CrossRef]
- Fath-Tabar, G.H.; Gutman, I.; Nasiri, R. Extremely irregular trees. Bull. Acad. Serbe Sci. Arts (Cl. Sci. Math. Nat.) 2013, 38, 1–8. [Google Scholar]
- Henning, M.A.; Rautenbach, D. On the irregularity of bipartite graphs. Discret. Math. 2007, 307, 1467–1472. [Google Scholar] [CrossRef]
- Réti, T.; Dimitrov, D. On irregularities of bidegreed graphs. Acta Polytech. Hung. 2013, 10, 117–134. [Google Scholar]
- Tavakoli, M.; Rahbarnia, F.; Ashrafi, A.R. Some new results on irregularity of graphs. J. Appl. Math. Inform. 2014, 32, 675–685. [Google Scholar] [CrossRef]
- Zhou, B.; Luo, W. On irregularity of graphs. Ars Comb. 2008, 88, 55–64. [Google Scholar]
- Gutman, I.; Togan, M.; Yurttas, A.; Cevik, A.S.; Cangul, I.N. Inverse problem for sigma index. Match Commun. Math. Comput. Chem. 2018, 79, 491–508. [Google Scholar]
- Abdo, H.; Dimitrov, D.; Gutman, I. Graphs with maximal σ irregularity. Discret. Appl. Math. 2018, 250, 57–64. [Google Scholar] [CrossRef]
- Gutman, I. Stepwise irregular graphs. Appl. Math. Comput. 2018, 325, 234–238. [Google Scholar] [CrossRef]
- Réti, T. On some properties of graph irregularity indices with a particular regard to the σ-index. Appl. Math. Comput. 2019, 344–345, 107–115. [Google Scholar]
- Abdo, H.; Dimitrov, D.; Gao, W. On the irregularity of some molecular structures. Can. J. Chem. 2017, 95, 174–183. [Google Scholar] [CrossRef]
- Gutman, I.; Hansen, P.; Mélot, H. Variable neighborhood search for extremal graphs 10. Comparison of irregularity indices for chemical trees. J. Chem. Inf. Model. 2005, 45, 222–230. [Google Scholar] [CrossRef]
- Iqbal, Z.; Aslam, A.; Ishaq, M.; Aamir, M. Characteristic study of irregularity measures of some nanotubes. Can. J. Phys. 2019. [Google Scholar] [CrossRef]
- Badetti, E.; Lloveras, V.; Muñoz-Gómez, J.L.; Sebastián, R.M.; Caminade, A.M.; Veciana, J.; Vidal-Gancedo, J. Radical dendrimers: A family of five generations of phosphorus dendrimers functionalized with TEMPO radicals. Macromolecules 2014, 47, 7717–7724. [Google Scholar] [CrossRef]
- Kang, S.M.; Iqbal, Z.; Ishaq, M.; Sarfraz, R.; Aslam, A.; Nazeer, W. On eccentricity-based topological indices and polynomials of phosphorus-containing dendrimers. Symmetry 2018, 10, 237–246. [Google Scholar] [CrossRef]
- Vestberg, R.; Nyström, A.; Lindgren, M.; Malmström, E.; Hult, A. Porphyrin-cored 2,2-bis (methylol) propionic acid dendrimers. Chem. Mater. 2004, 16, 2794–2804. [Google Scholar] [CrossRef]
- Gao, W.; Iqbal, Z.; Ishaq, M.; Sarfraz, R.; Aamir, M.; Aslam, A. On eccentricity-based topological indices study of a class of porphyrin-cored dendrimers. Biomolecules 2018, 8, 71–81. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Xu, Z.; Yin, M. Perylenediimide-cored dendrimers and their bioimaging and gene delivery applications. Prog. Polym. Sci. 2015, 46, 25–54. [Google Scholar] [CrossRef]
- Iqbal, Z.; Ishaq, M.; Farooq, R. Computing different versions of atom-bond connectivity index of dendrimers. J. Inform. Math. Sci. 2017, 9, 217–229. [Google Scholar]
- Iqbal, Z.; Ishaq, M.; Aamir, M. On eccentricity-based topological descriptors of dendrimers. Iran. J. Sci. Technol. Trans. Sci. 2018. [Google Scholar] [CrossRef]
- Iqbal, Z.; Ishaq, M.; Aslam, A.; Gao, W. On eccentricity-based topological descriptors of water-soluble dendrimers. Z. Nat. 2018, 74, 25–33. [Google Scholar] [CrossRef]
- Gajjar, D.; Wadia, D.; Patel, R.M.; Patel, P.M. Development, Characterization of hydroxyl terminated dendritic macromolecules as prospective drug carriers. Am. J. Polym. Sci. Eng. 2015, 3, 201500632. [Google Scholar]
- Jishkariani, D.; MacDermaid, C.M.; Timsina, Y.N.; Grama, S.; Gillani, S.S.; Divar, M.; Yadavalli, S.S.; Moussodia, R.-O.; Leowanawat, P.; Berrios Camacho, A.M. Self-interrupted synthesis of sterically hindered aliphatic polyamide dendrimers. Proc. Natl. Acad. Sci. USA 2017, 1, E2275–E2284. [Google Scholar] [CrossRef] [PubMed]


| Name of Dendrimer | Growth Stage of | irr( | var( | ||
|---|---|---|---|---|---|
| Phosphorus-containing dendrimers | First generation | 474 | 12,226.5 | 930 | |
| second generation | 1026 | 60,034.5 | 1986 | ||
| Porphyrin-cored dendrimer | First generation | 88 | 1504 | 136 | |
| second generation | 184 | 4432 | 328 | ||
| PDI-cored dendrimers | First generation | 40 | 576 | 56 | |
| second generation | 72 | 1568 | 96 | ||
| Triazine-based dendrimer | First generation | 20 | 352 | 20 | |
| second generation | 84 | 5504 | 84 | ||
| Aliphatic polyamide dendrimers | First generation | 28 | 84 | 52 | |
| second generation | 76 | 504 | 148 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Aamir, M.; Iqbal, Z.; Ishaq, M.; Aslam, A. On Irregularity Measures of Some Dendrimers Structures. Mathematics 2019, 7, 271. https://doi.org/10.3390/math7030271
Gao W, Aamir M, Iqbal Z, Ishaq M, Aslam A. On Irregularity Measures of Some Dendrimers Structures. Mathematics. 2019; 7(3):271. https://doi.org/10.3390/math7030271
Chicago/Turabian StyleGao, Wei, Muhammad Aamir, Zahid Iqbal, Muhammad Ishaq, and Adnan Aslam. 2019. "On Irregularity Measures of Some Dendrimers Structures" Mathematics 7, no. 3: 271. https://doi.org/10.3390/math7030271
APA StyleGao, W., Aamir, M., Iqbal, Z., Ishaq, M., & Aslam, A. (2019). On Irregularity Measures of Some Dendrimers Structures. Mathematics, 7(3), 271. https://doi.org/10.3390/math7030271






