1. Introduction
The topology of an interconnection network is usually modelled by a simple connected graph
, where
is the vertex set representing the set of processors and
is the set of edges, i.e., communication links in the network. A modern multiprocessor network typically contains tens of thousands of processors, and the reliability and fault-tolerance of such systems are of critical importance, as a local breakdown may cause the fragmentation of the whole network [
1,
2].
The first graph-theoretic measure of reliability is perhaps the connectivity of
G, denoted by
, which is the minimum number of vertices whose removal results in a disconnected graph or a single vertex. A graph is said to be
k-connected if
. Evidently, the larger
is, the more reliable the network becomes. The concept of super connectivity was introduced in [
3,
4] as a more realistic and refined index of reliability as the probability that all processors directly connected to a processor fail at the same time is very small in large-scale communication networks. Specifically, a subset
is called a super vertex-cut if
is not connected and every component contains at least two vertices. The super connectivity
is the minimum cardinality over all super vertex-cuts in
G, if there is any, and is set to be
otherwise. We say that a graph
G is
k-super connected if
. The super connectivity has been investigated extensively for a variety of graphs; see, e.g., [
5,
6,
7,
8,
9,
10] and the references therein. Super connectivity provides a more realistic measure of reliability for multiprocessor systems since an isolated node has very limited influence on the system performance [
4], which also echoes the idea of considering the giant components in network resilience, while ignoring isolated nodes or small components [
2,
11].
In this letter, we study the super connectivity of two classical Erdős–Rényi random graphs of order
n, namely the uniform model
and the binomial model
[
12]. The graph
can be obtained by starting with an empty graph on
n vertices and inserting
M edges in such a way that all possible
choices are equally likely, while the graph
with
is obtained by including each possible edge with probability
p independently of others. Since the introduction of Erdős–Rényi random graphs in the 1950s, they have been developed into an extremely prolific and highly active field in mathematics. We refer the readers to the monographs [
12,
13] for a variety of results and the recent textbook [
11] for some additional variant models in relation to complex networks. The connectivity of Erdős–Rényi random graphs has been well understood so far. The following result due to Erdő and Rényi is well known (see [
14]; [
12], Thm7.7).
Theorem 1 ([
14])
. Let , , and . Then:and: Basically, in this letter, we manage to derive threshold-like results (see Theorem 2 below) for super connectivity in Erdős–Rényi random graphs based on Theorem 1. To our knowledge, this is the first attempt to deal with super connectivity in the setting of random graphs. Here, we are interested in the limit of a large graph size, i.e., as n tends to infinity, which is customary in the theory of random graphs.
Remark 1. In [15], a graph G is said to be super connected, or simply super-κ, if every minimum vertex cut is the neighbourhood of a vertex in G, that is every minimum vertex cut isolates a vertex. We clarify that a graph is super-κ does not mean that it is one-super connected. A triangle having a dangling vertex attached is a counterexample. On the other hand, a graph is one-super connected does not imply that it is super-κ either (consider the bow-tie graph on five vertices). 2. Main Results
The following lemma on the existence of perfect matchings in is useful.
Lemma 1 ([
16]; [
12], Cor.7.21)
. If n is even, , and , then: Let
be the minimum degree of a graph
G. The property that “
is less than a constant” is a monotone graph property. Therefore, the “asymptotic equivalence” (see [
13], Cor. 1.16) between the two models
and
for monotone properties and Theorem 3.2 in [
11] (or Exercise 3.2 in [
12]), which was originally stated for
model, readily give rise to the following estimate.
Lemma 2. Suppose that is an integer, , where , as . Then: Our main result reads as follows.
Theorem 2. Let be an integer, , and as .
- (i)
If , then: - (ii)
If , then:
Note that
r-super connectedness is an increasing graph property in the sense that adding edges will never violate the property. It follows immediately from the “asymptotic equivalence” ([
13], Cor. 1.16) between the two models
and
that the following corollary holds for the binomial model.
Corollary 1. Let be an integer, , and as .
- (i)
If , then: - (ii)
If , then:
We observe from the above results that there is still a gap, namely for the model and for the model, to pinpoint the sharp threshold for r-super connectedness. It would be very interesting to determine the asymptotic probability distribution of r-super connectedness within these parameter windows (perhaps in a similar flavour as Theorem 1).
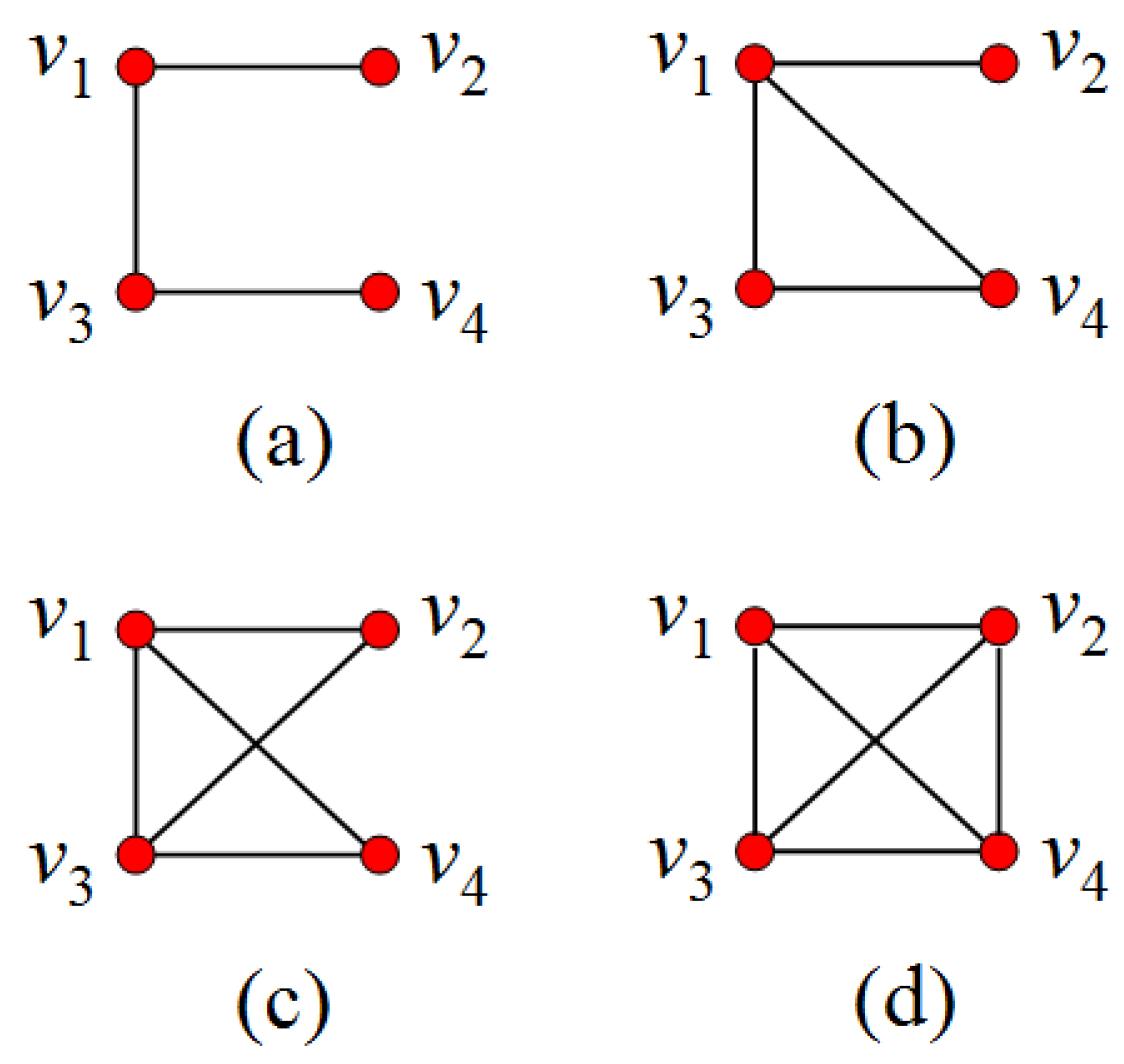
Proof of Theorem 2. To show (i), it suffices to show the statement when . For , the result follows from the fact that as n goes to infinity (see Theorem 1). In the following, we assume that .
First, we assume that
n is even. Lemma 1 implies that
has a one-factor asymptotically almost surely (a.a.s.) as
. For a given one-factor, we contract
by shrinking each edge in the one-factor to a single vertex and reducing (possible) multiple edges into a single edge. The resulting graph is denoted by
, which has
vertices and
N edges. Theorem 1 implies that
is connected a.a.s., and hence,
. Indeed, this can be easily seen by noting that the above construction procedure removes at least half of the edges in
(see
Figure 1 for an illustration). Thus,
can be viewed as a subgraph (in the sense of graph instance) of
.
By our construction, if
is
r-super connected, then
is
-connected. Since
r-super connectedness is an increasing property, it remains to show:
In view of Lemma 2, we obtain
. Recall that
holds for any graph
G. We hence arrive at
, which yields (
1).
Now if n is odd, the probability that the vertex is isolated turns out to be (when ). Hence, the above proof strategy still works.
To prove (ii), we note that as by using Theorem 1. □
3. Concluding Remarks
In this letter, we have obtained some asymptotic almost sure results on the
r-super connectivity for Erdős–Rényi models
and
. A more general concept of conditional connectivity with respect to a graph property
proposed by Harary [
17] is defined as the minimum cardinality of a set of vertices, if any, whose deletion disconnects the graph, and every remaining component has property
. From this viewpoint, the super connectivity here is the special case where
is the property of having more than two vertices. On the other hand, connectivity properties of varied random graph models (including both relational models, e.g., Erdős–Rényi graphs and geometric models) have been reported recently; see, e.g., [
18,
19,
20,
21]. It is hoped that this work will stimulate further research effort in these interesting (yet demanding) topics in the realm of random graphs.