Abstract
Various Cahn–Hilliard (CH) energy functionals have been introduced to model phase separation in multi-component system. Mathematically consistent models have highly nonlinear terms linked together, thus it is not well-known how to split this type of energy. In this paper, we propose a new convex splitting and a constrained Convex Splitting (cCS) scheme based on the splitting. We show analytically that the cCS scheme is mass conserving and satisfies the partition of unity constraint at the next time level. It is uniquely solvable and energy stable. Furthermore, we combine the convex splitting with the specially designed implicit–explicit Runge–Kutta method to develop a high-order (up to third-order) cCS scheme for the multi-component CH system. We also show analytically that the high-order cCS scheme is unconditionally energy stable. Numerical experiments with ternary and quaternary systems are presented, demonstrating the accuracy, energy stability, and capability of the proposed high-order cCS scheme.
1. Introduction
The Cahn–Hilliard (CH) equation was originally introduced as a phenomenological model of phase separation in a binary alloy [1] and has been applied to a wide range of problems [2]. The CH equation is derived from the Ginzburg–Landau energy functional:
where c is the concentration field defined in and are the free energy and gradient energy coefficients. The CH equation is a gradient flow for in the -inner product, thus is nonincreasing in time.
Generalizations of for more than two components can be applied to wide range of problems, thus have been studied intensively [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. A great deal of research has been focused on the ternary system [10] such as:
where is the concentration field of the phase i. There are many other forms of energy functional for the ternary system and some of them are equivalent. For example, under the constraint , the first term in can be rewritten [11] as follows:
One of the most important criteria for the multi-component model is to avoid the generation of spurious phases. To be more precise, we think a physically reasonable model must satisfy the following two fundamental criteria:
- (A)
- (Consistency of null-phase) If a phase is absent at the initial time, it should not appear at any time.
- (B)
- (No additional phase on interface) The interface including multiple junction should be free of additional phases.
The model with and many other models with three components obey both criteria; however, it is not well-known how to construct an energy functional for more than three components satisfying mathematical and physical criteria including these two. For example, the following generalization introduced by Lee and Kim [12] for the vector-valued concentration field :
does not satisfy Criteria A and B when .
In this paper, we consider the following energy functional satisfying Criteria A and B:
where
The energy functional introduced by Tóth et al. [14] is a non-trivial extension of for more than three component system in the sense that it is equivalent to when and when . We develop a high-order energy stable numerical method for this energy with quadratically mixed terms to study phase separation in multi-component systems.
The -gradient flow for is given by
under the partition of unity constraint,
where is the vector-valued chemical potential, is the chemical potential of the phase i, denotes the variational derivative with respect to , , , is a Lagrange multiplier to ensure the constraint [8,10,11,12,13,16,17], and ∈. We consider the boundary conditions for and as the zero Neumann boundary conditions:
where is a unit normal vector to . We refer to Equation (2) as the vector-valued CH (vCH) equation. Because the vCH equation is of gradient type, is nonincreasing in time as the constraint holds:
The vCH equation is a fourth-order nonlinear partial differential equation and the N unknowns are linked through the constraint. Therefore, accurate and efficient numerical methods are desirable to study the dynamics of the vCH equation. In this paper, we propose a constrained Convex Splitting (cCS) scheme for the vCH equation, which is based on a convex splitting of under the constraint. For and 3, has a straightforward convex–concave splitting. However, there is a difficulty with since in is neither convex nor concave. To apply the convex splitting idea [18,19,20] for all N, we add and subtract an auxiliary term in . Then, a convex–concave decomposition is available. We show analytically that the cCS scheme is mass conserving and satisfies the constraint at the next time level. It is uniquely solvable and energy stable. Furthermore, we combine the convex splitting with the implicit–explicit Runge–Kutta (RK) method [21,22] to develop a high-order (up to third-order) cCS scheme. We employ the specially designed implicit–explicit RK tables [23] to have both high-order time accuracy and unconditional energy stability. We also show analytically that the high-order cCS scheme is unconditionally energy stable.
This paper is organized as follows. In Section 2, we describe the convex splitting with an auxiliary term. We propose the (first-order) cCS scheme for the vCH equation and prove its unconditional unique solvability and energy stability. In Section 3, we construct the high-order cCS scheme with a proof of unconditional energy stability. In Section 4, we present numerical examples showing the accuracy, energy stability, and capability of the proposed scheme. Finally, conclusions are drawn in Section 5.
2. Constrained Convex Splitting Scheme
The convex splitting of when is trivial; however, it is not well-known how to split for into convex and concave parts. Therefore, we here propose to split for according to with
where
Lemma 1.
Both and in (4) are convex.
Proof.
For any ,
where , is the Hessian matrix of , and
From the positive semi-definiteness of , we obtain
For ,
where . Then, we have
Thus, the convexity of and is assured. □
We now present the cCS scheme for the vCH Equation (2) by treating implicitly and explicitly under the partition of unity constraint in Equation (3):
where , , , and .
Lemma 2.
Proof.
Let be a solution of the cCS scheme. From Equation (5), we have
where we used the zero Neumann boundary condition for . It follows that . □
Lemma 3.
The cCS scheme satisfies the constraint at any time , i.e., if an initial condition satisfies .
Proof.
Theorem 1.
The cCS scheme with an initial condition satisfying is uniquely solvable for any time step .
Proof.
We consider the following functional on :
where and denote the - and -inner products, respectively, and (we refer to [24] for the definition of the -inner product). It may be shown that is the unique minimizer of if and only if it solves, for any ,
because is strictly convex by the convexity of . Equation (7) is true for any if and only if Equation (5) holds. Hence, minimizing the strictly convex functional is equivalent to solving Equation (5). □
Lemma 4.
The convexity of and yields the following inequality:
Proof.
Since both and are convex, we obtain
Subtracting these inequalities yields
□
Theorem 2.
The cCS scheme with an initial condition satisfying is unconditionally energy stable, meaning that, for any ,
Proof.
Setting and in Equation (8), we have
□
3. Extension of the Constrained Convex Splitting Scheme To High-Order Time Accuracy
The cCS scheme in Equation (5),
is first-order accurate in time and its order of time accuracy can be improved by various approaches. One of them is to combine with an s-stage implicit–explicit RK method [21]: let ,
where and are RK coefficients for , and then
by using the stiffly accurate condition.
Recently, the authors of [23] proved that a Convex Splitting Runge–Kutta scheme for a gradient flow is unconditionally energy stable under the resemble condition ( for and ). Applying the resemble condition to Equation (9), we have the following s-stage high-order cCS scheme for the vCH equation (2):
where .
Lemma 5.
The s-stage high-order cCS scheme in Equation (10) is also mass conserving, satisfies the constraint at any time , and is uniquely solvable for any time step , provided that for .
Proof.
The proofs are similar to Lemmas 2 and 3 and Theorem 1, thus we omit the details here. □
Before proving the energy stability of the s-stage high-order cCS scheme, we define an matrix as for and for , and an matrix as with .
Theorem 3.
Suppose that is positive definite. The s-stage high-order cCS scheme with for and an initial condition satisfying is unconditionally energy stable, meaning that for any ,
Proof.
The analogous proof can be found in [23]. Using Lemma 4, we have
where the last equality follows from the fact that
Let . Since is positive definite,
where for and . It follows that . □
Remark 1.
The first-order cCS scheme can be viewed as the one-stage cCS scheme with and .
4. Numerical Experiments
The s-stage high-order cCS scheme in Equation (10) can be rewritten as follows: for ,
where . The nonlinearity of the scheme comes from and and these can be handled using a Newton-type linearization [24,25,26,27]: for ,
where . We then develop a Newton-type fixed point iteration method for the scheme as
where ,
for , and we set
if a relative -norm of the consecutive error is less than a tolerance . In this paper, the biconjugate gradient (BICG) method is used to solve the system in Equation (11) and we use the following preconditioner P to accelerate the convergence speed of the BICG algorithm:
where and is the average value of . The stopping criterion for the BICG iteration is that the relative residual norm is less than .
For first-, second-, and third-order accuracy, we use the following matrices , respectively [23]:
and
The positive definiteness of is easily seen by showing eigenvalues of are all positive. The eigenvalues of are , , and for Equation (13), and approximately , , , , , and for Equation (14).
We used the Fourier spectral method for the spatial discretization and the discrete cosine transform in MATLAB was applied for the whole numerical simulations to solve the vCH equation with the zero Neumann boundary condition.
4.1. Convergence Test
We demonstrate the convergence of the proposed schemes with the initial conditions
on . We set and compute for . The grid size is fixed to , which provides enough spatial accuracy. To estimate the convergence rate with respect to , simulations are performed by varying . We take the quadruply over-resolved numerical solution using the third-order scheme as the reference solution. Figure 1a,b shows the evolution of for the reference solution and the relative -errors of (this time is indicated by a dashed line in Figure 1a) for various time steps, respectively. It is observed that the schemes give desired order of accuracy in time.
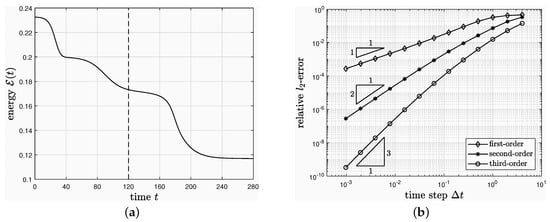
Figure 1.
(a) Evolution of for the reference solution with and . (b) Relative -errors of for various time steps.
4.2. Energy Stability of the Proposed Schemes
To investigate the energy stability of the proposed schemes, we consider the phase separation of a ternary system with the initial conditions
on . Here, is a random number between and , and we use and . Figure 2 shows the evolution of using the first-, second-, and third-order schemes with different time steps. All energy curves are nonincreasing in time even for sufficiently large time steps. Figure 3 shows the evolution of using the third-order scheme with .
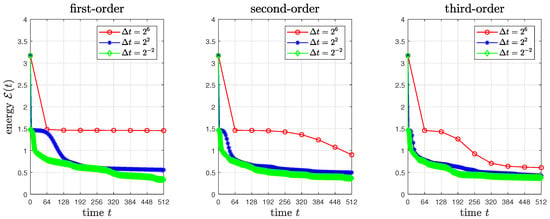
Figure 2.
Evolution of using the first-, second-, and third-order schemes with different time steps.
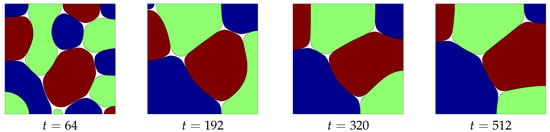
Figure 3.
Evolution of using the third-order scheme with , , and . In each snapshots, the red, green, and blue regions indicate , , and , respectively, and contour lines represent .
4.3. Consistency of Null-Phase
To confirm whether consistency of null-phase guarantees, we consider that only three phases are present but the simulation is performed using a quaternary system, i.e., we take the initial conditions as
on . For , we employ the convex splitting in [17] and also apply the third-order scheme in Equation (10) with in (14). We use , , and the third-order scheme and compute for . Figure 4a,b shows obtained with and for various time steps, respectively, for two models and . As shown in Figure 4, generates , even though the initial condition for is zero. We believe that this generation is not a result of numerical computation but a consequence of the model error not satisfying Criterion A. On the other hand, for , the maximum of is only controlled by the accuracy of the numerical scheme.
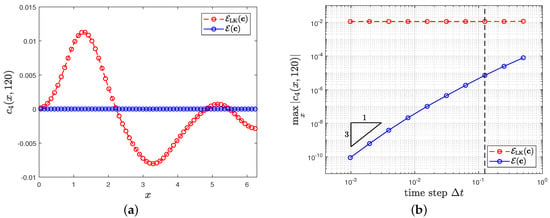
Figure 4.
(a) obtained with (this time step is indicated by a dashed line in (b)). (b) for various time steps.
4.4. No Additional Phase Generation on Interface
To test whether spurious phase generation takes place on interfaces, we consider the phase separation of a quaternary system with the initial conditions
on . Here, is a random number between and . For , we employ the convex splitting in [17] and also apply the third-order scheme in Equation (10) with in Equation (14). We use , , and . Figure 5 and Figure 6 show and local maximum of for using the third-order scheme for two models and , respectively.
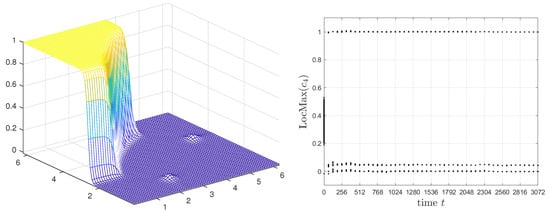
Figure 5.
and local maxima of for the model .
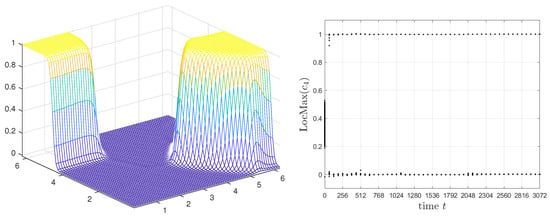
Figure 6.
and local maxima of for the model .
As shown in Figure 5, generates spurious phase at two triple junction points where the first, second, and third components meet. On the other hand, in Figure 6 suppresses the formation of spurious phases on interfaces almost completely. To quantify the spurious phase generation, we define at time t as a set of local maxima of in . We observe many local maxima near at the beginning of evolution but only two maxima 0 and 1 are expected for the fully separated phases. The model with shown in Figure 6 gives well separated phases over time, whereas the model with has another local maximum at about due to the spurious phases at the junction points. We believe that this spurious phases generation is not a result of numerical computation but a consequence of the model error not satisfying Criterion B.
5. Conclusions
In this paper, we consider the multi-component CH system where all phase variables are nonlinearly coupled. To study the dynamics of this system, we propose the high-order energy stable scheme based on the convex splitting idea. To handle the nonconvex, nonconcave term in the energy, we add an auxiliary term, which yields a convex–concave decomposition of the energy. We combine the convex splitting with the specially designed implicit–explicit RK method thus developed the high-order cCS scheme. We confirmed that the schemes give desired order of accuracy in time and are unconditionally energy stable. By using the scheme, we also demonstrated that the use of is crucial and gives very significant qualitative improvement of the results compared to the additive model .
Author Contributions
Writing–original draft, H.G.L., J.S. and J.-Y.L. H.G.L., J.S. and J.-Y.L. contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Korea government MSIP (2017R1D1A1B0-3032422, 2017R1E1A1A0- 3070161, and 2019R1C1C1011112).
Acknowledgments
The authors thank the reviewers for their constructive and helpful comments on the revision of this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Chen, L.-Q. Phase-field models for microstructure evolution. Annu. Rev. Mater. Res. 2000, 32, 113–140. [Google Scholar] [CrossRef]
- Fontaine, D. A Computer Simulation of the Evolution of Coherent Composition Variations in Solid Solutions; Northwestern University: Evanston, IL, USA, 1967. [Google Scholar]
- Morral, J.E.; Cahn, J.W. Spinodal decomposition in ternary systems. Acta Metall. 1971, 19, 1037–1045. [Google Scholar] [CrossRef]
- Elliott, C.M.; Luckhaus, S. A generalised diffusion equation for phase separation of a multi-component mixture with interfacial free energy. IMA Prepr. Ser. 1991, 887. [Google Scholar]
- Eyre, D.J. Systems of Cahn–Hilliard equations. SIAM J. Appl. Math. 1993, 53, 1686–1712. [Google Scholar] [CrossRef]
- Blowey, J.F.; Copetti, M.I.M.; Elliott, C.M. Numerical analysis of a model for phase separation of a multicomponent alloy. IMA J. Numer. Anal. 1996, 16, 111–139. [Google Scholar] [CrossRef]
- Garcke, H.; Nestler, B.; Stoth, B. On anisotropic order parameter models for multi-phase systems and their sharp interface limits. Physics D 1998, 115, 87–108. [Google Scholar] [CrossRef]
- Kim, J.; Kang, K.; Lowengrub, J. Conservative multigrid methods for ternary Cahn–Hilliard systems. Commun. Math. Sci. 2004, 2, 53–77. [Google Scholar]
- Folch, R.; Plapp, M. Quantitative phase-field modeling of two-phase growth. Phys. Rev. E 2005, 72, 011602. [Google Scholar] [CrossRef]
- Boyer, F.; Lapuerta, C. Study of a three component Cahn–Hilliard flow model. ESAIM M2AN 2006, 40, 653–687. [Google Scholar] [CrossRef]
- Lee, H.G.; Kim, J. A second-order accurate non-linear difference scheme for the N-component Cahn–Hilliard system. Physics A 2008, 387, 4787–4799. [Google Scholar] [CrossRef]
- Lee, H.G.; Choi, J.-W.; Kim, J. A practically unconditionally gradient stable scheme for the N-component Cahn–Hilliard system. Physics A 2012, 391, 1009–1019. [Google Scholar] [CrossRef]
- Tóth, G.I.; Pusztai, T.; Gránásy, L. Consistent multiphase-field theory for interface driven multidomain dynamics. Phys. Rev. B 2015, 92, 184105. [Google Scholar] [CrossRef]
- Tavakoli, R. Unconditionally energy stable time stepping scheme for Cahn–Morral equation: Application to multi-component spinodal decomposition and optimal space tiling. J. Comput. Phys. 2016, 304, 441–464. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, J.; Wang, Q.; Shen, J. Numerical approximations for a three-component Cahn–Hilliard phase-field model based on the invariant energy quadratization method. Math. Models Meth. Appl. Sci. 2017, 27, 1993–2030. [Google Scholar] [CrossRef]
- Lee, H.G.; Lee, J.-Y.; Shin, J. A constrained convex splitting scheme for the vector-valued Cahn–Hilliard equation. J. KSIAM 2019, 23, 1–17. [Google Scholar]
- Elliott, C.M.; Stuart, A.M. The global dynamics of discrete semilinear parabolic equations. SIAM J. Numer. Anal. 1993, 30, 1622–1663. [Google Scholar] [CrossRef]
- Eyre, D.J. Unconditionally gradient stable time marching the Cahn–Hilliard equation. MRS Proc. 1998, 529, 39–46. [Google Scholar] [CrossRef]
- Badalassi, V.E.; Ceniceros, H.D.; Banerjee, S. Computation of multiphase systems with phase field models. J. Comput. Phys. 2003, 190, 371–397. [Google Scholar] [CrossRef]
- Ascher, U.M.; Ruuth, S.J.; Spiteri, R.J. Implicit–explicit Runge–Kutta methods for time-dependent partial differential equations. Appl. Numer. Math. 1997, 25, 151–167. [Google Scholar] [CrossRef]
- Shin, J.; Lee, H.G.; Lee, J.-Y. Convex Splitting Runge–Kutta methods for phase-field models. Comput. Math. Appl. 2017, 73, 2388–2403. [Google Scholar] [CrossRef]
- Shin, J.; Lee, H.G.; Lee, J.-Y. Unconditionally stable methods for gradient flow using Convex Splitting Runge–Kutta scheme. J. Comput. Phys. 2017, 347, 367–381. [Google Scholar] [CrossRef]
- Lee, H.G.; Shin, J.; Lee, J.-Y. First- and second-order energy stable methods for the modified phase field crystal equation. Comput. Methods Appl. Mech. Engrg. 2017, 321, 1–17. [Google Scholar] [CrossRef]
- Hu, Z.; Wise, S.M.; Wang, C.; Lowengrub, J.S. Stable and efficient finite-difference nonlinear-multigrid schemes for the phase field crystal equation. J. Comput. Phys. 2009, 228, 5323–5339. [Google Scholar] [CrossRef]
- Baskaran, A.; Hu, Z.; Lowengrub, J.S.; Wang, C.; Wise, S.M. Zhou, P. Energy stable and efficient finite-difference nonlinear multigrid schemes for the modified phase field crystal equation. J. Comput. Phys. 2013, 250, 270–292. [Google Scholar] [CrossRef]
- Shin, J.; Lee, H.G.; Lee, J.-Y. First and second order numerical methods based on a new convex splitting for phase-field crystal equation. J. Comput. Phys. 2016, 327, 519–542. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).